Benchmarking Dynamic Balancing Controllers for Humanoid Robots
Abstract
1. Introduction
2. Balancing Strategies
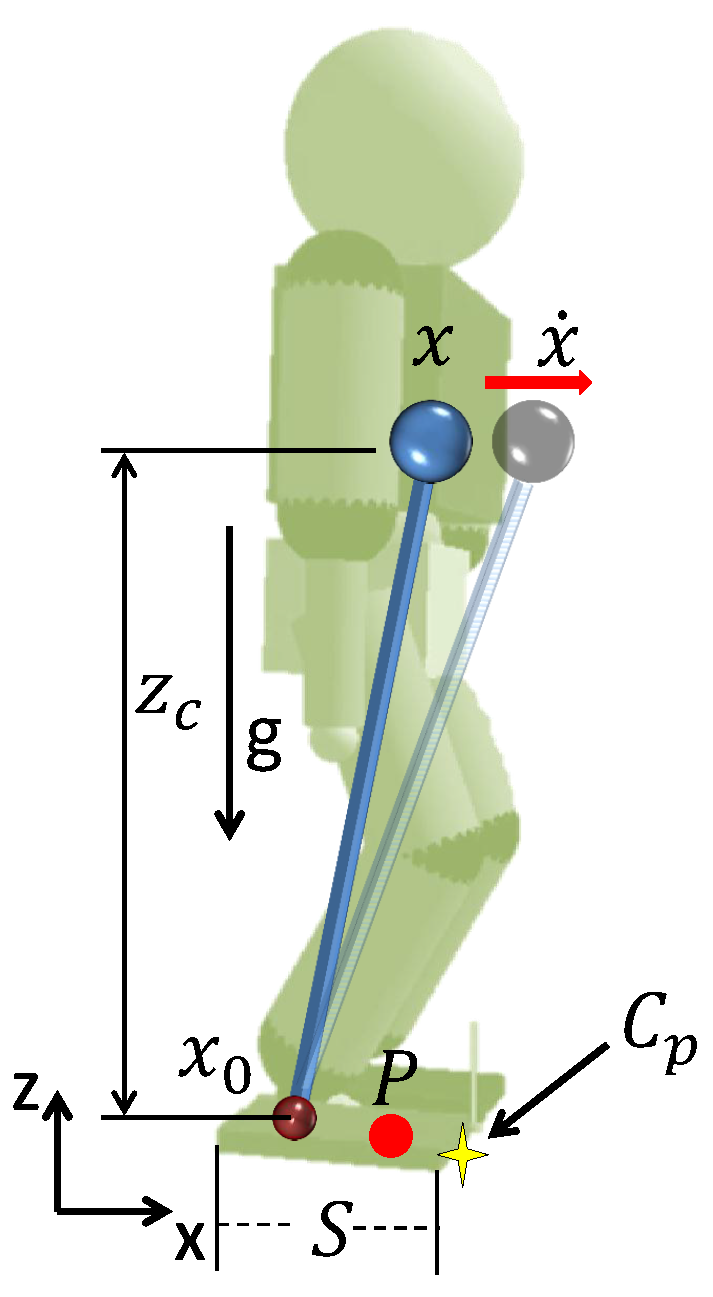
2.1. CoM Stabilizer—A Capture Point Approach
2.2. CoM Stabilizer—A Virtual Spring-Damper Approach
2.3. Attitude Controller
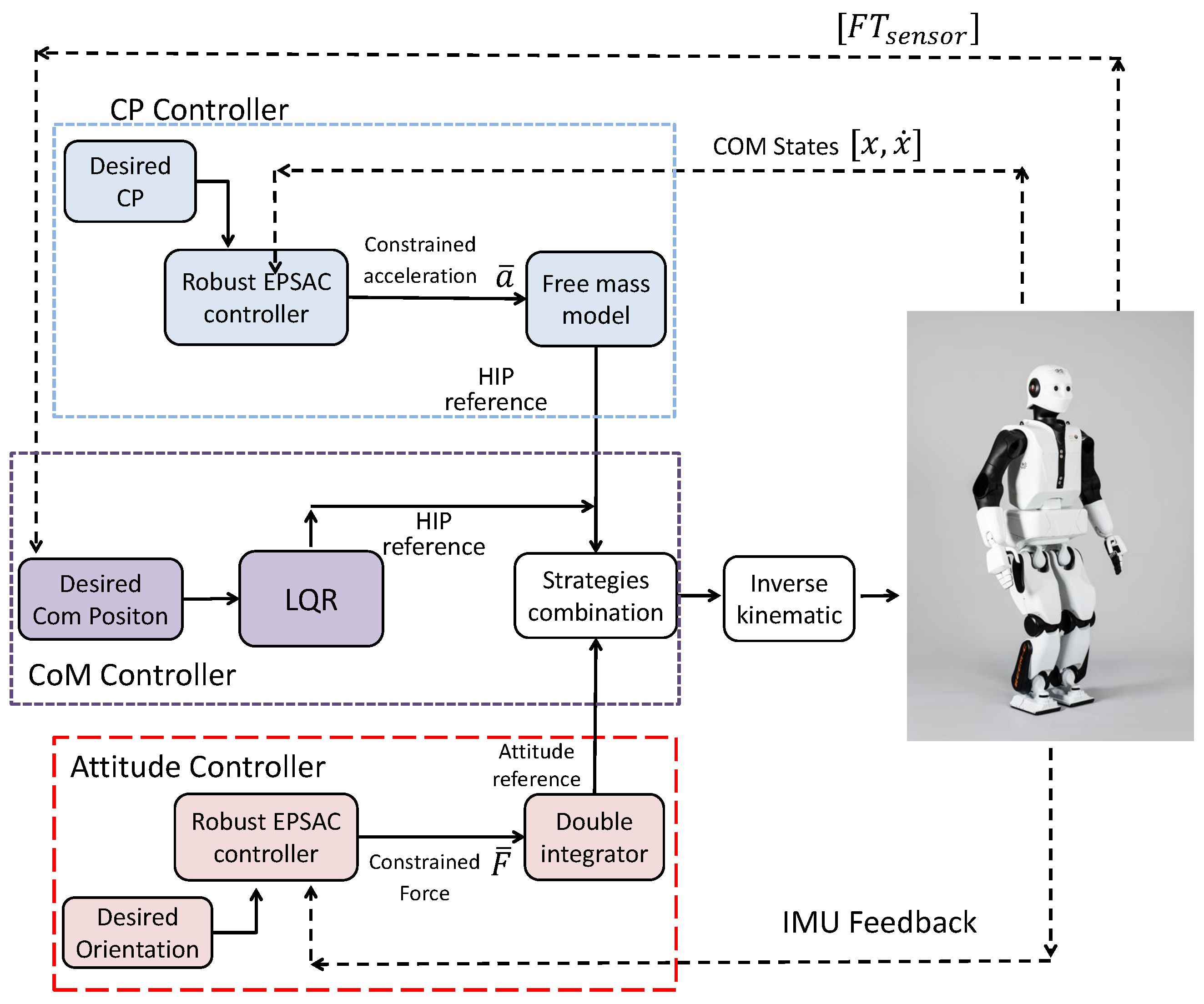
3. Experimental Protocols
4. Simulation Results
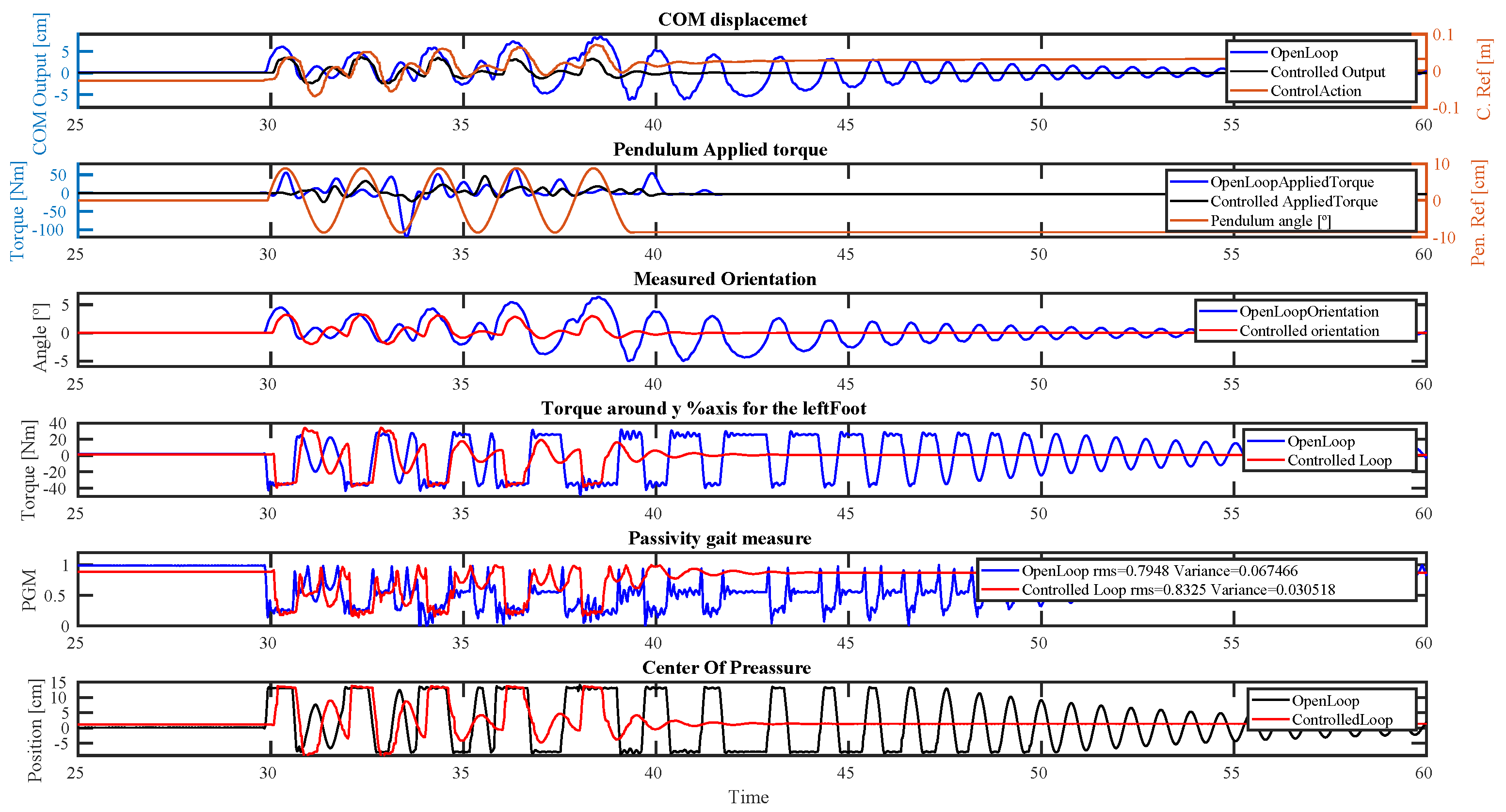
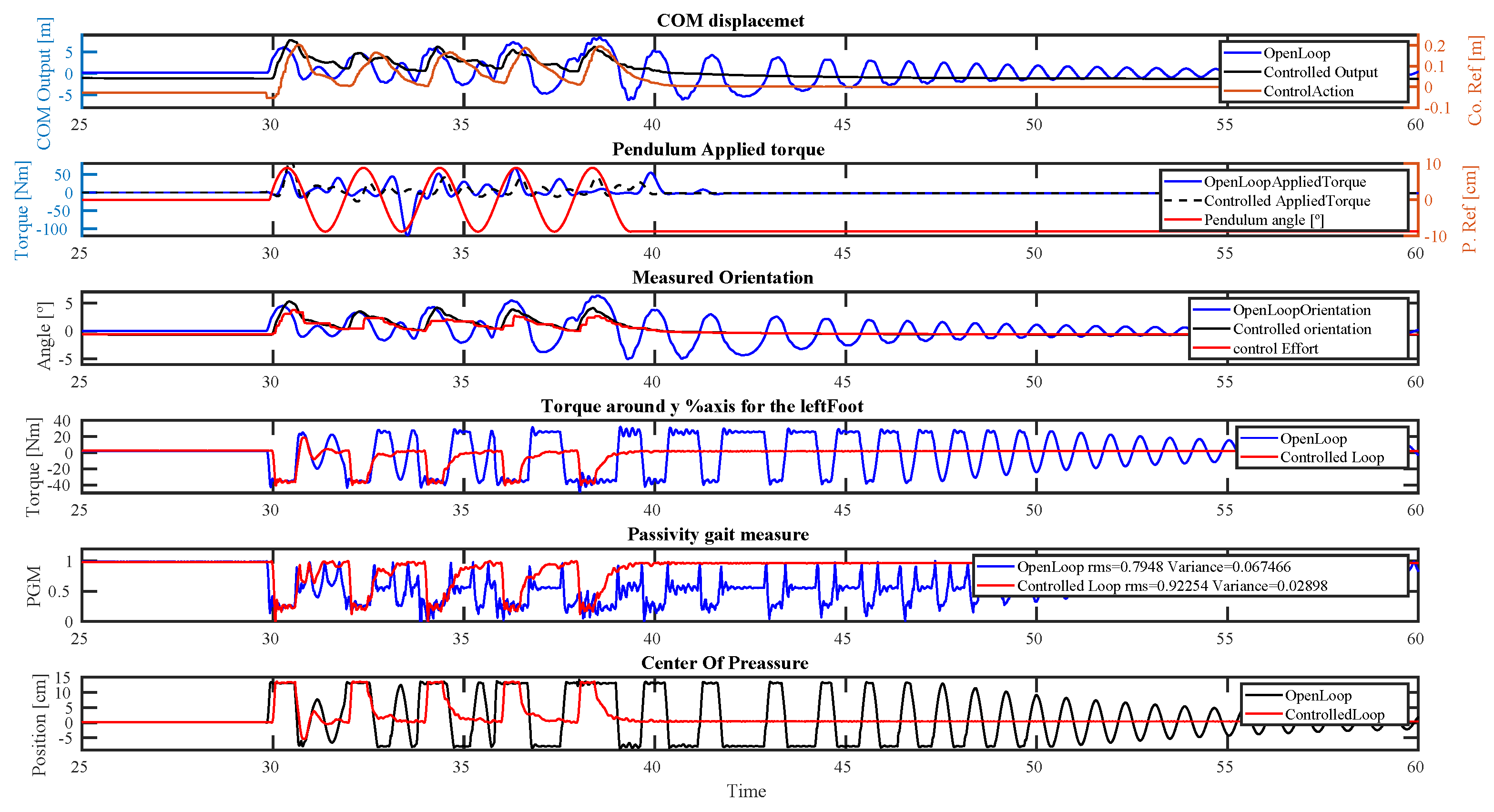
4.1. Simulations
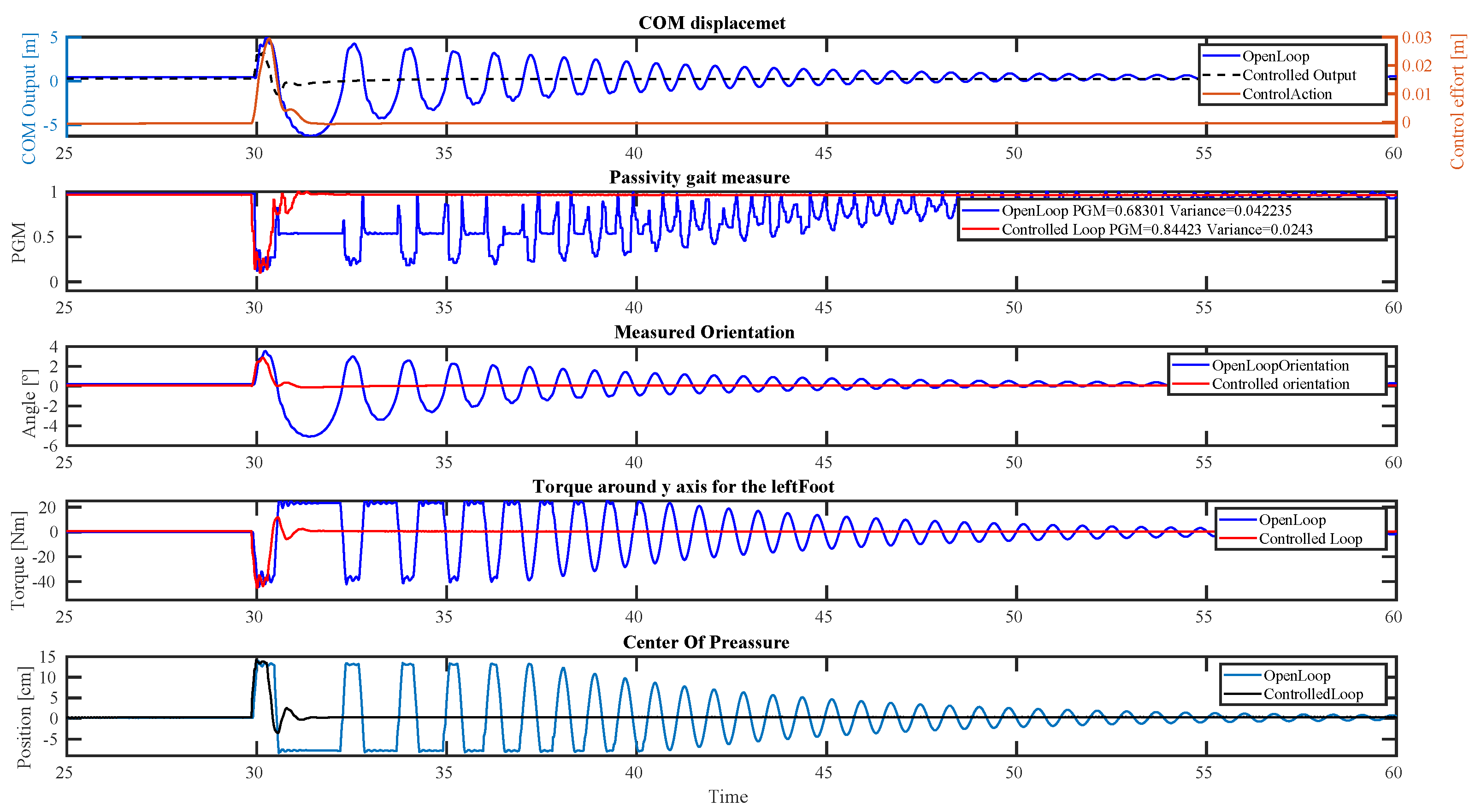
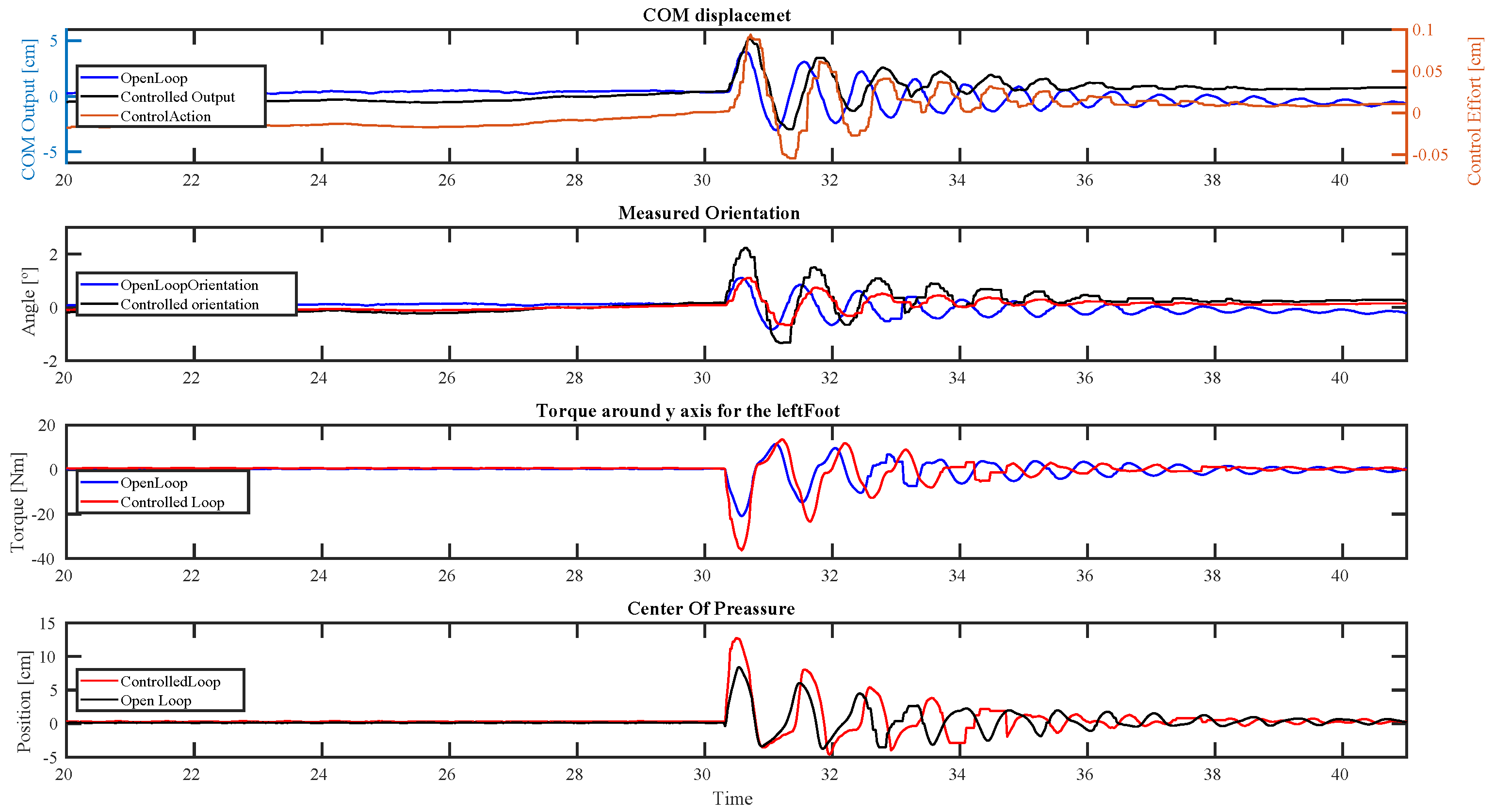
4.2. Impulsive Disturbance
- deviation;
- Passive Gait Measure;
- Measured Orientation;
- Torque around the Y-axis for the left foot;
- .
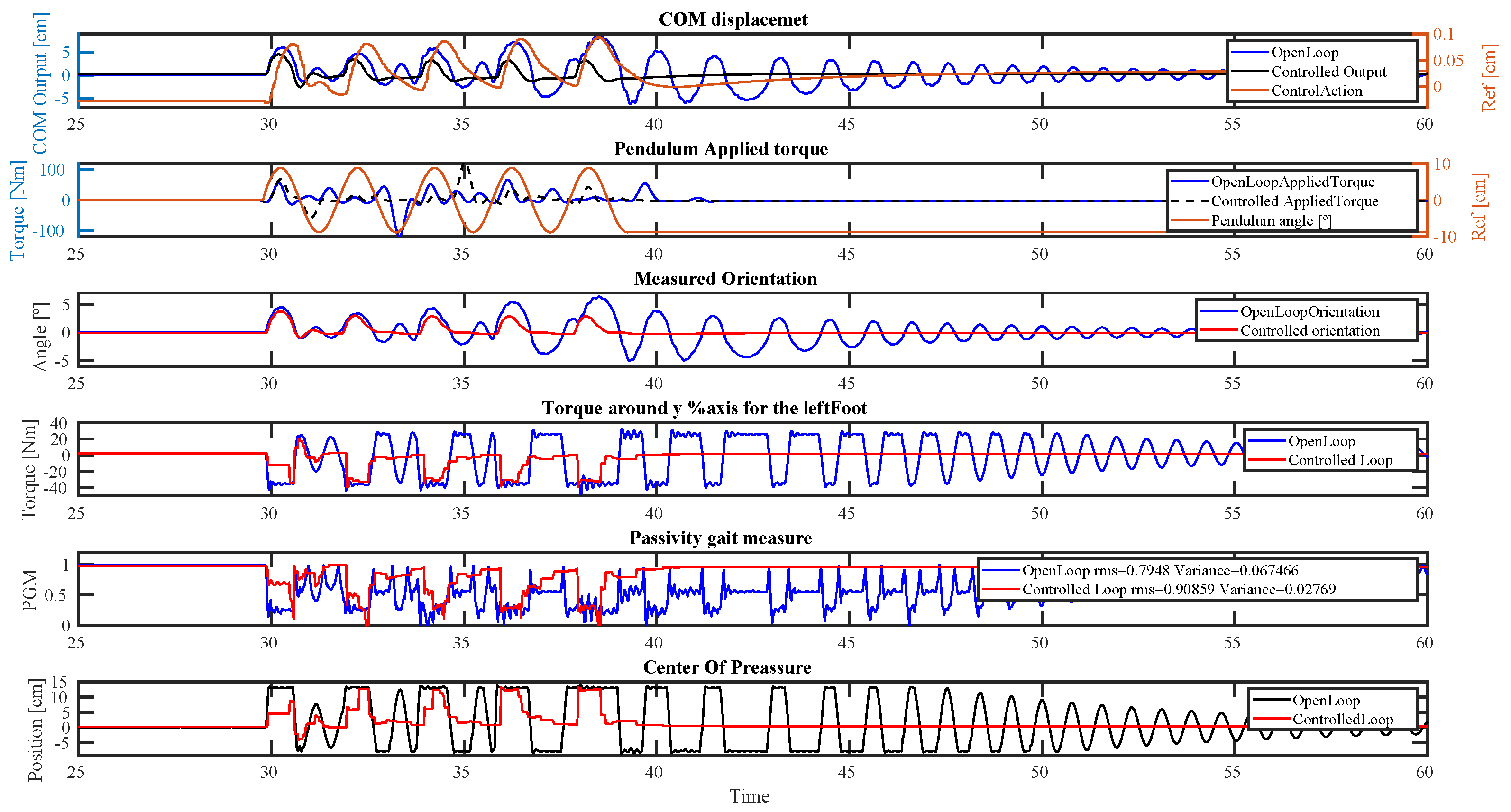
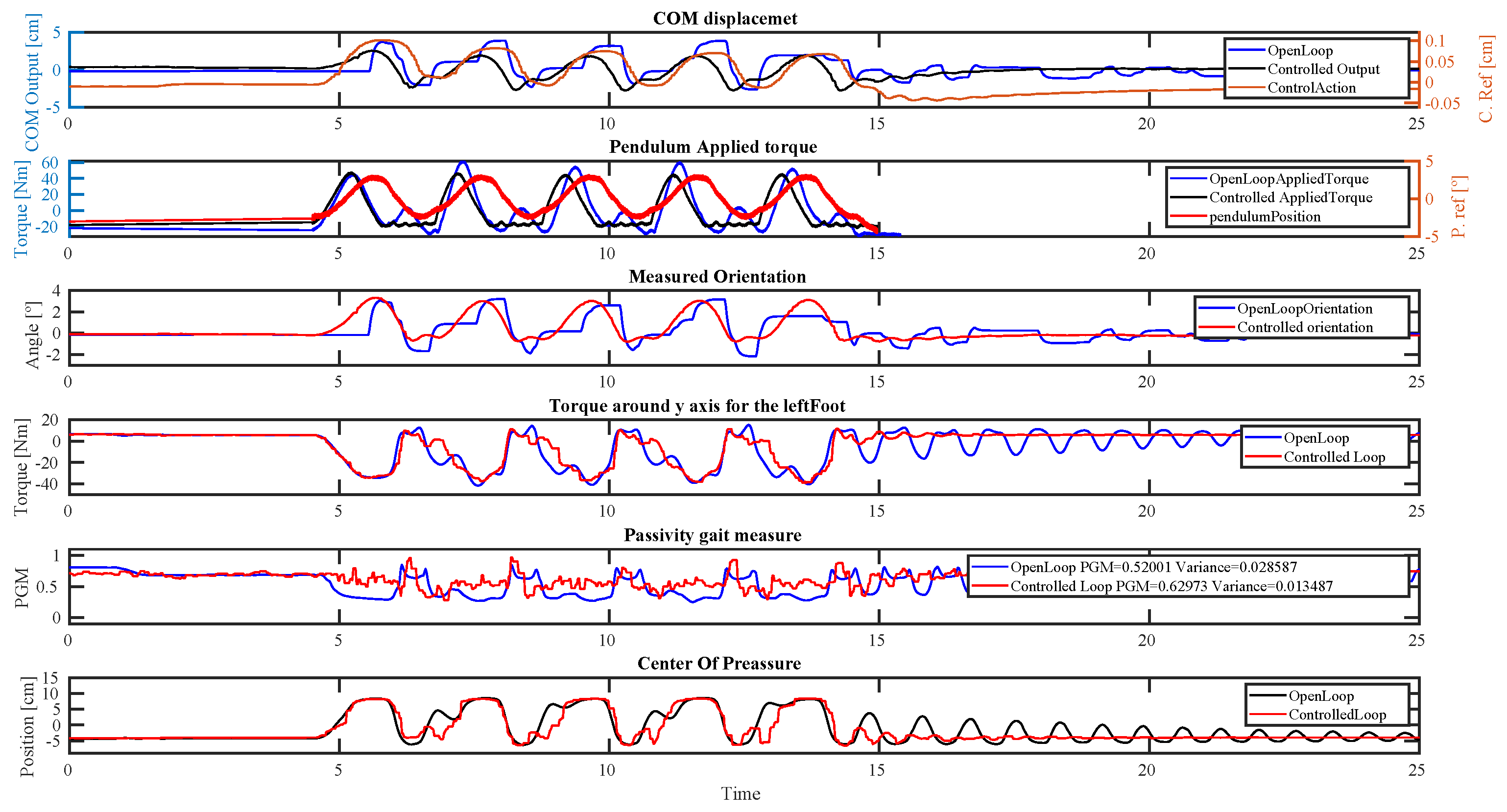
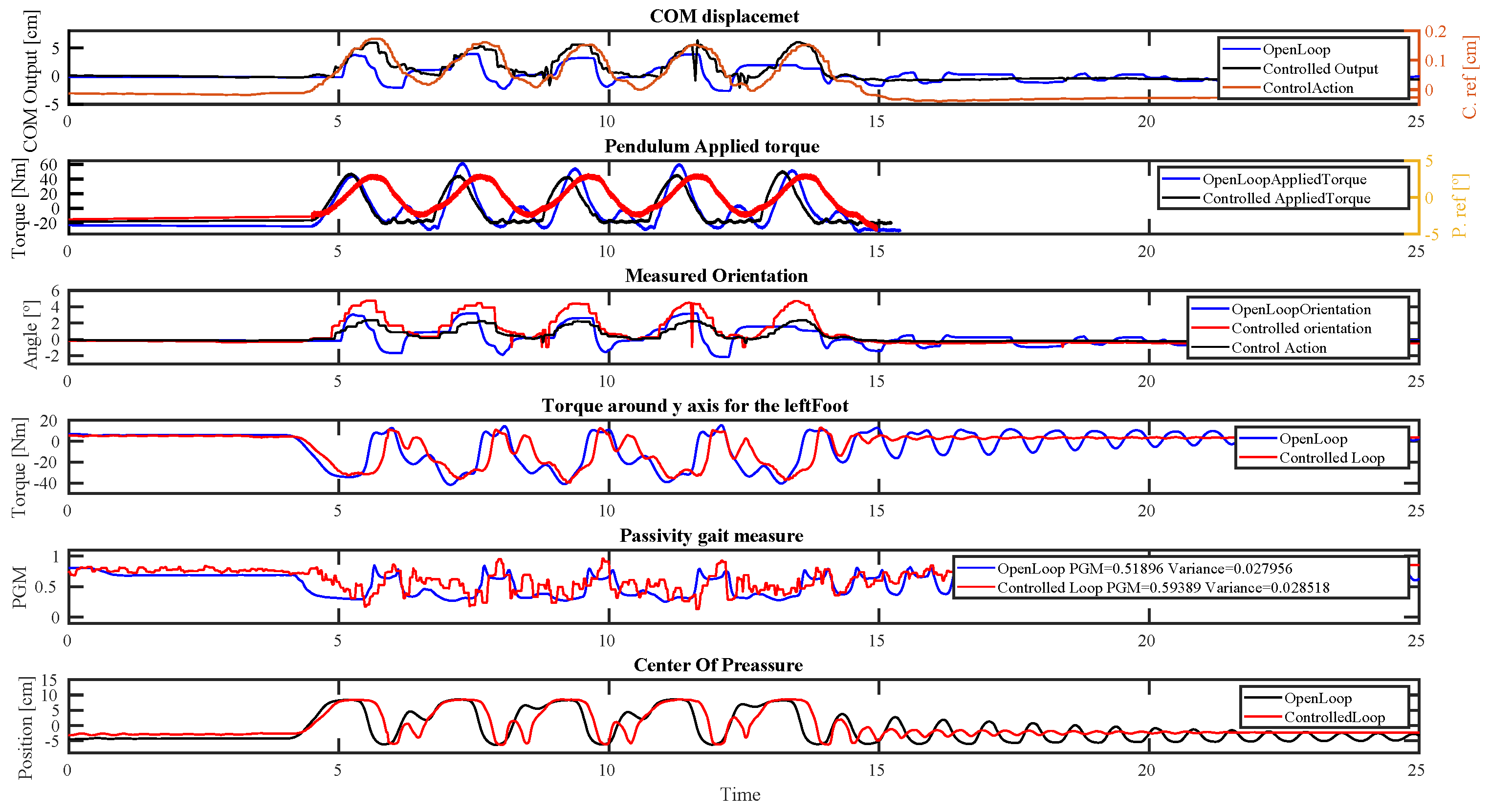
4.3. Periodic Quasi-Static Disturbance
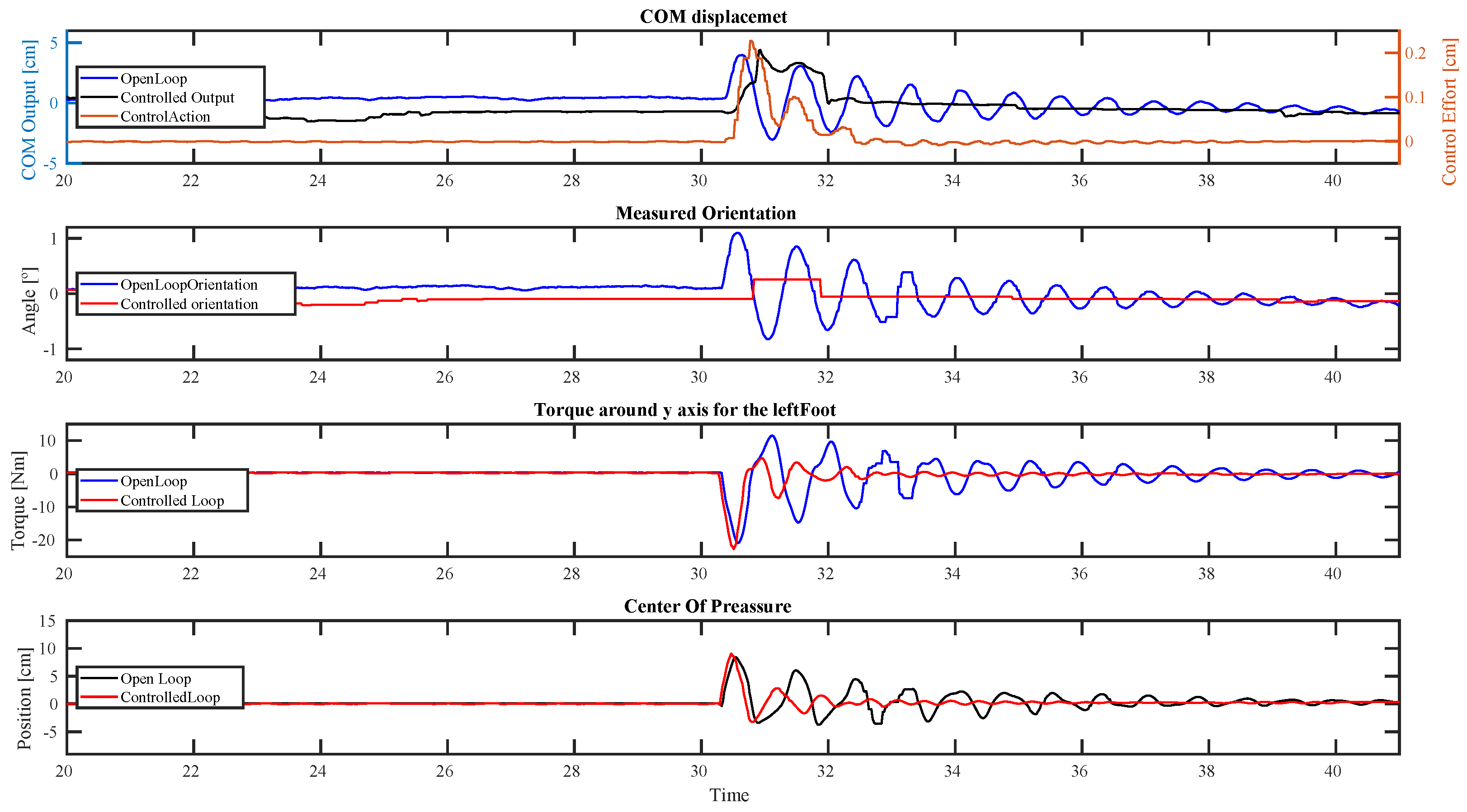
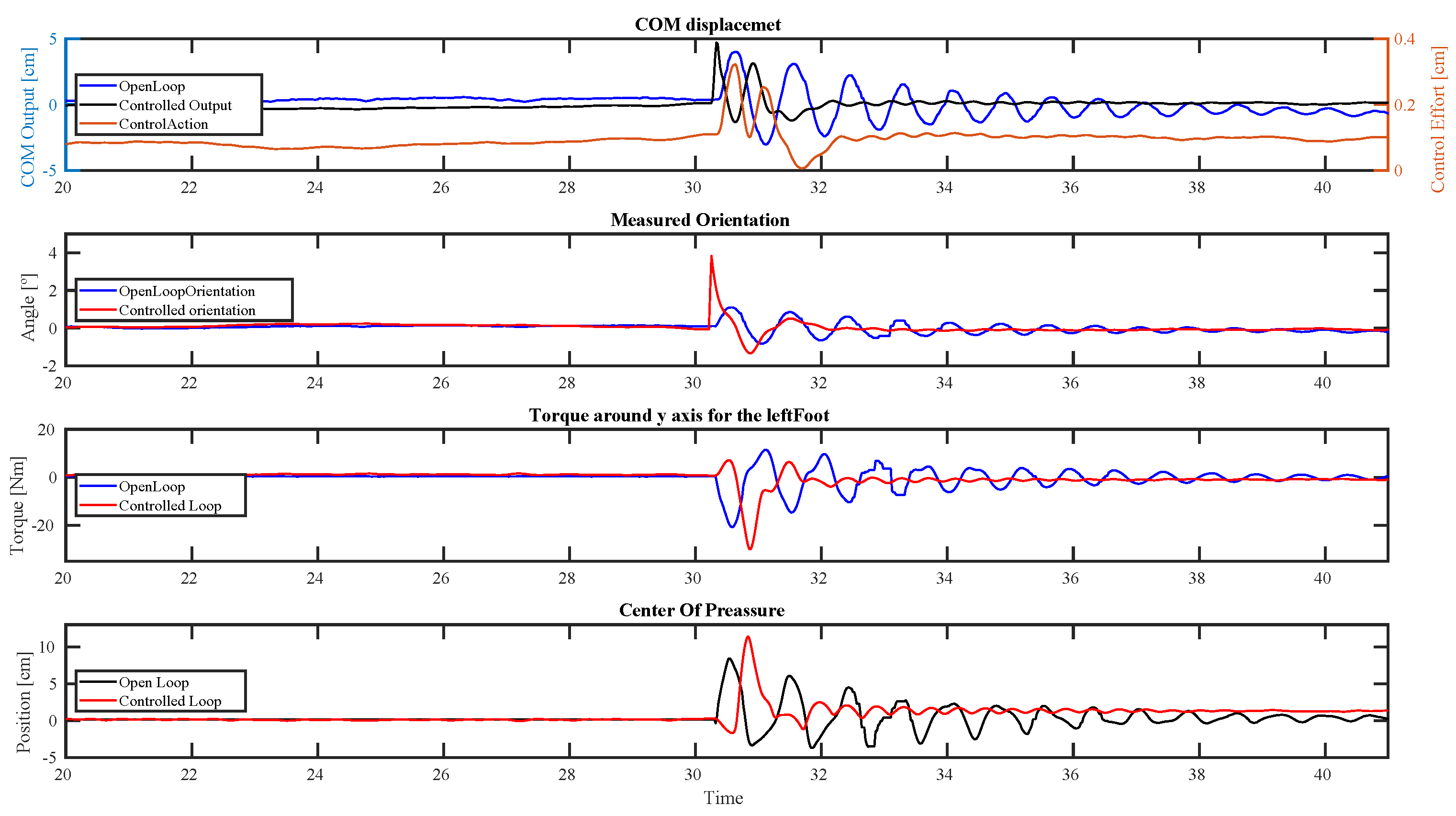
5. Experimental Results
5.1. Impulsive Disturbance
5.2. Quasi-Static Periodic Disturbance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Z.; Zhou, C.; Tsagarakis, N.; Caldwell, D. Compliance Control for Stabilizing a Humanoid on the Changing Slope Based on Terrain Inclination Estimation. Auton. Robot. 2016, 40, 955–971. [Google Scholar] [CrossRef]
- Ott, C.; Henze, B.; Hettich, G.; Seyde, T.N.; Roa, M.A.; Lippi, V.; Mergner, T. Good Posture, Good Balance: Comparison of Bioinspired and Model-Based Approaches for Posture Control of Humanoid Robots. IEEE Robot. Autom. Mag. 2016, 23, 22–33. [Google Scholar] [CrossRef]
- Kanamiya, Y.; Ota, S.; Sato, D. Ankle and hip balance control strategies with transitions. In Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, Alaska, 3–8 May 2010; pp. 3446–3451. [Google Scholar]
- Kouppas, C.; Saada, M.; Meng, Q.; King, M.; Majoe, D. Hybrid autonomous controller for bipedal robot balance with deep reinforcement learning and pattern generators. Robot. Auton. Syst. 2021, 146, 103891. [Google Scholar] [CrossRef]
- Asano, Y.; Nakashima, S.; Yanokura, I.; Onitsuka, M.; Kawaharazuka, K.; Tsuzuki, K.; Koga, Y.; Omura, Y.; Okada, K.; Inaba, M. Ankle-hip-stepping stabilizer on tendon-driven humanoid Kengoro by integration of muscle-joint-work space controllers for knee-stretched humanoid balance. In Proceedings of the IEEE-RAS 19th International Conference on Humanoid Robots, Toronto, ON, Canada, 15–17 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Nenchev, D.N.; Nishio, A. Ankle and hip strategies for balance recovery of a biped subjected to an impact. Robotica 2008, 26, 643–653. [Google Scholar] [CrossRef]
- Nishio, A.; Takahashi, K.; Nenchev, D. Balance Control of a Humanoid Robot Based on the Reaction Null Space Method. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 1996–2001. [Google Scholar] [CrossRef]
- Stephens, B. Integral control of humanoid balance. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 4020–4027. [Google Scholar] [CrossRef]
- Morisawa, M.; Kajita, S.; Kanehiro, F.; Kaneko, K.; Miura, K.; Yokoi, K. Balance control based on Capture Point error compensation for biped walking on uneven terrain. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots, Osaka, Japan, 29 November–1 December 2012; pp. 734–740. [Google Scholar] [CrossRef]
- Sugihara, T. Standing stabilizability and stepping maneuver in planar bipedalism based on the best COM-ZMP regulator. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 1966–1971. [Google Scholar] [CrossRef]
- Vanderborght, B. Dynamic Stabilisation of the Biped Lucy Powered by Actuators with Control stiffness; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Joe, H.-M.; Oh, J.-H. A Robust Balance-Control Framework for the Terrain-Blind Bipedal Walking of a Humanoid Robot on Unknown and Uneven Terrain. Sensors 2019, 19, 4194. [Google Scholar] [CrossRef] [PubMed]
- Vukpbratovic, M.; Boravac, B. Zero-moment point—Thirty five years of its life. Int. J. Humanoid Robot. 2004, 1, 157–173. [Google Scholar] [CrossRef]
- Borovac, B.; Nikoli, M.; Raković, M. How to compensate for the disturbances that jeopardize dynamic balance of a humanoid robot? Int. J. Hum. Robot. 2011, 8, 533–578. [Google Scholar] [CrossRef]
- Monteleone, S.; Negrello, F.; Grioli, G.; Catalano, M.G.; Garabini, M.; Bicchi, A. Dysturbance: DYnamic and STatic pUsheR to Benchmark bAlaNCE. In Proceedings of the 2nd Italian Conference on Robotics and Intelligent Machines, Fisciano, Italy, 7–18 December 2020. [Google Scholar]
- Castano, J.A.; Zhou, C.; Li, Z.; Tsagarakis, N. Robust Model Predictive Control for humanoids standing balancing. In Proceedings of the International Conference on Advanced Robotics and Mechatronics, Macau, China, 18–20 August 2016; pp. 147–152. [Google Scholar] [CrossRef]
- Zhou, C.; Li, Z.; Castano, J.; Dallali, H.; Tsagarakis, N.; Caldwell, D. A passivity based compliance stabilizer for humanoid robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Hong Kong, China, 31 May–7 June 2014; pp. 1487–1492. [Google Scholar] [CrossRef]
- Zhou, C.; Li, Z.; Wang, X.; Tsagarakis, N.; Caldwell, D. Stabilization of Bipedal Walking Based on Compliance Control. Auton. Robot. 2016, 40, 1041–1057. [Google Scholar] [CrossRef][Green Version]
- Castano, J.A.; Hoffman, E.M.; Laurenzi, A.; Muratore, L.; Karnedula, M.; Tsagarakis, N.G. A Whole Body Attitude Stabilizer for Hybrid Wheeled-Legged Quadruped Robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Brisbane, Australia, 21–25 May 2018; pp. 706–712. [Google Scholar] [CrossRef]
- Castano, J.A.; Hernandez, A.; Li, Z.; Tsagarakis, N.G.; Caldwell, D.G.; Keyser, R.D. Enhancing the robustness of the EPSAC predictive control using a Singular Value Decomposition approach. Robot. Auton. Syst. 2015, 74, 283–295. [Google Scholar] [CrossRef]
- Castano, J.A.; Hernandez, A.; Li, Z.; Zhou, C.; Tsagarikis, N.G.; Caldwell, D.; Keyser, R.D. Implementation of Robust EPSAC on dynamic walking of COMAN Humanoid. In Proceedings of the 19th World Congress the International Federation of Automatic Control, Cape Town, South Africa, 24–29 August 2014; pp. 8384–8390. [Google Scholar]
- Pratt, J.; Carff, J.; Drakunov, S.; Goswami, A. Capture Point: A Step toward Humanoid Push Recovery. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots, Genova, Italy, 4–6 December 2006; pp. 200–207. [Google Scholar]
- Zhou, C.; Wang, X.; Li, Z.; Tsagarakis, N. Overview of Gait Synthesis for the Humanoid COMAN. J. Bionic Eng. 2017, 14, 15–25. [Google Scholar] [CrossRef]
- Hoffman, E.M.; Clement, B.; Zhou, C.; Tsagarakis, N.; Mouret, J.B.; Ivaldi, S. Whole-Body Compliant Control of iCub: First results with OpenSoT. In Proceedings of the IEEE ICRA Workshop on Dynamic Legged Locomotion in Realistic Terrains, Brisbane, Australia, 21–25 May 2018. [Google Scholar]
- Rao, V.; Bernstein, D. Naive control of the double integrator: A comparison of a dozen diverse controllers under off-nominal conditions. In Proceedings of the American Control Conference, San Diego, CA, USA, 2–4 June 1999; Volume 2, pp. 1477–1481. [Google Scholar] [CrossRef]
- Aller, F.; Pinto-Fernandez, D.; Torricelli, D.; Pons, J.L.; Mombaur, K. From the State of the Art of Assessment Metrics Toward Novel Concepts for Humanoid Robot Locomotion Benchmarking. IEEE Robot. Autom. Lett. 2020, 5, 914–920. [Google Scholar] [CrossRef]
- Torricelli, D.; Gonzalez-Vargas, J.; Veneman, J.F.; Mombaur, K.; Tsagarakis, N.; del Ama, A.J.; Gil-Agudo, A.; Moreno, J.C.; Pons, J.L. Benchmarking Bipedal Locomotion: A Unified Scheme for Humanoids, Wearable Robots, and Humans. IEEE Robot. Autom. Mag. 2015, 22, 103–115. [Google Scholar] [CrossRef]
- Lippi, V.; Mergner, T.; Seel, T.; Maurer, C. COMTEST Project: A Complete Modular Test Stand for Human and Humanoid Posture Control and Balance. arXiv 2021, arXiv:abs/2104.11935. [Google Scholar]
- Koenig, N.; Howard, A. Design and use paradigms for gazebo, an open-source multi-robot simulator. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Sendai, Japan, 28 September–2 October 2004; Volume 3, pp. 2149–2154. [Google Scholar]
- Wang, L. Model Predictive Control System Design and Implementation Using MATLAB®; Advances in Industrial Control; Springer: London, UK, 2010. [Google Scholar]











| openloop | 19.08 | 5.03 | 3.53 | 0.68 | 0.042 | 28.3 | −44.3 | 14 | −8.37 |
| COM1 | 1.4 | 3.48 | 2.73 | 0.84 | 0.024 | 11 | −44.98 | 14.12 | −3.51 |
| COM2 | 2.6 | 3.3 | 2.8 | 0.8 | 0.011 | 28.31 | −43.1 | 14.07 | −8.2 |
| Attitude | 7.74 | 6.44 | 3.72 | 0.76 | 0.03 | 26.71 | −43.21 | 13.9 | −8.13 |
| COM1+A | 2.14 | 3.07 | 2.38 | 0.856 | 0.012 | 8.7 | −44.24 | 13.85 | −2.88 |
| COM2+A | 1.33 | 4.55 | 2.9 | 0.856 | 0.013 | 8.34 | −41.606 | 12.81 | −4.3 |
| openloop | 26.2 | 8.3 | 6.19 | 0.79 | 0.067 | 30.35 | −48 | 14.15 | −8.16 |
| COM1 | 9.9 | 4.4 | 3.74 | 0.9 | 0.027 | 20.12 | −38.8 | 13.13 | −4.06 |
| COM2 | 10.5 | 3.31 | 3.17 | 0.83 | 0.03 | 33.76 | −37.11 | 13.68 | −8.7 |
| Attitude | 14.2 | 10.74 | 6.21 | 0.907 | 0.04 | 23.7 | −39.75 | 13.5 | −8.16 |
| COM1+A | 10.2 | 7.62 | 5.15 | 0.92 | 0.028 | 17.7 | −40 | 13.46 | −5.38 |
| COM2+A | 9.6 | 9.86 | 6.75 | 0.92 | 0.02595 | 6.9 | −41.6 | 13.26 | −3.22 |
| openloop | 20+ | 3.96 | 1.08 | 11.21 | −20.86 | 4.28 | −7.71 |
| COM1 | 2.45 | 4.05 | 0.3 | 4 | −22.7 | 8.46 | −3.2 |
| COM1+A | 2.04 | 4.48 | 0.98 | 5.44 | −16.54 | 7.68 | −3.15 |
| COM2+A | 1.8 | 4.4 | 1.96 | 1.56 | −33.35 | 8.9 | −7.08 |
| openloop | 13 | 3.7 | 4.12 | 0.52 | 0.028 | 17.08 | −30.75 | 8.52 | −6.24 |
| COM1 | 10.2 | 2.54 | 3.28 | 0.629 | 0.013 | 11.43 | −38.35 | 8.54 | −6.29 |
| COM1+A | 10 | 5.7 | 4.72 | 0.593 | 0.028 | 11.62 | −39.65 | 8.52 | −6.17 |
| COM2+A | 10.7 | 5 | 1.97 | 0.58 | 0.02842 | 17.08 | −30.7 | 8.52 | −6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castano, J.A.; Humphreys, J.; Mingo Hoffman, E.; Fernández Talavera, N.; Rodriguez Sanchez, M.C.; Zhou, C. Benchmarking Dynamic Balancing Controllers for Humanoid Robots. Robotics 2022, 11, 114. https://doi.org/10.3390/robotics11050114
Castano JA, Humphreys J, Mingo Hoffman E, Fernández Talavera N, Rodriguez Sanchez MC, Zhou C. Benchmarking Dynamic Balancing Controllers for Humanoid Robots. Robotics. 2022; 11(5):114. https://doi.org/10.3390/robotics11050114
Chicago/Turabian StyleCastano, Juan A., Joseph Humphreys, Enrico Mingo Hoffman, Noelia Fernández Talavera, Maria Cristina Rodriguez Sanchez, and Chengxu Zhou. 2022. "Benchmarking Dynamic Balancing Controllers for Humanoid Robots" Robotics 11, no. 5: 114. https://doi.org/10.3390/robotics11050114
APA StyleCastano, J. A., Humphreys, J., Mingo Hoffman, E., Fernández Talavera, N., Rodriguez Sanchez, M. C., & Zhou, C. (2022). Benchmarking Dynamic Balancing Controllers for Humanoid Robots. Robotics, 11(5), 114. https://doi.org/10.3390/robotics11050114









