VLP Landmark and SLAM-Assisted Automatic Map Calibration for Robot Navigation with Semantic Information
Abstract
:1. Introduction
2. Related Work
2.1. Robot Positioning and Navigation
2.2. Map Merging and Map Alignment Method
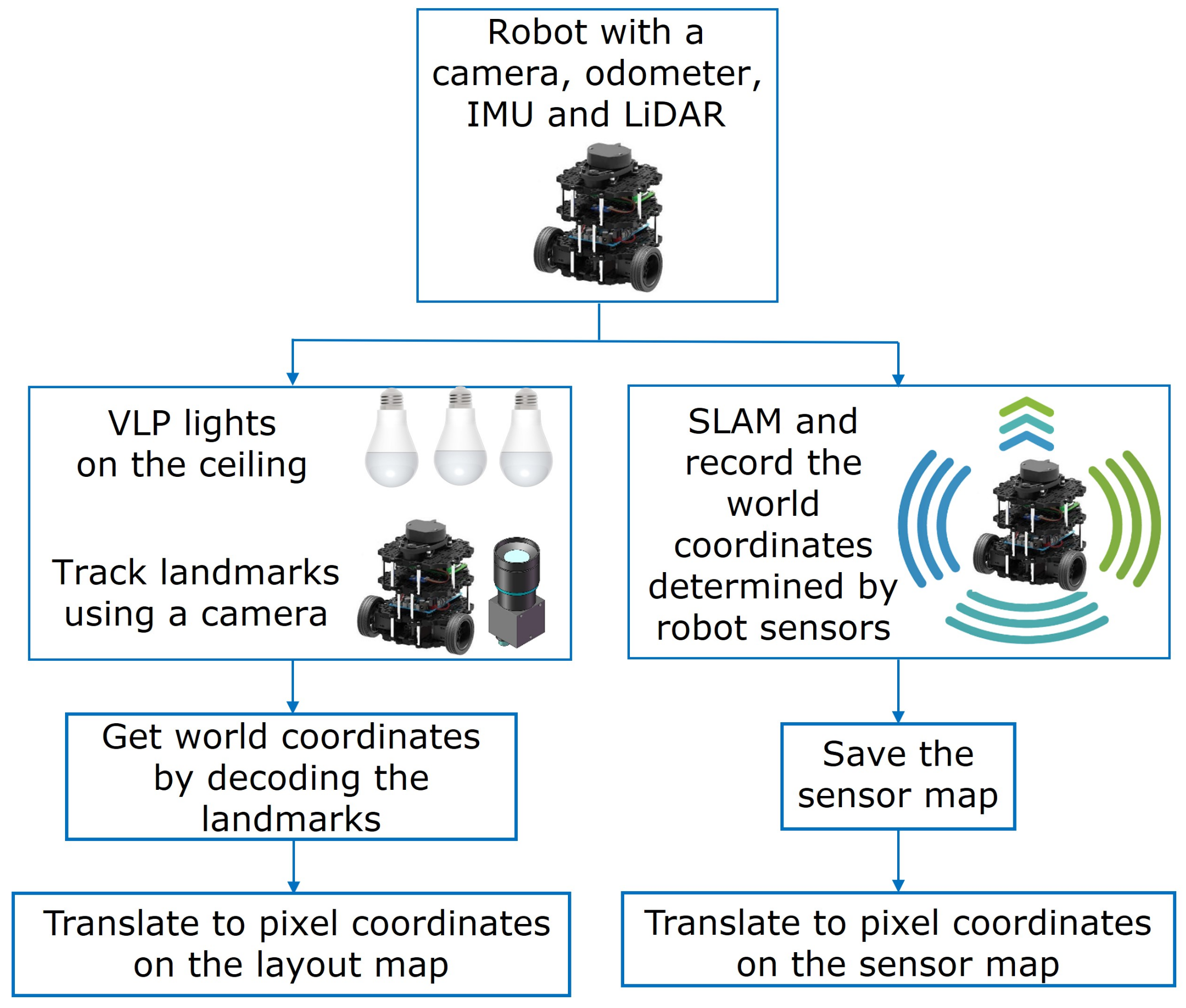
3. Mapping System
3.1. Occupancy Grid Mapping System
3.2. Map Transformation
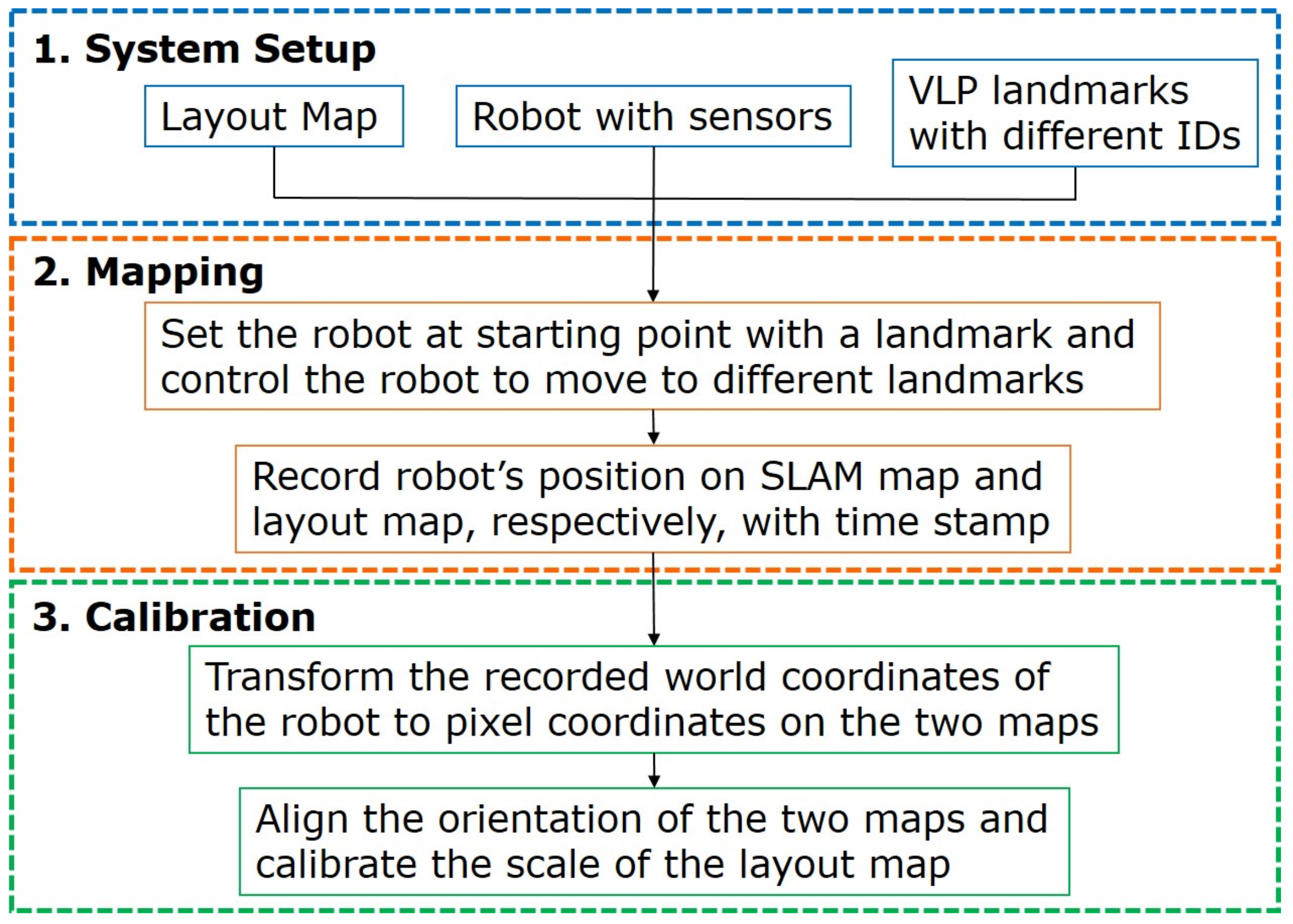
3.3. Overview of the Proposed Map Calibration System
4. Map Calibration Method
4.1. Positioning on Two Different Maps
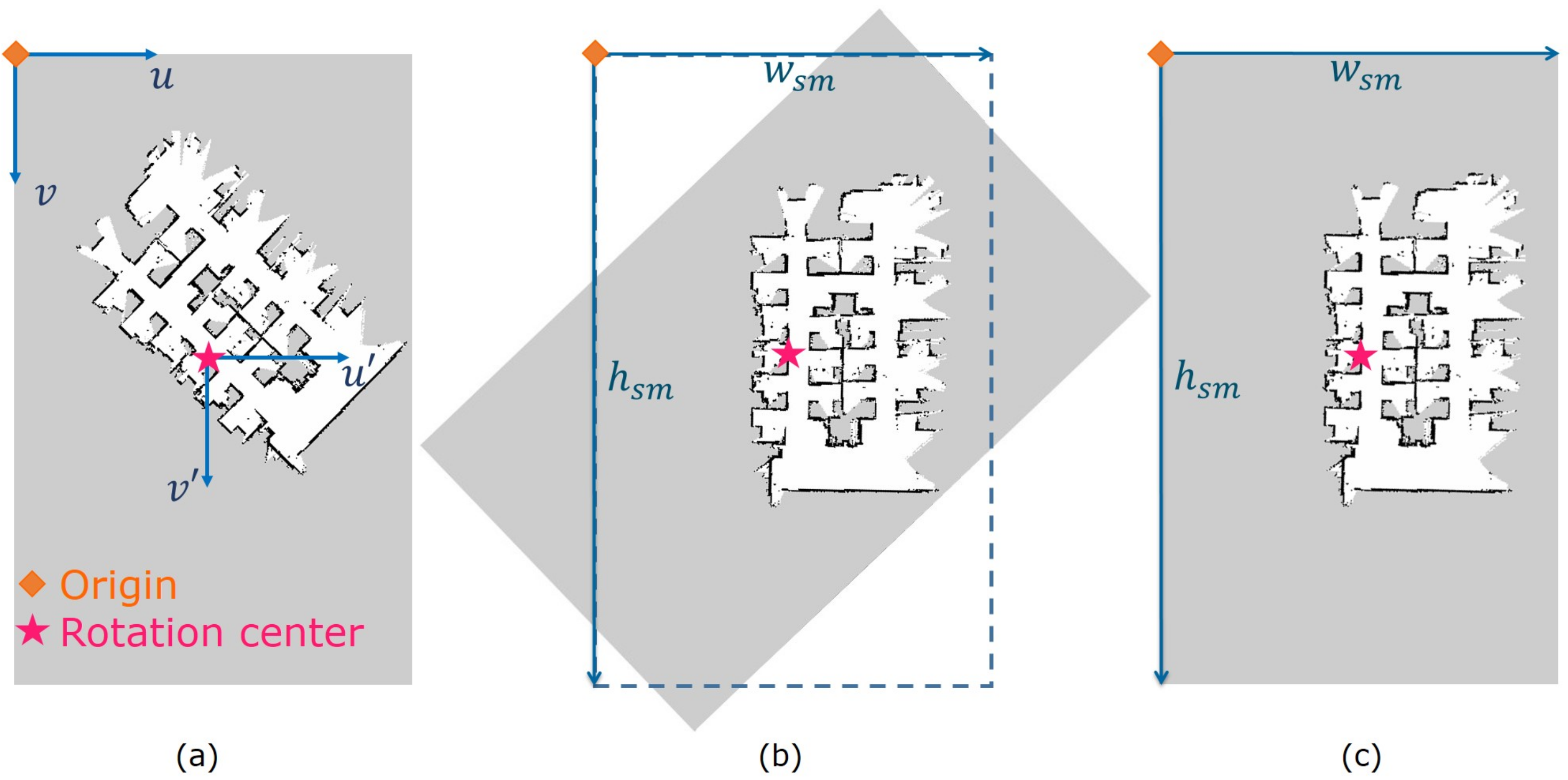
4.2. Calibration of the Orientation
4.3. Calibration of the Scale
5. Experimental Results
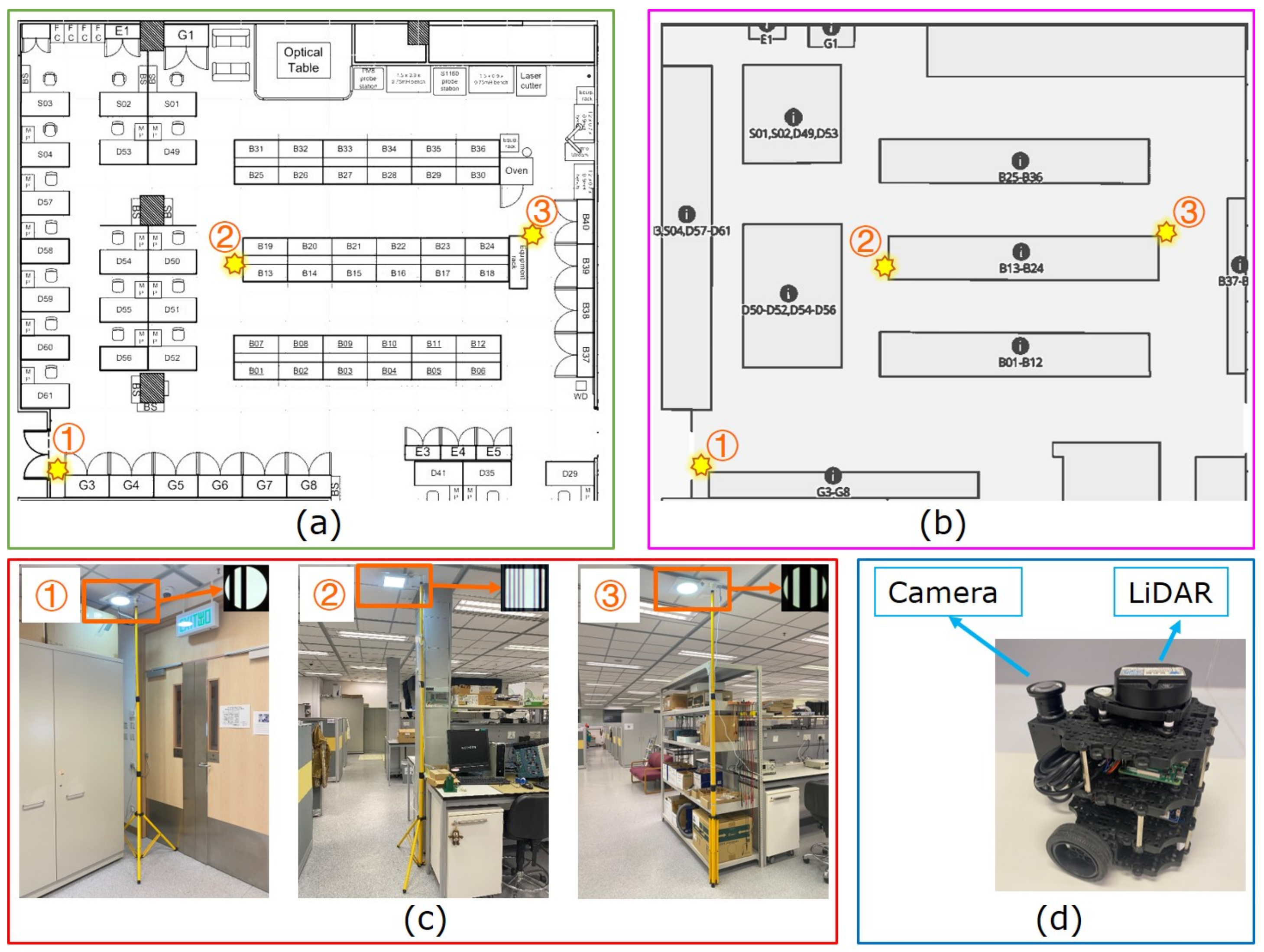
5.1. Experiment Setup
5.2. Mapping Process and Alignment Results
5.3. Navigation on Calibrated Map
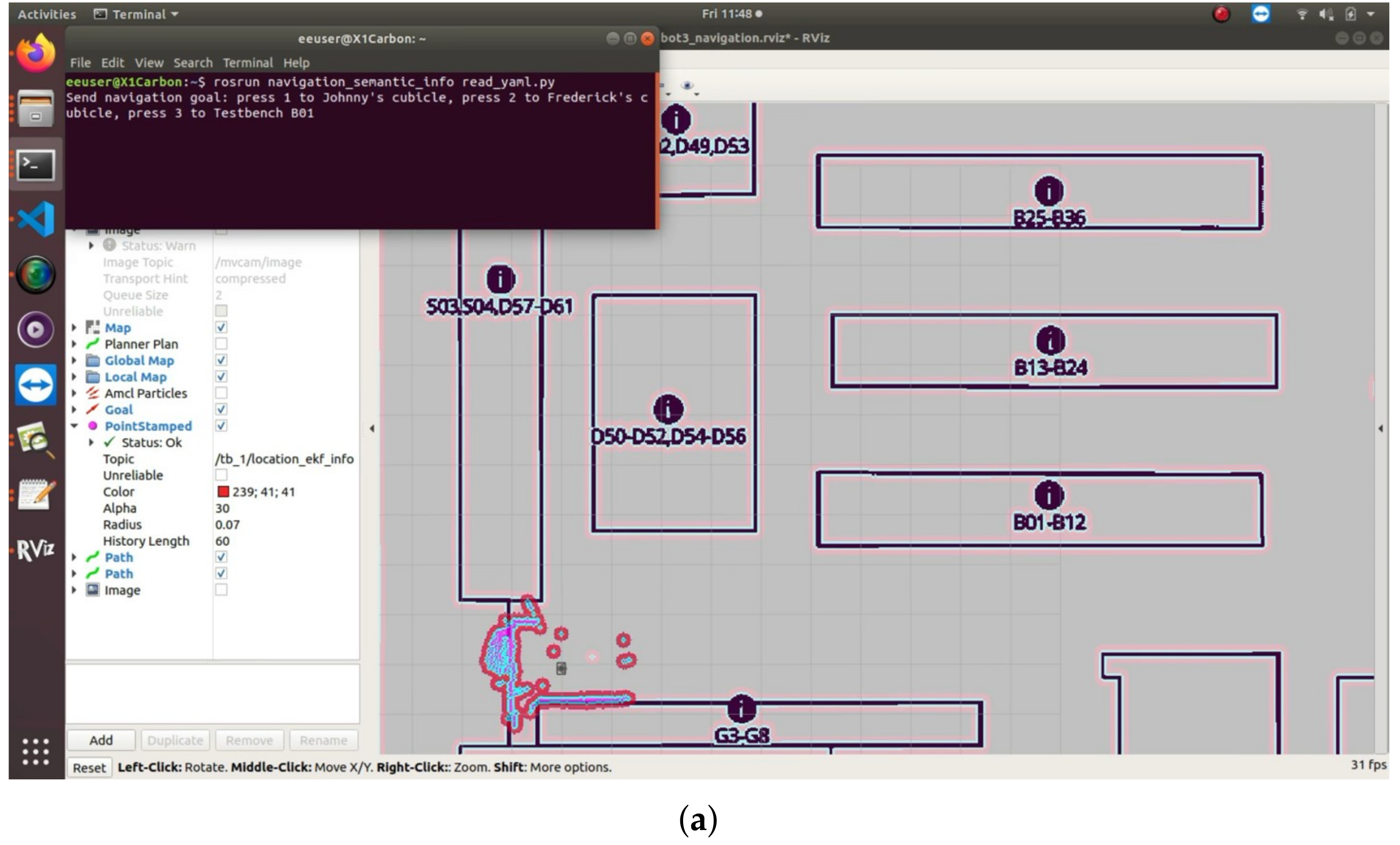
5.4. Navigation with Semantic Information
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Su, H.; Qi, W.; Schmirander, Y.; Ovur, S.E.; Cai, S.; Xiong, X. A human activity-aware shared control solution for medical human–robot interaction. Assem. Autom. 2022, 42, 388–394. [Google Scholar] [CrossRef]
- Qi, W.; Ovur, S.E.; Li, Z.; Marzullo, A.; Song, R. Multi-sensor guided hand gesture recognition for a teleoperated robot using a recurrent neural network. IEEE Robot. Autom. Lett. 2021, 6, 6039–6045. [Google Scholar] [CrossRef]
- Liu, C.; Tomizuka, M. Algorithmic safety measures for intelligent industrial co-robots. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 3095–3102. [Google Scholar]
- Peternel, L.; Kim, W.; Babič, J.; Ajoudani, A. Towards ergonomic control of human-robot co-manipulation and handover. In Proceedings of the 2017 IEEE-RAS 17th International Conference on Humanoid Robotics (Humanoids), Birmingham, UK, 15–17 November 2017; pp. 55–60. [Google Scholar]
- Zhuang, Y.; Hua, L.; Qi, L.; Yang, J.; Cao, P.; Cao, Y.; Wu, Y.; Thompson, J.; Haas, H. A survey of positioning systems using visible LED lights. IEEE Commun. Surv. Tutor. 2018, 20, 1963–1988. [Google Scholar] [CrossRef] [Green Version]
- Guan, W.; Huang, L.; Hussain, B.; Yue, C.P. Robust robotic localization using visible light positioning and inertial fusion. IEEE Sens. J. 2021, 22, 4882–4892. [Google Scholar] [CrossRef]
- Wang, Y.; Hussain, B.; Yue, C.P. Arbitrarily Tilted Receiver Camera Correction and Partially Blocked LED Image Compensation for Indoor Visible Light Positioning. IEEE Sens. J. 2021, 22, 4800–4807. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, X.; Yuan, J.; Song, J.; Fang, Y. A novel global localization approach based on structural unit encoding and multiple hypothesis tracking. IEEE Trans. Instrum. Meas. 2019, 68, 4427–4442. [Google Scholar] [CrossRef]
- Huletski, A.; Kartashov, D.; Krinkin, K. VinySLAM: An indoor SLAM method for low-cost platforms based on the transferable belief model. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Cannada, 24–28 September 2017; pp. 6770–6776. [Google Scholar]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, present, and future of simultaneous localization and mapping: Toward the robust-perception age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef] [Green Version]
- Kshirsagar, J.; Shue, S.; Conrad, J.M. A Survey of Implementation of Multi-Robot Simultaneous Localization and Mapping. In Proceedings of the SoutheastCon 2018, St. Petersburg, FL, USA, 19–22 April 2018; pp. 1–7. [Google Scholar]
- Bresson, G.; Alsayed, Z.; Yu, L.; Glaser, S. Simultaneous localization and mapping: A survey of current trends in autonomous driving. IEEE Trans. Intell. Transp. Syst. 2017, 2, 194–220. [Google Scholar] [CrossRef] [Green Version]
- Tan, H.; Song, J. Design of An Intelligent Transfer Robot with Color Recognition. In Proceedings of the 2021 3rd International Conference on Applied Machine Learning (ICAML), Chengdu, China, 14–16 May 2021; pp. 287–291. [Google Scholar]
- Patil, A.; Bae, J.; Park, M. An Algorithm for Task Allocation and Planning for a Heterogeneous Multi-Robot System to Minimize the Last Task Completion Time. Sensors 2022, 22, 5637. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, Y.; Liu, Y.; Li, Q.; Cao, F.; Feng, M.; Wu, H.; Li, W.; Kang, Y. Development Status and Multilevel Classification Strategy of Medical Robots. Electronics 2021, 10, 1278. [Google Scholar] [CrossRef]
- Khan, Z.H.; Siddique, A.; Lee, C.W. Robotics utilization for healthcare digitization in global COVID-19 management. Int. J. Environ. Res. Public Health 2020, 17, 3819. [Google Scholar] [CrossRef]
- Kostavelis, I.; Kargakos, A.; Skartados, E.; Peleka, G.; Giakoumis, D.; Sarantopoulos, I.; Agriomallos, I.; Doulgeri, Z.; Endo, S.; Stüber, H.; et al. Robotic Assistance in Medication Intake: A Complete Pipeline. Appl. Sci. 2022, 12, 1379. [Google Scholar] [CrossRef]
- Iqbal, J.; Xu, R.; Sun, S.; Li, C. Simulation of an autonomous mobile robot for LiDAR-based in-field phenotyping and navigation. Robotics 2020, 9, 46. [Google Scholar] [CrossRef]
- Santos, L.; Santos, F.; Mendes, J.; Costa, P.; Lima, J.; Reis, R.; Shinde, P. Path planning aware of robot’s center of mass for steep slope vineyards. Robotica 2020, 38, 684–698. [Google Scholar] [CrossRef]
- Al Khatib, E.I.; Jaradat, M.A.K.; Abdel-Hafez, M.F. Low-cost reduced navigation system for mobile robot in indoor/outdoor environments. IEEE Access 2020, 8, 25014–25026. [Google Scholar] [CrossRef]
- Lv, W.; Kang, Y.; Qin, J. Indoor localization for skid-steering mobile robot by fusing encoder, gyroscope, and magnetometer. IEEE Trans. Syst. Man Cybern. Syst. 2017, 49, 1241–1253. [Google Scholar] [CrossRef]
- Murata, Y.; Murakami, T. Estimation of Posture and Position Based on Geometric Calculation Using IMUs. In Proceedings of the IECON 2019-45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; Volume 1, pp. 5388–5393. [Google Scholar]
- McGregor, A.; Dobie, G.; Pearson, N.R.; MacLeod, C.N.; Gachagan, A. Determining position and orientation of a 3-wheel robot on a pipe using an accelerometer. IEEE Sens. J. 2020, 20, 5061–5071. [Google Scholar] [CrossRef]
- Da Mota, F.A.; Rocha, M.X.; Rodrigues, J.J.; De Albuquerque, V.H.C.; De Alexandria, A.R. Localization and navigation for autonomous mobile robots using Petri nets in indoor environments. IEEE Access 2018, 6, 31665–31676. [Google Scholar] [CrossRef]
- Zhang, J.; Lyu, Y.; Patton, J.; Periaswamy, S.C.; Roppel, T. BFVP: A probabilistic UHF RFID tag localization algorithm using Bayesian filter and a variable power RFID model. IEEE Trans. Ind. Electron. 2018, 65, 8250–8259. [Google Scholar] [CrossRef]
- Su, D.; Kong, H.; Sukkarieh, S.; Huang, S. Necessary and Sufficient Conditions for Observability of SLAM-Based TDOA Sensor Array Calibration and Source Localization. IEEE Trans. Robot. 2021, 37, 1451–1468. [Google Scholar] [CrossRef]
- Naab, C.; Zheng, Z. Application of the unscented Kalman filter in position estimation a case study on a robot for precise positioning. Rob. Auton. Syst. 2022, 147, 103904. [Google Scholar] [CrossRef]
- Schouten, G.; Steckel, J. A biomimetic radar system for autonomous navigation. IEEE Trans. Robot. 2019, 35, 539–548. [Google Scholar] [CrossRef]
- Liu, X.; Xu, Q.; Mu, Y.; Yang, J.; Lin, L.; Yan, S. High-Precision Camera Localization in Scenes with Repetitive Patterns. ACM Trans. Intell. Syst. Technol. 2018, 9, 1–21. [Google Scholar] [CrossRef]
- Wang, Y.; Guan, W.; Hussain, B.; Yue, C.P. High Precision Indoor Robot Localization Using VLC Enabled Smart Lighting. In Proceedings of the Optical Fiber Communication Conference, San Francisco, CA, USA, 6–10 June 2021; p. M1B-8. [Google Scholar]
- Bonanni, T.M.; Della Corte, B.; Grisetti, G. 3-D map merging on pose graphs. IEEE Robot. Autom. Lett. 2017, 2, 1031–1038. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhu, J.; Li, Y.; Wang, J.; Li, Z.; Lu, H. Simultaneous merging multiple grid maps using the robust motion averaging. J. Intell. Robot. Syst. 2019, 94, 655–668. [Google Scholar] [CrossRef] [Green Version]
- Guo, C.X.; Sartipi, K.; DuToit, R.C.; Georgiou, G.A.; Li, R.; O’Leary, J.; Nerurkar, E.D.; Hesch, J.A.; Roumeliotis, S.I. Resource-aware large-scale cooperative three-dimensional mapping using multiple mobile devices. IEEE Trans. Robot. 2018, 34, 1349–1369. [Google Scholar] [CrossRef]
- Hernández, C.A.V.; Ortiz, F.A.P. A real-time map merging strategy for robust collaborative reconstruction of unknown environments. Expert Syst. Appl. 2020, 145, 113109. [Google Scholar] [CrossRef]
- Amigoni, F.; Li, A.Q. Comparing methods for merging redundant line segments in maps. Robot. Autom. Syst. 2018, 99, 135–147. [Google Scholar] [CrossRef]
- Ramachandran, R.K.; Kakish, Z.; Berman, S. Information correlated Lévy walk exploration and distributed mapping using a swarm of robots. IEEE Trans. Robot. 2020, 36, 1422–1441. [Google Scholar] [CrossRef]
- Kakuma, D.; Tsuichihara, S.; Ricardez, G.A.G.; Takamatsu, J.; Ogasawara, T. Alignment of occupancy grid and floor maps using graph matching. In Proceedings of the 2017 IEEE 11th International Conference on Semantic Computing (ICSC), San Diego, CA, USA, 30 January–1 February 2017; pp. 57–60. [Google Scholar]
- Georgiou, C.; Anderson, S.; Dodd, T. Constructing informative bayesian map priors: A multi-objective optimisation approach applied to indoor occupancy grid mapping. Int. J. Rob. Res. 2017, 36, 274–291. [Google Scholar] [CrossRef]
- Shahbandi, S.G.; Magnusson, M.; Iagnemma, K. Nonlinear optimization of multimodal two-dimensional map alignment with application to prior knowledge transfer. IEEE Robot. Autom. Lett. 2018, 3, 2040–2047. [Google Scholar] [CrossRef] [Green Version]
- Hou, J.; Kuang, H.; Schwertfeger, S. Fast 2D map matching based on area graphs. In Proceedings of the 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO), Dali, China, 6–8 December 2019; pp. 1723–1729. [Google Scholar]
- Qi, W.; Aliverti, A. A multimodal wearable system for continuous and real-time breathing pattern monitoring during daily activity. IEEE J. Biomed. Health Inform. 2019, 24, 2199–2207. [Google Scholar] [CrossRef]
- Elfes, A. Using occupancy grids for mobile robot perception and navigation. Computer 1989, 22, 46–57. [Google Scholar] [CrossRef]
- Reineking, T.; Clemens, J. Dimensions of uncertainty in evidential grid maps. In Proceedings of the International Conference on Spatial Cognition, Bremen, Germany, 15–19 September 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 283–298. [Google Scholar]
- Grisetti, G.; Stachniss, C.; Burgard, W. Improved techniques for grid mapping with Rao-Blackwellized particle filters. IEEE Trans. Robot. 2007, 23, 34–46. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Y.; Lin, Z. The augmented homogeneous coordinates matrix-based projective mismatch removal for partial-duplicate image search. IEEE Trans. Image Process. 2018, 28, 181–193. [Google Scholar] [CrossRef]
- Hussain, B.; Lau, C.; Yue, C.P. Li-Fi based secure programmable QR code (LiQR). In Proceedings of the JSAP-OSA Joint Symposia, Fukuoka, Japan, 18–21 September 2017; Optical Society of America: Washington, DC, USA, 2017; p. 6p_A409_6. [Google Scholar]
- Thrun, S.; Fox, D.; Burgard, W.; Dellaert, F. Robust Monte Carlo localization for mobile robots. Artif. Intell. 2001, 128, 99–141. [Google Scholar] [CrossRef] [Green Version]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef] [Green Version]
- Fox, D.; Burgard, W.; Thrun, S. The dynamic window approach to collision avoidance. IEEE Robot. Autom. Mag. 1997, 4, 23–33. [Google Scholar] [CrossRef] [Green Version]










| LED Height | 2.7 m |
| LED Diameter | 0.175 m |
| LED Power | 18 w |
| Camera Resolution | 2048 × 1536 |
| Points | Sensor Map (cm) | Building Blueprint (cm) | Floor Map (cm) |
|---|---|---|---|
| ➀ | 65 | 45 | 49 |
| ➁ | 67 | 46 | 50 |
| ➂ | 83 | 57 | 59 |
| ➃ | 88 | 60 | 59 |
| ➄ | 90 | 62 | 63 |
| Average | 78.6 | 54 | 56 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Hussain, B.; Yue, C.P. VLP Landmark and SLAM-Assisted Automatic Map Calibration for Robot Navigation with Semantic Information. Robotics 2022, 11, 84. https://doi.org/10.3390/robotics11040084
Wang Y, Hussain B, Yue CP. VLP Landmark and SLAM-Assisted Automatic Map Calibration for Robot Navigation with Semantic Information. Robotics. 2022; 11(4):84. https://doi.org/10.3390/robotics11040084
Chicago/Turabian StyleWang, Yiru, Babar Hussain, and Chik Patrick Yue. 2022. "VLP Landmark and SLAM-Assisted Automatic Map Calibration for Robot Navigation with Semantic Information" Robotics 11, no. 4: 84. https://doi.org/10.3390/robotics11040084
APA StyleWang, Y., Hussain, B., & Yue, C. P. (2022). VLP Landmark and SLAM-Assisted Automatic Map Calibration for Robot Navigation with Semantic Information. Robotics, 11(4), 84. https://doi.org/10.3390/robotics11040084







