Abstract
Hybrid mobile robots with two motion modes of a wheeled vehicle and truss structure with the ability to climb poles have significant flexibility. The motion planning of this kind of robot on a pole has been widely studied, but few studies have focused on the transition of the robot from the ground to the pole. In this study, a locomotion strategy of wheeled-legged pole-climbing robots (the WL_PCR) is proposed to solve the problem of ground-to-pole transition. By analyzing the force of static and dynamic process in the ground-to-pole transition, the condition of torque provided by the gripper and moving joint is proposed. The mathematical expression of Centre of Mass (CoM) of the wheeled-legged pole-climbing robots is utilized, and the conditions for the robot to smoothly transition from the ground to the vertical pole are proposed. Finally, the feasibility of this method is proved by the simulation and experimentation of a locomotion strategy on wheeled-legged pole-climbing robots.
1. Introduction
Climbing robots have significant potential applications in industry, which can be used to inspect and maintain large structures, such as dams [1], bridges [2], hulls [3], and large industrial boilers [4]. Therefore, great efforts have been made to develop robots that can climb in truss structures [5,6]. On the other hand, due to their high speed and high energy efficiency, wheeled vehicles have existed and developed for hundreds of years. How to integrate the best performance of two completely different mobile systems into a hybrid platform is a hot topic in robot research, which provides more possibilities for improving the robot’s ability to adapt to the environment [7,8,9]. In order to solve this problem, this paper studies the mechanism of wheeled-legged robots and how the motion planning of hybrid motion contributes to the motion control scheme for the hybrid locomotion of wheeled-legged robots.
The hybrid motion system with wheels improves the flexibility and environmental adaptability of the system and provides more gait. The Centaur robot is equipped with wheel steering and articulated legs to adjust its supporting gait in response to unknown disturbances [7]. The design method of hybrid legged/wheeled mobile robots is demonstrated, and the walking, rolling, gliding and skating motions were generated by the novel trajectory optimization formulation [8]. A Transleg was installed with four transformable leg-wheel mechanisms, similar to the compliant spine mechanism, which can realize the turning movement in legged-wheeled mode and the jumping gait in legged mode [9]. By adding the wheel structure to improve the mechanism of the PCR [10], the research on gait control can improve the flexibility and environmental adaptability of the PCR [10].
From the perspective of structural design, pole-climbing robots can be divided into three types: soft climbing robots, legged climbing robots, and wheeled climbing robots. The inspiration of the soft climbing robot is inspired by bionics. The soft climbing robot is based on dielectric-elastomer artificial muscles and electroadhesive feet. The movement is realized by controlling the voltage applied to the actuator and foot to synchronize the body deformation and foot adhesion. This movement mechanism imitates the crawling caused by the movement of caterpillars. Therefore, auxiliary wheel execution cannot be added to this structure [11].
The Climbot is a bio-inspired biped climbing robot composed of five joint modules and two grippers in a series [6]. The cable climbing robot adopts a bilateral-wheeled mechanical structure to perform dynamic obstacle surmounting, which is composed of driving wheels and driven wheels. The task of climbing the cable is completed by the analysis of the track and torque of the wheel. This structure allows the wheels to complete the climbing cable, and limits their movement on the ground, so it does not have the function of the wheel in the normal sense [12].
For a multi-degree-of-freedom connecting rod robot, the trajectory of the robot needs to be optimized. There are two main directions for solving the problem of optimal control: direct and indirect approaches. The direct approach reduces the optimal control problem to a nonlinear programming problem [13] that provides the transition from the optimization problem in the infinite-dimensional space to the optimization problem in the finite-dimensional space; thus, it is more convenient and can be readily solved within a wider convergence region. The indirect approach based on the Pontryagin’s maximum principle (PMP) [14] solves optimal control by formulating it as a boundary value problem where it is necessary to find the initial conditions for a system of differential equations for conjugate variables. The PMP was originally proposed to maximize the terminal speed of a rocket in space orbit, and it was also used to find the optimal control signal of the robot. In robot control optimization, the optimization of PMP was represented by Lagrangian and Hamiltonian mechanics [15,16,17]. The free-floating planar manipulator of a flexible spacecraft simulator was built, and the optimal control of the model was carried out by using the Hamilton principle [15].
The PMP principle and dynamic programming (DP) method can be used to plan the optimal motion mode of robots [16]. The principle of PMP can also plan the vehicle path and realize it in the dynamic process [17]. The PMP principle, combined with Newton mechanics, can find the best combination of static balance and trajectory planning in the process of robot motion [18]. Its optimal solution has high accuracy, but it is very sensitive to the description of additional conditions that must be met for control, and it also guarantees the maximum value of the Hamiltonian method. For problems with complex phase constraints, the Hamiltonian method is usually difficult to set in practice.
However, these works generally focus on the nominal trajectory performance without considering possible uncertainties. In practice, on the right-hand sides of the models, there are objectively some uncertainties of various nature. As a rule, they are not taken into account, but the presence of such uncertainties can lead to the loss of optimality of the obtained control [19].
There are also some methods to consider the influence of uncertainty when designing the reference orbit in advance [20,21,22]. For example, in the process of motion control, the uncertain performance of parameters was used to establish the optimal control scheme [20]. Desensitization optimal control [22] modifies the nominal optimal trajectory to reduce its sensitivity to uncertain parameters. This involves constructing an appropriate sensitivity cost that, when penalized, provides solutions that are relatively insensitive to parametric uncertainties.
Model Predictive Control (MPC) scheme is an optimal model-based control strategy that has been quite popular in the process industry in the last decades, while in recent years, there has been a major shift for its adoption in the area of robotics [23].
Due to the complexity of kinematics models with joint structures, the numerical method is an effective method for solving kinematics models. The sequential quadratic programming (SQP) method is one of the most successful methods to solve the problem of nonlinear constraint minimization [24]. The SQP algorithm is used to solve the inverse kinematics problem of humanoid robots with a redundancy [25].
In this study, we designed and developed a wheeled-legged pole-climbing robot named the WL_PCR. The WL_PCR consists of a two-legged structure and a four-wheeled structure that achieves the locomotion of the climbing pole and ground travel. The main contributions of the study are as follows.
We designed and developed the WL_PCR.
We had developed a movement strategy for the ground-to-pole transition, which has not done with the other pole-climbing robot.
We used the sequential quadratic programming algorithm to do the force analysis of static and dynamic process, and a flip locomotion control scheme to determine its motion conditions.
We explored the possibilities of motion strategies through simulation analysis. We proved the performance of the WL_PCR through experiments.
The rest of this article is organized as follows. In the second section, the design of the WL_PCR is introduced. The third section analyzes the ground-to-pole transition, including the static force analysis, the force analysis of dynamic process and the flip locomotion. The experimental results are presented and discussed in Section 4. Finally, the conclusions are summarized in Section 5.
2. System Design
2.1. The WL_PCR Design
The WL_PCR is an improved pole-climbing robot [10,26] developed in our laboratory. It was developed for the hybrid motion of pole-climbing and ground-walking. The primary characteristic of the WL_PCR is the design of its leg structure and wheel structure, which enables ground travel, climbing poles and the transition from the ground to climbing a pole. The leg structure of the WL_PCR is designed to climb pole-like objects, as presented in Figure 1. The leg structure is composed of four bar linkages (, , , , ), four joints (, , , ), two supports (, ) and two grippers (, ). and are designed to support and reduce the torque requirements of the servomotor when it is climbing, as shown in Figure 2a. All variables used in this paper are defined in Table A1 in Appendix A.
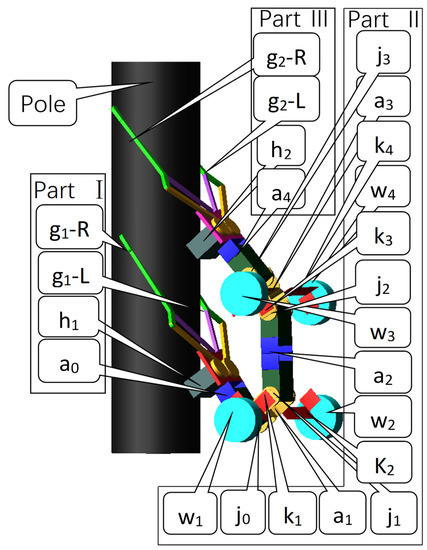
Figure 1.
3D model of the pole-climbing robot.

Figure 2.
(a) Photos of the robot’s climbing posture. (b) Photos of the robot’s ground posture.
The wheel structure of the WL_PCR is designed to travel on the ground, as shown in Figure 2b.
For small mobile robots like the WL_PCR, it is required to simplify the complexity of the mechanism due to the inertial effect and limited structural stress [27]. Therefore, we determined the most simple and feasible mechanism under careful consideration to reduce the complexity of the WL_PCR’s structure to the greatest extent. Only four wheels (, , , ) and four fixed poles (, , , ) are added to the PCR [10] structure. , , and are driven by a DC motor. The model of the motor is JGA25-370, and its parameters are shown in Table 1. , , , and , are driven by a servomotor. The model of the servomotor is DS5160, and its parameters are shown in Table 2.

Table 1.
DC motor parameters.

Table 2.
Servomotor parameters.
2.2. The WL_PCR Design
The dimensions of each component of the WL_PCR are summarized in Table 3. According to the relative motion between structures during the three stages of transition, the structure of the WL_PCR is divided into three parts: Part I, Part II and Part III, as shown in Figure 1. The weight of each part is shown in Table 4. In the process of the ground-to-pole transition, each part moves relatively, and the interior of each part remains relatively static.

Table 3.
Dimensions of robot components.

Table 4.
Mass of robot parts.
In order to simplify the analysis of the WL_PCR, we assume that the mass distribution of the WL_PCR is uniform, and the center of mass of each part is located at its geometric center.
3. Ground-to-Pole Transition Analysis
3.1. Problem Definition
The WL_PCR can perform four gaits: traveling on the ground, climbing on a pole, transiting from the ground to the pole, and transiting from the pole to the ground. The latter two processes are inverse to each other. This paper only studies the transiting from the ground to the pole. Traveling on the ground is executed by driving , , , and the way it is executed is discussed in many papers [28,29]. Climbing on a pole is achieved by two grippers, and , which alternately clamp the pole as described in [26]. Our focus is the special gait of transiting from the ground to the pole.
Transiting from the ground to the pole can be divided into three stages. Stage 1: The WL_PCR uses one gripper , to clamp the pole, rotates to make Part II and Part III lose the support of the ground and keeps itself stable on the pole. Stage 2: continues to be rotated, causing Part II and Part III to uniformly rotate in the direction of the pole. Until the other gripper grasps the pole, stops rotating. Stage 3: The WL_PCR uses to clamp the pole, and turns itself over to prepare for climbing on the pole. During stage 1, the static force of the WL_PCR is analyzed, and the force condition provided by the gripper is obtained to ensure that the robot can be stably lifted from the ground. During stage 2, the dynamic torque of the WL_PCR is analyzed, and the torque condition of the servomotor at (or ) is obtained. During stage 3, the flip locomotion of the WL_PCR is analyzed to ensure that the WL_PCR can complete the first flip without collision.
3.2. Force Analysis of Static State
In stage 1, the WL_PCR uses to grasp the pole, and rotates to make Part II and Part III off the ground at time , as shown in Figure 3a. At , the robot is in a static state and the resultant moment of the WL_PCR system is 0. The moment at , and points can be described as follows:
where is the gravity of the WL_PCR at the center of mass , , , , and are the supporting force, , and are the static coefficients of frictions between the gripper and the pole, , , , and are the frictions between the pole and the robot, , and are the projections of the arm of forces , , and on the x-axis respectively, as shown in Figure 3.
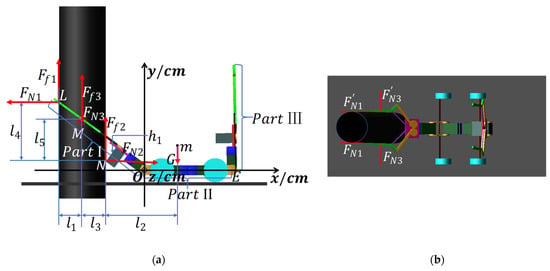
Figure 3.
(a) The Front View of Force analysis of the WL_PCR. (b) The Vertical View of Force analysis of the WL_PCR.
According to Equations (4)–(6), , , and increased with increasing , , and which are related to the clamping force of the gripper. Due to the symmetry of the mechanical structure in Figure 3b, and . Then and by Equations (4)–(6). Set , , and , then can be obtained.
is the reaction of the clamping force generated by the gripper . is provided by the servomotor mounted at the support frame . To ensure the completion of the locomotion in stage 1, the equivalent force produced by the torque of meets the following Condition 1:
According to Equation (8), Figure 4 can be obtained. The range of the ’s rotation angle ω is between . In this range, increases with the increase of ω. Thus, the minimum value of is 20.6 N; the maximum value of is 41.4 N.
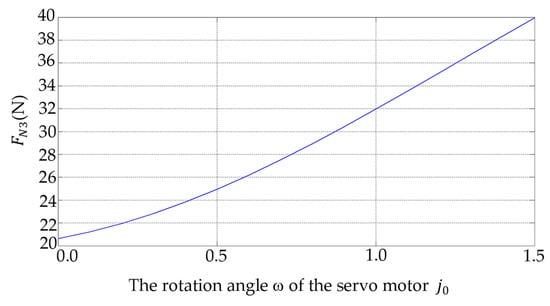
Figure 4.
The relationship between and the rotation angle of the servomotor .
3.3. Force Analysis of Dynamic Process
3.3.1. Analysis of the Trajectory of Mass Center
The WL_PCR performs the locomotion of stage 2 from to . continues to rotate until the other gripper grasps the pole at .
To simplify the analysis, we made assumptions as follows:
Assumption 1: rotates at a constant speed in the second stage.
Assumption 2: The relative positions between Part II and Part III remain unchanged during the rotation process.
The coordinate system of is represented by X-Y-Z as shown in Figure 4. Let the center of mass of Part III be A (), the center of mass of Part II be B , and the center of mass of Part II and Part III be D . can be calculated by Equation (11).
where is the mass of Part II, and m3 is the mass of Part III.
In the X-Y-Z coordinate system, the coordinate values of () are (26.0, 16.0, 0) and is (13.0, 0, 0) at according to the dimensions of each part in Table 3. Then are (17.9, 6.0, 0) at according to Equation (11).
changes with the rotation of the servomotor . Under Assumption 2, its trajectory is a circle, which centers on the origin of the coordinate and has radius r described in Equation (12). During stage 2, the trajectory of point D is shown by the dotted line in Figure 5.
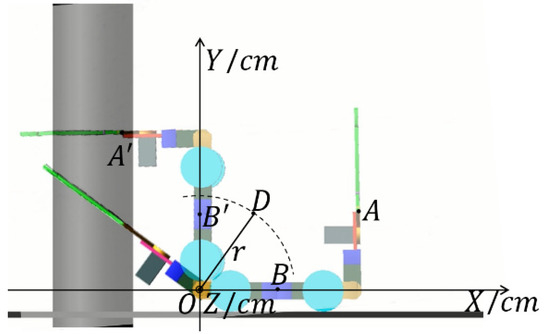
Figure 5.
The trajectory of mass center.
3.3.2. Torque Analysis of the WL_PCR
The servomotor installed at provides the torque for part II and part III to rotate.
where is the gravity arm of . can be obtained by Equations (15) and (16).
where α ( 90°) is the angle between OD and OE and ω is the angle between OE and the X-axis.
decreases with the increase of ω () and then increase according to Equations (15) and (16). When 90°, the minimum value of is 0. The range of can be obtained by Equation (17).
The range of can be obtained by Equation (18). The torque of meets the following Condition 2:
According to Equations (13)–(16), Figure 6 can be obtained. The minimum value of is 0, the maximum value of is 34.8 . The movement process of stage2 is shown in Figure 7.
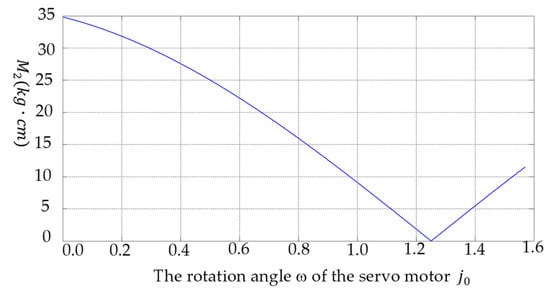
Figure 6.
The relationship between and the rotation angle of the servomotor .
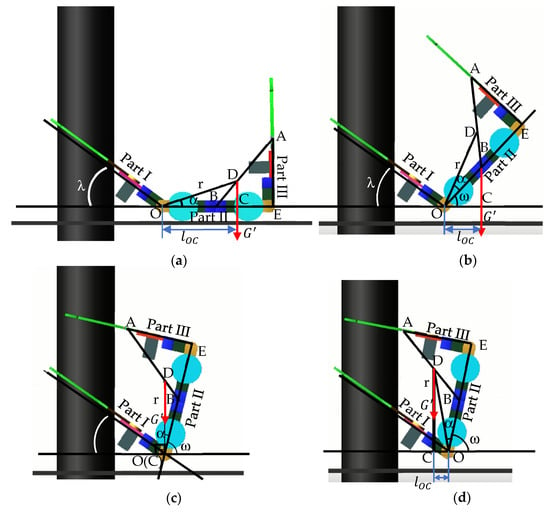
Figure 7.
(a) Start rotating Parts II and III and at . (b) decreases with the rotation of ω and 90° at ; (c) and 90° at ; and (d) increases with the rotation of ω and at . B is the center of mass of Part II; A is the center of mass of Part III; D is the total center of mass of Part II and Part III; O is the rotating shaft of Part II and Part III during the movement of the robot; C is the intersection of the vertical line passing through D to the x-axis and the x-axis; λ ( ) is the angle between the axis of Part I and the horizontal direction; ω is the angle between the axis of Part II of the robot and the horizontal direction; is for the servomotor say, the gravity arms of Part II and Part III.
3.4. Load Analysis of the WL_PCR
The robot is required to have a certain carrying capacity to carry special equipment for special tasks. Since the WL_PCR is a symmetrical structure and two clamping devices are loaded alternately, the optimal position of the loading weight of the WL_PCR should be in the center of the robot structure.
Let the mass of the heavy object be .
During stage 1, with load can be obtained according to Equation (8).
where is the arm of gravity to N.
with load is provided by the servomotor mounted at the support frame .
Therefore, in the case of load, needs to meet the following condition 3:
The position of the total center of mass of Part II, Part III and the load is and its trajectory are still circular with the rotation of . Let the trajectory radius be .
Let the torque for Part II, Part III and the load be .
When the robot is loaded, the torque of meets the following Condition 4:
where is the total gravity of Part II, Part III and the load, is the gravity arm of , and is the angle between OD’ and OE.
The change of is the same as that of , which first decreases and then increases with the rotation of ω. When 90°, the minimum value of is 0. The range of can be obtained by Equation (29).
In this paper, the same type of servomotor is used for driving the grippers and joints, and the torque of the servomotor is 60.0 kg∙cm. When condition 3 is satisfied, the maximum mass of the load is 8.7 kg according to Equations (19)–(22); when condition 4 is satisfied, the maximum mass of the load is 1.9 kg according to Equations (23)–(29). Therefore, the maximum mass of the WL_PCR’s load is 1.9 kg.
3.5. Flip Locomotion
3.5.1. Flip Condition
Stage 3: The flip locomotion of the WL_PCR was conducted to prepare for climbing on the pole. According to the execution of the first stage and second stage, several control schemes were selected to perform the flip locomotion as described in Figure 8 and Figure 9. During the transition from Figure 8a,b, the WL_PCR controls to keep λ approach to the pole until grasps the pole. The specified tasks of Stage 1 described in Section 3.1 are completed. Then, the WL_PCR controls grasp the highest point on the pole within the reachable range. The specified functions of stage 2 described in Section 3.1 are completed, as illustrated in Figure 8c,d. starts to rotate and drives part I and part II to rotate together, during which part I and part II remain relatively stationary, as illustrated in Figure 8e. Figure 8e shows the key stage of the flip action, and its collision-free completion determines the successful execution of the flip locomotion. , , and rotate harmoniously until clamps the pole as shown in Figure 8f. The posture in Figure 8f is the initial posture of the flip locomotion in [28]. Figure 8e,f describe a scheme in which the flip locomotion is successfully performed.
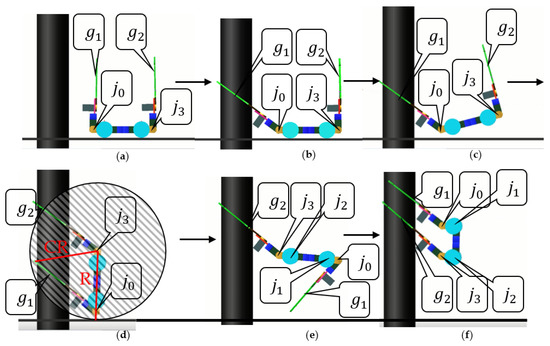
Figure 8.
The successful execution of the flip locomotion. (a) Approach to the pole. (b) The gripper grasps the pole. (c) rotates and the robot leaves the ground. (d) The gripper grasps the pole. (e) rotates and the robot complete the flip action. (f) The robot completes the flip, the gripper grasps the pole again.
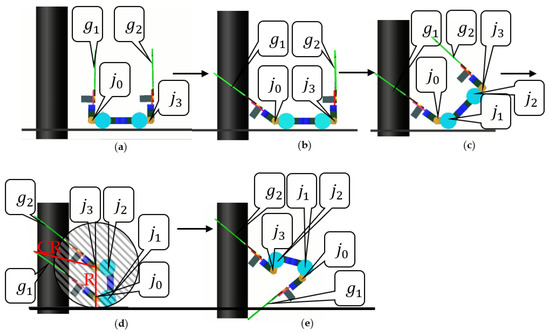
Figure 9.
The failed execution of the flip locomotion. (a) Approach to the pole. (b) The gripper grasps the pole. (c) rotates and the robot leaves the ground. (d) The gripper grasps the pole. (e) rotates but the robot can’t complete the flip action.
λ is controlled to a fixed value during the approach to the climbing pole, and grasps the pole, as shown in Figure 9a,b. Then the WL_PCR controls grasp the lowest point on the pole within the reachable range. The specified functions of stage 2 are conducted from Figure 9c,d. As shown in Figure 9, failed to drive part I and part II to complete the locomotion. In the process of rotation, touches the ground and is hindered by the ground and forced to halt.
The last posture in the second stage is planned as the initial posture of the flip locomotion, as shown in Figure 8 and Figure 9. Condition 5 for completing the flip locomotion is as follows:
Condition 5: Draw a circle CR with as the center and the distance from to the ground as the radius R. If CR contains all the components of part I and part II, the robot completes the flip locomotion smoothly; otherwise, it fails. As shown in Figure 10.
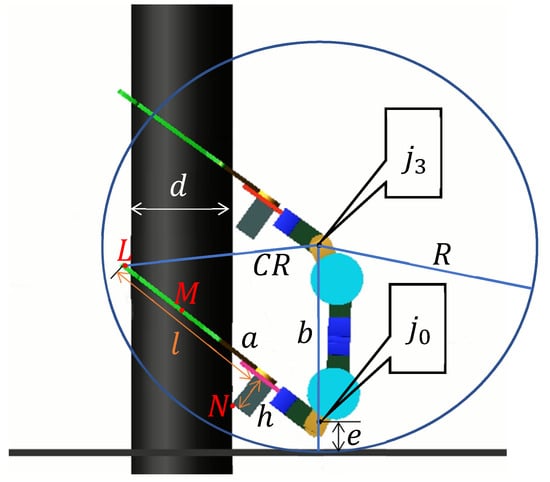
Figure 10.
The last posture in the second stage.
In Figure 8d, CR surrounds all the components of part I and part II, which satisfies condition 3. The flip locomotion is executed smoothly, as shown in Figure 8e,f. In Figure 9d, CR cannot surround all the components of part I and part II, which violates condition 5. The flip action fails to be executed, as shown in Figure 9e.
The quantitative expression of condition 5 can be calculated by Equations (30)–(32).
where b is the length from to , e is the length from to the ground, a is the length from to the tip of the gripper , CR is the distance from to the tip of the gripper , d is the diameter of the pole, h is the height of the support frame , and l is the distance from the tip of the gripper to the support frame , as illustrated in Figure 8.
According to the dimensions in Table 3, CR is the longest distance point from to parts I and II. When Equation (32) is satisfied, condition 5 is satisfied. The structure and size of the WL_PCR are determined, then e is fixed. According to Equation (30), R depends on b. Condition 5 can be expressed as follows:
3.5.2. Control Scheme
The control scheme is realized by adjusting , , and to satisfy Equation (33). The rotation angles , and of the servomotor , and determine b, as shown in Figure 11. The control quantities of between b and , and can be calculated by Equation (34).
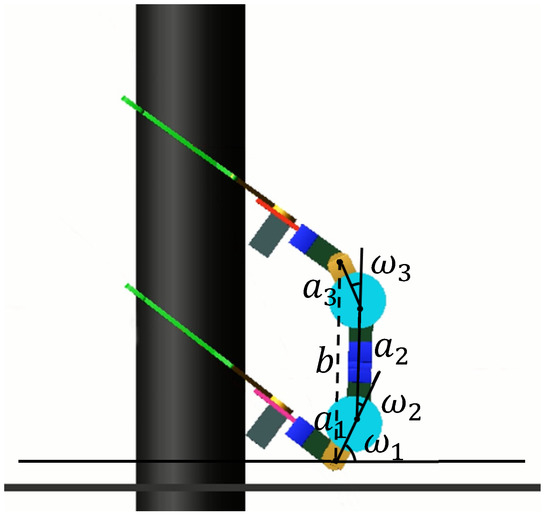
Figure 11.
The control relationship of b with , and .
In order to keep the WL_PCR as balanced as possible when climbing the pole, the control scheme is to adjust , and to keep the robot’s posture as symmetrical as possible. According to Equation (33), we simulate the extreme action of the flip locomotion, as illustrated in Figure 12. When 63°, 26° and 28°, the WL_PCR can complete the flip locomotion according to condition 5. Under the limit condition, .

Figure 12.
The extreme locomotion of the flip locomotion. (a) Approach to the pole. (b) The gripper grasps the pole. (c) rotates and the robot leaves the ground. (d) The gripper grasps the pole. (e) rotates and the robot complete the flip action. (f) The robot completes the flip, the gripper grasps the pole again.
4. Experiments
According to the motion planning and control scheme of the ground-to-pole transition, the feasibility of simulation results is verified by experiments.
In the experiment, the trunk with a diameter of 14 cm was selected as the climbing pole. The tree grows evenly and the diameter of the selected climbing area of the trunk is almost the same. We set three groups of control parameters to control the transition gait of the robot, and the parameters are shown in Table 5.

Table 5.
Three groups of control parameters.
According to the structure size of the WL_PCR (see Table 3) and the selected trunk diameter, 48°. By executing the first set of control parameters, the WL_PCR’s gait execution results are illustrated in Figure 13. The WL_PCR completes the actions of stage 1, stage 2 and stage 3 according to the predetermined plan. The WL_PCR has no touch with the ground and completes the flip action smoothly.

Figure 13.
Climbing experiment with the first group of control parameters. (a) Approach to the pole. (b) The gripper grasps the pole. (c) rotates and the robot leaves the ground. (d) The gripper grasps the pole. (e) rotates and the robot complete the flip action. (f) The robot completes the flip, the gripper grasps the pole again.
By executing the second set of control parameters, the WL_PCR ‘s gait execution results are illustrated in Figure 14. The WL_PCR completes stage 1 and stage 2 according to the predetermined plan. However, in stage 3, the WL_PCR’s body is blocked by the ground and fails to complete the scheduled action.

Figure 14.
Climbing experiment with the second group of control parameters. (a) Approach to the pole. (b) The gripper grasps the pole. (c) rotates and the robot leaves the ground. (d) The gripper grasps the pole. (e) rotates but the robot can’t complete the flip action.
By executing the third set of control parameters, the WL_PCR ‘s gait execution results are illustrated in Figure 15. The robot can complete the actions of stage 1, stage 2 and stage 3 according to the predetermined plan. In the third stage, the tip of the gripper of the robot skims over the ground. Under this limit condition, the WL_PCR completes the third stage of the turning action.

Figure 15.
Climbing experiment with the third group of control parameters. (a) Approach to the pole. (b) The gripper grasps the pole. (c) rotates and the robot leaves the ground. (d) The gripper grasps the pole. (e) rotates and the robot complete the flip action. (f) The robot completes the flip, the gripper grasps the pole again.
5. Conclusions
In this study, we designed and manufactured the WL_PCR based on the original PCR [10,26]. The WL_PCR is composed of the original PCR’s leg structure and the wheel structure. It can be moved on the ground through the wheel structure and on the pole through the leg structure.
The WL_PCR can perform four gaits: traveling on the ground, climbing on a pole, transiting from the ground to the pole and transiting from the pole to the ground. This paper studies the transiting from the ground to the pole. We study the force analysis of WL_PCR and motion planning during the transition process. By analyzing the force of static and dynamic processes in the ground-to-pole transition, the condition of the joint providing force to the WL_PCR is proposed. The motion planning of the WL_PCR is analyzed by the flipping scheme, which provides joints for the WL_PCR to complete the ground-to-pole motion smoothly.
The experimental verification of the transition posture determination conditions proposed in this paper is confirmed. The average time to complete the whole transition is 14 s, the maximum climbing height is 26.0 cm and the minimum climbing height is 24.5 cm in the transition.
The transition process of the robot from the ground to the climbing pole is an important part of the unmanned detection system of the climbing pole robot, which can reduce the workload of the operator in the dangerous environment and avoid harming the environment and people. This research will be helpful in the application of climbing robots for pipeline inspections in dangerous environments, such as inspecting leakages in nuclear pipelines.
Author Contributions
Conceptualization, Y.W. and Q.D.; data curation, Y.W.; formal analysis, Y.W.; investigation, Y.W., T.Z., C.X. and Q.D.; methodology, Y.W.; software, Y.W.; writing—original draft preparation, Y.W.; writing—review and editing, Y.W. and Q.D.; visualization, Y.W.; supervision, Q.D.; project administration, Q.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data supporting reported results can be found by contacting the coordinating author at wangyk19@mails.jlu.edu.cn.
Acknowledgments
This work was supported by Jilin Province Science and Technology Development Plan Project (20190303008SF), Talent Program of Hainan Medical University(XRC180010, HYPY201905, XRC180006), and the Hundred-Talent Program (Hainan 2018).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
All variables used in the manuscript.
Table A1.
All variables used in the manuscript.
| Variable | Variable Name |
|---|---|
| bar linkages | , , , , |
| joints | , , , |
| supports | , |
| grippers | , |
| wheels | , , , |
| fixed poles | , , , |
| Contact point between robot’s Part I front end with pole | L |
| Contact point between robot’s Part I middle end with pole | M |
| Contact point between support with pole | N |
| Static friction coefficient at point L | |
| Static friction coefficient at point N | |
| Static friction coefficient at point M | |
| Acceleration of gravity | g |
| The supporting force of pole on the gripper at L point | , |
| The supporting force of pole on the gripper at M point | , |
| The supporting force of pole on the support at N point | |
| The frictional force between gripper with pole at L point | , |
| The frictional force between gripper with pole at M point | , |
| The frictional force between support with pole at N point | |
| Center of mass of robot | m |
| Gravity of robot | G |
| Arm of force , to point M | |
| Arm of force G to point N | |
| Arm of force to point M | |
| Arm of force , to point N | |
| Arm of force to point M | |
| Quality of Part I | |
| Quality of Part II | |
| Quality of Part III | |
| Quality of load | |
| The pressure exerted by the gripper on the pole | |
| Maximum force provided by gripper | |
| Center of mass of Part II | B |
| Center of mass of Part III | A |
| Center of mass of Part II and Part III | D |
| Center of mass of Part II, Part III and load | |
| The position of | O |
| The position of | E |
| Gravity of Part II and Part III | |
| Arm of force to point O | |
| Distance between point O and D | r |
| Distance between point O and | |
| The angle between and OE | α |
| The angle between O and OE | |
| Angle between OE and horizontal line | ω |
| Angle between Part I and horizontal line | λ |
| Torque of servomotor at when there is no load | |
| Torque of servomotor at when there is a load | |
| Gravity of robot and load | |
| Gravity of Part II, Part III and load | |
| Arm of force to point O | |
| The supporting force of pole on the gripper at M point when there is a load | |
| Distance from the top of the gripper to the support | a |
| Distance from to | b |
| Distance from the top of the gripper to . | CR |
| Diameter of pole | d |
| Distance from to the ground | e |
| Length of support | h |
| Distance from to the ground | R |
| Rotation angle of servomotor at | |
| Rotation angle of servomotor at | |
| Rotation angle of servomotor at | |
| Length of bar linkage | |
| Length of bar linkage | |
| Length of bar linkage |
References
- Yao, M.; Zhou, Y.; Zhang, Z.; He, B.; Sun, R.; Zhang, X. The Measuring Method of the Inner Deformation for High Concrete Faced Rockfill Dam with Pipe-robot Monitoring System. In Proceedings of the 2016 10th International Conference on Sensing Technology, Nanjing, China, 11–13 November 2016. [Google Scholar]
- Hung Manh, L.; Tran Hiep, D.; Nhan Huu, P.; Quang Phuc, H.; Anh Quyen, P. Automated robotic monitoring and inspection of steel structures and bridges. Robotica 2019, 37, 947–967. [Google Scholar]
- Enjikalayil Abdulkader, R.; Veerajagadheswar, P.; Htet Lin, N.; Kumaran, S.; Vishaal, S.R.; Elara, M.R. Sparrow: A Magnetic Climbing Robot for Autonomous Thickness Measurement in Ship Hull Maintenance. J. Mar. Sci. Eng. 2020, 8, 469. [Google Scholar] [CrossRef]
- Lu, X.; Qiu, R.; Liu, G.; Huang, F. The Design of an Inspection Robot for Boiler Tubes Inspection. In Proceedings of the 2009 International Conference on Artificial Intelligence and Computational Intelligence, Shanghai, China, 7–8 November 2009; pp. 313–317. [Google Scholar] [CrossRef]
- Guan, Y.; Jiang, L.; Zhu, H.; Wu, W.; Zhou, X.; Zhang, H.; Zhang, X. Climbot: A Bio-Inspired Modular Biped Climbing Robot-System Development, Climbing Gaits, and Experiments. J. Mech. Robot.-Trans. ASME 2016, 8, 021026. [Google Scholar] [CrossRef]
- Chen, W.; Gu, S.; Zhu, L.; Zhang, H.; Zhu, H.; Guan, Y. Representation of truss-style structures for autonomous climbing of biped pole-climbing robots. Robot. Auton. Syst. 2018, 101, 126–137. [Google Scholar] [CrossRef]
- Kamedula, M.; Tsagarakis, N.G. Reactive Support Polygon Adaptation for the Hybrid Legged-Wheeled CENTAURO Robot. IEEE Robot. Autom. Lett. 2020, 5, 1734–1741. [Google Scholar] [CrossRef]
- Ceilinger, M.; Poranne, R.; Desai, R.; Thomaszewski, B.; Coros, S. Skaterbots: Optimization-based design and motion synthesis for robotic creatures with legs and wheels. ACM Trans. Graph. 2018, 37, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Wei, Z.; Song, G.; Qiao, G.; Zhang, Y.; Sun, H. Design and Implementation of a Leg-Wheel Robot: Transleg. J. Mech. Robot.-Trans. ASME 2017, 9, 051001. [Google Scholar] [CrossRef]
- Du, Q.; Lu, X.; Wang, Y.; Liu, S. The obstacle-surmounting analysis of a pole-climbing robot. Int. J. Adv. Robot. Syst. 2020, 17, 17. [Google Scholar]
- Guo, Y.; Zhang, J.; Ju, Y.; Guo, X. Climbing Reconnaissance Drone Design. In Proceedings of the 2018 3rd International Conference on Insulating Materials, Material Application and Electrical Engineering, IMMAEE 2018, Melbourne, VIC, Australia, 15–16 September 2018. [Google Scholar]
- Xi, F.; Jiang, Q. Dynamic obstacle-surmounting analysis of a bilateral-wheeled cable-climbing robot for cable-stayed bridges. Ind. Robot-Int. J. Robot. Res. Appl. 2019, 46, 431–443. [Google Scholar]
- Asgari, M.; Nikoobin, A. Analysis of Optimal Dynamic Manipulation for Robotic Manipulator Based on Pontryagin’s Minimum Principle. Arab. J. Sci. Eng. 2020, 45, 9159–9169. [Google Scholar] [CrossRef]
- Arutyunov, A.; Karamzin, D. A Survey on Regularity Conditions for State-Constrained Optimal Control Problems and the Non-degenerate Maximum Principle. J. Optim. Theory Appl. 2020, 184, 697–723. [Google Scholar] [CrossRef]
- Sands, T. Optimization Provenance of Whiplash Compensation for Flexible Space Robotics. Aerospace 2019, 6, 93. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, A.; Ren, J.; Huang, X.S.; Ouda, A.N.; Abdo, G.M. Comparative study of dynamic programming and Pontryagin’s minimum principle for autonomous multi-wheeled combat vehicle path planning. Int. J. Heavy Veh. Syst. 2019, 26, 565–577. [Google Scholar] [CrossRef]
- Rathinam, S.; Manyam, S.G.; Zhang, Y.T. Near-Optimal Path Planning for a Car-Like Robot Visiting a Set of Waypoints With Field of View Constraints. IEEE Robot. Autom. Lett. 2019, 4, 391–398. [Google Scholar] [CrossRef]
- Nikoobin, A.; Moradi, M. Analysis of Optimal Balancing for Robotic Manipulators in Repetitive Motions. J. Dyn. Syst. Meas. Control-Trans. ASME 2018, 140, 8. [Google Scholar] [CrossRef]
- Diveev, A.; Shmalko, E.; Serebrenny, V.; Zentay, P. Fundamentals of Synthesized Optimal Control. Mathematics 2020, 9, 21. [Google Scholar] [CrossRef]
- Shah, R.; Sands, T. Comparing Methods of DC Motor Control for UUVs. Appl. Sci. 2021, 11, 4972. [Google Scholar] [CrossRef]
- Hu, H.J.; Zhu, S.Y.; Cui, P.Y. Desensitized optimal trajectory for landing on small bodies with reduced landing error. Aerosp. Sci. Technol. 2016, 48, 178–185. [Google Scholar] [CrossRef]
- Makkapati, V.R.; Dor, M.; Tsiotras, P. Trajectory Desensitization in Optimal Control Problems. In Proceedings of the 2018 IEEE Conference on Decision and Control, Miami Beach, FL, USA, 17–19 December 2018; pp. 2478–2483. [Google Scholar]
- Papadimitriou, A.; Andrikopoulos, G.; Nikolakopoulos, G. On the Optimal Adhesion Control of a Vortex Climbing Robot. J. Intell. Robot. Syst. 2021, 102, 1–15. [Google Scholar] [CrossRef]
- Boggs, P.T.; Tolle, J.W. Sequential quadratic programming for large-scale nonlinear optimization. J. Comput. Appl. Math. 2000, 124, 123–137. [Google Scholar] [CrossRef]
- Xu, J.X.; Wang, W. Two optimization algorithm for solving robotics inverse kinematics with redundancy. In Proceedings of the 2007 IEEE International Conference on Control and Automation, Guangzhou, China, 30 May–1 June 2007; IEEE: New York, NY, USA, 2007; pp. 1142–1149. [Google Scholar]
- Du, Q.; Li, Y.; Liu, S. Design of a micro pole-climbing robot. Int. J. Adv. Robot. Syst. 2019, 16, 1729881419852813. [Google Scholar]
- Xie, D.; Liu, J.; Kang, R.; Zuo, S. Fully 3D-Printed Modular Pipe-Climbing Robot. IEEE Robot. Autom. Lett. 2021, 6, 462–469. [Google Scholar] [CrossRef]
- Grigore, L.S.; Gorgoteanu, D.; Molder, C.; Alexa, O.; Oncioiu, I.; Stefan, A.; Constantin, D.; Lupoae, M.; Balasa, R.-I. A Dynamic Motion Analysis of a Six-Wheel Ground Vehicle for Emergency Intervention Actions. Sensors 2021, 21, 1618. [Google Scholar] [CrossRef] [PubMed]
- Qi, L.; Zhang, T.; Xu, K.; Pan, H.; Zhang, Z.; Yuan, Y. A novel terrain adaptive omni-directional unmanned ground vehicle for underground space emergency: Design, modeling and tests. Sustain. Cities Soc. 2021, 65, 102621. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).