Abstract
In this paper, we present a novel adaptation rule to optimize the exoskeleton assistance in rehabilitation tasks. The proposed method adapts the exoskeleton contribution to user impairment severity without any prior knowledge about the user motor capacity. The proposed controller is a combination of an adaptive feedforward controller and a low gain adaptive PD controller. The PD controller guarantees the stability of the human-exoskeleton system during feedforward torque adaptation by utilizing only the human-exoskeleton joint positions as the sensory feedback for assistive torque optimization. In addition to providing a convergence proof, in order to study the performance of our method we applied it to a simplified 2-DOF model of human-arm and a generic 9-DOF model of lower limb to perform walking. In each simulated task, we implemented the impaired human torque to be insufficient for the task completion. Moreover, the scenarios that violate our convergence proof assumptions are considered. The simulation results show a converging behavior for the proposed controller; the maximum convergence time of 20 s is observed. In addition, a stable control performance that optimally supplements the remaining user motor contribution is observed; the joint angle tracking error in steady condition and its improvement compared to the start of adaptation are as follows: shoulder (); elbow (); hip (); knee (); and ankle (). The presented simulation results verify the robustness of proposed adaptive method in cases that differ from our mathematical assumptions and indicate its potentials to be used in practice.
1. Introduction
Every year, millions of people suffer from motor impairments around the world due to Spinal Cord Injury (SCI), Stroke, and Cerebral Palsy. These individuals suffer from reduced muscle control ability, which demonstrates itself in reduced torque generation and lack of ability to modulate mechanical impedance about the joints. They often suffer from symptomatic muscle control, for instance, due to spasticity [1,2]. A high portion of these individuals could benefit from rehabilitation techniques for restoring their motor capacity [3]. Several methods have been developed to reconnect the lesion site in SCI such as stem cell techniques or by bypassing the lesion using neuroprosthetics [4,5]. Neuroprosthetic technologies [6] such as pharmacological stimulation [7] and functional electrical stimulation [8,9] have been used to recover the affected movements. Intensive activity-therapy based rehabilitation showed evidence for long-term motor recovery in SCI [10,11]. In addition to rehabilitation purposes, locomotor training with exoskeletons have huge potentials for improving individuals’ experience of daily activities, improving their mental condition, and preventing muscle loss in the long term; see [12].
In order to maximize rehabilitation outcome, the rehabilitation and assistance level should maximally engage each individual user in the motor task. Developed work on Assist as Needed (AAN) strategies for exoskeleton control are aimed towards reaching this goal [13,14]. Hence, we can enable the users to continue intensive training while remaining engaged.
These benefits of locomotor training have motivated several research studies to present new rehabilitation controller strategies. An effective control strategy should partially assist the user while allowing voluntary active movements and permit the users to maximally engage their neuromuscular system [13,14]. This strategy promotes neuroplasticity [15] and, in the long term, may result in neural control recovery of the affected limbs [10,11]. From this perspective, the main challenge for controller design is to identify the borders of the affected neuromuscular system capabilities: how much user can contribute? Accordingly, the control structure should be tunable for each individual and account for the alternations of user performance during training, i.e., it should be adaptive.
There are several perspectives in the robotic field that can address this property. For instance, in human–robot interaction, the reference trajectories are adapted to the human’s intended trajectory through interaction force minimization; see [13,16,17,18,19,20,21]. For instance, Jezernik et al. [19] presented three different control strategies for minimizing the interaction force between exoskeleton and user during walking, however, none of them could guarantee the convergence to a cyclic, stable, and reliable walking pattern. The main assumption behind reference trajectory adaptation based on interaction force minimization is that the user can generate cyclic and reliable patterns. This assumption is not valid for individuals with motor impairment and, thus, we cannot fully rely on their exhibited trajectory and trajectory adaptation by means of interaction force minimization as it might results in a failure; this is already addressed in [19] where even changes in the control structure cannot improve the performance of trajectory adaptation.
From another perspective, the AAN controller can be realized by the minimization of exoskeleton actuator torque while tracking error is reduced; it forces the exoskeleton to only compensate for tracking error reduction and prevents any further contribution. There are several works which address this idea to adapt the reference trajectory and to guarantee reliable performance (see [22,23,24,25]). In [22], a classic control (similar to LQR) cost function is suggested to train the robot motions and to extract a control rule, which is the AAN. In the next step, this work is developed (in [23]) for rehabilitation during walking. Moreover, refs. [24,25] present impedance/compliant control approaches to optimize the exoskeleton contribution to the gait. Another perspective is to design a vector field for the assistive torque profile, which applies torque to the joints proportional with velocity (see [26,27]).
Adaptation in muscle level (using myoelectric sensors) is another alternative to having an AAN controller. In this scenario, the controller command is adapted according to real-time biofeedback from EMG muscles to regulate (maximize/minimize) the user contribution to the motion. For instance, Nasiri et al. [28] introduced a general adaptation rule to optimize the robotic assistive torque which minimizes the actuator torque. This adaptation rule is extended for wearable robots in [29,30] and its generality for lower limb exoskeletons is studied in [31]. However, in SCI individuals, the muscles’ EMG signals are not sufficiently reliable for controller adaptation.
Human dynamics can resemble a multi-joint manipulator system and, accordingly, an alternative approach is to employ the adaptive control approach suggested for robotic systems [32,33,34,35]. By using a similar perspective, in this paper, instead of trajectory adaptation, we adapt the assistive torque profile of the exoskeleton while a low gain adaptive PD controller guarantees the stability of close loop during assistive torque adaptation. Although the PD controller tries to control the user joints over a reference trajectory, in our method the PD gains are sufficiently low to allow the user to have voluntary motions around the reference trajectory and most of the task is performed by adaptation of assistive torque which assists as needed, i.e., our controller is a type of AAN.
2. Problem Statement
Consider Figure 1 which describes the control schematics of the Adaptive Assistance Controller (AAC). In this block diagram, the user applied torque () indicates the contribution of the human to the gait/motion. AAC assists the human-exoskeleton system to perform the desired task and the AAC controller command () contains four main blocks: reference trajectory (), required torque (), PD controller (), and the adaptation rule block which optimizes the exoskeleton assistive torque () and updates the PD controller gains. Note that in our mathematics are matrix, vector, and scalar, respectively.
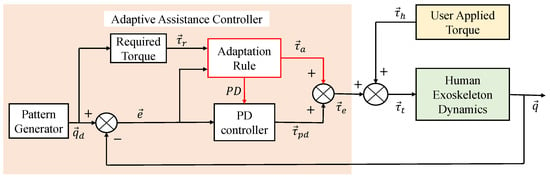
Figure 1.
The overall schematic for the Adaptive Assistance Controller (AAC).
The exoskeleton controller compensates for the user applied torque to perform the desired trajectory (, where n is number of the joints) using the human-exoskeleton joint position () as the only sensory feedback. The required torque block generates the required torque profile () as a function of the desired trajectory; the required torque is a torque profile, which is sufficient to move the human-exoskeleton system over the desired trajectory. Here, we assume that the user is performing a rehabilitation task in which the desired motion is designed by physiotherapist and it is provided; hence, both and are known.
The adaptation block utilizes the tracking error () and the required torque () to optimize the assistive torque profile () and, accordingly, updates the PD controller gains. The adaptive PD controller () is considered in the control loop to ensure the stability of the system during assistive torque () adaptation. The PD controller torque is equal to where are diagonal matrices with positive values which contain time-varying proportional and derivative gains for each joint.
Here we present an adaptation rule to optimize the assistive torque profile for human-exoskeleton system. The optimal assistive torque () profile supplements the human applied torque () to perform the desired task, i.e., [29].
3. Mathematics
Consider the dynamical equations of the human-exoskeleton system as follows:
where represents the dynamical equations of human-exoskeleton system. Similar equation can be used for upper limbs or lower limbs. If the joint trajectories moves on the desired trajectory, then . In this case, the PD controller torque is and we can replace with in dynamical equations and compute the required torque to move over the desired trajectory as: . However, in general, the human-exoskeleton system’s actual trajectory would have errors with respect to the reference trajectory (), where the PD controller can guarantee an upper bound for the tracking error, i.e., . In this case, the dynamical equations can be rewritten as follows:
where is the error torque added to model inconsistency between the required torque and dynamical equations; if . In the rest of the mathematical analysis, without loss of generality and for the sake of simplicity, we focus on one joint of the system and develop the mathematics only for that joint; clearly, all of the presented mathematics can also be presented in the vector and matrix format.
3.1. Optimal Assistive Torque
The optimal assistive torque profile is the torque profile that supplements the human torque profile as . From another perspective, by using Equation (2), the assistive torque profile is optimal if and only if the contribution of PD controller in movement control is minimized. Hence, to optimize the assistive torque profile in an online manner, we consider a cost function based on the minimization of PD controller torque.
The torque applied by the PD controller is a summation of proportional and derivative terms, with the proportional term providing a greater contribution in low dynamic regimes. Hence, in order to minimize the contribution of PD controller and optimize assistive torque profile, the indirect chosen cost function is the squared of tracking error . Minimization of this cost function results in minimization of the PD controller torque, which indirectly optimizes the assistive torque profile.
3.2. Assistive Torque Adaptation
In order to extract the adaptation rule for the assistive torque optimization, we define where is the exoskeleton contribution gain and determines what percentage of required torque should be compensated by exoskeleton. Therefore, if means zero exoskeleton contribution then the task is completely performed by the user, while if means exoskeleton maximum contribution then the task is completely performed by exoskeleton. The values between mean a portion of the required torque is applied by the user and if , then it means the user is resisting against exoskeleton assistance. Finally, for rehabilitation purposes, we can choose and the exoskeleton resists against the user and will require him/her to apply extra torque to perform the task. In this paper, the users with motor impairments, , have been considered.
The optimization of exoskeleton contribution gain () is equivalent to optimizing the assistive torque (). In order to extract the adaptation rule for optimization of , we apply gradient decent over the defined cost function as . By replacing and in Equation (1), we can compute as . Hence, the adaptation rule is computed as follows:
where is the adaptation rate; increasing (decreasing) increases (decreases) the rate of adaption and consequently affects the convergence precision. Hence, the exact determination of is a trade-off between speed and accuracy of converged solution.
The proposed adaptation rule (in Equation (3)) only utilizes the tracking error and required torque to optimize the exoskeleton contribution. It does not require any information about user impairment level and it is completely autonomous. In addition, it is important to note that this adaptation rule is extracted without any strong assumption on the dynamics of the human-exoskeleton system or any assumptions with respect to human applied torque; it is general and applicable for both upper limb and lower limb exoskeletons. Finally, the adaptation rule is extracted without any assumptions on the desired reference trajectory as long as the trajectory is known; hence, it is applicable for periodic and non-periodic tasks.
3.3. Convergence Proof
Assuming that the user can apply a portion of the required torque as . In this case, the optimal contribution gain () is computed using optimal assistive torque equation () as follows.
In order to prove the convergence of the adaption rule (Equation (3)) to the optimal contribution gain (), we compute the tracking error using Equation (2) as follows.
By replacing and we have the following.
Assuming that the PD controller can guarantee small tracking error; we have . Hence, we can write the following adaptation dynamics.
By considering a Lyapunov function as , the time derivative of the Lyapunov function is computed as follows.
The derivative of the Lyapunov function is a negative definite function of . Hence, based on the Lyapunov stability theorem [36], the system is globally asymptotically stable and convergent towards .
3.4. Adaptive PD Controller
An appropriate PD controller for engaging human assistance tasks is a low gain PD controller that does not impose the trajectory to the joints. However, since the user cannot perform the task alone and, in the course of assistive torque adaptation, the PD controller should guarantee closed-loop stability. Therefore, the PD gains in the course of adaptation should be increased and, after the convergence of the assistive torque profile to its optimal value, the gains can be reduced. In order to adapt the PD gains, we utilize again Equation (3). In the process of adaptation, increases and, once the adaptation is converged, diminishes to zero. Accordingly, we set the PD gains to a moving average of plus a minimum value as follows:
where are minimum PD gains, is the window size, and are PD gain amplifiers. In this format, once a new adaptation is triggered, increases and it amplifies the PD gains by magnitude of to ensure the closed-loop stability in the course of adaptation. Moreover, once the adaptation is settled (), the PD gains return to their minimum values .
4. Results
In order to study the performance of the proposed adaptation method to optimize exoskeleton contribution gain and to ensure the stability of closed-loop system, we utilized two different simulation models: (1) a 2-DOF manipulator system which is a representation of simplified human-arm performing task in sagittal plane; (2) a detailed dynamic walking model of the human lower limb with 9-DOF; see Figure 2.
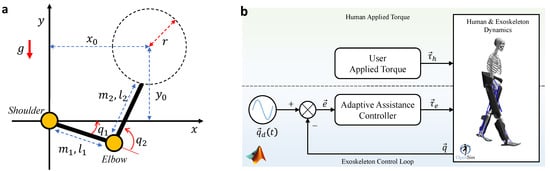
Figure 2.
(a) The simplified model of human-arm performing a cyclic task. (b) The detailed model of human dynamic walking performing normal walking task.
The first model is a nonlinear 2-DOF manipulator with unit masses ( m) and lengths ( kg) and gravity acceleration ( m/s2) simulated in MATLAB SimMechanics. The second model is a generic dynamical model of human lower limb with 9-DOF, human body mass distribution, and human anthropometry. This model is simulated in OpenSim [37] and controlled using MATLAB Simulink; for more details about our simulator, please refer to ([38], Sec IV).
4.1. Human Simplified Arm Simulation
The task is to move the hand on a circle with radius of m and frequency of rad/s where the circle origin position w.r.t. shoulder is at (1 m, 1 m). The required torque for each joint is recorded using precise dynamics of the model. In this simulation, the controller parameters are set as follows: adaptation rate , PD initial gains , PD gain amplifiers , and moving average window size s.
Here, we consider two different scenarios. Scenario 1: Human torque is proportional to the required torque (), which is exactly the same as it is assumed in our mathematics; this case has resemblance to incomplete SCI cases [39]. In Scenario 2, we consider the human torque as a nonlinear function of the required torque, i.e., , in contrast to our convergence assumption. Scenario 2 allows testing the generality and robustness of the adaptation rule in cases that drastically violate our considered assumptions.
In Scenario 1, it is assumed that user contribution to the gait at the start of task is for shoulder joint and for the elbow joint; in this case, the exoskeleton optimal contribution gains are for the shoulder joint and for the elbow joint. In order to check the performance of adaptation and stability of the control loop, the user contribution at s suddenly increases to for the shoulder and for the elbow joints; in this case, the exoskeleton optimal contributions are for the shoulder joint and for the elbow joint.
In Scenario 2, a dead-zone function is considered to create the nonlinear and non-smooth relation between human torque and required torque (). The dead-bands for the shoulder and elbow joints are Nm and Nm, respectively. In this case, the optimal exoskeleton contribution cannot be computed analytically.
Figure 3 illustrates the simulation results for Scenario 1. It can be observed that for s, the exoskeleton contribution gains for both joints converged to their optimal values in 15 s, i.e., at shoulder joint and at the elbow joint. For s, the change in human applied torque re-triggered the adaptation, which converges to its corresponding optimal contribution gains in 5 s; for shoulder joint and for the elbow joint. Figure 3b,c shows the adaptive PD controller gains demonstrating an increase in PD gains at the start of simulation and at s to ensure the stability of control loop. Comparing Figure 3a–c shows that once the adaptation is converged, the PD gains are lessened to their minimum values. Tracking error is depicted in Figure 3d manifesting the stability of the closed-loop human-exoskeleton system thanks to the concurrent adaptation of feedforward contribution gain () and the PD controller gains; joint tracking error (mean ± s.t.d.) and error reduction for shoulder and elbow joints are reported in Table 1. After the adaptation settles to the optimal contribution gains, the tracking error magnitude remains below 2°; minimization of tracking error is our main adaptation objective. Finally, the desired trajectory and the required torque profile for each joint are reported in Figure 3e,f.
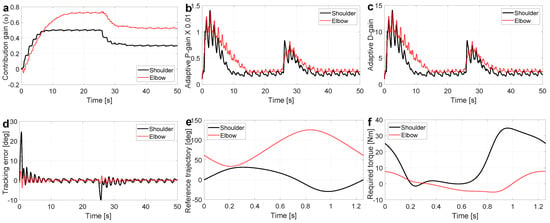
Figure 3.
The simulation results for the case that human-arm torque is proportional with the required torque; Scenario 1. (a) shows that the adaptation rule performance indicates a convergence behavior. (b,c) are the time-varying proportional and derivative gains for the adaptive PD controller. (d) is the tracking error, which indicates the stability of the system in the course of adaptation. (e) is the desired trajectory. (f) is the required torque profile to perform the desired trajectory.

Table 1.
Human-arm: AAC controller performance in terms of tracking error (degree).
Scenario 2 simulation results are presented in Figure 4. Despite violation of the convergence assumption in this scenario, the adaptation rule successfully adapts the exoskeleton contribution gains to their optimal values in 15 s (see the converging gains in Figure 4a). Similar to Scenario 1, while the adaptation rule optimizes the exoskeleton contribution gain, the PD controller gains are increased to maintain the stability of the closed-loop system (see Figure 4b,c). Interestingly, in this challenging scenario, the human-exoskeleton system can guarantee a minimum level of tracking error while the adaptive PD controller gains are diminished to their minimum values (see Figure 4d where tracking error is lower than 5°). Joint tracking error (mean ± s.t.d.) and error reduction for shoulder and elbow joints are reported in Table 1. Finally, the torque profiles for both shoulder and elbow joints are reported in Figure 4e,f, respectively. In these figures, the exoskeleton torque supplements the human torque such that their summation is approximately equal to the required torque, i.e., it proves that the contribution gain is converged to an optimal value.
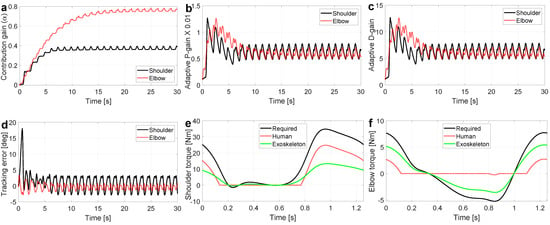
Figure 4.
The simulation results for the case that human-arm torque is a nonlinear function of the required torque; Scenario 2. (a) shows the adaptation rule performance that indicates a convergence behavior. (b,c) are the time-varying proportional and derivative gains for the adaptive PD controller. (d) is the tracking error, which indicates the stability of the system in course of adaptation. (e,f) compare the required torque, human torque, and the optimal assistive torque profiles for both joints.
4.2. Human Dynamic Walking Simulation
The task is to perform a normal dynamic walking with forward velocity of m/s. In order to perform normal walking, the desired ankle, knee, and hip trajectories are set the same as human normal walking (in sagittal plane) (see Figure 5e). In addition, the joint required torques are selected according to the human inverse dynamics torque to perform normal walking; see Figure 5f. The first 60% of each stride percentage is stance phase and the rest 40% is the swing phase. The controller parameters are reported in Table 2. The initial PD gains () are set high, since the controller should ensure both closed-loop stability and a movement stability, i.e., a non diverging movement. A significant miss-match with referent trajectory can results in a falling scenario. In this simulation, we significantly violated our assumptions for the convergence proof, where walking has hybrid dynamics with several zero dynamics [40]; human dynamics during walking cannot be expressed by Equation (1).
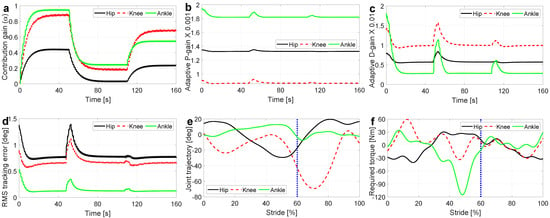
Figure 5.
The simulation results for human dynamic walking. (a) is the instantaneous exoskeleton contribution gains which indicates the performance of adaptation rule. (b,c) describe variations of PD controller gains in the course of adaptation. (d) shows tracking error and illustrates the performance of the AAC controller to guarantee the closed-loop stability. (e,f) report the reference joint trajectories and required torques to perform a dynamic walking task; is the stance phase and is the swing phase.

Table 2.
AAC controller parameters for dynamic walking simulation.
In order to investigate the adaptation performance of AAC in the face of variations in user applied torque, for each joint, the user contribution gain () is changed twice during the normal walking task; the variation times are s and s. The human contribution gains () are selected based on [39] to simulate an individual with motor capacity reduction with some similarities to an incomplete Spinal Cord Injury (i-SCI); the more distal the joint, the less torque the person can apply with less contribution gain. For each time interval and joint, the human contribution gains () and the resultant exoskeleton optimal contribution gains () are reported in Table 3.

Table 3.
Human contribution gain () and exoskeleton optimal contribution gain ().
The simulation results for lower limb assisted walking are reported in Figure 5. As it can be observed in Figure 5a, for each time interval the exoskeleton contribution gains for each joint are converged to their optimal values reported in Table 3; the maximum convergence time is 20 s at the first interval . In addition, Figure 5b,c illustrates the adaptation of PD gains in the course of walking. Based on these figures, each variation in the human contribution gains triggers a new adaptation process for the exoskeleton contribution gain and, consequently, amplifies the PD controller gains. The RMS tracking error is reported in Figure 5d, which indicates the performance of AAC to track the desired trajectory; joint tracking error (mean ± s.t.d.) and error reduction for hip, knee, and ankle joints are reported in Table 4. Regardless of significant changes in the user applied torque ( and ), ACC can guarantee stable dynamic walking. In dynamic walking, stability contains mechanical and state stability. Mechanical stability means that the model should not fall during walking and state stability indicates the stability of the joint positions and velocities. Accordingly, this complex simulation on 9-DOF model of human walking demonstrates the potential of the proposed controller to be used in lower limb exoskeletons.

Table 4.
Walking task: AAC controller performance in terms of tracking error (degree).
5. Discussion and Conclusions
In this paper, we present a new adaptive control schematic in order to optimize the assistance level of an exoskeleton. The proposed controller is a combination of an adaptive feedforward and adaptive feedback controllers. The adaptive feedforward controller determines the assistance of the exoskeleton to perform the desired motion, while the adaptive feedback controller guarantees the stability of the closed-loop system in course of adaptation. In order to allow user voluntary motions relative to the reference trajectory, the initial PD gains are very low; however, once adaptation of the feedforward gain is triggered, the PD gains are also amplified deceptively to ensure the stability. The adaptation rule optimizes the feedforward controller by adapting a proportional gain, which is called exoskeleton contribution gain. This value determines the assistance level of the exoskeleton.
The increase in PD gain in our controller during the adaptation of feedforward torque is also in line with previous human motor control experiments indicating an increase in mechanical impedance in unstable tasks [41] and the benefits of co-contractions, which are equivalent to high gain PD control, in accelerating the internal model formation [42]. The human central nervous system modulates muscle activation to generate the required torque and variable mechanical impedance at our joints to move and stabilize our motion [43]. Despite existing efforts in identifying mechanical joint impedance [44,45,46,47], multi-joint mechanical impedance have not yet fully uncovered during motion. In order to improve our simulations, the variable impedance can be also implemented in the future.
The adaption rule can optimize the exoskeleton contribution gain relative to the severity of human impairment and compensates for the required torque to perform the desired task. All of these are performed without any knowledge about user impairment level or motor capacity; the adaptations are fully autonomous and the required torque and the reference trajectory are known. Here, we apply the method on a simplified 2-DOF model of human-arm and a generic 9-DOF model of lower limb by considering three different types of human impairments. (1) The impairment in the upper limb: A user who can provide the torque profile proportional to but lower than the required torque; (2) impairment in the upper limb: a user whose torque is not proportional to the required torque; (3) impairment in lower limb: a user with reduced torque generation capacity and control gains in more distal limbs. In all of the simulation scenarios, the adaptation method successfully converges to the optimal values and guarantees the mechanical and closed-loop stability of the systems. These simulation results investigate the applicability of the proposed method for rehabilitation purposes for both upper or lower limb exoskeletons.
As future work, we will consider developing this method for an upper/lower limb exoskeleton and test it first in a realistic closed-loop dynamical simulation, such as in [48]. Upon verification in realistic simulations, we will implement the proposed method in practice where we will validate the applicability of the method in real world. One of the most interesting usage of the proposed method is the presentation of a metric to measure the human and exoskeleton contribution relative to the gait/motion. The exoskeleton contribution gain can be used as a metric to measure the user impairment level at the start of rehabilitation process. It can also measure the improvement/performance of the user in the course of training; the lower the exoskeleton contribution gain, the higher the user contribution/performance.
Author Contributions
Conceptualization, R.N. and A.A.; methodology, R.N. and A.A.; writing, R.N. and A.A.; simulation, R.N. and M.S.; data analysis, R.N. and M.S.; visualization, R.N. and M.S.; review and editing, R.N. and A.A. and M.S.; funding acquisition A.A.; project administration A.A.; supervision, A.A. All authors have read and agreed to the published version of the manuscript.
Funding
New Frontiers in Research Fund—Exploration, grant number 2018-01698.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lance, J.W. The control of muscle tone, reflexes, and movement: Robert Wartenbeg Lecture. Neurology 1980, 30, 1303. [Google Scholar] [CrossRef] [PubMed]
- Cha, Y.; Arami, A. Quantitative modeling of spasticity for clinical assessment, treatment and rehabilitation. Sensors 2020, 20, 5046. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, I.; Meiner, Z. Robotic-assisted gait training in neurological patients: Who may benefit? Ann. Biomed. Eng. 2015, 43, 1260–1269. [Google Scholar] [CrossRef]
- Bakshi, A.; Hunter, C.; Swanger, S.; Lepore, A.; Fischer, I. Minimally invasive delivery of stem cells for spinal cord injury: Advantages of the lumbar puncture technique. J. Neurosurg. Spine 2004, 1, 330–337. [Google Scholar] [CrossRef]
- Moritz, C.T.; Ambrosio, F. Regenerative Rehabilitation: Combining Stem Cell Therapies and Activity Dependent Stimulation. Pediatr. Phys. Ther. Off. Publ. Sect. Pediatr. Am. Phys. Ther. Assoc. 2017, 29, S10. [Google Scholar] [CrossRef]
- Collinger, J.L.; Foldes, S.; Bruns, T.M.; Wodlinger, B.; Gaunt, R.; Weber, D.J. Neuroprosthetic technology for individuals with spinal cord injury. J. Spinal Cord Med. 2013, 36, 258–272. [Google Scholar] [CrossRef] [Green Version]
- Baptiste, D.C.; Fehlings, M.G. Pharmacological approaches to repair the injured spinal cord. J. Neurotrauma 2006, 23, 318–334. [Google Scholar] [CrossRef]
- Lynch, C.L.; Popovic, M.R. Functional electrical stimulation. IEEE Control Syst. Mag. 2008, 28, 40–50. [Google Scholar]
- Makowski, N.S.; Lombardo, L.M.; Foglyano, K.M.; Kobetic, R.; Pinault, G.; Selkirk, S.M.; Triolo, R.J. Walking after incomplete spinal cord injury with an implanted neuromuscular electrical stimulation system and a hinged knee replacement: A single-subject study. Spinal Cord Ser. Cases 2020, 6, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Jones, M.L.; Evans, N.; Tefertiller, C.; Backus, D.; Sweatman, M.; Tansey, K.; Morrison, S. Activity-based therapy for recovery of walking in individuals with chronic spinal cord injury: Results from a randomized clinical trial. Arch. Phys. Med. Rehabil. 2014, 95, 2239–2246. [Google Scholar] [CrossRef]
- Harvey, L.A. Physiotherapy rehabilitation for people with spinal cord injuries. J. Physiother. 2016, 62, 4–11. [Google Scholar] [CrossRef] [Green Version]
- Morawietz, C.; Moffat, F. Effects of locomotor training after incomplete spinal cord injury: A systematic review. Arch. Phys. Med. Rehabil. 2013, 94, 2297–2308. [Google Scholar] [CrossRef]
- Zhang, J.F.; Dong, Y.M.; Yang, C.J.; Geng, Y.; Chen, Y.; Yang, Y. 5-Link model based gait trajectory adaption control strategies of the gait rehabilitation exoskeleton for post-stroke patients. Mechatronics 2010, 20, 368–376. [Google Scholar] [CrossRef]
- Duschau-Wicke, A.; Von Zitzewitz, J.; Caprez, A.; Lunenburger, L.; Riener, R. Path control: A method for patient-cooperative robot-aided gait rehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 2009, 18, 38–48. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ding, Y.; Kastin, A.J.; Pan, W. Neural plasticity after spinal cord injury. Curr. Pharm. Des. 2005, 11, 1441–1450. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Y.; Ge, S.S. Human–robot collaboration based on motion intention estimation. IEEE/ASME Trans. Mechatron. 2013, 19, 1007–1014. [Google Scholar] [CrossRef]
- Khoramshahi, M.; Billard, A. A dynamical system approach to task-adaptation in physical human–robot interaction. Auton. Robot. 2019, 43, 927–946. [Google Scholar] [CrossRef] [Green Version]
- Wu, A.R.; Dzeladini, F.; Brug, T.J.; Tamburella, F.; Tagliamonte, N.L.; Van Asseldonk, E.H.; Van Der Kooij, H.; Ijspeert, A.J. An adaptive neuromuscular controller for assistive lower-limb exoskeletons: A preliminary study on subjects with spinal cord injury. Front. Neurorobot. 2017, 11, 30. [Google Scholar] [CrossRef]
- Jezernik, S.; Colombo, G.; Morari, M. Automatic gait-pattern adaptation algorithms for rehabilitation with a 4-DOF robotic orthosis. IEEE Trans. Robot. Autom. 2004, 20, 574–582. [Google Scholar] [CrossRef]
- Riener, R.; Lunenburger, L.; Jezernik, S.; Anderschitz, M.; Colombo, G.; Dietz, V. Patient-cooperative strategies for robot-aided treadmill training: First experimental results. IEEE Trans. Neural Syst. Rehabil. Eng. 2005, 13, 380–394. [Google Scholar] [CrossRef]
- Vallery, H.; Van Asseldonk, E.H.; Buss, M.; Van Der Kooij, H. Reference trajectory generation for rehabilitation robots: Complementary limb motion estimation. IEEE Trans. Neural Syst. Rehabil. Eng. 2008, 17, 23–30. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Emken, J.L.; Bobrow, J.E.; Reinkensmeyer, D.J. Robotic movement training as an optimization problem: Designing a controller that assists only as needed. In Proceedings of the 9th International Conference on Rehabilitation Robotics, ICORR 2005, Chicago, IL, USA, 28 June–1 July 2005; pp. 307–312. [Google Scholar]
- Emken, J.L.; Benitez, R.; Reinkensmeyer, D.J. Human-robot cooperative movement training: Learning a novel sensory motor transformation during walking with robotic assistance-as-needed. J. Neuroeng. Rehabil. 2007, 4, 8. [Google Scholar] [CrossRef] [Green Version]
- Wolbrecht, E.T.; Chan, V.; Reinkensmeyer, D.J.; Bobrow, J.E. Optimizing compliant, model-based robotic assistance to promote neurorehabilitation. IEEE Trans. Neural Syst. Rehabil. Eng. 2008, 16, 286–297. [Google Scholar] [CrossRef]
- Rosati, G.; Bobrow, J.E.; Reinkensmeyer, D.J. Compliant control of post-stroke rehabilitation robots: Using movement-specific models to improve controller performance. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Boston, MA, USA, 31 October–6 November 2008; Volume 48630, pp. 167–174. [Google Scholar]
- Martinez, A.; Lawson, B.; Durrough, C.; Goldfarb, M. A velocity-field-based controller for assisting leg movement during walking with a bilateral hip and knee lower limb exoskeleton. IEEE Trans. Robot. 2018, 35, 307–316. [Google Scholar] [CrossRef]
- Asl, H.J.; Narikiyo, T.; Kawanishi, M. An assist-as-needed velocity field control scheme for rehabilitation robots. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 3322–3327. [Google Scholar]
- Nasiri, R.; Khoramshahi, M.; Shushtari, M.; Ahmadabadi, M.N. Adaptation in variable parallel compliance: Towards energy efficiency in cyclic tasks. IEEE/ASME Trans. Mechatron. 2016, 22, 1059–1070. [Google Scholar] [CrossRef]
- Nasiri, R.; Rayati, M.; Ahmadabadi, M.N. Feedback from mono-articular muscles is sufficient for exoskeleton torque adaptation. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 2097–2106. [Google Scholar] [CrossRef]
- Nasiri, R.; Aftabi, H.; Rayati, M.; Ahmadabadi, M.N. Human-in-the-Loop Weight Compensation and Mass Estimation in Upper Limb Wearable Robots Towards Muscles Effort Minimization. bioRxiv 2020. [Google Scholar] [CrossRef]
- Aftabi, H.; Nasiri, R.; Ahmadabadi, M.N. Simulation-based biomechanical assessment of unpowered exoskeletons for running. Sci. Rep. 2021, 11, 11846. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Li, W. On the adaptive control of robot manipulators. Int. J. Robot. Res. 1987, 6, 49–59. [Google Scholar] [CrossRef]
- Aoi, S.; Manoonpong, P.; Ambe, Y.; Matsuno, F.; Wörgötter, F. Adaptive control strategies for interlimb coordination in legged robots: A review. Front. Neurorobot. 2017, 11, 39. [Google Scholar] [CrossRef]
- Zhang, D.; Wei, B. A review on model reference adaptive control of robotic manipulators. Annu. Rev. Control 2017, 43, 188–198. [Google Scholar] [CrossRef]
- Azar, A.T.; Serrano, F.E. Stabilization of port Hamiltonian chaotic systems with hidden attractors by adaptive terminal sliding mode control. Entropy 2020, 22, 122. [Google Scholar] [CrossRef] [Green Version]
- Khalil, H.K. Nonlinear Systems; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Delp, S.L.; Anderson, F.C.; Arnold, A.S.; Loan, P.; Habib, A.; John, C.T.; Guendelman, E.; Thelen, D.G. OpenSim: Open-Source Software to Create and Analyze Dynamic Simulations of Movement. IEEE Trans. Biomed. Eng. 2007, 54, 1940–1950. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shushtari, M.; Nasiri, R.; Arami, A. Online Reference Trajectory Adaptation: A Personalized Control Strategy for Lower Limb Exoskeletons. bioRxiv 2021. [Google Scholar] [CrossRef]
- Jayaraman, A.; Gregory, C.; Bowden, M.; Stevens, J.; Shah, P.; Behrman, A.; Vandenborne, K. Lower extremity skeletal muscle function in persons with incomplete spinal cord injury. Spinal Cord 2006, 44, 680–687. [Google Scholar] [CrossRef] [Green Version]
- Westervelt, E.R.; Grizzle, J.W.; Koditschek, D.E. Hybrid zero dynamics of planar biped walkers. IEEE Trans. Autom. Control 2003, 48, 42–56. [Google Scholar] [CrossRef] [Green Version]
- Burdet, E.; Osu, R.; Franklin, D.W.; Milner, T.E.; Kawato, M. The central nervous system stabilizes unstable dynamics by learning optimal impedance. Nature 2001, 414, 446–449. [Google Scholar] [CrossRef] [PubMed]
- Heald, J.B.; Franklin, D.W.; Wolpert, D.M. Increasing muscle co-contraction speeds up internal model acquisition during dynamic motor learning. Sci. Rep. 2018, 8, 16355. [Google Scholar] [CrossRef] [Green Version]
- Hogan, N. Mechanical impedance of single-and multi-articular systems. In Multiple Muscle Systems; Springer: Berlin/Heidelberg, Germany, 1990; pp. 149–164. [Google Scholar]
- Lee, H.; Hogan, N. Time-varying ankle mechanical impedance during human locomotion. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 23, 755–764. [Google Scholar] [CrossRef]
- Huang, H.Y.; Arami, A.; Farkhatdinov, I.; Formica, D.; Burdet, E. The influence of posture, applied force and perturbation direction on hip joint viscoelasticity. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 1138–1145. [Google Scholar] [CrossRef]
- Arami, A.; van Asseldonk, E.; van der Kooij, H.; Burdet, E. A Clustering-based Approach to Identify Joint Impedance during Walking. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 1808–1816. [Google Scholar] [CrossRef] [PubMed]
- Perreault, E.J.; Kirsch, R.F.; Crago, P.E. Multijoint dynamics and postural stability of the human arm. Exp. Brain Res. 2004, 157, 507–517. [Google Scholar] [CrossRef] [PubMed]
- Weng, J.; Hashemi, E.; Arami, A. Natural Walking With Musculoskeletal Models Using Deep Reinforcement Learning. IEEE Robot. Autom. Lett. 2021, 6, 4156–4162. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).