Protein Solvent-Accessibility Prediction by a Stacked Deep Bidirectional Recurrent Neural Network
Abstract
1. Introduction
2. Results
2.1. Measurement Evaluation
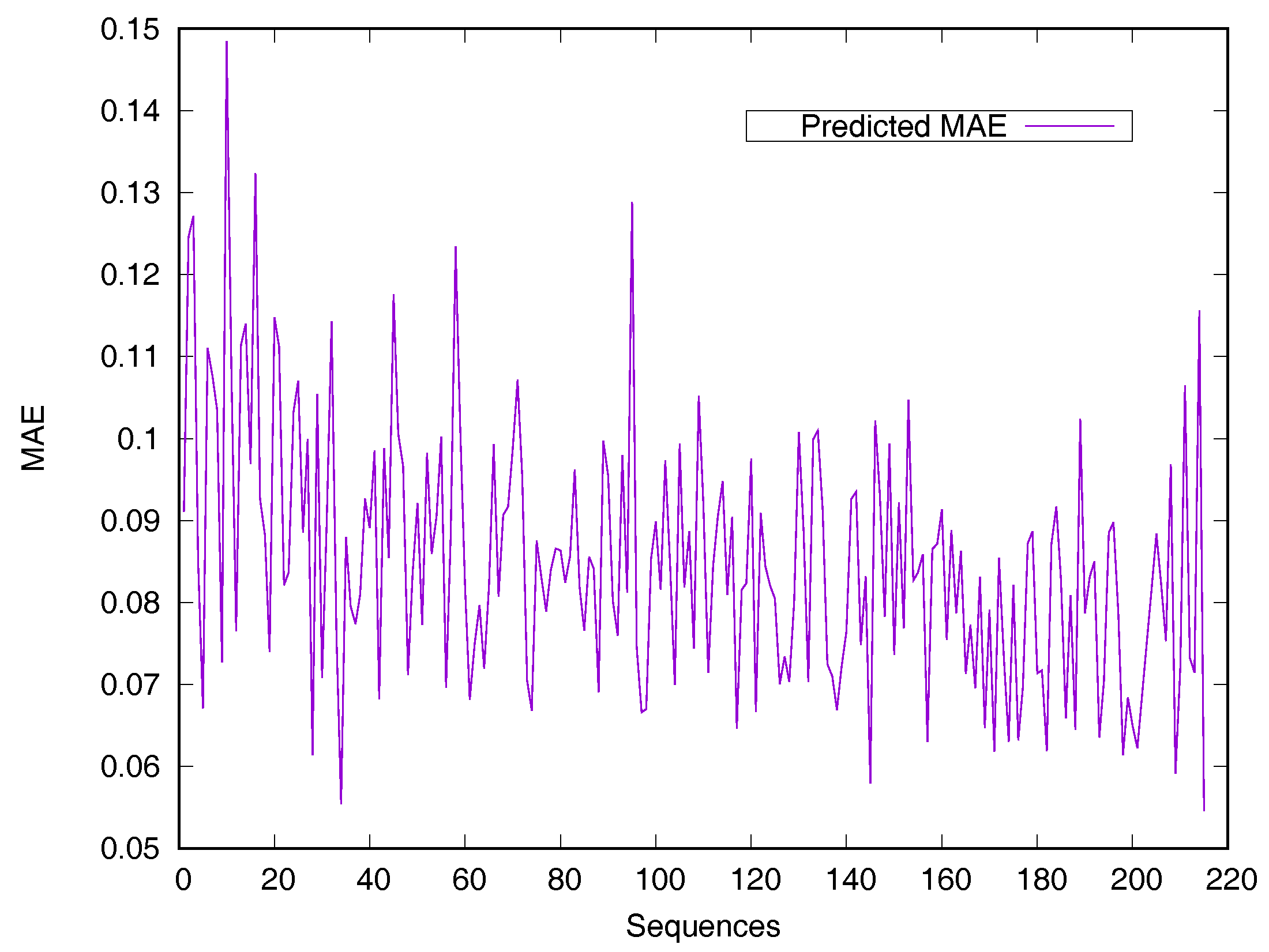
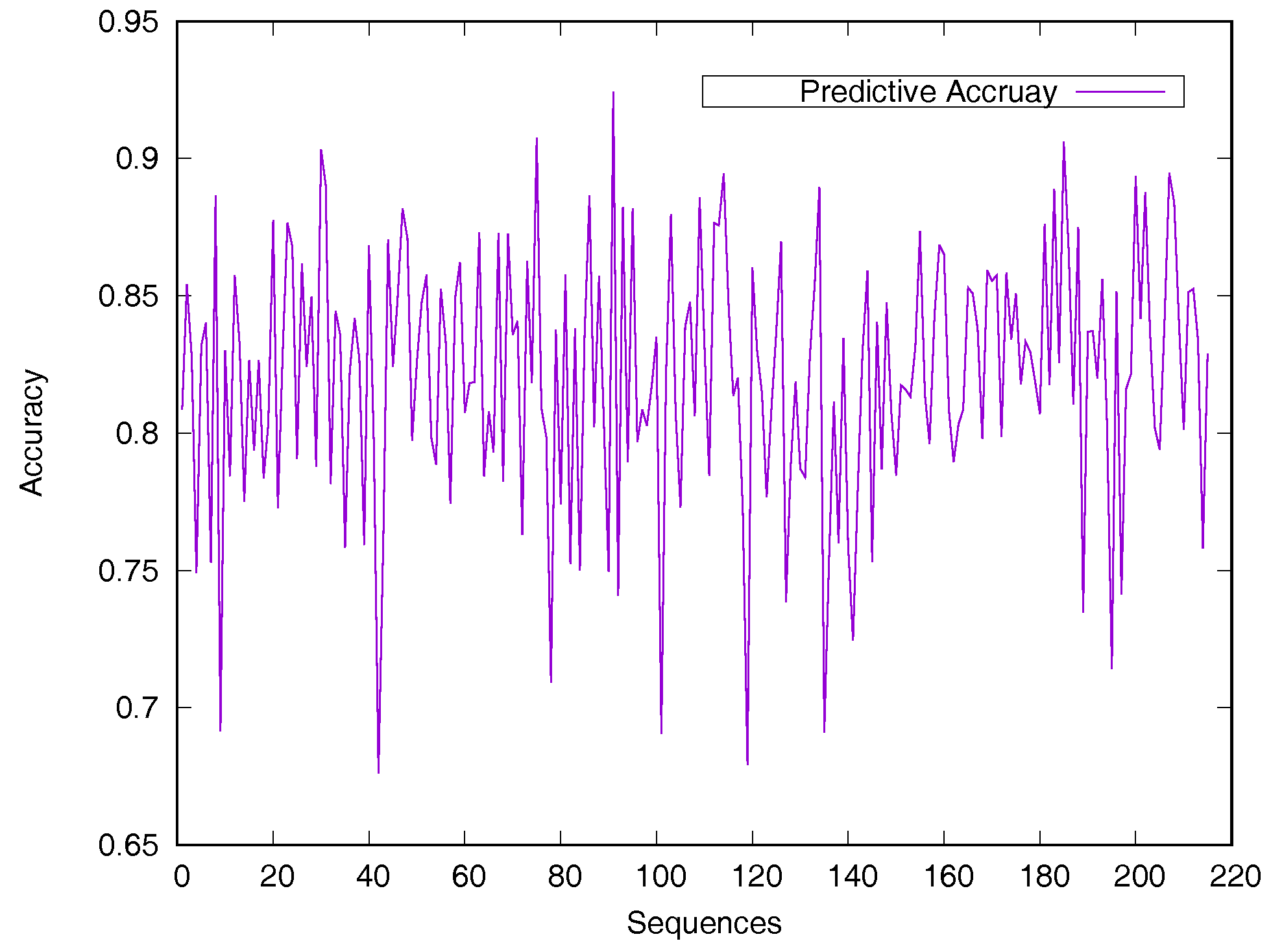
2.2. Performance on Relative Solvent-Accessible Area Prediction
2.3. Comparison of Different Classification Predictors
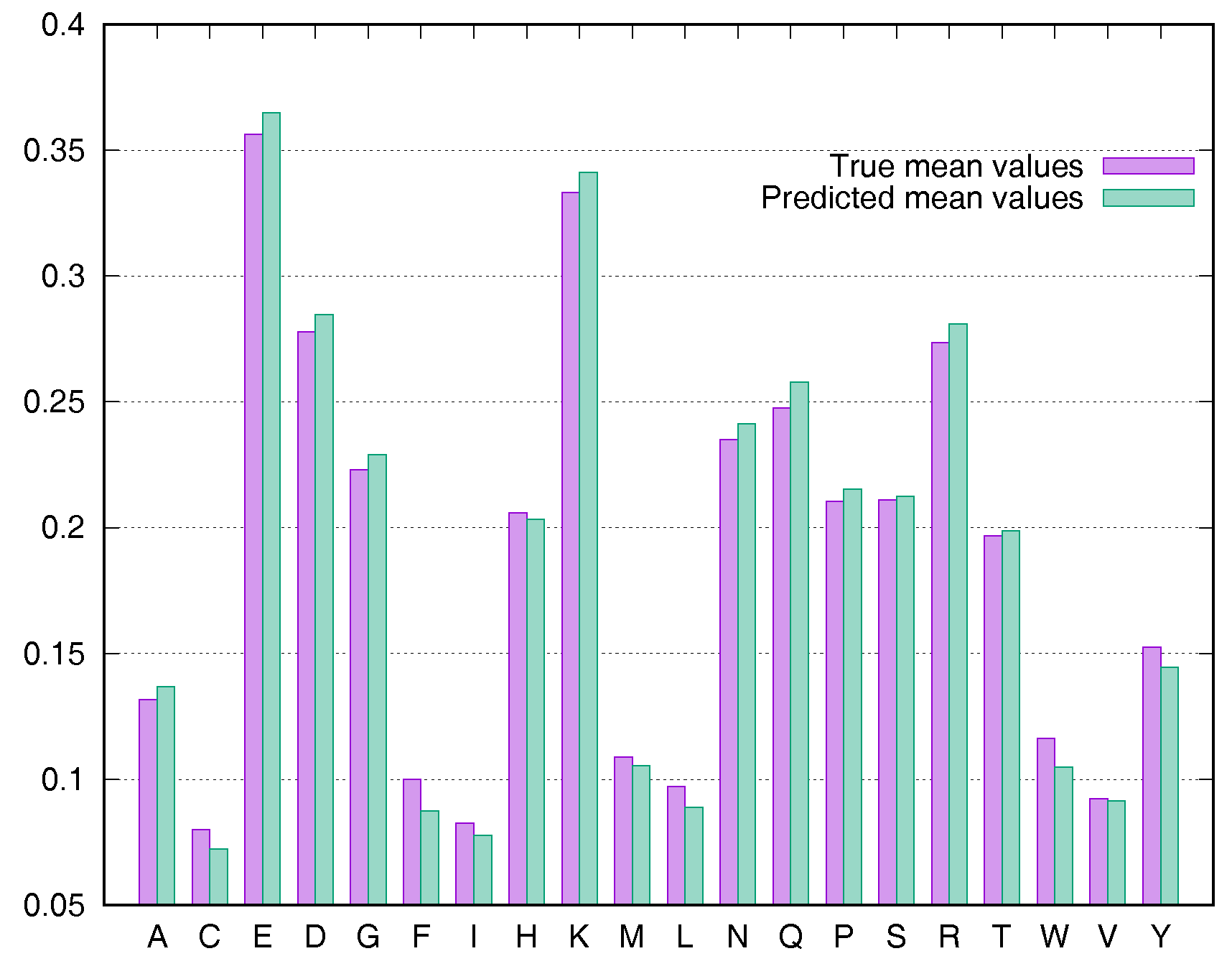
2.4. Residue-Specific Variation in Predictive Error
3. Discussion
4. Materials and Methods
4.1. Datasets and Input Features
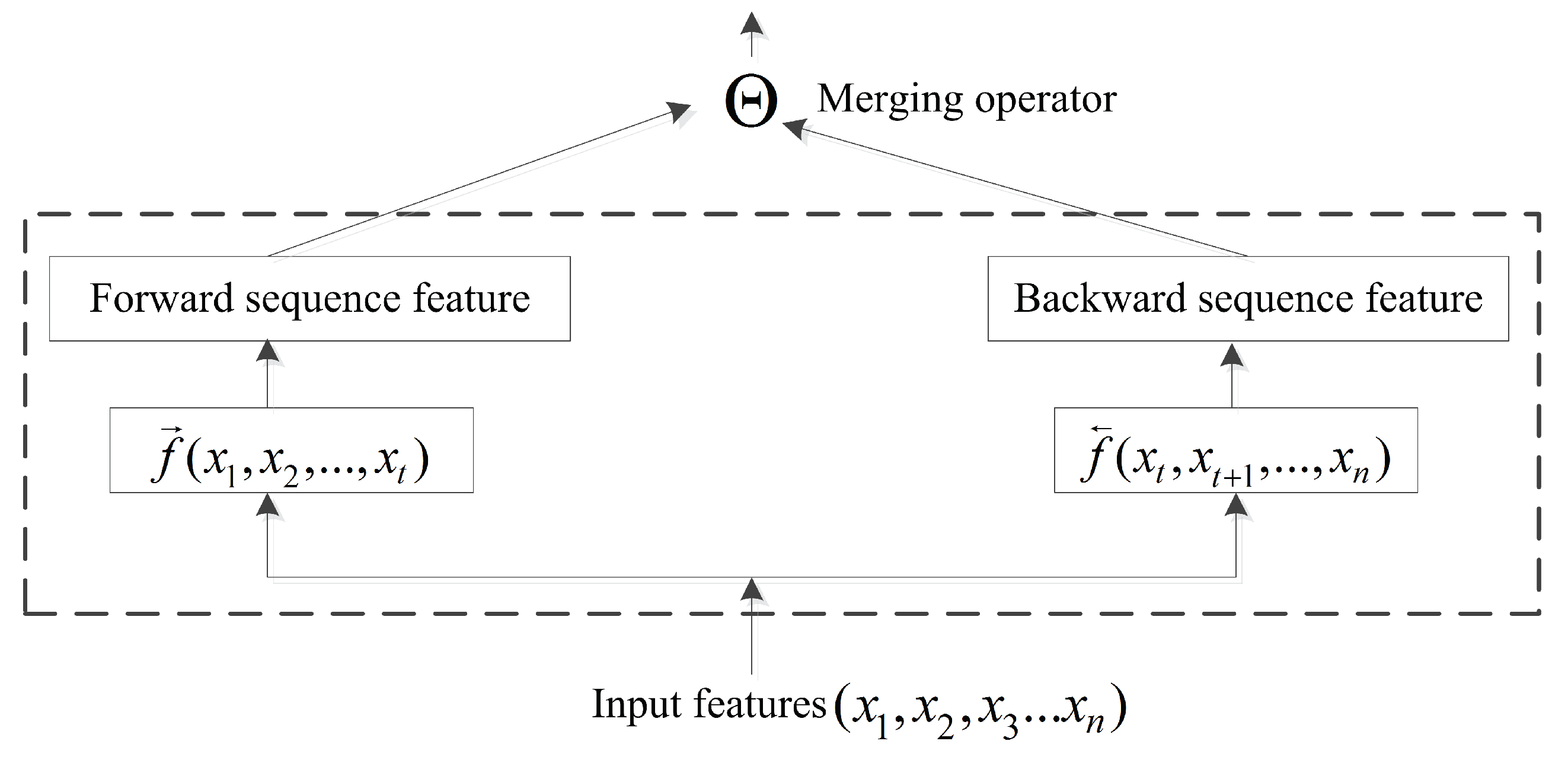
4.2. BRNN and Merging Operator
4.3. Model
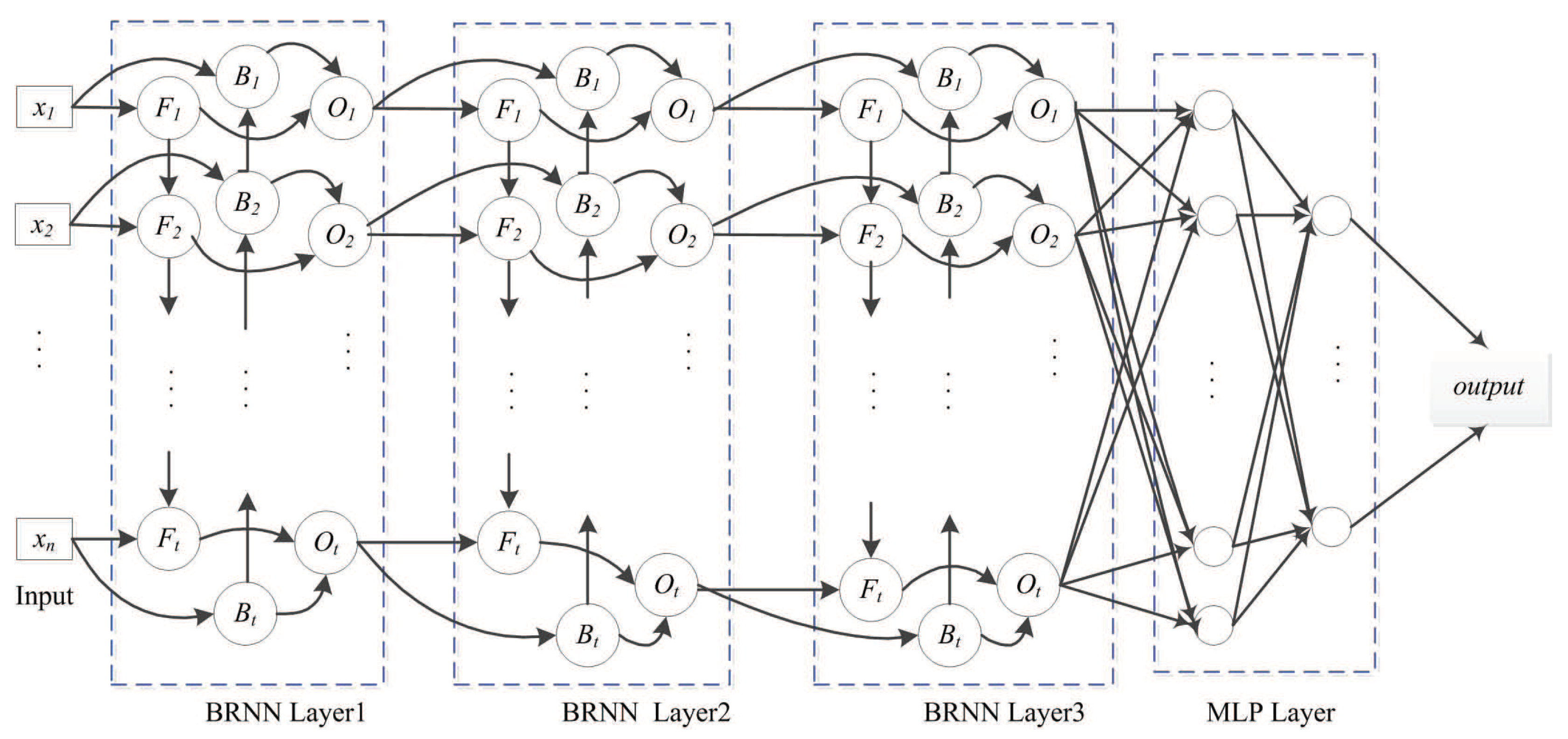
4.3.1. SDBRNN
4.3.2. Model Hyperparameters
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| RSA | Residue Solvent Accessibility |
| rASA | relative accessible solvent area |
| BLSTM | bidirectional long-short memory |
| SDBRNN | stacked deep bidirectional recurrent neural network |
| RNN | recurrent neural network |
| BRNN | bidirectional recurrent neural network |
| LSTM | long short-term memory |
| MLP | multi-layer perceptron |
| MAE | mean absolute error |
| PCC | Pearson’s correlation coefficient |
| MCC | Matthews’ correlation coefficient |
| ACC | Accuracy |
References
- Lee, B.; Richards, F.M. The interpretation of protein structures: Estimation of static accessibility. J. Mol. Biol. 1971, 55, 379–400. [Google Scholar] [CrossRef]
- Rost, B.; Sander, C. Conservation and prediction of solvent accessibility in protein families. Proteins Struct. Funct. Bioinform. 1994, 20, 216–226. [Google Scholar] [CrossRef] [PubMed]
- Wodak, S.J.; Janin, J. Location of structural domains in protein. Biochemistry 1981, 20, 6544–6552. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Zhang, C.; Liang, S.; Zhou, Y. Fold recognition by concurrent use of solvent accessibility and residue depth. Proteins Struct. Funct. Bioinform. 2007, 68, 636–645. [Google Scholar] [CrossRef] [PubMed]
- Mooney, C.; Pollastri, G.; Shields, D.C.; Haslam, N.J. Prediction of short linear protein binding regions. J. Mol. Biol. 2012, 415, 193–204. [Google Scholar] [CrossRef] [PubMed]
- Connolly, M.L. Solvent-accessible surfaces of proteins and nucleic acids. Science 1983, 221, 709–713. [Google Scholar] [CrossRef] [PubMed]
- Huang, B.; Schroeder, M. LIGSITE csc: Predicting ligand binding sites using the Connolly surface and degree of conservation. BMC Struct. Biol. 2006, 6, 19. [Google Scholar] [CrossRef] [PubMed]
- Janin, J. Surface and inside volumes in globular proteins. Nature 1979, 277, 491. [Google Scholar] [CrossRef] [PubMed]
- Rose, G.; Geselowitz, A.; Lesser, G.; Lee, R.; Zehfus, M. Hydrophobicity of amino acid residues in globular proteins. Science 1985, 229, 834–838. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, S.; Gromiha, M.M.; Sarai, A. Real value prediction of solvent accessibility from amino acid sequence. Proteins Struct. Funct. Bioinform. 2003, 50, 629–635. [Google Scholar] [CrossRef] [PubMed]
- Holbrook, S.R.; Muskal, S.M.; Kim, S.H. Predicting surface exposure of amino acids from protein sequence. Protein Eng. 1990, 3, 659–665. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, S.; Gromiha, M.M. NETASA: Neural network based prediction of solvent accessibility. Bioinformatics 2002, 18, 819–824. [Google Scholar] [CrossRef] [PubMed]
- Garg, A.; Kaur, H.; Raghava, G.P. Real value prediction of solvent accessibility in proteins using multiple sequence alignment and secondary structure. Proteins Struct. Funct. Bioinform. 2005, 61, 318–324. [Google Scholar] [CrossRef] [PubMed]
- Dor, O.; Zhou, Y. Real-SPINE: An integrated system of neural networks for real-value prediction of protein structural properties. Proteins Struct. Funct. Bioinform. 2007, 68, 76–81. [Google Scholar] [CrossRef] [PubMed]
- Faraggi, E.; Xue, B.; Zhou, Y. Improving the prediction accuracy of residue solvent accessibility and real-value backbone torsion angles of proteins by guided-learning through a two-layer neural network. Proteins Struct. Funct. Bioinform. 2009, 74, 847–856. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Park, H. Prediction of protein relative solvent accessibility with support vector machines and long-range interaction 3D local descriptor. Proteins Struct. Funct. Bioinform. 2004, 54, 557–562. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.Y.; Lee, H.M.; Ahmad, S. SVM-Cabins: Prediction of solvent accessibility using accumulation cutoff set and support vector machine. Proteins Struct. Funct. Bioinform. 2007, 68, 82–91. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.Y.; Lee, H.M.; Ahmad, S. Prediction and evolutionary information analysis of protein solvent accessibility using multiple linear regression. Proteins Struct. Funct. Bioinform. 2005, 61, 481–491. [Google Scholar] [CrossRef] [PubMed]
- Thompson, M.J.; Goldstein, R.A. Predicting solvent accessibility: Higher accuracy using Bayesian statistics and optimized residue substitution classes. Proteins Struct. Funct. Bioinform. 1996, 25, 38. [Google Scholar] [CrossRef]
- Joo, K.; Lee, S.J.; Lee, J. Sann: Solvent accessibility prediction of proteins by nearest neighbor method. Proteins Struct. Funct. Bioinform. 2012, 80, 1791. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, S.; Mishra, A.; Hoque, M.T. Improved prediction of accessible surface area results in efficient energy function application. J. Theor. Biol. 2015, 380, 380–391. [Google Scholar] [CrossRef] [PubMed]
- Fan, C.; Liu, D.; Huang, R.; Chen, Z.; Deng, L. PredRSA: A gradient boosted regression trees approach for predicting protein solvent accessibility. BMC Bioinform. 2016, 17, S8. [Google Scholar] [CrossRef] [PubMed]
- Heffernan, R.; Paliwal, K.; Lyons, J.; Dehzangi, A.; Sharma, A.; Wang, J.; Sattar, A.; Yang, Y.; Zhou, Y. Improving prediction of secondary structure, local backbone angles, and solvent accessible surface area of proteins by iterative deep learning. Sci. Rep. 2015, 5, 11476. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Chen, W.; Sun, P.; Zhao, X.; Ma, Z. Prediction of protein solvent accessibility using PSO-SVR with multiple sequence-derived features and weighted sliding window scheme. BioData Min. 2015, 8, 3. [Google Scholar] [CrossRef] [PubMed]
- Naderi-Manesh, H.; Sadeghi, M.; Arab, S.; Moosavi Movahedi, A.A. Prediction of protein surface accessibility with information theory. Proteins 2001, 42, 452–459. [Google Scholar] [CrossRef]
- Nepal, R.; Spencer, J.; Bhogal, G.; Nedunuri, A.; Poelman, T.; Kamath, T.; Chung, E.; Kantardjieff, K.; Gottlieb, A.; Lustig, B. Logistic regression models to predict solvent accessible residues using sequence- and homology-based qualitative and quantitative descriptors applied to a domain-complete X-ray structure learning set. J. Appl. Crystallogr. 2015, 48, 1976–1984. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, M.N.; Rajapakse, J.C. Prediction of protein relative solvent accessibility with a two-stage SVM approach. Proteins Struct. Funct. Bioinform. 2005, 59, 30–37. [Google Scholar] [CrossRef] [PubMed]
- Chang, D.T.; Huang, H.Y.; Syu, Y.T.; Wu, C.P. Real value prediction of protein solvent accessibility using enhanced PSSM features. BMC Bioinformat. 2008, 9, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Meshkin, A.; Sadeghi, M.; Ghasem-Aghaee, N. Prediction of relative solvent accessibility using pace regression. EXCLI J. 2009, 8, 211–217. [Google Scholar]
- Kashefi, A.H.; Meshkin, A.; Zargoosh, M.; Zahiri, J.; Taheri, M.; Ashtiani, S. Scatter-search with support vector machine for prediction of relative solvent accessibility. Excli J. 2013, 12, 52–63. [Google Scholar] [PubMed]
- Qian, N.; Sejnowski, T.J. Predicting the secondary structure of globular proteins using neural network models. J. Mol. Biol. 1988, 202, 865–884. [Google Scholar] [CrossRef]
- Rost, B.; Sander, C. Improved prediction of protein secondary structure by use of sequence profiles and neural networks. Proc. Natl. Acad. Sci. USA 1993, 90, 7558–7562. [Google Scholar] [CrossRef] [PubMed]
- Wan, S.; Mak, M.W.; Kung, S.Y. Transductive Learning for Multi-Label Protein Subchloroplast Localization Prediction. IEEE/ACM Trans. Comput. Biol. Bioinform. 2016, 14, 212–224. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C.; Shen, H.B. Cell-PLoc: A package of Web servers for predicting subcellular localization of proteins in various organisms. Nat. Protoc. 2008, 3, 153–162. [Google Scholar] [CrossRef] [PubMed]
- Wan, S.; Mak, M.W.; Kung, S.Y. FUEL-mLoc: Feature-unified prediction and explanation of multi-localization of cellular proteins in multiple organisms. Bioinformatics 2017, 33, 749–750. [Google Scholar] [CrossRef] [PubMed]
- Hayat, M.; Khan, A. MemHyb: Predicting membrane protein types by hybridizing SAAC and PSSM. J. Theor. Biol. 2012, 292, 93. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C.; Shen, H.B. MemType-2L: A web server for predicting membrane proteins and their types by incorporating evolution information through Pse-PSSM. Biochem. Biophys. Res. Commun. 2007, 360, 339–345. [Google Scholar] [CrossRef] [PubMed]
- Wan, S.; Mak, M.W.; Kung, S.Y. Mem-ADSVM: A two-layer multi-label predictor for identifying multi-functional types of membrane proteins. J. Theor. Biol. 2016, 398, 32–42. [Google Scholar] [CrossRef] [PubMed]
- Wan, S.; Mak, M.W.; Kung, S.Y. Ensemble linear neighborhood propagation for predicting subchloroplast localization of multi-location proteins. J. Proteome Res. 2016, 15, 4755–4762. [Google Scholar] [CrossRef] [PubMed]
- Meiler, J.; Müllerl, M.; Zeidler, A.; Schmäschke, F. Generation and evaluation of dimension-reduced amino acid parameter representations by artificial neural networks. J. Mol. Model. 2001, 7, 360–369. [Google Scholar] [CrossRef]
- Quan, L.; Lv, Q.; Zhang, Y. STRUM: Structure-based prediction of protein stability changes upon single-point mutation. Bioinformatics 2016, 32, 2936. [Google Scholar] [CrossRef] [PubMed]
- Bowie, J.U.; Luthy, R.; Eisenberg, D. A Method to Identify Protein Sequences that Fold into a Known Three- Dimensional Structure. Science 1991, 253, 164. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Wang, Z.; Cong, P.; Li, T. Accurate prediction of protein relative solvent accessibility using a balanced model. Biodata Min. 2017, 10, 1. [Google Scholar] [CrossRef] [PubMed]
- Kabsch, W.; Sander, C. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 1983, 22, 2577–2637. [Google Scholar] [CrossRef] [PubMed]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Jozefowicz, R.; Zaremba, W.; Sutskever, I. An Empirical Exploration of Recurrent Network Architectures. In Proceedings of the 32nd International Conference on Machine Learning (ICML), Lille, France, 6–11 July 2015; pp. 171–180. [Google Scholar]
- Li, Z.; Yu, Y. Protein Secondary Structure Prediction Using Cascaded Convolutional and Recurrent Neural Networks. In Proceedings of the 25th International Joint Conference on Artificial Intelligence(IJCAI), New York, NY, USA, 9–15 July 2016; pp. 2560–2567. [Google Scholar]
- Wan, F.; Zeng, J. Deep learning with feature embedding for compound-protein interaction prediction. bioRxiv 2016. [Google Scholar] [CrossRef]
- Zhou, J.; Troyanskaya, O.G. Deep Supervised and Convolutional Generative Stochastic Network for Protein Secondary Structure Prediction. In Proceedings of the 31st International Converenfe on Machine Learning (ICML), Beijing, China, 21–26 June 2014; pp. 745–753. [Google Scholar]
- Petersen, B.; Petersen, T.N.; Andersen, P.; Nielsen, M.; Lundegaard, C. A generic method for assignment of reliability scores applied to solvent accessibility predictions. BMC Struct. Biol. 2009, 9, 51. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Chaudhari, N.S. Cascaded Bidirectional Recurrent Neural Networks for Protein Secondary Structure Prediction. IEEE/ACM Trans. Comput. Biol. Bioinform. 2007, 4, 572–582. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Dunbrack, R.L., Jr. PISCES: A protein sequence culling server. Bioinformatics 2003, 19, 1589–1591. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Godzik, A. Cd-hit: A fast program for clustering and comparing large sets of protein or nucleotide sequences. Bioinformatics 2006, 22, 1658. [Google Scholar] [CrossRef] [PubMed]
- Cuff, J.; Barton, G. Application of multiple sequence alignment profiles to improve protein secondary structure prediction. Proteins 2000, 40, 502–511. [Google Scholar] [CrossRef]
- Altschul, S.F.; Gertz, E.M.; Agarwala, R.; Schaäffer, A.A.; Yu, Y.K. PSI-BLAST pseudocounts and the minimum description length principle. Nucleic Acids Res. 2009, 37, 815–824. [Google Scholar] [CrossRef] [PubMed]
- Nan, L.; Zhonghua, S.; Fan, J. Prediction of protein-protein binding site by using core interface residue and support vector machine. BMC Bioinform. 2009, 9, 553. [Google Scholar]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735. [Google Scholar] [CrossRef] [PubMed]
- Graves, A.; Jaitly, N.; Mohamed, A.R. Hybrid speech recognition with Deep Bidirectional LSTM. In Proceedings of the Automatic Speech Recognition and Understanding, Olomouc, Czech Republic, 8–12 December 2014; pp. 273–278. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Theano Development Team. Theano: A Python framework for fast computation of mathematical expressions. arXiv, 2016; arXiv:1605.02688. [Google Scholar]
| Work | Algorithm | Description of Features | MAE (%) |
|---|---|---|---|
| Ahmad, 2003 [10] | Neural network | Amino acid composition | 18.8 |
| Wang, 2005 [18] | Multiple linear regression | PSSM | 16.2 |
| Garg, 2005 [13] | Neural network | PSSM, secondary structure | 16.6 |
| Nguyen, 2006 [27] | Two-stage SVR | PSSM | 15.7 |
| Wang, 2007 [17] | Support vector machine | PSSM | 15.1 |
| Dor, 2007 [14] | Neural network | PSSM, physical properties | 14.3 |
| Chang, 2008 [28] | Support vector regression | Enhances PSSM-based features | 14.8 |
| Faraggi, 2009 [15] | Neural networks | PSSM, physical properties, secondary structure | 11.1 |
| Meshkin, 2009 [29] | Pace regression | PSSM | 13.4 |
| Joo, 2012 [20] | k-nearest neighbor | PSSM | 14.8 |
| Kashefi, 2013 [30] | SVR and scatter search methods | PSSM, qualitative physicochemical features | 12.31 |
| Zhang, 2015 [24] | Weighted sliding window | PSSM, secondary structure, native disorder, physicochemical propensities, sequence-based features | 14 |
| Fan, 2016 [22] | Gradient boosted regression trees | PSSM, secondary structure, native disorder, conservation score, side-chain environment | 9.4 |
| Method | CB502 | Manesh215 | ||
|---|---|---|---|---|
| MAE (%) | PCC | MAE (%) | PCC | |
| SARpred | 17.4 | 0.6 | 16.6 | 0.61 |
| SVR | 14.8 | 0.68 | 14.2 | 0.69 |
| Real-SPINE | 14.5 | 0.68 | 13.8 | 0.7 |
| NetSurfP | 14.3 | 0.71 | 13.6 | 0.7 |
| PredRSA | 9.4 | 0.73 | 9.0 | 0.75 |
| SDBRNN | 8.8 | 0.75 | 8.2 | 0.78 |
| Method | Accuracy for Two-State Prediction | ||||||
|---|---|---|---|---|---|---|---|
| 5% | 10% | 20% | 25% | 30% | 40% | 50% | |
| SARpred | 74.9 | 77.2 | 77.7 | - | 77.8 | 78.1 | 80.5 |
| PR | 76.8 | 74.8 | 75.3 | 76.7 | 77.7 | 79.8 | 86.3 |
| SVR | 80.9 | 80.1 | 78.7 | - | - | - | 80.8 |
| SS-SVM | 79.2 | 78.2 | 77.6 | 77.6 | 77.5 | 79.7 | 86.5 |
| Two-stage SVR | 81.1 | 78.7 | 77.6 | 77.3 | - | - | 79.5 |
| PredRSA | 80 | 81.6 | 80.9 | 81.1 | 82.2 | 87.1 | 93.2 |
| SDBRNN | 83.5 | 82.4 | 82.3 | 82.6 | 83.5 | 87.4 | 93 |
| Threshold (%) | Manesh215 | CB502 | CASP10 | |||
|---|---|---|---|---|---|---|
| PredRSA | SDBRNN | PredRSA | SDBRNN | PredRSA | SDBRNN | |
| 5 | 80.1 | 83.5 | 77.9 | 82.3 | 78.5 | 84 |
| 10 | 81.7 | 82.4 | 79 | 80.9 | 79.1 | 82.1 |
| 20 | 81 | 82.3 | 80.5 | 80.7 | 78.3 | 80.6 |
| 25 | 81.2 | 82.6 | 81 | 81.4 | 79.7 | 80.2 |
| 30 | 82.4 | 83.5 | 82.1 | 82.5 | 80.5 | 81.2 |
| 40 | 87.1 | 87.4 | 86.8 | 87 | 85 | 85.4 |
| 50 | 93.2 | 93 | 93 | 92.4 | 91.2 | 91.4 |
| Threshold (%) | Manesh215 | CB502 | CASP10 | |||
|---|---|---|---|---|---|---|
| PredRSA | SDBRNN | PredRSA | SDBRNN | PredRSA | SDBRNN | |
| 5 | 0.54 | 0.62 | 0.5 | 0.59 | 0.48 | 0.61 |
| 10 | 0.63 | 0.64 | 0.58 | 0.61 | 0.57 | 0.63 |
| 20 | 0.61 | 0.63 | 0.6 | 0.6 | 0.56 | 0.61 |
| 25 | 0.58 | 0.61 | 0.57 | 0.58 | 0.56 | 0.57 |
| 30 | 0.54 | 0.58 | 0.52 | 0.55 | 0.51 | 0.53 |
| 40 | 0.42 | 0.48 | 0.39 | 0.46 | 0.4 | 0.43 |
| 50 | 0.25 | 0.34 | 0.23 | 0.33 | 0.3 | 0.31 |
| Feature | MAE (%) | PCC |
|---|---|---|
| PSSM | 9.33 | 0.732 |
| PSSM + SC | 9.03 | 0.749 |
| PSSM + SC + CS | 9.00 | 0.750 |
| PSSM + SC + CS + PP | 8.95 | 0.750 |
| PSSM + SC + CS + PP + PC | 8.86 | 0.753 |
| Method | CB502 | Manesh215 | CASP10 | TS261 | ||||
|---|---|---|---|---|---|---|---|---|
| MAE (%) | PCC | MAE (%) | PCC | MAE (%) | PCC | MAE (%) | PCC | |
| LSTM | 9.8 | 0.694 | 9.4 | 0.722 | 10.0 | 0.698 | 10.0 | 0.695 |
| BLSTM_C | 9.0 | 0.74 | 8.44 | 0.772 | 9.33 | 0.734 | 9.0 | 0.748 |
| BLSTM_S | 8.93 | 0.744 | 8.33 | 0.775 | 9.26 | 0.739 | 8.96 | 0.747 |
| SDBRNN | 8.84 | 0.748 | 8.24 | 0.777 | 9.19 | 0.742 | 8.86 | 0.753 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, B.; Li, L.; Lü, Q. Protein Solvent-Accessibility Prediction by a Stacked Deep Bidirectional Recurrent Neural Network. Biomolecules 2018, 8, 33. https://doi.org/10.3390/biom8020033
Zhang B, Li L, Lü Q. Protein Solvent-Accessibility Prediction by a Stacked Deep Bidirectional Recurrent Neural Network. Biomolecules. 2018; 8(2):33. https://doi.org/10.3390/biom8020033
Chicago/Turabian StyleZhang, Buzhong, Linqing Li, and Qiang Lü. 2018. "Protein Solvent-Accessibility Prediction by a Stacked Deep Bidirectional Recurrent Neural Network" Biomolecules 8, no. 2: 33. https://doi.org/10.3390/biom8020033
APA StyleZhang, B., Li, L., & Lü, Q. (2018). Protein Solvent-Accessibility Prediction by a Stacked Deep Bidirectional Recurrent Neural Network. Biomolecules, 8(2), 33. https://doi.org/10.3390/biom8020033





