Factors Determining Kinesin Motors in a Predominant One-Head-Bound or Two-Heads-Bound State During Its Stepping Cycle
Abstract
1. Introduction
2. General Chemomechanical Pathway of Kinesin Dimer
3. Results and Discussion
3.1. General Theory on Fractions of 1HB and 2HB States
3.2. Fractions of 1HB and 2HB States Under Saturating ATP Concentrations, No Free ADP and No Load
3.3. Effect of ATP Concentration on Fractions of 1HB and 2HB States Under No Load and No Free ADP
3.4. Effect of Load on Fractions of 1HB and 2HB States at Saturating ATP Concentrations and No Free ADP
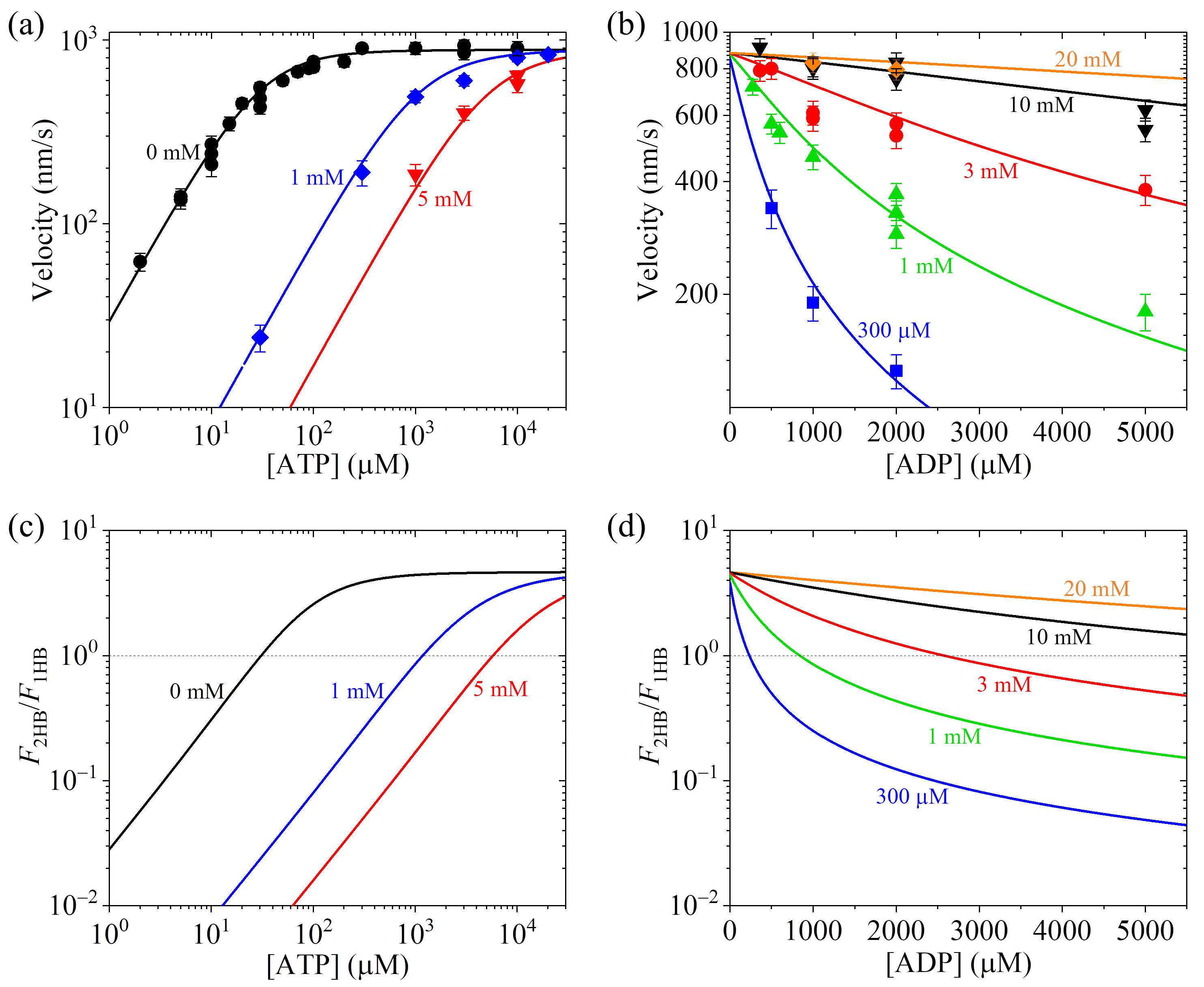
3.5. Effect of ADP Concentration on Velocity and Fractions of 1HB and 2HB States Under No Load
3.6. Applications of the Theory for Kinesin-1, Kinesin-2, Kinesin-3, Kinesin-5 and Kinesin-13 Motors
4. Conclusions
- (i)
- Under saturating ATP concentrations, no free ADP and no load—the fraction of the 2HB state, F2HB, and that of the 1HB state, F1HB, depend only on two parameters, , the ratio of the rate of ATP transition to ADP in the TH to the rate of ADP release from the MT-bound head, and , the ratio of the rate of NL docking of the ATP-head to the rate of ADP release from the MT-bound head. is determined mainly by and mildly by . For the motor having a large kNL, when < 1.62, the motor is in the predominant 2HB state, and as decreases, the fraction of the 2HB state increases sensitively, while when > 1.62, the motor is in the predominant 1HB state, and as increases, the fraction of the 1HB state increases sensitively.
- (ii)
- Under no free ADP and no load— increases with the increase in the ATP concentration at low ATP concentrations and becomes leveled off at high ATP concentrations. The motor having a small , such as kinesin-1 or kinesin-2, which is in the predominant 2HB at high ATP concentrations, can become in the predominant 1HB state at low ATP concentrations. The motor having a large , such as kinesin-3 KIF1A, is always in the predominant 1HB state, and the fraction of the 1HB state increases with the decrease in the ATP concentration.
- (iii)
- At saturating ATP concentrations and no free ADP— increases with the increase in the backward load, especially at a large . The motor having a large , such as kinesin-3 KIF1A, which is in the predominant 1HB under no load, can become in the predominant 2HB state under a high load. The motor having a small , such as kinesin-1 or kinesin-2, is always in the predominant 2HB state, and the fraction of the 2HB state increases with the increase in the backward load.
- (iv)
- Under no load—for a given ATP concentration and, in particular, for the ATP concentration not very large, decreases with the increase in the ADP concentration. For example, for kinesin-1 at 1 mM ATP molecules, the motor is in the predominant 2HB state under no free ADP and can become in the predominant 1HB state under high ADP concentrations.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lawrence, C.J.; Dawe, R.K.; Christie, K.R.; Cleveland, D.W.; Dawson, S.C.; Endow, S.A.; Goldstein, L.S.B.; Goodson, H.V.; Hirokawa, N.; Howard, J.; et al. A standardized kinesin nomenclature. J. Cell Biol. 2004, 167, 19–22. [Google Scholar] [CrossRef] [PubMed]
- Miki, H.; Okada, Y.; Hirokawa, N. Analysis of the kinesin superfamily: Insights into structure and function. Trends Cell Biol. 2005, 15, 467–476. [Google Scholar] [CrossRef] [PubMed]
- Hirokawa, N.; Noda, Y.; Tanaka, Y.; Niwa, S. Kinesin superfamily motor proteins and intracellular transport. Nat. Rev. Mol. Cell Biol. 2009, 10, 682. [Google Scholar] [CrossRef]
- Iino, R.; Kinbara, K.; Bryant, Z. Introduction: Molecular motors. Chem. Rev. 2020, 120, 1–4. [Google Scholar] [CrossRef]
- Kozielski, F.; Sack, S.; Marx, A.; Thormählen, M.; Schönbrunn, E.; Biou, V.; Thompson, A.; Mandelkow, E.M.; Mandelkow, E. The crystal structure of dimeric kinesin and implications for microtubule-dependent motility. Cell 1997, 91, 985–994. [Google Scholar] [CrossRef]
- Vale, R.D. The molecular motor toolbox for intracellular transport. Cell 2003, 112, 467–480. [Google Scholar] [CrossRef]
- Asbury, C.L.; Fehr, A.N.; Block, S.M. Kinesin moves by an asymmetric hand-over-hand mechanism. Science 2003, 302, 2130–2134. [Google Scholar] [CrossRef]
- Yildiz, A.; Tomishige, M.; Vale, R.D.; Selvin, P.R. Kinesin walks hand-over-hand. Science 2004, 303, 676–678. [Google Scholar] [CrossRef]
- Mori, T.; Vale, R.D.; Tomishige, M. How kinesin waits between steps. Nature 2007, 450, 750–754. [Google Scholar] [CrossRef]
- Alonso, M.C.; Drummond, D.R.; Kain, S.; Hoeng, J.; Amos, L.; Cross, R.A. An ATP gate controls tubulin binding by the tethered head of kinesin-1. Science 2007, 316, 120–123. [Google Scholar] [CrossRef][Green Version]
- Wolff, J.O.; Scheiderer, L.; Engelhardt, T.; Engelhardt, J.; Matthias, J.; Hell, S.W. MINFLUX dissects the unimpeded walking of kinesin-1. Science 2023, 379, 1004–1010. [Google Scholar] [CrossRef] [PubMed]
- Deguchi, T.; Iwanski, M.K.; Schentarra, E.-M.; Heidebrecht, C.; Schmidt, L.; Heck, J.; Weihs, T.; Schnorrenberg, S.; Hoess, P.; Liu, S.; et al. Direct observation of motor protein stepping in living cells using MINFLUX. Science 2023, 379, 1010–1015. [Google Scholar] [CrossRef] [PubMed]
- Isojima, H.; Iino, R.; Niitani, Y.; Noji, H.; Tomishige, M. Direct observation of intermediate states during the stepping motion of kinesin-1. Nat. Chem. Biol. 2016, 12, 290–297. [Google Scholar] [CrossRef]
- Mickolajczyk, K.J.; Hancock, W.O. Kinesin processivity is determined by a kinetic race from a vulnerable one-head-bound state. Biophys. J. 2017, 112, 2615–2623. [Google Scholar] [CrossRef]
- Sudhakar, S.; Kazem, M.; Tobias, A.; Jachowski, J.; Bugiel, M.; Jannasch, A.; Schäffer, E. Germanium nanospheres for ultraresolution picotensiometry of kinesin motors. Science 2021, 71, eabd9944. [Google Scholar] [CrossRef]
- Chen, G.-Y.; Mickolajczyk, K.J.; Hancock, W.O. The kinesin-5 chemomechanical cycle is dominated by a two-heads-bound state. J. Biol. Chem. 2016, 291, 20283–20294. [Google Scholar] [CrossRef]
- Zaniewski, T.M.; Gicking, A.M.; Fricks, J.; Hancock, W.O. A kinetic dissection of the fast and superprocessive kinesin-3 KIF1A reveals a predominant one-head-bound state during its chemomechanical cycle. J. Biol. Chem. 2020, 295, 17889–17903. [Google Scholar] [CrossRef]
- Saunders, A.M.; Powers, J.; Strome, S.; Saxton, W.M. Kinesin-5 acts as a brake in anaphase spindle elongation. Curr. Biol. 2007, 17, 453–454. [Google Scholar] [CrossRef]
- Shimamoto, Y.; Forth, S.; Kapoor, T.M. Measuring pushing and braking forces generated by ensembles of kinesin-5 crosslinking two microtubules. Dev. Cell 2015, 34, 669–681. [Google Scholar] [CrossRef]
- Xie, P. A model of tubulin removal and exchange caused by kinesin motor walking on microtubule lattices. J. Theor. Biol. 2025, 605, 112088. [Google Scholar] [CrossRef]
- Verhey, K.J.; Ohi, R. Causes, costs and consequences of kinesin motors communicating through the microtubule lattice. J. Cell Sci. 2023, 136, jcs260735. [Google Scholar] [CrossRef] [PubMed]
- Dumont, E.L.P.; Do, C.; Hess, H. Molecular wear of microtubules propelled by surface-adhered kinesins. Nat. Nanotechnol. 2015, 10, 166–169. [Google Scholar] [CrossRef] [PubMed]
- VanDelinder, V.; Adams, P.G.; Bachand, G.D. Mechanical splitting of microtubules into protofilament bundles by surface-bound kinesin-1. Sci. Rep. 2016, 6, 39408. [Google Scholar] [CrossRef]
- Andreu-Carbo, M.; Fernandes, S.; Velluz, M.C.; Kruse, K.; Aumeier, C. Motor usage imprints microtubule stability along the shaft. Dev. Cell 2022, 57, 5–18. [Google Scholar] [CrossRef]
- Budaitis, B.G.; Badieyan, S.; Yue, Y.; Blasius, T.L.; Reinemann, D.N.; Lang, M.J.; Cianfrocco, M.A.; Verhey, K.J. A kinesin-1 variant reveals motor-induced microtubule damage in cells. Curr. Biol. 2022, 32, 2416–2429. [Google Scholar] [CrossRef]
- Helenius, J.; Brouhard, G.; Kalaidzidis, Y.; Diez, S.; Howard, J. The depolymerizing kinesin MCAK uses lattice diffusion to rapidly target microtubule ends. Nature 2006, 441, 115–119. [Google Scholar] [CrossRef]
- Xie, P. Modeling study of kinesin-13 MCAK microtubule depolymerase. Eur. Biophys. J. 2024, 53, 339–354. [Google Scholar] [CrossRef]
- Mickolajczyk, K.J.; Deffenbaugh, N.C.; Arroyo, J.O.; Andrecka, J.; Kukura, P.; Hancock, W.O. Kinetics of nucleotide-dependent structural transitions in the kinesin-1 hydrolysis cycle. Proc. Natl. Acad. Sci. USA 2015, 112, E7186–E7193. [Google Scholar] [CrossRef]
- Takaki, R.; Mugnai, M.L.; Goldtzvik, Y.; Thirumalai, D. How kinesin waits for ATP affects the nucleotide and load dependence of the stepping kinetics. Proc. Natl. Acad. Sci. USA 2019, 116, 23091–23099. [Google Scholar] [CrossRef]
- Xie, P. ATP-concentration-dependent fractions of one-head-bound and two-heads-bound states of kinesin motor during its chemomechanical coupling cycle. J. Phys. Chem. Lett. 2024, 15, 3893–3899. [Google Scholar] [CrossRef]
- Xie, P. Effects of stalk orientation and size of trapped bead on force–velocity relation of kinesin motor determined using single molecule optical trapping methods. J. Biol. Phys. 2025, 51, 7. [Google Scholar] [CrossRef]
- Yildiz, A.; Tomishige, M.; Gennerich, A.; Vale, R.D. Intramolecular strain coordinates kinesin stepping behavior along microtubules. Cell 2008, 134, 1030–1041. [Google Scholar] [CrossRef]
- Moyer, M.L.; Gilbert, S.P.; Johnson, K.A. Pathway of ATP hydrolysis by monomeric and dimeric kinesin. Biochemistry 1998, 37, 800–813. [Google Scholar] [CrossRef] [PubMed]
- Okada, Y.; Hirokawa, N. A processive single-headed motor: Kinesin superfamily protein KIF1A. Science 1999, 283, 1152–1157. [Google Scholar] [CrossRef] [PubMed]
- Rosenfeld, S.S.; Fordyce, P.M.; Jefferson, G.M.; King, P.H.; Block, S.M. Stepping and stretching: How kinesin uses internal strain to walk processively. J. Biol. Chem. 2003, 278, 18550–18556. [Google Scholar] [CrossRef]
- Xie, P. A model for chemomechanical coupling of kinesin-3 motor. Cell. Mol. Bioeng. 2024, 17, 137–151. [Google Scholar] [CrossRef]
- Rosenfeld, S.S.; Jefferson, G.M.; King, P.H. ATP reorients the neck linker of kinesin in two sequential steps. J. Biol. Chem. 2001, 276, 40167–40174. [Google Scholar] [CrossRef]
- Gilbert, S.P.; Moyer, M.L.; Johnson, K.A. Alternating Site Mechanism of the Kinesin ATPase. Biochemistry 1998, 37, 792–799. [Google Scholar] [CrossRef]
- Cross, R.A. The kinetic mechanism of kinesin. Trends Biochem. Sci. 2004, 29, 301–309. [Google Scholar] [CrossRef]
- Schief, W.R.; Clark, R.H.; Crevenna, A.H.; Howard, J. Inhibition of kinesin motility by ADP and phosphate supports a hand-over-hand mechanism. Proc. Natl. Acad. Sci. USA 2004, 101, 1183–1188. [Google Scholar] [CrossRef]
- Rosenfeld, S.S.; van Duffelen, M.; Behnke-Parks, W.M.; Beadle, C.; Corrreia, J.; Xing, J. The ATPase Cycle of the Mitotic Motor CENP-E. J. Biol. Chem. 2009, 284, 32858–32868. [Google Scholar] [CrossRef] [PubMed]
- Friel, C.T.; Howard, J. The kinesin-13 MCAK has an unconventional ATPase cycle adapted for microtubule depolymerization. EMBO J. 2011, 30, 3928–3939. [Google Scholar] [CrossRef] [PubMed]
- Cooper, J.R.; Wagenbach, M.; Asbury, C.L.; Wordeman, L. Catalysis of the microtubule on-rate is the major parameter regulating the depolymerase activity of MCAK. Nat. Struct. Mol. Biol. 2010, 17, 77. [Google Scholar] [CrossRef] [PubMed]
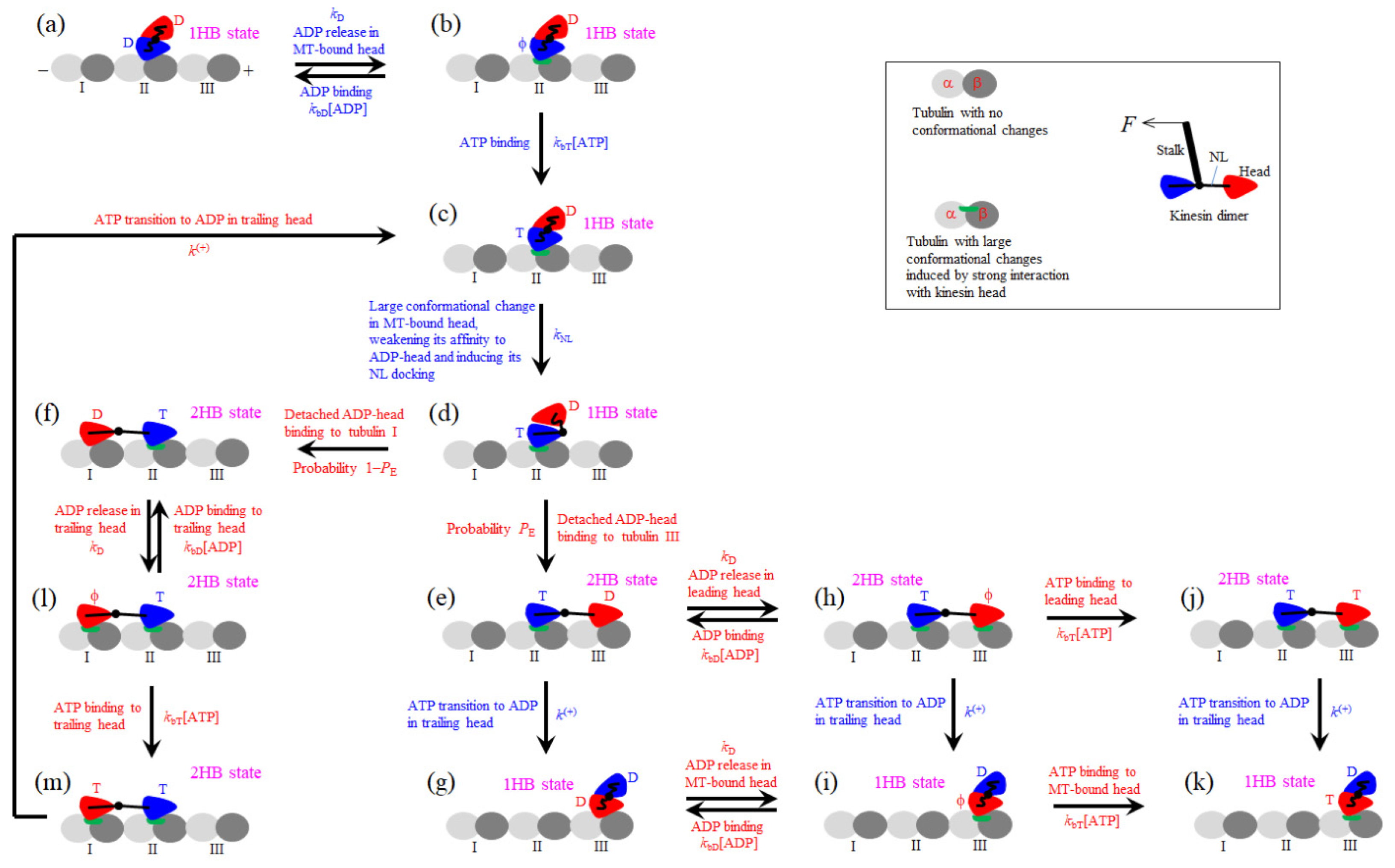
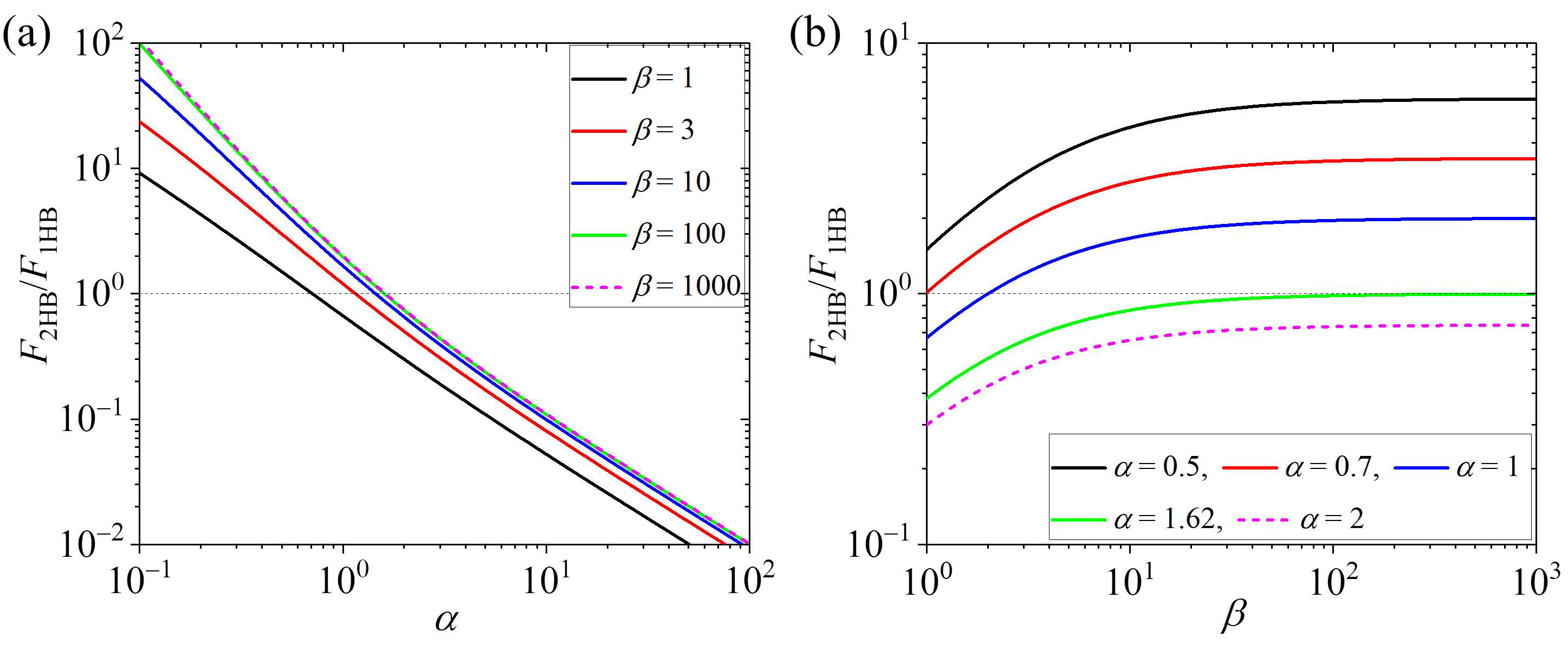



| Ratio of rate of ATP transition to ADP in TH to that of ADP release from MT-bound head |
| Ratio of rate of NL docking in ATP-head to that of ADP release from MT-bound head |
| Ratio of the rate of the second-order ATP-binding rate to that of ADP release from the MT-bound head |
| Ratio of the rate of the second-order ADP-binding rate to that of ADP release from the MT-bound head |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, X.-X.; Liu, Y.-R.; Xie, P. Factors Determining Kinesin Motors in a Predominant One-Head-Bound or Two-Heads-Bound State During Its Stepping Cycle. Biomolecules 2025, 15, 717. https://doi.org/10.3390/biom15050717
Shi X-X, Liu Y-R, Xie P. Factors Determining Kinesin Motors in a Predominant One-Head-Bound or Two-Heads-Bound State During Its Stepping Cycle. Biomolecules. 2025; 15(5):717. https://doi.org/10.3390/biom15050717
Chicago/Turabian StyleShi, Xiao-Xuan, Yu-Ru Liu, and Ping Xie. 2025. "Factors Determining Kinesin Motors in a Predominant One-Head-Bound or Two-Heads-Bound State During Its Stepping Cycle" Biomolecules 15, no. 5: 717. https://doi.org/10.3390/biom15050717
APA StyleShi, X.-X., Liu, Y.-R., & Xie, P. (2025). Factors Determining Kinesin Motors in a Predominant One-Head-Bound or Two-Heads-Bound State During Its Stepping Cycle. Biomolecules, 15(5), 717. https://doi.org/10.3390/biom15050717






