Multi-Target In Silico Prediction of Inhibitors for Mitogen-Activated Protein Kinase-Interacting Kinases
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dataset and Calculation of Molecular Descriptors
2.2. Model Development and Evaluation
2.2.1. Linear mt-QSAR Models
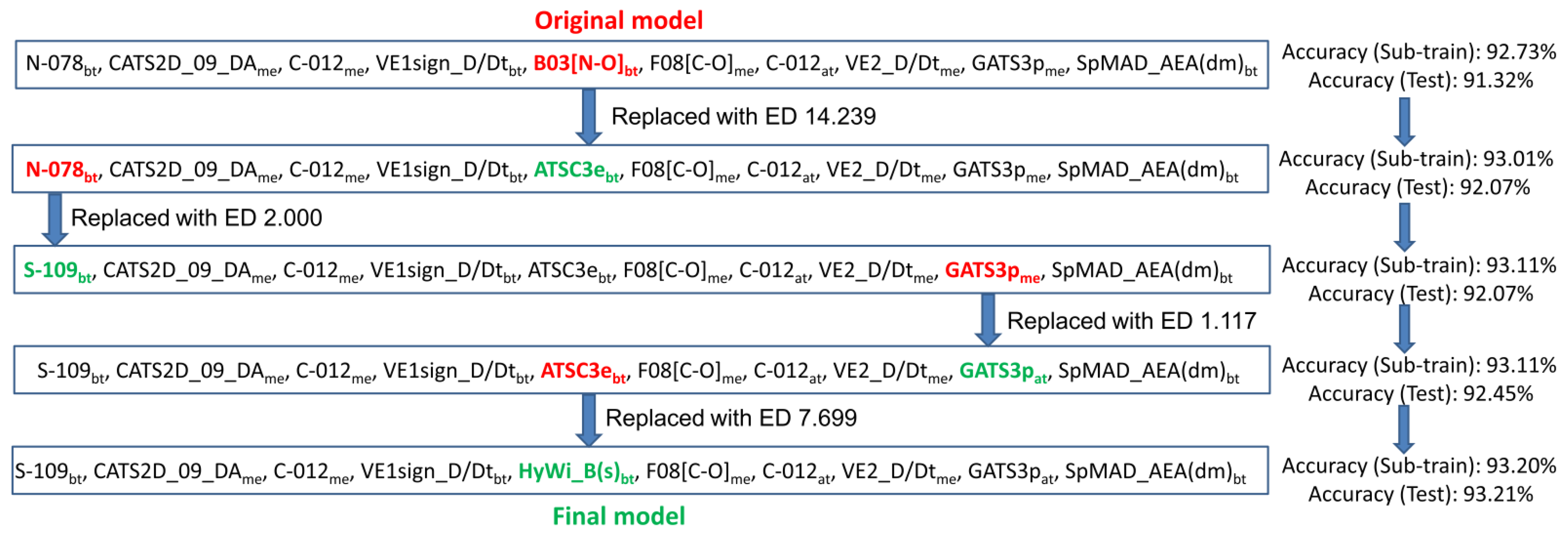
2.2.2. Post-Selection Similarity Search-Based Modification
2.2.3. Non-Linear mt-QSAR Models
2.2.4. Model Evaluation
2.3. Similarity Search Analysis
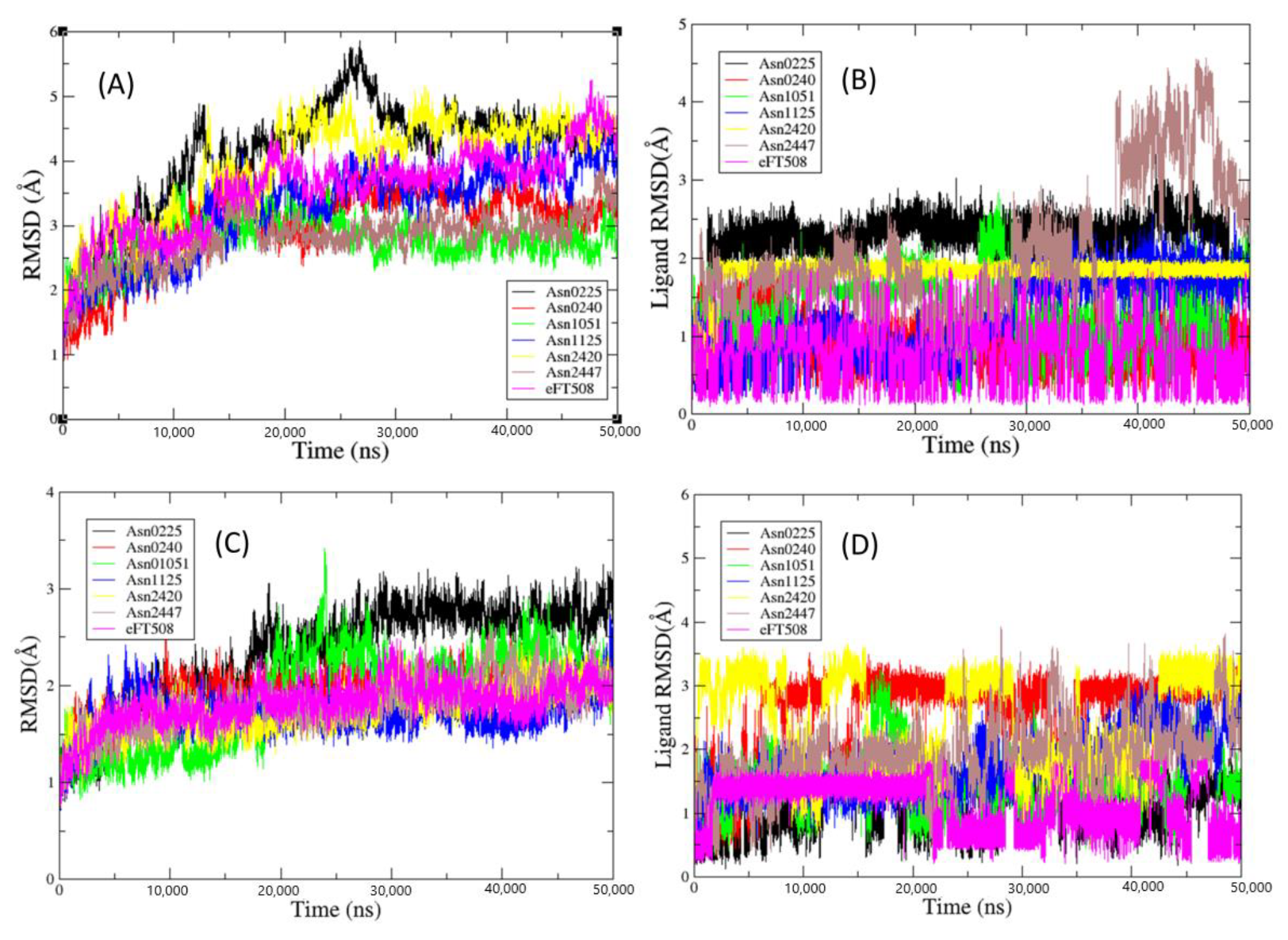
2.4. Molecular Dynamics Simulations
3. Results and Discussion
3.1. Multi-Target QSAR Models
3.2. Virtual Screening of Potential Hits
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bitterman, P.B.; Polunovsky, V.A. EIF4E-mediated translational control of cancer incidence. Biochim. Biophys. Acta 2015, 1849, 774–780. [Google Scholar] [CrossRef] [PubMed]
- Diab, S.; Kumarasiri, M.; Yu, M.; Teo, T.; Proud, C.; Milne, R.; Wang, S. MAP kinase-interacting kinases-emerging targets against cancer. Chem. Biol. 2014, 21, 441–452. [Google Scholar] [CrossRef] [PubMed]
- Kwiatkowski, J.; Liu, B.; Pang, S.; Ahmad, N.H.B.; Wang, G.; Poulsen, A.; Yang, H.; Poh, Y.R.; Tee, D.H.Y.; Ong, E.; et al. Stepwise evolution of fragment hits against mapk interacting kinases 1 and 2. J. Med. Chem. 2020, 63, 621–637. [Google Scholar] [CrossRef] [PubMed]
- Buxade, M.; Parra-Palau, J.L.; Proud, C.G. The MNKs: MAP kinase-interacting kinases (MAP kinase signal-integrating kinases). Front. Biosci. 2008, 13, 5359–5373. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Yu, R.; Wang, X.; Proud, C.G.; Jiang, T. Progress in developing MNK inhibitors. Eur. J. Med. Chem. 2021, 219, 113420. [Google Scholar] [CrossRef]
- Xie, J.; Merrett, J.E.; Jensen, K.B.; Proud, C.G. The MAP kinase-interacting kinases (MNKs) as targets in oncology. Expert Opin. Ther. Targets 2019, 23, 187–199. [Google Scholar] [CrossRef]
- Abdelaziz, A.M.; Yu, M.; Wang, S. MNK inhibitors: A patent review. Pharm. Pat. Anal. 2021, 10, 25–35. [Google Scholar] [CrossRef]
- Diab, S.; Li, P.; Basnet, S.K.; Lu, J.; Yu, M.; Albrecht, H.; Milne, R.W.; Wang, S. Unveiling new chemical scaffolds as Mnk inhibitors. Future Med. Chem. 2016, 8, 271–285. [Google Scholar] [CrossRef]
- Gagic, Z.; Ruzic, D.; Djokovic, N.; Djikic, T.; Nikolic, K. In silico methods for design of kinase inhibitors as anticancer drugs. Front. Chem. 2020, 7, 873. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Speck-Planche, A.; Kleandrova, V.V.; Cordeiro, M.N.D.S. Chemoinformatics for rational discovery of safe antibacterial drugs: Simultaneous predictions of biological activity against Streptococci and toxicological profiles in laboratory animals. Bioorg. Med. Chem. 2013, 21, 2727–2732. [Google Scholar] [CrossRef]
- Speck-Planche, A.; Cordeiro, M.N.D.S. Multitasking Models for quantitative structure-biological effect relationships: Current status and future perspectives to speed up drug discovery. Expert Opin. Drug Discov. 2015, 10, 245–256. [Google Scholar] [CrossRef]
- Speck-Planche, A.; Cordeiro, M.N.D.S. Speeding up early drug discovery in antiviral research: A fragment-based in silico approach for the design of virtual anti-hepatitis c leads. ACS Comb. Sci. 2017, 19, 501–512. [Google Scholar] [CrossRef] [PubMed]
- Kleandrova, V.V.; Scotti, L.; Bezerra Mendonca Junior, F.J.; Muratov, E.; Scotti, M.T.; Speck-Planche, A. QSAR modeling for multi-target drug discovery: Designing simultaneous inhibitors of proteins in diverse pathogenic parasites. Front. Chem. 2021, 9, 634663. [Google Scholar] [CrossRef] [PubMed]
- ChemAxon. Standardizer, Version 15.9.14.0 Software; ChemAxon: Budapest, Hungary, 2010. [Google Scholar]
- Alvascience srl. alvaDesc (Software for Molecular Descriptors Calculation). 2019. Available online: https://www.alvascience.com/ (accessed on 12 June 2021).
- Sushko, I.; Novotarskyi, S.; Korner, R.; Pandey, A.K.; Rupp, M.; Teetz, W.; Brandmaier, S.; Abdelaziz, A.; Prokopenko, V.V.; Tanchuk, V.Y.; et al. Online Chemical Modeling Environment (OCHEM): Web platform for data storage, model development and publishing of chemical information. J. Comput. Aided Mol. Des. 2011, 25, 533–554. [Google Scholar] [CrossRef] [Green Version]
- Sadowski, J.; Gasteiger, J.; Klebe, G. Comparison of automatic three-dimensional model builders using 639 X-ray structures. J. Chem. Inf. Comput. Sci. 1994, 34, 1000–1008. [Google Scholar] [CrossRef]
- Halder, A.K.; Cordeiro, M.N.D.S. QSAR-Co-X: An open source toolkit for multitarget QSAR modelling. J. Cheminform. 2021, 13, 29. [Google Scholar] [CrossRef]
- Ambure, P.; Halder, A.K.; Gonzalez Diaz, H.; Cordeiro, M.N.D.S. QSAR-Co: An open source software for developing robust multitasking or multitarget classification-based QSAR models. J. Chem. Inf. Model. 2019, 59, 2538–2544. [Google Scholar] [CrossRef] [PubMed]
- Halder, A.K.; Cordeiro, M.N.D.S. Development of multi-target chemometric models for the inhibition of class I PI3K enzyme isoforms: A case study using QSAR-Co tool. Int. J. Mol. Sci. 2019, 20, 4191. [Google Scholar] [CrossRef] [Green Version]
- Cover, T.M.; Hart, P.E. Nearest neighbor pattern classification. IEEE Trans. Inform. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- McCallum, A.; Nigam, K. A comparison of event models for naive bayes text classification. In Proceedings in Workshop on Learning for Text Categorization, AAAI’98; The AAAI Press: Menlo Park, CA, USA, 1998; Volume 752, pp. 41–48. [Google Scholar]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the Fifth Annual Workshop on Computational Learning Theory ACM 144–152, Pittsburgh, PA, USA, 27–29 July 1992. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Huang, G.B.; Babri, H.A. Upper bounds on the number of hidden neurons in feedforward networks with arbitrary bounded nonlinear activation functions. IEEE Trans. Neural Netw. 1998, 9, 224–229. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Urias, R.W.; Barigye, S.J.; Marrero-Ponce, Y.; Garcia-Jacas, C.R.; Valdes-Martini, J.R.; Perez-Gimenez, F. IMMAN: Free software for information theory-based chemometric analysis. Mol. Divers. 2015, 19, 305–319. [Google Scholar] [CrossRef]
- Sosnin, S.; Karlov, D.; Tetko, I.V.; Fedorov, M.V. Comparative study of multitask toxicity modeling on a broad chemical space. J. Chem. Inf. Model. 2019, 59, 1062–1072. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wilks, S.S. Certain generalizations in the analysis of variance. Biometrika 1932, 24, 471–494. [Google Scholar] [CrossRef]
- Ojha, P.K.; Roy, K. Comparative QSARs for antimalarial endochins: Importance of descriptor-thinning and noise reduction prior to feature selection. Chemom. Intell. Lab. Syst. 2011, 109, 146–161. [Google Scholar] [CrossRef]
- Lučić, B.; Batista, J.; Bojović, V.; Lovrić, M.; Kržić, A.S.; Bešlo, D.; Nadramija, D.; Vikić-Topić, D. Estimation of random accuracy and its use in validation of predictive quality of classification models within predictive challenges. Croat. Chem. Acta 2019, 92, 379–391. [Google Scholar] [CrossRef] [Green Version]
- Batista, J.; Vikić-Topić, D.; Lučić, B. The difference between the accuracy of real and the corresponding random model is a useful parameter for validation of two-state classification model quality. Croat. Chem. Acta 2016, 89, 527–534. [Google Scholar] [CrossRef]
- Bajusz, D.; Rácz, A.; Héberger, K. Why is Tanimoto index an appropriate choice for fingerprint-based similarity calculations? J. Cheminform. 2015, 7, 20. [Google Scholar] [CrossRef] [Green Version]
- Capecchi, A.; Probst, D.; Reymond, J.L. One molecular fingerprint to rule them all: Drugs, biomolecules, and the metabolome. J. Cheminform. 2020, 12, 43. [Google Scholar] [CrossRef]
- Awale, M.; Reymond, J.L. Web-Based tools for polypharmacology prediction. Methods. Mol. Biol. 2019, 1888, 255–272. [Google Scholar]
- Matsui, Y.; Yasumatsu, I.; Yoshida, K.I.; Iimura, S.; Ikeno, Y.; Nawano, T.; Fukano, H.; Ubukata, O.; Hanzawa, H.; Tanzawa, F.; et al. A novel inhibitor stabilizes the inactive conformation of MAPK-interacting kinase 1. Acta Crystallogr. F Struct. Biol. Commun. 2018, 74, 156–160. [Google Scholar] [CrossRef]
- Reich, S.H.; Sprengeler, P.A.; Chiang, G.G.; Appleman, J.R.; Chen, J.; Clarine, J.; Eam, B.; Ernst, J.T.; Han, Q.; Goel, V.K.; et al. Structure-based Design of Pyridone–Aminal eFT508 targeting dysregulated translation by selective mitogen-activated protein kinase interacting kinases 1 and 2 (MNK1/2) Inhibition. J. Med. Chem. 2018, 61, 3516–3540. [Google Scholar] [CrossRef] [PubMed]
- Bernstein, F.C.; Koetzle, T.F.; Williams, G.J.; Meyer, E.F., Jr.; Brice, M.D.; Rodgers, J.R.; Kennard, O.; Shimanouchi, T.; Tasumi, M. The Protein Data Bank: A computer-based archival file for macromolecular structures. Arch. Biochem. Biophys. 1978, 185, 584–591. [Google Scholar] [CrossRef]
- Morris, G.M.; Huey, R.; Lindstrom, W.; Sanner, M.F.; Belew, R.K.; Goodsell, D.S.; Olson, A.J. AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility. J. Comput. Chem. 2009, 30, 2785–2791. [Google Scholar] [CrossRef] [Green Version]
- Halder, A.K.; Giri, A.K.; Cordeiro, M.N.D.S. Multi-target chemometric modelling, fragment analysis and virtual screening with ERK inhibitors as potential anticancer agents. Molecules 2019, 24, 3909. [Google Scholar] [CrossRef] [Green Version]
- Case, D.A.; Cheatham, T.E.; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M., Jr.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salomon-Ferrer, R.; Case, D.A.; Walker, R.C. An overview of the Amber biomolecular simulation package. WIREs Comput. Mol. Sci. 2013, 3, 198–210. [Google Scholar] [CrossRef]
- Dolinsky, T.J.; Czodrowski, P.; Li, H.; Nielsen, J.E.; Jensen, J.H.; Klebe, G.; Baker, N.A. PDB2PQR: Expanding and upgrading automated preparation of biomolecular structures for molecular simulations. Nucleic Acids Res. 2007, 35, W522–W525. [Google Scholar] [CrossRef] [PubMed]
- Harvey, M.J.; De Fabritiis, G. An implementation of the smooth particle mesh ewald method on GPU hardware. J. Chem. Theory Comput. 2009, 5, 2371–2377. [Google Scholar] [CrossRef] [PubMed]
- Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of N-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef] [Green Version]
- Halder, A.K.; Honarparvar, B. Molecular alteration in drug susceptibility against subtype B and C-SA HIV-1 proteases: MD study. Struct. Chem. 2019, 30, 1715–1727. [Google Scholar] [CrossRef]
- Srinivasan, J.; Cheatham, T.E.; Cieplak, P.; Kollman, P.A.; Case, D.A. Continuum solvent studies of the stability of DNA, RNA, and phosphoramidate−DNA helices. J. Am. Chem. Soc. 1998, 120, 9401–9409. [Google Scholar] [CrossRef]
- Muratov, E.N.; Bajorath, J.; Sheridan, R.P.; Tetko, I.V.; Filimonov, D.; Poroikov, V.; Oprea, T.I.; Baskin, I.I.; Varnek, A.; Roitberg, A.; et al. QSAR without borders. Chem. Soc. Rev. 2020, 49, 3525–3564. [Google Scholar] [CrossRef] [PubMed]
- Speck-Planche, A. Multicellular target QSAR model for simultaneous prediction and design of anti-pancreatic cancer agents. ACS Omega 2019, 4, 3122–3132. [Google Scholar] [CrossRef]
- Reutlinger, M.; Koch, C.P.; Reker, D.; Todoroff, N.; Schneider, P.; Rodrigues, T.; Schneider, G. Chemically Advanced Template Search (CATS) for scaffold-hopping and prospective target prediction for ‘orphan’ molecules. Mol. Inform. 2013, 32, 133–138. [Google Scholar] [CrossRef] [Green Version]
- Pawellek, R.; Krmar, J.; Leistner, A.; Djajić, N.; Otašević, B.; Protić, A.; Holzgrabe, U. Charged aerosol detector response modeling for fatty acids based on experimental settings and molecular features: A machine learning approach. J. Cheminform. 2021, 13, 53. [Google Scholar] [CrossRef]
- Consonni, V.; Todeschini, R. Handbook of Molecular Descriptors; Wiley-VCH: Weinheim, Germany; New York, NY, USA, 2000. [Google Scholar]
- Neves, B.J.; Braga, R.C.; Melo-Filho, C.C.; Moreira-Filho, J.T.; Muratov, E.N.; Andrade, C.H. QSAR-based virtual screening: Advances and applications in drug discovery. Front. Pharmacol. 2018, 9, 1275. [Google Scholar] [CrossRef] [Green Version]
- Daina, A.; Michielin, O.; Zoete, V. SwissADME: A free web tool to evaluate pharmacokinetics, drug-likeness and medicinal chemistry friendliness of small molecules. Sci. Rep. 2017, 7, 42717. [Google Scholar] [CrossRef] [Green Version]
- Lipinski, C.A. Lead- and drug-like compounds: The rule-of-five revolution. Drug Discov. Today Technol. 2004, 1, 337–341. [Google Scholar] [CrossRef]
- Veber, D.F.; Johnson, S.R.; Cheng, H.-Y.; Smith, B.R.; Ward, K.W.; Kopple, K.D. Molecular properties that influence the oral bioavailability of drug candidates. J. Med. Chem. 2002, 45, 2615–2623. [Google Scholar] [CrossRef] [PubMed]
| Parameters | Linear Model (Ten-Descriptor; FS-LDA) | Non-Linear Model (Ten-Descriptor; RF) | Non-Linear Model (All Descriptor; GB) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Sub-Train | Test | Validation | Sub-Train | Test | Validation | Sub-Train | Test | Validation | |
| TP | 308 | 88 | 147 | 314 | 81 | 148 | 318 | 87 | 150 |
| TN | 674 | 154 | 362 | 653 | 152 | 361 | 660 | 158 | 365 |
| FP | 20 | 11 | 20 | 41 | 13 | 21 | 34 | 7 | 17 |
| FN | 57 | 12 | 39 | 51 | 19 | 38 | 47 | 13 | 36 |
| Sensitivity | 97.12 | 93.33 | 94.76 | 86.03 | 92.12 | 94.51 | 87.12 | 95.76 | 95.55 |
| Specificity | 84.38 | 88.00 | 79.03 | 94.09 | 81.00 | 79.57 | 95.10 | 87.00 | 80.64 |
| Accuracy | 92.73 | 91.32 | 89.61 | 91.31 | 87.92 | 89.61 | 92.35 | 92.45 | 90.67 |
| F1-score | 88.89 | 88.44 | 83.29 | 87.22 | 83.50 | 83.38 | 88.70 | 89.69 | 84.98 |
| MCC | 0.838 | 0.815 | 0.76 | na | 0.741 | 0.760 | na | 0.838 | 0.785 |
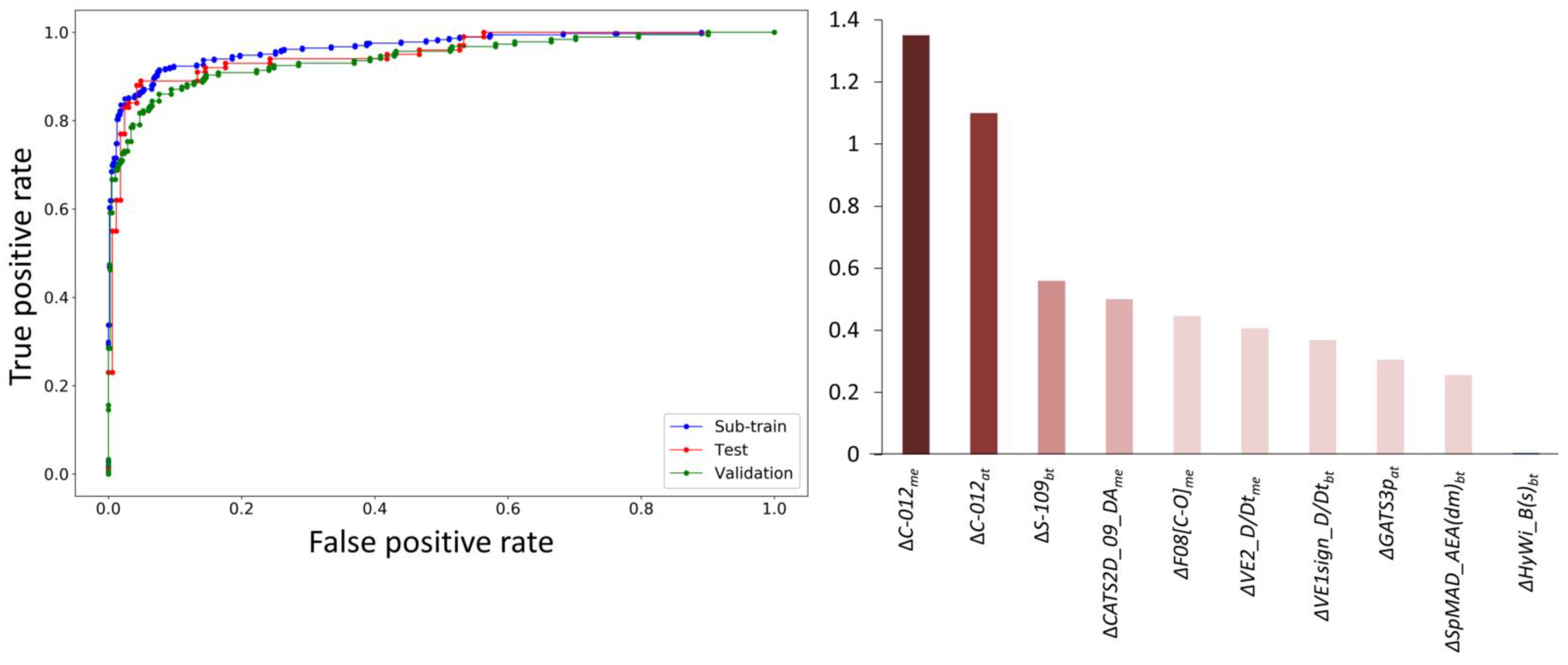
| AUROC | 0.907 | 0.907 | 0.869 | na | 0.866 | 0.870 | na | 0.914 | 0.881 |
| Model | Equation | Sub-Training | Test | Validation |
|---|---|---|---|---|
| Original (FS-LDA) | Wilks λ = 0.319, F = 224.16, p < 10−16 | TP = 308 TN = 674 FP = 20 FN = 57 Sn = 97.12 Sp = 84.38 Acc = 92.73 F1 = 88.89 MCC = 0.838 | TP = 88 TN = 154 FP = 11 FN = 12 Sn = 93.33 Sp = 88.00 Acc = 91.32 F1 = 88.44 MCC = 0.815 | TP = 147 TN = 362 FP = 20 FN = 39 Sn = 94.76 Sp = 79.03 Acc = 89.61 F1 = 83.29 MCC = 0.760 |
| Final (PS3M) | Wilks λ = 0.329, F = 212.86, p < 10−16 | TP = 310 TN = 677 FP = 17 FN = 55 Sn = 97.55 Sp = 84.93 Acc = 93.20 F1 = 89.59 MCC = 0.848 | TP = 89 TN = 158 FP = 7 FN = 11 Sn = 95.76 Sp = 89.00 Acc = 93.20 F1 = 90.82 MCC = 0.855 | TP = 148 TN = 367 FP = 15 FN = 38 Sn = 96.07 Sp = 79.57 Acc = 90.67 F1 = 8 4.81 MCC = 0.785 |
| Condition | me | at | bt | Test Set | External Validation Set | ||
|---|---|---|---|---|---|---|---|
| #Instances | %Accuracy | #Instances | %Accuracy | ||||
| 1 | IC50 | B | MNK-2 | 189 | 88.36 | 107 | 92.52 |
| 2 | IC50 | B | MNK-1 | 104 | 88.46 | 40 | 92.50 |
| 3 | Kd | B | MNK-2 | 20 | 95.00 | 11 | 90.91 |
| 4 | Kd | B | MNK-1 | 31 | 96.77 | 9 | 100.00 |
| 5 | Ki | B | MNK-2 | 19 | 84.21 | 1 | 0.00 |
| 6 | Ki | B | MNK-1 | 15 | 93.33 | 5 | 100.00 |
| 7 | Ki | F | MNK-2 | 190 | 93.16 | 92 | 94.57 |
| Query Compounds | Number of Matches | Average MNK-1/2 Activity b | Average Similarity |
|---|---|---|---|
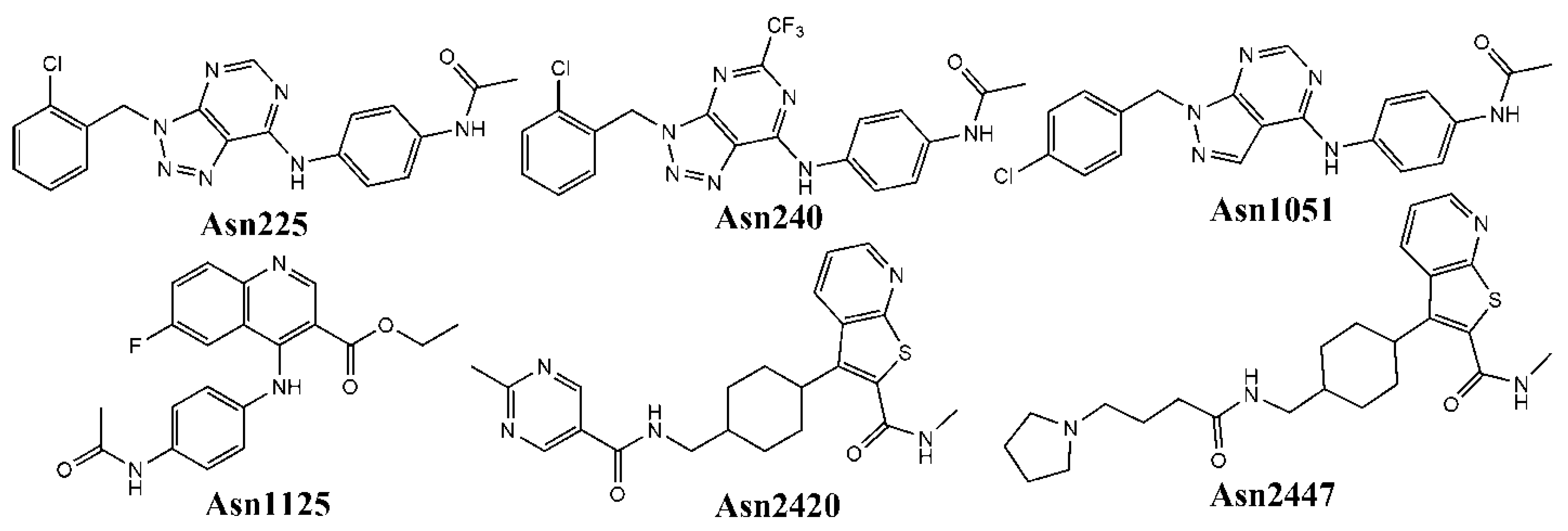
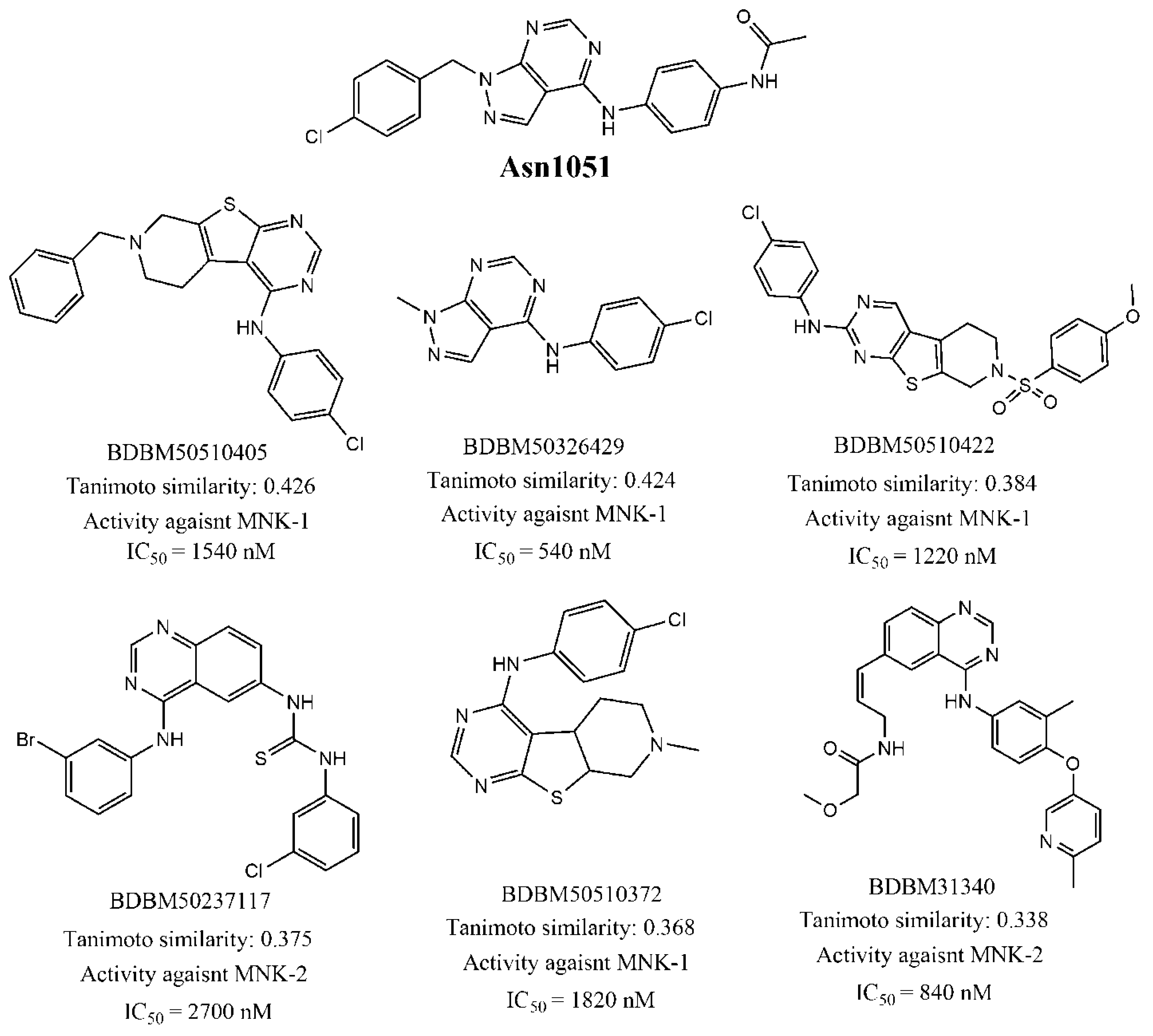
| Asn1051 | 45 | 1085.78 | 0.33 |
| Asn0225 | 30 | 1218.10 | 0.32 |
| Asn1125 | 14 | 646.57 | 0.32 |
| Asn2420 | 14 | 36.36 | 0.32 |
| Asn0240 | 12 | 608.00 | 0.32 |
| Asn2447 | 6 | 22.50 | 0.32 |
| Asn0252 | 4 | 2100.00 | 0.33 |
| Asn2416 | 3 | 35.00 | 0.32 |
| Asn2471 | 3 | 45.00 | 0.31 |
| Asn2459 | 2 | 36.50 | 0.31 |
| Asn2466 | 2 | 49.00 | 0.32 |
| Asn4780 | 2 | 1032.00 | 0.33 |
| Asn2422 | 1 | 46.00 | 0.31 |
| Asn2458 | 1 | 46.00 | 0.32 |
| Compound | ESOL a Class | GI b Absorption | BBB c Permeant | p-gp d Substrate | Lipinski #Violations | Veber #Violations | Synthetic Accessibility |
|---|---|---|---|---|---|---|---|
| Asn0225 | Moderate | High | No | No | 0 | 0 | 3.06 |
| Asn0240 | Moderate | High | No | No | 0 | 0 | 3.28 |
| Asn1051 | Moderate | High | No | No | 0 | 0 | 2.77 |
| Asn1125 | Moderate | High | No | No | 0 | 0 | 2.67 |
| Asn2420 | Moderate | High | No | Yes | 0 | 0 | 4.18 |
| Asn2447 | Moderate | High | No | Yes | 0 | 0 | 4.44 |
| Query Compounds | MNK-1 | MNK-2 |
|---|---|---|
| Asn1051 | −40.20 | −37.21 |
| Asn0225 | −52.97 | −35.21 |
| Asn1125 | −32.32 | −37.45 |
| Asn2420 | −38.38 | −48.94 |
| Asn0240 | −32.33 | −42.28 |
| Asn2447 | −31.88 | −29.71 |
| eFT508 | −36.41 | −44.82 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Halder, A.K.; Cordeiro, M.N.D.S. Multi-Target In Silico Prediction of Inhibitors for Mitogen-Activated Protein Kinase-Interacting Kinases. Biomolecules 2021, 11, 1670. https://doi.org/10.3390/biom11111670
Halder AK, Cordeiro MNDS. Multi-Target In Silico Prediction of Inhibitors for Mitogen-Activated Protein Kinase-Interacting Kinases. Biomolecules. 2021; 11(11):1670. https://doi.org/10.3390/biom11111670
Chicago/Turabian StyleHalder, Amit Kumar, and M. Natália D. S. Cordeiro. 2021. "Multi-Target In Silico Prediction of Inhibitors for Mitogen-Activated Protein Kinase-Interacting Kinases" Biomolecules 11, no. 11: 1670. https://doi.org/10.3390/biom11111670
APA StyleHalder, A. K., & Cordeiro, M. N. D. S. (2021). Multi-Target In Silico Prediction of Inhibitors for Mitogen-Activated Protein Kinase-Interacting Kinases. Biomolecules, 11(11), 1670. https://doi.org/10.3390/biom11111670







