Computational Insights into the Binding Mechanism of OxyS sRNA with Chaperone Protein Hfq
Abstract
:1. Introduction
2. Materials and Methods
2.1. Molecular Dynamics Simulations
2.2. MM/GBSA Method
2.3. Interaction Entropy
2.4. Free Energy Perturbation Calculations
3. Results and Discussion
3.1. MD Simulation and Binding Free Energies
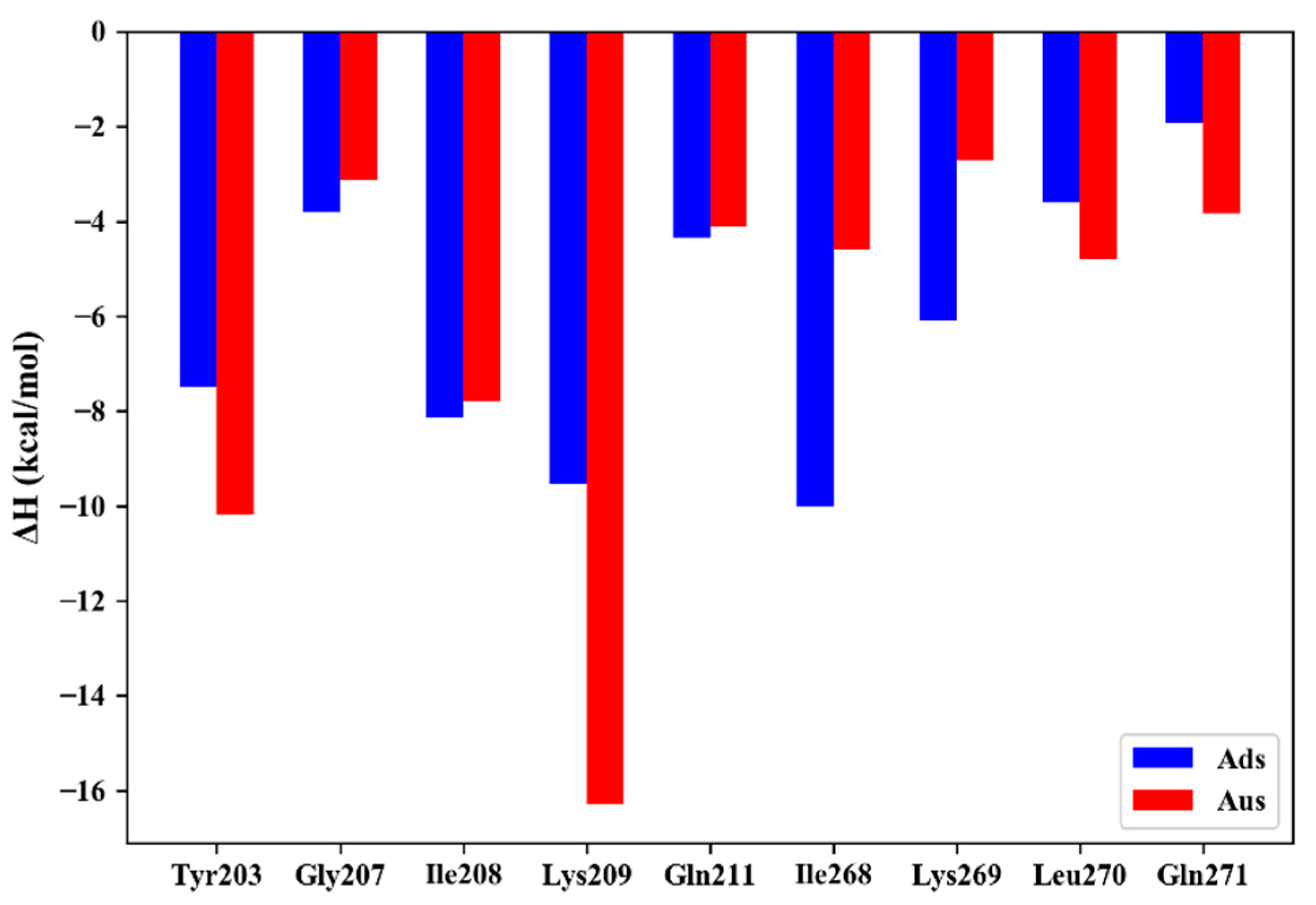
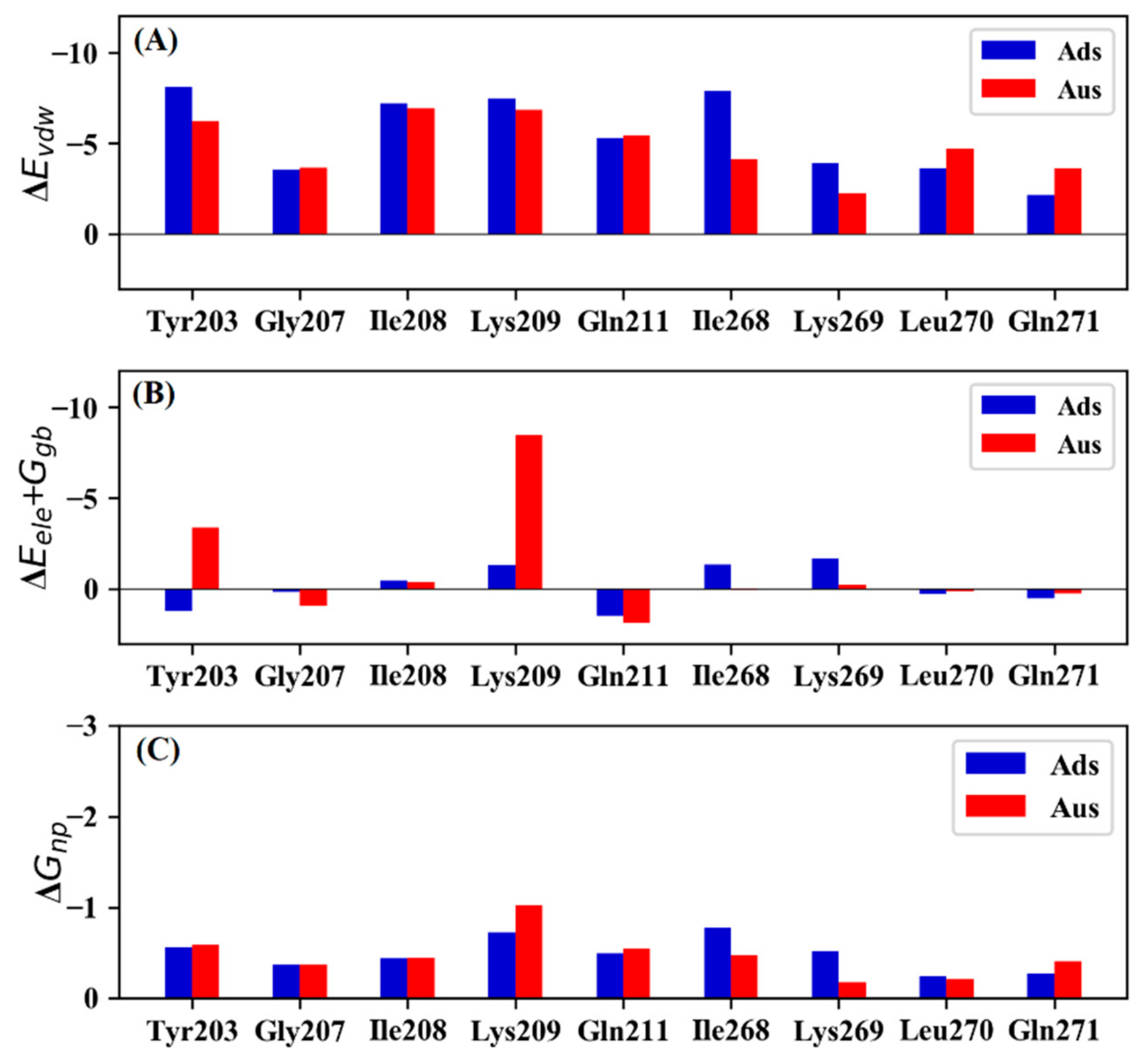
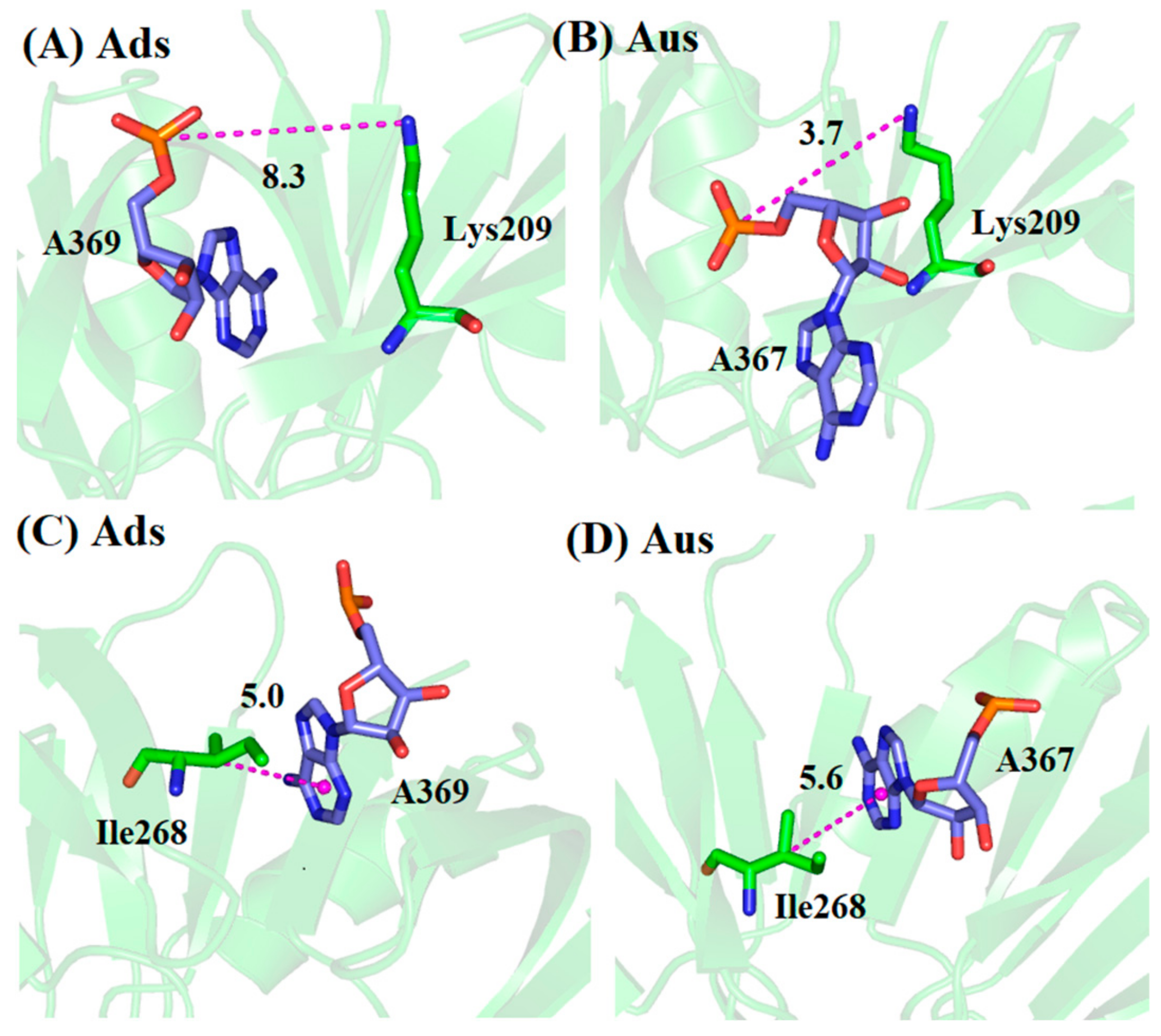
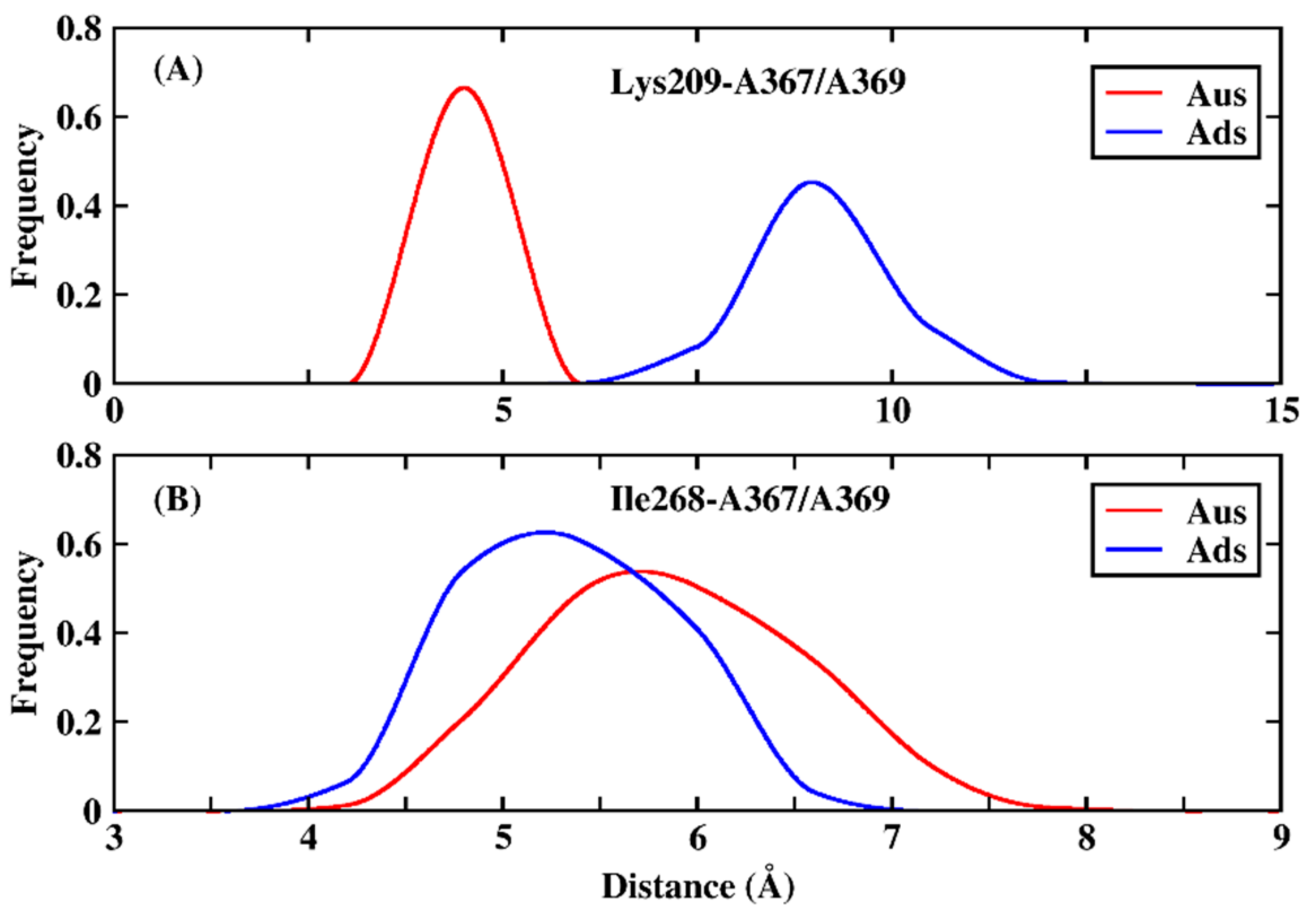
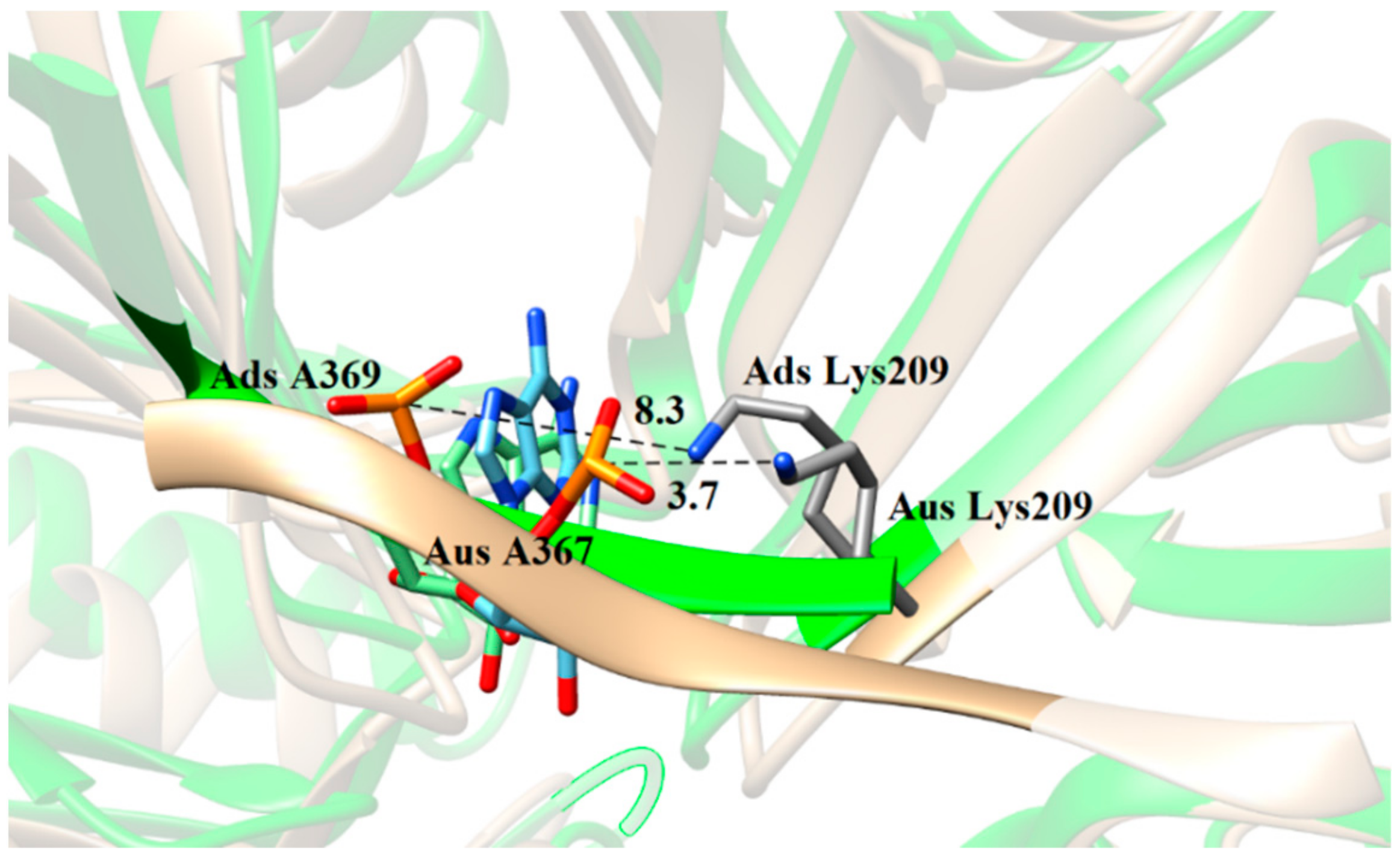
3.2. Comparison of Binding Mode of Ads and Aus
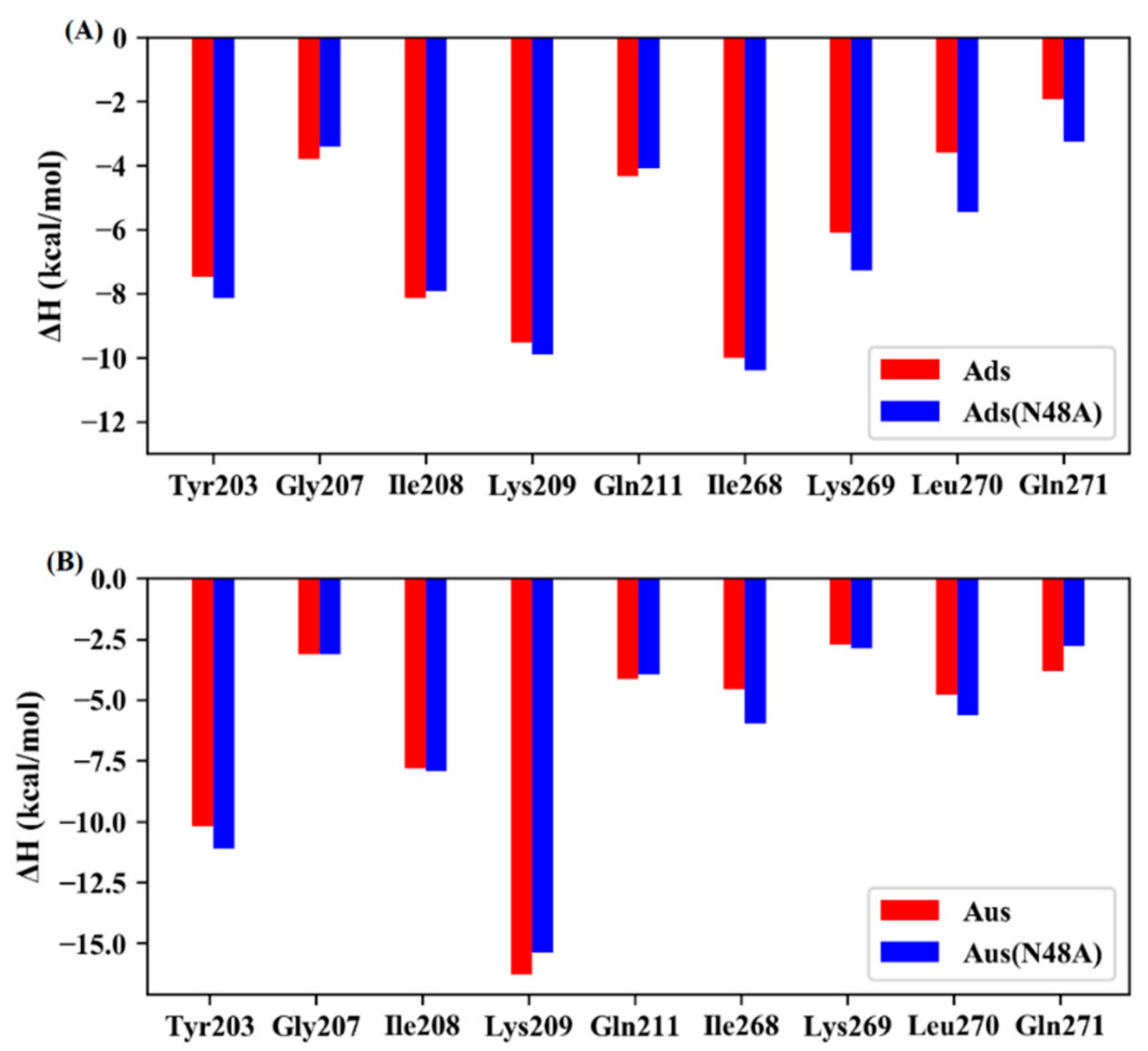
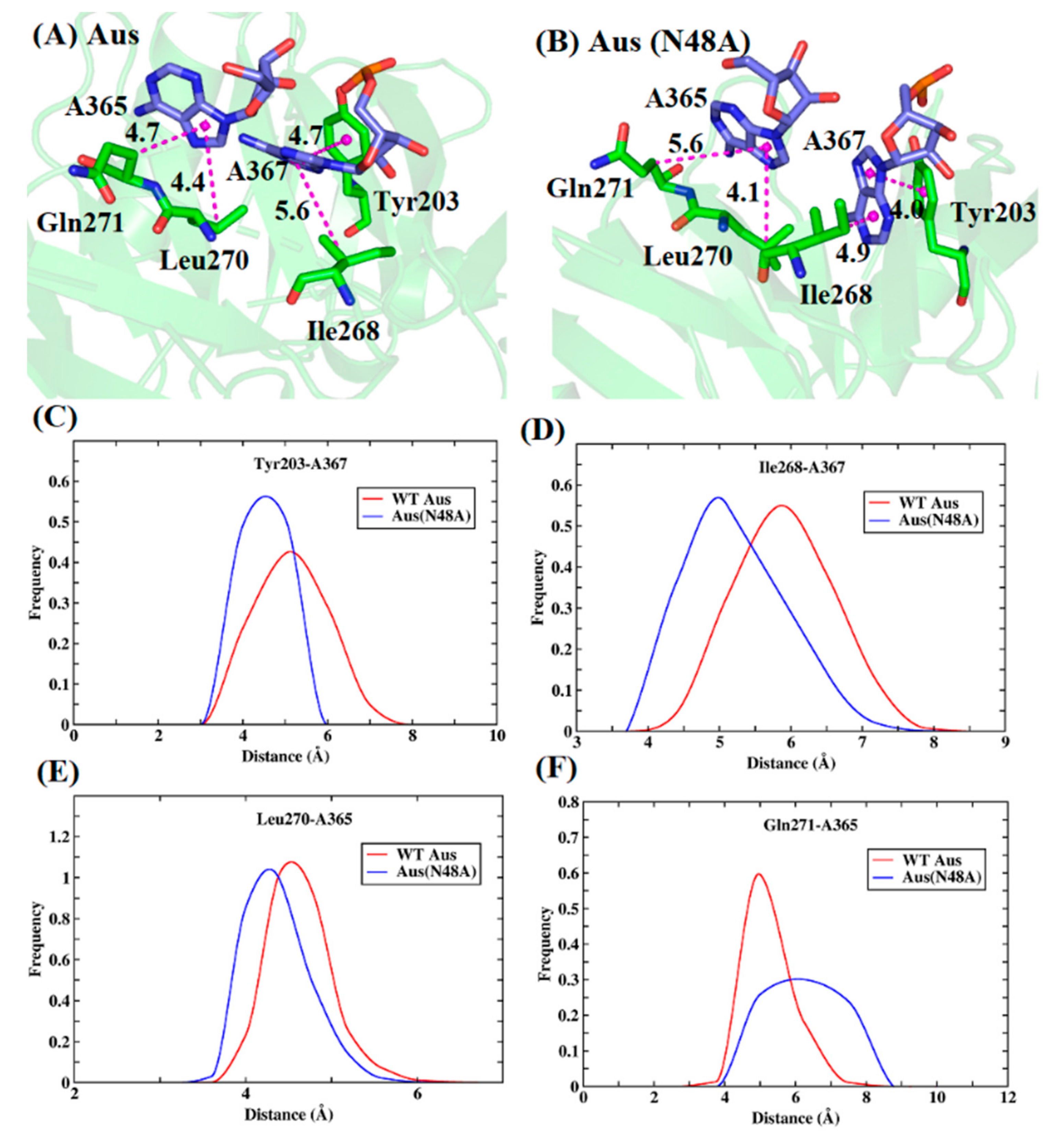
3.3. Mutational Effect of Ads and Aus
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Brosius, J.; Tiedge, H. RNomenclature. RNA Biol. 2004, 1, 81–83. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoe, C.-H.; Raabe, C.A.; Rozhdestvensky, T.S.; Tang, T.-H. Bacterial sRNAs: Regulation in stress. Int. J. Med. Microbiol. 2013, 303, 217–229. [Google Scholar] [CrossRef] [PubMed]
- Altuvia, S.; Weinstein-Fischer, D.; Zhang, A.; Postow, L.; Storz, G. A small, stable RNA induced by oxidative stress: Role as a pleiotropic regulator and antimutator. Cell 1997, 90, 43–53. [Google Scholar] [CrossRef] [Green Version]
- Chambers, J.R.; Sauer, K. Small RNAs and their role in biofilm formation. Trends Microbiol. 2013, 21, 39–49. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gottesman, S.; McCullen, C.; Guillier, M.; Vanderpool, C.; Majdalani, N.; Benhammou, J.; Thompson, K.; Fitzgerald, P.; Sowa, N.; Fitzgerald, D. Small RNA regulators and the bacterial response to stress. Cold Spring Harb. Symp. Quant. Biol. 2006, 71, 1–11. [Google Scholar] [CrossRef]
- De Lay, N.; Schu, D.J.; Gottesman, S. Bacterial small RNA-based negative regulation: Hfq and its accomplices. J. Biol. Chem. 2013, 288, 7996–8003. [Google Scholar] [CrossRef] [Green Version]
- Bossi, L.; Figueroa-Bossi, N. Competing endogenous RNAs: A target-centric view of small RNA regulation in bacteria. Nat. Rev. Genet. 2016, 14, 775–784. [Google Scholar] [CrossRef] [Green Version]
- Lalaouna, D.; Simoneau-Roy, M.; Lafontaine, D.; Massé, E. Regulatory RNAs and target mRNA decay in prokaryotes. Biochim. Biophys. Acta Bioenerg. 2013, 1829, 742–747. [Google Scholar] [CrossRef]
- Chinni, S.; Raabe, C.A.; Zakaria, R.; Randau, G.; Hoe, C.H.; Zemann, A.; Brosius, J.; Tang, T.-H.; Rozhdestvensky, T.S. Experimental identification and characterization of 97 novel npcRNA candidates in Salmonella enterica serovar Typhi. Nucleic Acids Res. 2010, 38, 5893–5908. [Google Scholar] [CrossRef] [Green Version]
- Waters, L.S.; Storz, G. Regulatory RNAs in Bacteria. Cell 2009, 136, 615–628. [Google Scholar] [CrossRef] [Green Version]
- Saramago, M.; Bárria, C.; dos Santos, R.F.; Silva, I.; Pobre, V.; Domingues, S.; Andrade, J.; Viegas, S.; Arraiano, C.M. The role of RNases in the regulation of small RNAs. Curr. Opin. Microbiol. 2014, 18, 105–115. [Google Scholar] [CrossRef] [PubMed]
- Quendera, A.; Seixas, A.F.; Dos Santos, R.F.; Santos, I.; Silva, J.P.N.; Arraiano, C.M.; Andrade, J.M. RNA-binding proteins driving the regulatory activity of small non-coding RNAs in bacteria. Front. Mol. Biosci. 2020, 7, 9. [Google Scholar] [CrossRef] [PubMed]
- Shimoni, Y.; Friedlander, G.; Hetzroni, G.; Niv, G.; Altuvia, S.; Biham, O.; Margalit, H. Regulation of gene expression by small non-coding RNAs: A quantitative view. Mol. Syst. Biol. 2007, 3, 138. [Google Scholar] [CrossRef] [PubMed]
- Schulz, E.C.; Seiler, M.; Zuliani, C.; Voigt, F.; Rybin, V.; Pogenberg, V.; Mücke, N.; Wilmanns, M.; Gibson, T.J.; Barabas, O. Intermolecular base stacking mediates RNA-RNA interaction in a crystal structure of the RNA chaperone Hfq. Sci. Rep. 2017, 7, 9903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sauter, C.; Basquin, J.; Suck, D. Sm-like proteins in Eubacteria: The crystal structure of the Hfq protein from Escherichia coli. Nucleic Acids Res. 2003, 31, 4091–4098. [Google Scholar] [CrossRef] [Green Version]
- Weichenrieder, O. RNA binding by Hfq and ring-forming (L)Sm proteins A trade-off be-tween optimal sequence readout and RNA backbone conformation. RNA Biol. 2014, 11, 537–549. [Google Scholar] [CrossRef] [Green Version]
- Brennan, R.G.; Link, T.M. Hfq structure, function and ligand binding. Curr. Opin. Microbiol. 2007, 10, 125–133. [Google Scholar] [CrossRef]
- Møller, T.; Franch, T.; Højrup, P.; Keene, D.R.; Bächinger, H.P.; Brennan, R.G.; Valentin-Hansen, P. Hfq: A bacterial Sm-like protein that mediates RNA-RNA interaction. Mol. Cell 2002, 9, 23–30. [Google Scholar] [CrossRef]
- Otaka, H.; Ishikawa, H.; Morita, T.; Aiba, H. PolyU tail of rho-independent terminator of bacterial small RNAs is essential for Hfq action. Proc. Natl. Acad. Sci. USA 2011, 108, 13059–13064. [Google Scholar] [CrossRef] [Green Version]
- Kovach, A.R.; Hoff, K.E.; Canty, J.; Orans, J.; Brennan, R.G. Recognition of U-rich RNA by Hfq from the Gram-positive pathogenListeria monocytogenes. RNA 2014, 20, 1548–1559. [Google Scholar] [CrossRef] [Green Version]
- Sauer, E.; Schmidt, S.; Weichenrieder, O. Small RNA binding to the lateral surface of Hfq hexamers and structural rearrangements upon mRNA target recognition. Proc. Natl. Acad. Sci. USA 2012, 109, 9396–9401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Papenfort, K.; Vanderpool, C.K. Target activation by regulatory RNAs in bacteria. FEMS Microbiol. Rev. 2015, 39, 362–378. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chao, Y.; Vogel, J. The role of Hfq in bacterial pathogens. Curr. Opin. Microbiol. 2010, 13, 24–33. [Google Scholar] [CrossRef]
- Papenfort, K.; Vogel, J. Regulatory RNA in bacterial pathogens. Cell Host Microbe 2010, 8, 116–127. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chambers, J.R.; Bender, K.S. The RNA chaperone Hfq is important for growth and stress tolerance in Francisella novicida. PLoS ONE 2011, 6, e19797. [Google Scholar] [CrossRef] [Green Version]
- Zhang, A.; Wassarman, K.M.; Ortega, J.; Steven, A.C.; Storz, G. The Sm-like Hfq protein increases OxyS RNA interaction with target mRNAs. Mol. Cell 2002, 9, 11–22. [Google Scholar] [CrossRef]
- Updegrove, T.B.; Wartell, R.M. The influence of Escherichia coli Hfq mutations on RNA binding and sRNA•mRNA duplex formation in rpoS riboregulation. Biochim. Biophys. Acta Bioenerg. 2011, 1809, 532–540. [Google Scholar] [CrossRef]
- Henderson, C.A.; Vincent, H.A.; Casamento, A.; Stone, C.M.; Phillips, J.O.; Cary, P.D.; Sobott, F.; Gowers, D.M.; Taylor, J.E.; Callaghan, A.J. Hfq binding changes the structure of Escherichia coli small noncoding RNAs OxyS and RprA, which are involved in the riboregulation of rpoS. RNA 2013, 19, 1089–1104. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Wang, W.; Li, F.; Zhang, J.; Wu, J.; Gong, Q.; Shi, Y. Structural insights into the recognition of the internal A-rich linker from OxyS sRNA by Esche-richia coli Hfq. Nucleic Acids Res. 2015, 43, 2400–2411. [Google Scholar] [CrossRef] [Green Version]
- McCammon, J.A.; Gelin, B.R.; Karplus, M. Dynamics of folded proteins. Nat. Cell Biol. 1977, 267, 585–590. [Google Scholar] [CrossRef]
- Elcock, A.H. Molecular simulations of diffusion and association in multimacromolecular systems. In Numerical Computer Methods; Pt, D., Brand, L., Johnson, M.L., Eds.; Elsevier Academic Press Inc.: San Diego, CA, USA, 2004; Volume 383, pp. 166–198. [Google Scholar]
- Winkler, D.A. Ligand Entropy is hard but should not be ignored. J. Chem. Inf. Model. 2020, 60, 4421–4423. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Qiu, L.; Zhang, J.Z. Erratum on “An efficient method for computing excess free energy of liquid”. Sci. China Chem. 2018, 61, 1638. [Google Scholar] [CrossRef] [Green Version]
- Qiu, L.; Yan, Y.; Sun, Z.; Song, J.; Zhang, J.Z. Interaction entropy for computational alanine scanning in protein-protein binding. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2017, 8, e1342. [Google Scholar] [CrossRef]
- Zou, Y.; Qian, Z.; Sun, Y.; Wei, G.; Zhang, Q. Orcein-related small molecule O4 desta-bilizes hIAPP protofibrils by interacting mostly with the Amyloidogenic core region. J. Phys. Chem. B 2017, 121, 9203–9212. [Google Scholar] [CrossRef] [PubMed]
- Thai, N.Q.; Nguyen, H.L.; Linh, H.Q.; Li, M.S. Protocol for fast screening of multi-target drug candidates: Application to Alzheimer’s disease. J. Mol. Graph. Model. 2017, 77, 121–129. [Google Scholar] [CrossRef] [PubMed]
- Shirts, M.R.; Pitera, J.W.; Swope, W.C.; Pande, V.S. Extremely precise free energy calculations of amino acid side chain analogs: Comparison of common molecular mechanics force fields for proteins. J. Chem. Phys. 2003, 119, 5740–5761. [Google Scholar] [CrossRef] [Green Version]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The protein data bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [Green Version]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. ff14SB: Improving the accuracy of protein side chain and backbone parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef] [Green Version]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Ryckaert, J.-P.; Ciccotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef] [Green Version]
- Duan, L.; Liu, X.; Zhang, J.Z. Interaction entropy: A new paradigm for highly efficient and reliable computation of protein–ligand binding free energy. J. Am. Chem. Soc. 2016, 138, 5722–5728. [Google Scholar] [CrossRef] [PubMed]

| System | Simulation | ||||
|---|---|---|---|---|---|
| Ads | No. 1 | −62.4 ± 0.4 | 33.8 ± 0.0 | −28.6 ± 0.4 | −8.0 |
| No. 2 | −60.3 ± 0.5 | 35.1 ± 0.0 | −25.2 ± 0.5 | ||
| No. 3 | −62.4 ± 0.5 | 33.3 ± 0.0 | −29.2 ± 0.5 | ||
| Ave | −61.7 | 34.0 | −27.7 | ||
| Ads (N48A) | No. 1 | −65.4 ± 0.4 | 36.5 ± 0.0 | −28.9 ± 0.4 | −9.6 |
| No. 2 | −66.5 ± 0.4 | 38.2 ± 0.0 | −28.3 ± 0.4 | ||
| No. 3 | −64.1 ± 0.3 | 31.5 ± 0.0 | −32.6 ± 0.3 | ||
| Ave | −65.3 | 35.4 | −29.9 | ||
| Aus | No. 1 | −61.3 ± 0.4 | 30.7 ± 0.0 | −30.6 ± 0.4 | −10.5 |
| No. 2 | −64.2 ± 0.4 | 32.7 ± 0.0 | −31.5 ± 0.4 | ||
| No. 3 | −67.5 ± 0.4 | 40.4 ± 0.0 | −27.2 ± 0.4 | ||
| Ave | −64.3 | 34.6 | −29.7 | ||
| Aus (N48A) | No. 1 | −68.7 ± 0.4 | 37.8 ± 0.0 | −30.9 ± 0.4 | −10.6 |
| No. 2 | −67.7 ± 0.3 | 33.3 ± 0.0 | −34.4 ± 0.3 | ||
| No. 3 | −65.8 ± 0.4 | 37.1 ± 0.0 | −28.7 ± 0.4 | ||
| Ave | −67.4 | 36.1 | −31.3 |
| Acceptor | Donor | Occupancy (%) | Distance (Å) | Angle (°) | |
|---|---|---|---|---|---|
| Ads | A369@OP2 a | Tyr203@OH | 0.0 | 5.3 | 111.0 |
| U368@OP1 | Lys269@N | 62.1 | 3.8 | 154.8 | |
| Aus | A367@OP2 a | Tyr203@OH | 95.5 | 2.7 | 163.4 |
| U366@OP1 | Lys269@N | 0.0 | 11.9 | 132.9 |
| System | |||
|---|---|---|---|
| Ads (N48A) | −2.2 | −2.9 | −1.6 |
| Aus (N48A) | −1.6 | −4.1 | −0.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Cong, Y.; Qi, Y.; Zhang, J.Z.H. Computational Insights into the Binding Mechanism of OxyS sRNA with Chaperone Protein Hfq. Biomolecules 2021, 11, 1653. https://doi.org/10.3390/biom11111653
Li M, Cong Y, Qi Y, Zhang JZH. Computational Insights into the Binding Mechanism of OxyS sRNA with Chaperone Protein Hfq. Biomolecules. 2021; 11(11):1653. https://doi.org/10.3390/biom11111653
Chicago/Turabian StyleLi, Mengxin, Yalong Cong, Yifei Qi, and John Z. H. Zhang. 2021. "Computational Insights into the Binding Mechanism of OxyS sRNA with Chaperone Protein Hfq" Biomolecules 11, no. 11: 1653. https://doi.org/10.3390/biom11111653
APA StyleLi, M., Cong, Y., Qi, Y., & Zhang, J. Z. H. (2021). Computational Insights into the Binding Mechanism of OxyS sRNA with Chaperone Protein Hfq. Biomolecules, 11(11), 1653. https://doi.org/10.3390/biom11111653







