When Order Meets Disorder: Modeling and Function of the Protein Interface in Fuzzy Complexes
Abstract
1. Introduction
2. Modeling Tools for Fuzzy Complexes
2.1. All-Atom Force Fields
2.2. Alternate Protein and Solvent Models
2.3. Algorithms
2.4. Integrating Experimental Data
2.5. Measuring and Comparing Disorder
3. Functional Role of the Fuzzy Interface in the Cell
3.1. Interactions between the C-Terminal Tails of α,β-Tubulin Dimers and the Tubulin Core
3.2. Role of the RecA Protein C-Terminal Tails in Homologous Recombination
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anfinsen, C.B. Principles that govern the folding of protein chains. Science 1973, 181, 223–230. [Google Scholar] [CrossRef]
- Wright, P.E.; Dyson, H.J. Intrinsically unstructured proteins: Re-assessing the protein structure-function paradigm. J. Mol. Biol. 1999, 293, 321–331. [Google Scholar] [CrossRef] [PubMed]
- Perdigao, N.; Heinrich, J.; Stolte, C.; Sabir, K.S.; Buckley, M.J.; Tabor, B.; Signal, B.; Gloss, B.S.; Hammang, C.J.; Rost, B.; et al. Unexpected features of the dark proteome. Proc. Natl. Acad. Sci. USA 2015, 112, 15898–15903. [Google Scholar] [CrossRef] [PubMed]
- Bhowmick, A.; Brookes, D.H.; Yost, S.R.; Dyson, H.J.; Forman-Kay, J.D.; Gunter, D.; Head-Gordon, M.; Hura, G.L.; Pande, V.S.; Wemmer, D.E.; et al. Finding Our Way in the Dark Proteome. J. Am. Chem. Soc. 2016, 138, 9730–9742. [Google Scholar] [CrossRef]
- Uversky, V.N. The mysterious unfoldome: Structureless, underappreciated, yet vital part of any given proteome. J. Biomed. Biotechnol. 2010, 2010, 568068. [Google Scholar] [CrossRef]
- Tompa, P. Unstructural biology coming of age. Curr. Opin. Struct. Biol. 2011, 21, 419–425. [Google Scholar] [CrossRef] [PubMed]
- Xie, H.; Vucetic, S.; Iakoucheva, L.M.; Oldfield, C.J.; Dunker, A.K.; Uversky, V.N.; Obradovic, Z. Functional anthology of intrinsic disorder. 1. Biological processes and functions of proteins with long disordered regions. J. Proteome Res. 2007, 6, 1882–1898. [Google Scholar] [CrossRef]
- Wright, P.E.; Dyson, H.J. Intrinsically disordered proteins in cellular signalling and regulation. Nat. Rev. Mol. Cell Biol. 2015, 16, 18–29. [Google Scholar] [CrossRef]
- Monzon, A.M.; Necci, M.; Quaglia, F.; Walsh, I.; Zanotti, G.; Piovesan, D.; Tosatto, S.C.E. Experimentally Determined Long Intrinsically Disordered Protein Regions Are Now Abundant in the Protein Data Bank. Int. J. Mol. Sci. 2020, 21, 4496. [Google Scholar] [CrossRef]
- Fuxreiter, M. Fuzziness in Protein Interactions-A Historical Perspective. J. Mol. Biol. 2018, 430, 2278–2287. [Google Scholar] [CrossRef]
- Tompa, P.; Fuxreiter, M. Fuzzy complexes: Polymorphism and structural disorder in protein-protein interactions. Trends Biochem. Sci. 2008, 33, 2–8. [Google Scholar] [CrossRef]
- Fuxreiter, M. Classifying the Binding Modes of Disordered Proteins. Int. J. Mol. Sci. 2020, 21, 8615. [Google Scholar] [CrossRef]
- Freiberger, M.I.; Wolynes, P.G.; Ferreiro, D.U.; Fuxreiter, M. Frustration in Fuzzy Protein Complexes Leads to Interaction Versatility. J. Phys. Chem. B 2021, 125, 2513–2520. [Google Scholar] [CrossRef]
- Ross, E.D.; Edskes, H.K.; Terry, M.J.; Wickner, R.B. Primary sequence independence for prion formation. Proc. Natl. Acad. Sci. USA 2005, 102, 12825–12830. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Hamkalo, B.; Parseghian, M.H.; Hansen, J.C. Chromatin condensing functions of the linker histone C-terminal domain are mediated by specific amino acid composition and intrinsic protein disorder. Biochemistry 2009, 48, 164–172. [Google Scholar] [CrossRef] [PubMed]
- Fuxreiter, M.; Tompa, P. Fuzzy complexes: A more stochastic view of protein function. Adv. Exp. Med. Biol. 2012, 725, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Li, S.; Landsman, D.; Panchenko, A.R. Histone tails as signaling antennas of chromatin. Curr. Opin. Struct. Biol. 2021, 67, 153–160. [Google Scholar] [CrossRef]
- Rauscher, S.; Gapsys, V.; Gajda, M.J.; Zweckstetter, M.; de Groot, B.L.; Grubmuller, H. Structural Ensembles of Intrinsically Disordered Proteins Depend Strongly on Force Field: A Comparison to Experiment. J. Chem. Theory Comput. 2015, 11, 5513–5524. [Google Scholar] [CrossRef]
- Best, R.B.; Buchete, N.V.; Hummer, G. Are current molecular dynamics force fields too helical? Biophys. J. 2008, 95, L07–L09. [Google Scholar] [CrossRef]
- Best, R.B. Computational and theoretical advances in studies of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2017, 42, 147–154. [Google Scholar] [CrossRef]
- Robustelli, P.; Piana, S.; Shaw, D.E. Developing a molecular dynamics force field for both folded and disordered protein states. Proc. Natl. Acad. Sci. USA 2018, 115, E4758–E4766. [Google Scholar] [CrossRef]
- Mu, J.; Liu, H.; Zhang, J.; Luo, R.; Chen, H.F. Recent Force Field Strategies for Intrinsically Disordered Proteins. J. Chem. Inf. Model. 2021, 61, 1037–1047. [Google Scholar] [CrossRef] [PubMed]
- Best, R.B.; Hummer, G. Optimized molecular dynamics force fields applied to the helix-coil transition of polypeptides. J. Phys. Chem. B 2009, 113, 9004–9015. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Li, D.W.; Bruschweiler, R. Balanced Amino-Acid-Specific Molecular Dynamics Force Field for the Realistic Simulation of Both Folded and Disordered Proteins. J. Chem. Theory Comput. 2020, 16, 1311–1318. [Google Scholar] [CrossRef] [PubMed]
- Lindorff-Larsen, K.; Piana, S.; Palmo, K.; Maragakis, P.; Klepeis, J.L.; Dror, R.O.; Shaw, D.E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins 2010, 78, 1950–1958. [Google Scholar] [CrossRef]
- Piana, S.; Lindorff-Larsen, K.; Shaw, D.E. How robust are protein folding simulations with respect to force field parameterization? Biophys. J. 2011, 100, L47–L49. [Google Scholar] [CrossRef]
- Robertson, M.J.; Tirado-Rives, J.; Jorgensen, W.L. Improved Peptide and Protein Torsional Energetics with the OPLSAA Force Field. J. Chem. Theory Comput. 2015, 11, 3499–3509. [Google Scholar] [CrossRef]
- Harder, E.; Damm, W.; Maple, J.; Wu, C.; Reboul, M.; Xiang, J.Y.; Wang, L.; Lupyan, D.; Dahlgren, M.K.; Knight, J.L.; et al. OPLS3: A Force Field Providing Broad Coverage of Drug-like Small Molecules and Proteins. J. Chem. Theory Comput. 2016, 12, 281–296. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, H.; Yang, S.; Luo, R.; Chen, H.F. Well-Balanced Force Field ff03CMAP for Folded and Disordered Proteins. J. Chem. Theory Comput. 2019, 15, 6769–6780. [Google Scholar] [CrossRef]
- Nettels, D.; Muller-Spath, S.; Kuster, F.; Hofmann, H.; Haenni, D.; Ruegger, S.; Reymond, L.; Hoffmann, A.; Kubelka, J.; Heinz, B.; et al. Single-molecule spectroscopy of the temperature-induced collapse of unfolded proteins. Proc. Natl. Acad. Sci. USA 2009, 106, 20740–20745. [Google Scholar] [CrossRef]
- Piana, S.; Klepeis, J.L.; Shaw, D.E. Assessing the accuracy of physical models used in protein-folding simulations: Quantitative evidence from long molecular dynamics simulations. Curr. Opin. Struct. Biol. 2014, 24, 98–105. [Google Scholar] [CrossRef] [PubMed]
- Piana, S.; Donchev, A.G.; Robustelli, P.; Shaw, D.E. Water dispersion interactions strongly influence simulated structural properties of disordered protein states. J. Phys. Chem. B 2015, 119, 5113–5123. [Google Scholar] [CrossRef]
- Abriata, L.A.; Dal Peraro, M. Assessment of transferable forcefields for protein simulations attests improved description of disordered states and secondary structure propensities, and hints at multi-protein systems as the next challenge for optimization. Comput. Struct. Biotechnol. J. 2021, 19, 2626–2636. [Google Scholar] [CrossRef] [PubMed]
- Uversky, V.N. Intrinsically disordered proteins and their environment: Effects of strong denaturants, temperature, pH, counter ions, membranes, binding partners, osmolytes, and macromolecular crowding. Protein J. 2009, 28, 305–325. [Google Scholar] [CrossRef] [PubMed]
- Kjaergaard, M.; Norholm, A.B.; Hendus-Altenburger, R.; Pedersen, S.F.; Poulsen, F.M.; Kragelund, B.B. Temperature-dependent structural changes in intrinsically disordered proteins: Formation of alpha-helices or loss of polyproline II? Protein Sci. 2010, 19, 1555–1564. [Google Scholar] [CrossRef]
- Wuttke, R.; Hofmann, H.; Nettels, D.; Borgia, M.B.; Mittal, J.; Best, R.B.; Schuler, B. Temperature-dependent solvation modulates the dimensions of disordered proteins. Proc. Natl. Acad. Sci. USA 2014, 111, 5213–5218. [Google Scholar] [CrossRef]
- Jephthah, S.; Staby, L.; Kragelund, B.B.; Skepo, M. Temperature Dependence of Intrinsically Disordered Proteins in Simulations: What are We Missing? J. Chem. Theory Comput. 2019, 15, 2672–2683. [Google Scholar] [CrossRef]
- Kaminski, G.A.; Stern, H.A.; Berne, B.J.; Friesner, R.A.; Cao, Y.X.; Murphy, R.B.; Zhou, R.; Halgren, T.A. Development of a polarizable force field for proteins via ab initio quantum chemistry: First generation model and gas phase tests. J. Comput. Chem. 2002, 23, 1515–1531. [Google Scholar] [CrossRef]
- Huang, J.; MacKerell, A.D., Jr. Force field development and simulations of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2018, 48, 40–48. [Google Scholar] [CrossRef]
- Wang, A.; Zhang, Z.; Li, G. Higher Accuracy Achieved in the Simulations of Protein Structure Refinement, Protein Folding, and Intrinsically Disordered Proteins Using Polarizable Force Fields. J. Phys. Chem. Lett. 2018, 9, 7110–7116. [Google Scholar] [CrossRef]
- Inakollu, V.S.; Geerke, D.P.; Rowley, C.N.; Yu, H. Polarisable force fields: What do they add in biomolecular simulations? Curr. Opin. Struct. Biol. 2020, 61, 182–190. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Xia, Z.; Zhang, J.; Best, R.; Wu, C.; Ponder, J.W.; Ren, P. The Polarizable Atomic Multipole-based AMOEBA Force Field for Proteins. J. Chem. Theory Comput. 2013, 9, 4046–4063. [Google Scholar] [CrossRef] [PubMed]
- Patel, S.; Mackerell, A.D., Jr.; Brooks, C.L., III. CHARMM fluctuating charge force field for proteins: II protein/solvent properties from molecular dynamics simulations using a nonadditive electrostatic model. J. Comput. Chem. 2004, 25, 1504–1514. [Google Scholar] [CrossRef] [PubMed]
- Lopes, P.E.M.; Huang, J.; Shim, J.; Luo, Y.; Li, H.; Roux, B.; MacKerell, A.D. Polarizable Force Field for Peptides and Proteins Based on the Classical Drude Oscillator. J. Chem. Theory Comput. 2013, 9, 5430–5449. [Google Scholar] [CrossRef]
- Cieplak, P.; Caldwell, J.; Kollman, P. Molecular mechanical models for organic and biological systems going beyond the atom centered two body additive approximation: Aqueous solution free energies of methanol and N-methyl acetamide, nucleic acid base, and amide hydrogen bonding and chloroform/water partition coefficients of the nucleic acid bases. J. Comput. Chem. 2001, 22, 1048–1057. [Google Scholar] [CrossRef]
- Shoemaker, B.A.; Portman, J.J.; Wolynes, P.G. Speeding molecular recognition by using the folding funnel: The fly-casting mechanism. Proc. Natl. Acad. Sci. USA 2000, 97, 8868–8873. [Google Scholar] [CrossRef]
- Rogers, J.M.; Oleinikovas, V.; Shammas, S.L.; Wong, C.T.; De Sancho, D.; Baker, C.M.; Clarke, J. Interplay between partner and ligand facilitates the folding and binding of an intrinsically disordered protein. Proc. Natl. Acad. Sci. USA 2014, 111, 15420–15425. [Google Scholar] [CrossRef]
- Knott, M.; Best, R.B. Discriminating binding mechanisms of an intrinsically disordered protein via a multi-state coarse-grained model. J. Chem. Phys. 2014, 140, 175102. [Google Scholar] [CrossRef]
- Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936. [Google Scholar] [CrossRef]
- Cragnell, C.; Rieloff, E.; Skepo, M. Utilizing Coarse-Grained Modeling and Monte Carlo Simulations to Evaluate the Conformational Ensemble of Intrinsically Disordered Proteins and Regions. J. Mol. Biol. 2018, 430, 2478–2492. [Google Scholar] [CrossRef]
- Baul, U.; Chakraborty, D.; Mugnai, M.L.; Straub, J.E.; Thirumalai, D. Sequence Effects on Size, Shape, and Structural Heterogeneity in Intrinsically Disordered Proteins. J. Phys. Chem. B 2019, 123, 3462–3474. [Google Scholar] [CrossRef] [PubMed]
- Shea, J.E.; Best, R.B.; Mittal, J. Physics-based computational and theoretical approaches to intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2021, 67, 219–225. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Wolynes, P.G.; Papoian, G.A. AWSEM-IDP: A Coarse-Grained Force Field for Intrinsically Disordered Proteins. J. Phys. Chem. B 2018, 122, 11115–11125. [Google Scholar] [CrossRef]
- Rutter, G.O.; Brown, A.H.; Quigley, D.; Walsh, T.R.; Allen, M.P. Testing the transferability of a coarse-grained model to intrinsically disordered proteins. Phys. Chem. Chem. Phys. 2015, 17, 31741–31749. [Google Scholar] [CrossRef]
- Nguyen, P.H.; Derreumaux, P. Structures of the intrinsically disordered Abeta, tau and alpha-synuclein proteins in aqueous solution from computer simulations. Biophys. Chem. 2020, 264, 106421. [Google Scholar] [CrossRef]
- Sieradzan, A.K.; Niadzvedtski, A.; Scheraga, H.A.; Liwo, A. Revised Backbone-Virtual-Bond-Angle Potentials to Treat the l- and d-Amino Acid Residues in the Coarse-Grained United Residue (UNRES) Force Field. J. Chem. Theory Comput. 2014, 10, 2194–2203. [Google Scholar] [CrossRef]
- Klein, F.; Barrera, E.E.; Pantano, S. Assessing SIRAH’s Capability to Simulate Intrinsically Disordered Proteins and Peptides. J. Chem. Theory Comput. 2021, 17, 599–604. [Google Scholar] [CrossRef]
- Schuler, B.; Soranno, A.; Hofmann, H.; Nettels, D. Single-Molecule FRET Spectroscopy and the Polymer Physics of Unfolded and Intrinsically Disordered Proteins. Annu. Rev. Biophys. 2016, 45, 207–231. [Google Scholar] [CrossRef]
- Lin, Y.H.; Forman-Kay, J.D.; Chan, H.S. Sequence-Specific Polyampholyte Phase Separation in Membraneless Organelles. Phys. Rev. Lett. 2016, 117, 178101. [Google Scholar] [CrossRef] [PubMed]
- Dignon, G.L.; Zheng, W.; Kim, Y.C.; Best, R.B.; Mittal, J. Sequence determinants of protein phase behavior from a coarse-grained model. PLoS Comput. Biol. 2018, 14, e1005941. [Google Scholar] [CrossRef] [PubMed]
- Still, W.C.; Tempczyk, A.; Hawley, R.C.; Hendrickson, T. Semianalytical treatment of solvation for molecular mechanics and dynamics. J. Am. Chem. Soc. 1990, 112, 6127–6129. [Google Scholar] [CrossRef]
- Kleinjung, J.; Fraternali, F. Design and application of implicit solvent models in biomolecular simulations. Curr. Opin. Struct. Biol. 2014, 25, 126–134. [Google Scholar] [CrossRef] [PubMed]
- Bottaro, S.; Lindorff-Larsen, K.; Best, R.B. Variational Optimization of an All-Atom Implicit Solvent Force Field to Match Explicit Solvent Simulation Data. J. Chem. Theory Comput. 2013, 9, 5641–5652. [Google Scholar] [CrossRef]
- Lee, K.H.; Chen, J. Optimization of the GBMV2 implicit solvent force field for accurate simulation of protein conformational equilibria. J. Comput. Chem. 2017, 38, 1332–1341. [Google Scholar] [CrossRef]
- Das, P.; Matysiak, S.; Mittal, J. Looking at the Disordered Proteins through the Computational Microscope. ACS Cent. Sci. 2018, 4, 534–542. [Google Scholar] [CrossRef]
- Lazaridis, T.; Karplus, M. Effective energy function for proteins in solution. Proteins 1999, 35, 133–152. [Google Scholar] [CrossRef]
- Vitalis, A.; Pappu, R.V. ABSINTH: A new continuum solvation model for simulations of polypeptides in aqueous solutions. J. Comput. Chem. 2009, 30, 673–699. [Google Scholar] [CrossRef]
- Choi, J.M.; Pappu, R.V. Improvements to the ABSINTH Force Field for Proteins Based on Experimentally Derived Amino Acid Specific Backbone Conformational Statistics. J. Chem. Theory Comput. 2019, 15, 1367–1382. [Google Scholar] [CrossRef] [PubMed]
- Mollica, L.; Bessa, L.M.; Hanoulle, X.; Jensen, M.R.; Blackledge, M.; Schneider, R. Binding Mechanisms of Intrinsically Disordered Proteins: Theory, Simulation, and Experiment. Front. Mol. Biosci. 2016, 3, 52. [Google Scholar] [CrossRef] [PubMed]
- Ikebe, J.; Umezawa, K.; Higo, J. Enhanced sampling simulations to construct free-energy landscape of protein-partner substrate interaction. Biophys. Rev. 2016, 8, 45–62. [Google Scholar] [CrossRef] [PubMed]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef]
- Laio, A.; Gervasio, F.L. Metadynamics: A method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science. Rep. Prog. Phys. 2008, 71, 126601. [Google Scholar] [CrossRef]
- Higo, J.; Umezawa, K. Free-energy landscape of intrinsically disordered proteins investigated by all-atom multicanonical molecular dynamics. Adv. Exp. Med. Biol. 2014, 805, 331–351. [Google Scholar] [CrossRef] [PubMed]
- Han, M.; Xu, J.; Ren, Y.; Li, J. Simulation of coupled folding and binding of an intrinsically disordered protein in explicit solvent with metadynamics. J. Mol. Graph. Model. 2016, 68, 114–127. [Google Scholar] [CrossRef]
- Wostenberg, C.; Kumar, S.; Noid, W.G.; Showalter, S.A. Atomistic simulations reveal structural disorder in the RAP74-FCP1 complex. J. Phys. Chem. B 2011, 115, 13731–13739. [Google Scholar] [CrossRef] [PubMed]
- Ithuralde, R.E.; Roitberg, A.E.; Turjanski, A.G. Structured and Unstructured Binding of an Intrinsically Disordered Protein as Revealed by Atomistic Simulations. J. Am. Chem. Soc. 2016, 138, 8742–8751. [Google Scholar] [CrossRef] [PubMed]
- Pierce, L.C.T.; Salomon-Ferrer, R.; De Oliviera, C.A.F.; McCammon, J.A.; Walker, R.C. Routine Access to Millisecond Time Scale Events with Accelerated Molecular Dynamics. J. Chem. Theory Comput. 2012, 8, 2997–3002. [Google Scholar] [CrossRef]
- Scholes, N.S.; Weinzierl, R.O. Molecular Dynamics of “Fuzzy” Transcriptional Activator-Coactivator Interactions. PLoS Comput. Biol. 2016, 12, e1004935. [Google Scholar] [CrossRef]
- Sugita, Y.; Kamiya, M.; Oshima, H.; Re, S. Replica-Exchange Methods for Biomolecular Simulations. Methods Mol. Biol 2019, 2022, 155–177. [Google Scholar] [CrossRef]
- Gerlach, G.J.; Carrock, R.; Stix, R.; Stollar, E.J.; Ball, K.A. A disordered encounter complex is central to the yeast Abp1p SH3 domain binding pathway. PLoS Comput. Biol. 2020, 16, e1007815. [Google Scholar] [CrossRef]
- Zou, R.; Zhou, Y.; Wang, Y.; Kuang, G.; Agren, H.; Wu, J.; Tu, Y. Free Energy Profile and Kinetics of Coupled Folding and Binding of the Intrinsically Disordered Protein p53 with MDM2. J. Chem. Inf. Model. 2020, 60, 1551–1558. [Google Scholar] [CrossRef] [PubMed]
- Bui, J.M.; McCammon, J.A. Protein complex formation by acetylcholinesterase and the neurotoxin fasciculin-2 appears to involve an induced-fit mechanism. Proc. Natl. Acad. Sci. USA 2006, 103, 15451–15456. [Google Scholar] [CrossRef] [PubMed]
- Gangupomu, V.K.; Wagner, J.R.; Park, I.H.; Jain, A.; Vaidehi, N. Mapping conformational dynamics of proteins using torsional dynamics simulations. Biophys. J. 2013, 104, 1999–2008. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Rezaei-Ghaleh, N.; Parigi, G.; Soranno, A.; Holla, A.; Becker, S.; Schuler, B.; Luchinat, C.; Zweckstetter, M. Local and Global Dynamics in Intrinsically Disordered Synuclein. Angewandte Chemie Int. Ed. 2018, 57, 15262–15266. [Google Scholar] [CrossRef] [PubMed]
- Ozenne, V.; Bauer, F.; Salmon, L.; Huang, J.R.; Jensen, M.R.; Segard, S.; Bernado, P.; Charavay, C.; Blackledge, M. Flexible-meccano: A tool for the generation of explicit ensemble descriptions of intrinsically disordered proteins and their associated experimental observables. Bioinformatics 2012, 28, 1463–1470. [Google Scholar] [CrossRef]
- Barozet, A.; Molloy, K.; Vaisset, M.; Simeon, T.; Cortes, J. A reinforcement-learning-based approach to enhance exhaustive protein loop sampling. Bioinformatics 2020, 36, 1099–1106. [Google Scholar] [CrossRef]
- Arbesu, M.; Maffei, M.; Cordeiro, T.N.; Teixeira, J.M.; Perez, Y.; Bernado, P.; Roche, S.; Pons, M. The Unique Domain Forms a Fuzzy Intramolecular Complex in Src Family Kinases. Structure 2017, 25, 630–640. [Google Scholar] [CrossRef]
- Brookes, D.H.; Head-Gordon, T. Experimental Inferential Structure Determination of Ensembles for Intrinsically Disordered Proteins. J. Am. Chem. Soc. 2016, 138, 4530–4538. [Google Scholar] [CrossRef]
- Boomsma, W.; Ferkinghoff-Borg, J.; Lindorff-Larsen, K. Combining experiments and simulations using the maximum entropy principle. PLoS Comput. Biol. 2014, 10, e1003406. [Google Scholar] [CrossRef]
- Lazar, T.; Martinez-Perez, E.; Quaglia, F.; Hatos, A.; Chemes, L.B.; Iserte, J.A.; Mendez, N.A.; Garrone, N.A.; Saldano, T.E.; Marchetti, J.; et al. PED in 2021: A major update of the protein ensemble database for intrinsically disordered proteins. Nucleic Acids Res. 2021, 49, D404–D411. [Google Scholar] [CrossRef]
- Miskei, M.; Antal, C.; Fuxreiter, M. FuzDB: Database of fuzzy complexes, a tool to develop stochastic structure-function relationships for protein complexes and higher-order assemblies. Nucleic Acids Res. 2017, 45, D228–D235. [Google Scholar] [CrossRef] [PubMed]
- Horvath, A.; Miskei, M.; Ambrus, V.; Vendruscolo, M.; Fuxreiter, M. Sequence-based prediction of protein binding mode landscapes. PLoS Comput. Biol. 2020, 16, e1007864. [Google Scholar] [CrossRef] [PubMed]
- Miskei, M.; Horvath, A.; Vendruscolo, M.; Fuxreiter, M. Sequence-Based Prediction of Fuzzy Protein Interactions. J. Mol. Biol. 2020, 432, 2289–2303. [Google Scholar] [CrossRef] [PubMed]
- Asakawa, H.; Ikegami, K.; Setou, M.; Watanabe, N.; Tsukada, M.; Fukuma, T. Submolecular-scale imaging of alpha-helices and C-terminal domains of tubulins by frequency modulation atomic force microscopy in liquid. Biophys. J. 2011, 101, 1270–1276. [Google Scholar] [CrossRef]
- Laurin, Y.; Eyer, J.; Robert, C.H.; Prevost, C.; Sacquin-Mora, S. Mobility and Core-Protein Binding Patterns of Disordered C-Terminal Tails in beta-Tubulin Isotypes. Biochemistry 2017, 56, 1746–1756. [Google Scholar] [CrossRef]
- Koukos, P.I.; Bonvin, A. Integrative Modelling of Biomolecular Complexes. J. Mol. Biol. 2020, 432, 2861–2881. [Google Scholar] [CrossRef]
- Yang, S.; Bernado, P. Integrative Biophysics: Protein Interaction and Disorder. J. Mol. Biol. 2020, 432, 2843–2845. [Google Scholar] [CrossRef]
- Dudas, E.F.; Palfy, G.; Menyhard, D.K.; Sebak, F.; Ecsedi, P.; Nyitray, L.; Bodor, A. Tumor-Suppressor p53TAD(1-60) Forms a Fuzzy Complex with Metastasis-Associated S100A4: Structural Insights and Dynamics by an NMR/MD Approach. ChemBioChem 2020, 21, 3087–3095. [Google Scholar] [CrossRef]
- Spreitzer, E.; Usluer, S.; Madl, T. Probing Surfaces in Dynamic Protein Interactions. J. Mol. Biol. 2020, 432, 2949–2972. [Google Scholar] [CrossRef]
- Tsytlonok, M.; Hemmen, K.; Hamilton, G.; Kolimi, N.; Felekyan, S.; Seidel, C.A.M.; Tompa, P.; Sanabria, H. Specific Conformational Dynamics and Expansion Underpin a Multi-Step Mechanism for Specific Binding of p27 with Cdk2/Cyclin A. J. Mol. Biol. 2020, 432, 2998–3017. [Google Scholar] [CrossRef] [PubMed]
- Grawert, T.W.; Svergun, D.I. Structural Modeling Using Solution Small-Angle X-ray Scattering (SAXS). J. Mol. Biol. 2020, 432, 3078–3092. [Google Scholar] [CrossRef] [PubMed]
- Bonomi, M.; Camilloni, C.; Vendruscolo, M. Metadynamic metainference: Enhanced sampling of the metainference ensemble using metadynamics. Sci. Rep. 2016, 6, 31232. [Google Scholar] [CrossRef]
- Bonomi, M.; Pellarin, R.; Vendruscolo, M. Simultaneous Determination of Protein Structure and Dynamics Using Cryo-Electron Microscopy. Biophys. J. 2018, 114, 1604–1613. [Google Scholar] [CrossRef] [PubMed]
- Brotzakis, Z.F.; Lindstedt, P.R.; Taylor, R.; Bernardes, G.J.L.; Vendruscolo, M. A Structural Ensemble of a Tau-Microtubule Complex Reveals Regulatory Tau Phosphorylation and Acetylation Mechanisms. bioRxiv 2020. [Google Scholar] [CrossRef]
- Kellogg, E.H.; Hejab, N.M.A.; Poepsel, S.; Downing, K.H.; DiMaio, F.; Nogales, E. Near-atomic model of microtubule-tau interactions. Science 2018, 360, 1242–1246. [Google Scholar] [CrossRef]
- Ramanathan, A.; Ma, H.; Parvatikar, A.; Chennubhotla, S.C. Artificial intelligence techniques for integrative structural biology of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2021, 66, 216–224. [Google Scholar] [CrossRef]
- Ramanathan, A.; Parvatikar, A.; Chennubhotla, S.C.; Mei, Y.; Sinha, S.C. Transient Unfolding and Long-Range Interactions in Viral BCL2 M11 Enable Binding to the BECN1 BH3 Domain. Biomolecules 2020, 10, 1308. [Google Scholar] [CrossRef]
- Demerdash, O.; Shrestha, U.R.; Petridis, L.; Smith, J.C.; Mitchell, J.C.; Ramanathan, A. Using Small-Angle Scattering Data and Parametric Machine Learning to Optimize Force Field Parameters for Intrinsically Disordered Proteins. Front. Mol. Biosci. 2019, 6, 64. [Google Scholar] [CrossRef]
- Lazar, T.; Guharoy, M.; Vranken, W.; Rauscher, S.; Wodak, S.J.; Tompa, P. Distance-Based Metrics for Comparing Conformational Ensembles of Intrinsically Disordered Proteins. Biophys. J. 2020, 118, 2952–2965. [Google Scholar] [CrossRef] [PubMed]
- Weinzierl, R.O.J. Molecular Dynamics Simulations of Human FOXO3 Reveal Intrinsically Disordered Regions Spread Spatially by Intramolecular Electrostatic Repulsion. Biomolecules 2021, 11, 856. [Google Scholar] [CrossRef]
- Cuevas-Velazquez, C.L.; Dinneny, J.R. Organization out of disorder: Liquid-liquid phase separation in plants. Curr. Opin. Plant Biol. 2018, 45, 68–74. [Google Scholar] [CrossRef] [PubMed]
- Darling, A.L.; Liu, Y.; Oldfield, C.J.; Uversky, V.N. Intrinsically Disordered Proteome of Human Membrane-Less Organelles. Proteomics 2018, 18, e1700193. [Google Scholar] [CrossRef] [PubMed]
- Borgia, A.; Borgia, M.B.; Bugge, K.; Kissling, V.M.; Heidarsson, P.O.; Fernandes, C.B.; Sottini, A.; Soranno, A.; Buholzer, K.J.; Nettels, D.; et al. Extreme disorder in an ultrahigh-affinity protein complex. Nature 2018, 555, 61–66. [Google Scholar] [CrossRef] [PubMed]
- Khazanov, N.; Levy, Y. Sliding of p53 along DNA can be modulated by its oligomeric state and by cross-talks between its constituent domains. J. Mol. Biol. 2011, 408, 335–355. [Google Scholar] [CrossRef] [PubMed]
- Vuzman, D.; Levy, Y. Intrinsically disordered regions as affinity tuners in protein-DNA interactions. Mol. Biosyst. 2012, 8, 47–57. [Google Scholar] [CrossRef] [PubMed]
- Shishmarev, D.; Wang, Y.; Mason, C.E.; Su, X.C.; Oakley, A.J.; Graham, B.; Huber, T.; Dixon, N.E.; Otting, G. Intramolecular binding mode of the C-terminus of Escherichia coli single-stranded DNA binding protein determined by nuclear magnetic resonance spectroscopy. Nucleic Acids Res. 2014, 42, 2750–2757. [Google Scholar] [CrossRef]
- Mondal, A.; Bhattacherjee, A. Mechanism of Dynamic Binding of Replication Protein A to ssDNA. J. Chem. Inf. Model. 2020, 60, 5057–5069. [Google Scholar] [CrossRef]
- Shereda, R.D.; Bernstein, D.A.; Keck, J.L. A central role for SSB in Escherichia coli RecQ DNA helicase function. J. Biol. Chem. 2007, 282, 19247–19258. [Google Scholar] [CrossRef]
- Marceau, A.H.; Bahng, S.; Massoni, S.C.; George, N.P.; Sandler, S.J.; Marians, K.J.; Keck, J.L. Structure of the SSB-DNA polymerase III interface and its role in DNA replication. EMBO J. 2011, 30, 4236–4247. [Google Scholar] [CrossRef]
- Protopopova, A.D.; Litvinov, R.I.; Galanakis, D.K.; Nagaswami, C.; Barinov, N.A.; Mukhitov, A.R.; Klinov, D.V.; Weisel, J.W. Morphometric characterization of fibrinogen’s alphaC regions and their role in fibrin self-assembly and molecular organization. Nanoscale 2017, 9, 13707–13716. [Google Scholar] [CrossRef]
- Bigman, L.S.; Levy, Y. Modulating Microtubules: A Molecular Perspective on the Effects of Tail Modifications. J. Mol. Biol. 2021, 433, 166988. [Google Scholar] [CrossRef] [PubMed]
- Bigman, L.S.; Levy, Y. Tubulin tails and their modifications regulate protein diffusion on microtubules. Proc. Natl. Acad. Sci. USA 2020, 117, 8876–8883. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharyya, B.; Sackett, D.L.; Wolff, J. Tubulin, hybrid dimers, and tubulin S. Stepwise charge reduction and polymerization. J. Biol. Chem. 1985, 260, 10208–10216. [Google Scholar] [CrossRef]
- Fan, H.F.; Su, S. The regulation mechanism of the C-terminus of RecA proteins during DNA strand-exchange process. Biophys. J. 2021, 120, 3166–3179. [Google Scholar] [CrossRef]
- Ferreiro, D.U.; Komives, E.A.; Wolynes, P.G. Frustration in biomolecules. Q. Rev. Biophys. 2014, 47, 285–363. [Google Scholar] [CrossRef]
- Carvaillo, J.-C. From Assembly Unit to Capsid: In Silico Application to Norovirus and Hepatitis B Virus; Université Paris-Saclay: Gif-sur-Yvette, France, 2021. [Google Scholar]
- Bell, J.C.; Kowalczykowski, S.C. RecA: Regulation and Mechanism of a Molecular Search Engine. Trends Biochem. Sci. 2016, 41, 491–507. [Google Scholar] [CrossRef]
- Lusetti, S.L.; Shaw, J.J.; Cox, M.M. Magnesium ion-dependent activation of the RecA protein involves the C terminus. J. Biol. Chem. 2003, 278, 16381–16388. [Google Scholar] [CrossRef]
- Kim, R.; Kanamaru, S.; Mikawa, T.; Prevost, C.; Ishii, K.; Ito, K.; Uchiyama, S.; Oda, M.; Iwasaki, H.; Kim, S.K.; et al. RecA requires two molecules of Mg2+ ions for its optimal strand exchange activity in vitro. Nucleic Acids Res. 2018, 46, 2548–2559. [Google Scholar] [CrossRef]
- Kurumizaka, H.; Aihara, H.; Ikawa, S.; Kashima, T.; Bazemore, L.R.; Kawasaki, K.; Sarai, A.; Radding, C.M.; Shibata, T. A possible role of the C-terminal domain of the RecA protein. A gateway model for double-stranded DNA binding. J. Biol. Chem. 1996, 271, 33515–33524. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Yang, H.; Pavletich, N.P. Mechanism of homologous recombination from the RecA–ssDNA/dsDNA structures. Nature 2008, 453, 489–494. [Google Scholar] [CrossRef]
- Yang, D.; Boyer, B.; Prevost, C.; Danilowicz, C.; Prentiss, M. Integrating multi-scale data on homologous recombination into a new recognition mechanism based on simulations of the RecA-ssDNA/dsDNA structure. Nucleic Acids Res. 2015, 43, 10251–10263. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Boyer, B.; Danilowicz, C.; Prentiss, M.; Prevost, C. Weaving DNA strands: Structural insight on ATP hydrolysis in RecA-induced homologous recombination. Nucleic Acids Res. 2019, 47, 7798–7808. [Google Scholar] [CrossRef] [PubMed]
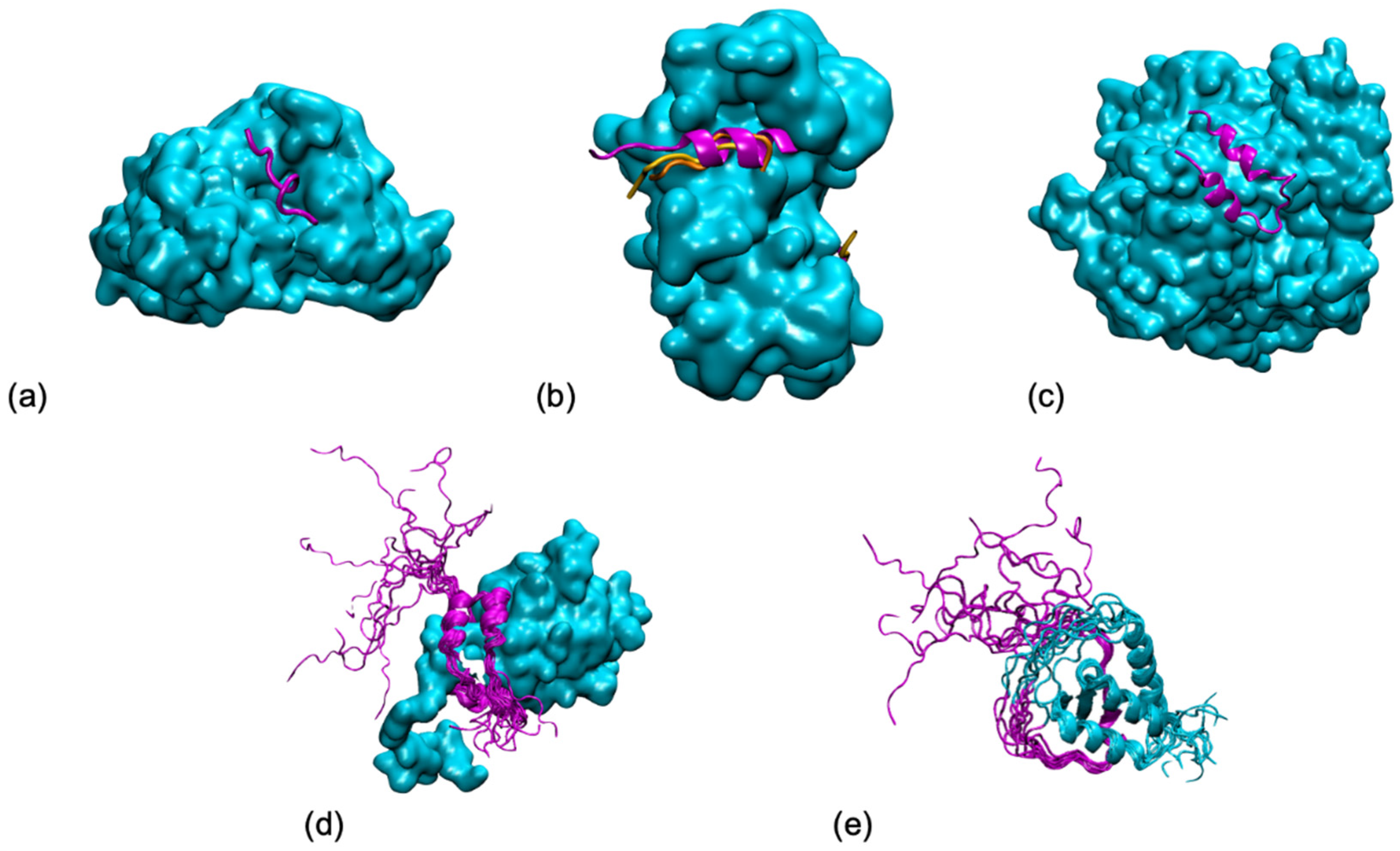
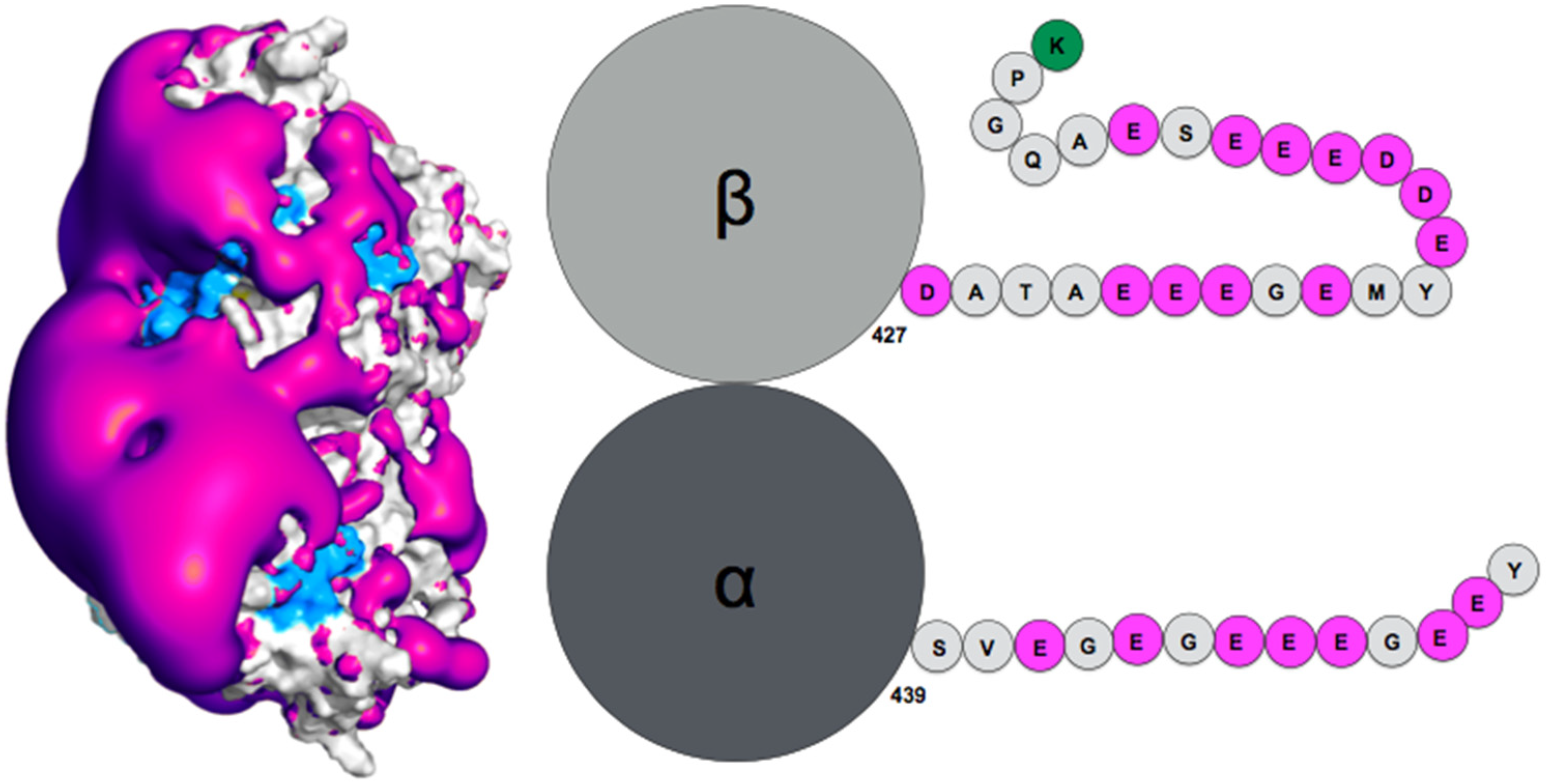
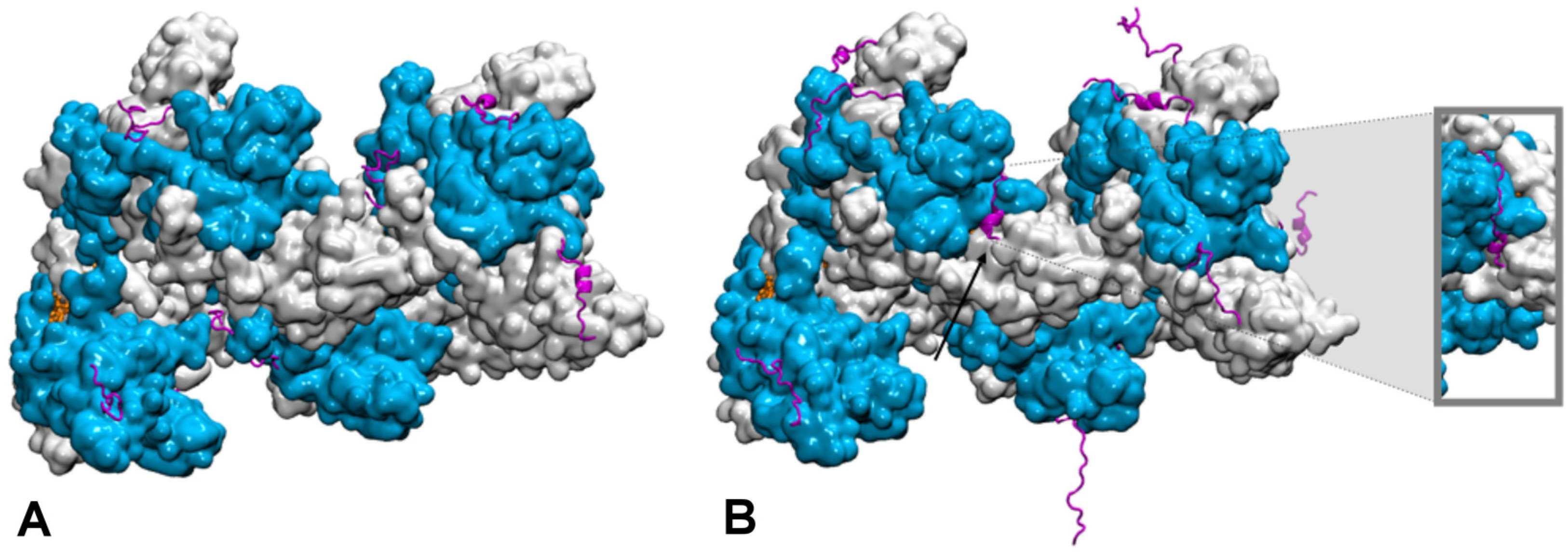
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sacquin-Mora, S.; Prévost, C. When Order Meets Disorder: Modeling and Function of the Protein Interface in Fuzzy Complexes. Biomolecules 2021, 11, 1529. https://doi.org/10.3390/biom11101529
Sacquin-Mora S, Prévost C. When Order Meets Disorder: Modeling and Function of the Protein Interface in Fuzzy Complexes. Biomolecules. 2021; 11(10):1529. https://doi.org/10.3390/biom11101529
Chicago/Turabian StyleSacquin-Mora, Sophie, and Chantal Prévost. 2021. "When Order Meets Disorder: Modeling and Function of the Protein Interface in Fuzzy Complexes" Biomolecules 11, no. 10: 1529. https://doi.org/10.3390/biom11101529
APA StyleSacquin-Mora, S., & Prévost, C. (2021). When Order Meets Disorder: Modeling and Function of the Protein Interface in Fuzzy Complexes. Biomolecules, 11(10), 1529. https://doi.org/10.3390/biom11101529




