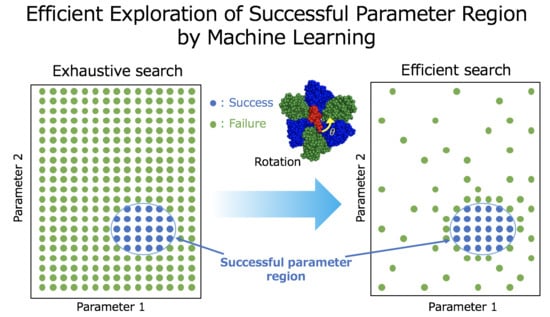
Exploring Successful Parameter Region for Coarse-Grained Simulation of Biomolecules by Bayesian Optimization and Active Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Machine Learning Based Region Search of Successful Parameters
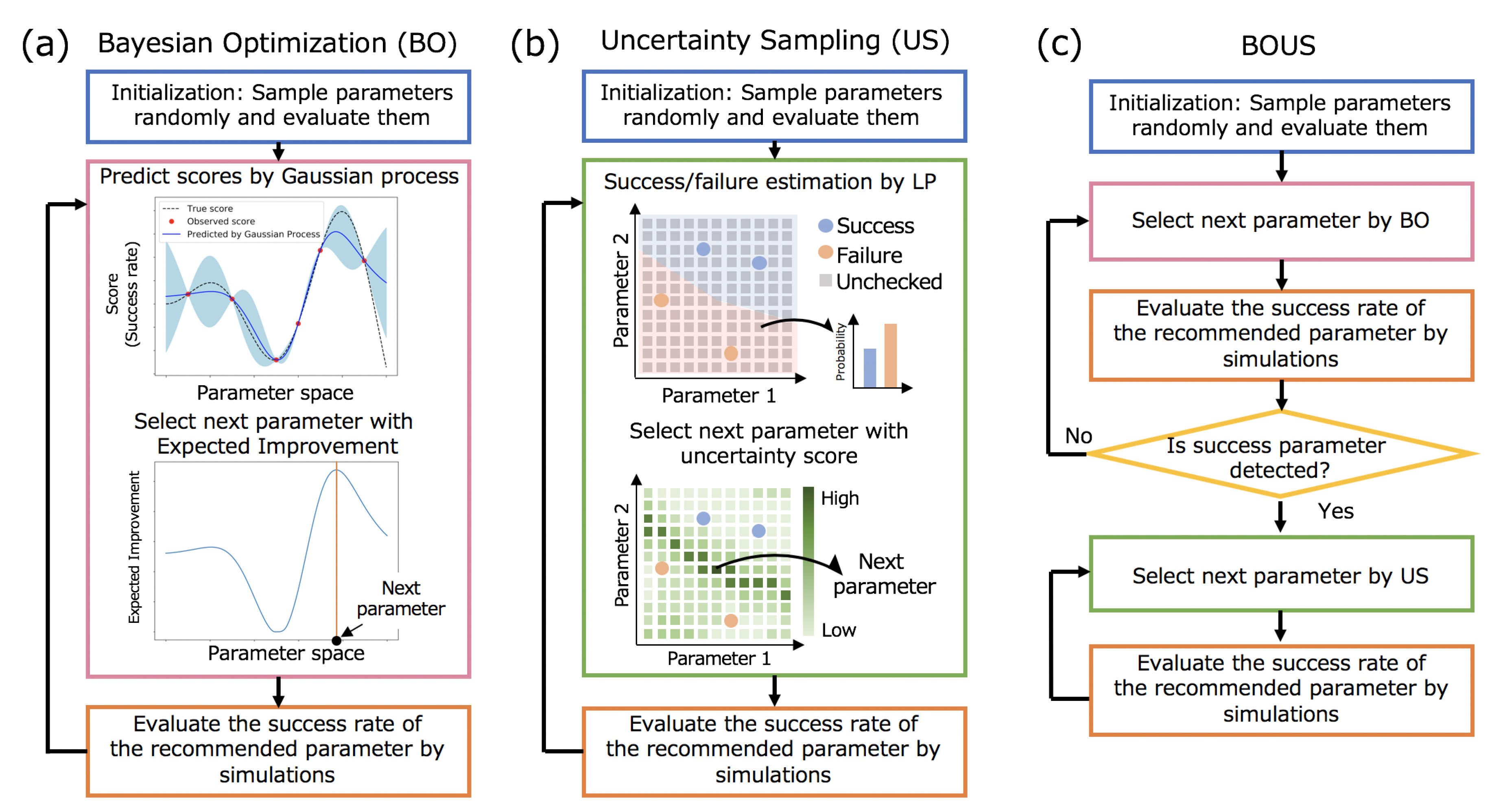
2.1.1. Parameter Sampling By Bo
2.1.2. Parameter Sampling by Us
2.1.3. Combination of BO and US
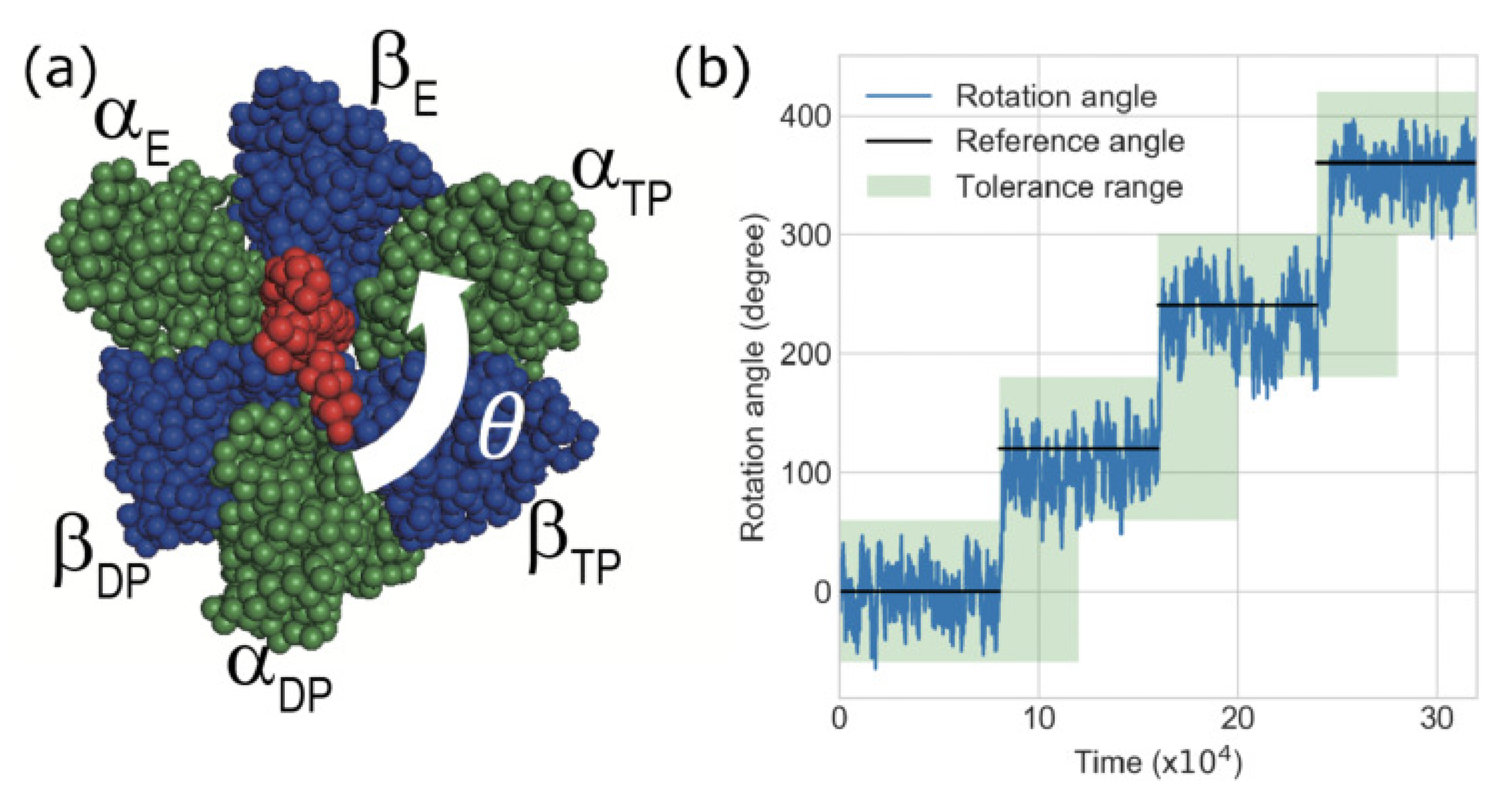
2.2. F1-Motor and CG-MD Simulation
2.3. Simulation Dynamics and Sampled Parameter Space
2.4. Definition of Success Rate for the Rotation of Subunit in F1-Motor
3. Results
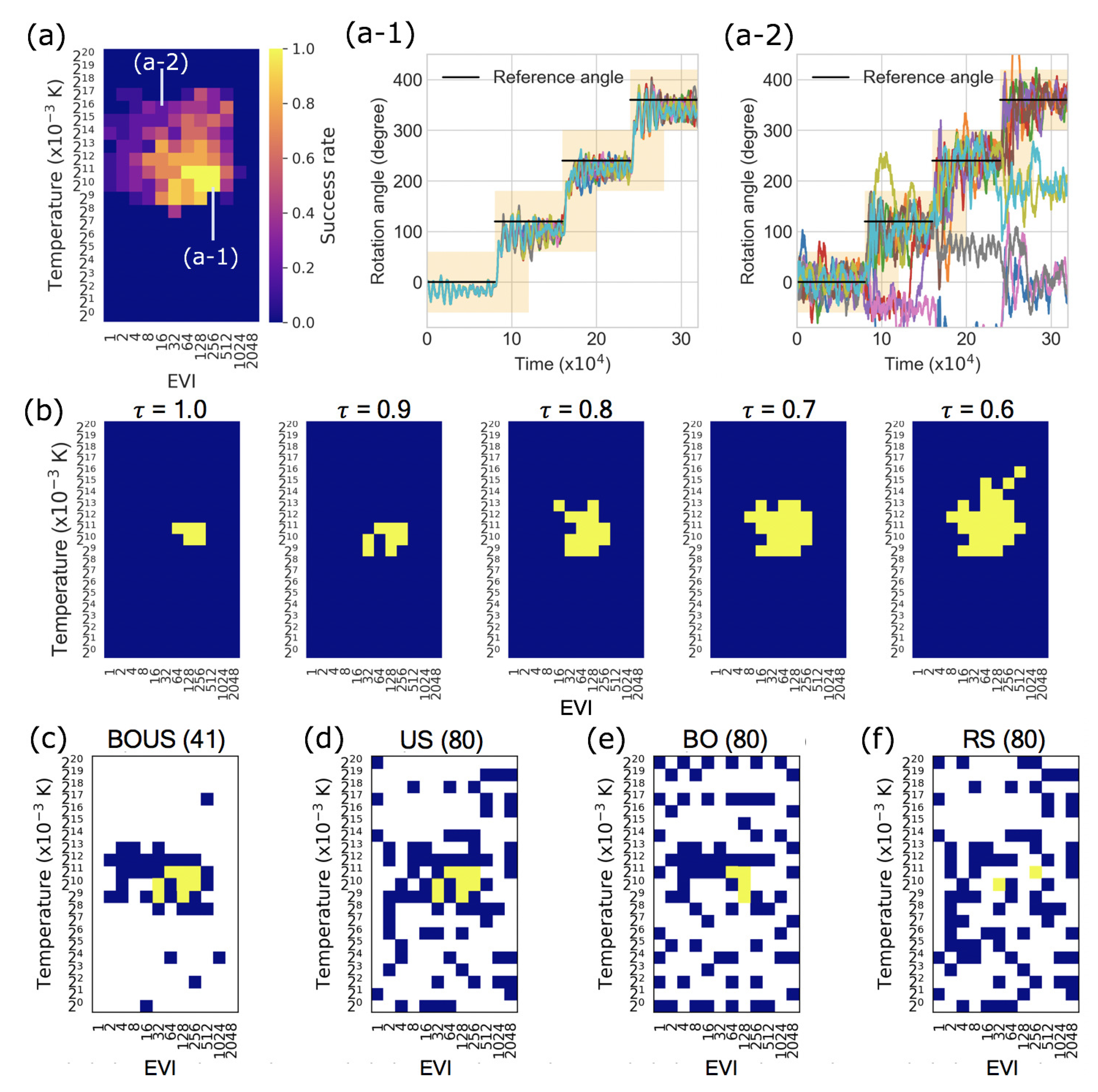
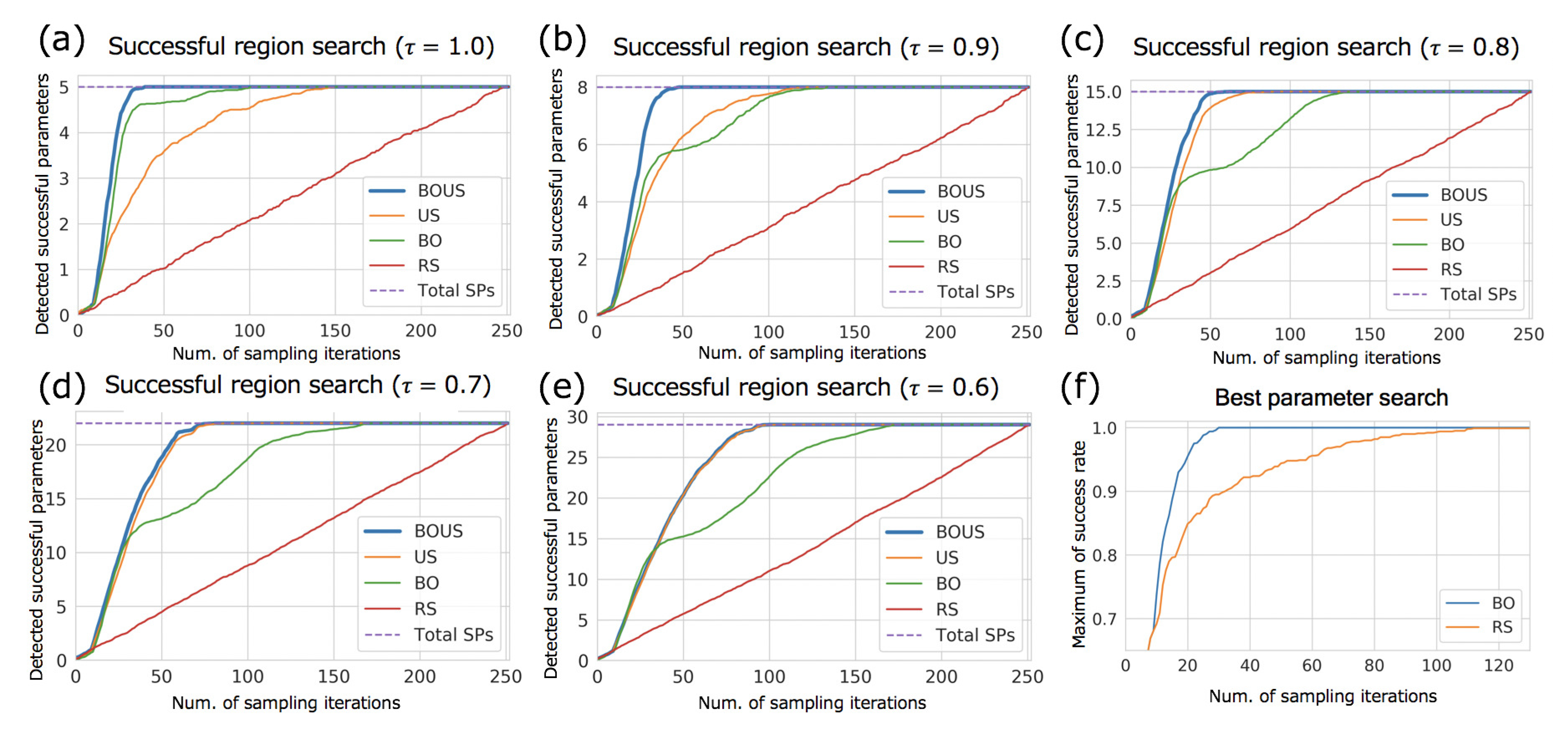
3.1. Sampling Performances for F1-Motor Simulations Using Newtonian Dynamics
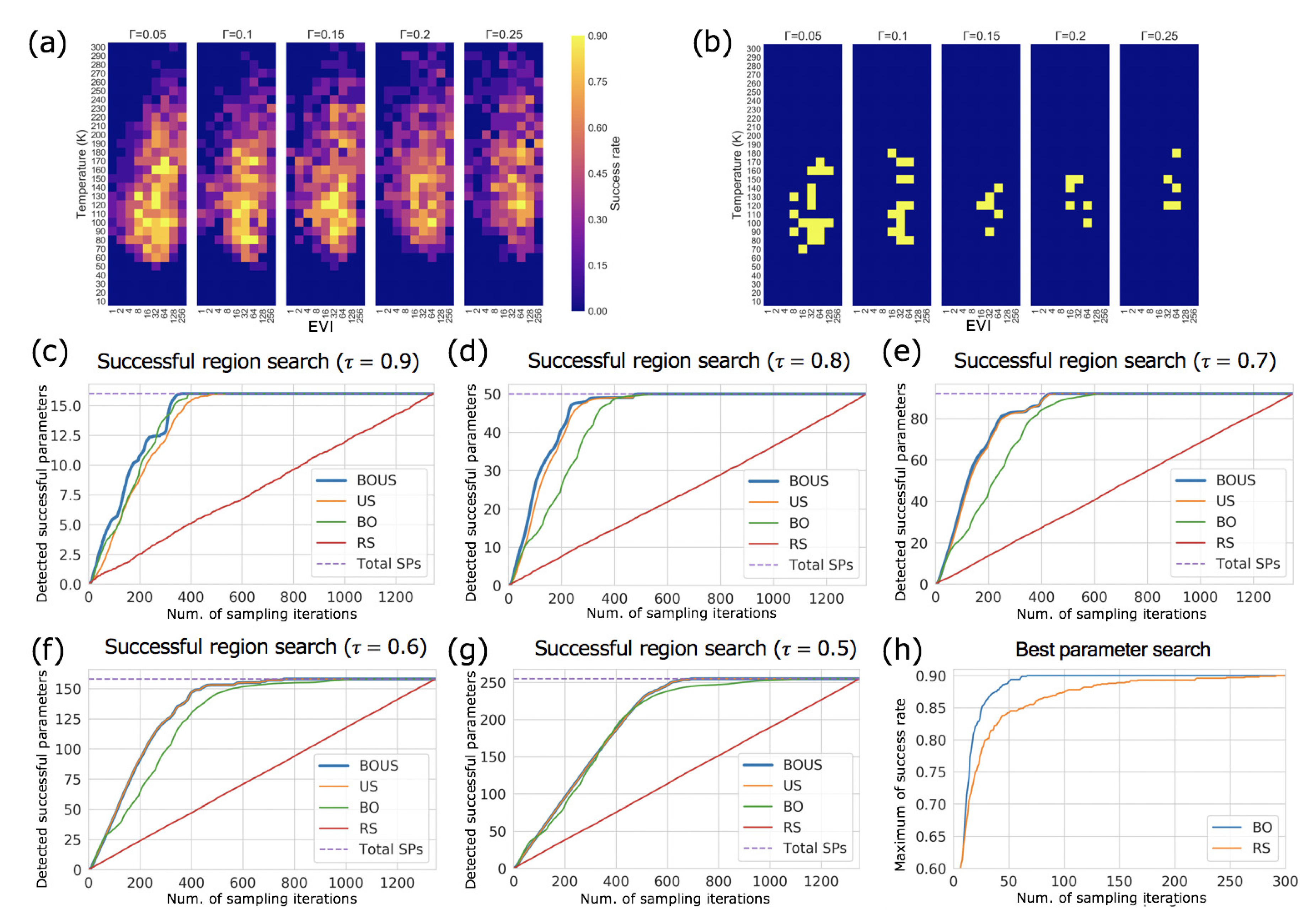
3.2. Sampling Performance of F1-Motor Simulations Using Langevin Dynamics
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Shaw, D.E.; Deneroff, M.M.; Dror, R.O.; Kuskin, J.S.; Larson, R.H.; Salmon, J.K.; Young, C.; Batson, B.; Bowers, K.J.; Chao, J.C.; et al. Anton, a special-purpose machine for molecular dynamics simulation. Commun. ACM 2008, 51, 91–97. [Google Scholar] [CrossRef]
- Takada, S.; Kanada, R.; Tan, C.; Terakawa, T.; Li, W.; Kenzaki, H. Modeling Structural Dynamics of Biomolecular Complexes by Coarse-Grained Molecular Simulations. Accounts Chem. Res. 2015, 48, 3026–3035. [Google Scholar] [CrossRef] [PubMed]
- Koga, N.; Takada, S. Folding-based molecular simulations reveal mechanisms of the rotary motor F1–ATPase. Proc. Natl. Acad. Sci. USA 2006, 103, 5367–5372. [Google Scholar] [CrossRef] [PubMed]
- Okazaki, K.i.; Takada, S. Dynamic energy landscape view of coupled binding and protein conformational change: Induced-fit versus population-shift mechanisms. Proc. Natl. Acad. Sci. USA 2008, 105, 11182–11187. [Google Scholar] [CrossRef] [PubMed]
- Koga, N.; Kameda, T.; Okazaki, K.i.; Takada, S. Paddling mechanism for the substrate translocation by AAA+ motor revealed by multiscale molecular simulations. Proc. Natl. Acad. Sci. USA 2009, 106, 18237–18242. [Google Scholar] [CrossRef]
- Kanada, R.; Terakawa, T.; Kenzaki, H.; Takada, S. Nucleosome Crowding in Chromatin Slows the Diffusion but Can Promote Target Search of Proteins. Biophys. J. 2019, 116, 2285–2295. [Google Scholar] [CrossRef]
- Levy, Y.; Onuchic, J.N.; Wolynes, P.G. Fly-Casting in Protein-DNA Binding: Frustration between Protein Folding and Electrostatics Facilitates Target Recognition. J. Am. Chem. Soc. 2007, 129, 738–739. [Google Scholar] [CrossRef]
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; de Vries, A.H. The MARTINI Force Field: Coarse Grained Model for Biomolecular Simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef]
- Hills, R.D.; Lu, L.; Voth, G.A. Multiscale coarse-graining of the protein energy landscape. PLoS Comput. Biol. 2010, 6, e1000827. [Google Scholar] [CrossRef]
- Wang, J.; Olsson, S.; Wehmeyer, C.; Pérez, A.; Charron, N.E.; de Fabritiis, G.; Noé, F.; Clementi, C. Machine Learning of Coarse-Grained Molecular Dynamics Force Fields. ACS Cent. Sci. 2019, 5, 755–767. [Google Scholar] [CrossRef]
- Bahar, I.; Rader, A. Coarse-grained normal mode analysis in structural biology. Curr. Opin. Struct. Biol. 2005, 15, 586–592. [Google Scholar] [CrossRef] [PubMed]
- Sambriski, E.J.; Schwartz, D.C.; de Pablo, J.J. A mesoscale model of DNA and its renaturation. Biophys. J. 2009, 96, 1675–1690. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Okazaki, K.; Koga, N.; Takada, S.; Onuchic, J.N.; Wolynes, P.G. Multiple-basin energy landscapes for large-amplitude conformational motions of proteins: Structure-based molecular dynamics simulations. Proc. Natl. Acad. Sci. USA 2006, 103, 11844–11849. [Google Scholar] [CrossRef] [PubMed]
- Izvekov, S.; Voth, G.A. A Multiscale Coarse-Graining Method for Biomolecular Systems. J. Phys. Chem. B 2005, 109, 2469–2473. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Wolynes, P.G.; Takada, S. Frustration, specific sequence dependence, and nonlinearity in large-amplitude fluctuations of allosteric proteins. Proc. Natl. Acad. Sci. USA 2011, 108, 3504–3509. [Google Scholar] [CrossRef] [PubMed]
- Yao, X.Q.; Kenzaki, H.; Murakami, S.; Takada, S. Drug export and allosteric coupling in a multidrug transporter revealed by molecular simulations. Nat. Commun. 2010, 1, 117. [Google Scholar] [CrossRef] [PubMed]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; De Freitas, N. Taking the human out of the loop: A review of Bayesian optimization. Proc. IEEE 2015, 104, 148–175. [Google Scholar] [CrossRef]
- Snoek, J.; Larochelle, H.; Adams, R.P. Practical Bayesian Optimization of Machine Learning Algorithms. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–8 December 2012; pp. 2951–2959. [Google Scholar]
- Jaderberg, M.; Dalibard, V.; Osindero, S.; Czarnecki, W.M.; Donahue, J.; Razavi, A.; Vinyals, O.; Green, T.; Dunning, I.; Simonyan, K. Population based training of neural networks. arXiv Prepr. 2017, arXiv:1711.09846. [Google Scholar]
- Seko, A.; Togo, A.; Hayashi, H.; Tsuda, K.; Chaput, L.; Tanaka, I. Prediction of Low-Thermal-Conductivity Compounds with First-Principles Anharmonic Lattice-Dynamics Calculations and Bayesian Optimization. Phys. Rev. Lett. 2015, 115, 205901. [Google Scholar] [CrossRef]
- Saito, Y.; Oikawa, M.; Nakazawa, H.; Niide, T.; Kameda, T.; Tsuda, K.; Umetsu, M. Machine-learning-guided mutagenesis for directed evolution of fluorescent proteins. ACS Synth. Biol. 2018, 7, 2014–2022. [Google Scholar] [CrossRef]
- Terayama, K.; Tamura, R.; Nose, Y.; Hiramatsu, H.; Hosono, H.; Okuno, Y.; Tsuda, K. Efficient construction method for phase diagrams using uncertainty sampling. Phys. Rev. Mater. 2019, 3, 033802. [Google Scholar] [CrossRef]
- Terayama, K.; Tsuda, K.; Tamura, R. Efficient recommendation tool of materials by an executable file based on machine learning. Jpn. J. Appl. Phys. 2019, 58, 098001. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Jones, D.R.; Schonlau, M.; Welch, W.J. Efficient global optimization of expensive black-box functions. J. Glob. Optim. 1998, 13, 455–492. [Google Scholar] [CrossRef]
- Ueno, T.; Rhone, T.D.; Hou, Z.; Mizoguchi, T.; Tsuda, K. COMBO: An efficient Bayesian optimization library for materials science. Mater. Discov. 2016, 4, 18–21. [Google Scholar] [CrossRef]
- Rahimi, A.; Recht, B. Random features for large-scale kernel machines. In Proceedings of the 20th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 3–6 December 2007; pp. 1177–1184. [Google Scholar]
- Zhu, X.; Ghahramani, Z.; Lafferty, J.D. Semi-supervised learning using gaussian fields and harmonic functions. In Proceedings of the 20th International Conference on Machine Learning, Washington, DC, USA, 21–24 August 2003; pp. 912–919. [Google Scholar]
- Lewis, D.D.; Gale, W.A. A sequential algorithm for training text classifiers. In Proceedings of the 17th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Dublin, Ireland, 3–6 July 1994; Springer: New York, NY, USA, 1994; pp. 3–12. [Google Scholar]
- Abrahams, J.P.; Leslie, A.G.W.; Lutter, R.; Walker, J.E. Structure at 2.8 Â resolution of F1-ATPase from bovine heart mitochondria. Nature 1994, 370, 621–628. [Google Scholar] [CrossRef] [PubMed]
- Yasuda, R.; Noji, H.; Kinosita, K.; Yoshida, M. F1-ATPase Is a Highly Efficient Molecular Motor that Rotates with Discrete 120 Steps. Cell 1998, 93, 1117–1124. [Google Scholar] [CrossRef]
- Kenzaki, H.; Koga, N.; Hori, N.; Kanada, R.; Li, W.; Okazaki, K.i.; Yao, X.Q.; Takada, S. CafeMol: A Coarse-Grained Biomolecular Simulator for Simulating Proteins at Work. J. Chem. Theory Comput. 2011, 7, 1979–1989. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Academic Press: Cambridge, UK, 1996; p. 443. [Google Scholar]
- Berendsen, H.J.; Postma, J.P.; Van Gunsteren, W.F.; Dinola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984. [Google Scholar] [CrossRef]
- Yasuda, R.; Noji, H.; Yoshida, M.; Kinosita, K.; Itoh, H. Resolution of distinct rotational substeps by submillisecond kinetic analysis of F1-ATPase. Nature 2001, 410, 898–904. [Google Scholar] [CrossRef]
- Wang, Z.; Zoghi, M.; Hutter, F.; Matheson, D.; De Freitas, N. Bayesian optimization in high dimensions via random embeddings. In Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence, Beijing, China, 3–19 August 2013. [Google Scholar]
- Wang, Z.; Li, C.; Jegelka, S.; Kohli, P. Batched high-dimensional bayesian optimization via structural kernel learning. In Proceedings of the 34th International Conference on Machine, Sydney, Australia, 6–11 August 2017; pp. 3656–3664. [Google Scholar]
| SP | BOUS | US | BO | RS | |
|---|---|---|---|---|---|
| 1.0 | 5 (1.98%) | 31 (12.3%) | 115 (45.6%) | 67 (26.6%) | 237 (94.0%) |
| 0.9 | 8 (3.17%) | 36 (14.3%) | 90 (35.7%) | 100 (39.7%) | 241 (95.6%) |
| 0.8 | 15 (5.95%) | 45 (17.9%) | 56 (22.2%) | 114 (45.2%) | 242 (96.0%) |
| 0.7 | 22 (8.73%) | 60 (23.8%) | 65 (25.8%) | 129 (51.2%) | 238 (94.4%) |
| 0.6 | 29 (11.5%) | 80 (31.7%) | 82 (32.5%) | 146 (57.9%) | 241 (95.6%) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanada, R.; Tokuhisa, A.; Tsuda, K.; Okuno, Y.; Terayama, K. Exploring Successful Parameter Region for Coarse-Grained Simulation of Biomolecules by Bayesian Optimization and Active Learning. Biomolecules 2020, 10, 482. https://doi.org/10.3390/biom10030482
Kanada R, Tokuhisa A, Tsuda K, Okuno Y, Terayama K. Exploring Successful Parameter Region for Coarse-Grained Simulation of Biomolecules by Bayesian Optimization and Active Learning. Biomolecules. 2020; 10(3):482. https://doi.org/10.3390/biom10030482
Chicago/Turabian StyleKanada, Ryo, Atsushi Tokuhisa, Koji Tsuda, Yasushi Okuno, and Kei Terayama. 2020. "Exploring Successful Parameter Region for Coarse-Grained Simulation of Biomolecules by Bayesian Optimization and Active Learning" Biomolecules 10, no. 3: 482. https://doi.org/10.3390/biom10030482
APA StyleKanada, R., Tokuhisa, A., Tsuda, K., Okuno, Y., & Terayama, K. (2020). Exploring Successful Parameter Region for Coarse-Grained Simulation of Biomolecules by Bayesian Optimization and Active Learning. Biomolecules, 10(3), 482. https://doi.org/10.3390/biom10030482