Effect of a Bio-Based Dispersing Aid (Einar® 101) on PLA-Arbocel® Biocomposites: Evaluation of the Interfacial Shear Stress on the Final Mechanical Properties
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
- Poly (lactic) acid (PLA) 2003D, purchased from NatureWorks (Minnesota, Minneapolis, MN, USA), was used. It derives completely from renewable resources and this grade contains about 4% od D-lactic acid units in order to lower the melting point and the crystallization tendency. PLA2003D is a transparent general-purpose extrusion grade biopolymer that can be used naturally or as part of formulated blends or composites. Thanks to its high molecular weight, this PLA grade can be easily processed on conventional extrusion equipment. According to the producer’s data sheet, PLA 2003D has a density of 1.24 g/cm3, a melt flow index (MFI) of 6 g/10 min (210 °C, 2.16 kg) and a nominal average molar mass of 200,000 g/mol.
- Arbocel® 600 BE/PU, provided by J Rettenmaier and Söhne (Rosenberg, Germany), are 100% natural ultra-short, highly pure white micro-cellulose fibers (mean diameter 20 µm, mean fiber length 60 µm, and consequently, mean aspect ratio of 3, bulk density: 200–260 g/L, fiber density 1.44 g/cm3). In the following paper, these fibers will be named Arbocel.
- Einar® 101 provided by Palsgaard (Juelsminde, Denmark), is yellowish viscous and food-grade, entirely based on vegetable oils dispersing aid (density: 1.62g/cm3, viscosity: 7 Pa s). It is a Polyglycerol ricinoleate oil with a maximum acid value of 3 mg KOH/g and a saponification value of 170 mg KOH/g. The addition of Einar® 101 should enable a better fiber dispersion and at the same time, should enable to reach higher fiber loads, decreasing the melt viscosity during the processing. In the following paper, this dispersing aid will be named Einar.
2.2. Composites’ Preparation
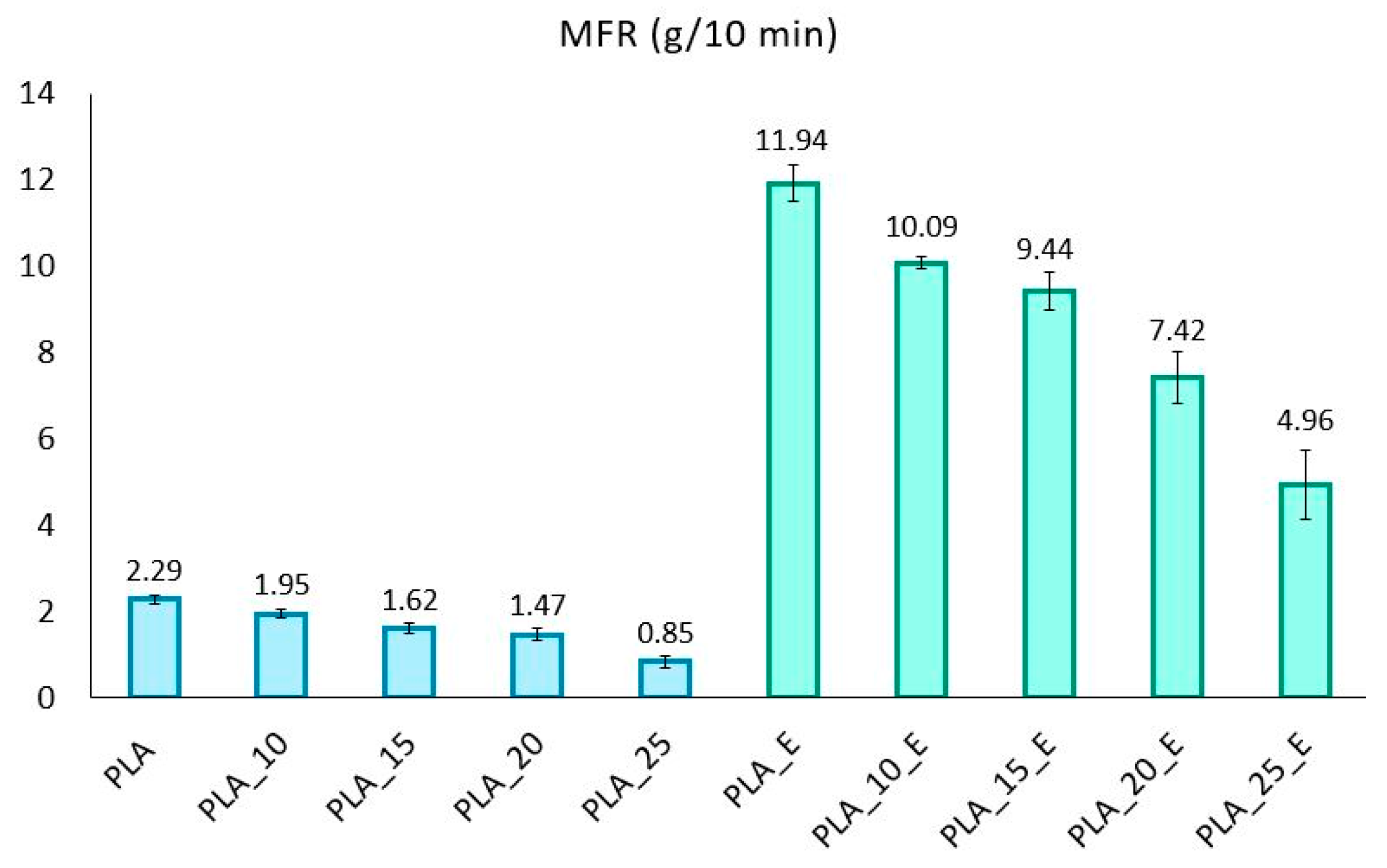
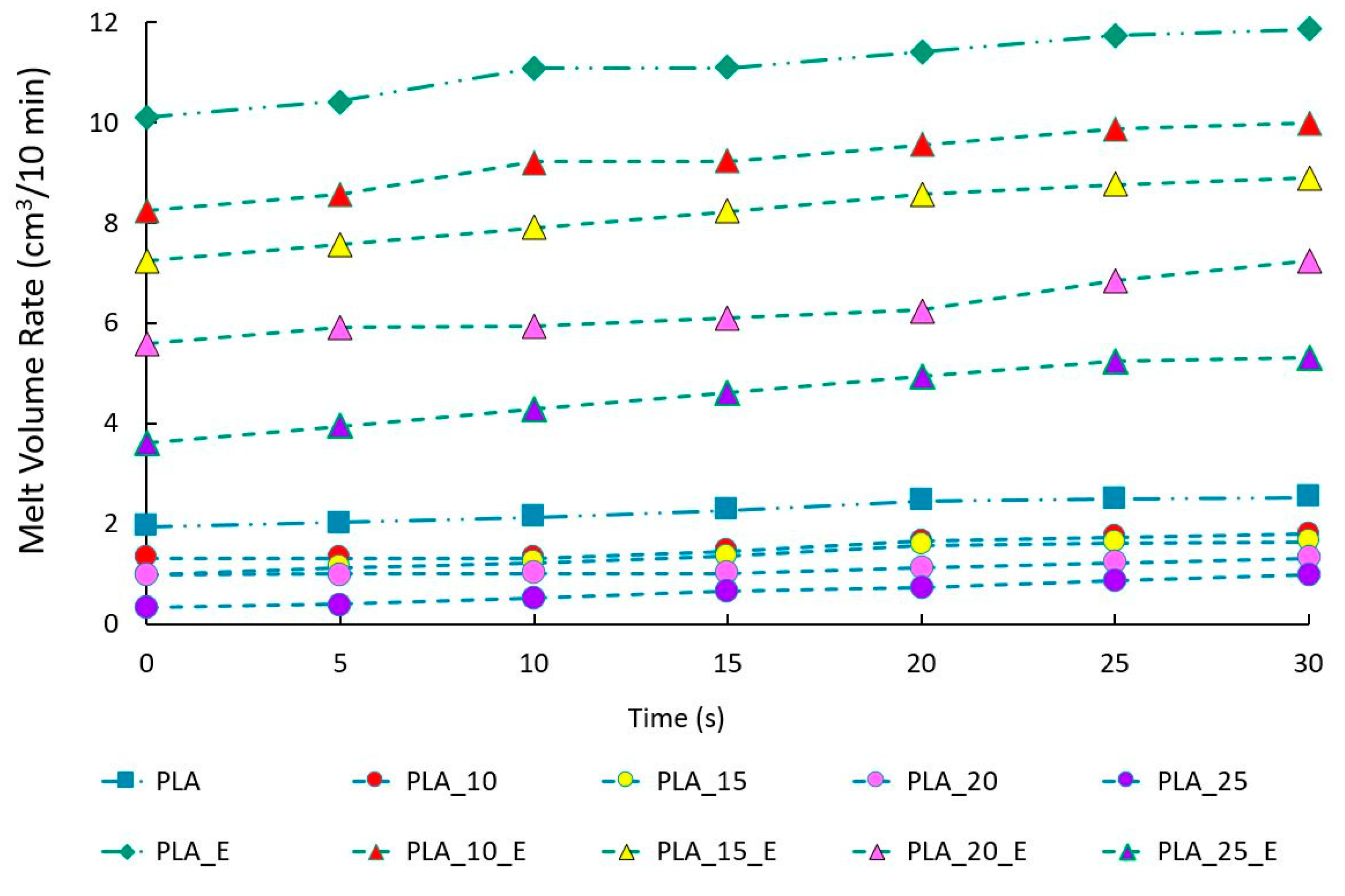
2.3. Melt Flow Rate
2.4. Specimens Preparation
2.5. Mechanical Tests
2.6. Scanning Electron Microscopy Analysis (SEM)
2.7. Thermo-Mechanical Analysis
3. Theoretical Analysis
3.1. Indirect Approach
3.2. Direct Approach
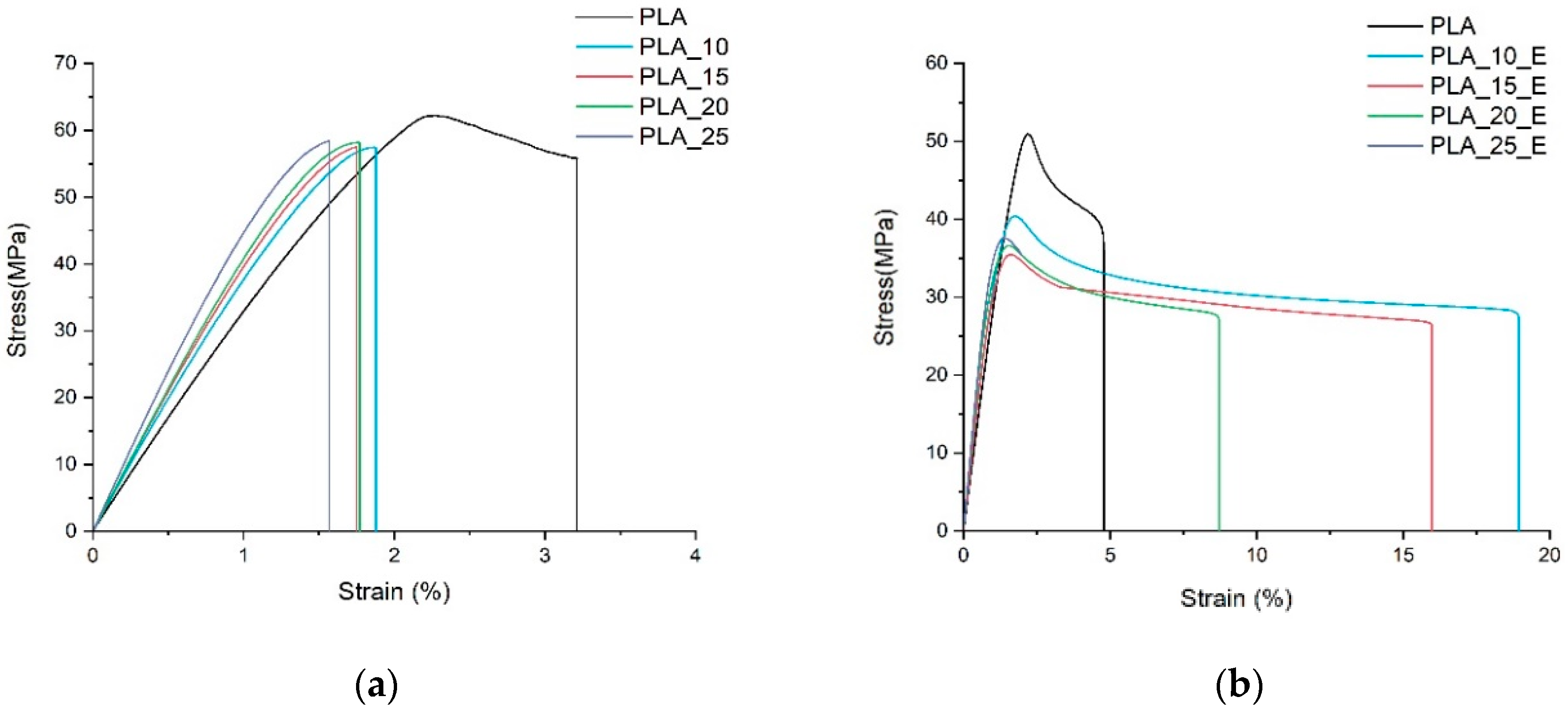
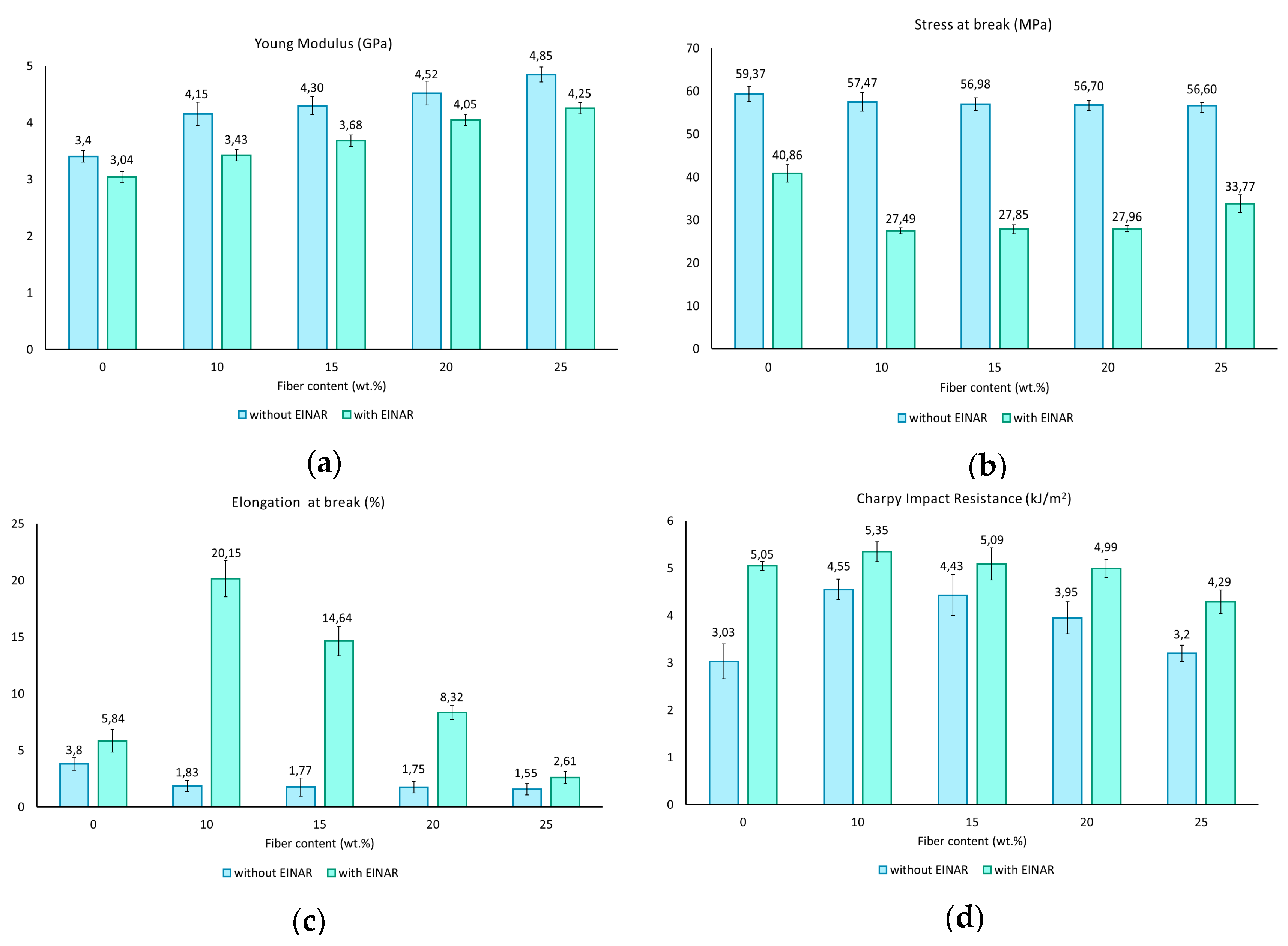
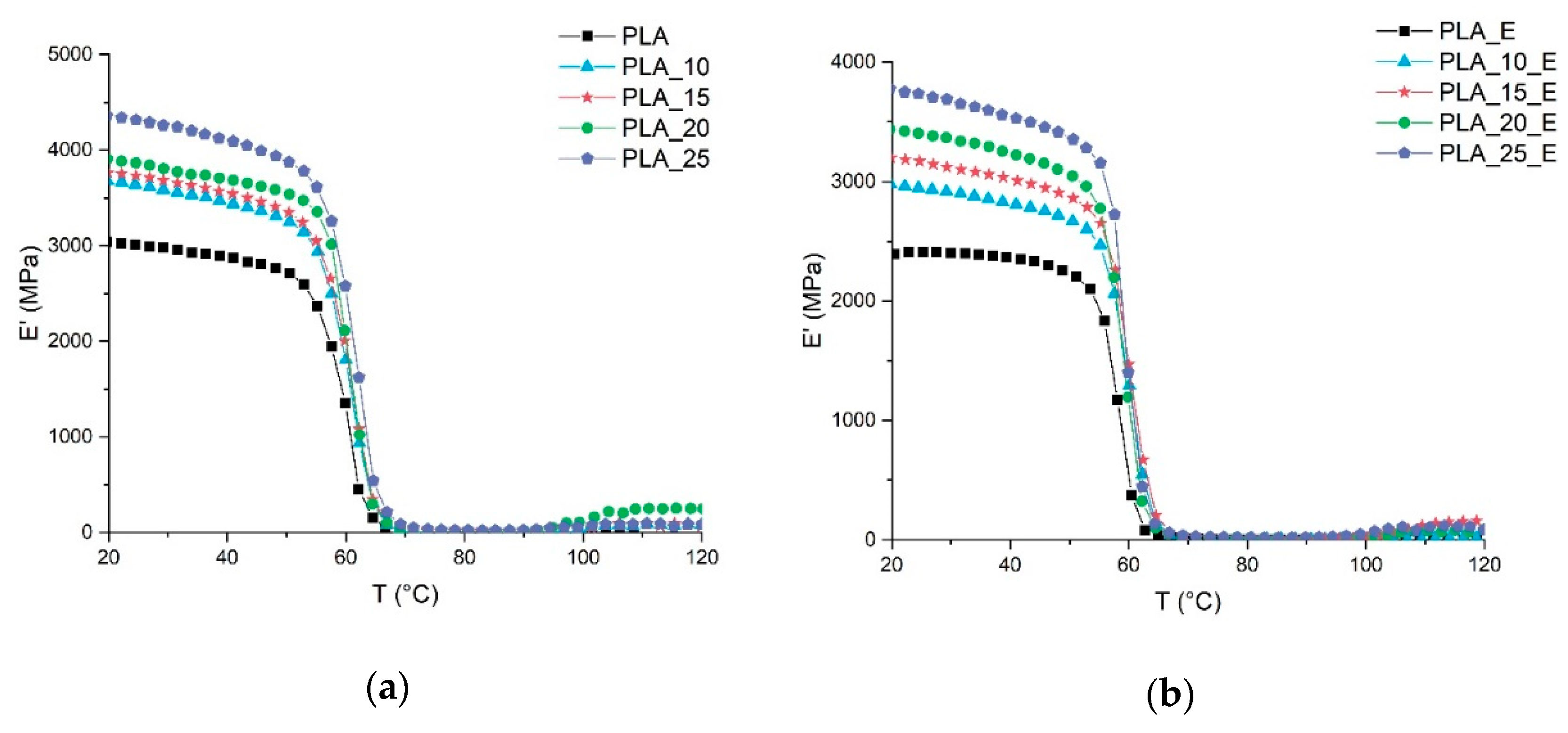
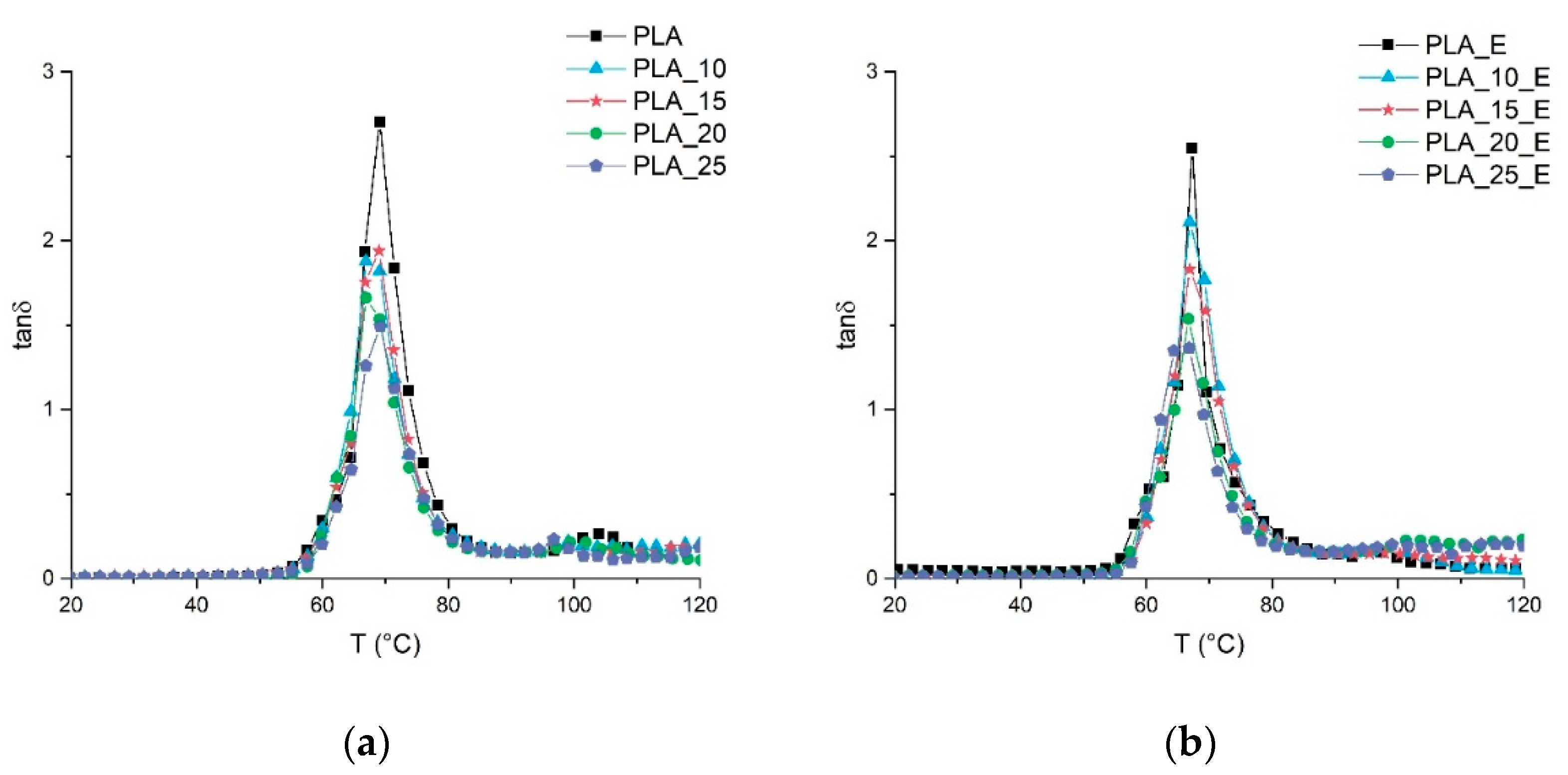
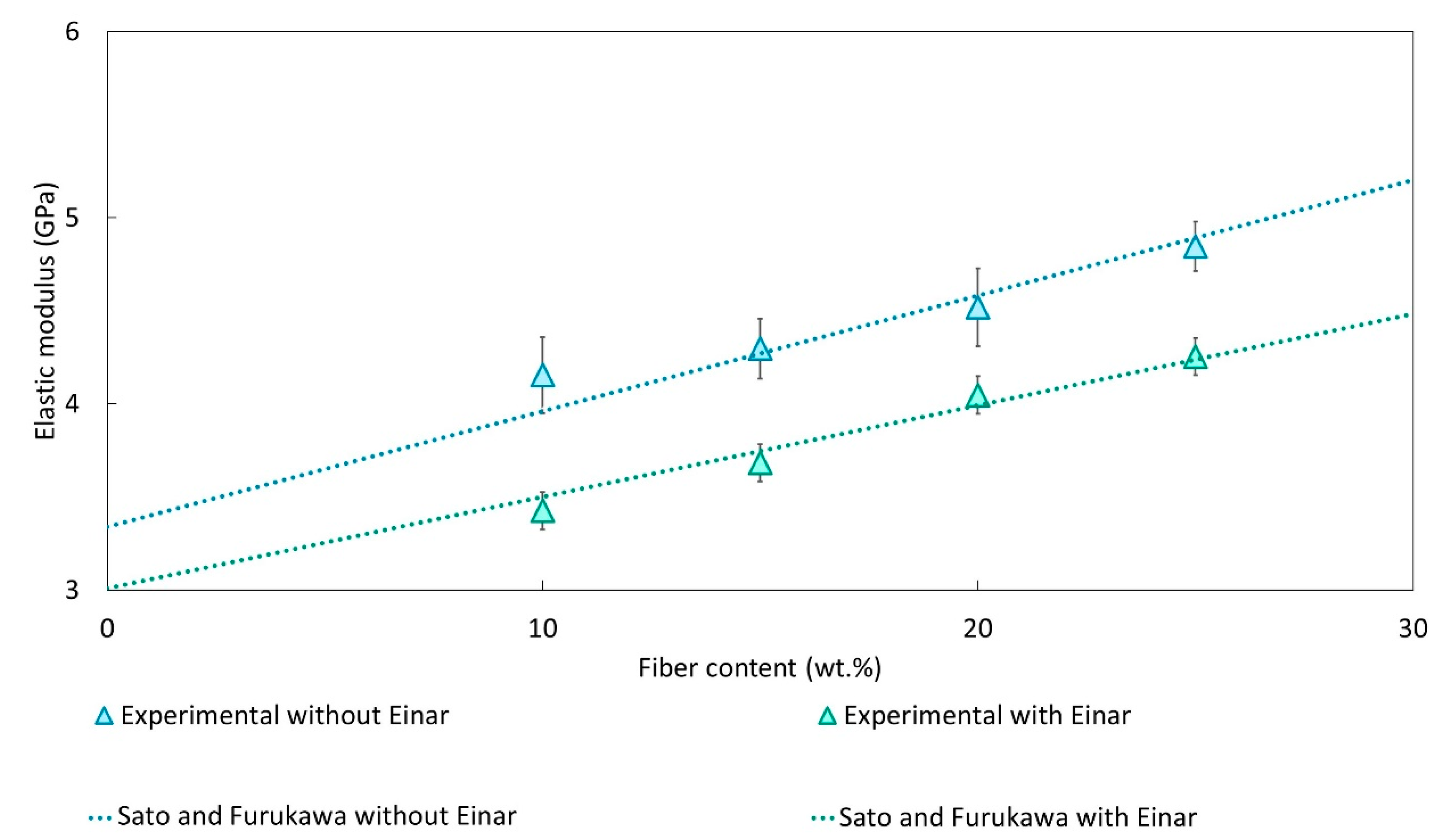
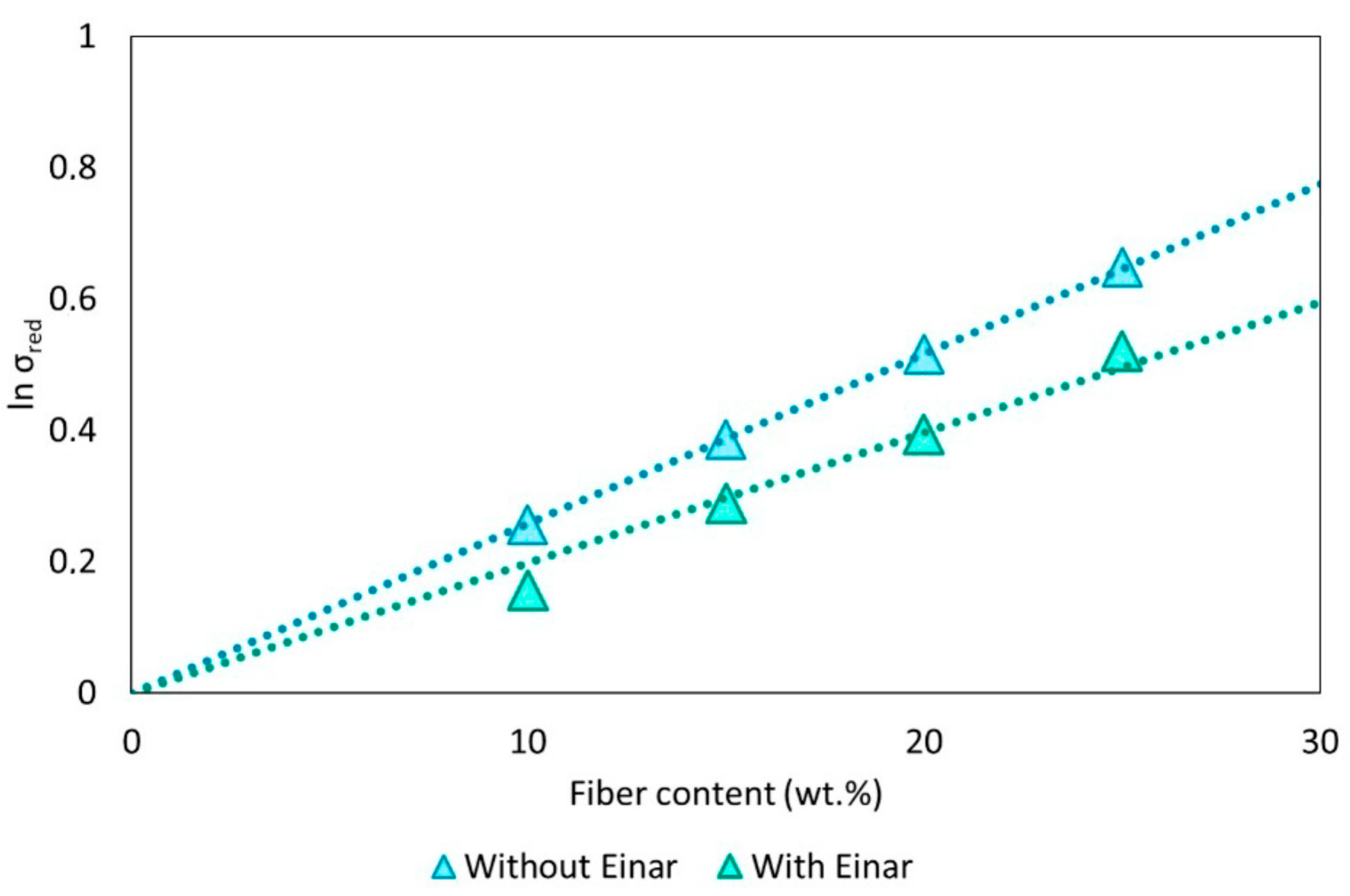
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gurunathan, T.; Mohanty, S.; Nayak, S.K. A review of the recent developments in biocomposites based on natural fibres and their application perspectives. Compos. Part A Appl. Sci. Manuf. 2015, 77, 1–25. [Google Scholar] [CrossRef]
- La Mantia, F.P.; Morreale, M. Green composites: A brief review. Compos. Part A Appl. Sci. Manuf. 2011, 42, 579–588. [Google Scholar] [CrossRef]
- Mohanty, A.K.; Misra, M.; Drzal, L.T. Sustainable bio-composites from renewable resources: opportunities and challenges in the green materials world. J. Polym. Environ. 2002, 10, 19–26. [Google Scholar] [CrossRef]
- Râpă, M.; Popa, M.; Cinelli, P.; Lazzeri, A.; Burnichi, R.; Mitelut, A.; Grosu, E. Biodegradable Alternative to Plastics for Agriculture Application. Rom. Biotechnol. Lett. 2011, 16, 59–64. [Google Scholar]
- Garrison, T.F.; Murawski, A.; Quirino, R.L. Bio-Based Polymers with Potential for Biodegradability. Polymers (Basel) 2016, 8, 262. [Google Scholar] [CrossRef] [PubMed]
- Righetti, M.C.; Cinelli, P.; Mallegni, N.; Massa, C.A.; Aliotta, L.; Lazzeri, A. Thermal, Mechanical, Viscoelastic and Morphological Properties of Poly ( lactic acid ) based Biocomposites with Potato Pulp Powder Treated with Waxes. Materials (Basel) 2019, 12, 990. [Google Scholar] [CrossRef]
- Dungani, R.; Karina, M.; Sulaeman, A.; Hermawan, D.; Hadiyane, A. Agricultural waste fibers towards sustainability and advanced utilization: A review. Asian J. Plant Sci. 2016, 15, 42–55. [Google Scholar] [CrossRef]
- Mohanty, A.K.; Vivekanandhan, S.; Pin, J.-M.; Misra, M. Composites from renewable and sustainable resources: Challenges and innovations. Science 2018, 362, 536–542. [Google Scholar] [CrossRef]
- Bledzki, A.K.; Gassan, J. Composites reinforced with cellulose based fibres. Prog. Polym. Sci. 1999, 24, 221–274. [Google Scholar] [CrossRef]
- Satyanarayana, K.G.; Arizaga, G.G.C.; Wypych, F. Biodegradable composites based on lignocellulosic fibers—An overview. Prog. Polym. Sci. 2009, 34, 982–1021. [Google Scholar] [CrossRef]
- Faruk, O.; Bledzki, A.K.; Fink, H.P.; Sain, M. Biocomposites reinforced with natural fibers: 2000-2010. Prog. Polym. Sci. 2012, 37, 1552–1596. [Google Scholar] [CrossRef]
- Pickering, K.L.; Efendy, M.G.A.; Le, T.M. A review of recent developments in natural fibre composites and their mechanical performance. Compos. Part A Appl. Sci. Manuf. 2016, 83, 98–112. [Google Scholar] [CrossRef]
- Raquez, J.M.; Habibi, Y.; Murariu, M.; Dubois, P. Polylactide (PLA)-based nanocomposites. Prog. Polym. Sci. 2013, 38, 1504–1542. [Google Scholar] [CrossRef]
- Aliotta, L.; Cinelli, P.; Coltelli, M.B.; Righetti, M.C.; Gazzano, M.; Lazzeri, A. Effect of nucleating agents on crystallinity and properties of poly (lactic acid) (PLA). Eur. Polym. J. 2017, 93, 822–832. [Google Scholar] [CrossRef]
- Scaffaro, R.; Lopresti, F.; Botta, L. PLA based biocomposites reinforced with Posidonia oceanica leaves. Compos. Part B Eng. 2018, 139, 1–11. [Google Scholar] [CrossRef]
- Aliotta, L.; Gigante, V.; Acucella, O.; Signori, F.; Lazzeri, A. Thermal, Mechanical and Micromechanical Analysis of PLA/PBAT/POE-g-GMA Extruded Ternary Blends. Front. Mater. 2020, 7, 1–14. [Google Scholar] [CrossRef]
- Gross, R.A.; Kalra, B. Biodegradable Polymers for the Environment. Science 2002, 297, 803–807. [Google Scholar] [CrossRef]
- Scaffaro, R.; Botta, L.; Lopresti, F.; Maio, A.; Sutera, F. Polysaccharide nanocrystals as fillers for PLA based nanocomposites. Cellulose 2017, 24, 447–478. [Google Scholar] [CrossRef]
- Chen, Y.; Geever, L.M.; Killion, J.A.; Lyons, J.G.; Higginbotham, C.L.; Devine, D.M. Review of multifarious applications of poly (lactic acid). Polym. Plast. Technol. Eng. 2016, 55, 1057–1075. [Google Scholar] [CrossRef]
- Nagarajan, V.; Mohanty, A.K.; Misra, M. Perspective on Polylactic Acid (PLA) based Sustainable Materials for Durable Applications: Focus on Toughness and Heat Resistance. ACS Sustain. Chem. Eng. 2016, 4, 2899–2916. [Google Scholar] [CrossRef]
- Barletta, M.; Aversa, C.; Puopolo, M.; Vesco, S. Ultra-flexible PLA-based blends for the manufacturing of biodegradable tamper-evident screw caps by injection molding. J. Appl. Polym. Sci. 2020, 137, 49428. [Google Scholar] [CrossRef]
- Aliotta, L.; Gigante, V.; Coltelli, M.B.; Cinelli, P.; Lazzeri, A. Evaluation of Mechanical and Interfacial Properties of Bio-Composites Based on Poly (Lactic Acid ) with Natural Cellulose Fibers. Int. J. Mol. Sci. 2019, 20, 960. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Zhang, J. Research progress in toughening modification of poly(lactic acid). J. Polym. Sci. Part B Polym. Phys. 2011, 49, 1051–1083. [Google Scholar] [CrossRef]
- Aliotta, L.; Lazzeri, A. A proposal to modify the Kelly-Tyson equation to calculate the interfacial shear strength (IFSS ) of composites with low aspect ratio fibers. Compos. Sci. Technol. 2020, 186, 107920. [Google Scholar] [CrossRef]
- Rezaei, F.; Yunus, R.; Ibrahim, N.A.; Mahdi, E.S. development of short-carbon-fiber-reinforced polypropylene composite for car bonnet Development of short-carbon-fiber-reinforced polypropylene composite for car bonnet. Polym. Plast. Technol. Eng. 2008, 47, 351–357. [Google Scholar] [CrossRef]
- Tao, Y.U.; Yan, L.I.; Jie, R.E.N. Preparation and properties of short natural fiber reinforced poly (lactic acid) composites. Trans. Nonferrous Met. Soc. China 2009, 19, s651–s655. [Google Scholar]
- Fu, S.-Y.; Lauke, B.; Mäder, E.; Yue, C.-Y.; Hu, X. Tensile properties of short-glass-fiber-and short-carbon-fiber-reinforced polypropylene composites. Compos. Part A Appl. Sci. Manuf. 2000, 31, 1117–1125. [Google Scholar] [CrossRef]
- Mohanty, A.K.; Misra, M.; Hinrichsen, G. Biofibres, biodegradable polymers and biocomposites: An overview. Macromol. Mater. Eng. 2000, 276–277, 1–24. [Google Scholar] [CrossRef]
- Aliotta, L.; Gigante, V.; Coltelli, M.-B.; Cinelli, P.; Lazzeri, A.; Seggiani, M. Thermo-mechanical properties of PLA/short flax fiber biocomposites. Appl. Sci. 2019, 9, 3797. [Google Scholar] [CrossRef]
- Gigante, V.; Cinelli, P.; Righetti, M.C.; Sandroni, M.; Tognotti, L.; Seggiani, M.; Lazzeri, A. Evaluation of Mussel Shells Powder as Reinforcement for PLA-Based Biocomposites. Int. J. Mol. Sci. 2020, 21, 5364. [Google Scholar] [CrossRef]
- Alimuzzaman, S.; Gong, R.H.; Akonda, M. Nonwoven polylactic acid and flax biocomposites. Polym. Compos. 2013, 34, 1611–1619. [Google Scholar] [CrossRef]
- Ibrahim, N.A.; Md Zin Wan Yunus, W.; Othman, M.; Abdan, K.; Hadithon, K.A. Poly(Lactic Acid) (PLA)-reinforced kenaf bast fiber composites: The effect of triacetin. J. Reinf. Plast. Compos. 2010, 29, 1099–1111. [Google Scholar] [CrossRef]
- Botta, L.; Fiore, V.; Scalici, T.; Valenza, A.; Scaffaro, R. New polylactic acid composites reinforced with artichoke fibers. Materials (Basel) 2015, 8, 7770–7779. [Google Scholar] [CrossRef]
- Mohanty, A.K.; Misra, M.; Drzal, L.T. Surface modifications of natural fibers and performance of the resulting biocomposites: An overview. Compos. Interfaces 2001, 8, 313–343. [Google Scholar] [CrossRef]
- Mathew, A.P.; Oksman, K.; Sain, M. Mechanical properties of biodegradable composites from poly lactic acid (PLA) and microcrystalline cellulose (MCC). J. Appl. Polym. Sci. 2005, 97, 2014–2025. [Google Scholar] [CrossRef]
- Venkateshwaran, N.; Elaya Perumal, A.; Arunsundaranayagam, D. Fiber surface treatment and its effect on mechanical and visco-elastic behaviour of banana/epoxy composite. Mater. Des. 2013, 47, 151–159. [Google Scholar] [CrossRef]
- Sawpan, M.A.; Pickering, K.L.; Fernyhough, A. Effect of fibre treatments on interfacial shear strength of hemp fibre reinforced polylactide and unsaturated polyester composites. Compos. Part A Appl. Sci. Manuf. 2011, 42, 1189–1196. [Google Scholar] [CrossRef]
- Yan, L.; Chouw, N.; Yuan, X. Improving the mechanical properties of natural fibre fabric reinforced epoxy composites by alkali treatment. J. Reinf. Plast. Compos. 2012, 31, 425–437. [Google Scholar] [CrossRef]
- Baley, C.; Morvan, C.; Grohens, Y. Influence of the absorbed water on the tensile strength of flax fibers. In Proceedings of the Macromolecular Symposia; Wiley Online Library: Hoboken, NJ, USA, 2005; Volume 222, pp. 195–202. [Google Scholar]
- Abdelhak, B.; Noureddine, M.; Hacen, M. Improvement of the interfacial adhesion between fiber and matrix. Mech. Mech. Eng. 2018, 22, 885–893. [Google Scholar] [CrossRef]
- Valadez-Gonzalez, A.; Cervantes-Uc, J.M.; Olayo, R.; Herrera-Franco, P.J. Effect of fiber surface treatment on the fiber–matrix bond strength of natural fiber reinforced composites. Compos. Part B Eng. 1999, 30, 309–320. [Google Scholar] [CrossRef]
- Carman, G.P.; Reifsnider, K.L. Micromechanics of short-fiber composites. Compos. Sci. Technol. 1992, 43, 137–146. [Google Scholar] [CrossRef]
- Fu, S.Y.; Lauke, B. Effects of fiber length and fiber orientation distributions on the tensile strength of short-fiber-reinforced polymers. Compos. Sci. Technol. 1996, 56, 1179–1190. [Google Scholar] [CrossRef]
- Herrera-Franco, P.J.; Valadez-Gonzalez, A. A study of the mechanical properties of short natural-fiber reinforced composites. Compos. Part B Eng. 2005, 36, 597–608. [Google Scholar] [CrossRef]
- Abrate, S. The mechanics of short-fiber-reinfroced composites: A review. Rubber Chem. Technol. 1986, 59, 384–404. [Google Scholar] [CrossRef]
- Zainudin, E.S.; Sapuan, S.M.; Sulaiman, S.; Ahmad, M.M.H.M. Fiber orientation of short fiber reinforced injection molded thermoplastic composites: A review. J. Inject. Molding Technol. 2002, 6, 1–10. [Google Scholar]
- Prashanth, S.; Subbaya, K.M.; Nithin, K.; Sachhidananda, S. Fiber reinforced composites-a review. J. Mater. Sci. Eng. 2017, 6, 22–2169. [Google Scholar]
- Capela, C.; Oliveira, S.E.; Pestana, J.; Ferreira, J.A.M. Effect of fiber length on the mechanical properties of high dosage carbon reinforced. Procedia Struct. Integr. 2017, 5, 539–546. [Google Scholar] [CrossRef]
- Bigg, D.M. Effect of compounding on the properties of short fiber reinforced injection moldable thermoplastic composites. Polym. Compos. 1985, 6, 20–28. [Google Scholar] [CrossRef]
- Aliotta, L.; Cinelli, P.; Coltelli, M.B.; Lazzeri, A. Rigid filler toughening in PLA-Calcium Carbonate composites: Effect of particle surface treatment and matrix plasticization. Eur. Polym. J. 2019, 113, 78–88. [Google Scholar] [CrossRef]
- Lazzeri, A.; Zebarjad, S.M.; Pracella, M.; Cavalier, K.; Rosa, R. Filler toughening of plastics. Part 1—the effect of surface interactions on physico-mechanical properties and rheological behaviour of ultrafine CaCO3/HDPE nanocomposites. Polymer (Guildf.) 2005, 46, 827–844. [Google Scholar] [CrossRef]
- Garg, P.; Singh, B.P.; Kumar, G.; Gupta, T.; Pandey, I.; Seth, R.K.; Tandon, R.P.; Mathur, R.B. Effect of dispersion conditions on the mechanical properties of multi-walled carbon nanotubes based epoxy resin composites. J. Polym. Res. 2011, 18, 1397–1407. [Google Scholar] [CrossRef]
- Bowyer, W.H.; Bader, M.G. On the re-inforcement of thermoplastics by imperfectly aligned discontinuous fibres. J. Mater. Sci. 1972, 7, 1315–1321. [Google Scholar] [CrossRef]
- Thomason, J.L. Interfacial strength in thermoplastic composites-At last an industry friendly measurement method? Compos. Part A Appl. Sci. Manuf. 2002, 33, 1283–1288. [Google Scholar] [CrossRef]
- Tripathi, D.; Turton, T.; Chen, F.; Jones, F.R. A new method to normalize the effect of matrix properties on the value of interfacial shear strength obtained from the fragmentation test. J. Mater. Sci. 1997, 32, 4759–4765. [Google Scholar] [CrossRef]
- Pukánszky, B. Influence of interface interaction on the ultimate tensile properties of polymer composites. Composites 1990, 21, 255–262. [Google Scholar] [CrossRef]
- Sato, Y.; Furukawa, J. A molecular theory of filler reinforcement based upon the conception of internal deformation (a rough approximation of the internal deformation). Rubber Chem. Technol. 1963, 36, 1081–1106. [Google Scholar] [CrossRef]
- International Organization for Standardization ISO 1133-1:2011: Determination of the melt mass-flow rate (MFR) and melt volume-flow rate (MVR) of thermoplastics - Part 1. Geneva 2011, 2011, 24.
- Lazzeri, A.; Phuong, V.T. Dependence of the Pukánszky’s interaction parameter B on the interface shear strength (IFSS) of nanofiller- and short fiber-reinforced polymer composites. Compos. Sci. Technol. 2014, 93, 106–113. [Google Scholar] [CrossRef]
- Huber, T.; Mussig, J. Fibre matrix adhesion of natural fibres cotton, flax and hemp in polymeric matrices analyzed with the single fibre fragmentation test. Compos. Interfaces 2008, 15, 335–349. [Google Scholar] [CrossRef]
- Vallejos, M.E.; Espinach, F.X.; Julián, F.; Torres, L.; Vilaseca, F.; Mutjé, P. Micromechanics of hemp strands in polypropylene composites. Compos. Sci. Technol. 2012, 72, 1209–1213. [Google Scholar] [CrossRef]
- Li, Y.; Pickering, K.L.; Farrell, R.L. Determination of interfacial shear strength of white rot fungi treated hemp fibre reinforced polypropylene. Compos. Sci. Technol. 2009, 69, 1165–1171. [Google Scholar] [CrossRef]
- Gigante, V.; Aliotta, L.; Phuong, V.T.; Coltelli, M.B.; Cinelli, P.; Lazzeri, A. Effects of waviness on fiber-length distribution and interfacial shear strength of natural fibers reinforced composites. Compos. Sci. Technol. 2017, 152, 129–138. [Google Scholar] [CrossRef]
- del Rey, R.; Serrat, R.; Alba, J.; Perez, I.; Mutje, P.; Espinach, F.X. Effect of sodium hydroxide treatments on the tensile strength and the interphase quality of hemp core fiber-reinforced polypropylene composites. Polymers (Basel) 2017, 9, 377. [Google Scholar] [CrossRef] [PubMed]
- Andersons, J.; Modniks, J.; Joffe, R.; Madsen, B.; Nättinen, K. Apparent interfacial shear strength of short-flax-fiber/starch acetate composites. Int. J. Adhes. Adhes. 2016, 64, 78–85. [Google Scholar] [CrossRef]
- Raharjo, W.P.; Soenoko, R.; Purnowidodo, A.; Choiron, M.A. Experimental and micromechanical modelling of randomly oriented zalacca fibre/low-density polyethylene composites fabricated by hot-pressing method. Cogent Eng. 2018, 5, 1518966. [Google Scholar] [CrossRef]
- Modniks, J.; Poriķe, E.; Andersons, J.; Joffe, R. Evaluation of the apparent interfacial shear strength in short-flax-fiber/PP composites. Mech. Compos. Mater. 2012, 48, 571–578. [Google Scholar] [CrossRef]
- Thomason, J.L. The influence of fibre length and concentration on the properties of glass fibre reinforced polypropylene: 5. Injection moulded long and short fibre PP. Compos. Part A Appl. Sci. Manuf. 2002, 33, 1641–1652. [Google Scholar] [CrossRef]
- Kelly, A.; Tyson, W.R. Tensile properties of fibre-reinforced metals: Copper/tungsten and copper/molybdenum. J. Mech. Phys. Solids 1965, 13, 329–350. [Google Scholar] [CrossRef]
- Sanadi, A.R.; Young, R.A.; Clemons, C.; Rowell, R.M. Recycled Newspaper Fibers as Reinforcing Fillers in Thermoplastics: Part I-Analysis of Tensile and Impact Properties in Polypropylene. J. Reinf. Plast. Compos. 1994, 13, 54–67. [Google Scholar] [CrossRef]
- Anderson, K.S.; Schreck, K.M.; Hillmyer, M.A. Toughening Polylactide. Polym. Rev. 2008, 48, 85–108. [Google Scholar] [CrossRef]
- Phuong, V.T.; Gigante, V.; Aliotta, L.; Coltelli, M.B.; Cinelli, P.; Lazzeri, A. Reactively extruded ecocomposites based on poly(lactic acid)/bisphenol A polycarbonate blends reinforced with regenerated cellulose microfibers. Compos. Sci. Technol. 2017, 139, 127–137. [Google Scholar] [CrossRef]
- Cinelli, P.; Mallegni, N.; Gigante, V.; Montanari, A.; Seggiani, M.; Coltelli, B.; Bronco, S.; Lazzeri, A. Biocomposites Based on Polyhydroxyalkanoates and Natural Fibres from Renewable Byproducts. Appl. Food Biotechnol. 2019, 6, 35–43. [Google Scholar]
- Argon, A.S.; Bartczak, Z.; Cohen, R.E.; Muratoglu, O.K. Novel mechanisms of toughening semi-crystalline polymers. In Toughening of Plastics; ACS Publications: Washington, DC, USA, 2000; ISBN 1947-5918. [Google Scholar]
- Wilbrink, M.W.L.; Argon, A.S.; Cohen, R.E.; Weinberg, M. Toughenability of Nylon-6 with CaCO3 filler particles: New findings and general principles. Polymer (Guildf.) 2001, 42, 10155–10180. [Google Scholar] [CrossRef]
- Formela, K.; Hejna, A.; Piszczyk, Ł.; Saeb, M.R.; Colom, X. Processing and structure–property relationships of natural rubber/wheat bran biocomposites. Cellulose 2016, 23, 3157–3175. [Google Scholar] [CrossRef]
- Aliotta, L.; Gazzano, M.; Lazzeri, A.; Righetti, M.C. Constrained Amorphous Interphase in Poly (L -lactic acid): Estimation of the Tensile Elastic Modulus. ACS Omega 2020, 5, 20890–20902. [Google Scholar] [CrossRef]
- Cox, H.L. The elasticity and strength of paper and other fibrous materials. Br. J. Appl. Phys. 1952, 3, 72–79. [Google Scholar] [CrossRef]
- Serrano, A.; Espinach, F.X.; Julian, F.; Del Rey, R.; Mendez, J.A.; Mutje, P. Estimation of the interfacial shears strength, orientation factor and mean equivalent intrinsic tensile strength in old newspaper fiber/polypropylene composites. Compos. Part B Eng. 2013, 50, 232–238. [Google Scholar] [CrossRef]
- Pegoretti, A.; Della Volpe, C.; Detassis, M.; Migliaresi, C.; Wagner, H.D. Thermomechanical behaviour of interfacial region in carbon fibre/epoxy composites. Compos. Part A Appl. Sci. Manuf. 1996, 27, 1067–1074. [Google Scholar] [CrossRef]
- Shenoy, A.V. Rheology of Filled Polymer Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; ISBN 9401592136. [Google Scholar]
- Gasner, G.E.; Bigio, D.; Marks, C.; Magnus, F.; Kiehl, C. A new approach to analyzing residence time and mixing in a co-rotating twin screw extruder. Polym. Eng. Sci. 1999, 39, 286–298. [Google Scholar] [CrossRef]


| Name | PLA-Arbocel wt.% | Einar 101 wt.% |
|---|---|---|
| PLA | 100–0 | - |
| PLA_10 | 90–10 | - |
| PLA_15 | 85–15 | - |
| PLA_20 | 80–20 | - |
| PLA_25 | 75–25 | - |
| PLA_E | 100–0 | 5 |
| PLA_10_E | 90–10 | 5 |
| PLA_15_E | 85–15 | 5 |
| PLA_20_E | 80–20 | 5 |
| PLA_25_E | 75–25 | 5 |
| Main Injection Molding Parameters | Composites without Einar | Composites with Einar |
|---|---|---|
| Temperature profile from feeder to injection zone (°C) | 180–185–180 | 170–175–170 |
| Mold temperature (°C) | 60 | 60 |
| Injection holding time (s) | 5 | 5 |
| Cooling time (s) | 25 | 25 |
| Injection pressure (bar) 1 | 90–110 | 90–110 |
| Symbol | Meaning |
|---|---|
| εc | Composite strain |
| η0 | Fiber orientation factor |
| σc | Composite stress at break |
| σ*f | Fiber stress at break |
| σ’m | Stress of the matrix at εc |
| Ef,m | Elastic modulus of fiber (f) or matrix (m) |
| ar | Fiber aspect ratio |
| Vf | Volume fraction of the fibers in the composite |
| τ | Interfacial Shear Strength (IFSS) |
| D | Average fiber diameter |
| Lc | Critical fiber length |
| Li,j | Fiber length below (i) and above (j) the critical fiber length |
| Composite System | Sato and Furukawa ξ Parameter | Pukánszky B Parameter |
|---|---|---|
| PLA/Arbocel | 0.13 | 2.58 |
| PLA/Arbocel/Einar | 0.37 | 1.98 |
| Composite System | IFSS (MPa) According to Classic B-B Model (Equation (7)) | IFSS (MPa) According to Modified B-B Model (Equation (8)) | IFSS (MPa) Von Mises Threshold |
|---|---|---|---|
| PLA/Arbocel | 55.92 | 34.44 | 37.20 |
| PLA/Arbocel/Einar | 23.20 | 8.20 | 25.98 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aliotta, L.; Gigante, V.; Cinelli, P.; Coltelli, M.-B.; Lazzeri, A. Effect of a Bio-Based Dispersing Aid (Einar® 101) on PLA-Arbocel® Biocomposites: Evaluation of the Interfacial Shear Stress on the Final Mechanical Properties. Biomolecules 2020, 10, 1549. https://doi.org/10.3390/biom10111549
Aliotta L, Gigante V, Cinelli P, Coltelli M-B, Lazzeri A. Effect of a Bio-Based Dispersing Aid (Einar® 101) on PLA-Arbocel® Biocomposites: Evaluation of the Interfacial Shear Stress on the Final Mechanical Properties. Biomolecules. 2020; 10(11):1549. https://doi.org/10.3390/biom10111549
Chicago/Turabian StyleAliotta, Laura, Vito Gigante, Patrizia Cinelli, Maria-Beatrice Coltelli, and Andrea Lazzeri. 2020. "Effect of a Bio-Based Dispersing Aid (Einar® 101) on PLA-Arbocel® Biocomposites: Evaluation of the Interfacial Shear Stress on the Final Mechanical Properties" Biomolecules 10, no. 11: 1549. https://doi.org/10.3390/biom10111549
APA StyleAliotta, L., Gigante, V., Cinelli, P., Coltelli, M.-B., & Lazzeri, A. (2020). Effect of a Bio-Based Dispersing Aid (Einar® 101) on PLA-Arbocel® Biocomposites: Evaluation of the Interfacial Shear Stress on the Final Mechanical Properties. Biomolecules, 10(11), 1549. https://doi.org/10.3390/biom10111549









