Abstract
We reinvestigate a key process in electron-atom collision physics, the elastic scattering of electrons from helium atoms. Specifically, results from a special-purpose relativistic polarized-orbital method, which is designed to treat elastic scattering only, are compared with those from a very extensive, fully ab initio, general-purpose B-spline R-matrix (close-coupling) code.
1. Introduction
One of the most-frequently investigated collision problems in atomic physics has been the elastic scattering of electrons from helium atoms. Although often considered a “solved problem”, especially when it comes to modelling applications in plasmas or astrophysics, attempts to increase the accuracy of the predictions continue to be reported. In fact, many special-purpose computational approaches have been developed solely to achieve this goal. The most recent example of such an attempt is the paper by Wan et al. [1] who state in their abstract: “Our calculated phaseshifts improve the best published results by at least one order of magnitude.”
While the method employed by Wan et al. is indeed capable of determining highly accurate phaseshifts, there are certain aspects of their approach, and others like it, which ultimately require sacrificing the rigour of the underlying physics to achieve these impressive gains in numerical accuracy. We note, for example, that Equation (1) of Wan et al. [1] contains a model potential with an approximate form of a local dipole-polarization potential. Both the cut-off radius and the actual form of the cut-off function, while known to be working well, are not based on first principles. Furthermore, the parameters chosen by Wan et al. yield a highly accurate nonrelativistic total energy of the ground state for an infinite nuclear mass, but this is not the actual energy of the system. As pointed out by those authors themselves, going from an infinite nuclear mass to the proper reduced mass will change the results, and so will relativistic and even quantum electrodynamic effects. In addition to such inaccuracies based on the omission of some known (or even unknown) physics in a model, the numerical accuracy of any computational method is limited as well.
Oleg Zatsarinny, to whom this Special Issue is dedicated, was well aware of both the physical and numerical limitations of calculations for structure and particularly collision problems. He would first define the physics (e.g., non-relativistic, semi-relativistic, or full-relativistic) of his approach and then try to solve the resulting equations as best he could with the computational resources available. He would compare with experiment, but use experimental data only reluctantly to further “improve” his ab initio calculations. For example, he might adjust the theoretical energies from his structure calculations to the values recommended by his colleagues and friends at the National Institute of Standards and Technology (NIST) [2], but only if that seemed necessary to allow for a direct comparison with experimental data that would have a smaller uncertainty in their energy resolution than the deviations between his theoretical threshold values and the NIST recommendations.
For many practical collision experiments, such high accuracy is not easy to achieve. Furthermore, experimental data for cross sections often have relatively large uncertainties due to the difficulties associated with their absolute calibration. The e-He collision system remains very important, since results for this problem are often utilized as a reference for both the energy scale and to normalize relative data for electron collisions with more complex targets via a relative-flow technique [3].
The purpose of the present contribution to this Special Issue is to investigate how predictions from a very general approach developed by Oleg to treat elastic scattering, excitation, and ionization not only from the ground state but also from and between excited states of atomic and ionic targets (including helium), compare to those from models that were designed to treat just one. Elastic e-He (a closed-shell target) scattering below the first excitation threshold, specifically below the famous resonance at eV [4], is such a process. There are numerous special-purpose methods around, some of which are mentioned by Wan et al. [1]. Here we present results from another such special-purpose method, the relativistic polarized orbital (RPO) approach described in the next section.
The B-spline R-matrix (BSR) approach developed by Oleg is a general-purpose approach. It is, in principle, applicable to any atom or ion, since it treats all electrons explicitly, i.e., N in the target plus the projectile. There are, of course, practical limitations due to the number of configurations and channels that can be handled. An overview of the method and many applications to structure, photoionization, and electron collision problems can be found in [5]. In 2006, Oleg published the code [6] and continuously worked on further extensions and improvements. The latest version of his programs (including a relativistic D(irac)BSR version) are freely available from Oleg’s GitHub repository [7]. Furthermore, the BSR version is being preserved through the Atomic, Molecular, and Optical Sciences (AMOS) Gateway [8], where the source code as well as many sample input files and run scripts for test cases are made available to all interested users.
This paper is organized as follows. In Section 2, we summarize the most important aspects of the RPO and BSR methods. This is followed by our results in Section 3. The latter section is divided into subsections starting with some representative phaseshifts, followed by extraction of the scattering length, and finally the presentation of the angle-integrated elastic and momentum-transfer cross sections. In addition to comparing with the results of Wan et al. [1], we show representative data obtained by Nesbet [9] using his early benchmark variational approach for elastic scattering as well as extensive multi-channel close-coupling calculations, specifically the momentum-space convergence close-coupling (CCC) approach of Fursa and Bray [10] and the coordinate-space R-matrix with pseudostates (RMPS) method used by Hudson et al. [11]. Finally, our findings and conclusions are summarized in Section 4.
2. Numerical Methods
We now briefly describe the numerical methods used to obtain the results presented in this paper. For more details, the reader should consult the references provided during the description. Unless indicated otherwise, atomic units (a.u.) are used throughout, i.e., energies (E) are given in Hartree ( eV), linear momenta are obtained as since relativistic effects are very small, lengths are given in multiples of the Bohr radius m, and angular momenta in multiples of .
2.1. Relativistic Polarized Orbital Approach
With this method, the various phaseshifts and cross sections were calculated using the relativistic optical potential method as originally described in [12]. This method is based upon an approximate solution of the Dirac-Fock scattering equations. It includes the static, polarization and exchange interactions as well as a complex optical potential to simulate excitation and ionization processes. However, since we are only considering elastic scattering here, this optical potential is not required. The computer code has recently been used to describe electron and positron scattering from other two-electron systems, namely Be [13] and Mg [14].
The Dirac wavefunctions for the ground state of He were obtained in a single-configuration calculation using the multi-configuration Dirac-Fock code [15]. This simple procedure yields a total energy of a.u., i.e., practically identical to the single-configuration nonrelativistic Hartree-Fock result ( a.u.) [16]. Using only one configuration misses a substantial amount of the correlation energy (see below).
Since we are dealing with just elastic scattering here, only three interactions need to be considered. The first two are given by the local potential , where is the static potential and is the (long-range) polarization potential. The third interaction is given by the (short-range) nonlocal exchange terms.
The static potential was determined in the usual manner from the ground-state atomic orbitals, while the polarization potential was generated by the polarized-orbital method [17]. It included the first five static multipole potentials plus the corresponding dynamic polarization potential. The precise form of this dynamic potential is discussed in McEachran and Stauffer [18,19] and references therein. Finally, the exchange interaction was given by anti-symmetrizing the total scattering wavefunction. The polarized-orbital method yielded dipole and quadrupole polarizabilities of 1.3222 and 2.3362 , respectively. The dipole and quadrupole polarization potentials were then scaled to 1.3840 [20] and 2.4459 [21] to account for as much of the relevant physics as possible. Since there are no absorption processes, we refer to this method as the relativistic polarized-orbital method (RPO). Apart from the above scaling of the dipole and quadrupole polarization potentials, the RPO method is ab initio.
The radial integral equations for the large and small components of the scattering wavefunctions, and , can be expressed in matrix form as
Here the functions and are the corresponding free-particle wavefunctions given in terms of Riccati-Bessel functions, while and are the large and small components of the exchange terms. The parameter is the relativistic angular momentum of the incident electron. The energy E and the wavenumber k of the incident electron are related according to . Here is the usual relativistic parameter, where v is the speed of the incident electron and is the speed of light in vacuum and is the fine-structure constant. In the cases considered here, and hence . The Green’s function can be expressed in terms of Riccati-Bessel and Riccati-Neumann functions (see Equation (23) of [12] for details).
Equations (1) were solved in a noniterative manner, and the corresponding phaseshifts were determined from the asymptotic form of the large component of the scattering wavefunctions. Here and are the spin-up and spin-down phaseshifts respectively corresponding to , where j and ℓ are the total and orbital angular momenta of the incident electron. From these phaseshifts, the elastic cross section is obtained as
Since relativistic effects in He are small, the spin-up and spin-down phaseshifts are very similar, with the difference increasing as the incident energy increases. The largest difference of 0.00002 occurred in the P-wave at the highest energy (19.59 eV) considered here, and hence Equation (2) essentially reduces to the well-known nonrelativistic form.
2.2. Nonrelativistic B-Spline R-Matrix with Pseudostates
The present BSR calculations are based on the work described by Zatsarinny and Bartschat [22]. Specifically, it is a nonrelativistic model with 498 states included in the close-coupling expansion. We will refer to this model as BSR-498 below. With the R-matrix radius chosen as 40, the lowest 11 bound states up to a principal quantum number are fairly well-described physical states, while the remaining states squeezed into this box are so-called pseudostates that represent coupling to the high-lying Rydberg states (the next 16) as well as the ionization continuum (the remaining 471). The highest state included had an energy of ≈76 eV.
For elastic scattering in the energy region discussed in this paper, the BSR-498 model appears to be a vast overkill. On the other hand, it is interesting to see how far one can get with a fully ab initio all-purpose approach (in contrast to special-purpose models designed to handle elastic scattering alone), like BSR-498, without adjusting any parameter. This particular model yields a ground-state energy of , i.e., it includes more than 99.6% of the nonrelativistic correlation energy obtained by subtracting the highly accurate correlated result [23] from the single-configuration Hartree-Fock prediction. The static dipole polarizability comes out as 1.355, which is within 2% of the result given in [20].
3. Results and Discussion
We now present and discuss our results for the phaseshift of the partial waves with orbital angular momentum (in this particular case , due to the target state) and compare them with a few selected predictions from other calculations. Since the spin-up and spin-down results for the RPO model are very close (practically identical to the number of figures given), the results shown here are the average of the two. We then concentrate on the S-wave at very low energies to extract the scattering length. We finish this section with a presentation of the angle-integrated elastic and momentum-transfer cross sections.
3.1. Scattering Phase
Table 1, Table 2 and Table 3 give the phaseshifts for the S-, P-, and D-waves, as obtained with the current RPO and BSR-498 models and compared to the results of Nesbet [9], Wan et al. [1], and Hudson et al. [11]. The latter model was the first extensive application of the then newly developed R-matrix with pseudostates (RMPS) method [24] in the framework of the widely-used Belfast R-matrix code [25].

Table 1.
S-wave phaseshift as a function of linear momentum k for infinite nuclear mass.

Table 2.
P-wave phaseshift as a function of linear momentum k for infinite nuclear mass.

Table 3.
D-wave phaseshift as a function of linear momentum k for infinite nuclear mass.
As expected, the overall agreement between the predictions from the various models is very good, with the largest deviations occurring in the S-wave. Especially in the low-energy region, this partial wave gives by far the largest contribution to the cross section, as will be further discussed below. The contribution from the D-wave is already very small. Interestingly, the predictions of all D-wave phaseshifts except for the one reported by Wan et al. [1] agree very well with the effective-range result of O’Malley et al. [26], which gives 0.0502 as the D-wave phaseshift for when using the more accurate dipole polarizability, and 0.0490 when using the dipole polarizability included in the BSR-498 model. Assuming that the numbers in Table II of [1] are for finite nuclear mass, a nearly 10% difference from the effective-range formula due to this effect alone seems large. As noted already by Nesbet [9], partial waves with total orbital angular momenta can be even better described by the simple formula of O’Malley et al. [26].
3.2. Scattering Length
Table 4 gives the S-wave predictions for very small k-values that allow the extraction of the scattering length. In the present work, we do this as follows. The RPO equations can be solved in a stable way for arbitrary energies, including , and hence the scattering length can be determined directly. For the BSR-498 calculations, the asymptotic coupled-channel equations are usually solved with the STGF [27] or FARM [28] packages. These codes have limitations and, consequently, parameters that need to be set regarding how close to a threshold (from both above and below) one can go before the results become numerically unstable. Consequently, we use a similar method as Wan et al. [1]. Specifically, we use their Equation (14) up to the term of order , calculate the value of the scattering length for each k, and then extrapolate to .

Table 4.
S-wave phaseshift used to extract the scattering length for infinite nuclear mass.
The result is shown in Figure 1. The BSR-498 model suggests a scattering length of about 1.187 with a numerical uncertainty of less than 0.002, provided we extract it from the results generated by FARM. The largest uncertainty is most likely coming from the point at , where the extracted results start to deviate from a straight line. That such deviations will occur is more clearly seen in the STGF results. At large values of they agree well with those from FARM, but start to deviate from the latter and the almost straight line when k is smaller than about 0.07. This issue could likely be addressed by changing the default numerical parameters, but our goal is to illustrate that care is required when using these general codes in such relatively extreme situations.
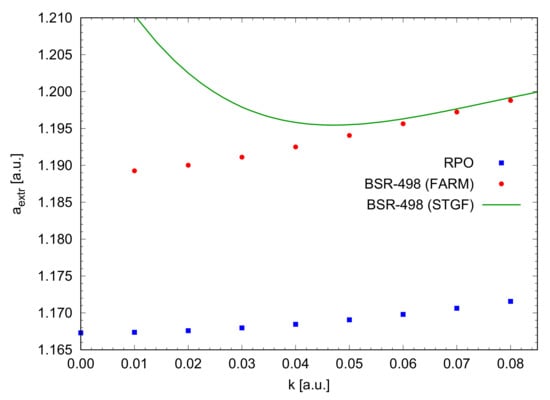
Figure 1.
Extraction of the scattering length. Due to the limitations of the asymptotic FARM and STGF codes (see text for details), the smallest k-value in the BSR-498 calculation is 0.01, while the RPO code allows the calculation at zero collision energy.
Looking at the FARM and RPO results, we see that the purely numerical uncertainty is much smaller (by at least an order of magnitude) than the differences between the actual results from the two models. The reasons for these differences, therefore, lie in the physics included in the two models.
3.3. Cross Sections
We now use these phaseshifts to calculate both the angle-integrated total elastic and momentum-transfer cross sections. Looking at Figure 2, we see that the RPO results are systematically lower than those obtained with BSR-498 and CCC [10], and also by Wan et al. [1]. This can be traced back to the S-wave, which accounts for more than 90% of the total cross section at the maximum around 1 eV and also (albeit in combination with the P-wave) essentially determines the momentum-transfer cross section. Even at the highest energy of 18 eV shown here, the D-wave only contributes about 1% of the total cross section, with the remaining 99% coming from the S- and P-waves at an approximate ratio of 3:1. For all practical purposes, all other partial waves are negligible in the energy regime considered here. This is an example where authors have put significant effort into optimizing tiny corrections [29] rather than concentrating on the physics of the partial waves that matter most.
Given the small differences in the theoretical predictions, it is no simple task to suggest which one of those may be most accurate. Looking at Figure 1 of Wan et al. [1], at low energies almost all the theoretical results fall within the margin of error of the experimentally obtained cross section, making selection by way of best agreement with experiment difficult. Somewhat more promising is the consensus expressed in Figure 1 of the review by Alves et al. [30]. Note that this consensus was not reached by including CCC results (they were accidentally omitted) or BSR-498 predictions. Instead, it was based on data from swarm measurements that are used extensively by the plasma community. The inset of this figure shows the momentum-transfer cross section peaking near 2 eV with a height between and . This confidence range includes the BSR-498 predictions, while the peak height of the RPO results () appears to be slightly too low.
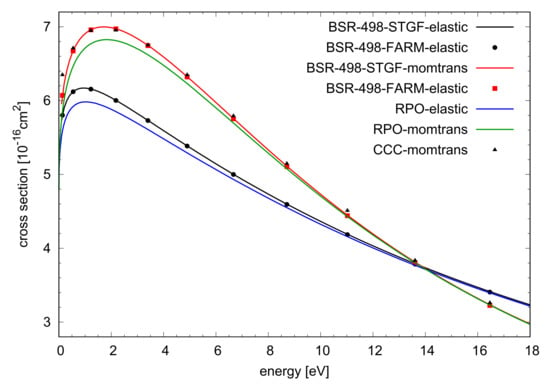
Figure 2.
Angle-integrated elastic and momentum-transfer (momtrans) cross section for e-He scattering. The lines show the present results obtained with RPO and the STGF asymptotic code for the BSR-498 model. The symbols show the same results for the FARM asymptotic package and the CCC results of Fursa and Bray [10] taken from the LXCat database [31].
4. Conclusions
In this contribution, we compared results for elastic electron scattering from helium atoms obtained in a number of special-purpose (elastic scattering only) and general-purpose (multi-channel close-coupling) approaches. These included our current RPO and BSR-498 results. As expected, relativistic effects in this collision system are for all practical purposes negligible compared to other important physics, such as using a finite nuclear mass [1] and channel coupling. We obtain excellent agreement with other sophisticated calculations, even if no adjustments at all (such as using a more accurate value for the dipole polarizability) are made in the BSR-498 calculation. At collision energies below ≈2 eV, the differences between the RPO and BSR-498 results are as large as 3.5%, almost entirely due to the differences in the S-wave phaseshifts in this energy region. Furthermore, we have shown that the much simpler RPO method, which attempts to accurately represent the polarization interaction, can compete favorably with much more sophisticated methods (BSR and CCC) in the elastic scattering region. While one may argue which theoretical predictions are more accurate, we note that the BSR-498 results agree somewhat better with the consensus reached by the plasma community. Overall, it seems appropriate to assign a remaining uncertainty of a few percent to any of these predictions.
Finally, if the desired accuracy is indeed even higher than what has been achieved so far, it seems clear that efforts should be directed to solidifying the S-wave and P-wave results in this purely elastic energy region, rather than worrying about small corrections to less significant contributions. This approach, of pursuing the fullest description of the physics of a problem rather than simply aiming for the greatest accuracy, was the true modus operandi of Oleg Zatsarinny. We believe that he would be very proud of what could be achieved with his approach to the e-He collision problem.
Author Contributions
The project was conceived R.P.M. who also carried out the RPO calculations. The BSR-calculations were performed by K.R.H. and K.B. Most of the manuscript was prepared by K.B. All authors have read and agreed to the published version of the manuscript.
Funding
The work of K.R.H. and K.B. was supported by the NSF under grant Nos. PHY-1803844, OAC-1834740, PHY-2110023, and the XSEDE allocation TG-PHY-090031.
Data Availability Statement
The data shown in the manuscript are available in tabular form from the authors upon request.
Acknowledgments
The authors gratefully acknowledge the contributions of Oleg Zatsarinny to ref. [22], which is the basis for the BSR calculations reported in this manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| RPO | Relativistic Polarized Orbital |
| BSR | B-Spline R-matrix |
References
- Wan, J.Y.; Wu, M.S.; Zhang, J.Y.; Yan, Z.C. Confined variational calculations of low-energy electron-helium scattering. Phys. Rev. A 2021, 103, 042814. [Google Scholar] [CrossRef]
- Atomic Spectra Database. Available online: https://www.nist.gov/pml/atomic-spectra-database (accessed on 12 September 2021).
- Brunger, M.J.; Buckman, S.J. Electron–molecule scattering cross-sections. I. Experimental techniques and data for diatomic molecules. Phys. Rep. 2002, 357, 215–458. [Google Scholar] [CrossRef]
- Gopalan, A.; Bömmels, J.; Götte, S.; Landwehr, A.; Franz, K.; Ruf, M.W.; Hotop, H.; Bartschat, K. A novel electron scattering apparatus combining a laser photoelectron source and a triply differentially pumped supersonic beam target: Characterization and results for the He−(1s2s2) resonance. Eur. Phys. J. D 2002, 22, 17–29. [Google Scholar] [CrossRef]
- Zatsarinny, O.; Bartschat, K. The B-spline R-matrix method for atomic processes: Application to atomic structure, electron collisions, and photoionization. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 112001. [Google Scholar] [CrossRef]
- Zatsarinny, O. BSR: B-Spline Atomic R-Matrix Codes. Comp. Phys. Commun. 2006, 174, 273. [Google Scholar] [CrossRef]
- Oleg Zatsarinny’s GitHub Repository. Available online: https://github.com/zatsaroi (accessed on 12 September 2021).
- Atomic, Molecular, and Optical Sciences Gateway. Available online: https://ampgateway.org (accessed on 12 September 2021).
- Nesbet, R.K. Variational calculations of accurate e--He cross sections below 19 eV. Phys. Rev. A 1979, 20, 58–70. [Google Scholar] [CrossRef]
- Fursa, D.V.; Bray, I. Calculation of electron-helium scattering. Phys. Rev. A 1995, 52, 1279. [Google Scholar] [CrossRef] [PubMed]
- Hudson, E.T.; Bartschat, K.; Scott, M.P.; Burke, P.G.; Burke, V.M. Electron scattering from helium atoms. Phase shifts, resonance parameters and total cross sections. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 5513. [Google Scholar] [CrossRef]
- Chen, S.; McEachran, R.P.; Stauffer, A.D. Ab initio optical potentials for elastic electron and positron scattering from the heavy noble gases. J. Phys. B At. Mol. Opt. Phys. 2008, 41, 025201. [Google Scholar] [CrossRef]
- McEachran, R.P.; Blanco, F.; García, G.; Brunger, M.J. A Relativistic Complex Optical Potential Calculation for Electron–Beryllium Scattering: Recommended Cross Sections. J. Phys. Chem. Ref. Data 2018, 47, 033103. [Google Scholar] [CrossRef]
- McEachran, R.P.; Blanco, F.; García, G.; Stokes, P.W.; White, R.D.; Brunger, M.J. Integral Cross Sections for Electron–Magnesium Scattering Over a Broad Energy Range (0–5000 eV). J. Phys. Chem. Ref. Data 2018, 47, 043104. [Google Scholar] [CrossRef]
- Grant, I.; McKenzie, B.; Norrington, P.; Mayers, D.; Pyper, N. An atomic multiconfigurational Dirac-Fock package. Comput. Phys. Commun. 1980, 21, 207–231. [Google Scholar] [CrossRef]
- Hibbert, A. Energies and Oscillator Strengths Using Configuration Interaction Wavefunctions. In Computational Atomc Physics; Bartschat, K., Ed.; Springer: Heidelberg, Germany; New York, NY, USA, 1996; Chapter 3; pp. 27–64. [Google Scholar]
- McEachran, R.P.; Morgan, D.L.; Ryman, A.G.; Stauffer, A.D. Positron scattering from noble gases: Corrected results for helium. J. Phys. B At. Mol. Phys. 1978, 11, 951–953. [Google Scholar] [CrossRef]
- McEachran, R.P.; Stauffer, A.D. Dynamic distortion effects in electron-atom scattering. J. Phys. B At. Mol. Opt. Phys. 1990, 23, 4605–4614. [Google Scholar] [CrossRef]
- McEachran, R.P.; Stauffer, A.D. Relativistic Effects in Low-Energy Electron–Argon Scattering. Aust. J. Phys. 1997, 50, 511–5244. [Google Scholar] [CrossRef][Green Version]
- Puchalski, M.; Szalewicz, K.; Lesiuk, M.; Jeziorski, B. QED calculation of the dipole polarizability of helium atom. Phys. Rev. A 2020, 101, 022505. [Google Scholar] [CrossRef]
- Wang, Y.S.; Kar, S.; Ho, Y.K. Dynamic Multipole Polarizabilities of Helium and Screened-Helium Atoms. Atoms 2020, 8, 90. [Google Scholar] [CrossRef]
- Zatsarinny, O.; Bartschat, K. Nonperturbative B-spline R-matrix-with-pseudostates calculations for electron-impact ionization of helium. Phys. Rev. A 2012, 85, 062709. [Google Scholar] [CrossRef]
- Pekeris, C.L. 11S and 23S States of Helium. Phys. Rev. 1959, 115, 1216–1221. [Google Scholar] [CrossRef]
- Bartschat, K.; Hudson, E.T.; Scott, M.P.; Burke, P.G.; Burke, V.M. Electron-atom scattering at low and intermediate energies using a pseudo-state/R-matrix basis. J. Phys. B At. Mol. Phys. 1996, 29, 115. [Google Scholar] [CrossRef]
- Berrington, K.A.; Eissner, W.; Norrington, P.H. RMATRIX-I: Belfast Atomic R-Matrix Codes. Comput. Phys. Commun. 1995, 92, 290. [Google Scholar] [CrossRef]
- O’Malley, T.F.; Spruch, L.; Rosenberg, L. Modification of Effective-Range Theory in the Presence of a Long-Range (r−4) Potential. J. Math. Phys. 1961, 2, 491. [Google Scholar] [CrossRef]
- Fernández-Menchero, L.; Conroy, A.; Ballance, C.; Badnell, N.; Mitnik, D.; Gorczyca, T.; Seaton, M. PSTGF: Time-independent R-matrix atomic electron-impact code. Comput. Phys. Commun. 2020, 256, 107489. [Google Scholar] [CrossRef]
- Burke, V.; Noble, C. Farm—A flexible asymptotic R-matrix package. Comput. Phys. Commun. 1995, 85, 471–500. [Google Scholar] [CrossRef]
- Ali, M.K.; Fraser, P.A. The contribution of long-range forces to low-energy phaseshifts. J. Phys. B At. Mol. Phys. 1977, 10, 3091–3104. [Google Scholar] [CrossRef]
- Alves, L.L.; Bartschat, K.; Biagi, S.F.; Bordage, M.C.; Pitchford, L.C.; Ferreira, C.M.; Hagelaar, G.J.M.; Morgan, W.L.; Pancheshnyi, S.; Phelps, A.V.; et al. Comparisons of sets of electron–neutral scattering cross sections and swarm parameters in noble gases: II. Helium and neon. J. Phys. D Appl. Phys. 2013, 46, 334002. [Google Scholar] [CrossRef]
- LXCat Database. Available online: https://nl.lxcat.net (accessed on 14 September 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).