Three-Photon Ionization with One-Photon Resonance between Excited Levels

Abstract

Within the framework of a three-level model, the process of three-photon ionization with one-photon resonance between two excited levels (with the lower one being initially unpopulated) is considered using the density matrix method. It is shown that such resonance can result in the appearance of a maximum in the three-photon ionization spectrum when detuning between the resonance wavenumber and the wavenumber of the transition responsible for the lower excited level being populated exceeds the laser radiation linewidth by more than three orders of magnitude.

In memory of Oleg Zatsarinny

In order to carry out experimental and theoretical studies of the multiphoton ionization of many-electron atoms, a group of scientists was formed in the former Soviet Union in the late 1970s and early 1980s. Under the leadership of N. Delone, the group included scientists from Moscow, Voronezh, Uzhgorod, and Tashkent. It was as a member of this group that Oleg Zatsarinny, already at that time a recognized authority in the field of research and calculation on atomic and ionic structures, studied the role of autoionization states in the process of multiphoton ionization. After the collapse of the Soviet Union and the breaking up of the group, Oleg moved away from this area of research and continued his scientific activity in the field of electron-atom and electron-ion collisions. Nevertheless, he remained constantly interested in our results on multiphoton ionization, especially our calculations using the density matrix method. It was Oleg who, in the summer of 2019, encouraged us to begin the calculations presented in this work, offering his assistance in calculating the matrix elements of one- and two-photon transitions for the barium, strontium, and calcium atoms. Unfortunately, his plans were not destined to come true. This article is dedicated to the memory of our friend and colleague Oleg Zatsarinny.

1. Introduction

Interest in the study of multiphoton ionization has remained consistently high for more than half a century [1,2,3,4,5,6]. Such studies are important both for a deeper understanding of the nonlinear dynamics of quantum systems exposed to an intense electromagnetic field as well as for their relevance to a number of applied problems, in particular the physics of laser plasma. The resonantly enhanced three-photon ionization, being the most promising method for studying the energy structure of atoms and molecules, is of particular interest.

The resonant processes of three-photon ionization of an atom A in a laser field with a wavenumber ω are in the vast majority of cases due to one-photon

A(1) + ħω→A(2) + 2ħω→A⁺ + e

(1)

and two-photon

A(1) + 2ħω→A(3) + ħω→A⁺ + e

(2)

excitation of atomic levels [1]. Here 1 is the ground level, while 2 and 3 are excited levels of the atom A. In the first case, the photon energy ħω is coincident with that of level 2 ($\hslash \omega =E_2$) while in the second case the energy of two photons 2ħω coincides with that of level 3 ($2\hslash \omega =E_3$). Note that in both cases the resonant transition is a one- or two-photon transition between the ground level and an excited level.

The resonant transitions (1) and (2) result in the appearance of maxima in the three-photon ionization spectra due to a considerable increase (up to several orders of magnitude) in the probability of the A⁺ ions’ formation. One- and two-photon resonantly enhanced three-photon ionization has been extensively studied via experiment, and to a lesser extent theoretically (see for example Refs. [7,8,9,10,11,12]).

It is evident that in the case of three-photon ionization, a process is also possible where the resonant transition is the one between excited levels 2→3 ($\hslash \omega =E_3-E_2$), while that between the ground and the lower excited levels 1→2 ($\hslash \omega \ne E_2$)is non-resonant;

A(1) + ħω→A(2) + ħω→A(3) + ħω → A⁺ + e

(3)

it is important to note that level 2 is initially unpopulated.

Experimental manifestation of transitions such as (3) has been observed at three-photon ionization of a number of atoms, in particular Na, Rb, Ba, and Yb (see for example Refs. [11,13,14,15]). Thus, at three-photon ionization of the Ba atom [11] in the vicinity of the maxima related to the one-photon $6s^2 {}^{1}S{}_0\to 6s6p {}^{1}P{}_1^{\mathrm{o}}$ (ω = 18,060 cm⁻¹) and two-photon $6s^2 {}^{1}S{}_0$→$5d6d {}^{3}D{}_2$ (ω = 18,100 cm⁻¹) transitions from the ground $6s^2 {}^{1}S{}_0$ level (transitions 1→2 and 1→3, respectively), a clear maximum corresponding to the one-photon $6s6p {}^{1}P{}_1^{\mathrm{o}}\to 5d6d {}^{3}D{}_2$ (ω = 18,140 cm⁻¹) transition between the excited levels (transition 2→3) was also observed. The detuning for the first photon transition ($6s^2 {}^{1}S{}_0\to 6s6p {}^{1}P{}_1^{\mathrm{o}}$) at the wavenumber ω = 18,140 cm⁻¹ was 80 cm⁻¹ which was more than an order of magnitude larger than the laser radiation linewidth (Δω ≈ 2–3 cm⁻¹). This indicates a substantially non-resonant character of the lower excited $6s6p {}^{1}P{}_1^{\mathrm{o}}$ level (level 2) population. The height of the maximum due to the one-photon $6s6p {}^{1}P{}_1^{\mathrm{o}}\to 5d6d {}^{3}D{}_2$ (2→3) transition was less than an order of magnitude ($A_{12}/A_{23}$ ≈ 60) lower than that corresponding to the one-photon $6s^2 {}^{1}S{}_0$→$6s6p {}^{1}P{}_1^{\mathrm{o}}$ (1→2) transition and more than two orders of magnitude ($A_{13}/A_{23}$ ≈ 560) lower than that related to the two-photon $6s^2 {}^{1}S{}_0\to 5d6d {}^{3}D{}_2$ (1→3) transition. Simultaneously, the height $A_{23}$ was higher by about an order of magnitude than the ion signal in the inter-resonance range. Note that here and elsewhere we use the transition wavenumbers in cm⁻¹. Recall that the conversion factor from eV to cm⁻¹ is 1 eV = 8065.544 cm⁻¹ [16].

It is worth noting that in Ref. [11] the maximum due to the $6s6p {}^{1}P{}_1^{\mathrm{o}}\to 5d6d {}^{3}D{}_2$ (2→3) transition was observed at a low field strength of ε ≈ 2.5⋅10⁴ V/cm (laser intensity ≈ 8.6·10⁵ W/cm²). This indicates that its nature is not related to the Stark shift of the excited $6s6p {}^{1}P{}_1^{\mathrm{o}}$ and $5d6d {}^{3}D{}_2$ levels in the laser radiation field, since at such a value of ε estimates show that their shifts are significantly less than the laser radiation linewidth.

In addition, both in the experiment [11] and in the above-mentioned works [13,14,15] the concentration of the studied atoms (in a beam or vapor) did not exceed 10¹² cm⁻³. This allows one to exclude the processes of collisions and multiphoton scattering from the possible mechanisms of population of the lower excited level 2, in this case $6s6p {}^{1}P{}_1^{\mathrm{o}}$.

At present, practically the only mechanism that makes it possible to explain the resonant transitions of type (3) is non-resonant population of the lower excited level 2 in the field of pulsed laser radiation [14]. There are no quantitative calculations in the literature that confirm and describe this process.

In this work, the process of three-photon ionization in the presence of an intermediate one-photon resonance between two excited levels was investigated within the framework of a three-level model using the density matrix method.

2. Calculation Details

The three-level system studied in the present work is shown schematically in Figure 1. Depending on the detuning values Δ₁ = ω–ω₁₂, Δ₂ = 2(ω–ω₁₃), and Δ₃ = ω–ω₂₃ (for the 1→2, 1→3, and 2→3 transitions, respectively) in the laser field with a wavenumber ω, three types of resonances are possible in the system under consideration: a one-photon resonance between the ground level 1 and the excited level 2 (Δ₁ = 0, Δ₂ ≠ 0, Δ₃ ≠ 0), a two-photon resonance between the ground level 1 and the excited level 3 (Δ₁ ≠ 0, Δ₂ = 0, Δ₃ ≠ 0), and a one-photon resonance between the excited levels 2 and 3 (Δ₁ ≠ 0, Δ₂ ≠ 0, Δ₃ = 0). Note that in the case of Δ₁ ≠ 0, Δ₂ ≠ 0, Δ₃ ≠ 0 one has a direct three-photon ionization [1].

Behavior of such a three-level system in the laser field within the framework of the density matrix method is described by a differential equation system

$$\begin{gathered} \frac{d{s}_{11}(t)}{dt}={\gamma }_{s2}\cdot s_{22}(t)+i \left[\frac{1}{2}{V}_{21}\cdot s_{12}(t)-\frac{1}{2}{V}_{12}\cdot s_{12}^{*}(t)+V_{31}^{(2)}\cdot s_{13}(t)-V_{13}^{(2)}\cdot s_{13}^{*}(t)\right], \\ \frac{d{s}_{22}(t)}{dt}=-{\gamma }_2(\epsilon )\cdot s_{22}(t)+{\gamma }_{s3}\cdot s_{33}(t)+\frac{i}{2}\left[V_{12}\cdot s_{12}^{*}(t)-V_{21}\cdot s_{12}(t)+V_{32}\cdot s_{23}t)-V_{23}\cdot s_{23}^{*}(t)\right], \\ \frac{d{s}_{33}(t)}{dt}=-{\gamma }_3(\epsilon )\cdot s_{33}(t)+i \left[V_{13}^{(2)}\cdot s_{13}^{*}(t)-V_{31}^{(2)}\cdot s_{13}(t)+\frac{1}{2}{V}_{23}\cdot s_{23}^{*}(t)-\frac{1}{2}{V}_{32}\cdot s_{23}(t)\right], \\ \frac{d{s}_{12}(t)}{dt}=i \left[{\overline{\Delta }}_1+\frac{i}{2}{\gamma }_2(\epsilon )\right] s_{12}(t)+i \left\{\frac{1}{2}{V}_{12} \left[s_{11}(t)-s_{22}(t)\right]+\frac{1}{2}{V}_{32}\cdot s_{13}(t)-V_{13}^{(2)}\cdot s_{23}^{*}(t)\right\}, \\ \frac{d{s}_{13}(t)}{dt}=i \left[{\overline{\Delta }}_2+\frac{i}{2}{\gamma }_3(\epsilon )\right] s_{13}(t)+i \left\{V_{13}^{(2)} \left[s_{11}(t)-s_{33}(t)\right]+\frac{1}{2}\left[V_{23}\cdot s_{12}(t)-V_{12}\cdot s_{23}^{*}(t)\right]\right\}, \\ \frac{d{s}_{23}(t)}{dt}=i \left[{\overline{\Delta }}_3+\frac{i}{2}\left({\gamma }_2(\epsilon )+{\gamma }_3(\epsilon )\right)\right] s_{23}(t)+i \left\{\frac{1}{2}{V}_{23} \left[s_{22}(t)-s_{33}(t)\right]-\frac{1}{2}{V}_{21}\cdot s_{13}(t)+V_{13}^{(2)}\cdot s_{12}^{*}(t)\right\} \end{gathered}$$

(4)

Here $s_{ij}(t)$ are slowly varying with time complex amplitudes of the density matrix elements ${\rho }_{ij}(t)$: ${\rho }_{11}(t)=s_{11}(t)$, ${\rho }_{22}(t)=s_{22}(t)$, ${\rho }_{33}(t)=s_{33}(t)$, ${\rho }_{12}(t)=s_{12}(t) \exp (i\omega t)$, ${\rho }_{13}(t)=s_{13}(t) \exp (i2\omega t)$, ${\rho }_{23}(t)=s_{23}(t) \exp (i\omega t)$, $s_{ij}^{*}(t)$ is the complex conjugate to the amplitude $s_{ij}(t)$, $V_{12}=0.5r_{12}\epsilon$, $V_{23}=0.5r_{23}\epsilon$, $V_{13}^{(2)}=r_{13}^{(2)}{\epsilon }^2$ with $r_{12}$, $r_{23}$, and $r_{13}^{(2)}$ being the dipole matrix elements of the one-photon 1→2, 2→3 transitions and composite matrix element of two-photon 1→3 transition, respectively, ${\overline{\Delta }}_1={\Delta }_1-V_{11}+V_{22}$, ${\overline{\Delta }}_2={\Delta }_2-V_{11}+V_{33}$, ${\overline{\Delta }}_3={\Delta }_3-V_{22}+V_{33}$ with $V_{11}$, $V_{22}$, and $V_{33}$ being Stark shifts of the ground level 1 and the excited levels 2 and 3 caused by the laser field of the strength ε, ${\gamma }_2(\epsilon )={\gamma }_{s2}+{\gamma }_{i2}^{(2)}(\epsilon )+{\gamma }_L$, ${\gamma }_3(\epsilon )={\gamma }_{s3}+{\gamma }_{i3}(\epsilon )+{\gamma }_L$ with ${\gamma }_{s2}$ and ${\gamma }_{s3}$ being the natural widths of the excited levels 2 and 3 related to their spontaneous decay to lower levels, ${\gamma }_{i2}^{(2)}(\epsilon )$ and ${\gamma }_{i3}(\epsilon )$ being the ionization widths of the levels 2 and 3 due to their one- and two-photon ionization, respectively, and ${\gamma }_L$ being the laser radiation linewidth.

It is important to note that the system (4) contains only transitions between levels 1, 2, and 3 with ionization from the excited levels 2 and 3 under laser radiation and does not include any additional processes that can result in an increase of the population of the lower excited level 2. Note also that it does not include three-photon ionization of the ground level 1 since the probability of such a process is well below those of the resonance processes under consideration.

For simplicity of calculation, the laser pulse profile was chosen to be Lorentzian for which the first-order correlation function is $e(t_1) e(t_2)={\epsilon }^2 \exp (-0.5 {\gamma }_L |t_1-t_2|)$ with e(t) being a stochastically fluctuating complex amplitude of the electric field. Note that the real laser profile is close to Gaussian. However, in this case the calculation becomes much more complicated without any substantial improvement. The laser pulse duration was chosen to be 2·10⁻⁸ s⁻¹.

In this calculation we approximate the region of focused laser radiation by a cylinder with a Gaussian intensity distribution over the cross section ${\epsilon }^2(r)={\epsilon }_0^2\exp [-{(r/r_0)}^2]$ ($r_0$ ≈ 5·10⁻³ cm). The number of ions produced by such a beam and normalized to the maximum number of ions that could be produced by a uniform beam of the same intensity (${\epsilon }^2(r)={\epsilon }_0^2$) is determined as follows:

$$N=\frac{2}{r_0^2}{\displaystyle \underset{0}{\overset{\infty }{\int }}P(\epsilon (r),t)\cdot r dr}.$$

(5)

The total probability of three-photon ionization $P(\epsilon (r),t)=1-s_{11}(t)-s_{22}(t)-s_{33}(t)$ at each point of the cross-section r was determined by solving the differential equation system (4) numerically using the 4th and 5th order Runge–Kutta method. In addition, at each point r the ionization widths depending on the field strength ε were also determined: ${\gamma }_{i3}(\epsilon )=8.5\cdot {10}^{-2} {\sigma }_{i3} {\epsilon }^2$ and ${\gamma }_{i2}^{(2)}(\epsilon )=2.98\cdot {10}^{14} {\sigma }_{i2}^2 {\epsilon }^4$ where ${\sigma }_{i3}$ and ${\sigma }_{i2}^2$ are the cross-sections of one- and two-photon ionization of the levels 3 and 2, respectively.

3. Results and Discussion

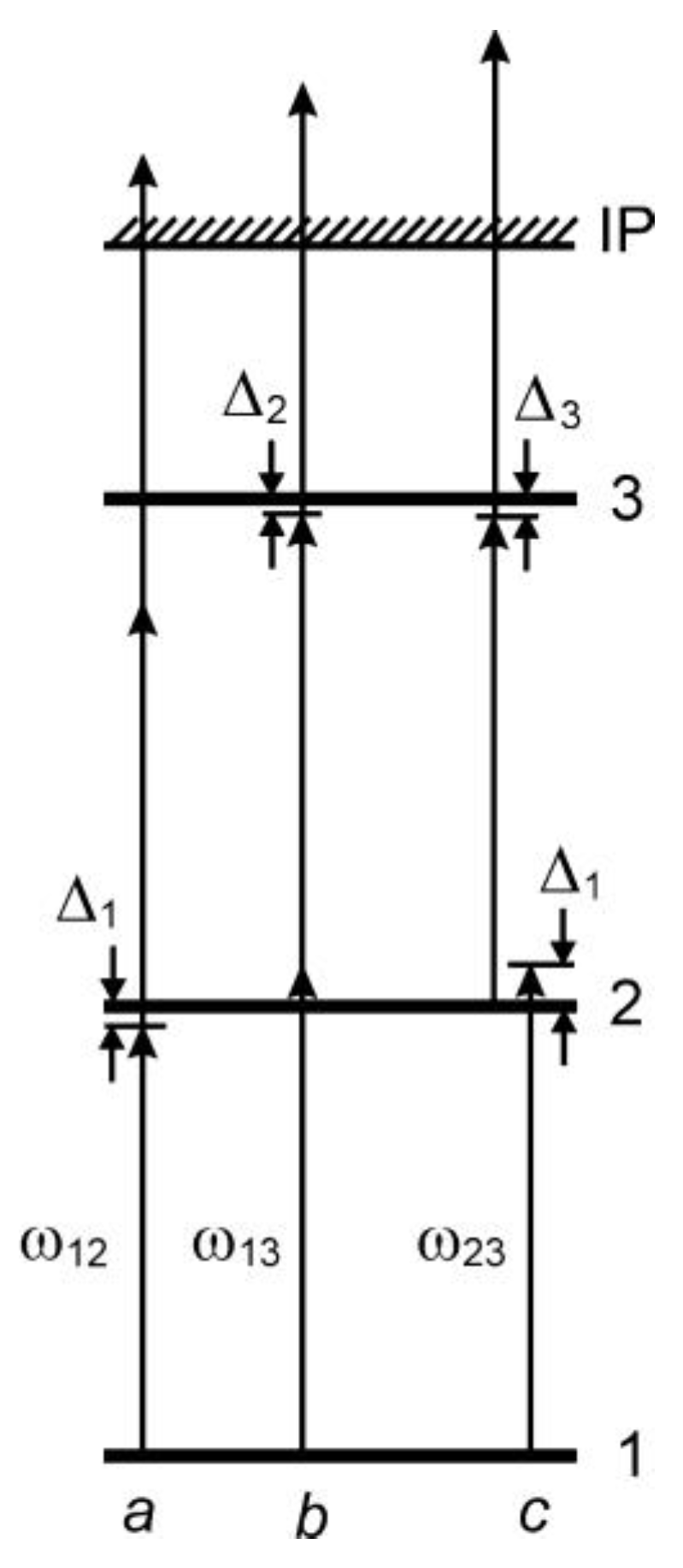
3.1. Three-Photon Ionization of the Ba Atom

To check the accuracy of the chosen model, we calculated the dependence of the single barium ion yield on the laser wavenumber N(ω) at three-photon ionization in the spectral range ω = 18,047–18,153 cm⁻¹ which contains transitions with participation of the $6s6p {}^{1}P{}_1^{\mathrm{o}}$ (${\omega }_{12}$ = 18,060.3 cm⁻¹ [17]) and $5d6d {}^{3}D{}_2$ ($2{\omega }_{13}$ = 36,200.4 cm⁻¹ [17]) levels, excitation of which was observed in Ref. [11]. 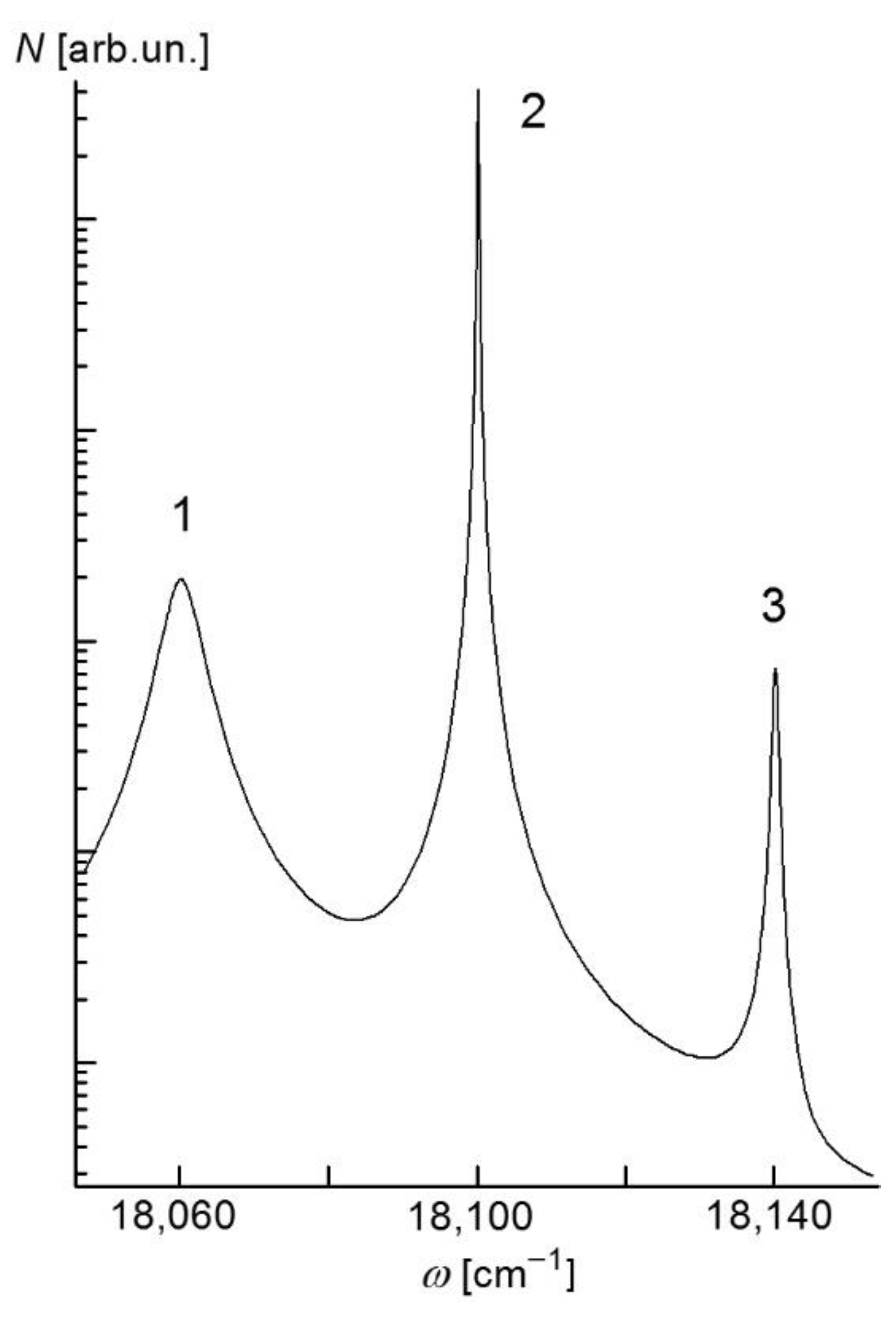In Figure 1 these are the levels 2 and 3, respectively. The resonance structure of the calculated N(ω) dependence (Figure 2) is due to the one-photon $6s^2 {}^{1}S{}_0\to 6s6p {}^{1}P{}_1^{\mathrm{o}}$ transition (maximum 1 at ω = 18,060.3 cm⁻¹), two-photon $6s^2 {}^{1}S{}_0\to 5d6d {}^{3}D{}_2$ transition (maximum 2 at ω = 18,100.2 cm⁻¹), and one-photon $6s6p {}^{1}P{}_1^{\mathrm{o}}$→$5d6d {}^{3}D{}_2$ transition between the excited levels (maximum 3 at ω = 18,140.1 cm⁻¹).

The N(ω) dependence shown in Figure 2 was calculated using the following values: $r_{12}$ = 5.5 a. u., $r_{13}^{(2)}$ = 679 a. u., $r_{23}$ = 0.09 a. u., ${\sigma }_{i3}$ = 10⁻¹⁷ cm², ${\sigma }_{i2}^2$ = 1.6·10⁻⁴⁶ cm⁴s, ${\gamma }_{s2}$ = ${\gamma }_{s3}$ = 10⁻⁴ cm⁻¹, $V_{11}$ = $V_{22}$ = $V_{33}$ = 0, ε = 2.5·10⁴ V/cm, and ${\gamma }_L$ = 0.2 cm⁻¹. The value ${\gamma }_L$ = 0.2 cm⁻¹ was chosen from the consideration that at such a value, in our opinion, the influence of the Lorentzian “wings” of the laser radiation spectrum on the probabilities of the transitions under study, first of all that of the non-resonant population of the $6s6p {}^{1}P{}_1^{\mathrm{o}}$ level, can be neglected.

As already mentioned above, the Stark shift of the levels in a field of strength ε = 2.5·10⁴ V/cm (laser intensity ≈ 8.6·10⁵ W/cm²) can be ignored. In particular, estimates show that even at the dynamic polarizability value of α = (2–3)·10³ a. u. [18] the Stark shift ΔE = α·ε²/4 is not more than 4·10⁻³ cm⁻¹. This is substantially less than the laser radiation linewidth ${\gamma }_L$ = 0.2 cm⁻¹. For this reason, the Stark shift of the levels was not taken into account in the calculation ($V_{11}$ = $V_{22}$ = $V_{33}$ = 0).

The value of the matrix element $r_{12}$ = 5.5 a. u. was determined on the basis of the known oscillator strength $f_{12}$ = 1.64 of the one-photon $6s^2 {}^{1}S{}_0\to 6s6p {}^{1}P{}_1^{\mathrm{o}}$ transition [19]. Unfortunately, there are no data in the literature on the oscillator strength f₂₃ of the $6s6p {}^{1}P{}_1^{\mathrm{o}}\to 5d6d {}^{3}D{}_2$ transition. For this reason, when determining the value of the matrix elements $r_{23}$ and $r_{13}^{(2)}$ we proceeded from the fact that the main contribution (not less than 95%) to the value of the composite matrix element $r_{13}^{(2)}$, because of the large value of r₁₂ and the relatively small detuning (${\omega }_{13}-{\omega }_{12}$ ≈ 40 cm⁻¹), comes from the matrix elements $r_{12}$ and $r_{23}$: $r_{13}^{(2)}=r_{12}\cdot r_{23}/4({\omega }_{13}-{\omega }_{12})$ [1]. The value of $r_{23}$ was chosen in such a way that the ratio of the heights ${(A_2/A_3)}_{\mathrm{calc}}$ of the maxima 2 and 3 of the calculated N(ω) dependence (Figure 2) coincided with the experimentally observed ratio ${(A_2/A_3)}_{\exp }$ [11]. At the above values of the matrix elements $r_{12}$ = 5.5 a. u., $r_{13}^{(2)}$ = 679 a. u., $r_{23}$ = 0.09 a. u. and the cross-section of one-photon ionization ${\sigma }_{i3}$ = 10⁻¹⁷ cm² [20] the ratio ${(A_2/A_3)}_{\mathrm{calc}}$ ≈ 555 is in good agreement with the experimentally observed one ${(A_2/A_3)}_{\exp }$ ≈ 560 [11]. In addition, the value of the composite matrix element $r_{13}^{(2)}$ = 679 a. u. obtained using the value of $r_{23}$ = 0.09 a. u. is, in our opinion, consistent with the fact that the maximum due to the two-photon $6s^2 {}^{1}S{}_0\to 5d6d {}^{3}D{}_2$ transition belongs to the group of the most intense maxima, as it follows from the N(ω) dependence experimentally measured in Ref. [11]. Note also that variation in the ${\sigma }_{i3}$ value within a range of 10⁻¹⁷–10⁻¹⁸ cm² results in a change of the absolute heights of the maxima 2 and 3; however, their ratio ${(A_2/A_3)}_{\mathrm{calc}}$ ≈ 555 remains practically unchanged.

The value of the cross-section ${\sigma }_{i2}^{(2)}$ for the two-photon ionization of the $6s6p {}^{1}P{}_1^{\mathrm{o}}$ level was chosen in such a way that the ratio of the heights ${(A_2/A_1)}_{\mathrm{calc}}$ of the maxima 2 and 1 of the calculated N(ω) dependence (Figure 2) coincided with the experimentally observed ratio ${(A_2/A_1)}_{\exp }$ [11]. At the above value ${\sigma }_{i2}^{(2)}$ = 1.6·10⁻⁴⁶ cm⁴s which, in our opinion, is quite reasonable [21,22], the ratio ${(A_2/A_1)}_{\mathrm{calc}}$ ≈ 209 is in good agreement with the experimentally observed one ${(A_2/A_1)}_{\exp }$  ≈ 210.

The natural widths ${\gamma }_{s2}$ and ${\gamma }_{s3}$ of the excited $6s6p {}^{1}P{}_1^{\mathrm{o}}$ and $5d6d {}^{3}D{}_2$ levels were chosen equal to 10⁻⁴ cm⁻¹ on the basis of the known lifetime τ ≈ 10⁻⁸ s of the $6s6p {}^{1}P{}_1^{\mathrm{o}}$ level [23]. Note that variation in the ${\gamma }_{s2}$ and ${\gamma }_{s3}$ values within a range of 10⁻³–10⁻⁵ cm⁻¹ did not noticeably affect the result of the calculation.

A qualitative and quantitative comparison of the calculated N(ω) dependence (Figure 2) with the one experimentally observed in Ref. [11] allows one to make two main conclusions: first, the proposed three-level model and the differential equation system (4) well describe the ion signal ratios of the maxima 1, 2, and 3; second, since the system (4) does not include any additional processes that can result in an increase of the population of the lower excited level 2 ($6s6p {}^{1}P{}_1^{\mathrm{o}}$ level in this case), one can argue that manifestation of the maximum 3 related to the one-photon $6s6p {}^{1}P{}_1^{\mathrm{o}}\to 5d6d {}^{3}D{}_2$ (2→3) transition in the N(ω) dependence is due to non-resonant population of the $6s6p {}^{1}P{}_1^{\mathrm{o}}$ (2) level with the detuning (${\Delta }_1$ ≈ 80 cm⁻¹) significantly exceeding the laser line width (${\gamma }_L$ = 0.2 cm⁻¹).

3.2. Conditions of Effective Manifestation of the One-Photon Resonance between Excited Levels at Three-Photon Ionization

We return now to the process of one-photon resonance between the excited levels (Figure 1, process c) and examine the influence of the values of the matrix elements $r_{12}$, $r_{23}$, ionization cross section ${\sigma }_{i3}$, and detuning ${\Delta }_1$ on the height of the maximum (denoted as A₂₃) due to the one-photon resonance 2→3 transition (${\Delta }_3$ = 0).

Since the differential equation system (4) is solved numerically, we fixed, for definiteness, the position of the upper excited level 3 by setting the resonance wavenumber ${\omega }_{13}$ of the two-photon 1→3 transition equal to 18,000 cm⁻¹. The position of the lower excited level 2 changes depending on the specified detuning value ${\Delta }_1$: ${\omega }_{12}=(2{\omega }_{13}-{\Delta }_1)/2$. The wavenumber of the resonant one-photon 2→3 transition in this case is determined as follows: ${\omega }_{23}=2{\omega }_{13}-{\omega }_{12}$. Note that the choice of the ${\omega }_{13}$ value is formal and does not affect the calculation result which, as follows from the system (4), depends on the detuning values ${\Delta }_1$, ${\Delta }_2$, and ${\Delta }_3$ but not on the absolute values of the resonant wavenumbers ${\omega }_{12}$, ${\omega }_{13}$, and ${\omega }_{23}$. Thus, one can fix the position of the lower excited level 2 and vary the position of the upper level 3 or even fix the distance between the excited levels 2 and 3 (${\omega }_{23}$ = const) and vary their position towards the ground level 1. We also set the ionization cross-section ${\sigma }_{i3}$ to 10⁻¹⁷ cm² and the laser linewidth ${\gamma }_L$ to 0.2 cm⁻¹.

We restricted ourselves to the case of a weak field (ε = 2.5·10⁵ V/cm), where the Stark shift of the levels 1, 2, and 3 and consequently a possible decrease of the detuning Δ₁ can be neglected. Note that for a correct quantitative determination of the level shifts due to the dynamic Stark effect under the action of the laser field, one has to know the absolute dependences α(ω) for the levels 1, 2, and 3 in the vicinity of the resonance wavenumber ${\omega }_{23}$.

For the estimation, we proceed from the ratio $A_2/A_0$ ≈ 10⁴ ($A_2$ is the height of the maximum due to the two-photon $6s6p {}^{1}P{}_1^{\mathrm{o}}\to 5d6d {}^{3}D{}_2$ transition, $A_0$ is the value of the ion signal in the inter-resonance range) experimentally observed in Ref. [11] and consider that the minimum height $A_{\min }$ of the maximum related to the one-photon resonance 2→3 transition, at which it already manifests in the dependence N(ω), is equal to $2A_0$ (or 2·10⁻⁴$A_2$). In our case (Figure 2), this value is $A_{\min }$ ≈ 8·10⁻⁴ arb. un. Note that the ratio $A_2/A_0$ ≈ 10⁴, in our opinion, is rather typical for the strong maxima due to two-photon transitions observed in the experiments using atomic beams and electron multipliers.

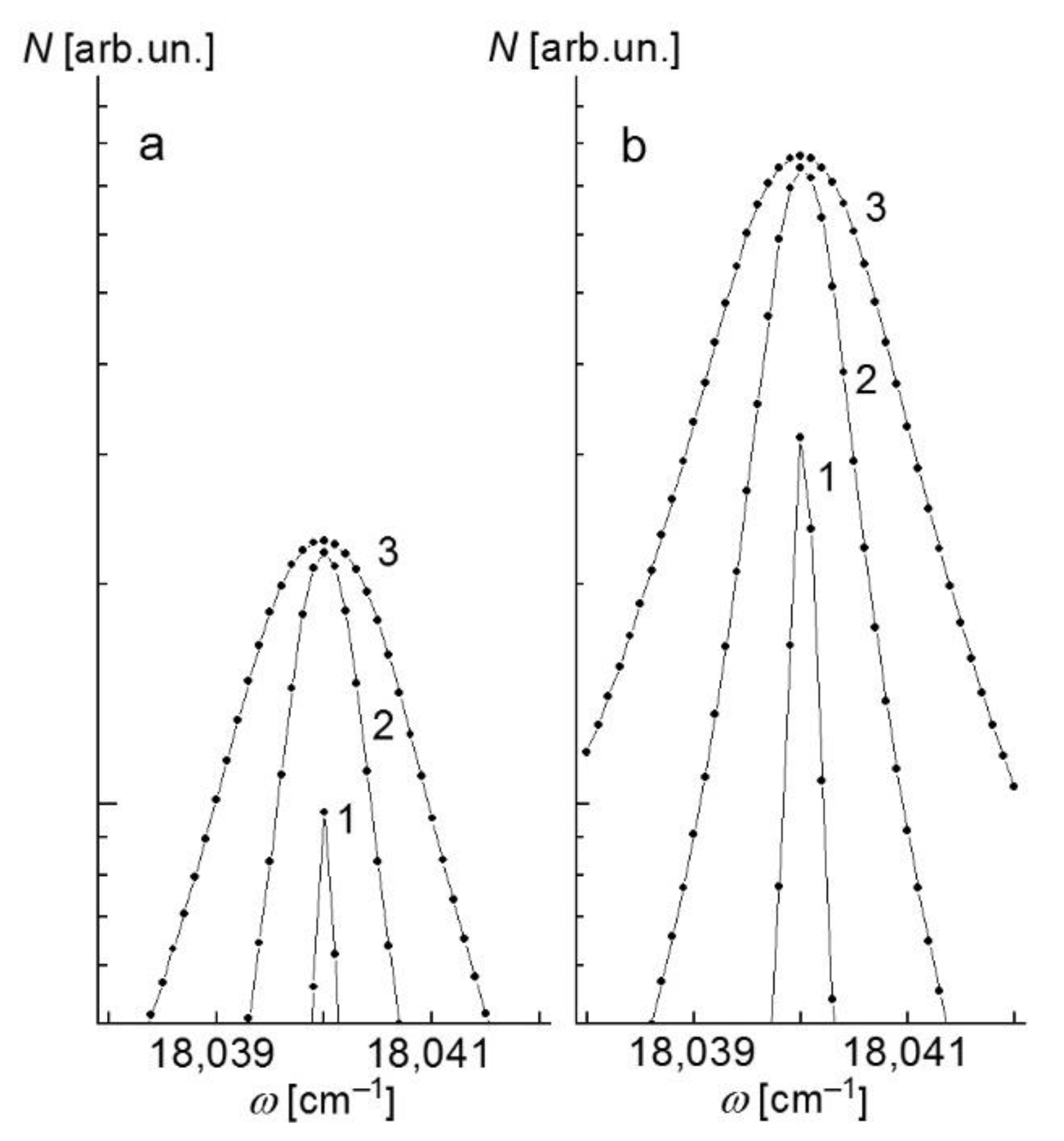
Figure 3 shows the dependences $A_{23}(r_{12})$ calculated for different values of the matrix element $r_{23}$ and detuning ${\Delta }_1$ = 80 cm⁻¹ (Figure 3a) and ${\Delta }_1$ = 160 cm⁻¹ (Figure 3b). The horizontal dashed line marks the $A_{\min }$ value. As can be seen, an increase of the matrix element r₁₂ results in an elevation of the $A_{23}$ height. Along with this, a slowdown in the rate of the $A_{23}$ height increase with $r_{12}$ is observed. It is also clearly seen that the minimum values of the matrix elements $r_{12}$ and $r_{23}$, for which the condition $A_{23}=A_{\min }$ is fulfilled, increase with detuning ${\Delta }_1$. In particular, the $r_{12}$ minimum value (at the maximum value $r_{23}$ = 0.2 a. u.) increases from 1.79 a. u. at ${\Delta }_1$ = 80 cm⁻¹ (Figure 3a, curve 1) to 3.55 a. u. at ${\Delta }_1$ = 160 cm⁻¹ (Figure 3b, curve 1) while the $r_{23}$ minimum value (at the maximum value $r_{12}$ = 5.5 a. u.) increases from 0.0087 a. u. at ${\Delta }_1$ = 80 cm⁻¹ (Figure 3a, point 6) to 0.02 a. u. at ${\Delta }_1$ = 160 cm ⁻¹ (Figure 3b, point 4). Note that the maximum value of the matrix element $r_{12}$, according to the available data on the oscillator strengths of the resonant S→P transitions in alkali and alkaline-earth metal atoms [23], is not greater than 5.5 a. u.

Figure 4 shows dependences $A_{23}(r_{23})$ calculated for different values of the matrix element $r_{12}$ and detuning ${\Delta }_1$ = 80 cm⁻¹ (Figure 4a) and ${\Delta }_1$ = 160 cm⁻¹ (Figure 4b). The dashed horizontal line marks the $A_{\min }$ value. As can be seen, an increase of the matrix element $r_{23}$ also results in an increasing $A_{23}$ height. However in this case, in contrast to the $A_{23}(r_{12})$ dependences (Figure 3), a more noticeable slowdown in the rate of the $A_{23}$ height increase with $r_{23}$ is observed (Figure 4). We restrict ourselves to the maximum value $r_{23}$ = 0.2 a. u. since the calculations show that a further practical increase of $r_{23}$ does not result in any further growth of the $A_{23}$ height.

It is clearly seen that similarly to the $A_{23}(r_{12})$ dependences (Figure 3), the minimum values of the matrix elements $r_{12}$ and $r_{23}$, for which the condition $A_{23}=A_{\min }$ is fulfilled, increase with detuning ${\Delta }_1$ (Figure 4). In particular, the $r_{23}$ minimum value (at the maximum value $r_{12}$ = 5.5 a. u.) increases from 0.0087 a. u. at ${\Delta }_1$ = 80 cm⁻¹ (Figure 4a, curve 1) to 0.0198 a. u. at ${\Delta }_1$ = 160 cm⁻¹ (Figure 4b, curve 1) while the $r_{12}$ minimum value (at the maximum value $r_{23}$ = 0.2 a. u.) increases from 1.79 a. u. at ${\Delta }_1$ = 80 cm⁻¹ (Figure 4a, point 9) to 3.55 a. u. at ${\Delta }_1$ = 160 cm⁻¹ (Figure 3b, point 10).

The slowdown in the rate of the $A_{23}$ height increase with matrix elements $r_{12}$ and $r_{23}$ is, in our opinion, due to a saturation of the ion signal owing to a close to unity probability of two-photon resonance ionization from the level 2. The strong saturation of the ion signal at large values of $r_{23}$ is most likely explained by the fact the 2→3 transition is resonant while in the case of the non-resonant 1→2 transition the increase of the r₁₂ value results in a weaker saturation of the ion signal.

The above argument is confirmed by N(ω) dependences calculated for different values of the matrix elements $r_{12}$, $r_{23}$ and detuning ${\Delta }_1$ = 80 cm⁻¹ (${\omega }_{23}$ = 18,040 cm⁻¹). They are shown in Figure 5. It is clearly seen that with the $r_{12}$ variation from 3.0 a. u. (Figure 5a) to 5.5 a. u. (Figure 5b) the $A_{23}$ height of the maximum related to the 2→3 transition increases but its width remains practically unchanged. In contrast, an increase of $r_{23}$ results in a growth of both the height and the width of the maximum. In particular, the maximum width increases from 0.26 cm⁻¹ at $r_{23}$ = 0.02 a. u. (Figure 5a,b, curve 1) to 1.77 cm⁻¹ at $r_{23}$ = 0.2 a. u. (Figure 5a,b, curve 3).

On the basis of the $A_{23}(r_{12})$ and $A_{23}(r_{23})$ dependences calculated for different values of the detuning ${\Delta }_1$, a relationship between the value of the maximum detuning ${\Delta }_{1\max }$ and the minimum values of the matrix elements $r_{12}$ and $r_{23}$ (for which the condition $A_{23}=A_{\min }$ is fulfilled) was found. As an example, Figure 6 shows dependences ${\Delta }_{1\max }(r_{12\min })$ calculated for $r_{23\min }$ = 0.2, 0.06, and 0.02 a. u. (curves 1, 2, and 3, respectively) whereas Figure 7 shows dependences ${\Delta }_{1\max }(r_{23\min })$ calculated for $r_{12\min }$ = 5.47, 3.0, and 0.5 a. u. (curves 1, 2, and 3, respectively). It is clearly seen that these dependences are of different nature. In particular, an increase of $r_{12\min }$ results in an almost linear growth of the ${\Delta }_{1\max }$ value while a significant slowdown in the ${\Delta }_{1\max }$ value increase with $r_{23\min }$ is observed. Such behavior of the ${\Delta }_{1\max }(r_{12\min })$ and ${\Delta }_{1\max }(r_{23\min })$ dependences agrees with the above $A_{23}(r_{12})$ and $A_{23}(r_{23})$ dependences and is caused by the stronger saturation of the ion signal in the case of the resonant 2→3 transition.

The maximum detuning values ${\Delta }_{1\max }$ for different values of $r_{12\min }$ = (0.5–5.5) a. u. and $r_{23\min }$ = (0.02–0.2) a. u. are presented in

Table 1. Maximum detuning ${\Delta }_{1\max }$ values (in cm⁻¹) for different $r_{12\min }$ and $r_{23\min }$ values.

${\mathit{r}}_{23\mathbf{min}},\mathbf{a}.\mathbf{u}.$	${\mathit{r}}_{12\mathbf{min}},\mathbf{a}.\mathbf{u}.$
	5.5	5.0	4.5	4.0	3.5	3.0	2.5	2.0	1.5	1.0	0.5
0.2	238	216	195	173	152	130	109	87	66	44	23
0.18	235	214	192	171	150	128	107	86	65	44	23
0.16	232	211	190	168	148	126	105	85	64	43	23
0.14	226	206	185	165	144	124	103	83	63	42	22
0.12	218	198	179	159	139	119	99	80	60	41	22
0.1	206	187	169	150	131	113	94	75	57	38	21
0.08	186	169	153	136	119	102	85	68	52	35	20
0.06	157	143	129	115	100	86	71	58	43	29	17
0.04	115	105	95	84	72	63	53	43	33	22	12
0.02	62	56	51	45	39	34	28	23	17	11	6

. Note that the maximum related to the one-photon 2→3 transition appears in the N(ω) dependence only where the conditions $r_{12}\ge r_{12\min }$, $r_{23}\ge r_{23\min }$, and ${\Delta }_1\le {\Delta }_{1\max }$ are fulfilled.

All the above dependences were obtained using the value ${\sigma }_{i3}$ = 10⁻¹⁷ cm² for ionization cross-section of the level 3. Study of the ${\sigma }_{i3}$ value influence on the $A_{23}$ height shows that the ${\Delta }_{1\max }$ value decreases by about a factor of three with ${\sigma }_{i3}$ decrease from 10⁻¹⁷ cm² down to 10⁻¹⁸ cm² regardless of the $r_{12\min }$ and $r_{23\min }$ values. As an example, Figure 8 shows the dependences ${\Delta }_{1\max }({\sigma }_{i3})$ calculated for different $r_{12\min }$ and $r_{23\min }$ values whereas

Table 2. The coefficient $k({\sigma }_{i3})$ values taking into account the ${\Delta }_{1\max }$ value decreasing with the ionization cross-section ${\sigma }_{i3}$ (×10⁻¹⁸ cm²) decrease.

${\mathit{\sigma }}_{\mathit{i}3}$	$\mathit{k}({\mathit{\sigma }}_{\mathit{i}3})$	${\mathit{\sigma }}_{\mathit{i}3}$	$\mathit{k}({\mathit{\sigma }}_{\mathit{i}3})$	${\mathit{\sigma }}_{\mathit{i}3}$	$\mathit{k}({\mathit{\sigma }}_{\mathit{i}3})$	${\mathit{\sigma }}_{\mathit{i}3}$	$\mathit{k}({\mathit{\sigma }}_{\mathit{i}3})$	${\mathit{\sigma }}_{\mathit{i}3}$	$\mathit{k}({\mathit{\sigma }}_{\mathit{i}3})$
1	3.00	3	1.78	5	1.41	7	1.19	9	1.05
2	2.15	4	1.55	6	1.28	8	1.10	10	1.00

presents the values of the coefficient $k({\sigma }_{i3})$ taking into account the ${\Delta }_{1\max }$ value decreasing with the cross-section ${\sigma }_{i3}$ decrease: ${\Delta }_{1\max }({\sigma }_{i3})$ = ${\Delta }_{1\max }$(${\sigma }_{i3}$ = 10⁻¹⁷ cm²)/$k({\sigma }_{i3})$.

The obtained results, in our opinion, are quite universal and can be used for the estimation of the conditions of manifestation of the resonance between two excited states at three-photon ionization of any atom. As an example,

Table 3. Data on possible one-photon transitions between two excited levels at three-photon ionization of the Ba, Sr, and Ca atoms.

Atom	Level 2	Level 3	${\mathit{E}}_3,{\mathbf{cm}}^{\text{−}1}$	${\mathit{\omega }}_{12},{\mathbf{cm}}^{\text{−}1}$	${\mathit{\omega }}_{23},{\mathbf{cm}}^{\text{−}1}$	${\mathbf{\Delta }}_1,{\mathbf{cm}}^{\text{−}1}$
Ba	$6s6p {}^{1}P{}_1^0$	5d6d 3D2	36,200.4	18,060.3	18,140.1	79.9
Sr	$5s5p {}^{1}P{}_1^0$	5s10s 1S0	43,512.2	21,698.5	21,813.7	115.2
Ca	$4s4p {}^{1}P{}_1^0$	4s10s 1S0	47,437.5	23,652.3	23,785.2	132.9

contains data on possible one-photon transitions between two excited levels (2→3) at three-photon ionization of the barium, strontium, and calcium atoms.

It is seen that in addition to the above $6s6p {}^{1}P{}_1^{\mathrm{o}}\to 5d6d {}^{3}D{}_2$ transition in the Ba atom, the transitions $5s5p {}^{1}P{}_1^{\mathrm{o}}\to 5s10s {}^{1}S{}_0$ in the Sr atom and $4s4p {}^{1}P{}_1^{\mathrm{o}}\to 4s10s {}^{1}S{}_0$ in the Ca atom are also possible. In both cases the one-photon ${}^{1}S{}_0\to {}^{1}P{}_1^{\mathrm{o}}$ transitions (1→2) are characterized by large matrix elements $r_{12}$ ≈ 5 a. u. [23]. Unfortunately, no data are available in the literature on the oscillator strengths of the $5s5p {}^{1}P{}_1^{\mathrm{o}}\to 5s10s {}^{1}S{}_0$ (Sr) and $4s4p {}^{1}P{}_1^{\mathrm{o}}\to 4s10s {}^{1}S{}_0$ (Ca) transitions, which does not allow for direct determination of the matrix elements for these transitions. As follows from the data presented in Table 1, in order for the transitions (2→3) under consideration to manifest in the N(ω) dependence ($A_{23}\ge A_{\min }$) at the detuning values ${\Delta }_1$ ≈ 115–133 cm⁻¹, the $r_{23}$ value for these transitions should be not less than 0.05 a. u. Taking into account the fact that in contrast to the intercombination two-electron $6s6p {}^{1}P{}_1^{\mathrm{o}}\to 5d6d {}^{3}D{}_2$ transition in the Ba atom ($r_{23}$ ≈ 0.09 a. u.) the transitions under consideration are one-electron dipole-allowed ones, one can expect that the $r_{23}$ value for these transitions can reach 0.1–0.2 a. u. Therefore, there are good reasons to expect that the $5s5p {}^{1}P{}_1^{\mathrm{o}}\to 5s10s {}^{1}S{}_0$ (Sr) and $4s4p {}^{1}P{}_1^{\mathrm{o}}\to 4s10s {}^{1}S{}_0$ (Ca) transitions will appear at three-photon ionization of these atoms. Unfortunately, there are no data in the literature on the three-photon ionization spectra of the Sr and Ca atoms measured in the wavelength range below 460 nm where these transitions occur. Thus, we are not able to judge unambiguously whether the maxima due to the $5s5p {}^{1}P{}_1^{\mathrm{o}}\to 5s10s {}^{1}S{}_0$ (Sr) and $4s4p {}^{1}P{}_1^{\mathrm{o}}\to 4s10s {}^{1}S{}_0$ (Ca) transitions are observed at three-photon ionization of these atoms.

4. Conclusions

Within the framework of the three-level model, the process of three-photon ionization with one-photon resonance between two excited levels (2→3) with the lower one being initially unpopulated is considered using the density matrix method. It is shown that such resonance can result in the maximum appearance in the three-photon ionization spectrum due to the non-resonant population of the lower excited level 2 with a detuning (Δ₁ = ω₂₃–ω₁₂) which can significantly exceed the laser radiation linewidth.

The detailed study of the influence of the values of the matrix elements $r_{12}$, $r_{23}$, ionization cross section ${\sigma }_{i3}$, and detuning ${\Delta }_1$ on the height of the maximum due to the one-photon 2→3 transition shows that it increases with the $r_{12}$, $r_{23}$, ${\sigma }_{i3}$ values as well as the ${\Delta }_1$ value decrease. Additionally, the $r_{23}$ increase results in the maximum broadening owing to the ion signal saturation due to a close to unity probability of two-photon resonant ionization from the level 2.

Estimations of the maximum possible detuning ${\Delta }_1$ value, at which the maximum due to the one-photon resonance between the two excited levels (2→3) is minimal but still appears in the N(ω) dependence, show that ${\Delta }_{1\max }$ increases with the matrix elements $r_{12}$ and $r_{23}$ as well as the ionization cross-section ${\sigma }_{i3}$ reaching the value of 238 cm⁻¹ at $r_{12}$ = 5.5 a. u., $r_{23}$ = 0.2 a. u., and ${\sigma }_{i3}$ = 10⁻¹⁷ cm², which is more than three orders of magnitude greater than the laser radiation linewidth ${\gamma }_L$ = 0.2 cm⁻¹.

Therefore, our results show that the maxima related to the one-photon transitions between two excited levels observed in the above-cited works [11,13,14,15] result from the non-resonant population of the lower excited level in the field of pulsed laser radiation. Such process, including non-resonant population of the excited level with subsequent one-photon resonantly enhanced two-photon ionization, should also be taken into account when interpreting the resonance structure of three-photon ionization spectra. In particular, a number of unidentified maxima observed at three-photon ionization of the Sm atom [24] are, in our opinion, related to exactly such resonant transitions.