One-Electron Energy Spectra of Heavy Highly Charged Quasimolecules: Finite-Basis-Set Approach
Abstract
:1. Introduction
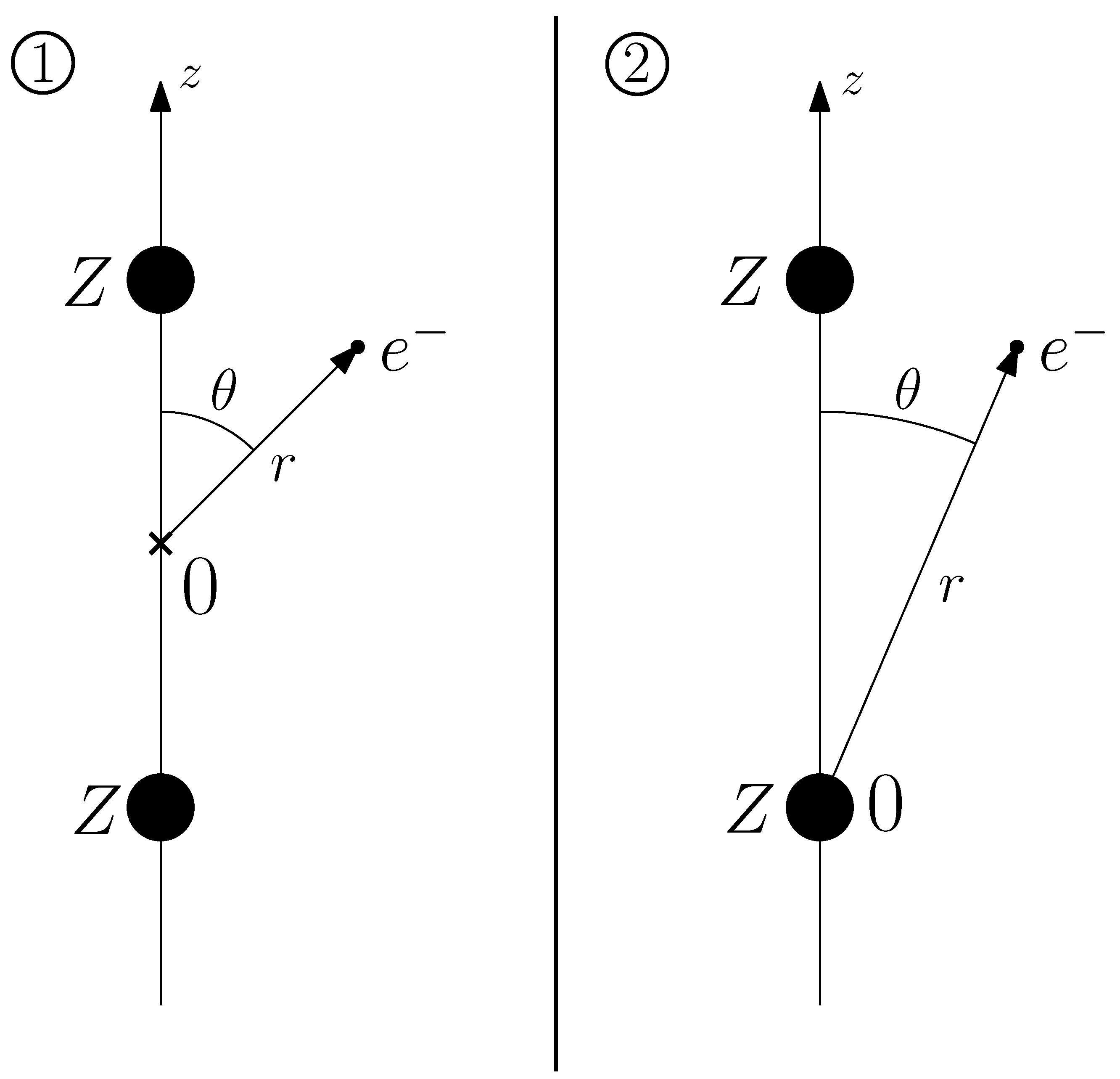
2. Method
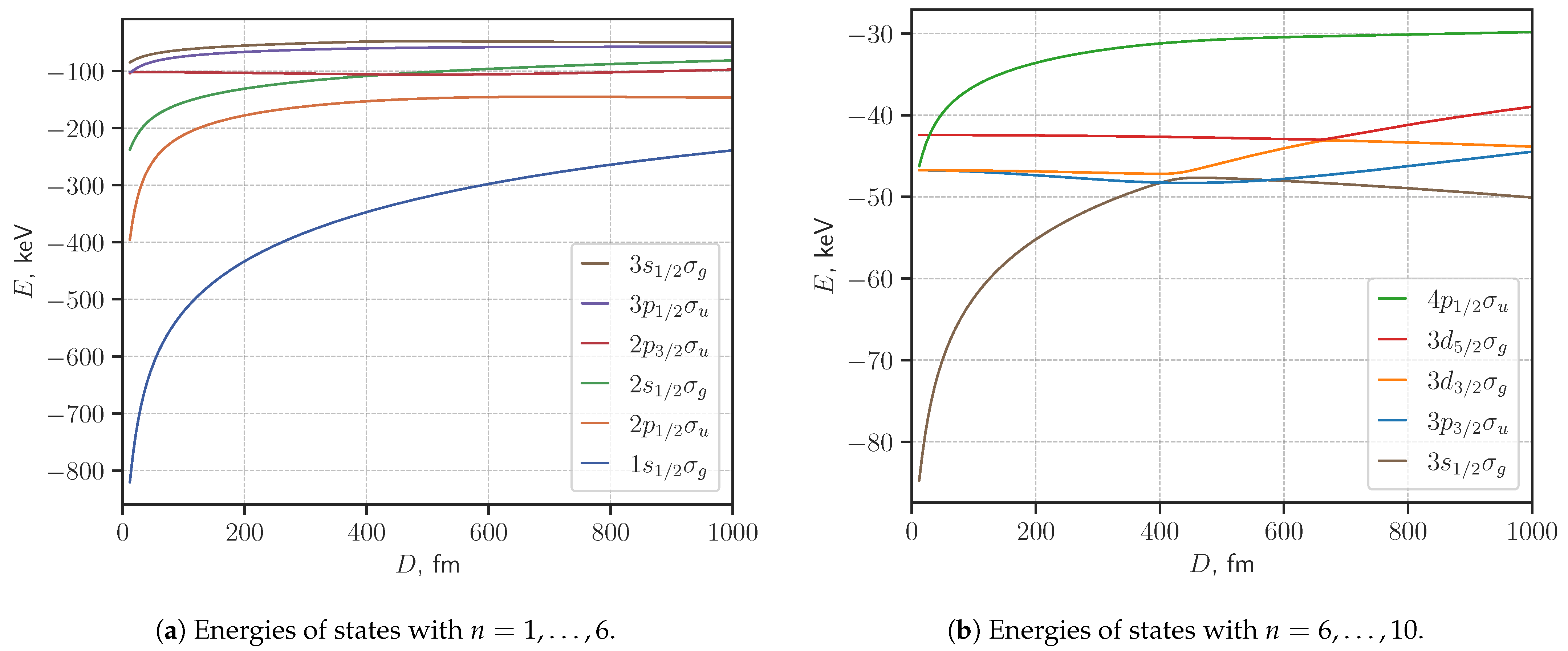
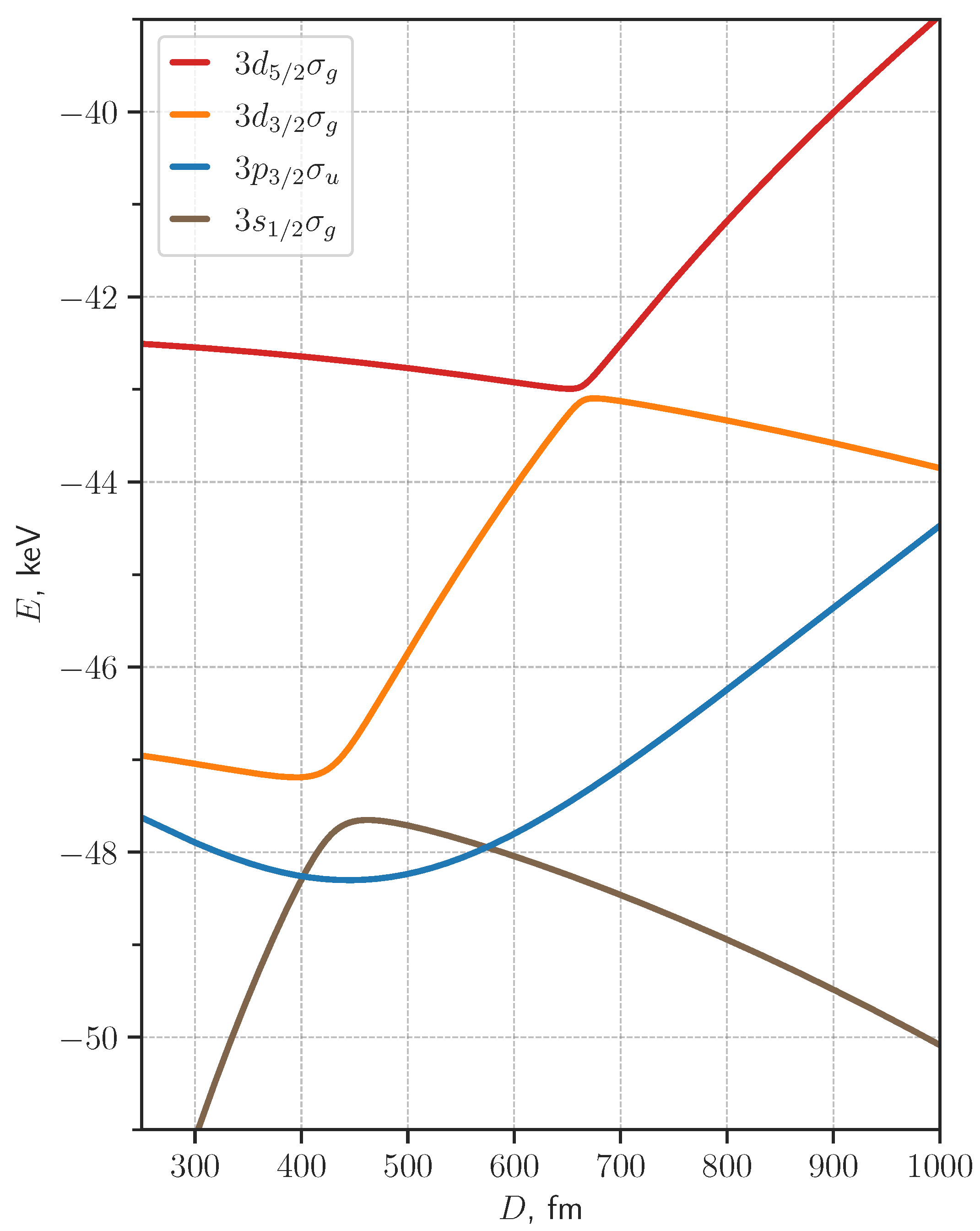
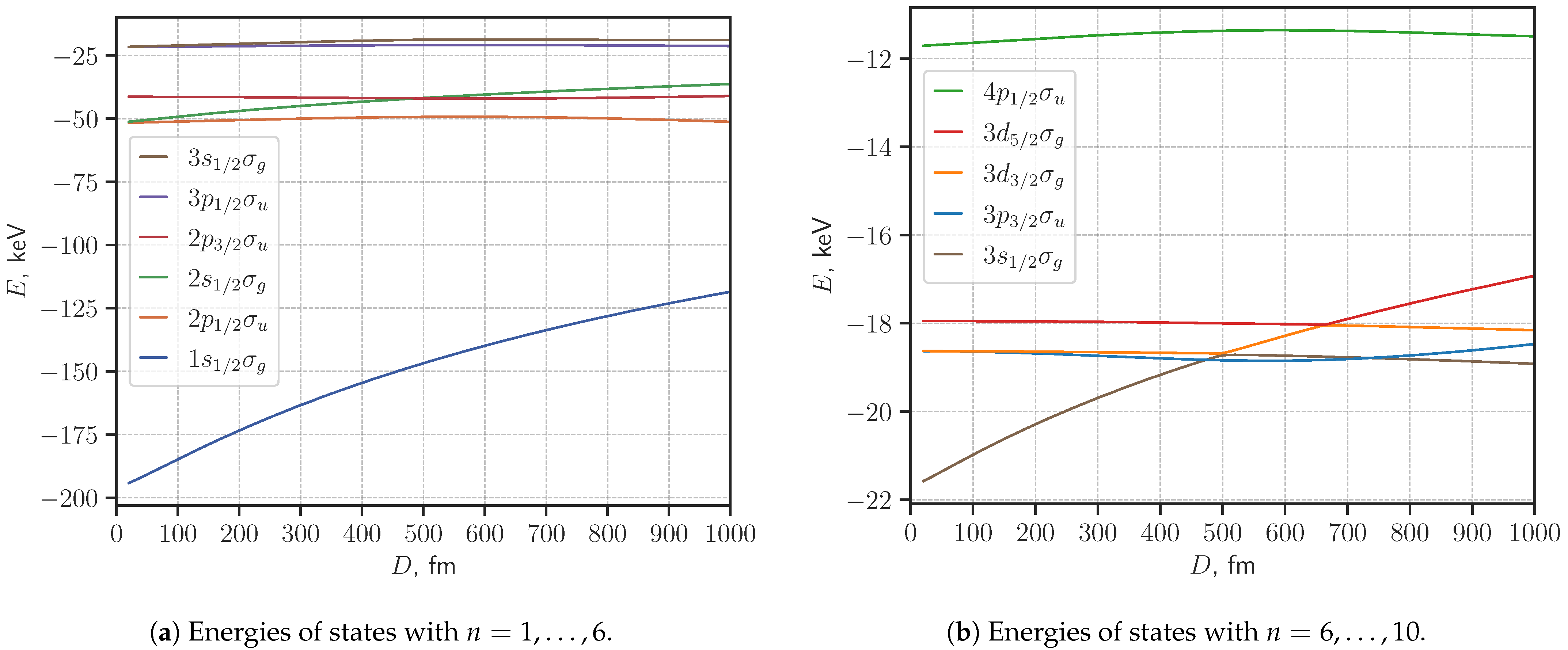
3. Results
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gerstein, S.S.; Zeldovich, Y.B. Positron Production during the Mutual Approach of Heavy Nuclei and the Polarization of the Vacuum. Sov. Phys. JETP 1969, 30, 358–361. [Google Scholar]
- Pieper, W.; Greiner, W. Interior electron shells in superheavy nuclei. Z. Phys. 1969, 218, 327–340. [Google Scholar] [CrossRef]
- Zeldovich, Y.B.; Popov, V.S. Electronic structure of superheavy atoms. Sov. Phys. Uspekhi 1972, 14, 673–694. [Google Scholar] [CrossRef]
- Rafelski, J.; Fulcher, L.P.; Klein, A. Fermions and bosons interacting with arbitrarily strong external fields. Phys. Rep. 1978, 38, 227–361. [Google Scholar] [CrossRef]
- Greiner, W.; Müller, B.; Rafelski, J. Quantum Electrodynamics of Strong Fields; Springer: Berlin, Germany, 1985. [Google Scholar]
- Shabaev, V.; Bondarev, A.; Glazov, D.; Kozhedub, Y.; Maltsev, I.; Malyshev, A.; Popov, R.; Tumakov, D.; Tupitsyn, I. QED with heavy ions: On the way from strong to supercritical fields. PoS Proc. Sci. 2019, 353, 052. [Google Scholar]
- Maltsev, I.A.; Shabaev, V.M.; Popov, R.V.; Kozhedub, Y.S.; Plunien, G.; Ma, X.; Stöhlker, T.; Tumakov, D.A. How to Observe the Vacuum Decay in Low-Energy Heavy-Ion Collisions. Phys. Rev. Lett. 2019, 123, 113401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Popov, R.V.; Shabaev, V.M.; Telnov, D.A.; Tupitsyn, I.I.; Maltsev, I.A.; Kozhedub, Y.S.; Bondarev, A.I.; Kozin, N.V.; Ma, X.; Plunien, G.; et al. How to access QED at a supercritical Coulomb field. Phys. Rev. D 2020, 102, 076005. [Google Scholar] [CrossRef]
- Voskresensky, D.N. Electron-Positron Vacuum Instability in Strong Electric Fields. Relativistic Semiclassical Approach. Universe 2021, 7, 104. [Google Scholar] [CrossRef]
- Verma, P.; Mokler, P.; Bräuning-Demian, A.; Bräuning, H.; Kozhuharov, C.; Bosch, F.; Liesen, D.; Hagmann, S.; Stöhlker, T.; Stachura, Z.; et al. Probing superheavy quasimolecular collisions with incoming inner shell vacancies. Nucl. Instrum. Meth. Phys. Res. B 2006, 245, 56–60. [Google Scholar] [CrossRef]
- Verma, P.; Mokler, P.; Bräuning-Demian, A.; Kozhuharov, C.; Bräuning, H.; Bosch, F.; Liesen, D.; Stöhlker, T.; Hagmann, S.; Chatterjee, S.; et al. Spectroscopy of superheavy quasimolecules. Radiat. Phys. Chem. 2006, 75, 2014–2018. [Google Scholar] [CrossRef]
- Hagmann, S.; Stöhlker, T.; Kozhuharov, C.; Shabaev, V.; Tupitsyn, I.; Kozhedub, Y.; Rothard, H.; Spillmann, U.; Reuschl, R.; Trotsenko, S.; et al. Electron Spectroscopy In Heavy-Ion Storage Rings: Resonant and Non-Resonant Electron Transfer Processes. AIP Conf. Proc. 2011, 1336, 115–118. [Google Scholar]
- Gumberidze, A.; Stöhlker, T.; Beyer, H.; Bosch, F.; Bräuning-Demian, A.; Hagmann, S.; Kozhuharov, C.; Kühl, T.; Mann, R.; Indelicato, P.; et al. X-ray spectroscopy of highly-charged heavy ions at FAIR. Nucl. Instrum. Meth. Phys. Res. B 2009, 267, 248–250. [Google Scholar] [CrossRef]
- Ter-Akopian, G.M.; Greiner, W.; Meshkov, I.N.; Oganessian, Y.T.; Reinhardt, J.; Trubnikov, G.V. Layout of new experiments on the observation of spontaneous electron–positron pair creation in supercritical Coulomb fields. Int. J. Mod. Phys. E 2015, 24, 1550016. [Google Scholar] [CrossRef]
- Ma, X.; Wen, W.; Zhang, S.; Yu, D.; Cheng, R.; Yang, J.; Huang, Z.; Wang, H.; Zhu, X.; Cai, X.; et al. HIAF: New opportunities for atomic physics with highly charged heavy ions. Nucl. Instrum. Meth. Phys. Res. B 2017, 408, 169–173. [Google Scholar] [CrossRef]
- Soff, G.; Greiner, W.; Betz, W.; Müller, B. Electrons in superheavy quasimolecules. Phys. Rev. A 1979, 20, 169–193. [Google Scholar] [CrossRef] [Green Version]
- Becker, U.; Grün, N.; Scheid, W.; Soff, G. Nonperturbative Treatment of Excitation and Ionization in U92+ + U91+ Collisions at 1 GeV/amu. Phys. Rev. Lett. 1986, 56, 2016–2019. [Google Scholar] [CrossRef]
- Eichler, J. Theory of relativistic ion-atom collisions. Phys. Rep. 1990, 193, 165–277. [Google Scholar] [CrossRef]
- Rumrich, K.; Soff, G.; Greiner, W. Ionization and pair creation in relativistic heavy-ion collisions. Phys. Rev. A 1993, 47, 215–228. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ionescu, D.C.; Belkacem, A. Relativistic Collisions of Highly-Charged Ions. Phys. Scr. 1999, T80, 128–132. [Google Scholar] [CrossRef]
- Tupitsyn, I.I.; Kozhedub, Y.S.; Shabaev, V.M.; Deyneka, G.B.; Hagmann, S.; Kozhuharov, C.; Plunien, G.; Stöhlker, T. Relativistic calculations of the charge-transfer probabilities and cross sections for low-energy collisions of H-like ions with bare nuclei. Phys. Rev. A 2010, 82, 042701. [Google Scholar] [CrossRef] [Green Version]
- Tupitsyn, I.I.; Kozhedub, Y.S.; Shabaev, V.M.; Bondarev, A.I.; Deyneka, G.B.; Maltsev, I.A.; Hagmann, S.; Plunien, G.; Stöhlker, T. Relativistic calculations of the K-K charge transfer and K-vacancy production probabilities in low-energy ion-atom collisions. Phys. Rev. A 2012, 85, 032712. [Google Scholar] [CrossRef] [Green Version]
- Müller, B.; Rafelski, J.; Greiner, W. Solution of the Dirac equation with two Coulomb centres. Phys. Lett. B 1973, 47, 5–7. [Google Scholar] [CrossRef]
- Rafelski, J.; Müller, B. The critical distance in collisions of heavy ions. Phys. Lett. B 1976, 65, 205–208. [Google Scholar] [CrossRef]
- Rafelski, J.; Müller, B. Magnetic Splitting of Quasimolecular Electronic States in Strong Fields. Phys. Rev. Lett. 1976, 36, 517–520. [Google Scholar] [CrossRef]
- Lisin, V.I.; Marinov, M.S.; Popov, V.S. Critical distance for the electron two-center problem. Phys. Lett. B 1977, 69, 141–142. [Google Scholar] [CrossRef]
- Lisin, V.I.; Marinov, M.S.; Popov, V.S. Critical electron state in heavy-ion collisions. Phys. Lett. B 1980, 91, 20–22. [Google Scholar] [CrossRef]
- Yang, L.; Heinemann, D.; Kolb, D. An accurate solution of the two-centre Dirac equation for H2+ by the finite-element method. Chem. Phys. Lett. 1991, 178, 213–215. [Google Scholar] [CrossRef]
- Parpia, F.A.; Mohanty, A.K. Numerical study of the convergence of the linear expansion method for the one-electron Dirac equation. Chem. Phys. Lett. 1995, 238, 209–214. [Google Scholar] [CrossRef]
- Deineka, G.B. Application of the Hermitian basis of B-splines for solution of diatomic molecular problems by the Hartree-Fock-Dirac method. Opt. Spectrosc. 1998, 84, 159–164. [Google Scholar]
- Matveev, V.I.; Matrasulov, D.U.; Rakhimov, H.Y. Two-center problem for the Dirac equation. Phys. Atom. Nucl. 2000, 63, 318–321. [Google Scholar] [CrossRef]
- Kullie, O.; Kolb, D. High accuracy Dirac-finite-element (FEM) calculations for and . Eur. Phus. J. D 2001, 17, 167–173. [Google Scholar] [CrossRef]
- Ishikawa, A.; Nakashima, H.; Nakatsuji, H. Solving the Schrödinger and Dirac equations of hydrogen molecular ion accurately by the free iterative complement interaction method. J. Chem. Phys. 2008, 128, 124103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Artemyev, A.N.; Surzhykov, A.; Indelicato, P.; Plunien, G.; Stöhlker, T. Finite basis set approach to the two-centre Dirac problem in Cassini coordinates. J. Phys. B 2010, 43, 235207. [Google Scholar] [CrossRef]
- Ishikawa, A.; Nakashima, H.; Nakatsuji, H. Accurate solutions of the Schrödinger and Dirac equations of , HD+, and HT+: With and without Born–Oppenheimer approximation and under magnetic field. Chem. Phys. 2012, 401, 62–72. [Google Scholar] [CrossRef]
- Tupitsyn, I.I.; Mironova, D.V. Relativistic calculations of ground states of single-electron diatomic molecular ions. Opt. Spectrosc. 2014, 117, 351–357. [Google Scholar] [CrossRef]
- Mironova, D.V.; Tupitsyn, I.I.; Shabaev, V.M.; Plunien, G. Relativistic calculations of the ground state energies and the critical distances for one-electron homonuclear quasi-molecules. Chem. Phys. 2015, 449, 10–13. [Google Scholar] [CrossRef] [Green Version]
- Artemyev, A.N.; Surzhykov, A. Quantum electrodynamical corrections to energy levels of diatomic quasimolecules. Phys. Rev. Lett. 2015, 114, 243004. [Google Scholar] [CrossRef] [PubMed]
- Shabaev, V.M.; Tupitsyn, I.I.; Yerokhin, V.A.; Plunien, G.; Soff, G. Dual kinetic balance approach to basis-set expansions for the Dirac equation. Phys. Rev. Lett. 2004, 93, 130405. [Google Scholar] [CrossRef] [Green Version]
- Rozenbaum, E.B.; Glazov, D.A.; Shabaev, V.M.; Sosnova, K.E.; Telnov, D.A. Dual-kinetic-balance approach to the Dirac equation for axially symmetric systems: Application to static and time-dependent fields. Phys. Rev. A 2014, 89, 012514. [Google Scholar] [CrossRef] [Green Version]
- Kotov, A.A.; Glazov, D.A.; Malyshev, A.V.; Vladimirova, A.V.; Shabaev, V.M.; Plunien, G. Ground-state energy of uranium diatomic quasimolecules with one and two electrons. X-ray Spectrom. 2020, 49, 110–114. [Google Scholar] [CrossRef] [Green Version]
- Shabaev, V.M. Finite nuclear size corrections to the energy levels of the multicharged ions. J. Phys. B 1993, 26, 1103–1108. [Google Scholar] [CrossRef]
- Tupitsyn, I.I.; Shabaev, V.M. Spurious States of the Dirac Equation in a Finite Basis Set. Opt. Spectrosc. 2008, 105, 183–188. [Google Scholar] [CrossRef]
- Johnson, W.R.; Blundell, S.A.; Sapirstein, J. Finite basis sets for the Dirac equation constructed from B splines. Phys. Rev. A 1988, 37, 307–315. [Google Scholar] [CrossRef]
- Sapirstein, J.; Johnson, W.R. The use of basis splines in theoretical atomic physics. J. Phys. B 1996, 29, 5213–5225. [Google Scholar] [CrossRef]
- Varentsova, A.S.; Agababaev, V.A.; Volchkova, A.M.; Glazov, D.A.; Volotka, A.V.; Shabaev, V.M.; Plunien, G. Third-order Zeeman effect in highly charged ions. Nucl. Instrum. Meth. Phys. Res. B 2017, 408, 80–83. [Google Scholar] [CrossRef]
- Volchkova, A.M.; Varentsova, A.S.; Zubova, N.A.; Agababaev, V.A.; Glazov, D.A.; Volotka, A.V.; Shabaev, V.M.; Plunien, G. Nuclear magnetic shielding in boronlike ions. Nucl. Instrum. Meth. Phys. Res. B 2017, 408, 89–92. [Google Scholar] [CrossRef]
- Volchkova, A.M.; Agababaev, V.A.; Glazov, D.A.; Volotka, A.V.; Fritzsche, S.; Shabaev, V.M.; Plunien, G. Helium-like ions in magnetic field: Application of the nonperturbative relativistic method for axially symmetric systems. arXiv 2009, arXiv:2009.00109. [Google Scholar]
| Z | This Work | Dirac–Sturm [37] |
|---|---|---|
| 1 | −1.1026433 | −1.102641581032 |
| 2 | −4.4106607 | −4.410654714140 |
| 10 | −110.33722 | −110.3371741499 |
| 20 | −442.23969 | −442.2392996469 |
| 30 | −998.4194 | −998.4214646525 |
| 40 | −1783.5479 | −1783.563450815 |
| 50 | −2804.5304 | −2804.571434254 |
| 60 | −4070.971 | −4071.036267926 |
| 70 | −5595.889 | −5595.926978290 |
| 80 | −7397.003 | −7397.028800116 |
| 90 | −9498.452 | −9498.588788490 |
| 92 | −9957.567 | −9957.775519122 |
| 100 | −11,935.89 | −11,936.41770218 |
| D, fm | ||||||
|---|---|---|---|---|---|---|
| 40 | −646,254 | −646,254 | −637,032 | −598,564 | 9222 | 38,468 |
| 50 | −614,504 | −614,504 | −604,643 | −568,188 | 9861 | 36,455 |
| 80 | −550,575 | −550,575 | −539,861 | −506,742 | 10,714 | 33,119 |
| 100 | −521,373 | −521,373 | −510,350 | −478,423 | 11,023 | 31,927 |
| 200 | −433,348 | −433,347 | −421,146 | −392,345 | 12,202 | 28,801 |
| 250 | −405,450 | −405,450 | −392,687 | −365,185 | 12,763 | 27,502 |
| 500 | −319,773 | −319,769 | −304,337 | −283,510 | 15,436 | 20,827 |
| −289,068 | −289,067 | −272,212 | −255,389 | 16,856 | 16,823 | |
| 700 | −279,462 | −279,464 | −262,095 | −246,756 | 17,367 | 15,339 |
| 1000 | −238,887 | −238,873 | −218,905 | −211,937 | 19,982 | 6968 |
| −212,020 | −212,003 | −189,652 | −190,174 | 22,368 | 522 |
| D, fm | ||||||
|---|---|---|---|---|---|---|
| 40 | −192,031 | −192,031 | −191,860 | −190,033 | 171 | 1827 |
| 50 | −190,845 | −190,845 | −190,607 | −188,314 | 238 | 2293 |
| 80 | −187,217 | −187,216 | −186,775 | −183,199 | 442 | 3576 |
| 100 | −184,805 | −184,805 | −184,228 | −179,895 | 577 | 4333 |
| 200 | −173,425 | −173,425 | −172,190 | −165,031 | 1235 | 7159 |
| 250 | −168,242 | −168,242 | −166,695 | −158,621 | 1547 | 8074 |
| 500 | −146,803 | −146,802 | −143,860 | −133,919 | 2943 | 9941 |
| 700 | −133,710 | −133,710 | −129,828 | −120,118 | 3882 | 9710 |
| −119,414 | −119,413 | −114,421 | −105,971 | 4993 | 8450 | |
| 1000 | −118,529 | −118,528 | −113,464 | −105,233 | 5065 | 8231 |
| −89,269 | −89,276 | −81,433 | −79,488 | 7836 | 1945 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kotov, A.A.; Glazov, D.A.; Shabaev, V.M.; Plunien, G. One-Electron Energy Spectra of Heavy Highly Charged Quasimolecules: Finite-Basis-Set Approach. Atoms 2021, 9, 44. https://doi.org/10.3390/atoms9030044
Kotov AA, Glazov DA, Shabaev VM, Plunien G. One-Electron Energy Spectra of Heavy Highly Charged Quasimolecules: Finite-Basis-Set Approach. Atoms. 2021; 9(3):44. https://doi.org/10.3390/atoms9030044
Chicago/Turabian StyleKotov, Artem A., Dmitry A. Glazov, Vladimir M. Shabaev, and Günter Plunien. 2021. "One-Electron Energy Spectra of Heavy Highly Charged Quasimolecules: Finite-Basis-Set Approach" Atoms 9, no. 3: 44. https://doi.org/10.3390/atoms9030044
APA StyleKotov, A. A., Glazov, D. A., Shabaev, V. M., & Plunien, G. (2021). One-Electron Energy Spectra of Heavy Highly Charged Quasimolecules: Finite-Basis-Set Approach. Atoms, 9(3), 44. https://doi.org/10.3390/atoms9030044






