Angular Distribution of Characteristic Radiation Following the Excitation of He-Like Uranium in Relativistic Collisions
Abstract
1. Introduction
2. Experiment
3. Results and Discussion
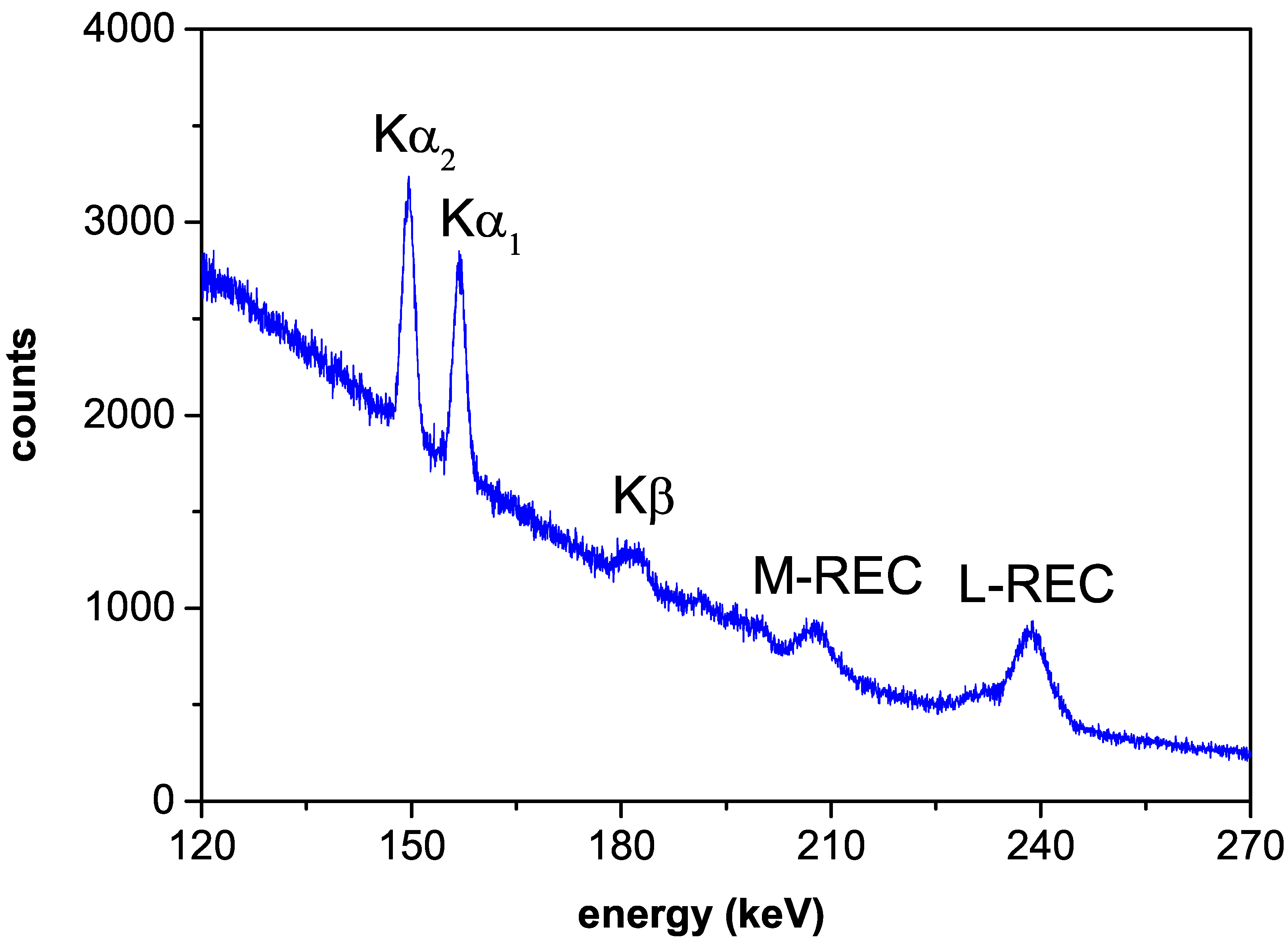
3.1. Experimental Data and Evaluation
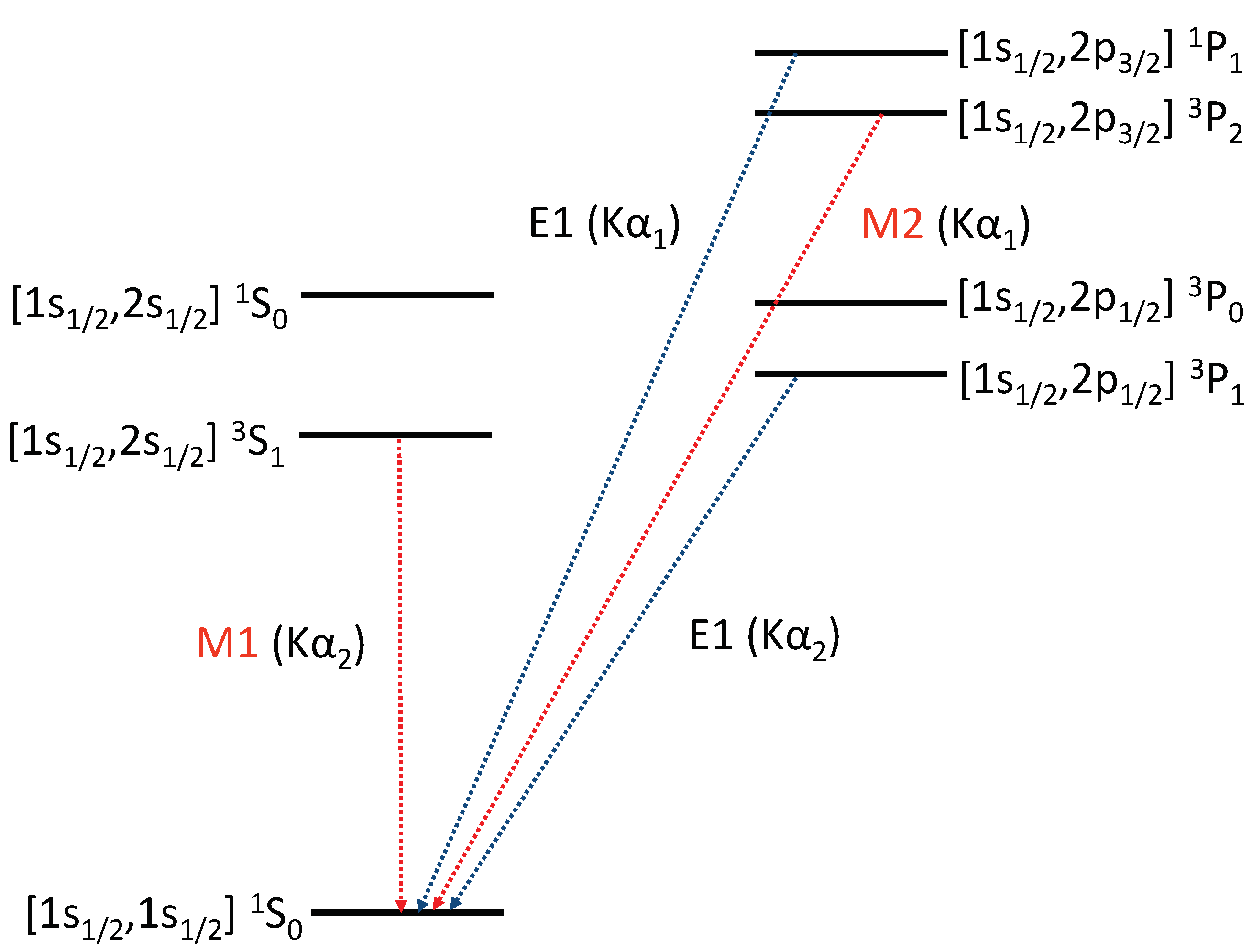
3.2. Theoretical Background
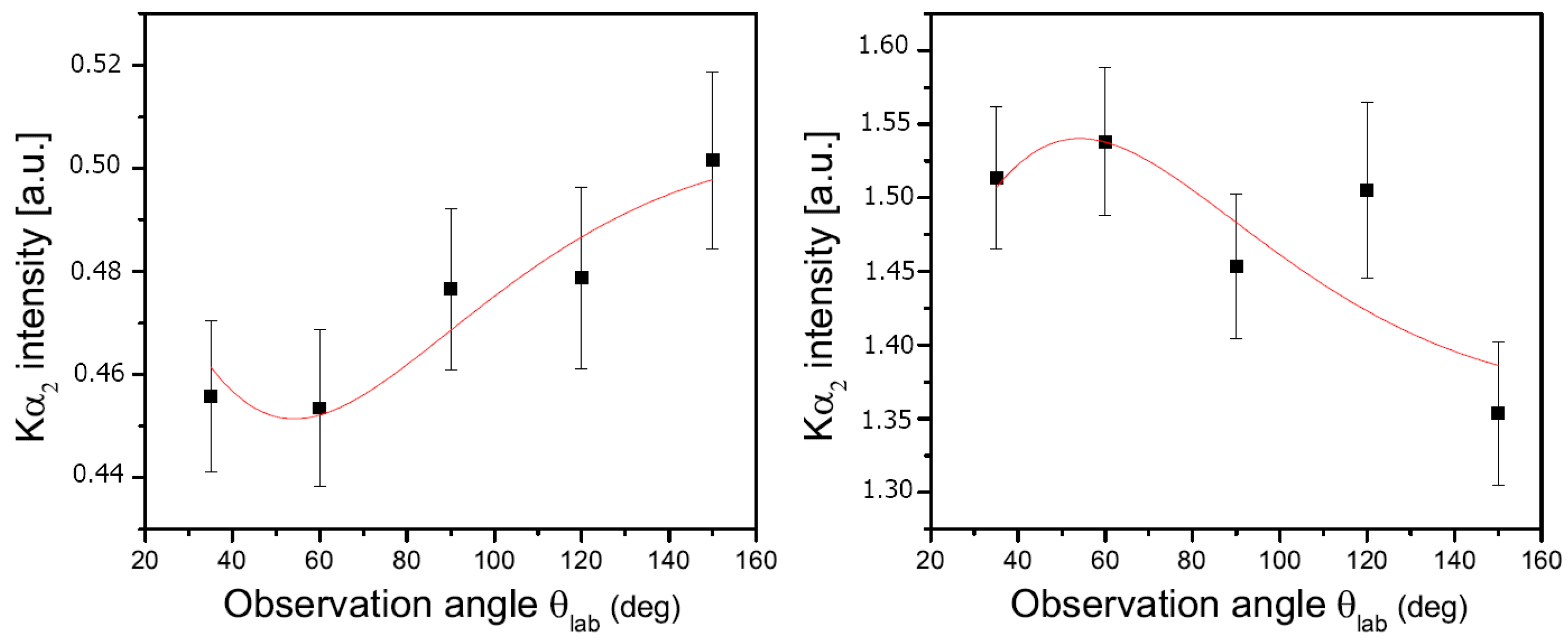
3.3. Comparison with Theory
4. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Detleffsen, D.; Anton, M.; Werner, A.; Schartner, K.H. Excitation of atomic hydrogen by protons and multiply charged ions at intermediate velocities. J. Phys. B 1994, 27, 4195. [Google Scholar] [CrossRef]
- Reymann, K.; Schartner, K.H.; Sommer, B.; Träbert, E. Scaling relation for total excitation cross sections of He in collisions with highly charged ions. Phys. Rev. A 1988, 38, 2290. [Google Scholar] [CrossRef]
- Anton, M.; Detleffsen, D.; Schartner, K.H.; Werner, A. Population of He 41D magnetic sublevels by collisions with protons and multiply charged ions in the intermediate velocity range. J. Phys. B 1993, 26, 2005. [Google Scholar] [CrossRef]
- Stolterfoht, N. Zero-degree Auger spectroscopy in energetic, highly charged ion-atom collisions. J. Electron Spectrosc. Relat. Phenom. 1993, 67, 309. [Google Scholar] [CrossRef]
- Stolterfoht, N.; Mattis, A.; Schneider, D.; Schiwietz, G.; Skogvall, B.; Sulik, B.; Ricz, S. Time-ordering effects in K-shell excitation of 170-MeV Ne7+ colliding with gas atoms: Double excitation. Phys. Rev. A 1995, 51, 350. [Google Scholar] [CrossRef] [PubMed]
- Wohrer, K.; Chetioui, A.; Rozet, J.P.; Jolly, A.; Fernandez, F.; Stephan, C.; Brendle, B.; Gayet, R. Target nuclear charge dependence of 1s2 to 1s2p and 1s2 to 1s3p excitation cross sections of Fe24+ projectiles in the intermediate velocity range. J. Phys. B 1986, 19, 1997. [Google Scholar] [CrossRef]
- Adoui, L.; Vernhet, D.; Wohrer, K.; Plante, J.; Chetioui, A.; Rozet, J.P.; Despiney, I.; Stephan, C.; Touati, A.; Ramillion, J.M.; et al. Excitation of Ar16+ projectiles in intermediate velocity collisions with neutrals. Nucl. Instrum. Methods Phys. Res. Sect. 1995, 98, 312. [Google Scholar] [CrossRef]
- Vernhet, D.; Rozet, J.P.; Wohrer, K.; Adoui, L.; Stephan, C.; Cassimi, A.; Ramillion, J.M. Excitation in swift heavy ion-atom collisions. Nucl. Instrum. Methods Phys. Res. Sect. 1996, 107, 71. [Google Scholar] [CrossRef]
- Brendle, B.; Gayet, R.; Rozet, J.P.; Wohrer, K. Application of the Schwinger Principle to Direct Excitation of Atoms or Ions by Impact of Bare Nuclei at Intermediate Velocities. Phys. Rev. Lett. 1985, 54, 2007. [Google Scholar] [CrossRef]
- Stöhlker, T.; Ionescu, D.C.; Rymuza, P.; Bosch, F.; Geissel, H.; Kozhuharov, C.; Ludziejewski, T.; Mokler, P.H.; Scheidenberger, C.; Stachura, Z.; et al. K-shell excitation studied for H- and He-like bismuth ions in collisions with low-Z target atoms. Phys. Rev. A 1998, 57, 845. [Google Scholar] [CrossRef]
- Gumberidze, A.; Fritzsche, S.; Bosch, F.; Ionescu, D.C.; Krämer, A.; Kozhuharov, C.; Stachura, Z.; Surzhykov, A.; Warczak, A.; Stöhlker, T. Shell- and subshell-resolved projectile excitation of hydrogenlike Au78+ ions in relativistic ion-atom collisions. Phys. Rev. A 2010, 82, 052712. [Google Scholar] [CrossRef]
- Gumberidze, A.; Fritzsche, S.; Hagmann, S.; Kozhuharov, C.; Ma, X.; Steck, M.; Surzhykov, A.; Warczak, A.; Stöhlker, T. Magnetic-sublevel population and alignment for the excitation of H- and He-like uranium in relativistic collisions. Phys. Rev. A 2011, 84, 042710. [Google Scholar] [CrossRef]
- Surzhykov, A.; Jentschura, U.D.; Stöhlker, T.; Gumberidze, A.; Fritzsche, S. Alignment of heavy few-electron ions following excitation by relativistic Coulomb collisions. Phys. Rev. A 2008, 77, 042722. [Google Scholar] [CrossRef]
- Feinberg, B.; Gould, H.; Meyerhof, W.E.; Belkacem, A.; Hülskötter, H.-P.; Alonso, J.R.; Blumenfeld, L.; Dillard, E.; Guardala, N. Relativistic electron- and proton-impact ionization of highly stripped heavy ions determined from projectile-electron loss in H2 and He. Phys. Rev. A 1993, 47, 2370. [Google Scholar] [CrossRef] [PubMed]
- Najjari, B.; Voitkiv, A.B. Excitation of heavy hydrogenlike ions by light atoms in relativistic collisions with large momentum transfers. Phys. Rev. A 2012, 85, 052712. [Google Scholar] [CrossRef]
- Zouros, T.J.M.; Lee, D.H.; Richard, P. Projectile 1s→2p excitation due to electron-electron interaction in collisions of O5+ and F6+ ions with H2 and He targets. Phys. Rev. Lett. 1989, 62, 2261. [Google Scholar] [CrossRef] [PubMed]
- Hülskötter, H.-P.; Meyerhof, W.E.; Gould, H.; Guardala, N. Evidence for Electron-Electron Interaction in Projectile JC-Shell Ionization. Phys. Rev. Lett. 1989, 63, 1938. [Google Scholar] [CrossRef]
- Chantrenne, S.; Beiersdorfer, P.; Cauble, R.; Schneider, M.B. Measurement of electron impact excitation cross sections for heliumlike titanium. Phys. Rev. Lett. 1992, 69, 265. [Google Scholar] [CrossRef]
- Wong, K.L.; Beiersdorfer, P.; Reed, K.J.; Vogel, D.A. Electron-impact excitation cross-section measurements of highly charged heliumlike and lithiumlike ions. Phys. Rev. A 1995, 51, 1214. [Google Scholar] [CrossRef]
- Robbins, D.L.; Beiersdorfer, P.; Faenov, A.Y.; Pikuz, T.A.; Thorn, D.B.; Chen, H.; Reed, K.J.; Smith, A.J.; Boyce, K.R.; Brown, G.V.; et al. Polarization measurements of the Lyman-α1 X-ray emission lines of hydrogenlike Ar17+ and Fe25+ at high electron-impact energies. Phys. Rev. A 2006, 74, 022713. [Google Scholar] [CrossRef]
- Lindroth, E.; Orban, I.; Trotsenko, S.; Schuch, R. Electron-impact recombination and excitation rates for charge-state-selected highly charged Si ions. Phys. Rev. A 2020, 101, 062706. [Google Scholar] [CrossRef]
- Kühnel, M.; Petridis, N.; Winters, D.F.A.; Popp, U.; Dörner, R.; Stöhlker, T.; Grisenti, R.E. Low- internal target from a cryogenically cooled liquid microjet source. Nucl. Instrum. Meth. A 2009, 602, 311. [Google Scholar] [CrossRef]
- Petridis, N.; Kalinin, A.; Popp, U.; Gostishchev, V.; Litvinov, Y.A.; Dimopoulou, C.; Nolden, F.; Steck, M.; Kozhuharov, C.; Thorn, D.B.; et al. Energy loss and cooling of relativistic highly charged uranium ions interacting with an internal hydrogen droplet target beam. Nucl. Instrum. Meth. A 2011, 656, 1. [Google Scholar] [CrossRef]
- Gumberidze, A.; Thorn, D.B.; Fontes, C.J.; Najjari, B.; Zhang, H.L.; Surzhykov, A.; Voitkiv, A.; Fritzsche, S.; Banas, D.; Beyer, H.; et al. Electron- and Proton-Impact Excitation of Hydrogenlike Uranium in Relativistic Collisions. Phys. Rev. Lett. 2013, 110, 213201. [Google Scholar] [CrossRef]
- Gumberidze, A.; Thorn, D.B.; Surzhykov, A.; Fontes, C.J.; Najjari, B.; Voitkiv, A.; Fritzsche, S.; Banas, D.; Beyer, H.; Chen, W.; et al. Electron- and proton-impact excitation of helium-like uranium in relativistic collisions. Phys. Rev. A 2019, 99, 032706. [Google Scholar] [CrossRef]
- Fontes, C.J.; Sampson, D.H.; Zhang, H.L. Inclusion of the generalized Breit interaction in excitation of highly charged ions by electron impact. Phys. Rev. A 1993, 47, 1009. [Google Scholar] [CrossRef]
- Fontes, C.J.; Sampson, D.H.; Zhang, H.L. Use of the factorized form for the collision strength in exploration of the effect of the generalized Breit interaction. Phys. Rev. A 1994, 49, 3704. [Google Scholar] [CrossRef] [PubMed]
- Gumberidze, A.; Thorn, D.B.; Fontes, C.J.; Najjari, B.; Zhang, H.L.; Surzhykov, A.; Voitkiv, A.; Fritzsche, S.; Banas, D.; Beyer, H.; et al. Ground-state excitation of heavy highly-charged ions. J. Phys. B 2015, 48, 144006. [Google Scholar] [CrossRef]
- Surzhykov, A.; Jentschura, U.D.; Stöhlker, T.; Fritzsche, S. Kα1 radiation from heavy, heliumlike ions produced in relativistic collisions. Phys. Rev. A 2006, 74, 052710. [Google Scholar] [CrossRef]
- Najjari, B.; Voitkiv, A.B. Excitation of highly charged hydrogenlike ions by the impact of equivelocity electrons and protons: A comparative study. Phys. Rev. A 2013, 87, 034701. [Google Scholar] [CrossRef]
| Beam Energy | Process | |||||
|---|---|---|---|---|---|---|
| 218 MeV/u | PIE | −0.1694 | 0.9864 | 0.4473 | 0.0135 | −0.1218 |
| PIE + EIE | −0.2161 | 0.7861 | −0.3517 | 0.2138 | −0.0751 | |
| 300 MeV/u | PIE | −0.0359 | 0.9843 | 0.4969 | 0.01567 | −0.0296 |
| PIE + EIE | −0.1367 | 0.8773 | −0.2874 | 0.1226 | −0.0637 |
| Beam Energy | Process | |||||
|---|---|---|---|---|---|---|
| 218 MeV/u | PIE | 0.1729 | 0.0442 | 0.1082 | 0.9557 | 0.0785 |
| PIE + EIE | 0.0361 | 0.2555 | −0.0731 | 0.7444 | −0.0320 | |
| 300 MeV/u | PIE | 0.1352 | 0.0449 | 0.2279 | 0.9550 | 0.1582 |
| PIE + EIE | 0.0658 | 0.1843 | 0.0227 | 0.8156 | 0.0217 |
| Beam Energy | Line | PIE Screened | Experiment |
|---|---|---|---|
| 218 MeV/u | K | −0.1201 | −0.12 ± 0.07 [12] |
| K | 0.0805 | 0.07 ± 0.02 | |
| 300 MeV/u | K | −0.0273 | 0.02 ± 0.02 |
| K | 0.1606 | 0.16 ± 0.03 |
| Beam Energy | Line | PIE | PIE + EIE | Experiment |
|---|---|---|---|---|
| 218 MeV/u | K | −0.1218 | −0.0751 | −0.11 ± 0.04 |
| K | 0.0785 | −0.0319 | −0.07 ± 0.03 | |
| 300 MeV/u | K | −0.0296 | −0.0637 | −0.02 ± 0.05 |
| K | 0.1582 | 0.0217 | 0.04 ± 0.02 |
| EIE | 0.7898 | 0.5319 |
| PIE | 0.3423 | 0.4407 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gumberidze, A.; Thorn, D.B.; Surzhykov, A.; Fontes, C.J.; Banaś, D.; Beyer, H.F.; Chen, W.; Grisenti, R.E.; Hagmann, S.; Hess, R.; et al. Angular Distribution of Characteristic Radiation Following the Excitation of He-Like Uranium in Relativistic Collisions. Atoms 2021, 9, 20. https://doi.org/10.3390/atoms9020020
Gumberidze A, Thorn DB, Surzhykov A, Fontes CJ, Banaś D, Beyer HF, Chen W, Grisenti RE, Hagmann S, Hess R, et al. Angular Distribution of Characteristic Radiation Following the Excitation of He-Like Uranium in Relativistic Collisions. Atoms. 2021; 9(2):20. https://doi.org/10.3390/atoms9020020
Chicago/Turabian StyleGumberidze, Alexandre, Daniel B. Thorn, Andrey Surzhykov, Christopher J. Fontes, Dariusz Banaś, Heinrich F. Beyer, Weidong Chen, Robert E. Grisenti, Siegbert Hagmann, Regina Hess, and et al. 2021. "Angular Distribution of Characteristic Radiation Following the Excitation of He-Like Uranium in Relativistic Collisions" Atoms 9, no. 2: 20. https://doi.org/10.3390/atoms9020020
APA StyleGumberidze, A., Thorn, D. B., Surzhykov, A., Fontes, C. J., Banaś, D., Beyer, H. F., Chen, W., Grisenti, R. E., Hagmann, S., Hess, R., Hillenbrand, P.-M., Indelicato, P., Kozhuharov, C., Lestinsky, M., Märtin, R., Petridis, N., Popov, R. V., Schuch, R., Spillmann, U., ... Stöhlker, T. (2021). Angular Distribution of Characteristic Radiation Following the Excitation of He-Like Uranium in Relativistic Collisions. Atoms, 9(2), 20. https://doi.org/10.3390/atoms9020020







