Abstract
High-resolution K-shell photoionization cross-sections for the C-like atomic nitrogen ion (N+) are reported in the 398 eV (31.15 Å) to 450 eV (27.55 Å) energy (wavelength) range. The results were obtained from absolute ion-yield measurements using the SOLEIL synchrotron radiation facility for spectral bandpasses of 65 meV or 250 meV. In the photon energy region 398–403 eV, autoionizing resonance states dominated the cross section spectrum. Analyses of the experimental profiles yielded resonance strengths and Auger widths. In the 415–440 eV photon region and resonances forming well-developed Rydberg series up , respectively, were identified in both the single and double ionization spectra. Theoretical photoionization cross-section calculations, performed using the R-matrix plus pseudo-states (RMPS) method and the multiconfiguration Dirac-Fock (MCDF) approach were bench marked against these high-resolution experimental results. Comparison of the state-of-the-art theoretical work with the experimental studies allowed the identification of new resonance features. Resonance strengths, energies and Auger widths (where available) are compared quantitatively with the theoretical values. Contributions from excited metastable states of the N+ ions were carefully considered throughout.
1. Introduction
X-ray spectra obtained by Chandra from sources such as Capella, Procyon, and HR 1099 provide challenges for contemporary plasma spectral modelling codes. For example, the X-ray spectrum of the bright blazar Mkn 421 observations by the Chandra LETG+HRC-S and subsequent modelling of the spectra indicated that high quality photoionization cross-section data of atomic carbon and its ions were required []. More recently, photoionization cross-section measurements on the atomic oxygen ion sequence [,,] were used to interpret the O VI differences between satellite observations in the UV spectra of galactic and extra-galactic sight lines compared to ground based measurements made at the SOLEIL synchrotron radiation facility [,].
Nitrogen is ubiquitous in astrophysical environments and the sixth most populous element in the cosmos. The photoionization of atomic nitrogen species has been the subject of a number of laboratory investigations. 1s photoionization of neutral nitrogen was investigated by Stolte et al. [] while Gharaibeh et al. measured K-shell cross-sections in N+ (carbon-like) [] and N2+ (B-like) [], Al-Shorman et al. investigated N3+ and N4+ []. Recently, ion yield spectra following X-ray absorption in the K threshold region of the N+, NH+, NH2+ and NH3+ species were obtained by Bari et al. []. For N+, these authors measured the double-ionisation yield (N3+) and provided resonance assignments based on both ab initio CI calculations using the General Atomic and Molecular Electronic Structure System (GAMESS) package [] and the results of []. Inner-shell photoionization and Auger processes in atomic nitrogen species have also been the subject of a number of theoretical works, see for example [,].
In this paper, we report high resolution absolute photoionization (PI) cross-section measurements for the singly ionised carbon-like atomic nitrogen ion N+ over the photon energy range 398–450 eV, covering the full 1s excitation region and photon energies beyond the K-threshold. N+ was one of the first ions to be studied on the Multi-Analysis Ion Apparatus (MAIA) photon-ion merged-beam facility at SOLEIL []. This early investigation was limited to the narrow 398–406 eV photon energy range and succeeded in detecting resonance features belonging to the strongest excitation only. Recent substantial improvements (discussed below) to the MAIA apparatus enabled us to: (1) detect the resonances with much improved statistical significance leading to the observation and assignment of several additional features; (2) estimate the experimental Auger widths and compare with theoretical values; (3) observe and identify regular series of resonances leading up to the K-shell ionisation limits and (4) provide improved absolute cross section measurements in both the single and double-ionisation channels.
State-of-the-art theoretical work from the Multi Configurational Dirac-Fock (MCDF) and R-matrix with pseudo-states (RMPS) methods are bench marked against these measurements. The comparison with theory allows the interpretation of resonance features found in the experimental spectra and an estimation of the metastable content of the ion beam.
2. Experimental Details
The present work was performed on the MAIA photon-ion merged-beam set-up available at the site of the SOLEIL synchrotron radiation facility []. MAIA allows the high-quality synchrotron photon beam to interact with a counter-propagating ion beam within a well-defined overlap region, and has been used for the last decade to investigate the relative and absolute cross section inner-shell photoionization behaviours of a range of atomic ions, see for example [,,]. More recently, similar studies on molecular species were initiated, see for example [,,]. Photoelectron-photo-ion coincidence studies on ionic species can also be performed with MAIA [].
Comprehensive descriptions of the apparatus and procedures used to obtain cross-sections in free ions are available from Bizau et al. [] and so only an outline of the main points is presented here. Molecular nitrogen was introduced into an electron cyclotron resonance (ECR) plasma source and heated by microwaves to produce ionisation. N+ ions, after extraction at a 4 kV voltage on the source, were selected from other multiply charged nitrogen ions by a dipole magnet and guided via an electrostatic deflector into the region of overlap with the counter-propagating monochromatized photon beam. The interaction of the synchrotron photons with the N+ ions resulted in the production of either N2+ or N3+ photo-ions which were separated, after exit from the interaction region, by a tuneable dipole magnet and detected by a channel plate detector. Photon energy scans of the N2+ and N3+ count rates were acquired to map out the relative single and double photoionization cross section behaviours, respectively. Absolute measurements of the N2+ and N3+ photon yield cross-section values were also carried out at a number of photon energies.
In a merged-beam experiment the ionisation cross section value is obtained from:
where is the counting rate of the photo-ions produced by the synchrotron photons of energy , is the electron charge, is the efficiency of the photodiode used to characterise the photon beam, is the velocity of the ions in the interaction region due to the extracting voltage, is the charge on the ion, is the current produced by the calibrated photodiode, is the ion current, is the efficiency of the channel plates used to measure the photo-ions and the integral takes account of the beam overlap geometry with which defines the ion beam propagation direction.
Table 1 provides a summary of the experimental parameters for the present experiments under the experimental conditions prevailing during the measurement of the absolute cross section near the maximum of the strongest resonance at 400 eV. The aforementioned experimental developments included an increased photon flux and an improved understanding and calibration of the merged beam configuration. The ion current has doubled and the reduced form factor reflects a tighter and better-defined interaction region. Most significantly, the signal-to-noise ratio for the experiment has been very much improved. Finally, of most significance for the absolute cross section measurements, a new ion detector involving focusing optics now ensures maximum collection efficiency of the photo-ions produced due to photoionization in the merged beam overlap region. Comparison with Gharaibeh et al. [] shows a substantial gain in overall performance and sensitivity due to the significant improvement of key experimental parameters. This is the justification for the revised cross-sectional values presented in the current work.

Table 1.
Values of experimental parameters used to evaluate the absolute photoionization cross-section at 400 eV photon energy.
Photon energies were determined by calibrating with the well-known and transitions in N2 [] and Ar [] gas, respectively, corrected for the Doppler shift resulting from the velocity of the N+ ions. The estimated energy uncertainty is 60 meV. Different photon energy bandpasses were used depending on the spectral region under investigation. For the strongest resonances in the 400 eV region a minimum photon bandpass of 65 meV was used for optimum spectral resolution, whereas for the higher lying resonances (425–450 eV) a mean energy bandpass of 225 meV was used. When carrying out measurements of the cross sections on an absolute basis a bandpass of 280 meV was used. We estimate the total relative experimental uncertainty in the absolute values of the cross sections to be no greater than 15%.
A complication in the interpretation of the MAIA experimental measurements may arise due to the possible presence in the overlap region of ions in long-lived metastable states that have remained populated during the journey from the ECR plasma source (this is the case for the present N+ experiment). The measured photo-ion spectra thus comprise ground and metastable initial states contributions, the relative strength of which depends in a non-trivial manner on the source (ECR plasma) conditions prevailing at extraction. Detailed comparisons between theoretical and experimental results can be used effectively to estimate the metastable fraction, e.g., [].
3. Theory
3.1. Relevant Decay Processes
Photon inner-shell excitation of a N+ ion in either the ground or metastable states produces highly energetic 1s hole states that may decay via autoionization (resonant Auger process), forming a stable N2+ ion and releasing a free electron. From the initial ground levels of N+, photo-excitation processes () produce or inner-shell states that autoionize into the (+) or (+) continua (channels) by Coulomb interactions, according to the coupling selection rules, leaving the ion in the ground state configuration of N2+. This decay scheme corresponds to the Auger process. Other Auger processes, namely or are possible that would leave the ion in the core-excited configurations or . More final state channels are open if the electron is excited to (higher ) states for the (higher ) electron can now either participate or spectate in the Auger process [] with the final core state configurations , or , , , respectively, e.g., [].
As noted earlier, the measured cross section data may be complicated by the presence of metastable states in the sample ion beam. Theoretical interpretation, thus, requires the computation of all the PI cross-sections from the relevant initially populated states that contribute. In the present case, these are (1.90 eV),(4.05 eV) and (5.80 eV), which all lie within a few eV above the ground state []. The state is radiatively coupled to the ground -levels with a total lifetime of 5.6 ms []. This time is sufficiently long for the initially extracted ions excited in the states to reach the interaction zone in our apparatus. Following () photo-excitation of , autoionization decay processes such as N+ N2+ + are allowed and similarly for () excitations in the and metastable states.
This brief analysis shows that the strength of the signal measured in this work in the single-ionization channel (N2+), at a given photon energy, will comprise simultaneous contributions from a variety of possible Auger decay processes involving several initial state channels. Theoretical modelling comprising the most important of these channels is necessary for the interpretation of the experimental data.
Further ionisation may also result from the initial X-ray absorption. The N3+ state lies about 77.0 eV [] above the N+ ground state and, thus, double-photoionization processes are, in principle, energetically possible following K-shell excitation in N+. Double-Auger decay, Auger cascade and electron shake-off are possible atomic processes that may contribute to double-ionization in the present case. For some of the final state configurations mentioned above, e.g., the Auger decay of the vacancy is not energetically possible, thus preventing the Auger cascade, and return to ground state is necessarily via radiative transitions.
A schematic energy level diagram showing the main excitation and decay processes involved in this work is shown in Figure 1. It is notable that the photon-excited states include several open shells and sub-shells. This makes the problem of accurate atomic structure calculations a very demanding one, e.g., [], and the case of N+ provides a particularly challenging test case for theoretical models. We have carried through extensive calculations using two different theoretical approaches, namely Multi-Configuration Dirac-Fock (MCDF) and R-matrix with Pseudo-States (RMPS) in order to evaluate their predictions compared with experiment and to help in the interpretation of the results.
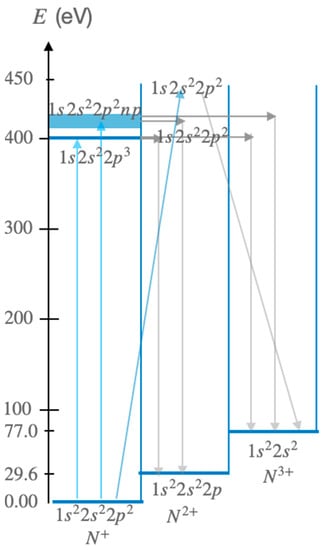
Figure 1.
Schematic energy level diagram showing the main excitation and decay processes (upward and downward arrows, respectively) involved in this work. The initial photon absorption process excites a 1s electron from the various states of the and configurations to the (near 400 eV) and (between 418 eV and 440 eV) states. The direct ionization process to in N2+ followed by Auger decay to in N3+ is also shown.
3.2. Multi-Configuration Dirac-Fock (MCDF)
Multi-configuration Dirac-Fock (MCDF) calculations, based on a full intermediate coupling scheme in a jj-basis, have been performed using a recent version of the code originally developed by Bruneau []. The N+ photoexcitation and photoionization cross-sections were computed in the Babushkin (velocity) gauge [] in the photon energy region of the K-edge. Calculations were restricted to electric-dipole (E1) transitions. The concept of the Slater transition state [] was used to optimize the one-electron wave functions. Photoexcitation and photoionization cross-sections were evaluated for the five J-levels ( and ) of the ground configuration and the lowest level of the configuration. The and configurations were added to optimize the initial state description. Photo-excited levels with were obtained based on the mixing of the , , , and , , odd and even parity configurations, respectively. With a view to optimise eigenenergies, different radial functions for the () orbitals were used in the initial and final configurations. The individual photoexcitation cross-sectional profiles were obtained by dressing each E1 transition with a Lorentzian line shape of full width at half maximum (FWHM) equal to 92.4 meV to represent the Auger width. The latter value was obtained from MCDF calculations performed to calculate the statistical average of the autoionization rates from the configuration to the , and configurations, respectively. The same value of 92.4 meV was used for all the members along the aforementioned Rydberg series. Continuum photoionization cross-sections were calculated using the reduced set of the , , and configurations.
Additionally, we note the work of Hasoǧlu et al. [] who used multiconfiguration Dirac-Fock (MCDF) and Breit-Pauli (MCBP) theoretical methodologies to calculate the K-shell Auger and radiative decay rates of the ten possible states along the iso-electronic sequence from to , showing the importance of both electron-electron correlation and relativistic effects even at low . Some of the Auger rates obtained by Hasoǧlu et al. [] for are amenable to direct comparison with the present experimental values (see Section 4.1).
3.3. R-Matrix (RMPS)
The photon energy range of the photoionization (PI) cross-sections presented in [] has been extended up to 440 eV to include the K-edge region. All PI cross sections were determined using the RMPS method [,,] in LS—coupling with the parallel version [] of the programs [,,]. The same 390-level model for the N2+ residual ion was used in the present close-coupling PI cross-section calculations as in the work of Gharaibeh et al. []. The RMPS resonance parameters were determined using the multi-channel R-matrix QB technique (applicable to atomic and molecular complexes) of Berrington and co- workers [], Quigley et al. [] and Ballance et al. []. The resonance width may be determined from the inverse of the energy derivative of the eigenphase sum at the position of the resonance energy via:
Further relevant theoretical details can be found in Gharaibeh et al. [].
4. Results and Analyses
The experimental results are presented in Figure 2 showing the measured cross-sections for single and double photo-ionization of N+ in the 398–450 eV photon energy region. The photon energies at which absolute measurements were carried out are indicated. Both spectra feature a strong discrete resonance region in the 399–405 eV photon range which corresponds with the decay of N+ ions following electron excitation. The four main peaks observed in the single ionization channel are seen to have counterparts in the double-ionization channel at the same photon energies. Additional, previously unobserved, resonance features appear in the 415–440 eV photon energy region in both the single and double ionisation channels. This is the region corresponding to the decay of N+ ions following excitations with . Some resonances are seen to form distinctive Rydberg series, particularly in the double-ionization channel, while continuum processes begin to contribute significantly to the cross-section upward of ~430 eV photon energy. Resonance series due to excitations in the and initial states converge to the , and inner ionisation limits in N2+, respectively. Excitations from the state will result in additional limits. Detailed analyses for the two photon regions 398–403 eV () and 415–450 eV () are given below in the light of the MCDF and RMPS theoretical results.
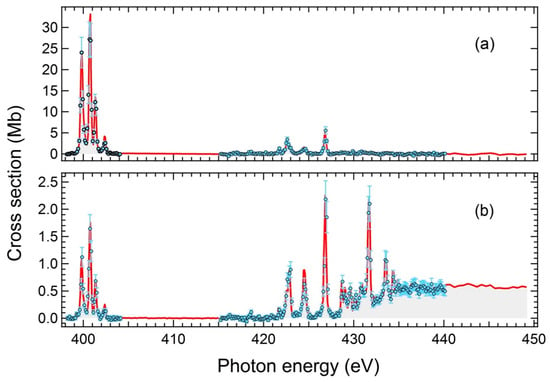
Figure 2.
N+ cross sections measured in (a) the single and (b) the double photoionisation channels, in the 398–450 eV photon energy range, respectively. In both figures, the photon energies for the absolute measurements (energy band pass of 280 meV) are shown with open circle points. Relative measurements were carried out with an energy band pass varying between 220 meV and 250 meV in the scanned range and shown by a continuous red line.
4.1. 1s → 2p Resonances
Figure 3 shows the ab initio results of our RMPS and MCDF total photoionization cross-section calculations for the resonances in the 398–404 eV region. These arise from the photon excitation of an inner shell 1s electron to a 2p valence shell, starting from the assumed initial levels and . Figure 4a shows a high-resolution experimental single-ionisation spectrum (65 meV band pass) in the same region which clearly reveals additional resonances not reported by Gharaibeh et al. []. The resonance features in Figure 4a are assigned the numerical labels that are used in Table 2, which provides the resonance identifications and atomic parameters. Figure 4a also shows the results of Voigt profile numerical deconvolutions of the measured lineshapes.
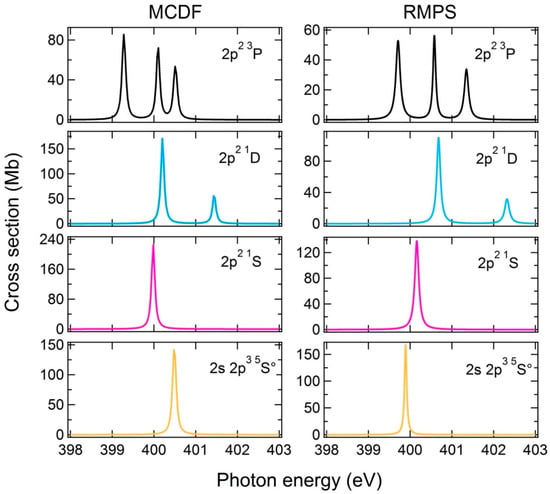
Figure 3.
Multiconfiguration Dirac-Fock (MCDF) and R-Matrix with pseudo-states (RMPS) theoretical calculations of the photoexcitation cross sections from the and states of N+, respectively.
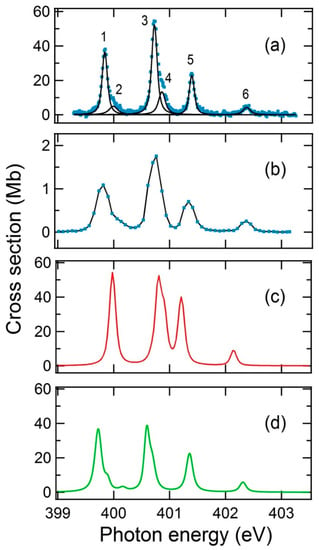
Figure 4.
Photoionization cross-sections of the N+ atomic ion in the photon energy region of the excitations. (a) Measured in the single ionisation channel (65 meV energy band pass). (b) Measured in the double ionisation channel (225 meV band pass). (c) Multiconfiguration Dirac-Fock (MCDF) simulation of the total photoabsorption cross-sections. The theoretical energy values are shifted by +0.7 eV in the figure. (d) R-matrix with pseudo-states theoretical (RMPS) simulation of the total photoionization cross-sections.

Table 2.
Experimentally determined atomic parameters (energy, Auger width and oscillator strength) of the main resonances (~400 eV photon energy) in the N+ photoionization cross-section spectrum, estimated from the absolute measurements of single-ionisation yields and comparison with theoretical values.
The and states lie 6.04 meV and 16.22 meV, respectively above the ground state. Such small energy differences are not amenable to discrimination in the present experimental conditions and we, thus, consider initial excitations from these three levels proportionally to their statistical weight. For the sake of simplifying the notation, we shall also generally omit the -value in the notation of the relevant states in the rest of the paper. From Figure 3, both theoretical approaches predict three strong resonances originating from the ground state to the states (in increasing order of energy). The strong experimental resonances 1, 3 and 5 in Figure 4a measured at 399.84 eV, 400.73 eV and 401.40 eV, respectively, are readily assigned to these transitions, respectively. The ab initio energies predicted by the MCDF (RMPS) theories are 399.28 (399.709) eV, 400.48 (400.579) eV and 400.53 (401.347) eV, corresponding to experimental vs. calculated energy differences of 0.56 (0.131) eV, 0.25 (0.149) eV and 0.87 (0.05) eV, for the same transitions, respectively. This comparison shows that the RMPS theory, as implemented in the manner described in Section 3, more accurately predicts the experimental values than the MCDF results which show differences of 0.25 eV or greater.
From the theoretical results of Figure 3, it is reasonable to assign the isolated resonance peak 6 observed at 402.36 eV to the transition (Table 2). It follows that the deconvolved shoulder at 400.85 eV, resonance 4 in Figure 4a, can be attributed to the transition. RMPS theory results for the resonance energies are again in closer agreement with experiment than the MCDF values (Table 2). Nevertheless, both theoretical approaches agree on these assignments.
Figure 4a shows a remaining (deconvolved) resonance 2 at 399.994 eV in the high-energy shoulder of the peak. Figure 3 shows the MCDF and RMPS predictions for transitions arising from the excited states and and differences exist here between the two theoretical approaches. MCDF suggests resonance 2 to be the transition. RMPS suggests instead that this is a contribution from the transition, theoretically predicted at 399.89 eV and closely matching the experimental resonance at 399.98 eV. Taking into account the generally very good agreement between the RMPS predicted energies and experimental values, we assign resonance 2 to the transition. We note further corroborating evidence for this assignment when the next member of the Rydberg series, for which resonance 2 in Table 2 is the first member, is unequivocally identified (the next member in question is resonance 1 in Table 5 of Section 4 below).
To provide a fuller comparison with experiment the ab initio MCDF and RMPS results of Figure 3 were convolved with Gaussian profiles of 65 meV FWHM to simulate the experimental broadening. The theoretical cross-section values, corresponding to the ground and excited state initial configurations, were weighted by numerical factors representing the relative populations of the initial states. The results are shown in Figure 4c,d. It is clear that the dominant initial configuration is the ground state , with smaller contributions from the and states. The ratios of the measured to the calculated cross-section values can provide an estimate of the initial state fractions. The sum of the integrated experimental intensities (single-ionisation channel only) of the resonances originating in the state is 6.0 + 9.1 + 3.7 = 18.8 MbeV, while for the RMPS predictions it is 10.1 + 6.8 + 6.3 = 23.2 MbeV, providing a ratio of 0.81 (Table 2). For the resonances, the numbers are 3.90 MbeV and 24.4 MbeV, respectively, with a ratio of 0.16, while for the ones the ratio would be . We note that these relative population values are quite close to those obtained for a Maxwell-Boltzmann equilibrium at a temperature of ~2.5 eV, for which the weighting factors would be 0.75 , 0.19 , 0.016 and 0.04 . This agreement may be somewhat fortuitous as it it realised that temperature may not be a meaningful physical concept in this case. However, such factors can be appropriately used to model theoretical cross-sections against experimental ones. Furthermore, the error bars on the experimental/theoretical cross-section ratios are large and include the relative error on the experimental integrated intensities of at least 10% (Table 2) and the contributions to the total cross-section due to the double-ionization channel. Figure 2 shows that the double ionization channel does contribute markedly in the 400 eV region with an estimated contribution of about 5%.
In Figure 4, we scale the theoretical cross-sections by factors of 0.75 , 0.19 , 0.016 and 0.04 to allow direct comparison with the experiment. The summed results are displayed in Figure 4c,d. From Figure 4, we conclude that the above analyses lead to an overall satisfactory agreement between the MCDF and RMPS theories and experiment in respect of the resonance strengths and energy positions. The RMPS results in Figure 4d reproduce well the experimental observations of Figure 4a in terms of resonance positions and relative intensities, whereas the MCDF peak absolute cross sections seem in better agreement with the experimental values. The very weak feature at 400.16 eV in the RMPS modelled spectrum is associated with the transition (labelled x in Table 2 and Table 3). The noise present in the measured data in this region together with an estimated very low scaling factor for prevent definite confirmation.

Table 3.
Resonance Assignments near 400 eV photon energy.
All the results from the RMPS and MCDF calculations in terms of energies (eV) and line strengths (Mb eV) are presented in Table 2 and compared with the experimental measurements. Table 2 also includes the measured line widths (meV) obtained from a Voigt profile numerical deconvolution of the experimental resonance shapes. This allows removal of the 65 meV FWHM Gaussian instrumental broadening from the measured total line width with the remaining Lorentzian FWHM representing mostly the Auger width of the final state of the resonance. The RMPS resonance widths (see Section 3) either match quite well (,,) or differ by no more than a factor of about two (,,) from the measured widths, taking into account the relative uncertainties from ~15% up to ~40%.
Inter-comparing the integrated intensities (resonance strengths) of the resonances originating from the same initial term allows a relative comparison with theory independent of the initial population fractions. The , and intensities are observed in the ratios of 1/1.5/0.6. This is to be compared to the ratio of 1/0.7/0.6 predicted by both the RMPS and MCDF theories. Agreement between experiment and the RMPS and MCDF theories is, thus, reasonably close, although for both theories this is less satisfactory for the state. Hasoğlu et al. [] discussed how peculiar spin-orbit mixing effects with affect the Auger and radiative rates of the state along the isoelectronic sequence. However, the authors show these effects peak around nuclear charge and play only a small part in the present case of nuclear charge. For the resonances originating in the excited state, the 1/0.36 experimental ratio is well reproduced by both the MCDF and RMPS theories. The total integrated experimental intensities of the six identified resonances, assuming the aforementioned initial state fractions, amounts to (83 ± 12) Mb eV, which is equivalent to a discrete oscillator strength of 0.76 ± 0.15 []. These figures compare very favourably with the theoretical RMPS values of 88.4 MbeV and 0.80, respectively, while the MCDF values of 118.6 MbeV and 1.1 are somewhat overestimated.
We have already mentioned the sizeable contribution (~5%) to the total cross section of decay processes leading to double ionisation of the final product (N3+). We see from Figure 3b that in the 400 eV region of excitations, the resonances structure for the doubly-ionisation spectrum is almost exactly coincident in energy and relative intensity with that in the single ionisation channel. This suggests the double-Auger process for the double-ionisation channel, whereby the inner-shell excited configuration non-radiatively decays to the final configuration of N3+ (Auger cascade is not possible here) with a electron filling the initial hole and the other two highly correlated electrons being simultaneously ejected.
The N3+ ion yield data of Bari et al. [] in the 400 eV region are in reasonable agreement with the present data of Figure 4b for both the main resonances energies and relative intensities. However, resonance assignments suggested by Bari et al. [], based on their own GAMESS configuration interaction (CI) calculations and the previous work of Garabeih et al. [], differ to some extent from those provided by the detailed analyses of the present work. The more complete comparisons shown between the present absolute measurements (see Section 2) and the results of extended atomic structure calculations from two theoretical approaches lead us to believe that the revised analyses of the present work are conclusive.
4.2. 1s → np (n ≥ 3) Resonances
Excitation of a electron into subshells from a ground state N+ ion, leads to the two main series: and converging to the and inner-shell limits, respectively. Additionally, if excitations from the ,and excited states have contributions, then we obtain several additional series converging on the , and limits, respectively. The contributions of the latter two to the measured total cross-sections are necessarily reduced compared to the ground state contributions as a result of the increasingly lower high n resonance strength coupled to the smaller fractional population factors established in the previous section. The RMPS and MCDF calculated series limits are shown in Table 4. No limits are calculated for the atomic states based on the configuration.

Table 4.
RMPS, MCDF and experimental (see text) N3+ series limits (eV).
In Figure 5, we show the ab initio MCDF and RMPS theoretical predictions for the higher energy range of 415–440 eV. These, together with those of Table 4 and Table 5, are used as the basis for the analyses of the experimental data presented in Figure 6. In Figure 6a, the absolute cross-sectional data for the single ionisation channel are shown. This channel contains no marked resonance contributions above noise at photon energies greater than ~427/8 eV. Resonance structure above this energy and up to ~436 eV is seen in the double ionisation, shown in Figure 6b, channel only, whereas this channel also contains resonance structures whose energies match those of the single ionisation channel in the region ~418–426 eV. The details of the resonance strengths and energy positions are given in Table 5.
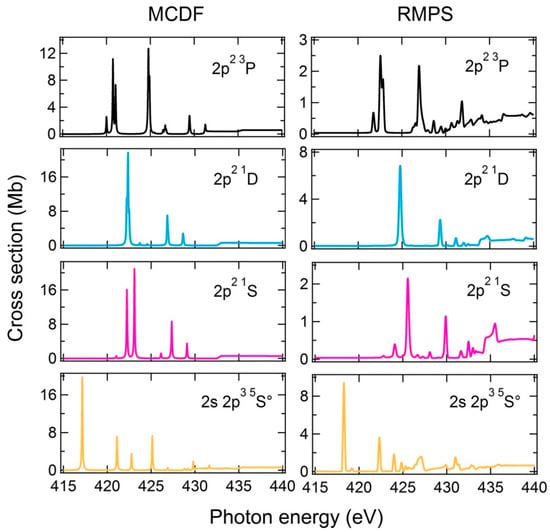
Figure 5.
Multiconfiguration Dirac-Fock (MCDF) and R-Matrix with pseudo-states (RMPS) theoretical calculations of the photoexcitation and photoionization cross sections from the and states of the ground and excited configurations of N+, respectively.

Table 5.
Experimentally determined energy and strength of the main resonances (415–440 eV photon energy) in the N+ photoionization cross-section spectrum, estimated from the absolute measurements of single-ionisation and double-ionization yields and comparison with theoretical energy values.
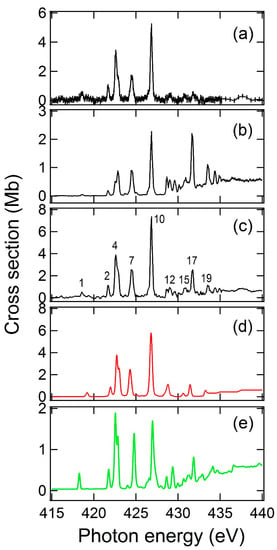
Figure 6.
Photoionization cross-sections of the N+ atomic ion in the photon energy region of the K-shell threshold ( excitations). (a) Absolute measurements in the single-ionisation channel (280 meV band pass). (b) Relative measurements in the double-ionisation channel normalised on the data of Figure 5a (250 meV band pass). (c) Summation of (a,b) with added resonance number labels used in the text of the paper. (d) Total photoionization cross-section simulation based on multiconfiguration Dirac-Fock calculations (MCDF). The theoretical energies are shifted by +2.0 eV in the figure. (e) Total photoionization cross-section simulation based on R-matrix with pseudo-states theoretical (RMPS) calculations.
These data are obtained from Voigt profile numerical fitting of the experimental resonance data profiles including a 250 meV FWHM Gaussian to simulate the energy band pass. Above 428 eV, for reasons of computational stability, Gaussian profiles only were used to extract resonance parameters. The resonances labelled #3, 6, 9, 16, 18, 23, 24 in Table 5 correspond to very low intensity features that are not readily identifiable as peaked atomic resonances, see Figure 6a,b. They arise during the experimental line fitting procedure and are the result of simulating either slightly asymmetric profiles or very weak spectral features and do not affect the general analyses of the data. As remarked earlier, the open shell nature of N+ means that the spectral density of resonances in this energy range is very high.
Both the RMPS and MCDF calculations confirm that the 418.58 eV resonance can only originate from the excited state connecting to several final states with dominant character (this notation is adopted in Table 4). This assignment was used in Section 4.1 above to establish the assignment of the low-energy resonance (labelled 2 in Table 2 and Table 3) in the 400 eV photon region.
The strong resonances at 421.74 eV, 422.61 eV and 422.96 eV are identified as the components of the member of the low energy Rydberg series, respectively. The corresponding single-valued theoretical energies for these and the higher Rydberg states shown in Table 4 are actually the result of the strength-averaged contributions of many mixed states with with almost overlapping energies. As the value of n increases, the energy differences between the (increasingly hydrogenic) states are almost indistinguishable, allowing Rydberg series analysis based on quantum defect values. The relatively strong resonance (#10) is the contribution of two components at 426.88 eV and 426.91 eV, in the single and double ionisation channels respectively, with about 8 Mb total peak intensity, see Figure 6a–c. Comparison with MCDF theoretical results shows that peak #10 is the blended contribution of the and resonances. Non-linear least-square fitting of the measured photon energies (eV) of the resonances numbered 10 (426.88 eV), 11, 13 and 14 to the Rydberg formula where δ is the quantum defect and the ionisation energy (eV) returns best-fit values of eV and δ = 0.56 ± 0.02. This value of is in good agreement with the RMPS and MCDF calculations and the value is typical for a electron orbit. These values allow the identification of the resonances up to . The agreement with the RMPS and MCDF calculated energies is noted. A similar approach for the resonances labelled 10 (426.91 eV), 17, 19, 20, 21 and 22 yields best-fit values of eV and δ = 0.59 ± 0.01. This is in good agreement with the RMPS calculations (Table 4 and Table 5) and allows the identification of the series up to . Above 431.4 eV photon energy the most likely process is direct ionisation to states followed by Auger decay in N2+ leading to a continuous ion signal in the double-ionisation channel only, as observed in Figure 5b. As discussed in Section 3.1, other double-ionisation processes are conceivable for excited configurations consisting of cascade or double-Auger participator and spectator decays. These processes are energetically possible below the 431.4 eV K-edge and explain satisfactorily the observations of Figure 6b. Single-electron autoionization decay of the and configurations are the main contributions to the single-ionisation channel as observed in Figure 6a.
Resonance #7 at 424.55 eV corresponds to transitions to states originating in the metastable state with roughly equal contributions in the single and double-ionisation channels. The resonances labelled 12 and 15 measured at 429.07 eV and 430.81 eV may tentatively be assigned to the and members of this series, respectively. Other contributions from excited states are extremely weak and unambiguous assignments are not possible.
To allow direct comparison with the theoretical data, the single and double ionisation experimental signals are added and the result shown in Figure 6c. In Figure 6d,e, the theoretical data of Figure 5 are adjusted in the manner used and discussed in Section 4.1, i.e., 0.75, 0.19, 0.016 and 0.04 initial state weight coefficients are applied following 225 meV FWHM Gaussian convolution. The MCDF theory shows a very satisfactory agreement with the measured cross-section profile in terms of relative energy positions and absolute intensities for the high energy resonances, although the absolute resonance energies are systematically too low by about 2 eV. Conversely, the RMPS theory predicts quite accurately the measured resonance energies while the peak intensities are typically too small by a factor of 2–3.
Only a qualitative comparison of the N3+ ion yield data by Bari et al. [] (their Figure 3b) is feasible. It indicates a reasonable agreement between the resonance energies and intensity patterns observed in the two works.
5. Conclusions
Enhanced experimental conditions at the MAIA crossed beam facility at SOLEIL allowed substantially improved single- and double-ionisation cross section measurements to be carried out for the N+ ion in the K-shell excitation regime. In addition to the strong resonances in the 398–405 eV range corresponding to excitations, several well-developed Rydberg resonance series corresponding to excitations were observed at higher photon energies running to K-shell ionization limits above 430 eV. With three open shells the calculation of such resonance series presents a considerable challenge to theory. Furthermore, contributions due to metastable states had also to be taken into account. Comparison of the measured results with theoretical photoionization cross-section calculations from large-scale MCDF and RMPS photoionization cross section calculations allowed interpretation of the experimental data and benchmarking of the different theoretical approaches. The present theoretical work may be incorporated into astrophysical modelling codes like CLOUDY [,], XSTAR [] and AtomDB [] used to numerically simulate the thermal and ionization structure of ionized astrophysical nebulae
Author Contributions
J.-P.M., E.T.K., J.-M.B., D.C. and S.G., were involved in the experiments and data taking. The theoretical aspects of the work were contributed by C.B. and B.M.M. The graphs and figures were prepared by J.-M.B. and D.C. All the authors contributed to the analyses presented in the work. J.-P.M., E.T.K., B.M.M. and J.-M.B. prepared the original draft. All the authors reviewed and edited the subsequent versions of the draft. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
J.-P.M. and E.T.K. wish to thank SOLEIL and the EC for financial assistance with travel, accommodation and subsistence costs. The authors would like to thank the SOLEIL and PLEIADES beam line staff, J. Bozek, C. Nicolas, A. Miloslajevic for their assistance throughout the experiment. This work has benefited from the LabEX PALM’s investments (ANR-10-LABX-0039-PALM). B.M.M. acknowledges financial support from the CNRS LabEX PALM programme. The University of Georgia at Athens is thanked for the award of an adjunct professorship, and Queen’s University Belfast for the award of a visiting research fellowship. The authors acknowledge this research used grants of computing time at the National Energy Research Scientific Computing Centre (NERSC), which is supported by the Office of Science of the U.S. Department of Energy (DOE) under Contract No. DE-AC02-05CH11231. The authors gratefully acknowledge the Gauss Centre for Supercomputing e.V. (www.gauss-centre.eu) for funding this project by providing computing time on the GCS Supercomputer hazel hen at Höchstleis-tungsrechenzentrum Stuttgart (www.hlrs.de). Itamp is supported in part by NSF Grant No. PHY-1607396.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hasoglu, M.F.; Abdel-Naby, S.H.A.; Gorczyca, T.; Drake, J.J.; McLaughlin, B.M. K-shell photoabsorption studies of the carbon isonuclear sequence. Astrophys. J. 2010, 724, 1296–1304. [Google Scholar] [CrossRef]
- McLaughlin, B.M.; Bizau, J.-M.; Cubaynes, D.; Al Shorman, M.M.; Guilbaud, S.; Sahko, I.; Blancard, C.; Gharaibeh, M.F. K-shell photoionization of B-like oxygen (O3+) ions: Experiment and theory. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 115201. [Google Scholar] [CrossRef]
- Bizau, J.-M.; Cubaynes, D.; Guilbaud, S.; Al Shorman, M.M.; Gharaibeh, M.F.; Ababneh, I.Q.; Blancard, C.; McLaughlin, B.M. K-shell photoionization of O+ and O2+ ions: Experiment and theory. Phys. Rev. A 2015, 92, 023401. [Google Scholar] [CrossRef]
- McLaughlin, B.M.; Bizau, J.-M.; Cubaynes, D.; Guilbaud, S.; Douix, S.; Al Shorman, M.M.; El Ghazaly, M.O.A.; Sakho, I.; Gharaibeh, M.F. K-shell photoionization of O4+ and O5+ ions: Experiment and theory. Mon. Not. R. Astron. Soc. 2017, 465, 4690–4702. [Google Scholar] [CrossRef]
- Mathur, S.; Nicastro, F.; Gupta, A.; Krongold, Y.; McLaughlin, B.M.; Brickhouse, N.; Pradhan, A. The O vi Mystery: Mismatch between X-Ray and UV Column Densities. Astrophys. J. 2017, 851, L7. [Google Scholar] [CrossRef]
- Leutenegger, M.A.; Kűhn, S.; Micke, P.; Steinbrűgge, R.; Stierhof, J.; Shah, C.; Hell, N.; Bissinger, M.; Hirsch, M.; Ballhasuen, R.; et al. High-Precision Determination of Oxygen Kα Transition Energy Excludes Incongruent Motion of Interstellar Oxygen. Phys. Rev. Lett. 2020, 125, 243001. [Google Scholar] [CrossRef] [PubMed]
- Stolte, W.C.; Jonauskas, V.; Lindle, D.W.; Sant’Anna, M.M.; Savin, D.W. Inner-shell photoionization studies of neutral atomic nitrogen. Astrophys. J. 2016, 818, 149. [Google Scholar] [CrossRef]
- Gharaibeh, M.F.; Bizau, J.M.; Cubaynes, D.; Guilbaud, S.; El Hassan, N.; Al Shorman, M.M.; Miron, C.; Nicolas, C.; Robert, E.; Blancard, C.; et al. K-shell photoionization of singly ionized atomic nitrogen: Experiment and theory. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 175208. [Google Scholar] [CrossRef]
- Gharaibeh, M.F.; Hassan, N.E.; Al Shorman, M.M.; Bizau, J.-M.; Cubaynes, D.; Guilbaud, S.; Sakho, I.; Blancard, C.; McLaughlin, B.M. K-shell photoionization of B-like atomic nitrogen ions: Experiment and theory. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 065201. [Google Scholar] [CrossRef]
- Al Shorman, M.M.; Gharaibeh, M.F.; Bizau, J.M.; Cubaynes, D.; Guilbaud, S.; El Hassan, N.; Miron, C.; Nicolas, C.; Robert, E.; Sakho, I.; et al. K-shell photoionization of Be-like and Li-like ions of atomic nitrogen: Experiment and theory. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 195701. [Google Scholar] [CrossRef]
- Bari, S.; Inhester, L.; Schubert, K.; Mertens, K.; Schunck, J.O.; Dörner, S.; Deinert, S.; Schwob, L.; Schippers, S.; Müller, A.; et al. Inner-shell X-ray absorption spectra of the cationic series NHy+ (y = 0–3). Phys. Chem. Chem. Phys. 2019, 21, 16505–16514. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Liang, L.; Zhou, C. K-shell photoionization of Be-like nitrogen from the ground state: Energies and Auger widths of the high-lying double-excited states for N IV. Can. J. Phys. 2018, 96, 1183–1191. [Google Scholar] [CrossRef]
- Peng, Y.-G.; Wu, Y.; Zhu, L.-F.; Zhang, S.B.; Wang, J.-G.; Liebermann, H.-P.; Buenker, R.J. Complex multireference configuration interaction calculations for the K-vacancy Auger states of Nq+ (q = 2-5) ions. J. Chem. Phys. 2016, 144, 054306. [Google Scholar] [CrossRef]
- Bizau, J.M.; Cubaynes, D.; Guilbaud, S.; El Hassan, N.; Al Shorman, M.M.; Bouisset, E.; Guigand, J.; Moustier, O.; Marié, A.; Nadal, E.; et al. A merged-beam setup at SOLEIL dedicated to photoelectron–photoion coincidence studies on ionic species. J. Electron Spectrosc. Relat. Phenom. 2016, 210, 5–12. [Google Scholar] [CrossRef]
- Blancard, C.; Cubaynes, D.; Guilbaud, S.; Bizau, J.-M. Absolute Photoionization Cross Section for Fe6+ to Fe10+ Ions in the Photon Energy Region of the 2p-3d Resonance Lines. Astrophys. J. 2018, 853, 32. [Google Scholar] [CrossRef]
- Khalal, M.A.; Lablanquie, P.; Andric, L.; Palaudoux, J.; Penent, F.; Bučar, K.; Žitnik, M.; Püttner, R.; Jänkälä, K.; Cubaynes, D.; et al. 4d-inner-shell ionization of Xe+ ions and subsequent Auger decay. Phys. Rev. A 2017, 96, 013412. [Google Scholar] [CrossRef]
- Bizau, J.-M.; Cubaynes, D.; Guilbaud, S.; Penent, F.; Lablanquie, P.; Andric, L.; Palaudoux, J.; Al Shorman, M.M.; Blancard, C. Photoelectron Spectroscopy of Ions: Study of the Auger Decay of the 4d -> nf (n=4,5) Resonances in Xe5+ Ion. Phys. Rev. Lett. 2016, 116, 103001. [Google Scholar] [CrossRef] [PubMed]
- Mosnier, J.-P.; Kennedy, E.T.; van Kampen, P.; Cubaynes, D.; Guilbaud, S.; Sisourat, N.; Puglisi, A.; Carniato, S.; Bizau, J.-M. Inner-shell photoexcitations as probes of the molecular ions CH+, OH+, and SiH+: Measurements and theory. Phys. Rev. A 2016, 93, 061401. [Google Scholar] [CrossRef]
- Puglisi, A.; Miteva, T.; Kennedy, E.T.; Mosnier, J.-P.; Bizau, J.-M.; Cubaynes, D.; Sisourat, N.; Carniato, S. X-ray photochemistry of carbon hydride molecular ions. Phys. Chem. Chem. Phys. 2018, 20, 4415–4421. [Google Scholar] [CrossRef] [PubMed]
- Carniato, S.; Bizau, J.-M.; Cubaynes, D.; Kennedy, E.T.; Guilbaud, S.; Sokell, E.; McLaughlin, B.M.; Mosnier, J.-P. Vibrationally and Spin-Orbit-Resolved Inner-Shell X-ray Absorption Spectroscopy of the NH+ Molecular Ion: Measurements and ab Initio Calculations. Atoms 2020, 8, 67. [Google Scholar] [CrossRef]
- Sodhi Rana, N.S.; Brion, C.E. Reference energies for inner shell electron energy-loss spectroscopy. J. Elec. Spec. Rel. Phenom. 1984, 34, 363–372. [Google Scholar] [CrossRef]
- Kato, M.; Morishita, Y.; Oura, M.; Yamaoka, H.; Tamenori, Y.; Okada, K.; Matsudo, T.; Gejo, T.; Suzuki, I.H.; Saito, N. Absolute photoionization cross sections with ultra-high energy resolution for Ar, Kr, Xe and N2 in inner-shell ionization regions. J. Elec. Spec. Rel. Phenom. 2007, 34, 39–48. [Google Scholar] [CrossRef]
- Mosnier, J.-P.; Sayyad, M.H.; Kennedy, E.T.; Bizau, J.-M.; Cubaynes, D.; Wuilleumier, F.J.; Champeaux, J.-P.; Blancard, C.; Varma, R.H.; Banerjee, T.; et al. Absolute photoionization cross sections and resonance structure of doubly ionized silicon in the region of the 2p-1 threshold: Experiment and theory. Phys. Rev. A 2003, 68, 052712. [Google Scholar] [CrossRef]
- Cooper, J.W. New directions in the study of atomic autoionizing states. J. Elec. Spec. Rel. Phenom. 1994, 67, 223–231. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (ver. 5.8). 2020. Available online: https://physics.nist.gov/asd (accessed on 18 February 2021).
- Tachiev, G.; Froese Fisher, C. Breit-Pauli energy levels for the carbonlike sequence. Can. J. Phys. 2001, 79, 955–976. [Google Scholar] [CrossRef]
- Martins, M. Photoionization of open-shell atoms: The chlorine 2p excitation. J. Phys. B At. Mol. Opt. Phys. 2001, 34, 1321–1355. [Google Scholar] [CrossRef]
- Bruneau, J. Correlation and relaxation effects in ns2-nsnp transitions. J. Phys. B At. Mol. Opt. Phys. 1984, 17, 3009–3028. [Google Scholar] [CrossRef]
- Grant, I.P. Gauge invariance and relativistic radiative transitions. J. Phys. B At. Mol. Opt. Phys. 1974, 7, 1458–1475. [Google Scholar] [CrossRef]
- Slater, J.C. Quantum Theory of Molecules and Solids Vol. 4: The Self-Consistent Field for Molecules and Solids; McGraw-Hill: New York, NY, USA, 1974. [Google Scholar]
- Hasoǧlu, M.F.; Nikolić, D.; Gorczyca, T.W.; Manson, S.T.; Chen, M.H.; Badnell, N.R. Nonmonotonic behavior as a function of nuclear charge of the K-shell Auger and radiative rates and fluorescence yields along the 1s2s2p3 isoelectronic sequence. Phys. Rev. A 2008, 78, 032509. [Google Scholar] [CrossRef]
- Burke, P.G. R-Matrix Theory of Atomic Collisions: Application to Atomic, Molecular and Optical Processes; Springer: New York, NY, USA, 2011. [Google Scholar]
- Burke, P.G.; Berrington, K.A. Atomic and Molecular Processes: An R-Matrix Approach; IOP Publishing: Bristol, UK, 1993. [Google Scholar]
- Berrington, K.A.; Eissner, W.; Norrington, P.H. RMATRX1: Belfast atomic R-matrix codes. Comput. Phys. Commun. 1995, 92, 290–420. [Google Scholar] [CrossRef]
- Ballance, C.P.; Griffin, D.C. Relativistic radiatively damped R-matrix calculation of the electron-impact excitation of W46+. J. Phys. B At. Mol. Opt. Phys. 2006, 39, 3617–3628. [Google Scholar] [CrossRef]
- Robicheaux, F.; Gorczyca, T.W.; Pindzola, M.S.; Badnell, N.R. Inclusion of radiation damping in the close-coupling equations for electron-atom scattering. Phys. Rev. A 1995, 52, 1319–1333. [Google Scholar] [CrossRef] [PubMed]
- Quigley, L.; Berrington, K.A. The QB method: Analysing resonances using R-matrix theory. Applications to C+, He and Li. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 4529–4542. [Google Scholar] [CrossRef]
- Quigley, L.; Berrington, K.A.; Pelan, J. The QB program: Analysing resonances using R-matrix theory. Comput. Phys. Commun. 1998, 114, 225–235. [Google Scholar] [CrossRef]
- Ballance, C.P.; Berrington, K.A.; McLaughlin, B.M. Detection and analysis of interloping molecular resonances. Phys. Rev. A 1995, 60, R4217(R). [Google Scholar] [CrossRef]
- Fano, U.; Cooper, J.W. Spectral Distribution of Oscillator Strengths. Rev. Mod. Phys. 1968, 40, 411. [Google Scholar] [CrossRef]
- Ferland, G.J. Quantitative Spectroscopy of Photoionized Clouds. Ann. Rev. Astron. Astr. 2003, 41, 517–554. [Google Scholar] [CrossRef]
- Ferland, G.J.; Korista, K.T.; Verner, D.A.; Ferguson, J.W.; Kingdon, J.B.; Verner, E.M. CLOUDY 90: Numerical Simulation of Plasmas and Their Spectra. Publ. Astron. Soc. Pac. 1998, 110, 761–778. [Google Scholar] [CrossRef]
- Bautista, M.A.; Kallman, T.R. The X-star Atomic Database. Astrophys. J. Suppl. 2001, 134, 139. [Google Scholar] [CrossRef]
- Foster, A.R.; Ji, L.; Smith, R.K.; Brickhouse, N.S. Updated Atomic Data and Calculations for X-ray Spectroscopy. Astrophys. J. 2012, 756, 128. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).