Simulations of Ion-Guiding Through Insulating Nanocapillaries of Varying Diameter: Interpretation of Experimental Results
Abstract
1. Introduction
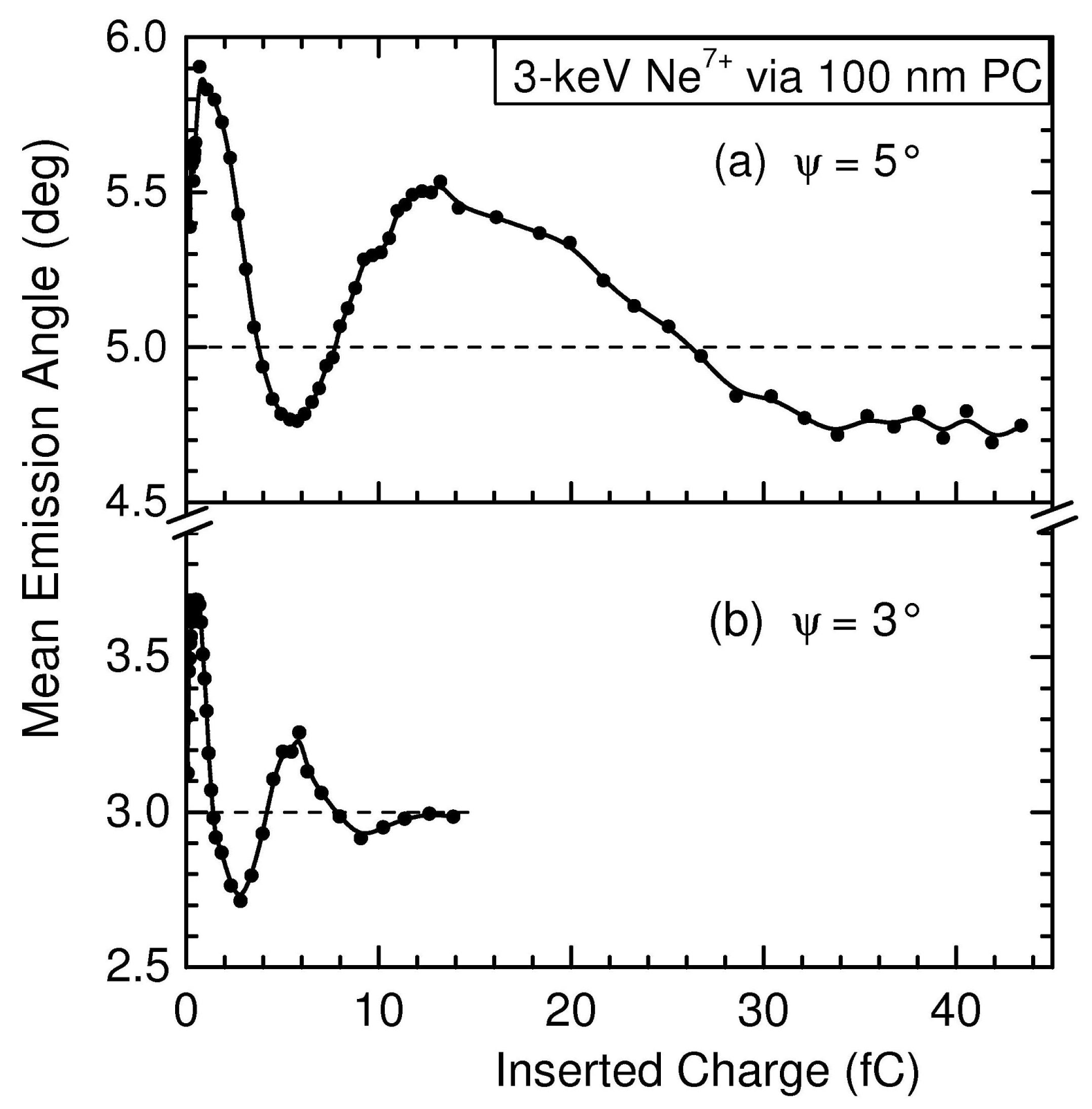
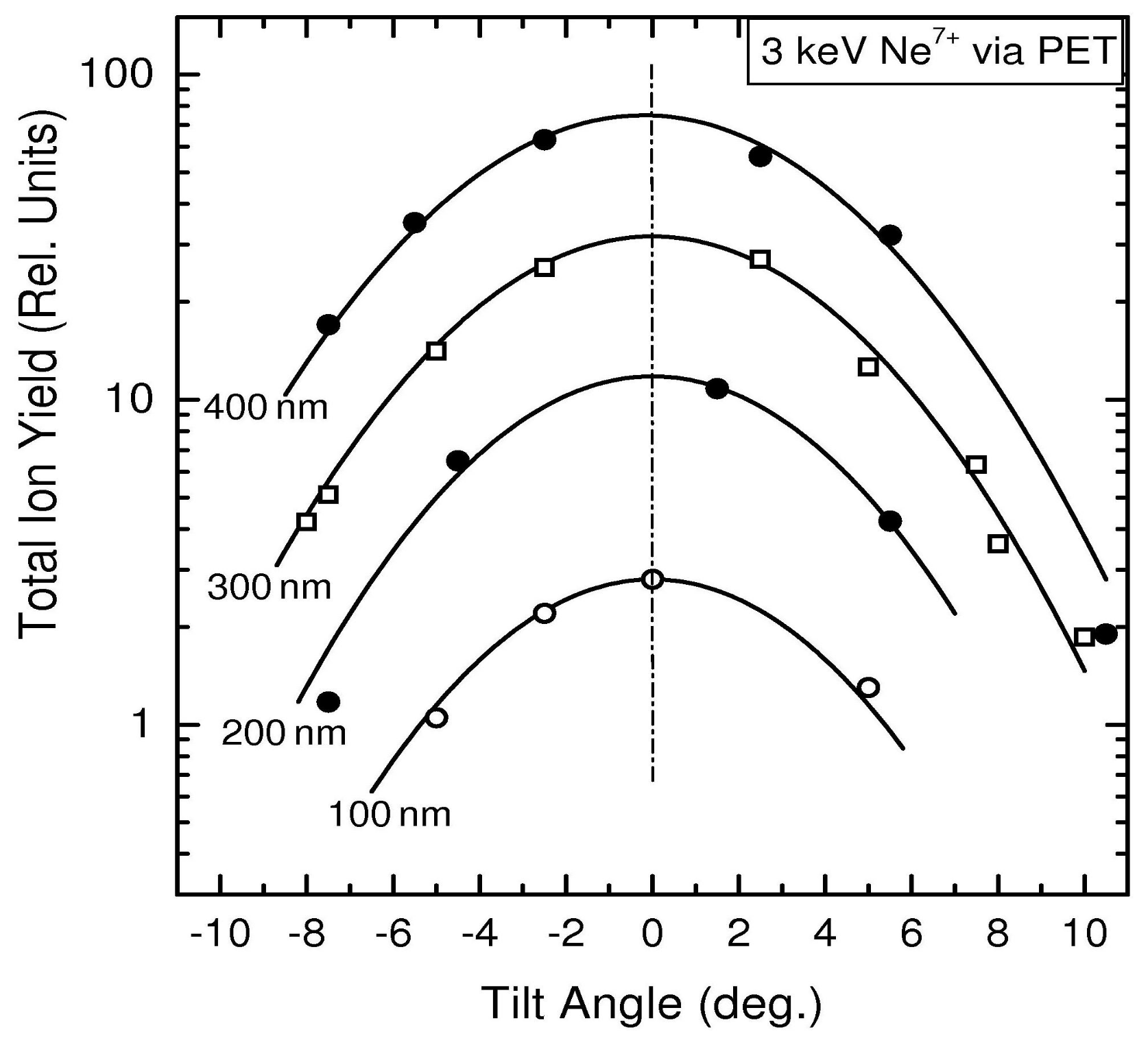
2. Overview of Previous Experiments
3. Theoretical Method
3.1. Basics of the Calculations
3.2. Example from Previous Simulations
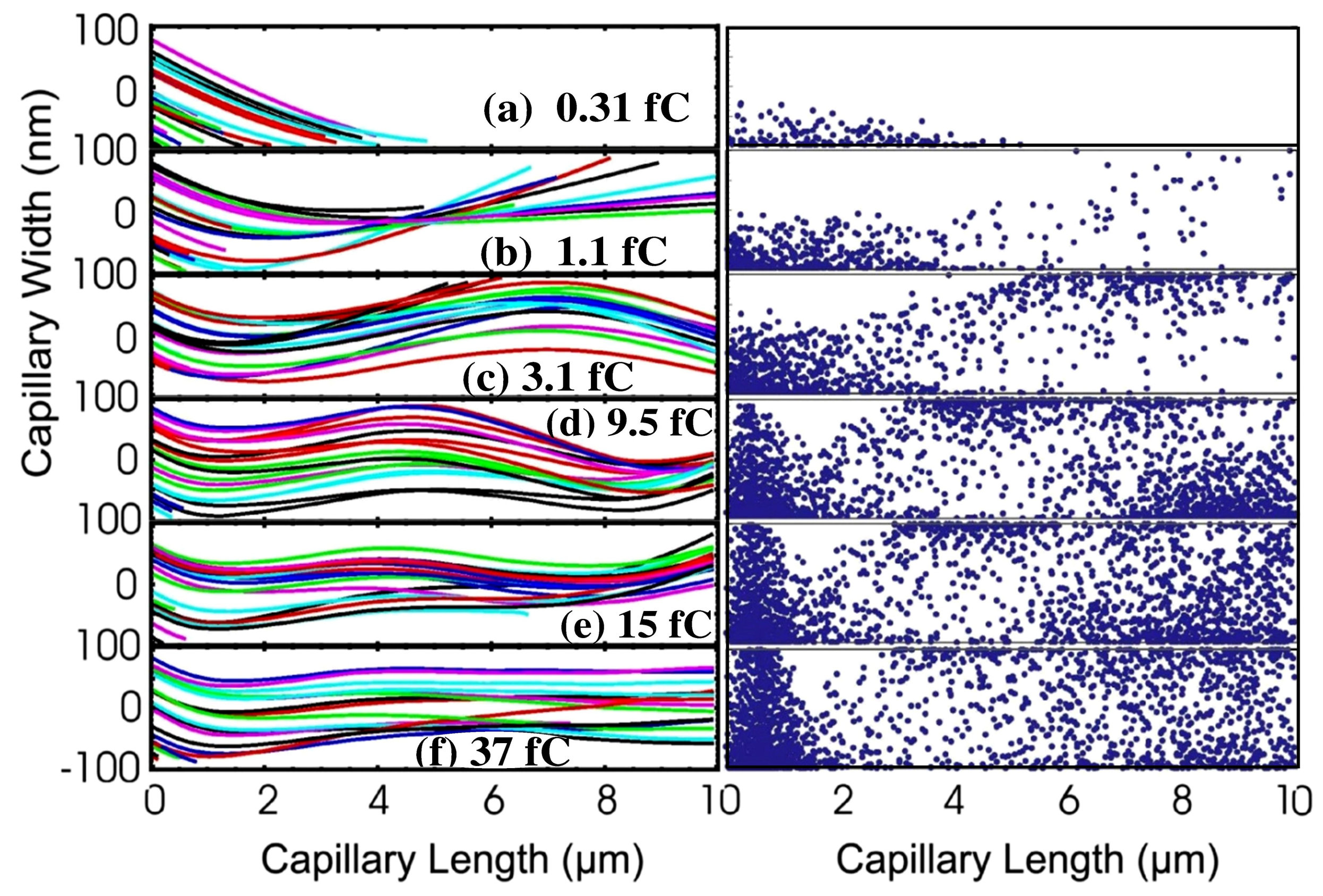
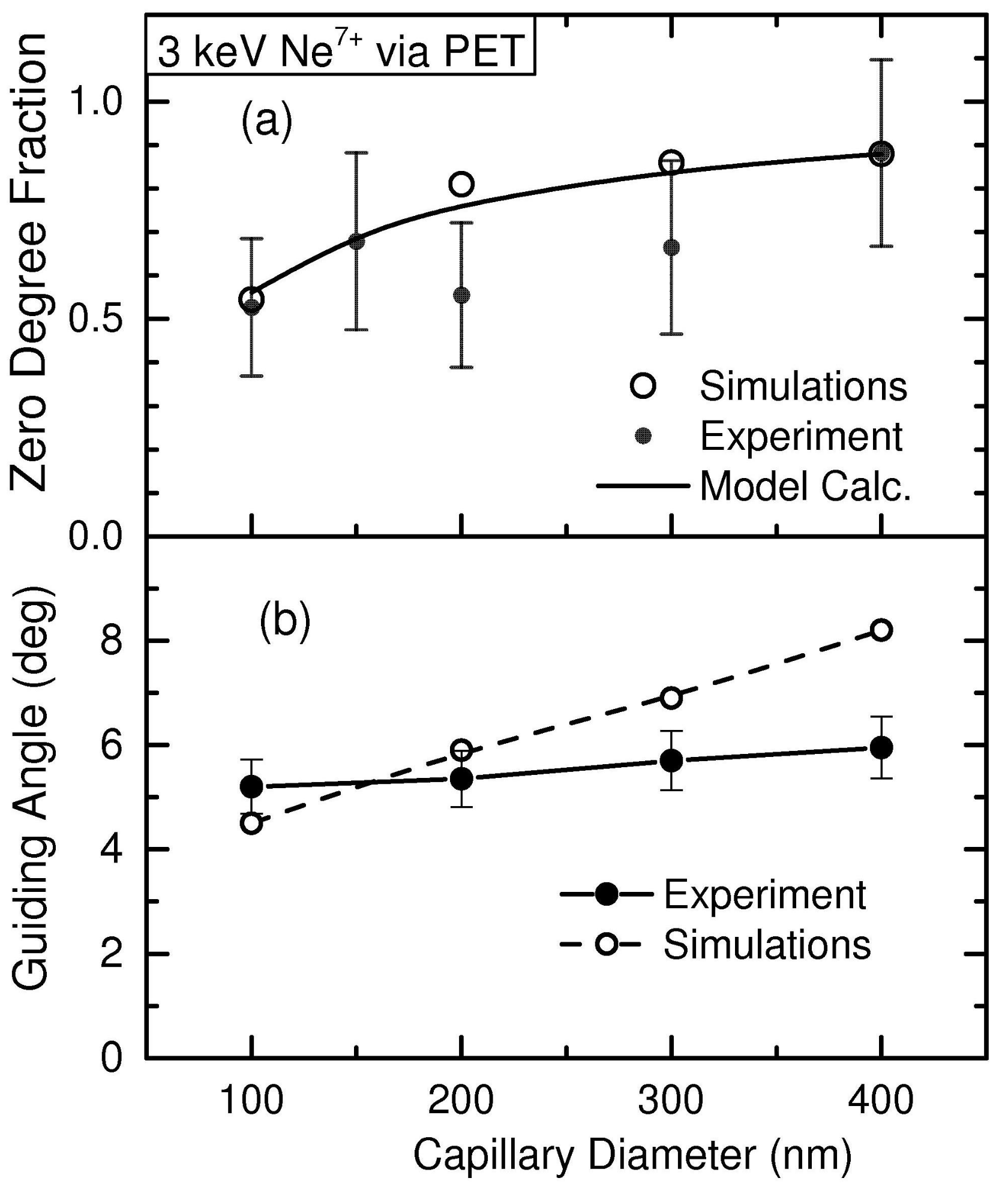
4. Results of the Simulations
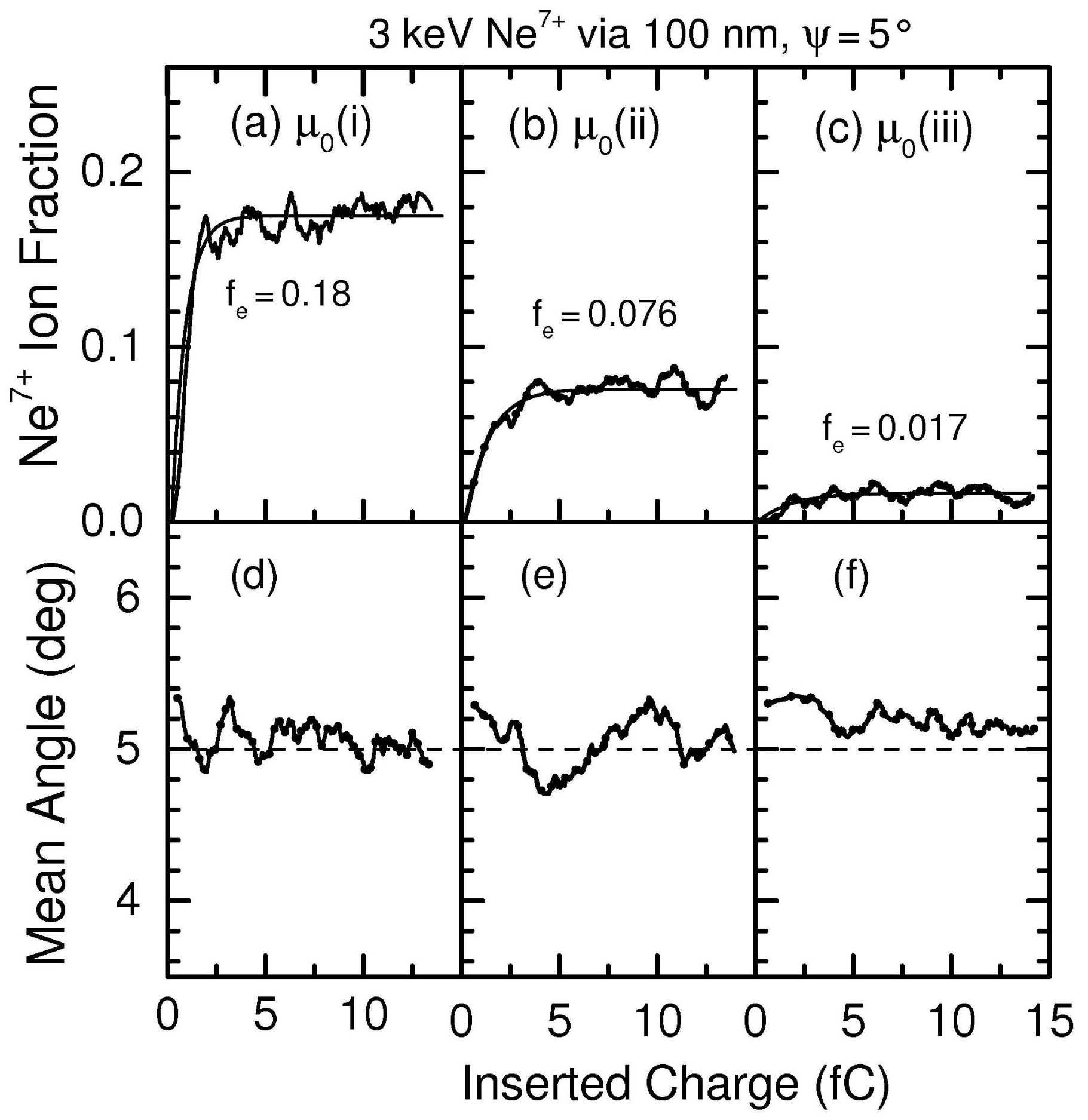
4.1. Analysis of the Surface Drift Mobility
4.2. Analysis of the Bulk Depletion Rate
4.3. Dependence on the Tilt Angle
4.4. Guiding Angle and Guiding Power
4.5. Rates for Surface and Bulk Discharge
5. Discussion and Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Stolterfoht, N.; Bremer, J.H.; Hoffmann, V.; Hellhammer, R.; Fink, D.; Petrov, A.; Sulik, B. Transmission of 3 keV Ne7+ ions through nanocapillaries etched in polymer foils: Evidence for capillary guiding. Phys. Rev. Lett. 2002, 88, 133201. [Google Scholar] [CrossRef] [PubMed]
- Stolterfoht, N.; Hellhammer, R.; Pešić, Z.D.; Hoffmann, V.; Bundesmann, J.; Petrov, A.; Fink, D.; Sulik, B. Guided transmission of Ne7+ ions through nanocapillaries in PET: Dependence on the tilt angle. Vacuum 2004, 73, 31–37. [Google Scholar] [CrossRef]
- Víkor, G.; Kumar, R.R.; Pešić, Z.; Stolterfoht, N.; Schuch, R. Guiding of slow highly charged ions by nanocapillaries in PET. Nucl. Instrum. Methods Phys. Res. B 2005, 233, 218–221. [Google Scholar] [CrossRef]
- Stolterfoht, N.; Hellhammer, R.; Bundesmann, J.; Fink, D.; Kanai, Y.; Hoshino, M.; Kambara, T.; Ikeda, T.; Yamazaki, Y. Guiding of slow Ne7+ ions through nanocapillaries in insulating PET polymers: Incident current dependence. Phys. Rev. A 2007, 76, 022712. [Google Scholar] [CrossRef]
- Kanai, Y.; Hoshino, M.; Kambara, T.; Ikeda, T.; Hellhammer, R.; Stolterfoht, N.; Yamazaki, Y. Two-dimensional images of transmitted slow neon ions gudided by nanocapillaries in polymer foils. Nucl. Instrum. Methods Phys. Res. B 2007, 258, 155–158. [Google Scholar] [CrossRef]
- Stolterfoht, N.; Hellhammer, R.; Juhász, Z.; Sulik, B.; Bayer, V.; Trautmann, C.; Bodewits, E.; de Nijs, A.J.; Dang, H.M.; Hoekstra, R. Guided transmission of Ne7+ ions through nanocapillaries in insulating polymers: Scaling laws for projectile energies up to 50 keV. Phys. Rev. A 2009, 79, 042902. [Google Scholar] [CrossRef]
- Stolterfoht, N.; Hellhammer, R.; Juhász, Z.; Sulik, B.; Bodewits, E.; Dang, H.M.; Hoekstra, R. Guided transmission of Ne7+ ions through nanocapillaries in insulating polymers: Dependence on the capillary diameter. Phys. Rev. A 2010, 82, 052902. [Google Scholar] [CrossRef]
- Juhász, Z.; Sulik, B.; Rácz, R.; Biri, S.; Bereczky, R.J.; Tökési, K.; Köver, Á.; Pálinkás, J.; Stolterfoht, N. Ion guiding accompanied by formation of neutrals in polyethylene terephthalate polymer nanocapillaries: Further insight into a self-organizing process. Phys. Rev. A 2010, 82, 062903. [Google Scholar] [CrossRef]
- Li, D.; Wang, Y.; Zhao, Y.; Xiao, G.; Zhao, D.; Xu, Z.; Li, F. The influence of the charged back side on the transmission of highly charged ions through PC nanocapillaries. Nucl. Instrum. Methods Phys. Res. B 2009, 267, 469–473. [Google Scholar] [CrossRef]
- Sahana, M.B.; Skog, P.; Víkor, G.; Rajendra-Kumar, R.T.; Schuch, R. Guiding of highly charged ions by highly-ordered SiO2 nanocapillaries. Phys. Rev. A 2006, 73, 040901(R). [Google Scholar] [CrossRef]
- Mátéfi-Tempfli, S.; Mátéfi-Tempfli, M.; Piraux, L.; Juhász, Z.; Biri, S.; Fekete, É.; Iván, I.; Gáll, F.; Sulik, B.; Víkor, G.; et al. Guided transmission of slow Ne6+ ions through the nanochannels of highly ordered anodic alumina. Nanotechnology 2006, 17, 3915–3920. [Google Scholar] [CrossRef]
- Skog, P.; Soroka, I.L.; Johansson, A.; Schuch, R. Guiding of highly charged ions through Al2O3 nanocapillaries. Nucl. Instrum. Methods Phys. Res. B 2007, 258, 145–149. [Google Scholar] [CrossRef]
- Chen, Y.F.; Chen, X.M.; Lou, F.J.; Zhang, J.Z.; Shao, J.X.; Sun, G.Z.; Wang, J.; Xi, F.Y.; Yin, Y.Z.; Wang, X.A.; et al. Guiding of 60 keV O6+ ions through nanocapillaries in uncoated Al2O3 membrane. Chin. Phys. B 2009, 18, 2739. [Google Scholar]
- Juhász, Z.; Sulik, B.; Biri, S.; Iván, I.; Tökési, K.; Fekete, É.; Mátéfi-Tempfli, S.; Mátéfi-Tempfli, M.; Víkor, G.; Takács, E.; et al. Ion guiding in alumina capillaries: MCP images of the transmitted ions. Nucl. Instrum. Methods Phys. Res. B 2009, 267, 321–325. [Google Scholar] [CrossRef]
- Zhang, H.Q.; Akram, N.; Skog, P.; Soroka, I.; Trautmann, C.; Schuch, R. Tailoring of keV-ion beams by image charge when transmitting through rhombic and rectangular shaped nanocapillaries. Phys. Rev. Lett. 2012, 108, 193202–193205. [Google Scholar] [CrossRef]
- Zhang, H.Q.; Akram, N.; Schuch, R. Transmission of highly charged ions through mica nanocapillaries of rectangular cross-section. Nucl. Instrum. Methods Phys. Res. B 2017, 408, 61–66. [Google Scholar] [CrossRef]
- Milosavljević, A.R.; Víkor, G.; Pešić, Z.D.; Kolarž, P.; Šević, D.; Marinković, B.P.; Mátéfi-Tempfli, S.; Mátéfi-Tempfli, M.; Piraux, L. Guiding of low-energy electrons by highly ordered Al2O3 nanocapillaries. Phys. Rev. A 2007, 75, 030901(R). [Google Scholar] [CrossRef]
- Das, S.; Dassanayake, B.S.; Winkworth, M.; Baran, J.L.; Stolterfoht, N.; Tanis, J.A. Inelastic guiding of electrons in polymer nanocapillaries. Phys. Rev. A 2007, 76, 042716. [Google Scholar] [CrossRef]
- Wickramarachchi, S.J.; Ikeda, T.; Dassanayake, B.S.; Keerthisinghe, D.; Tanis, J. Electron-beam transmission through a micrometer-sized tapered-glass capillary: Dependence on incident energy and angular tilt angle. Phys. Rev. A 2016, 94, 022701. [Google Scholar] [CrossRef]
- Ikeda, T.; Kanai, Y.; Kojima, T.M.; Iwai, Y.; Kambara, T.; Yamazaki, Y.; Hoshino, M.; Nebiki, T.; Narusawa, T. Production of a microbeam of slow highly charged ions with a tapered glass capillary. Appl. Phys. Lett. 2006, 89, 163502. [Google Scholar] [CrossRef]
- Ikeda, T.; Kojima, T.M.; Iwai, Y.; Kanai, Y.; Kambara, T.; Nebiki, T.; Narusawa, T.; Yamazaki, Y. Production of a nm sized slow HCI beam with a guiding effect. J. Phys. Conf. Ser. 2007, 58, 68–72. [Google Scholar] [CrossRef]
- Cassimi, A.; Muranaka, T.; Maunoury, L.; Lebius, H.; Manil, B.; Huber, B.A.; Ikeda, T.; Kanai, Y.; Kojima, T.M.; Iwai, Y.; et al. Multiply-charged ion nanobeams. Int. J. Nanotechnol. 2008, 5, 809–817. [Google Scholar] [CrossRef]
- Cassimi, A.; Ikeda, T.; Maunoury, L.; Zhou, C.L.; Guillous, S.; Mery, A.; Lebius, H.; Benyagoub, A.; Grygiel, C.; Khemliche, H.; et al. Dynamics of charge evolution in glass capillaries for 230-keV Xe23+ ions. Phys. Rev. A 2012, 86, 062902. [Google Scholar] [CrossRef]
- Gruber, E.; Stolterfoht, N.; Allinger, P.; Wampla, S.; Wang, Y.; Simon, M.J.; Aumayr, F. Temperature control of ion guiding through tapered capillaries. Nucl. Instrum. Methods Phys. Res. B 2014, 340, 1–4. [Google Scholar] [CrossRef]
- Giglio, E.; DuBois, R.; Cassimi, A.; Tökési, K. Low energy ion transmission through a conical insulating capillary with macroscopic dimensions. Nucl. Instrum. Methods Phys. Res. B 2015, 354, 82–85. [Google Scholar] [CrossRef]
- DuBois, R.D.; Tökési, K.; Giglio, E. Charge deposition, redistribution, and decay properties of insulating surfaces obtained from guiding of low-energy ions through capillaries. Phys. Rev. A 2019, 99, 062704. [Google Scholar] [CrossRef]
- Bereczky, R.; Kowarik, G.; Aumayr, F.; Tökési, K. Transmission of 4.5 keV Ar9+ ions through a single glass macro-capillary. Nucl. Instrum. Methods Phys. Res. B 2009, 267, 317–320. [Google Scholar] [CrossRef]
- Nakayama, R.; Tona, M.; Nakamura, N.; Watanabe, H.; Yoshiyasu, N.; Yamada, C.; Yamazaki, A.; Ohtani, S.; Sakurai, M. Guiding and blocking of highly charged ions through a single glass capillary. Nucl. Instrum. Methods Phys. Res. B 2009, 267, 2381–2384. [Google Scholar] [CrossRef]
- Gruber, E.; Kowarik, G.; Ladening, F.; Waclawek, J.P.; Aumayr, F.; Bereczky, R.J.; Tökési, K.; Gunacker, P.; Schweigler, T.; Lemell, C.; et al. Temperature control of ion guiding through insulating capillaries. Phys. Rev. A 2012, 86, 062901–062908. [Google Scholar] [CrossRef]
- Nagy, G.U.L.; Giglio, E.; Rajta, I.; Tökési, K. Transmission dynamics of 1 MeV H+ microbeam guided through an insulating macrocapillary. Nucl. Instrum. Methods Phys. Res. B 2019, 460, 216. [Google Scholar] [CrossRef]
- Nagy, G.U.L.; Rajta, I.; Tökési, K. Temporal evolution of the energy spectrum of proton beam guided through an insulating macrocapillary. Nucl. Instrum. Methods Phys. Res. B 2019, 458, 7–11. [Google Scholar] [CrossRef]
- Liu, S.D.; Zhao, Y.T. Simulations of transmission of 1 MeV protons through an insulating macrocapillary. J. Phys. D 2019, 53, 075103. [Google Scholar] [CrossRef]
- Kojima, T.M.; Ikeda, T.; Kanai, Y.; Yamazaki, Y.; Esaulov, V.A. Ion beam guiding with straight and curved teflon tubes. J. Phys. D 2011, 44, 355201. [Google Scholar] [CrossRef]
- Kojima, T.M. Ion guiding in macro-size insulating capillaries: straight, tapered, and curved shapes. J. Phys. B 2018, 51, 1042001. [Google Scholar] [CrossRef]
- Pokhil, G.P.; Cherdyntsev, V.V. Model of the Dynamics of Ion Propagation through Dielectric Capillaries. J. Surf. Investig. X-ray Synchrotron Neutron Tech. 2013, 7, 356–361. [Google Scholar] [CrossRef]
- Vokhmyanina, K.; Sotnikova, V.; Sotnikov, A.; Kaplii, A.; Nikulicheva, T.; Kubankin, A.; Kishin, I. Modeling the process of interaction of 10?keV electrons with a plane dielectric surface. Nucl. Instrum. Methods Phys. Res. B 2018, 422, 91–93. [Google Scholar] [CrossRef]
- Lemell, C.; Burgdörfer, J.; Aumayr, F. Interaction of charged particles with insulating capillary targets—The guiding effect. Progr. Surf. Sci. 2013, 88, 237–278. [Google Scholar] [CrossRef]
- Stolterfoht, N.; Yamazaki, Y. Guiding of charged particles through capillaries in insulating materials. Phys. Rep. 2016, 629, 1–107. [Google Scholar] [CrossRef]
- Schiessl, K.; Palfinger, W.; Lemell, C.; Burgdörfer, J. Simulation of guiding of highly charged projectiles through insulating nanocapillaries. Nucl. Instrum. Methods Phys. Res. B 2005, 232, 228–234. [Google Scholar] [CrossRef]
- Schiessl, K.; Palfinger, W.; Tökési, K.; Nowotny, H.; Lemell, C.; Burgdörfer, J. Simulation of guiding of multiply charged projectiles through insulating capillaries. Phys. Rev. A 2005, 72, 062902. [Google Scholar] [CrossRef]
- Schiessl, K.; Lemell, C.; Tökési, K.; Burgdörfer, J. Energy dependence of ion guiding through nanocapillaries. J. Phys. Conf. Ser. 2009, 163, 012081. [Google Scholar] [CrossRef]
- Pokhil, G.P.; Vokhmyanina, K.A. Drift Model of Ion Beam Guiding Using Capillaries. J. Surf. Investig. X-ray Synchrotron Neutron Tech. 2008, 2, 237–240. [Google Scholar] [CrossRef]
- Stolterfoht, N. Simulation and analysis of ion guiding through a nanocapillary in insulating polymers. Phys. Rev. A 2013, 87, 012902. [Google Scholar] [CrossRef]
- Stolterfoht, N. Simulation and analytic models of ion guiding through a nanocapillary in insulating polymers. Phys. Rev. A 2013, 87, 032901. [Google Scholar] [CrossRef]
- Liu, S.D.; Zhao, Y.T.; Wang, Y.Y. Simulations of guiding of low-energy ions through a single nanocapillary in insulating materials. Chin. Phys. B 2017, 26, 106104. [Google Scholar] [CrossRef]
- Frenkel, J. On pre-breakdown phenomena in insulators and electronic semi-conductors. Phys. Rev. 1938, 54, 647–648. [Google Scholar] [CrossRef]
- Giglio, E.; Tökési, K.; DuBois, R.D. Relaxation dynamics of charge patches formed inside an insulating capillary by ion impact. Nucl. Instrum. Methods Phys. Res. B 2019, 460, 234. [Google Scholar] [CrossRef]
- Giglio, E. Charge relaxation rates in insulating straight capillaries. Phys. Rev. A 2020, 101, 052707. [Google Scholar] [CrossRef]
- Skog, P.; Zhang, H.; Schuch, R. Evidence of sequentially formed charge patches guiding ions through nanocapillaries. Phys. Rev. Lett. 2008, 101, 223202. [Google Scholar] [CrossRef]
- Kanai, Y.; Hoshino, M.; Kambara, T.; Ikeda, T.; Hellhammer, R.; Stolterfoht, N.; Yamazaki, Y. Guiding of slow highly charged ions through nanocapillaries - dynamic aspect. J. Phys. Conf. Ser. 2009, 194, 012068. [Google Scholar] [CrossRef]
- Stolterfoht, N.; Hellhammer, R.; Fink, D.; Sulik, B.; Juhász, Z.; Bodewits, E.; Dang, H.M.; Hoekstra, R. Dynamic properties of ion guiding through nanocapillaries in an insulating polymer. Phys. Rev. A 2009, 79, 022901. [Google Scholar] [CrossRef]
- Zhang, H.; Skog, P.; Schuch, R. Dynamics of guiding highly charged ions through SiO2 nanocapillaries. Phys. Rev. A 2010, 82, 052901. [Google Scholar] [CrossRef]
- Stolterfoht, N.; Hellhammer, R.; Sulik, B.; Juhász, Z.; Bayer, V.; Trautmann, C.; Bodewits, E.; Hoekstra, R. Evidence of blocking effects on 3-keV Ne7+ ions guided through nanocapillaries in polycarbonate. Phys. Rev. A 2011, 83, 062901. [Google Scholar] [CrossRef]
- Unipan, M.; Robin, A.; Winters, D.F.A.; Morgenstern, R.; Hoekstra, R. Probing local spin ordering at surfaces by He2+ ions. Phys. Rev. A 2006, 74, 062901. [Google Scholar] [CrossRef]
- Stolterfoht, N.; Hellhammer, R.; Bundesmann, J.; Fink, D. Scaling laws for guiding of highly charged ios through nanocapillaries in an insulating polymer. Phys. Rev. A 2008, 77, 032905. [Google Scholar] [CrossRef]
- Gill, W.D. Drift mobilities in amorphous charge transfer complexes of trinitrofluorenone and poly-n-vinylcarbazole. J. Appl. Phys. 1972, 43, 5033–5040. [Google Scholar] [CrossRef]
- Davies, D.K. Carrier transport in polyethene. J. Phys. D 1972, 5, 162–168. [Google Scholar] [CrossRef]
- Hayashi, K.; Yoshino, K.; Inuishi, Y. Carrier mobilty in insulating polymers measured by time of flight method. Jpn. J. Appl. Phys. 1975, 14, 39–45. [Google Scholar] [CrossRef]
- Stolterfoht, N. Simulations of ion guiding through a straight macrocapillary: interpretation of an experiment and comparison with nanocapillaries. Phys. Rev. A 2014, 89, 062706. [Google Scholar] [CrossRef]
- Zhang, H.; He, S.; Chen, C.; Zheng, W.; Yan, Q. Electrical Conductivity of Melt Compounded Functionalized Graphene Sheets Filled Polyethyleneterephthalate Composites. In Physics and Applications of Graphene; Mikhailov, S., Ed.; IntechOpen: Rijeka, Croatia, 2011; Chapter 16. [Google Scholar] [CrossRef]
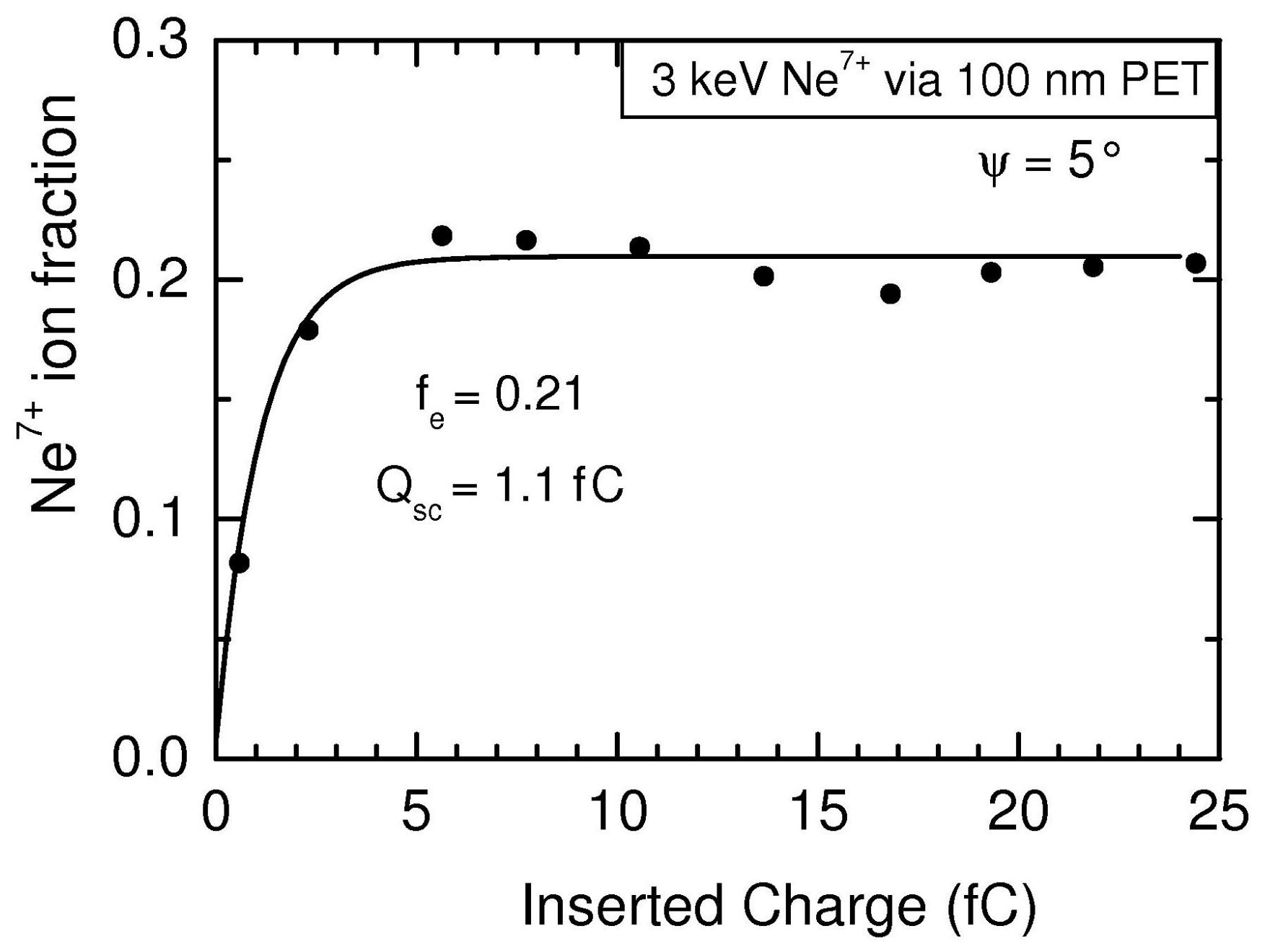
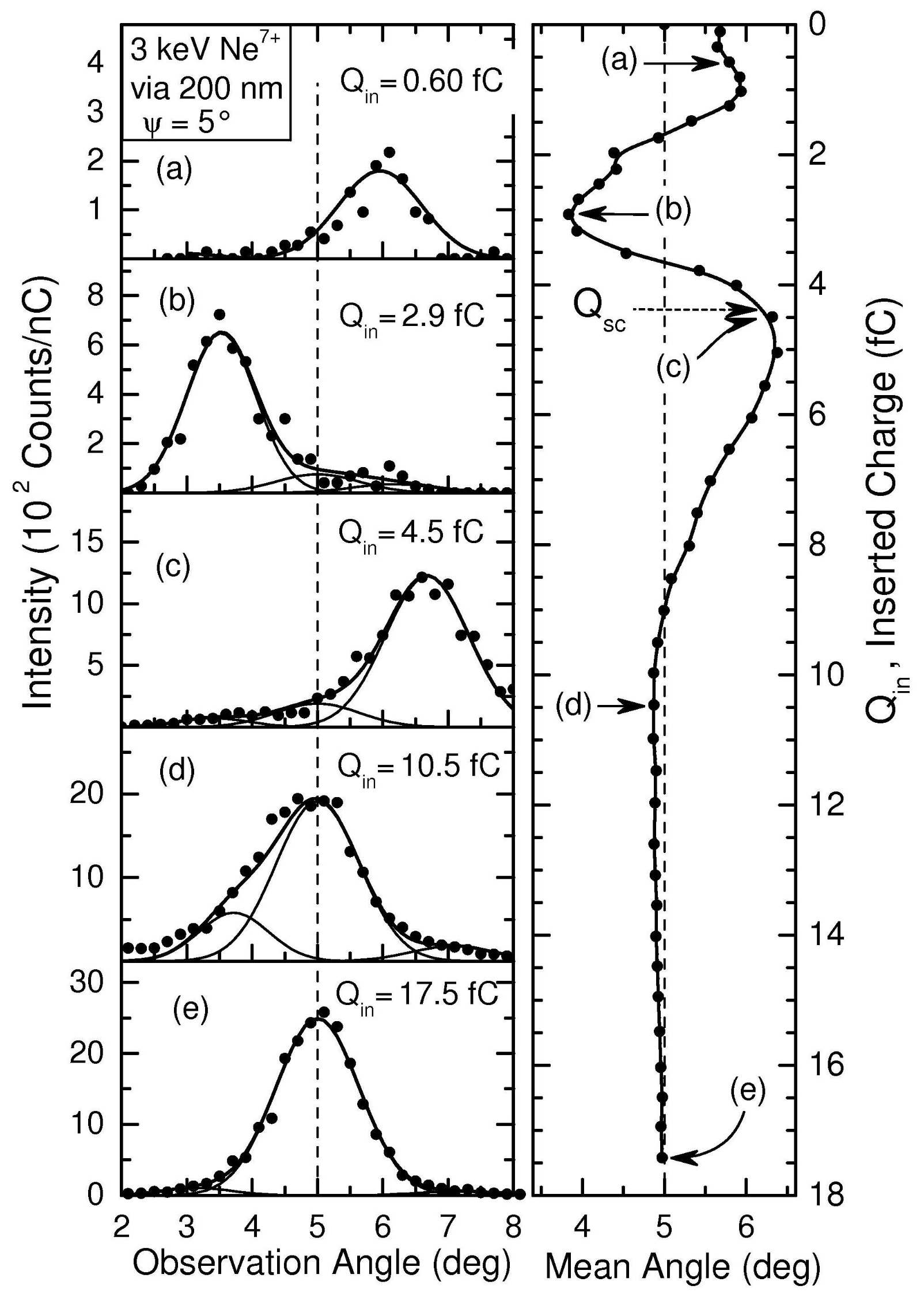
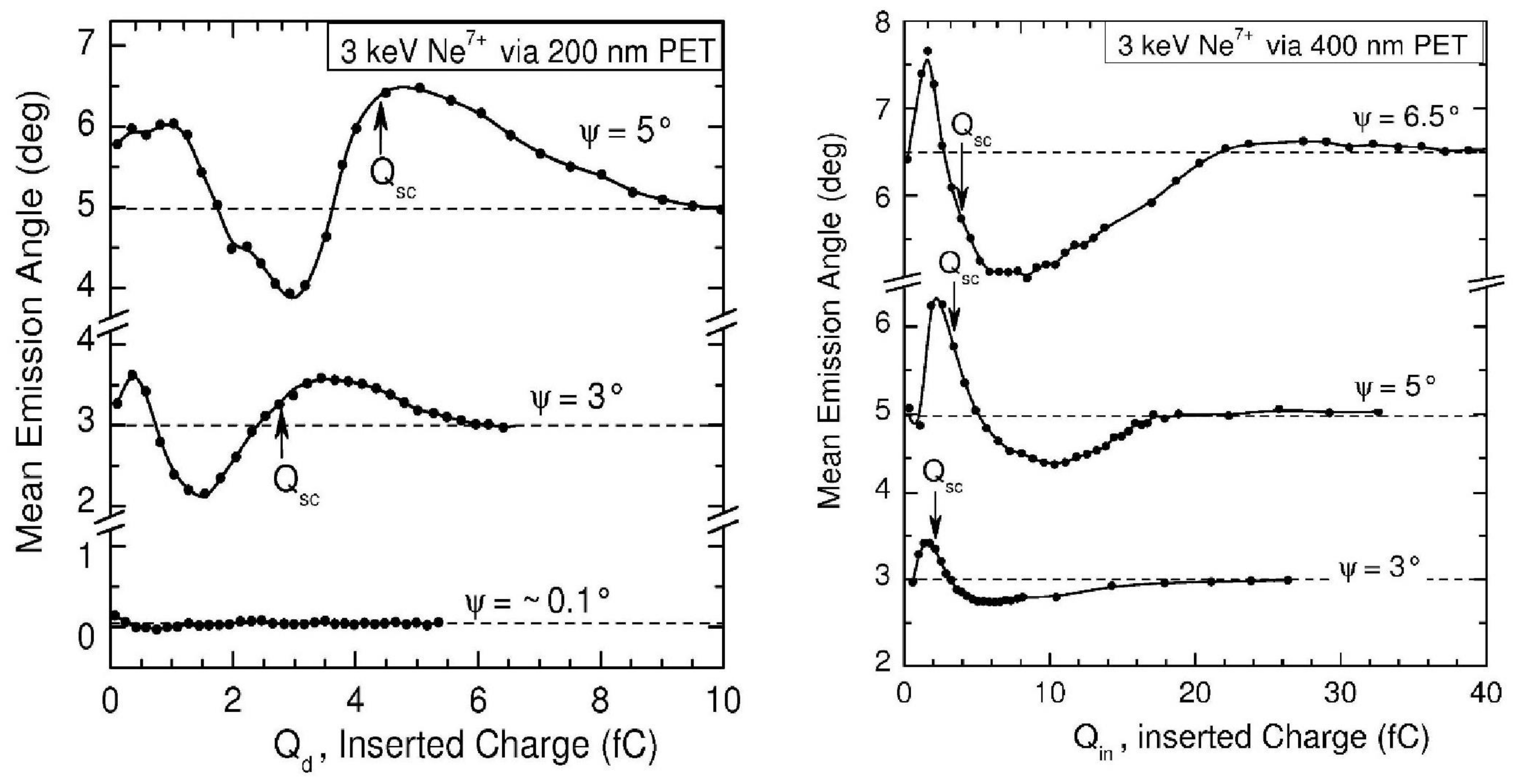
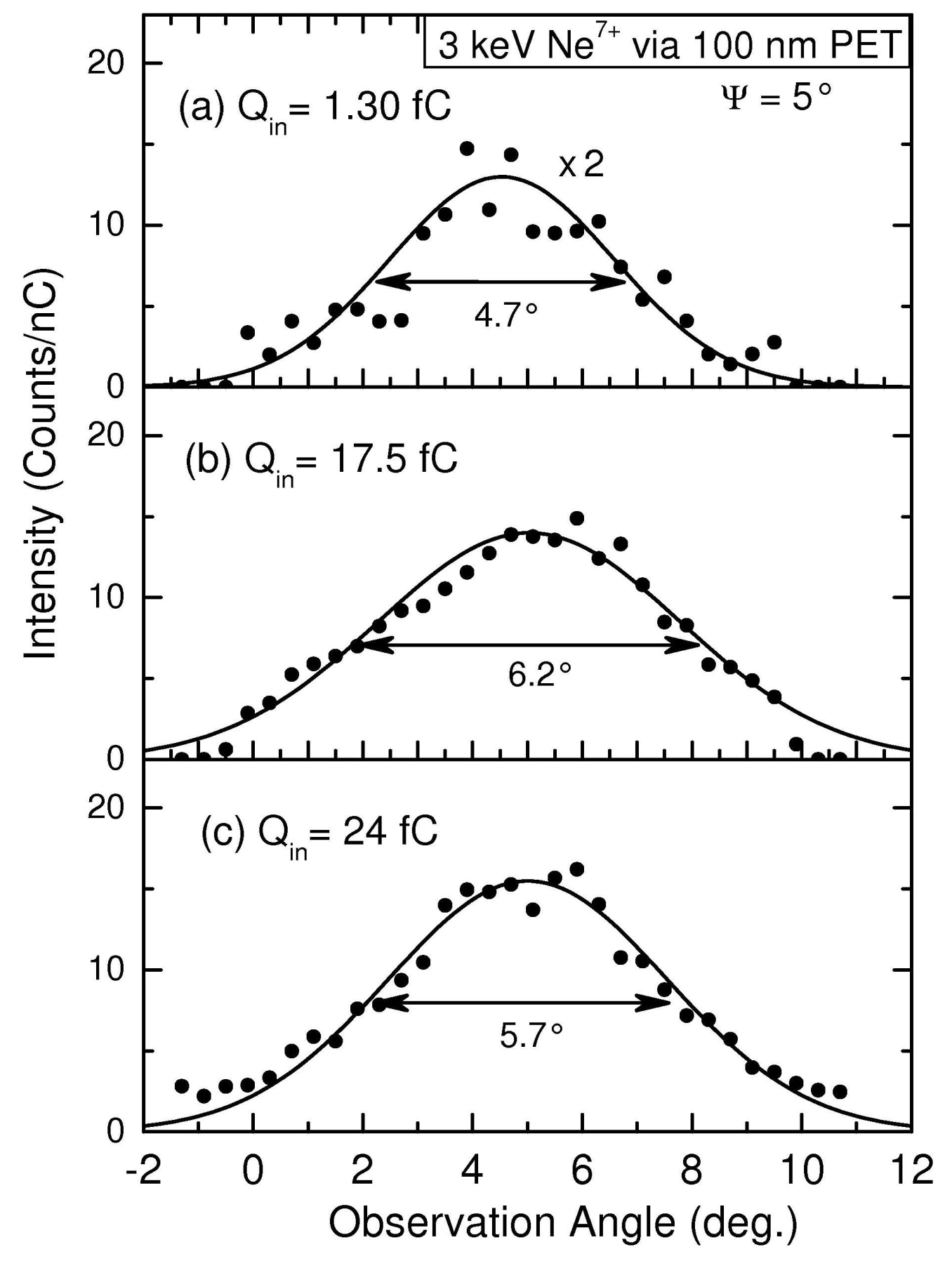
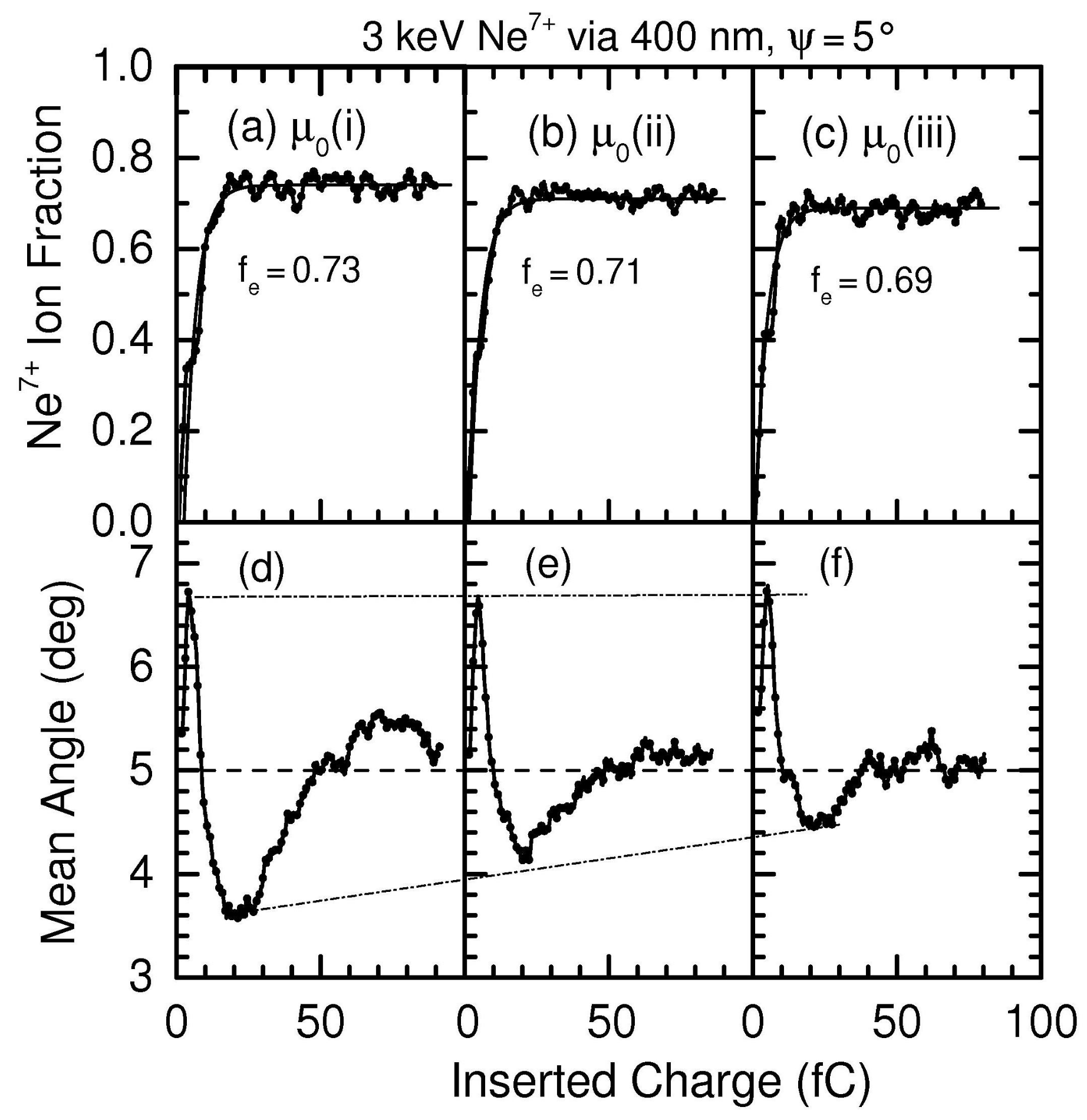
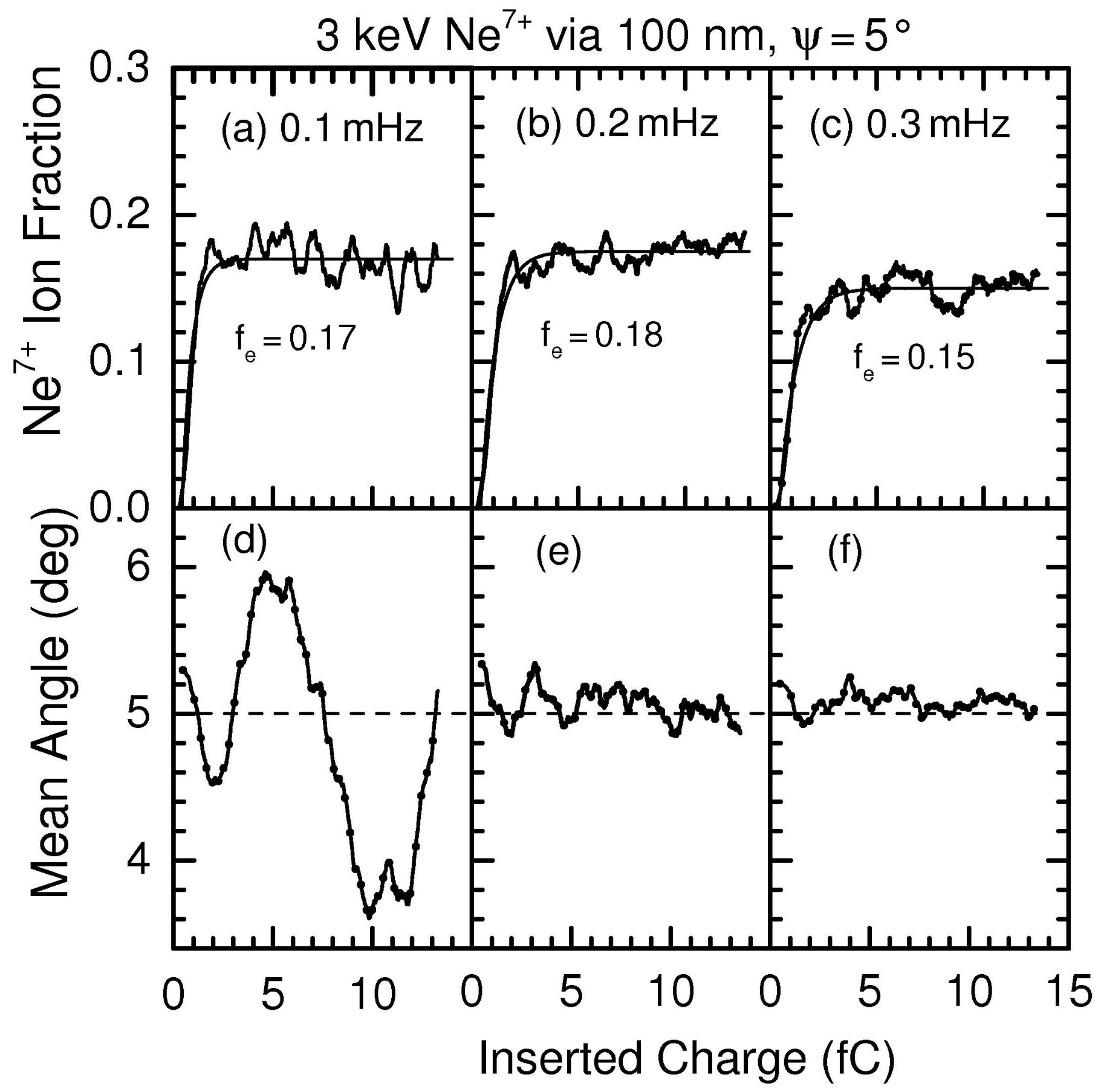
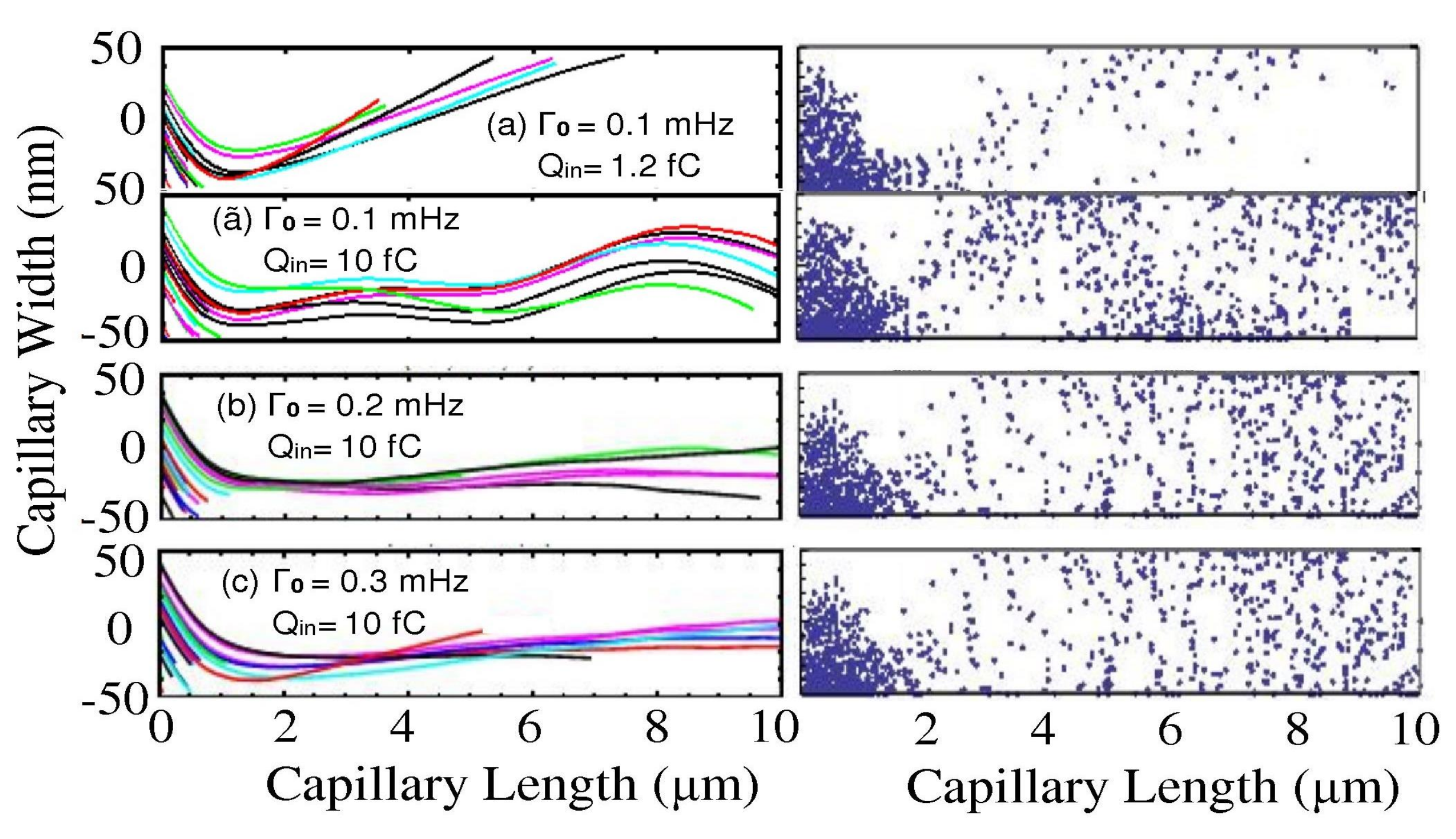
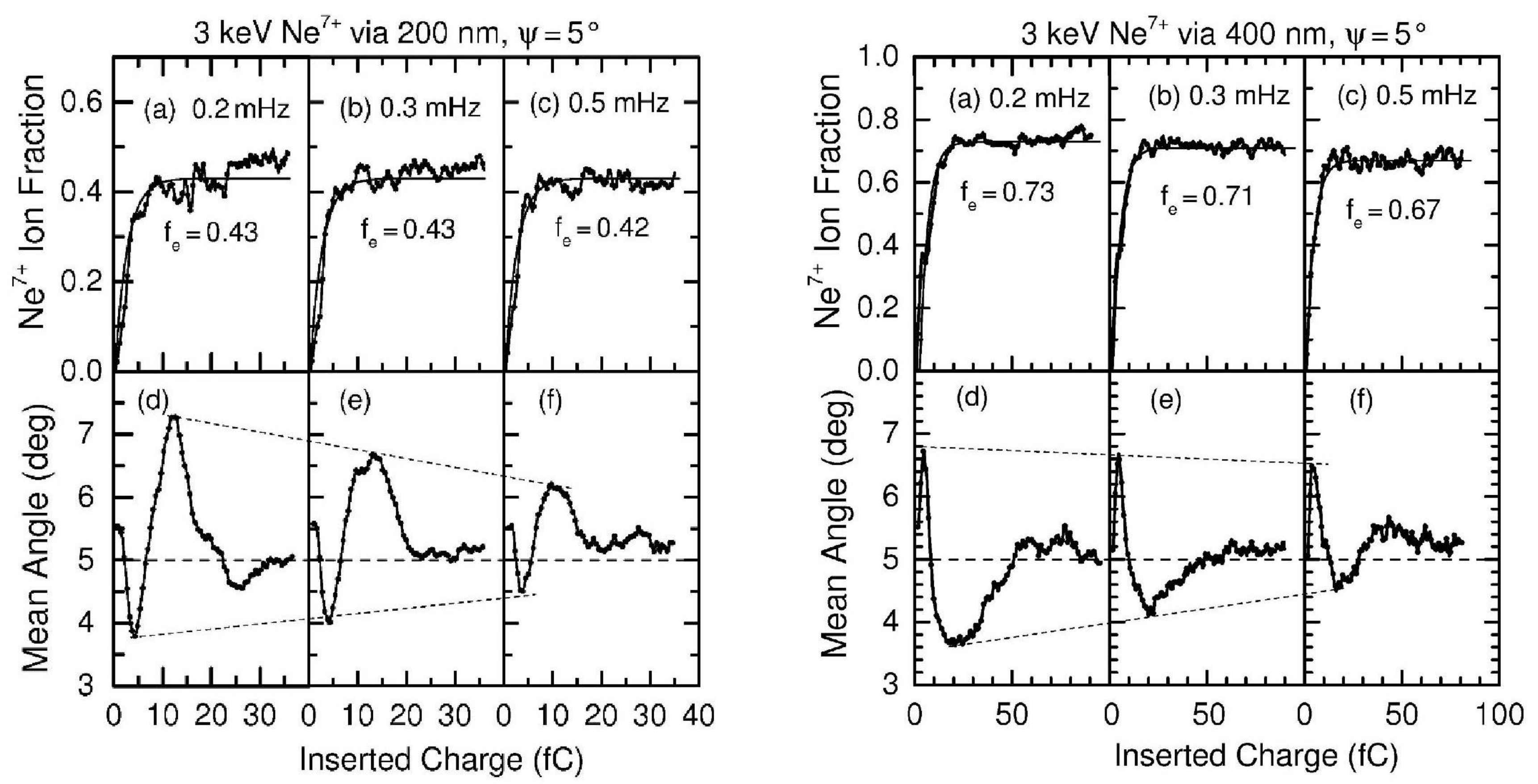
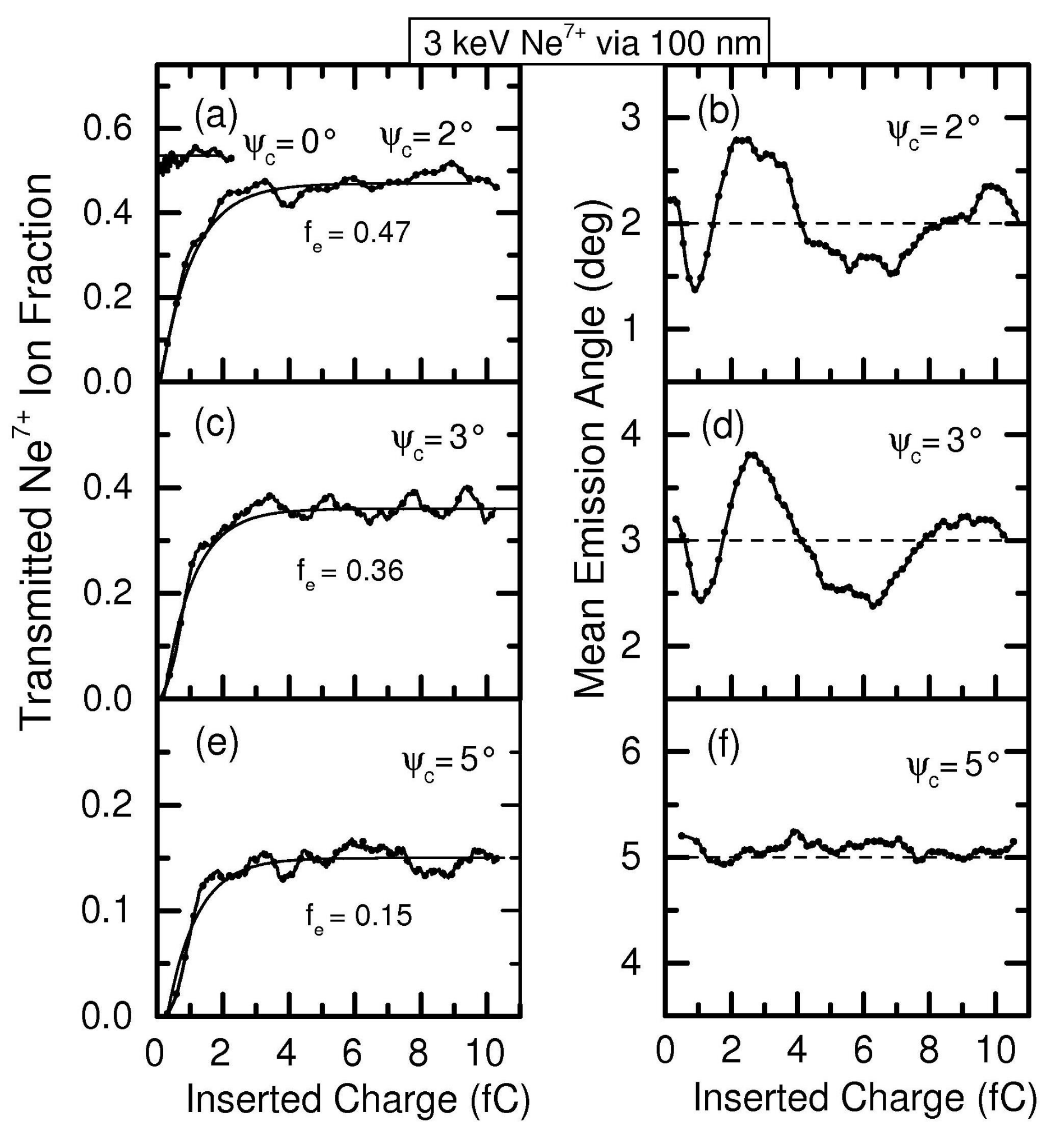
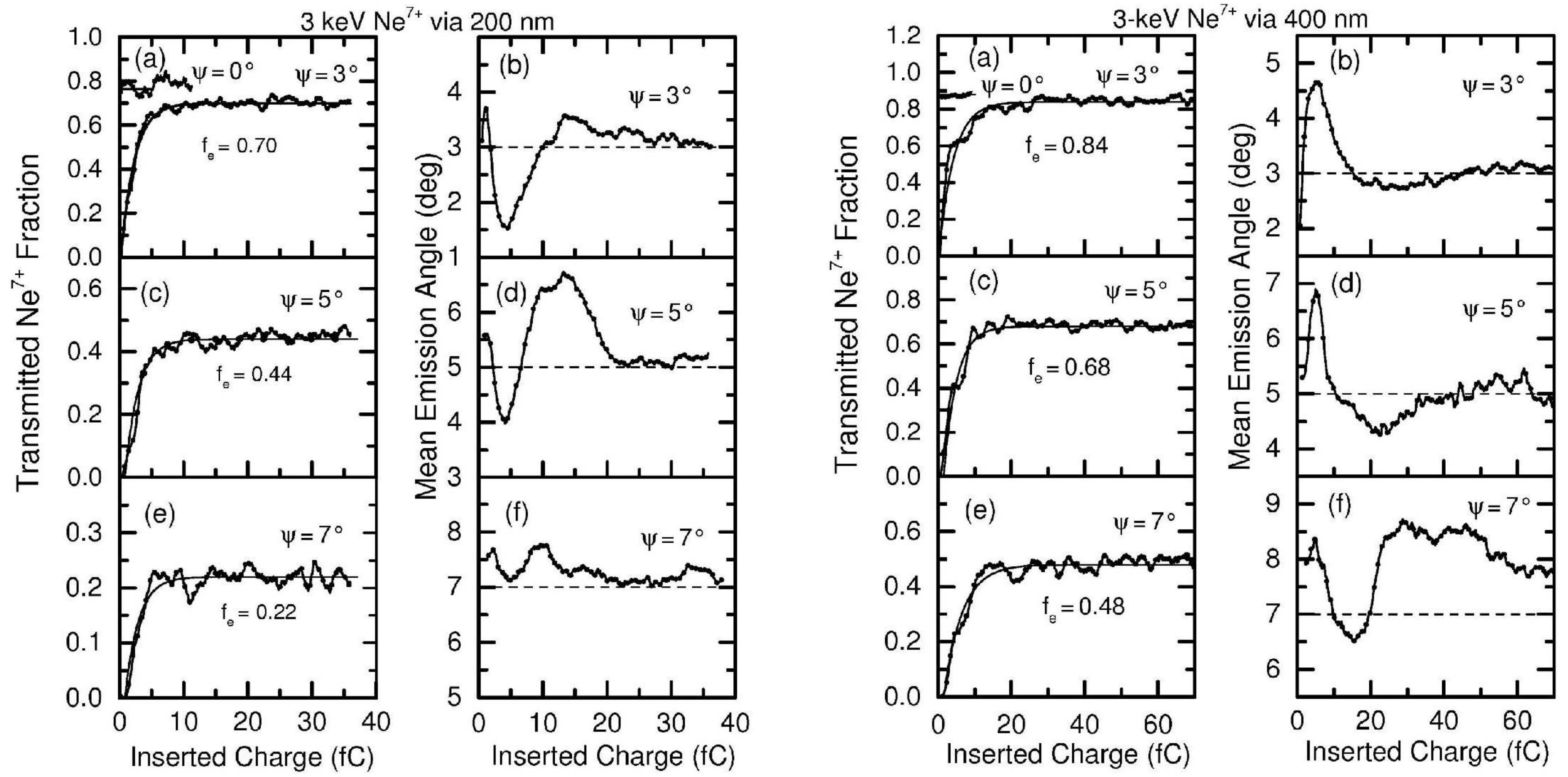
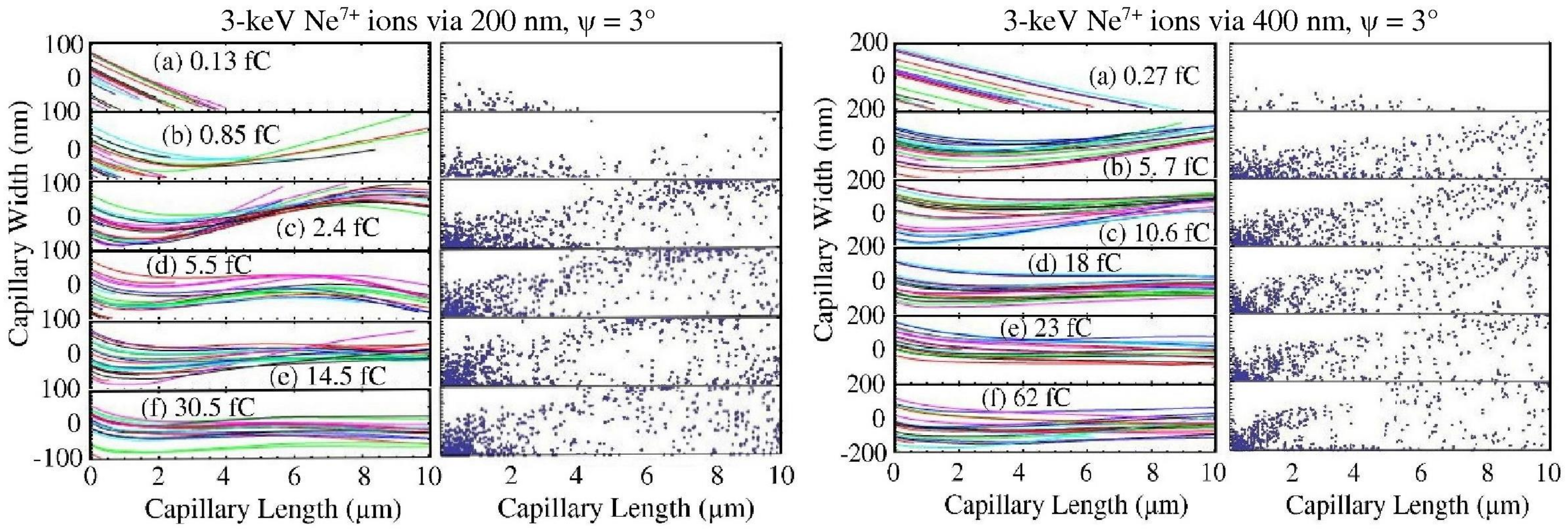
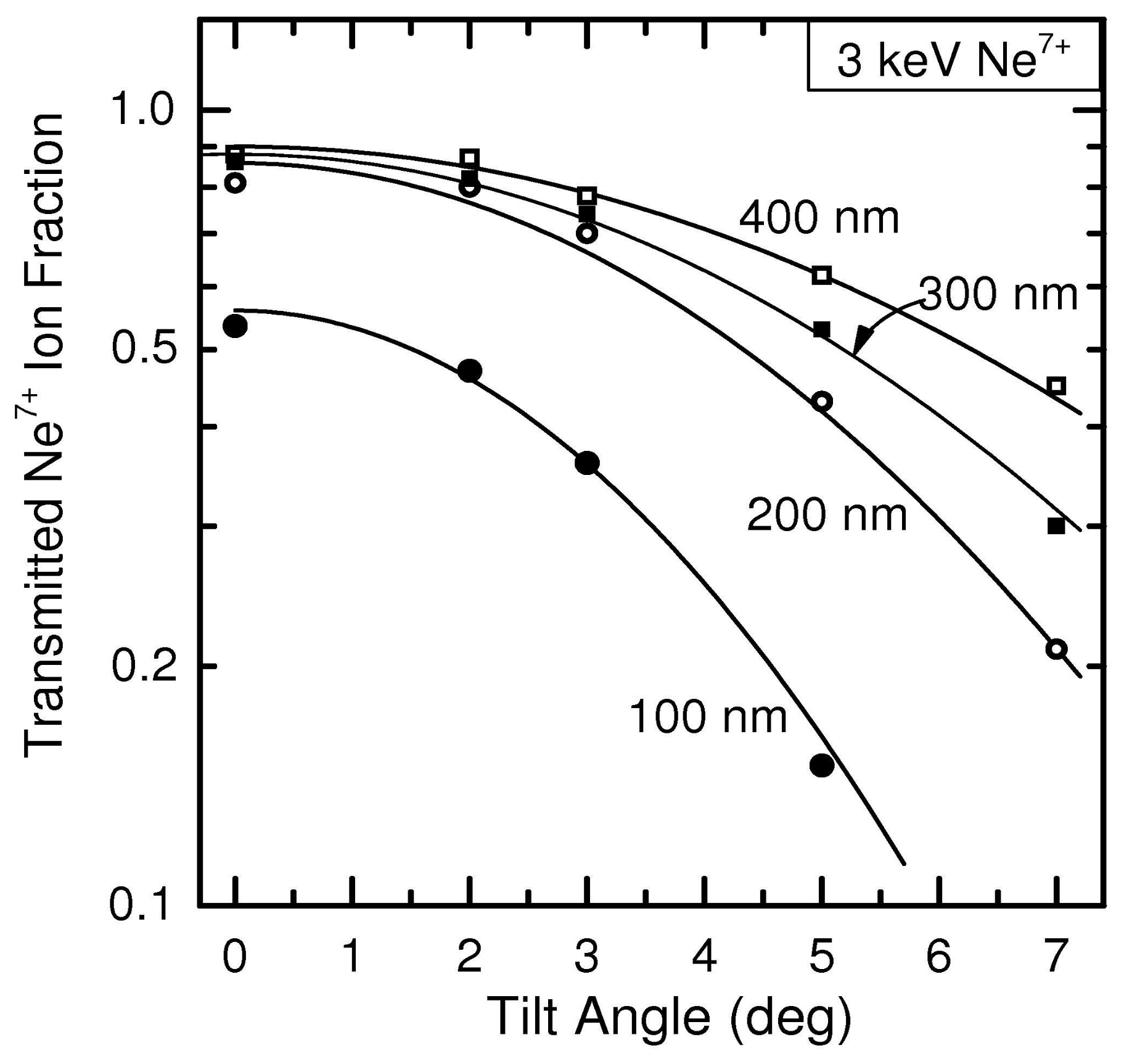
| Ion Energy, | Tot. Current, | Time, | Diameter | Length, L | Tilt Angle, |
|---|---|---|---|---|---|
| 3 keV | 100 pA | 1.4–22.4 s | 100–400 nm | 10–12 μm | 0°, 3°, 5°, 7° |
| Field, (V/μm) | 1.33 |
| Mobility, (nm/V·s ) | 0.001–0.01 |
| Rate, (mHz) | 0.1–0.5 |
| Notation | Mobility (nm/V·s) |
|---|---|
| (i) | 0.001 |
| (ii) | 0.003 |
| (iii) | 0.01 |
| d (nm) | (nm/V·s) | (mHz) | (mHz) | (mHz) | (mHz) | |
|---|---|---|---|---|---|---|
| 100 | 0.001 | 0.3 | 0.15 | 0.68 | 4.5 | 0.83 |
| 200 | 0.003 | 0.3 | 0.21 | 0.85 | 4.0 | 1.06 |
| 300 | 0.003 | 0.3 | 0.25 | 1.02 | 4.1 | 1.27 |
| 400 | 0.003 | 0.3 | 0.26 | 1.10 | 4.2 | 1.36 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stolterfoht, N. Simulations of Ion-Guiding Through Insulating Nanocapillaries of Varying Diameter: Interpretation of Experimental Results. Atoms 2020, 8, 48. https://doi.org/10.3390/atoms8030048
Stolterfoht N. Simulations of Ion-Guiding Through Insulating Nanocapillaries of Varying Diameter: Interpretation of Experimental Results. Atoms. 2020; 8(3):48. https://doi.org/10.3390/atoms8030048
Chicago/Turabian StyleStolterfoht, Nikolaus. 2020. "Simulations of Ion-Guiding Through Insulating Nanocapillaries of Varying Diameter: Interpretation of Experimental Results" Atoms 8, no. 3: 48. https://doi.org/10.3390/atoms8030048
APA StyleStolterfoht, N. (2020). Simulations of Ion-Guiding Through Insulating Nanocapillaries of Varying Diameter: Interpretation of Experimental Results. Atoms, 8(3), 48. https://doi.org/10.3390/atoms8030048




