Abstract
The opacity of the atmosphere of the Sun is due to processes such as Thomson scattering, bound–bound transitions and photodetachment (bound–free) of hydrogen and positronium ions. The well-studied free–free transitions involving photons, electrons, and hydrogen atoms are re-examined, while free–free transitions involving positrons are considered for the first time. Cross sections, averaged over a Maxwellian velocity distribution, involving positrons are comparable to those involving electrons. This indicates that positrons do contribute to the opacity of the atmosphere of the Sun. Accurate results are obtained because definitive phase shifts are known for electron–hydrogen and positron–hydrogen scattering.
1. Introduction
The variation of the solar spectral irradiance with wavelength shows the effects of bound–bound, bound–free, and free–free opacity of many elements in the solar atmosphere. In 1923, using a classical approach, Kramers [1] showed that the free–free absorption coefficient is given by
The solar medium is opaque between 4000 and 25000 Å because of various processes, such as Thomson scattering, bound–bound transitions, photodetachment (bound–free) or free–free transitions. In 1939, Wildt [2] suggested that an important source of opacity in the solar atmosphere could be due to the photodetachment of negative hydrogen ions:
The bound–free transitions explain the opaqueness of the Sun’s atmosphere between 4000 and 16,000 Å; beyond this range, free–free transitions account for the continuous spectrum of the Sun
If an electron with energy absorbs photon energy and the final energy of the electron in the continuum is , the change in energy is . These transitions also explain the opacity of late-type stellar atmospheres. Cross sections for bound–free and free–free transitions have been calculated by Chandrasekhar and Elbert [3] and Chandrasekhar and Breen [4], respectively. The cross section for free–free transition, given by the latter [4] is
where various quantities have the usual meaning and
The phase shifts and are the triplet and singlet phase shifts for the scattering of an electron from a hydrogen atom with momentum k. They were calculated using hybrid theory [5]. The present electron–hydrogen phase shifts are much more accurate compared to those used in earlier calculations for calculating cross sections for free–free transitions. The hybrid theory takes into account exchange, short-range correlations, and long-range correlations, at the same time. There are a number of earlier calculations. For example, the calculations in ref. [6] include only long-range correlations, while in ref. [7], only short-range correlations could be considered.
It has been known that there are positrons present in the Sun [8] and in interstellar space, as indicated by the detection of the 0.511 MeV line from the center of the galaxy due to the annihilation of the positron and electron pairs [9,10]. Positrons are produced due to various processes: when two protons collide, during the formation of 3He nuclei, the decay of radioactive nuclei, and the decay of positive pions to muons, which further decay into positrons [11]. Positrons produced by solar flares can reach the solar atmosphere and modulate the radiant flux passing through them during their lifetime.
Once positrons are available, the photodetachment of negative positronium ions
and free–free transitions of positrons on H are possible:
hν + Ps− → e− + Ps
For the latter, there is only one phase shift for a positron with an incident momentum k and Equation (6) takes the form
The positron–hydrogen phase shifts (δk) were calculated using hybrid theory [12]. An earlier calculation of reference [13] included only short-range correlations.
The cross section for photodetachment of H− is given by Ohmura and Ohmura [14] as
where and .
Photodetachment cross sections of negative positronium ions [15] were calculated using Ps− wave functions of the form used by Ohmura and Ohmura [14] for the negative hydrogen ion. This cross section is written in the form
where , and because is the binding energy, this gives a value of 0.024010 Ry [15]. In the above equations, k is the momentum of the outgoing electron. A measurement of this cross section was reported in [16].
We list the cross sections for bound–free and free–free transitions for electrons and positrons in Table 1 (and show them in Figure 1), where we have assumed a temperature of 6300 K and used the H−/H ratio given by Wheeler and Wildt [17]. This temperature has been used for many years as representative of a typical cool star, including the Sun at an optical depth of approximately 1. We see that the contribution of positrons cannot be neglected in calculations of the opacity of the Sun’s atmosphere.

Table 1.
Comparison of bound–free (σbf) and free–free (σff) cross sections (cm2) for electrons and positrons, T = 6300 K.
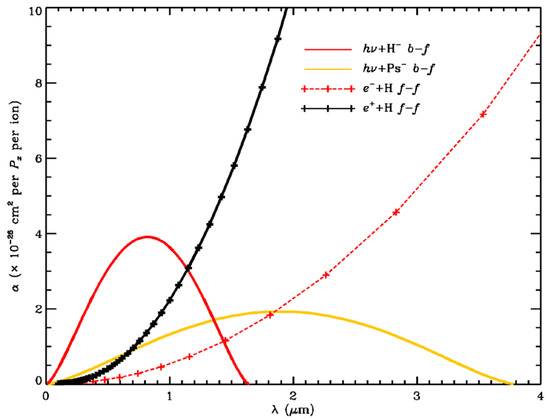
Figure 1.
Absorption coefficients of four scattering processes with T = 6300 K (θ = 0.8). The H− bound–free transitions are described by Equation (10) and the Ps− b–f transitions by Equation (11). The b–f absorption coefficients are formed by multiplying the cross sections by either the fraction of H−/H or Ps−/Ps, given by the Saha equation. The free–free transitions are for electrons on H (Equations (4) and (6)) and positrons on H (Equations (4) and (9)). The H b–f and f–f absorption coefficients are in units of 10−26 cm2 per Pe per H− atom, where Pe is the electron pressure. The Ps− bound–free coefficients are in units of 10−26 cm2 per Pe per Ps− atom. The positron–H free–free coefficients are in units of 10−26 cm2 per Pe+ per H− atom, where Pe+ is the thermal pressure of positrons.
Our results are shown in Figure 1. An examination of Figure 1 shows several effects. The most noticeable effect of positrons on the emergent spectrum would be an increase in the brightness temperature of wavelengths longer than 1 μm. The positron–H free–free opacity is larger than the electron–H free–free opacity at those wavelengths. The second effect is when the Ps abundance becomes appreciable and a broad region of opacity appears between 0.1 and 4 μm. A third effect, positron–Ps free–free transitions, will be described in a future work.
2. Conclusions
In addition to bound–free transitions, free–free transitions are important in the solar as well as stellar atmospheres. We have calculated cross sections for these processes and have shown that the free–free transitions involving electrons dominate at wavelengths longer than 16,000 Å. The same processes are present when positrons are involved in transitions instead of electrons. Two observable quantities, the locations of the maximum in the bound–free opacity and the transition from dominance of bound–free to free–free opacity, are both located at longer wavelengths when positrons and the negative positronium ions are considered. The presence of these shifted features would be a unique marker of an object with a measurable number of positrons in its atmosphere. Processes involving positrons cannot be neglected and their contribution to opacity could be comparable to those involving electrons.
Author Contributions
A.K.B. and W.D.P. contributed equally. All authors have read and agreed to the published version of the manuscript.
Funding
No funding was received for this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kramers, H.A. On the theory of X-ray absorption and the continuous X-ray spectrum. Philos. Mag. 1923, 46, 836–871. [Google Scholar] [CrossRef]
- Wildt, R. Electron affinity in astrophysics. Astrophys. J. 1939, 89, 295–301. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; Elbert, D.D. On the continuous absorption coefficient of the negative hydrogen ion. IV. Astrophys. J. 1958, 128, 633. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; Breen, F.H. On the continuous absorption coefficient of the negative hydrogen ion. Astrophys. J. 1946, 104, 430. [Google Scholar] [CrossRef]
- Bhatia, A.K. Hybrid theory of electron-hydrogen scattering. Phys. Rev. A 2007, 75, 032713. [Google Scholar] [CrossRef]
- Temkin, A.; Lamkin, J.C. Application of the Method of Polarized Orbitals to the Scattering of Electrons from Hydrogen. Phys. Rev. 1961, 121, 788. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Temkin, A. Complex correlation Kohn-T method of calculating total and elastic cross sections: Electron-Hydrogen elastic scattering. Phys. Rev. A 2001, 64, 032709. [Google Scholar] [CrossRef]
- Gopalswamy, N. Positron processes in the Sun. Atoms 2020, 8, 14. [Google Scholar] [CrossRef]
- Knödlseder, J.; Jean, P.; Lonjou, V.; Weidenspointner, G.; Guessoum, N.; Gillard, W.; Skinner, G.; von Ballmoos, P.; Vedrenne, G.; Roques, J.-P.; et al. The all-sky distribution of 511 keV electron-positron annihilation emission. Astron. Astrophys. 2005, 441, 513–532. [Google Scholar] [CrossRef]
- Leventhal, M. Recent Balloon Observation of the Galactic Center 511 keV annihilation line. Adv. Space Res. 1991, 11, 157. [Google Scholar] [CrossRef]
- Murphy, R.J.; Share, G.H.; Skibo, J.G.; Kozlovsky, B. The physics of positron annihilation in the solar atmosphere. Astrophys. J. Suppl. Ser. 2005, 161, 495. [Google Scholar] [CrossRef]
- Bhatia, A.K. Positron-Hydrogen scattering, annihilation and positronium formation. Atoms 2016, 4, 27. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Temkin, A.; Drachman, R.J.; Eiserike, H. Generalized Hylleraas calculations of Positron-Hydrogen Scattering. Phys. Rev. A 1971, 3, 1328. [Google Scholar] [CrossRef]
- Ohmura, T.; Ohmura, H. Electron-Hydrogen scattering at low energies. Phys. Rev. 1960, 118, 154. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Drachman, R.J. Photodetachment of positronium negative ion. Phys. Rev. A 1985, 32, 1745. [Google Scholar] [CrossRef] [PubMed]
- Michishio, K.; Tachibana, T.; Terabe, H.; Igarashi, A.; Wada, K.; Kuga, T.; Yagishita, A.; Hyodo, T.; Nagashima, Y. Photodetachment of positronium negative ions. Phys. Rev. Lett. 2011, 106, 153401. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, J.A.; Wildt, R. The absorption coefficient of the free-free transitions of the negative Hydrogen ion. Astrophys. J. 1942, 95, 281. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).