Radial and Angular Electron Ejection Patterns of Two-Electron Quantum Dots in THz Fields
Abstract
1. Introduction
2. Calculational Method of the Two-Electron QD Dynamics
2.1. Calculation of the QD Electronic Structure
2.2. Quantum Dot Laser Field Dynamics
3. Two-Electron Joint Radial Probability Distributions
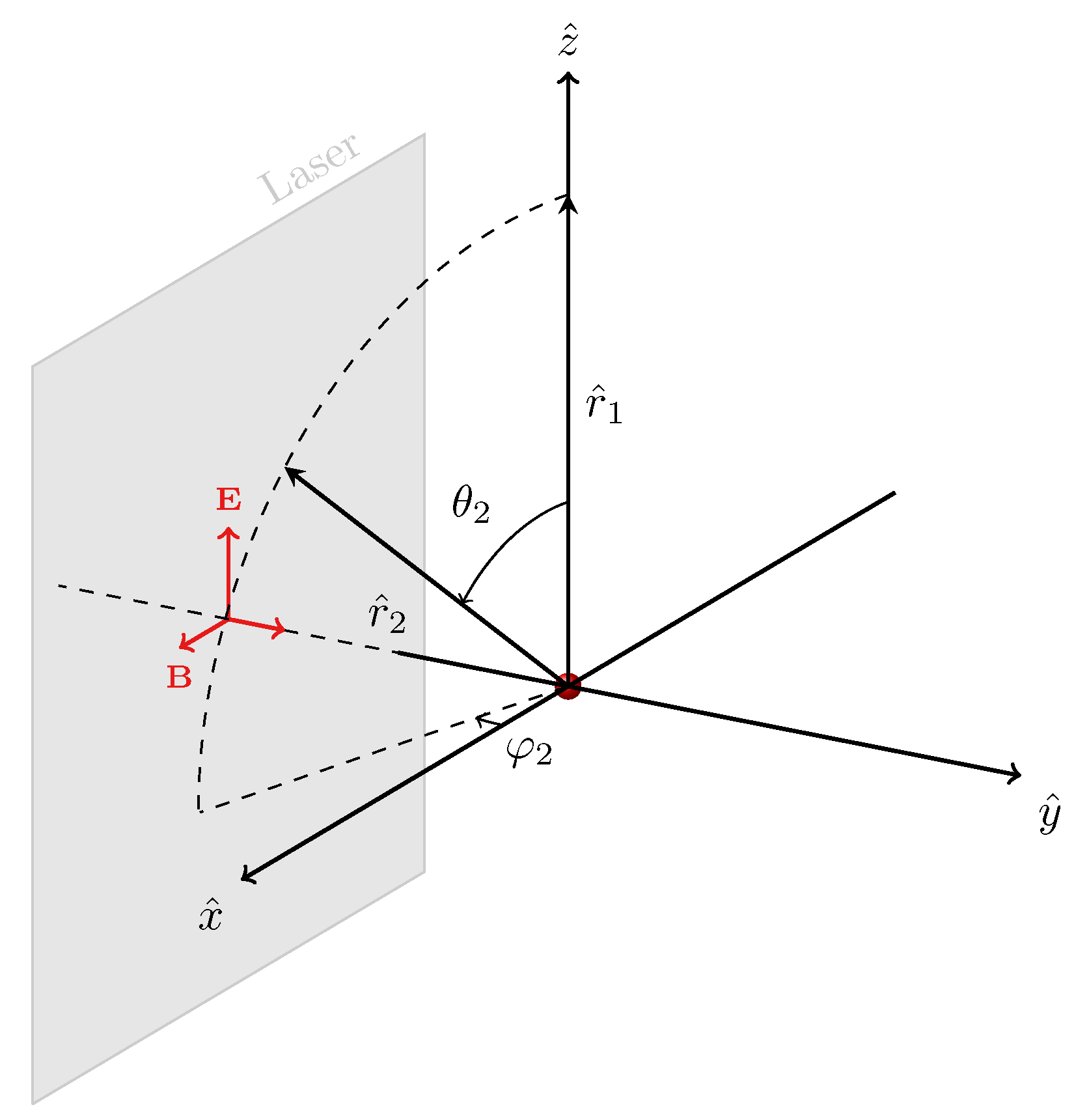
4. Two-Electron Joint Angular Probability Distribution
5. Results and Discussion
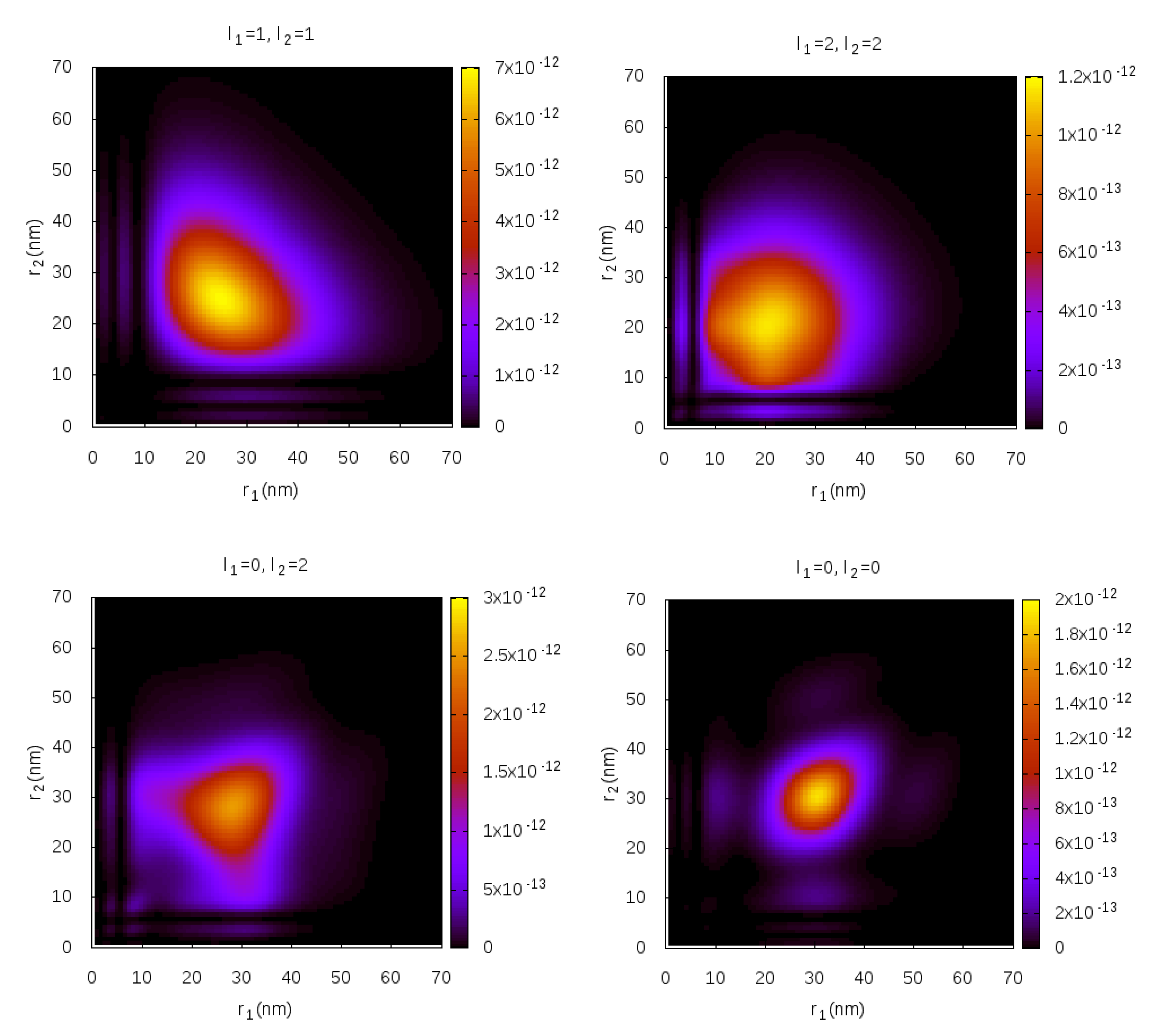
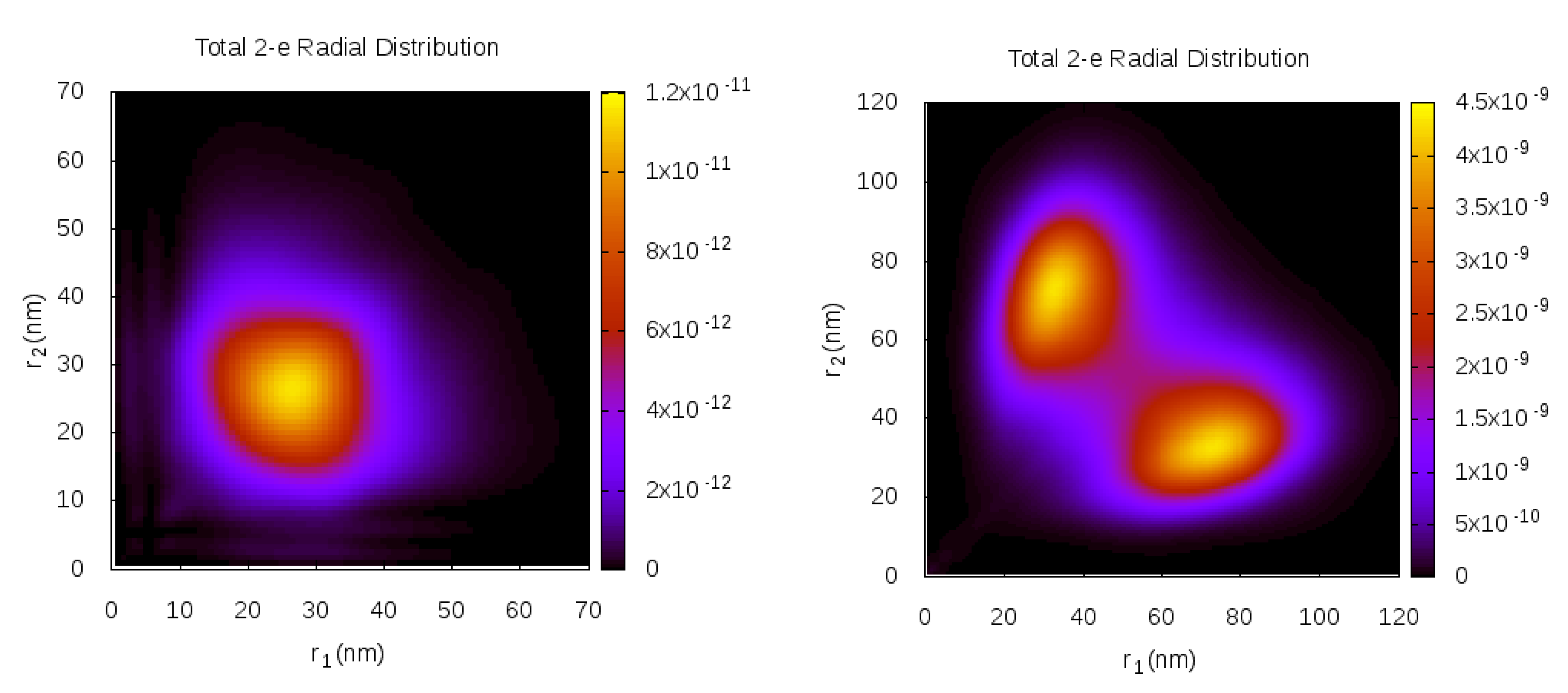
5.1. Radial Distributions
5.1.1. Direct Double Ionization Regime ( nm)
5.1.2. Sequential Double Ionization Regime ( nm)
5.2. Angular Distributions
Direct Double Ionization Regime (RQ = 4.6 nm)
5.3. Sequential Double Ionization Regime ( nm)
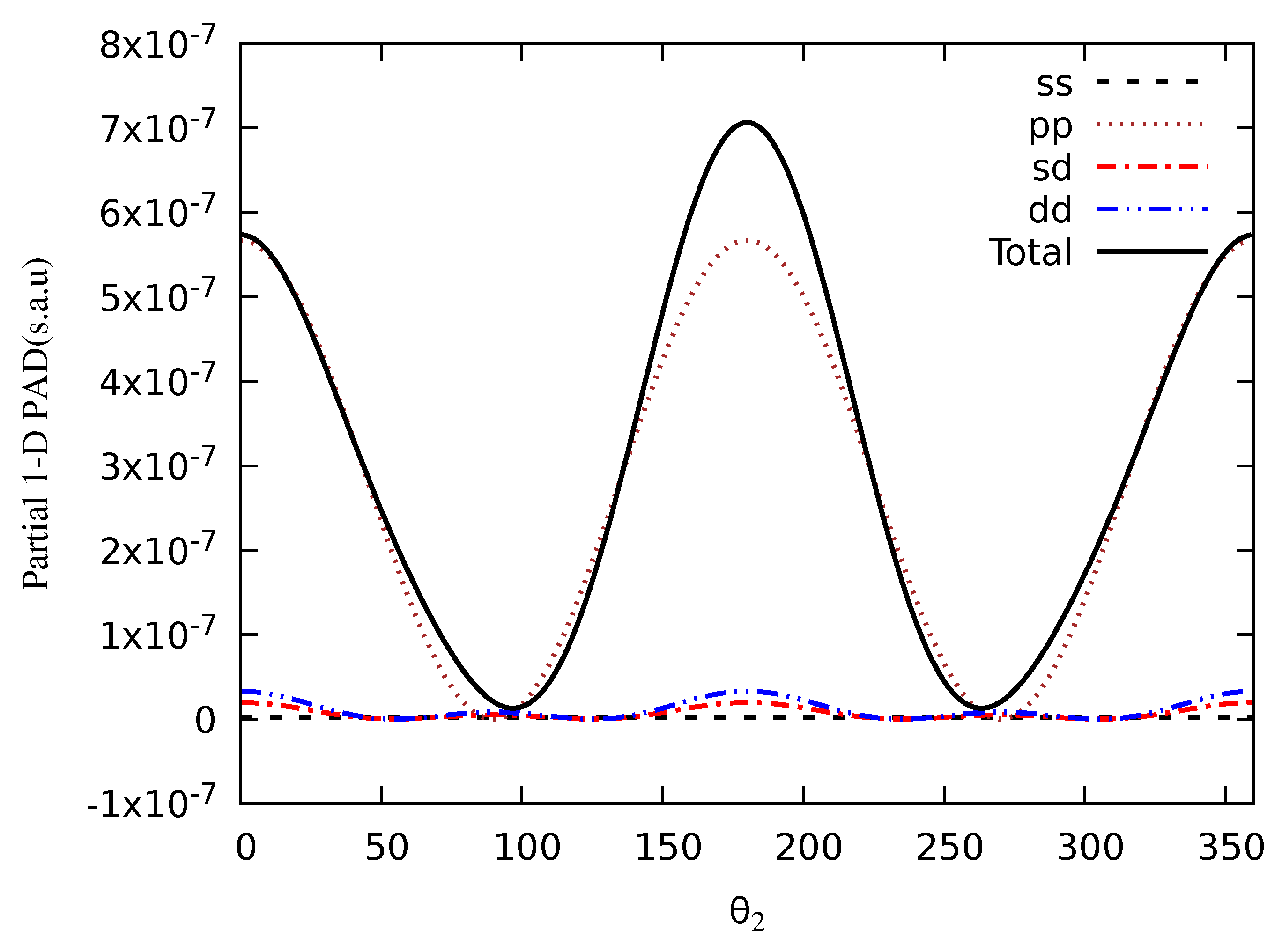
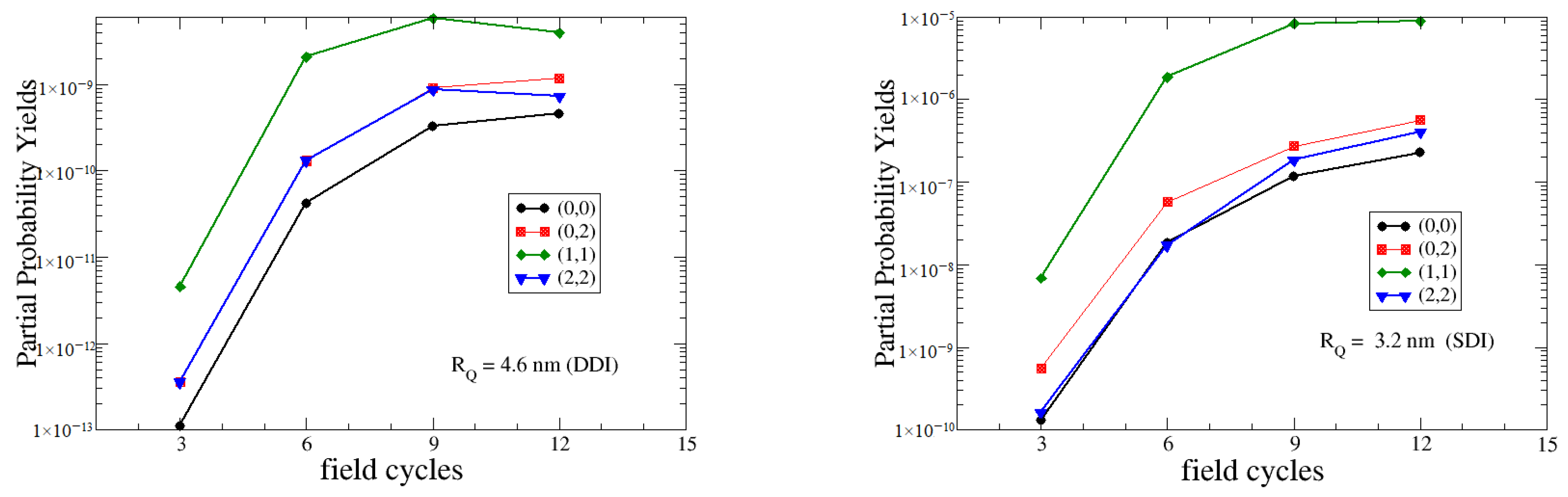
6. Partial Wave DI Probabilities
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SDI | Sequential Double Ionization |
| DDI | Direct Double Ionization |
| e-e | electron–electron |
| CI | Configuration Interaction |
References
- Harrison, P.; Vavanis, A. Quantum Wells, Wires and Dots, 4th ed.; John Wiley and Sons: Chichester, UK, 2016. [Google Scholar]
- Chakraborty, T. Quantum Dots, a Survey of the Properties of Artificial Atoms; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Mukamel, S. Principles of Nonlinear Optical Spectroscopy; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Langbein, W.; Patton, B. Heterodyne spectral interferometry for multidimensional nonlinear spectroscopy of individual quantum systems. Opt. Lett. 2006, 31, 1151. [Google Scholar] [CrossRef] [PubMed]
- Fejer, M.M.; Yoo, S.J.B.; Byer, R.L.; Harwit, A.; Harris, J.S., Jr. Observation of extremely large quadratic susceptibility at 9.6–10.8 μm in electric-field-biased AlGaAs quantum wells. Phys. Rev. Lett. 1989, 62, 1041. [Google Scholar] [CrossRef] [PubMed]
- Sirtori, C.; Capasso, F.; Sivco, D.L.; Cho, A.Y. Giant, triply resonant, third-order nonlinear susceptibility in coupled quantum wells. Phys. Rev. Lett. 1992, 68, 1010. [Google Scholar] [CrossRef] [PubMed]
- Heyman, J.N.; Craig, K.; Galdrikian, B.; Sherwin, M.S.; Campman, K.; Hopkins, P.F.; Gossard, A.C. Resonant harmonic generation and dynamic screening in a double quantum well. Phys. Rev. Lett. 1994, 72, 2183. [Google Scholar] [CrossRef] [PubMed]
- Gurnick, M.K.; DeTemple, T.A. Synthetic nonlinear semiconductors. IEEE J. Quant. Electr. 1983, 19, 791. [Google Scholar] [CrossRef]
- Indjin, D.; Ikonić, Z.; Milanović, V.; Radovanovi, J. Optimization of Resonant Second- and Third- Order Nonlinearities in Step and Continuously Graded Semiconductor Quantum Wells. IEEE J. Quant. Electr. 1998, 34, 795. [Google Scholar] [CrossRef]
- Catoire, F.; Bachau, H.; Wang, Z.; Blaga, C.; Agostini, P.; DiMauro, L.F. Wannier Representation of Intraband High-Order Harmonic Generation. Phys. Rev. Lett. 2018, 121, 143902. [Google Scholar] [CrossRef]
- Terzis, A.F.; Paspalakis, E. High-order harmonic generation in a two-electron quantum dot molecule. J. Appl. Phys. 2005, 97, 023523. [Google Scholar] [CrossRef]
- Bachau, H.; Cormier, E.; Decleva, P.; Hansen, J.E.; Martín, F. Applications of B-splines in atomic and molecular physics. Rep. Prog. Phys. 2001, 64, 1815–1943. [Google Scholar] [CrossRef]
- Catoire, F.; Bachau, H. Above-Threshold Ionization of Quasiperiodic Structures by Low-Frequency Laser Fields. Phys. Rev. Lett. 2015, 115, 163602. [Google Scholar] [CrossRef]
- Foumouo, E.; Hamido, A.; Antoine, P.H.; Piraux, B.; Bachau, H.; Shakeshaft, R. Time-dependent analysis of the mechanism for two-photon double escape in helium: From very long to attosecond time scales. J. Phys. B 2010, 43, 091001. [Google Scholar] [CrossRef]
- Bachau, H.; Dondera, M.; Florescu, V. Stimulated Compton Scattering in Two-Color Ionization of Hydrogen with keV Electromagnetic Fields. Phys. Rev. Lett. 2014, 112, 073001. [Google Scholar] [CrossRef]
- Nikolopoulos, L.A.A.; Nakajima, T.; Lambropoulos, P. Direct versus sequential double ionization of Mg with extreme-ultraviolet radiation. Phys. Rev. Lett. 2003, 90, 043003. [Google Scholar] [CrossRef] [PubMed]
- Nikolopoulos, L.A.A.; Kjeldsen, T.K.; Madsen, L.B. Spectral and partial-wave decomposition of time-dependent wave functions on a grid: Photoelectron specctru of H and H2+ in electromagnetic fields. Phys. Rev. A 2007, 75, 063426. [Google Scholar] [CrossRef]
- Papadogiannis, N.A.; Nikolopoulos, L.A.A.; Charalambidis, D.; Tsakiris, G.D.; Tzallas, P.; Witte, K. On the feasibility of performing non-linear autocorrelation with attosecond pulse trains. Appl. Phys. B 2003, 76, 721–727. [Google Scholar] [CrossRef]
- Nikolopoulos, L.A.A. Elements of Photoionization Quantum Dynamics Methods; Morgan & Claypool Publishers, IOP Concise Physics: London, UK, 2019. [Google Scholar]
- Nikolopoulos, L.A.A.; Bachau, H. Theory of photoionization of two-electron quantum dots in the resonance region in THz and mid-IR fields. Phys. Rev. A 2016, 94, 053409. [Google Scholar] [CrossRef]
- Bachau, H.; Nikolopoulos, L.A.A. Direct and Sequential Two-Photon Double Ionization of Two-Electron Quantum Dots. J. Phys. Chem. A 2018, 122, 1574. [Google Scholar] [CrossRef]
- Nikolopoulos, L.A.A. A package for the ab-initio calculation of one- and two-photon cross sections of two-electron atoms, using a CI B-splines method. Comput. Phys. Commun. 2003, 150, 140–165. [Google Scholar] [CrossRef]
- Hu, S.X.; Colgan, J.; Collins, J.A. Triple-differential cross-sections for two-photon double ionization of He near threshold. J. Phys. B 2005, 38, L35–L45. [Google Scholar] [CrossRef]
- Barna, I.F.; Wang, J.; Burgdörfer, J. Angular distribution in two-photon double ionization of helium by intense attosecond soft-X-ray pulses. Phys. Rev. A 2006, 73, 023402. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prior, A.; Bachau, H.; Nikolopoulos, L.A.A. Radial and Angular Electron Ejection Patterns of Two-Electron Quantum Dots in THz Fields. Atoms 2020, 8, 38. https://doi.org/10.3390/atoms8030038
Prior A, Bachau H, Nikolopoulos LAA. Radial and Angular Electron Ejection Patterns of Two-Electron Quantum Dots in THz Fields. Atoms. 2020; 8(3):38. https://doi.org/10.3390/atoms8030038
Chicago/Turabian StylePrior, Adam, Henri Bachau, and Lampros A. A. Nikolopoulos. 2020. "Radial and Angular Electron Ejection Patterns of Two-Electron Quantum Dots in THz Fields" Atoms 8, no. 3: 38. https://doi.org/10.3390/atoms8030038
APA StylePrior, A., Bachau, H., & Nikolopoulos, L. A. A. (2020). Radial and Angular Electron Ejection Patterns of Two-Electron Quantum Dots in THz Fields. Atoms, 8(3), 38. https://doi.org/10.3390/atoms8030038




