Element Abundances of Solar Energetic Particles and the Photosphere, the Corona, and the Solar Wind
Abstract
1. Introduction
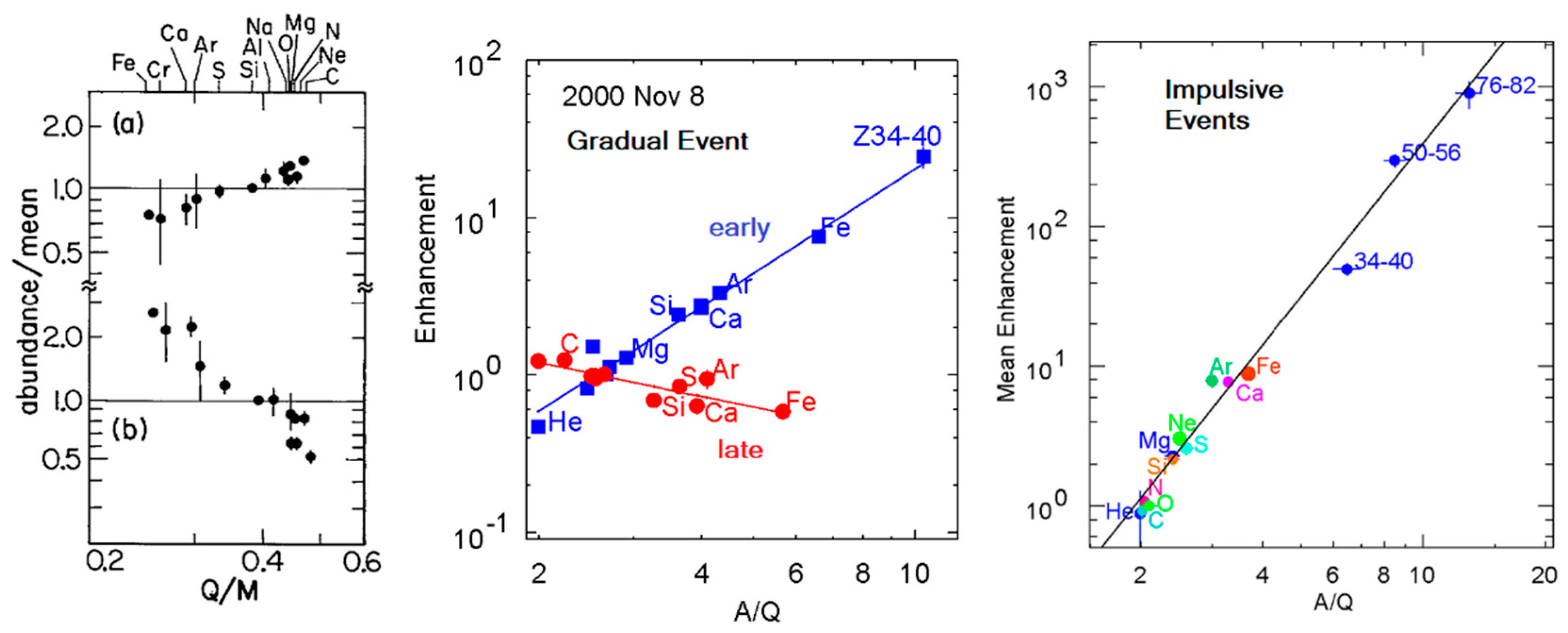
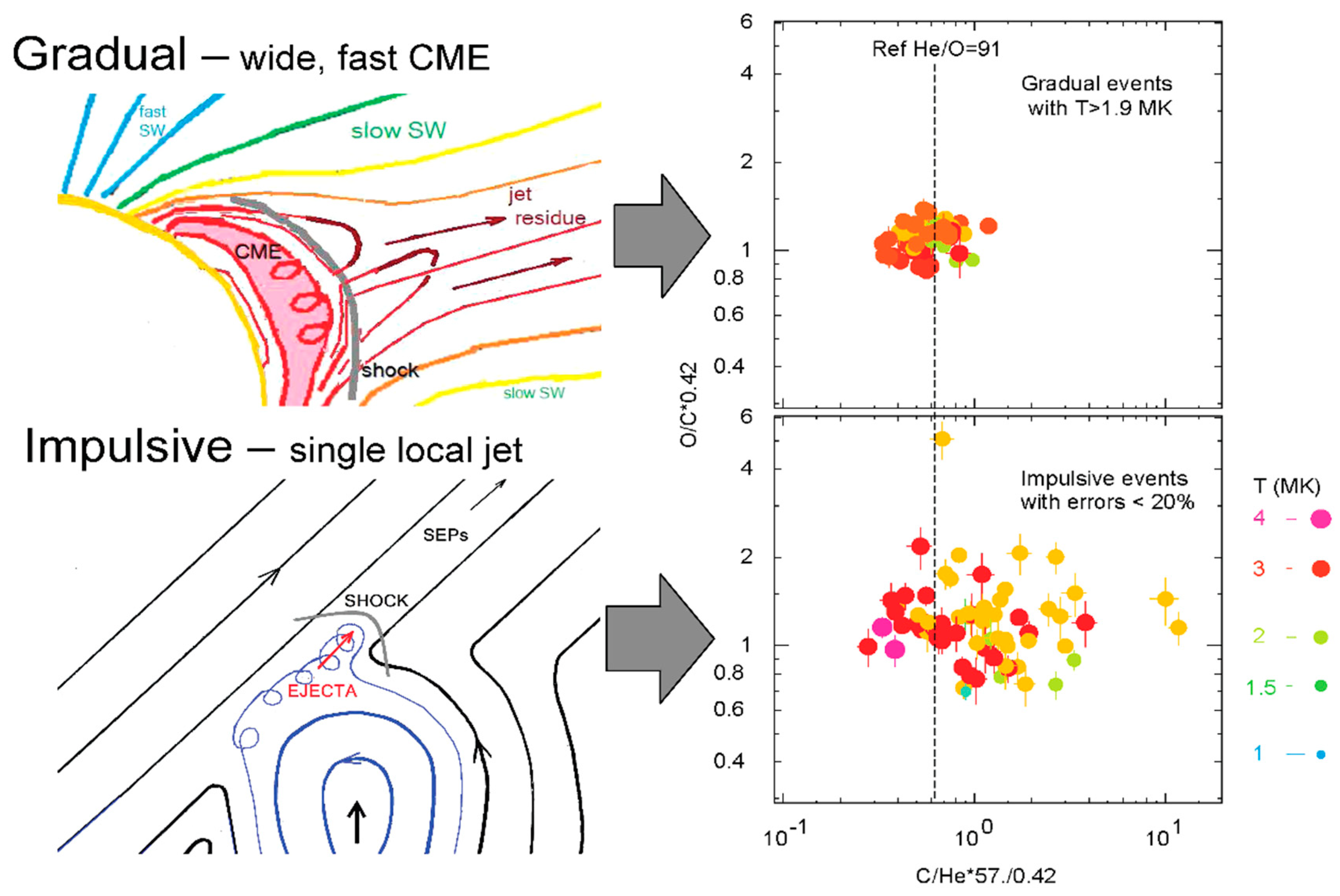
1.1. A Turbulent History: Gradual and Impulsive SEP Events
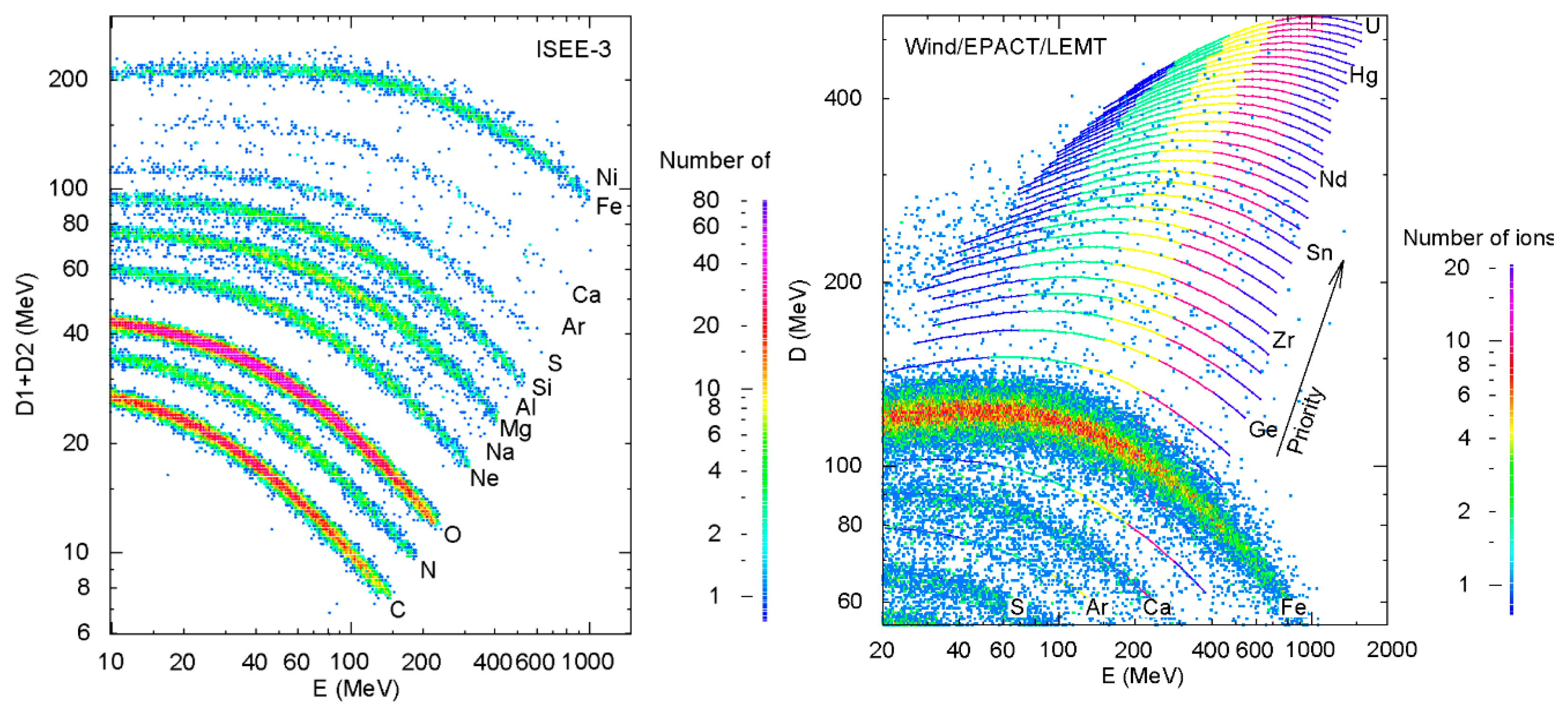
1.2. SEP Abundance Measuements
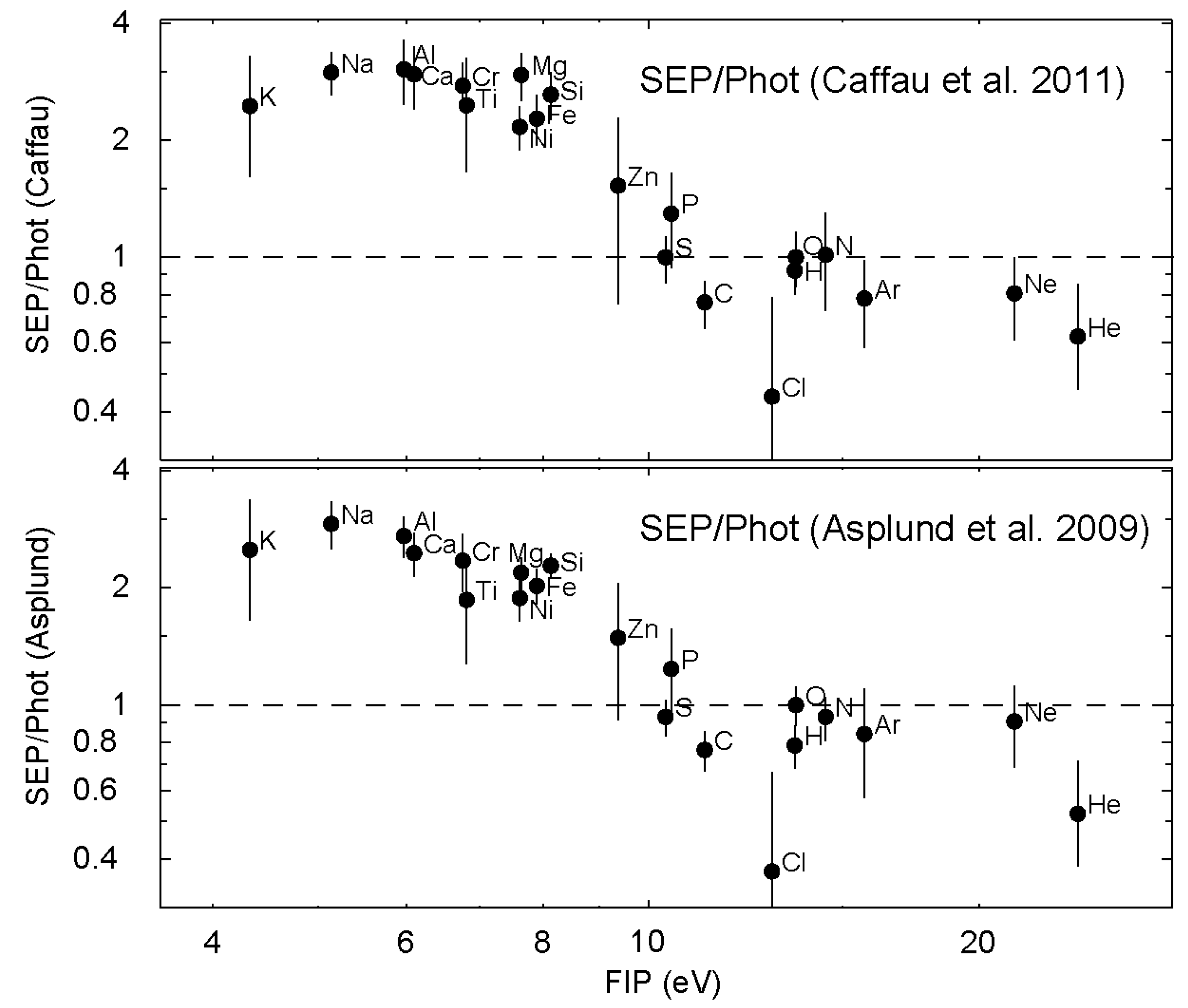
2. Abundances: Separating Dependence upon FIP and A/Q
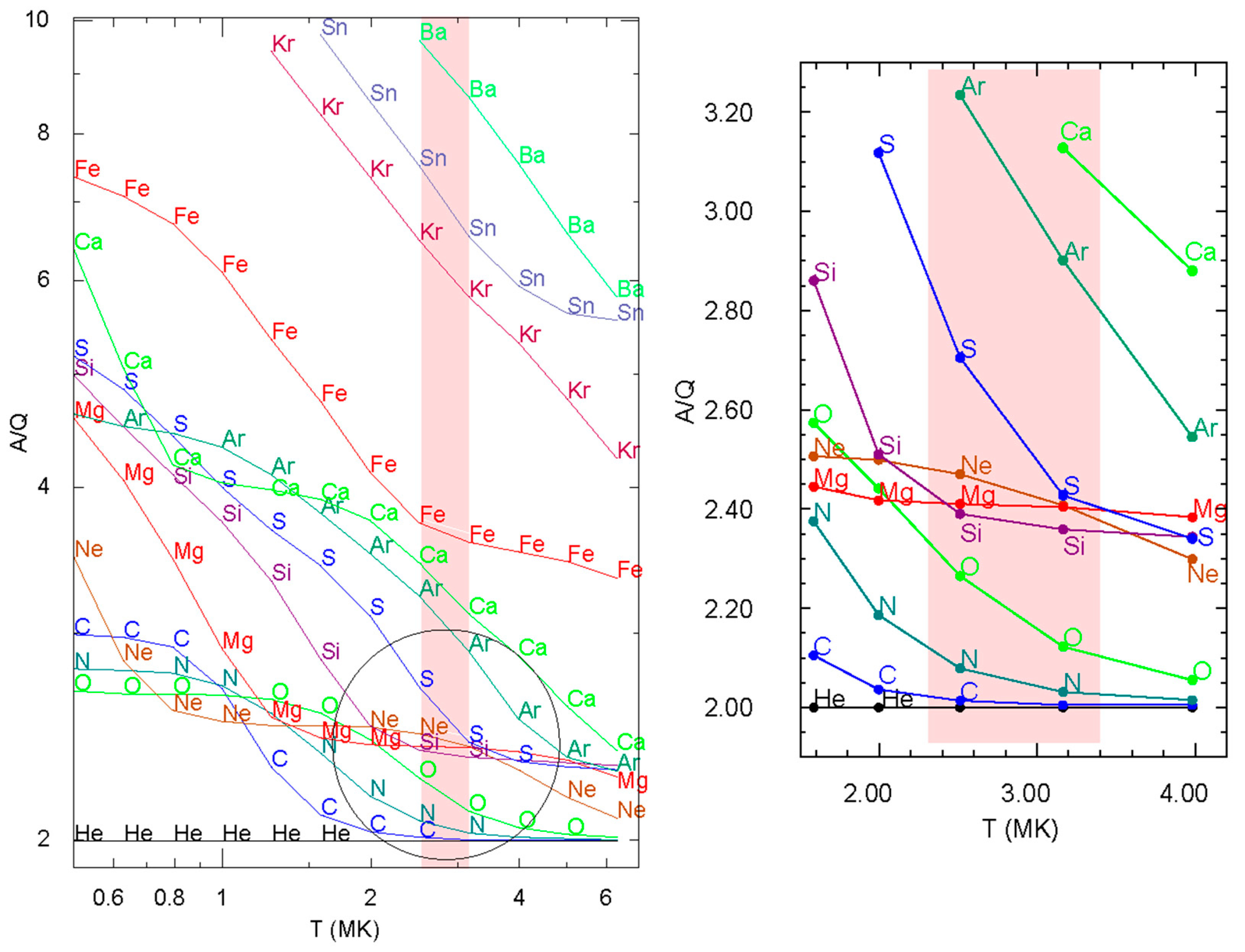
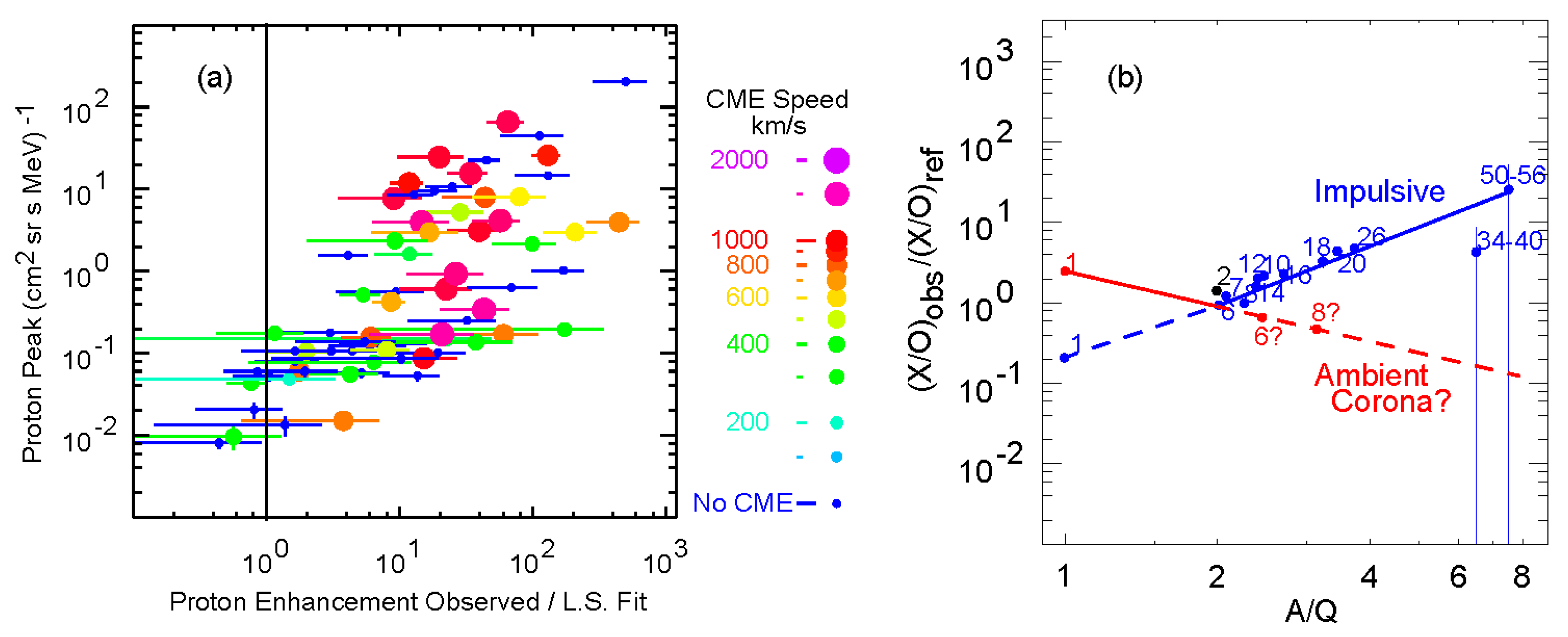
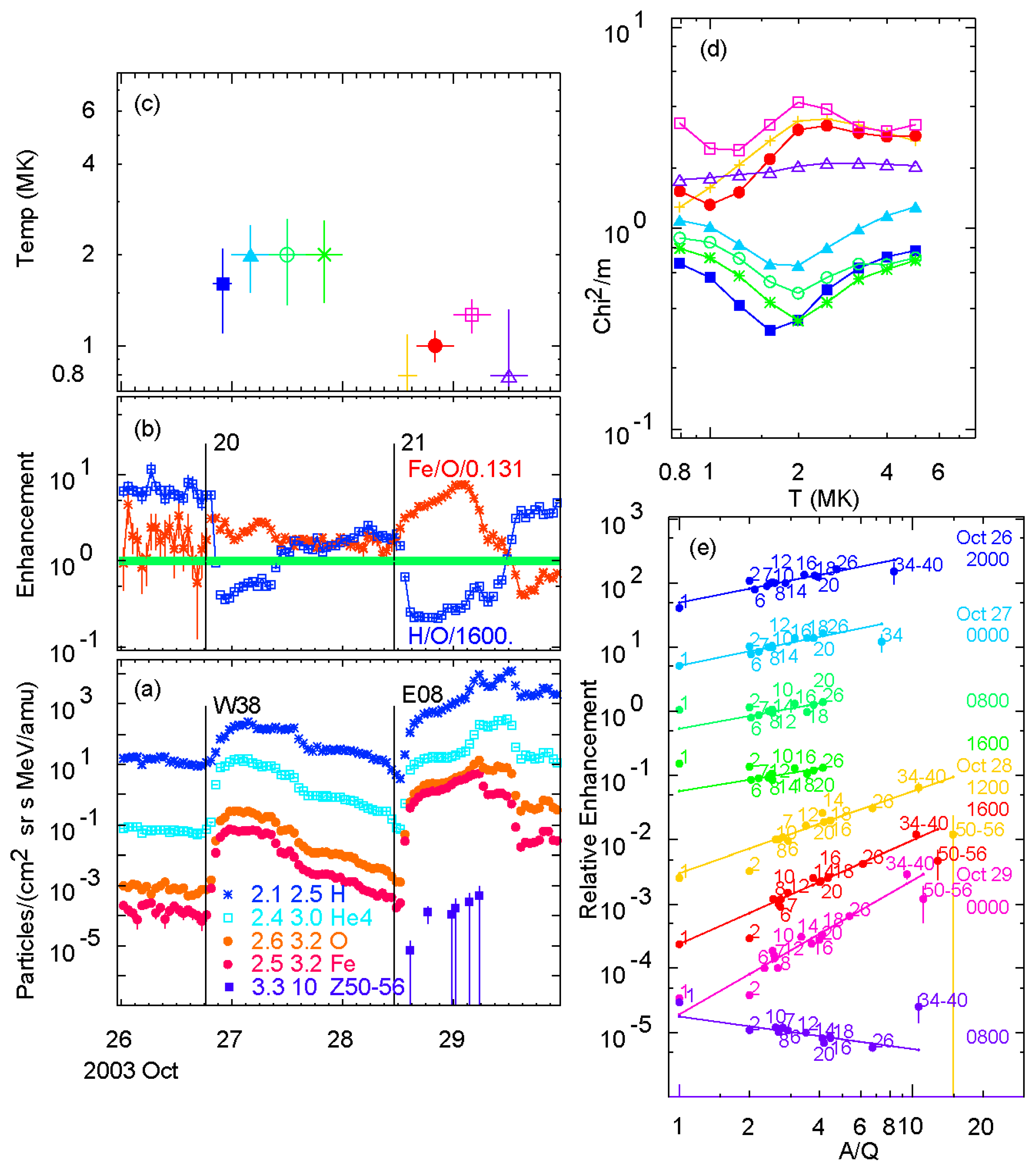
3. Source Temperatures and Power Laws in A/Q
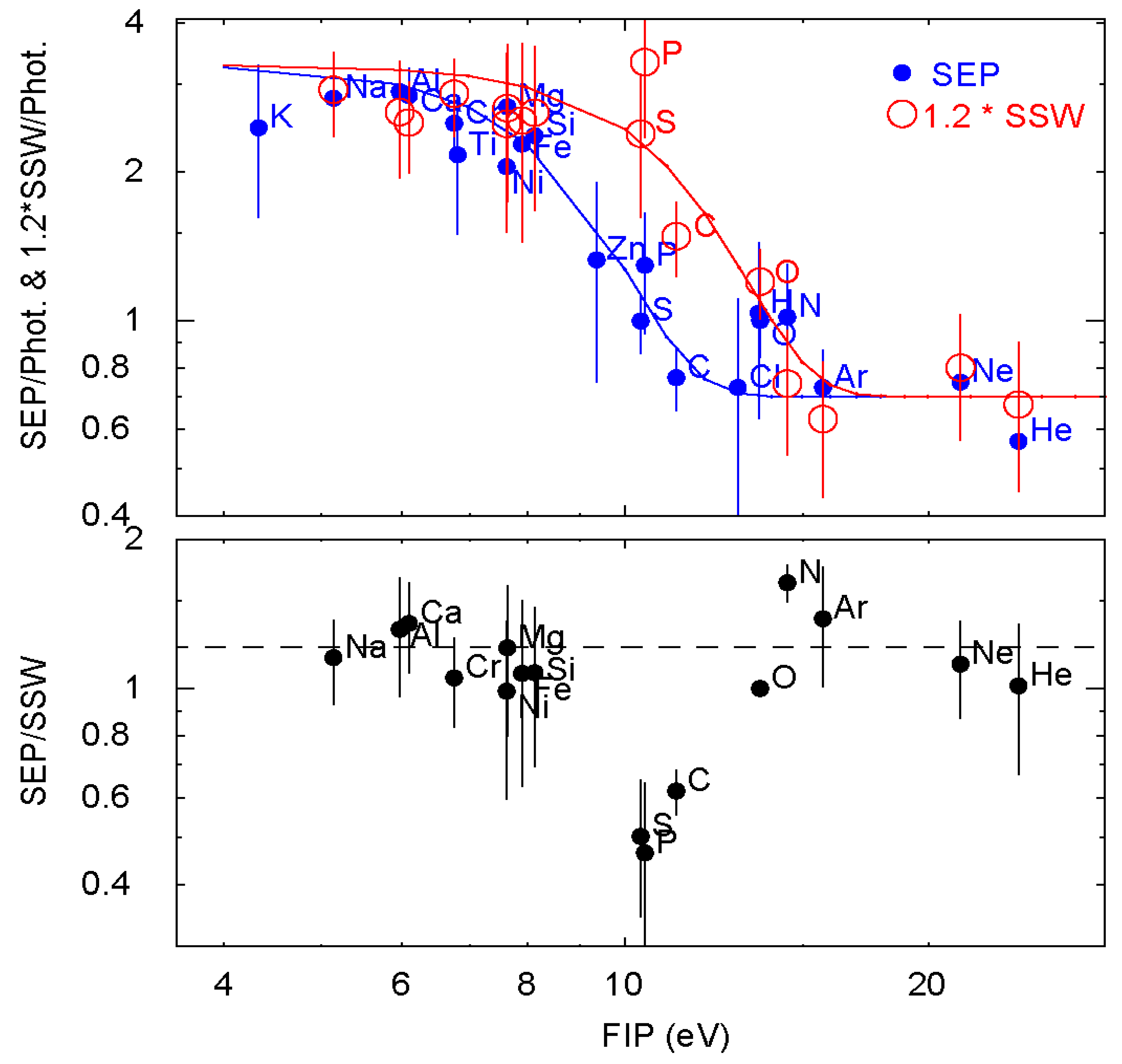
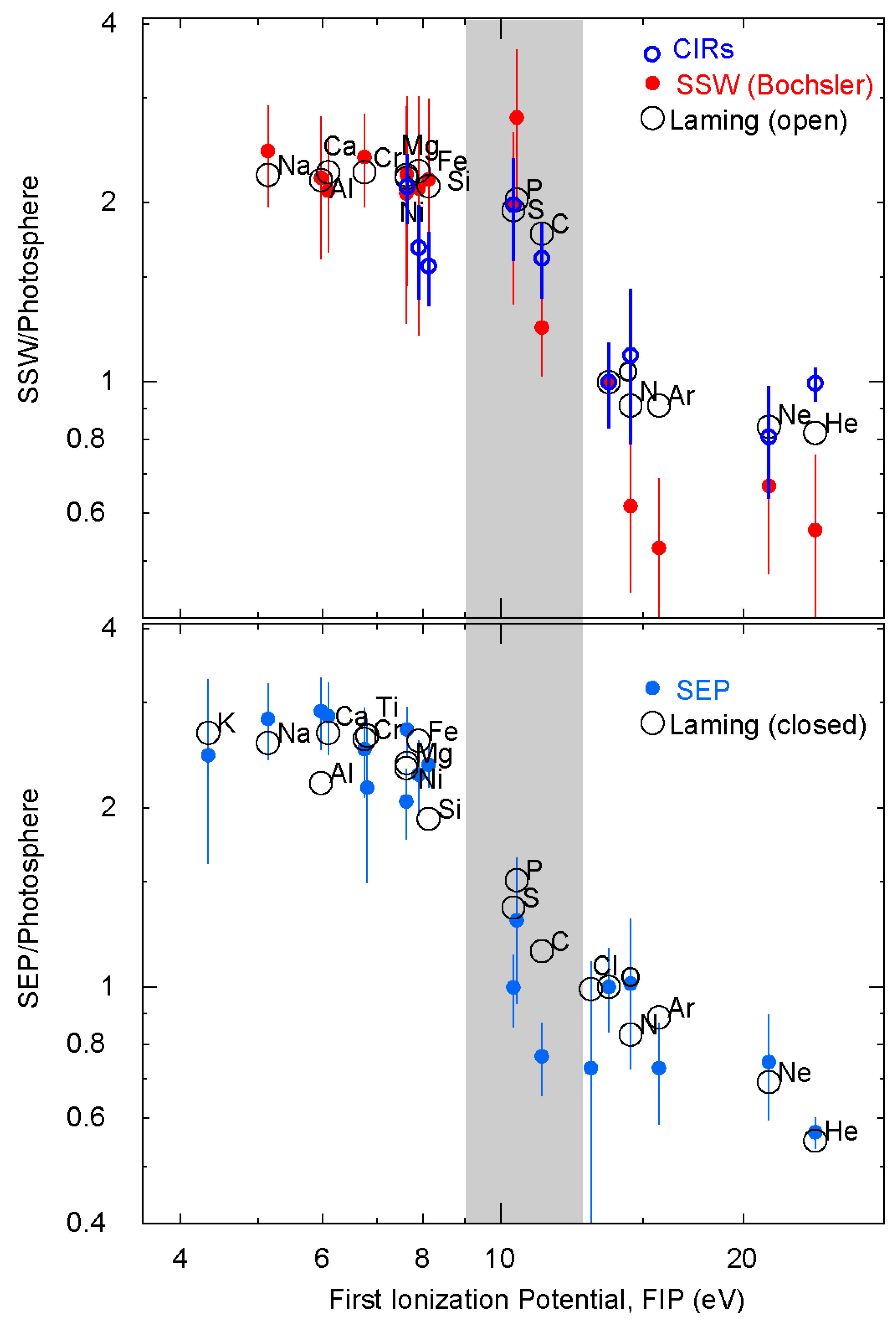
4. Comparing SEPs with the Solar Wind
5. Conclusions
- “Pure” impulsive SEPs from jets: Magnetic reconnection in jets produces steep power-law enhancements in A/Q from H to Pb and in 3He/4He from the ≈3 MK plasma at ≈1.5 RS. Jet ejecta are too slow to produce a shock wave. Flares involve similar physics on closed loops, but those energetic ions cannot escape to become SEPs; they deposit their energy in loop footpoints to produce hot, bright flares instead.
- Impulsive SEPs with shocks: An impulsive SEP jet where the CME from that same jet can drive a sufficiently fast shock to favor the reacceleration of the pre-enhanced ≈3 MK impulsive suprathermal ions, but also to sample protons from the ambient plasma to produce a proton excess.
- A weak gradual SEP event: A wide, moderately-fast (>500 km s−1) CME-driven shock wave sweeps up protons from the ambient corona, but strongly favors the faster pre-enhanced residual impulsive suprathermal ions that have accumulated in the corona from many small jets. The ≈3 MK impulsive ions dominate at Z >2, but there are excess protons.
- A strong gradual SEP event: A wide, fast (>1000 km s−1) CME-driven shock wave accelerates ions predominantly from the ambient 1–2 MK coronal plasma at 2–3 RS. Any impulsive suprathermal ions included are negligible.
Funding
Conflicts of Interest
Appendix A
| Z | FIP [eV] | Photosphere * [61,62] | Photosphere [60] | SEP [1,52,58] | SSW [85] | |
|---|---|---|---|---|---|---|
| H | 1 | 13.6 | (1.74 ± 0.04) × 106 * | (2.04 ± 0.05) × 106 | (1.6 ± 0.2) × 106 | – |
| He | 2 | 24.6 | (1.46 ± 0.07) × 105 | (1.74 ± 0.04) × 105 | (0.91 ± 0.03) × 105 | 90,000 ± 30,000 |
| C | 6 | 11.3 | 550 ± 76 * | 550 ± 63 | 420 ± 9 | 680 ± 70 |
| N | 7 | 14.5 | 126 ± 35 * | 138 ± 16 | 128 ± 3 | 78 ± 5 |
| O | 8 | 13.6 | 1000 ± 161 * | 1000 ± 115 | 1000 ± 10 | 1000 |
| Ne | 10 | 21.6 | 195 ± 45 | 174 ± 40 | 157 ± 10 | 140 ± 30 |
| Na | 11 | 5.1 | 3.47 ± 0.24 | 3.55 ± 0.33 | 10.4 ± 1.1 | 9.0 ± 1.5 |
| Mg | 12 | 7.6 | 60.3 ± 8.3 | 81.3 ± 7.5 | 178 ± 4 | 147 ± 50 |
| Al | 13 | 6.0 | 5.13 ± 0.83 | 5.75 ± 0.40 | 15.7 ± 1.6 | 11.9 ± 3 |
| Si | 14 | 8.2 | 57.5 ± 8.0 | 66.1 ± 4.6 | 151 ± 4 | 140 ± 50 |
| P | 15 | 10.5 | 0.501 ± 0.046 * | 0.525 ± 0.036 | 0.65 ± 0.17 | 1.4 ± 0.4 |
| S | 16 | 10.4 | 25.1 ± 2.9 * | 26.9 ± 1.9 | 25 ± 2 | 50 ± 15 |
| Cl | 17 | 13.0 | 0.55 ± 0.38 | 0.65 ± 0.45 | 0.24 ± 0.1 | – |
| Ar | 18 | 15.8 | 5.5 ± 1.3 | 5.1 ± 1.5 | 4.3 ± 0.4 | 3.1 ± 0.8 |
| K | 19 | 4.3 | 0.224 ± 0.046 * | 0.22 ± 0.045 | 0.55 ± 0.15 | – |
| Ca | 20 | 6.1 | 3.72 ± 0.60 | 4.47 ± 0.41 | 11 ± 1 | 8.1 ± 1.5 |
| Ti | 22 | 6.8 | 0.138 ± 0.019 | 0.182 ± 0.021 | 0.34 ± 0.1 | – |
| Cr | 24 | 6.8 | 0.759 ± 0.017 | 0.89 ± 0.08 | 2.1 ± 0.3 | 2.0 ± 0.3 |
| Fe | 26 | 7.9 | 57.6 ± 8.0 * | 64.6 ± 6.0 | 131 ± 6 | 122 ± 50 |
| Ni | 28 | 7.6 | 2.95 ± 0.27 | 3.39 ± 0.31 | 6.4 ± 0.6 | 6.5 ± 2.5 |
| Zn | 30 | 9.4 | 0.072 ± 0.025 | 0.074 ± 0.009 | 0.11 ± 0.04 | – |
References
- Reames, D.V. Solar Energetic Particles; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Forbush, S.E. Three unusual cosmic ray increases possibly due to charged particles from the Sun. Phys. Rev. 1946, 70, 771. [Google Scholar] [CrossRef]
- Newkirk, G., Jr.; Wenzel, D.G. Rigidity-independent propagation of cosmic rays in the solar corona. J. Geophys. Res. 1978, 83. [Google Scholar] [CrossRef]
- Mason, G.M.; Gloeckler, G.; Hovestadt, D. Temporal variations of nucleonic abundances in solar flare energetic particle events. II—Evidence for large-scale shock acceleration. Astrophys. J. 1984, 280, 902. [Google Scholar] [CrossRef]
- Kahler, S.W.; Sheeley, N.R., Jr.; Howard, R.A.; Koomen, M.J.; Michels, D.J.; McGuire, R.E.; von Rosenvinge, T.T.; Reames, D.V. Associations between coronal mass ejections and solar energetic proton events. J. Geophys. Res. 1984, 89, 9683. [Google Scholar] [CrossRef]
- Gosling, J.T. The solar flare myth. J. Geophys. Res. 1993, 98, 18937. [Google Scholar] [CrossRef]
- Zirin, H. Solar storminess. Sky and Telescope, 9 November 1994. [Google Scholar]
- Reames, D.V. Solar energetic particles: A paradigm shift. Revs. Geophys. Suppl. 1995, 33, 585. [Google Scholar] [CrossRef]
- Reames, D.V. The dark side of the solar flare myth. Eos Trans. AGU 1995, 76, 401. [Google Scholar] [CrossRef]
- Reames, D.V. Particle acceleration at the sun and in the heliosphere. Space Sci. Rev. 1999, 90, 413. [Google Scholar] [CrossRef]
- Reames, D.V. The two sources of solar energetic particles. Space Sci. Rev. 2013, 175, 53. [Google Scholar] [CrossRef]
- Reames, D.V. What are the sources of solar energetic particles? Element abundances and source plasma temperatures. Space Sci. Rev. 2015, 194, 303. [Google Scholar] [CrossRef]
- Reames, D.V. Abundances, ionization states, temperatures, and FIP in solar energetic particles. Space Sci. Rev. 2018, 214, 61. [Google Scholar] [CrossRef]
- Reames, D.V. Solar release times of energetic particles in ground-level events. Astrophys. J. 2009, 693, 812. [Google Scholar] [CrossRef]
- Reames, D.V. Solar energetic-particle release times in historic ground-level events. Astrophys. J. 2009, 706, 844. [Google Scholar] [CrossRef]
- Reames, D.V.; Barbier, L.M.; Ng, C.K. The spatial distribution of particles accelerated by coronal mass ejection-driven shocks. Astrophys. J. 1996, 466, 473. [Google Scholar] [CrossRef]
- Rouillard, A.C.; Odstrčil, D.; Sheeley, N.R., Jr.; Tylka, A.J.; Vourlidas, A.; Mason, G.; Wu, C.-C.; Savani, N.P.; Wood, B.E.; Ng, C.K.; et al. Interpreting the properties of solar energetic particle events by using combined imaging and modeling of interplanetary shocks. Astrophys. J. 2011, 735, 7. [Google Scholar] [CrossRef]
- Rouillard, A.; Sheeley, N.R., Jr.; Tylka, A.; Vourlidas, A.; Ng, C.K.; Rakowski, C.; Cohen, C.M.S.; Mewaldt, R.A.; Mason, G.M.; Reames, D.; et al. The longitudinal properties of a solar energetic particle event investigated using modern solar imaging. Astrophys. J. 2012, 752, 44. [Google Scholar] [CrossRef]
- Rouillard, A.P.; Plotnikov, I.; Pinto, R.F.; Tirole, M.; Lavarra, M.; Zucca, P.; Vainio, R.; Tylka, A.J.; Vourlidas, A.; De Rosa, M.L.; et al. Deriving the properties of coronal pressure fronts in 3D: Application to the 2012 May 17 ground level enhancement. Astrophys. J. 2016, 833, 45. [Google Scholar] [CrossRef]
- Gopalswamy, N.; Akiyama, S.; Yashiro, S. Major solar flares without coronal mass ejections. In Universal Heliophysical Processes; Gopalswamy, N., Webb, D.F., Eds.; Cambridge University Press: Cambridge, UK, 2009; Volume 257, p. 283. [Google Scholar] [CrossRef]
- Gopalswamy, N.; Xie, H.; Yashiro, S.; Akiyama, S.; Mäkelä, P.; Usoskin, I.G. Properties of Ground level enhancement events and the associated solar eruptions during solar cycle 23. Space Sci. Rev. 2012, 171, 23. [Google Scholar] [CrossRef]
- Kouloumvakos, A.; Rouillard, A.P.; Wu, Y.; Vainio, R.; Vourlidas, A.; Plotnikov, I.; Afanasiev, A.; Önel, H. Connecting the properties of coronal shock waves with those of solar energetic particles. Astrophys. J. 2019, 876, 80. [Google Scholar] [CrossRef]
- Luhn, A.; Klecker, B.; Hovestadt, D.; Gloeckler, G.; Ipavich, F.M.; Scholer, M.; Fan, C.Y.; Fisk, L.A. Ionic charge states of N, Ne, Mg, Si and S in solar energetic particle events. Adv. Space Res. 1984, 4, 161. [Google Scholar] [CrossRef]
- Luhn, A.; Klecker, B.; Hovestadt, D.; Möbius, E. The mean ionic charge of silicon in He-3-rich solar flares. Astrophys. J. 1987, 317, 951. [Google Scholar] [CrossRef]
- Mason, G.M.; Mazur, J.E.; Looper, M.D.; Mewaldt, R.A. Charge state measurements of solar energetic particles observed with SAMPEX. Astrophys. J. 1995, 452, 901. [Google Scholar] [CrossRef]
- Leske, R.A.; Cummings, J.R.; Mewaldt, R.A.; Stone, E.C.; von Rosenvinge, T.T. Measurements of the ionic charge states of solar energetic particles using the geomagnetic field. Astrophys. J. 1995, 452, L149. [Google Scholar] [CrossRef]
- Tylka, A.J.; Boberg, P.R.; Adams, J.H., Jr.; Beahm, L.P.; Dietrich, W.F.; Kleis, T. The mean ionic charge state of solar energetic Fe ions above 200 MeV per nucleon. Astrophys. J. Lett. 1995, 444, L109. [Google Scholar] [CrossRef]
- Reames, D.V. Temperature of the source plasma in gradual solar energetic particle events. Sol. Phys. 2016, 291, 911. [Google Scholar] [CrossRef]
- Zank, G.P.; Rice, W.K.M.; Wu, C.C. Particle acceleration and coronal mass ejection driven shocks: A theoretical model. J. Geophys. Res. 2000, 105, 25079. [Google Scholar] [CrossRef]
- Lee, M.A. Coupled hydromagnetic wave excitation and ion acceleration at an evolving coronal/interplanetary shock. Astrophys. J. Suppl. 2005, 158, 38. [Google Scholar] [CrossRef]
- Sandroos, A.; Vainio, R. Simulation results for heavy ion spectral variability in large gradual solar energetic particle events. Astrophys. J. 2007, 662, L127. [Google Scholar] [CrossRef]
- Ng, C.K.; Reames, D.V. Shock acceleration of solar energetic protons: The first 10 minutes. Astrophys. J. Lett. 2008, 686, L123. [Google Scholar] [CrossRef]
- Afanasiev, A.; Battarbee, M.; Vainio, R. Self-consistent Monte Carlo simulations of proton acceleration in coronal shocks: Effect of anisotropic pitch-angle scattering of particles. Astron. Astrophys. 2016, 584, 81. [Google Scholar] [CrossRef]
- Desai, M.I.; Giacalone, J. Large gradual solar energetic particle events. Living Rev. Sol. Phys. 2016, 13, 3. [Google Scholar] [CrossRef]
- Hu, J.; Li, G.; Ao, X.; Verkhoglyadova, O.; Zank, G. Modeling particle acceleration and transport at a 2D CME-driven shock. J. Geophys. Res. 2017, 122. [Google Scholar] [CrossRef]
- Kahler, S.W. The correlation between solar energetic particle peak intensities and speeds of coronal mass ejections: Effects of ambient particle intensities and energy spectra. J. Geophys. Res. 2001, 106, 20947. [Google Scholar] [CrossRef]
- Serlemitsos, A.T.; Balasubrahmanyan, V.K. Solar particle events with anomalously large relative abundance of 3He. Astrophys. J. 1975, 198, 195. [Google Scholar] [CrossRef]
- Reames, D.V.; von Rosenvinge, T.T.; Lin, R.P. Solar 3He-rich events and nonrelativistic electron events - A new association. Astrophys. J. 1985, 292, 716. [Google Scholar] [CrossRef]
- Reames, D.V.; Stone, R.G. The identification of solar 3He-rich events and the study of particle acceleration at the sun. Astrophys. J. 1986, 308, 902. [Google Scholar] [CrossRef]
- Temerin, M.; Roth, I. The production of 3He and heavy ion enrichment in 3He-rich flares by electromagnetic hydrogen cyclotron waves. Astrophys. J. Lett. 1992, 391, L105. [Google Scholar] [CrossRef]
- Reames, D.V. Abundances of trans-iron elements in solar energetic particle events. Astrophys. J. Lett. 2000, 540, L111. [Google Scholar] [CrossRef]
- Reames, D.V.; Ng, C.K. Heavy-element abundances in solar energetic particle events. Astrophys. J. 2004, 610, 510. [Google Scholar] [CrossRef]
- Mason, G.M.; Mazur, J.E.; Dwyer, J.R.; Jokippi, J.R.; Gold, R.E.; Krimigis, S.M. Abundances of heavy and ultraheavy ions in 3He-rich solar flares. Astrophys. J. 2004, 606, 555. [Google Scholar] [CrossRef]
- Reames, D.V.; Cliver, E.W.; Kahler, S.W. Abundance enhancements in impulsive solar energetic-particle events with associated coronal mass ejections. Sol. Phys. 2014, 289, 3817. [Google Scholar] [CrossRef]
- Drake, J.F.; Cassak, P.A.; Shay, M.A.; Swisdak, M.; Quataert, E. A magnetic reconnection mechanism for ion acceleration and abundance enhancements in impulsive flares. Astrophys. J. Lett. 2009, 700, L16. [Google Scholar] [CrossRef]
- Kahler, S.W.; Reames, D.V.; Sheeley, N.R., Jr. Coronal mass ejections associated with impulsive solar energetic particle events. Astrophys. J. 2001, 562, 558. [Google Scholar] [CrossRef]
- Bučík, R.; Innes, D.E.; Mason, G.M.; Wiedenbeck, M.E.; Gómez-Herrero, R.; Nitta, N.V. 3He-rich solar energetic particles in helical jets on the Sun. Astrophys. J. 2018, 852, 76. [Google Scholar] [CrossRef]
- Bučík, R.; Wiedenbeck, M.E.; Mason, G.M.; Gómez-Herrero, R.; Nitta, N.V.; Wang, L. 3He-rich solar energetic particles from sunspot jets. Astrophys. J. Lett. 2018, 869, L21. [Google Scholar] [CrossRef]
- Mandzhavidze, N.; Ramaty, R.; Kozlovsky, B. Determination of the abundances of subcoronal 4He and of solar flare-accelerated 3He and 4He from gamma-ray spectroscopy. Astrophys. J. 1999, 518, 918. [Google Scholar] [CrossRef]
- Murphy, R.J.; Ramaty, R.; Kozlovsky, B.; Reames, D.V. Solar abundances from gamma-ray spectroscopy: Comparisons with energetic particle, photospheric, and coronal abundances. Astrophys. J. 1991, 371, 793. [Google Scholar] [CrossRef]
- Murphy, R.J.; Kozlovsky, B.; Share, G.H. Evidence for enhanced 3He in flare-accelerated particles based on new calculations of the gamma-ray line spectrum. Astrophys. J. 2016, 833, 166. [Google Scholar] [CrossRef]
- Reames, D.V. Coronal Abundances determined from energetic particles. Adv. Space Res. 1995, 15, 41. [Google Scholar] [CrossRef]
- Von Rosenvinge, T.T.; Barbier, L.M.; Karsch, J.; Liberman, R.; Madden, M.P.; Nolan, T.; Reames, D.V.; Ryan, L.; Singh, S.; Trexel, H. The Energetic Particles: Acceleration, Composition, and Transport (EPACT) investigation on the Wind spacecraft. Space Sci. Rev. 1995, 71, 152. [Google Scholar] [CrossRef]
- Mason, G.M.; Gold, R.E.; Krimigis, S.M.; Mazur, J.E.; Andrews, G.B.; Daley, K.A.; Dwyer, J.R.; Heuerman, K.F.; James, T.L.; Kennedy, M.J.; et al. The Ultra-Low-Energy Isotope Spectrometer (ULEIS) for the ACE spacecraft. Space Sci. Rev. 1998, 86, 409. [Google Scholar] [CrossRef]
- Stone, E.C.; Cohen, C.M.S.; Cook, W.R.; Cummings, A.C.; Gauld, B.; Kecman, B.; Leske, R.A.; Mewaldt, R.A.; Thayer, M.R.; Dougherty, B.L.; et al. The Solar Isotope Spectrometer for the Advanced Composition Explorer. Space Sci. Rev. 1998, 86, 357. [Google Scholar] [CrossRef]
- Leske, R.A.; Mewaldt, R.A.; Cohen, C.M.S.; Cummings, A.C.; Stone, E.C.; Wiedenbeck, M.E.; von Rosenvinge, T.T. Solar isotopic composition as determined using solar energetic particles. Space Sci. Rev. 2007, 130, 195. [Google Scholar] [CrossRef]
- Webber, W.R. Solar and galactic cosmic ray abundances—A comparison and some comments. In Proceedings of the 14th International Cosmic Ray Conference, Munich, Germany, 15–29 August 1975; Volume 5, p. 1597. [Google Scholar]
- Reames, D.V. Element abundances in solar energetic particles and the solar corona. Sol. Phys. 2014, 289, 977. [Google Scholar] [CrossRef]
- Reames, D.V. The “FIP effect” and the origins of solar energetic particles and of the solar wind. Sol. Phys. 2018, 293, 47. [Google Scholar] [CrossRef]
- Asplund, M.; Grevesse, N.; Sauval, A.J.; Scott, P. The chemical composition of the sun. Ann. Rev. Astron. Astrophys. 2009, 47, 481. [Google Scholar] [CrossRef]
- Caffau, E.; Ludwig, H.-G.; Steffen, M.; Freytag, B.; Bonofacio, P. Solar chemical abundances determined with a CO5BOLD 3D model atmosphere. Sol. Phys. 2011, 268, 255. [Google Scholar] [CrossRef]
- Lodders, K.; Palme, H.; Gail, H.-P. Abundances of the elements in the solar system. In Landolt-Börnstein, New Series VI/4B; Trümper, J.E., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; Chapter 3.4; pp. 560–630. [Google Scholar]
- Meyer, J.-P. The baseline composition of solar energetic particles. Astrophys. J. Suppl. 1985, 57, 151. [Google Scholar] [CrossRef]
- Breneman, H.H.; Stone, E.C. Solar coronal and photospheric abundances from solar energetic particle measurements. Astrophys. J. Lett. 1985, 299, L57. [Google Scholar] [CrossRef]
- DiFabio, R.; Guo, Z.; Möbius, E.; Klecker, B.; Kucharek, H.; Mason, G.M.; Popecki, M. Energy-dependent charge states and their connection with ion abundances in impulsive solar energetic particle events. Astrophys. J. 2008, 687, 623. [Google Scholar] [CrossRef]
- Reames, D.V.; Meyer, J.P.; von Rosenvinge, T.T. Energetic-particle abundances in impulsive solar flare events. Astrophys. J. Suppl. 1994, 90, 649. [Google Scholar] [CrossRef]
- Reames, D.V.; Cliver, E.W.; Kahler, S.W. Variations in abundance enhancements in impulsive solar energetic-particle events and related CMEs and flares. Sol. Phys. 2014, 289, 4675. [Google Scholar] [CrossRef]
- Reames, D.V.; Cliver, E.W.; Kahler, S.W. Temperature of the source plasma for impulsive solar energetic particles. Sol. Phys. 2015, 290, 1761. [Google Scholar] [CrossRef]
- Reames, D.V. The abundance of helium in the source plasma of solar energetic particles. Sol. Phys. 2017, 292, 156. [Google Scholar] [CrossRef][Green Version]
- Reames, D.V. Helium suppression in impulsive solar energetic-particle events. Sol. Phys. 2019, 294, 32. [Google Scholar] [CrossRef]
- Laming, J.M. Non-WKB models of the first ionization potential effect: Implications for solar coronal heating and the coronal helium and neon abundances. Astrophys. J. 2009, 695, 954. [Google Scholar] [CrossRef]
- Mazzotta, P.; Mazzitelli, G.; Colafrancesco, S.; Vittorio, N. Ionization balance for optically thin plasmas: Rate coefficients for all atoms and ions of the elements H. to Ni. Astron. Astrophys. Suppl. 1998, 133, 403. [Google Scholar] [CrossRef]
- Post, D.E.; Jensen, R.V.; Tarter, C.B.; Grasberger, W.H.; Lokke, W.A. Steady-state radiative cooling rates for low-density, high temperature plasmas. At. Data Nucl. Data Tables 1977, 20, 397. [Google Scholar] [CrossRef]
- Reames, D.V. Hydrogen and the abundances of elements in impulsive solar energetic-particle events. Sol. Phys. 2019, 294, 37. [Google Scholar] [CrossRef]
- Reames, D.V. Excess H, suppressed He, and the abundances of elements in solar energetic particles. Sol. Phys. 2019, 294, 141. [Google Scholar] [CrossRef]
- Reames, D.V. Hydrogen and the abundances of elements in gradual solar energetic-particle events. Sol. Phys. 2019, 294, 69. [Google Scholar] [CrossRef]
- Tylka, A.J.; Cohen, C.M.S.; Dietrich, W.F.; Lee, M.A.; Maclennan, C.G.; Mewaldt, R.A.; Ng, C.K.; Reames, D.V. Shock geometry, seed populations, and the origin of variable elemental composition at high energies in large gradual solar particle events. Astrophys. J. 2005, 625, 474. [Google Scholar] [CrossRef]
- Tylka, A.J.; Lee, M.A. Spectral and compositional characteristics of gradual and impulsive solar energetic particle events. Astrophys. J. 2006, 646, 1319. [Google Scholar] [CrossRef]
- Reames, D.V. The origin of element abundance variations in solar energetic particles. Sol. Phys. 2016, 291, 2099. [Google Scholar] [CrossRef][Green Version]
- Desai, M.I.; Mason, G.M.; Dwyer, J.R.; Mazur, J.E.; Gold, R.E.; Krimigis, S.M.; Smith, C.W.; Skoug, R.M. Evidence for a suprathermal seed population of heavy ions accelerated by interplanetary shocks near 1 AU. Astrophys. J. 2003, 588, 1149. [Google Scholar] [CrossRef]
- Bučík, R.; Innes, D.E.; Mall, U.; Korth, A.; Mason, G.M.; Gómez-Herrero, R. Multi-spacecraft observations of recurrent 3He-rich solar energetic particles. Astrophys. J. 2014, 786, 71. [Google Scholar] [CrossRef]
- Bučík, R.; Innes, D.E.; Chen, N.H.; Mason, G.M.; Gómez-Herrero, R.; Wiedenbeck, M.E. Long-lived energetic particle source regions on the Sun. J. Phys. Conf. Ser. 2015, 642, 012002. [Google Scholar] [CrossRef]
- Chen, N.H.; Bučík, R.; Innes, D.E.; Mason, G.M. Case studies of multi-day 3He-rich solar energetic particle periods. Astron. Astrophys. 2015, 580, 16. [Google Scholar] [CrossRef][Green Version]
- Parker, E.N. Nanoflares and the solar X-ray corona. Astrophys. J. 1988, 330, 474. [Google Scholar] [CrossRef]
- Bochsler, P. Composition of matter in the heliosphere. Proc. IAU Symp. 2009, 257, 17. [Google Scholar] [CrossRef]
- Mewaldt, R.A.; Cohen, C.M.S.; Leske, R.A.; Christian, E.R.; Cummings, A.C.; Stone, E.C.; von Rosenvinge, T.T.; Wiedenbeck, M.E. Fractionation of solar energetic particles and solar wind according to first ionization potential. Adv. Space Res. 2002, 30, 79. [Google Scholar] [CrossRef]
- Laming, J.M. The FIP and inverse FIP effects in solar and stellar coronae. Living Rev. Sol. Phys. 2015, 12, 2. [Google Scholar] [CrossRef]
- Laming, J.M.; Vourlidas, A.; Korendyke, C.; Chua, D.; Cranmer, S.R.; Ko, Y.-K.; Kuroda, N.; Provornikova, E.; Raymond, J.C.; Raouafi, N.-E. Element abundances: A new diagnostic for the solar wind. Astrophys. J. 2019, 879, 124. [Google Scholar] [CrossRef]
- Cliver, E.W.; Kahler, S.W.; Reames, D.V. Coronal shocks and solar energetic proton events. Astrophys. J. 2004, 605, 902. [Google Scholar] [CrossRef]
- Reames, D.V. Corotating shock waves and the solar-wind source of energetic ion abundances: Power laws in A/Q. Sol. Phys 2018, 293, 144. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reames, D.V. Element Abundances of Solar Energetic Particles and the Photosphere, the Corona, and the Solar Wind. Atoms 2019, 7, 104. https://doi.org/10.3390/atoms7040104
Reames DV. Element Abundances of Solar Energetic Particles and the Photosphere, the Corona, and the Solar Wind. Atoms. 2019; 7(4):104. https://doi.org/10.3390/atoms7040104
Chicago/Turabian StyleReames, Donald V. 2019. "Element Abundances of Solar Energetic Particles and the Photosphere, the Corona, and the Solar Wind" Atoms 7, no. 4: 104. https://doi.org/10.3390/atoms7040104
APA StyleReames, D. V. (2019). Element Abundances of Solar Energetic Particles and the Photosphere, the Corona, and the Solar Wind. Atoms, 7(4), 104. https://doi.org/10.3390/atoms7040104




