Femtosecond Laser-Assisted Electron Scattering for Ultrafast Dynamics of Atoms and Molecules
Abstract
:1. Introduction
2. Theory of Laser-Assisted Electron Scattering (LAES)
3. Early LAES Experiments
4. Optical Gating and Optical Streaking of Electron Scattering Signals
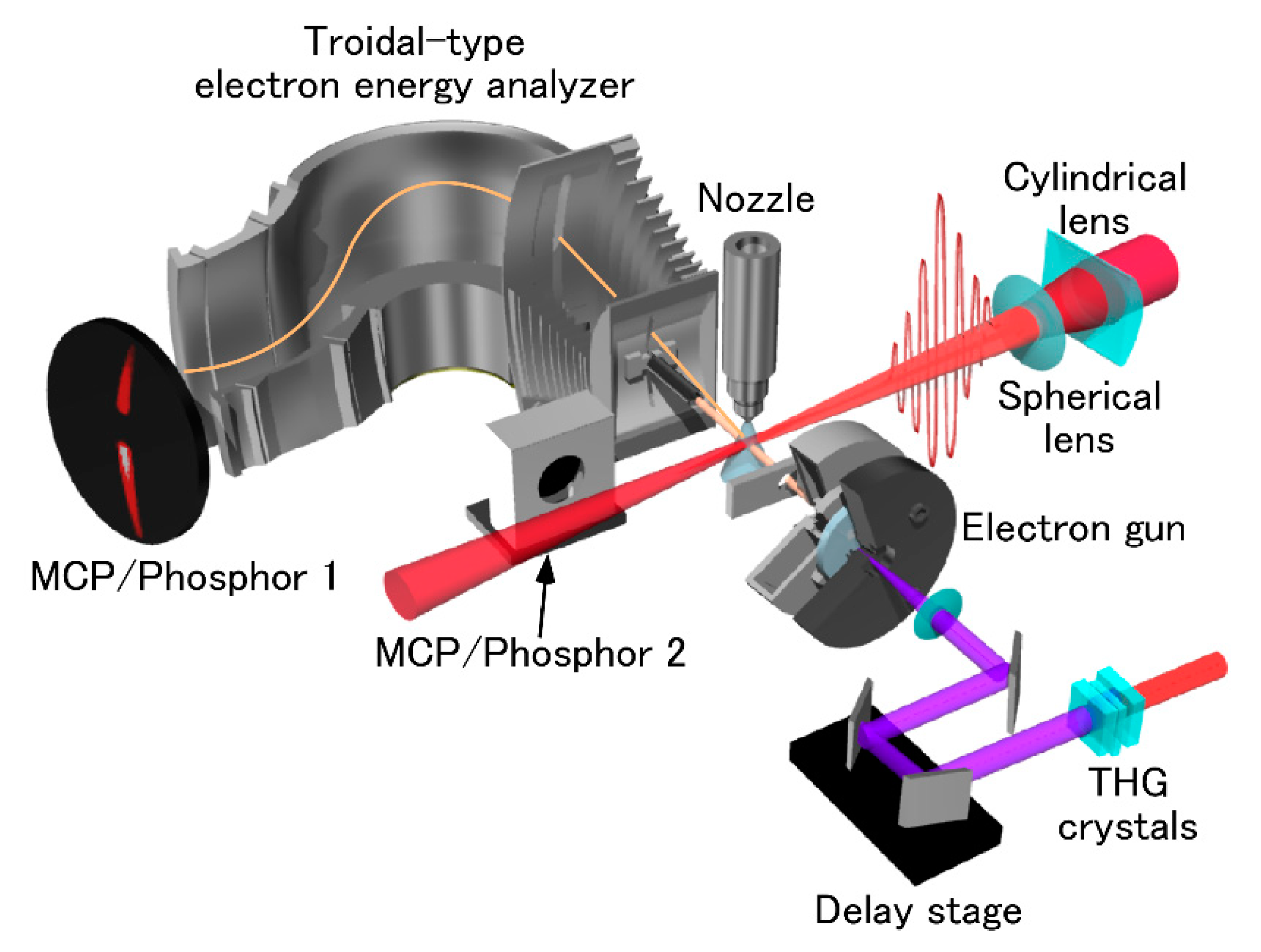
5. Experimental Setup for Recording Femtosecond-LAES Signals
6. Femtosecond LAES Experiments
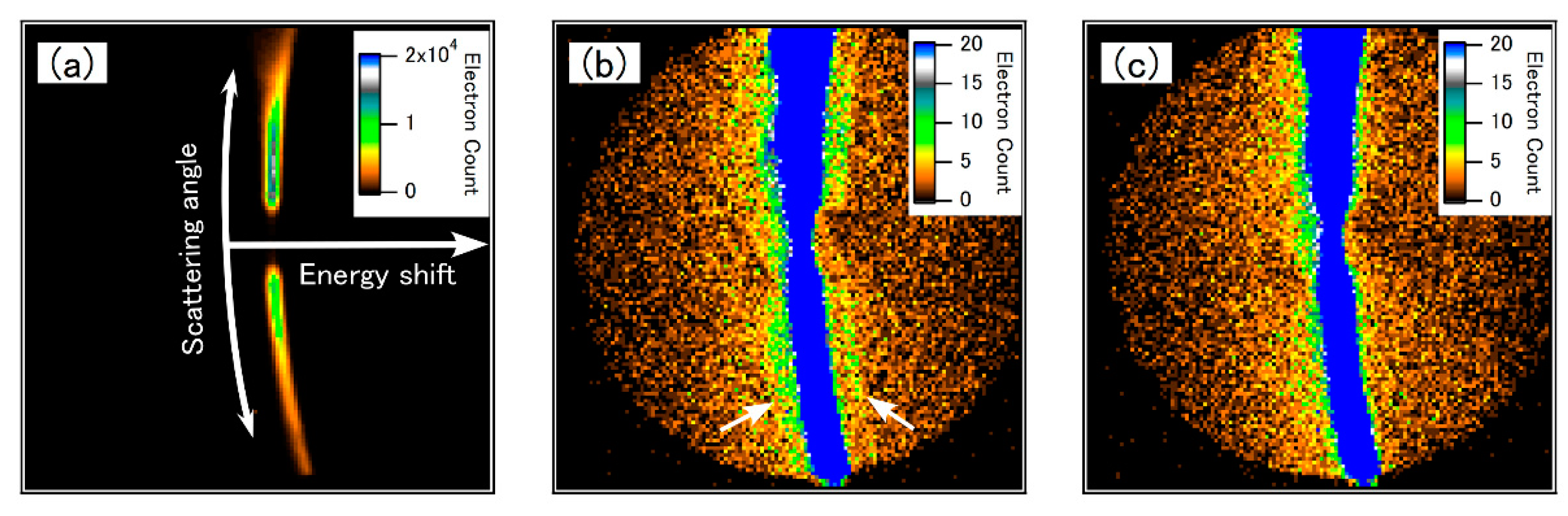
6.1. Measurements of Femtosecond-LAES Singals
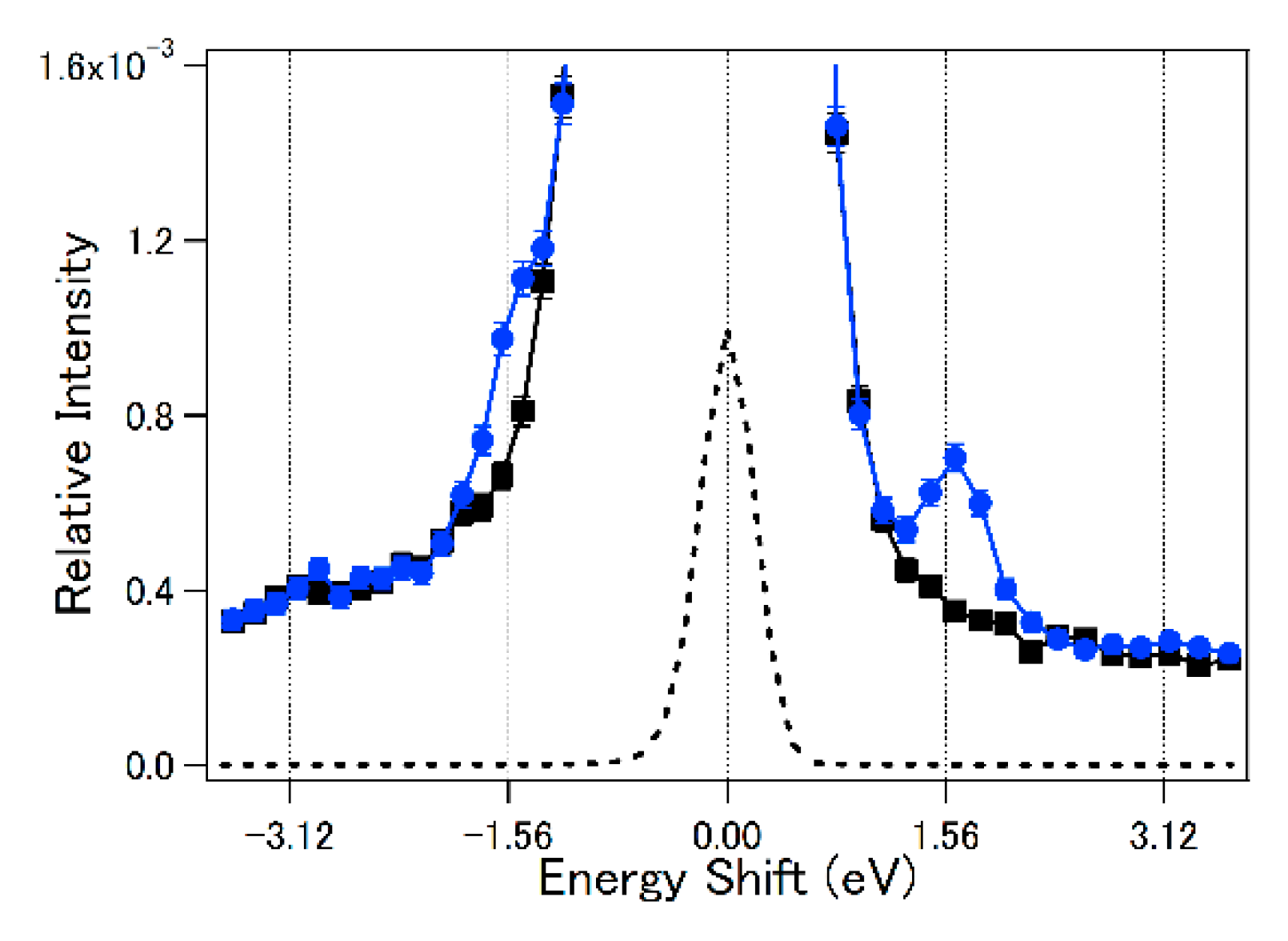
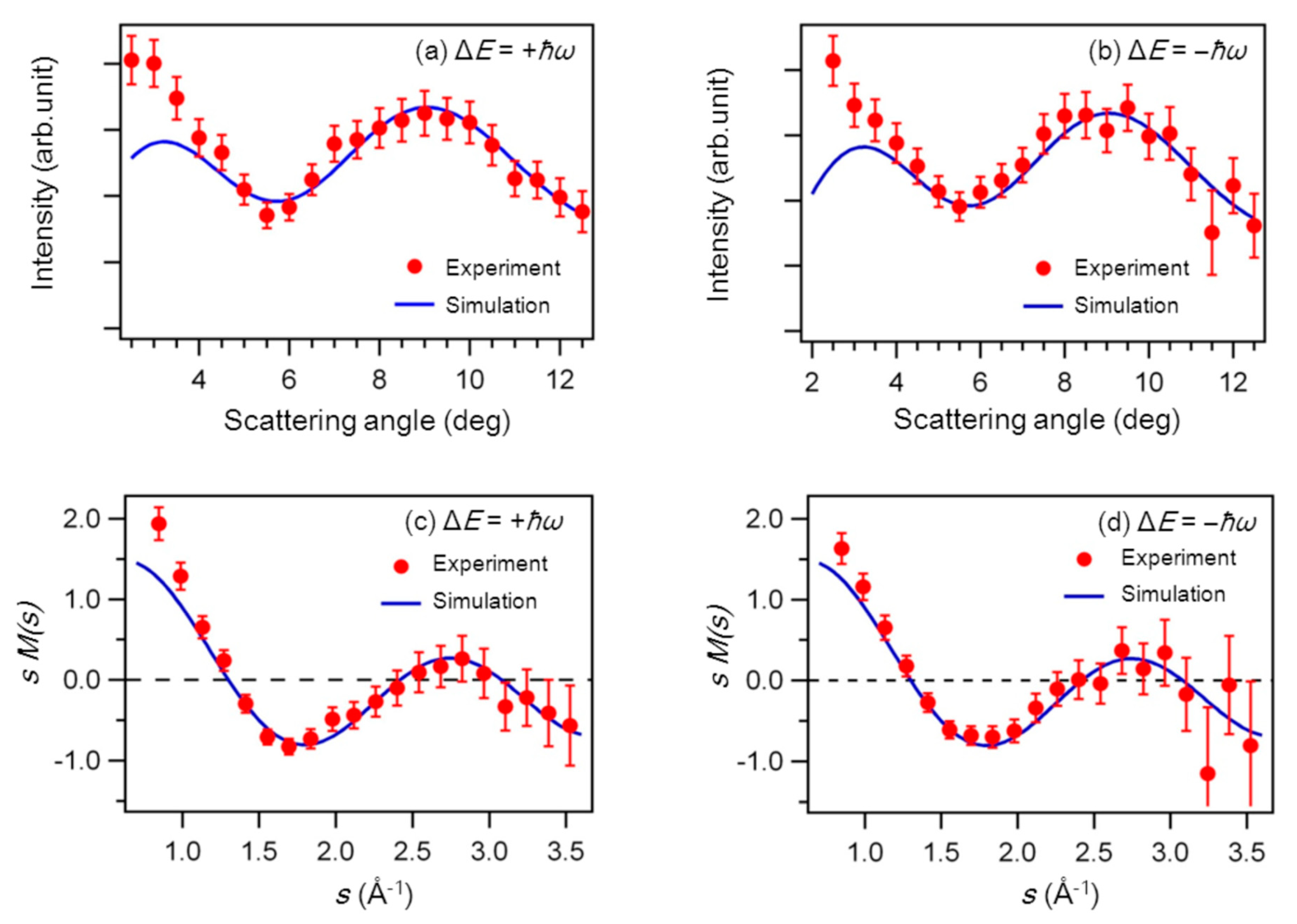
6.2. Light-Dressing Effect in Laser-Assisted Elastic Electron Scattering
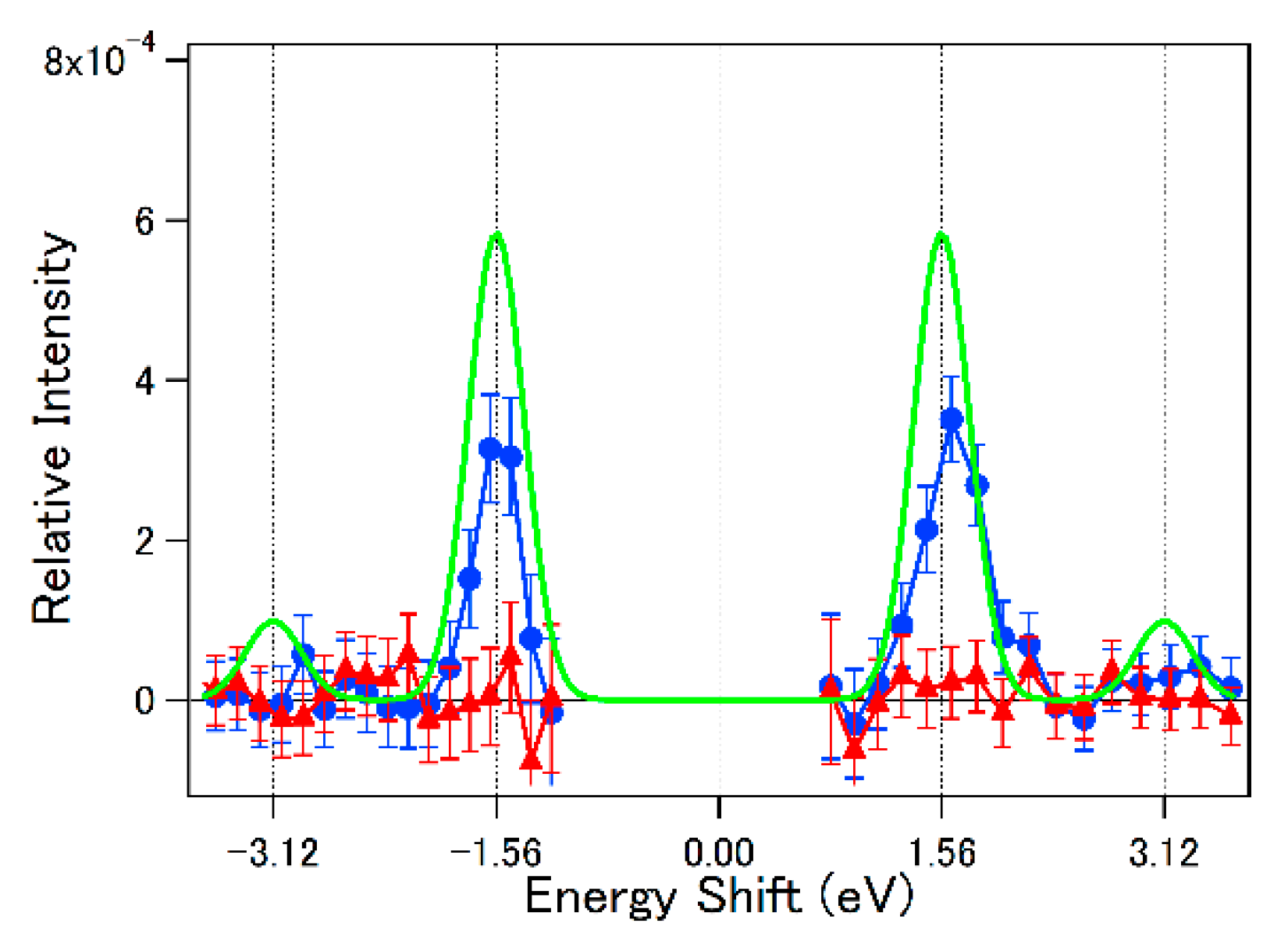
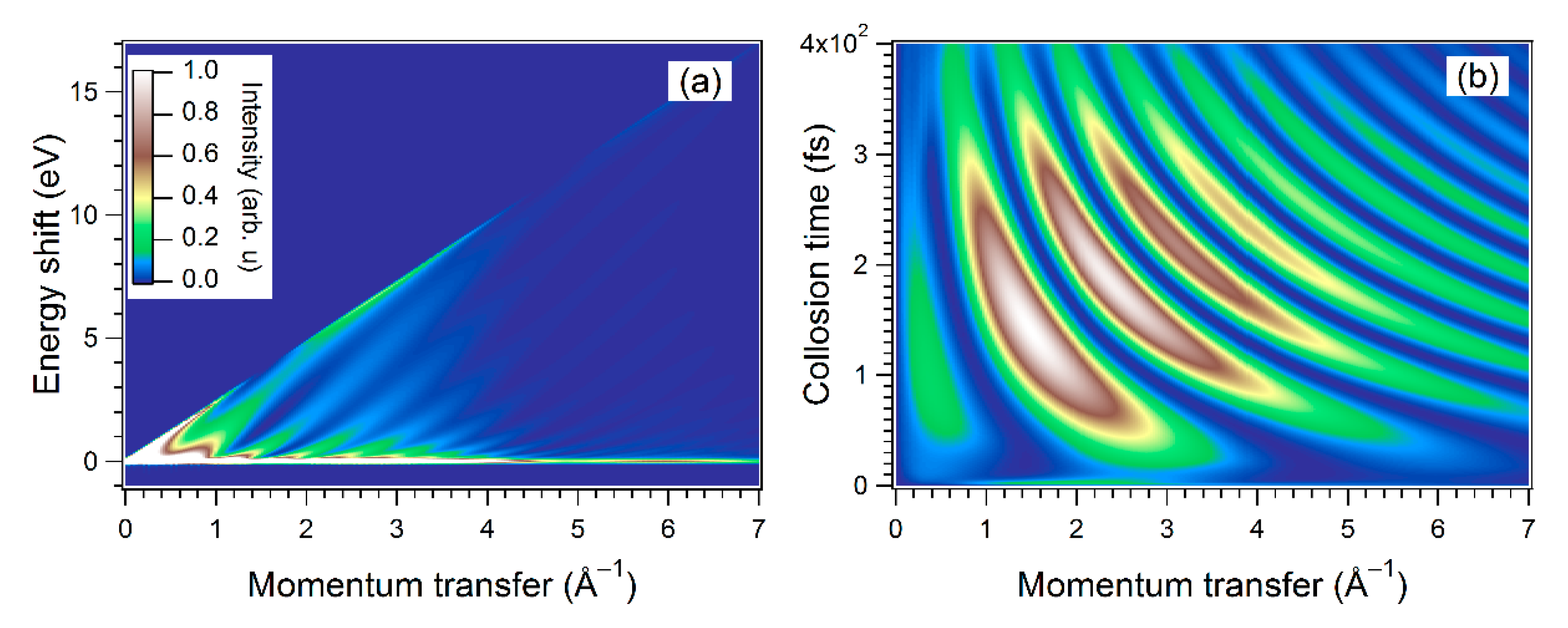
6.3. High-Order LAES Processes and Assignment of Collision Times
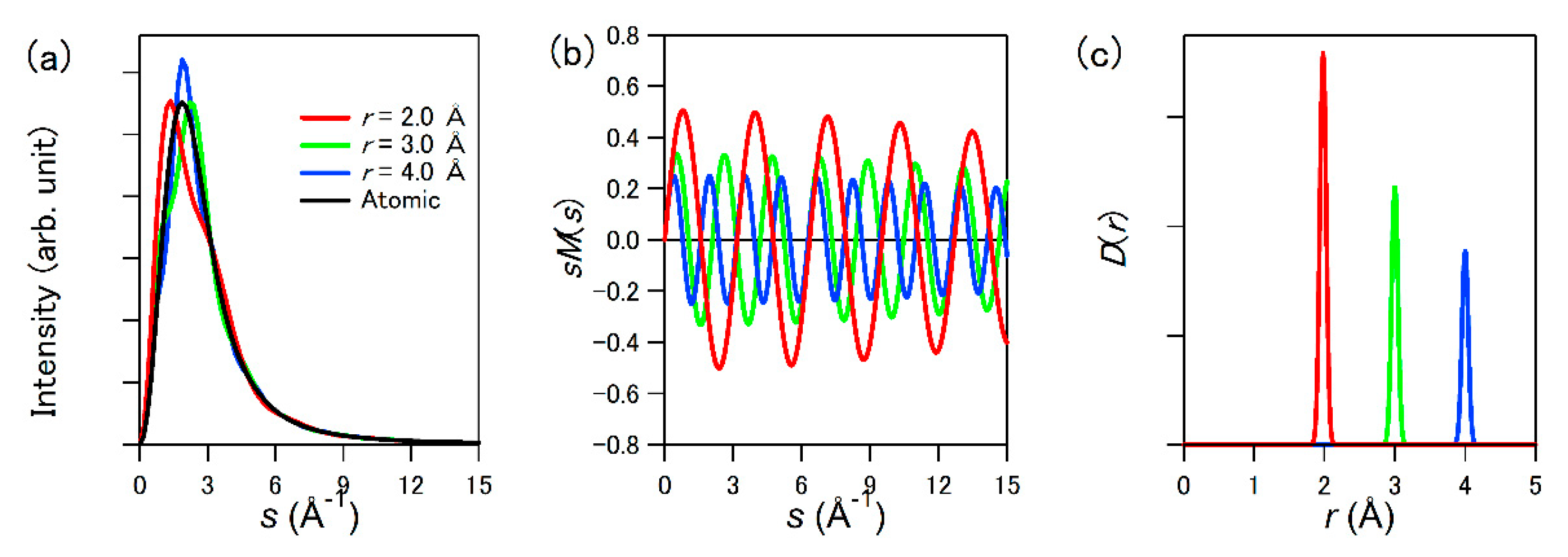
7. Ultrafast Gas Electron Diffraction by LAES Processes
7.1. Laser-Assisted Electron Diffraction
7.2. THz-Wave-Assisted Electron Diffraction
8. Future Prospects
Author Contributions
Funding
Conflicts of Interest
References
- Morgan, C.G. Laser-induced breakdown of gases. Rep. Prog. Phys. 1975, 38, 621–665. [Google Scholar] [CrossRef]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kulander, K.C.; Schafer, K.J.; Krause, J.L. Dynamics of Short-Pulse Excitation, Ionization and Harmonic Conversion. In Intercalation in Layered Materials; Springer Science and Business Media LLC: Berlin, Germany, 1993; Volume 316, pp. 95–110. [Google Scholar]
- Wilke, M.; Al-Obaidi, R.; Moguilevski, A.; Köthe, A.; Engel, N.; Metje, J.; Kiyan, I.Y.; Aziz, E. Laser-assisted electron scattering in strong-field ionization of dense water vapor by ultrashort laser pulses. New J. Phys. 2014, 16, 83032. [Google Scholar] [CrossRef]
- Barna, I.F.; Pocsai, M.A.; Varró, S. The influence of a strong infrared radiation field on the conductance properties of doped semiconductors. Eur. Phys. J. Appl. Phys. 2018, 84, 20101. [Google Scholar] [CrossRef]
- Weingartshofer, A.; Jung, C. Multiphoton free-free transitions. In Multiphoton Ionization of Atoms; Chin, S.L., Ed.; Academic Press: Toronto, ON, Canada, 1984; pp. 155–187. [Google Scholar]
- Masion, N.J. Laser-assisted electron-atom collisions. Rep. Prog. Phys. 1993, 56, 1275. [Google Scholar] [CrossRef]
- Ehlotzky, F.; Jaroń, A.; Kamiński, J. Electron–atom collisions in a laser field. Phys. Rep. 1998, 297, 63–153. [Google Scholar] [CrossRef]
- Kanya, R.; Morimoto, Y.; Yamanouchi, K. Observation of Laser-Assisted Electron-Atom Scattering in Femtosecond Intense Laser Fields. Phys. Rev. Lett. 2010, 105, 123202. [Google Scholar] [CrossRef]
- Morimoto, Y.; Kanya, R.; Yamanouchi, K. Light-Dressing Effect in Laser-Assisted Elastic Electron Scattering by Xe. Phys. Rev. Lett. 2015, 115, 123201. [Google Scholar] [CrossRef] [Green Version]
- Kanya, R.; Yamanouchi, K. Numerical simulation of THz-wave-assisted electron diffraction for ultrafast molecular imaging. Phys. Rev. A 2017, 95, 033416. [Google Scholar] [CrossRef]
- Bunkin, F.V.; Fedorov, M. Bremsstrahlung in a strong radiation field. Sov. Phys. JETP 1966, 22, 844. [Google Scholar]
- Gordon, W. Der Comptoneffekt nach der Schrödingerschen Theorie. Eur. Phys. J. A 1926, 40, 117–133. [Google Scholar]
- Volkov, D.M. Über eine Klasse von Lösungen der Diracschen Gleichung. Z. Phys. 1935, 94, 250. [Google Scholar]
- Kroll, N.M.; Watson, K.M. Charged-Particle Scattering in the Presence of a Strong Electromagnetic Wave. Phys. Rev. A 1973, 8, 804–809. [Google Scholar] [CrossRef] [Green Version]
- Jablonski, A.; Salvat, F.; Powell, C.J. NIST Electron Elastic-Scattering Cross-Section Database—Version 4.0. Natl. Inst. Stand. Technol. 2002. [Google Scholar]
- Gersten, J.I.; Mittleman, M.H. Electron scattering from atoms in the presence of a laser field. Phys. Rev. A 1976, 13, 123–130. [Google Scholar] [CrossRef]
- Mittleman, M.H. Electron scattering from atoms in the presence of a laser field. II. Phys. Rev. A 1976, 14, 1338–1344. [Google Scholar] [CrossRef]
- Mittleman, M.H. Electron scattering from atoms in the presence of a laser field. III. Phys. Rev. A 1977, 16, 1549–1551. [Google Scholar] [CrossRef]
- Mittleman, M.H. Electron scattering from atoms in the presence of a laser field. IV. Phys. Rev. A 1978, 18, 685–688. [Google Scholar] [CrossRef]
- Zon, B.A. Bremsstrahlung in collisions between electrons and atoms. Sov. Phys. JETP 1977, 46, 65. [Google Scholar]
- Zon, A.B.; Beilin, E.L. On the sum rule for multiphoton bremsstrahlung. J. Phys. B At. Mol. Phys. 1983, 16, L159–L161. [Google Scholar]
- Byron, F.W., Jr.; Joachain, C.J. Electron-atom collisions in a strong laser field. J. Phys. B At. Mol. Phys. 1984, 17, L295–L301. [Google Scholar] [CrossRef]
- Byron, F.W., Jr.; Francken, P.; Joachain, C.J. Laser-assisted elastic electron-atom collisions. J. Phys. B At. Mol. Phys. 1987, 20, 5487–5503. [Google Scholar] [CrossRef]
- Faisal, F.H.M. Theory of Multiphoton Processes; Springer: New York, NY, USA, 1987. [Google Scholar]
- Dörr, M.; Joachain, C.J.; Potvliege, R.M.; Vucic, S. Born-Floquet theory of laser-assisted electron-atom collisions. Phys. Rev. A 1994, 49, 4852–4863. [Google Scholar] [CrossRef] [PubMed]
- Burke, P.G.; Francken, P.; Joachain, C.J. R-matrix-Floquet theory of multiphoton processes. J. Phys. B At. Mol. Opt. Phys. 1991, 24, 761–790. [Google Scholar] [CrossRef]
- Terao-Dunseath, M.; Dunseath, K.M. R-matrix Floquet theory for laser-assisted electron-atom scattering. J. Phys. B 2002, 35, 125. [Google Scholar] [CrossRef]
- Cionga, A.; Dimou, L.; Faisal, F.H.M. Differential cross sections of low-energy electron - hydrogen scattering in a laser field. J. Phys. B At. Mol. Opt. Phys. 1997, 30, L361–L370. [Google Scholar] [CrossRef]
- Moore, L.; Lysaght, M.; Nikolopoulos, L.; Parker, J.; Van Der Hart, H.; Taylor, K.; Nikolopoulos, L. The RMT method for many-electron atomic systems in intense short-pulse laser light. J. Mod. Opt. 2011, 58, 1132–1140. [Google Scholar] [CrossRef]
- Andrick, D.; Langhans, L. Measurement of free-free transitions in e--Ar scattering. J. Phys. B At. Mol. Phys. 1976, 9, L459–L461. [Google Scholar] [CrossRef]
- Andrick, D.; Langhans, L. Measurement of the free-free cross section of e--Ar scattering. J. Phys. B At. Mol. Phys. 1978, 11, 2355–2360. [Google Scholar] [CrossRef]
- Langhans, L. Resonance structures in the free-free cross section of e--Ar scattering. J. Phys. B At. Mol. Phys. 1978, 11, 2361–2366. [Google Scholar] [CrossRef]
- Andrick, D.; Bader, H. Resonance structures in the cross section for free-free radiative transitions in e--He scattering. J. Phys. B At. Mol. Phys. 1984, 17, 4549–4555. [Google Scholar] [CrossRef]
- Bader, H. Resonance structures in the cross section for free-free radiative transitions in e--Ne and e--Ar scattering. J. Phys. B At. Mol. Phys. 1986, 19, 2177–2188. [Google Scholar] [CrossRef]
- Weingartshofer, A.; Holmes, J.K.; Caudle, G.; Clarke, E.M.; Krüger, H. Direct Observation of Multiphoton Processes in Laser-Induced Free-Free Transitions. Phys. Rev. Lett. 1977, 39, 269–270. [Google Scholar] [CrossRef]
- Wallbank, B.; Holmes, J.K.; MacIsaac, S.C.; Weingartshofer, A. Resonance structures in free-free cross sections for electron-helium scattering. J. Phys. B At. Mol. Opt. Phys. 1992, 25, 1265–1277. [Google Scholar] [CrossRef]
- Wallbank, B.; Holmes, J.K. Laser-assisted elastic electron-atom collisions. Phys. Rev. A 1993, 48, R2515–R2518. [Google Scholar] [CrossRef] [PubMed]
- Wallbank, B.; Holmes, J.K. Laser-assisted elastic electron-atom collisions: Low electron energy and small scattering angle. J. Phys. B At. Mol. Opt. Phys. 1994, 27, 1221–1231. [Google Scholar] [CrossRef]
- Wallbank, B.; Holmes, J.K. Low-energy electron - helium scattering in a laser field. J. Phys. B At. Mol. Opt. Phys. 1996, 29, 5881–5887. [Google Scholar] [CrossRef]
- Wallbank, B.; Holmes, J.K. Laser-assisted elastic electron scattering from helium. Can. J. Phys. 2001, 79, 1237–1246. [Google Scholar] [CrossRef]
- Nehari, D.; Holmes, J.; Dunseath, K.M.; Terao-Dunseath, M. Experimental and theoretical study of free–free electron–helium scattering in a CO2 laser field. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 25203. [Google Scholar] [CrossRef]
- Weingartshofer, A.; Clarke, E.M.; Holmes, J.K.; Jung, C. Experiments on multiphoton free-free transitions. Phys. Rev. A 1979, 19, 2371–2376. [Google Scholar] [CrossRef]
- Weingartshofer, A.; Holmes, J.K.; Sabbagh, J.; Chin, S.L. Electron scattering in intense laser fields. J. Phys. B At. Mol. Phys. 1983, 16, 1805–1817. [Google Scholar] [CrossRef]
- Wallbank, B.; Connors, V.W.; Holmes, J.K.; Weingartshofer, A. Experimental differential cross sections for one-photon free-free transitions. J. Phys. B At. Mol. Phys. 1987, 20, L833–L838. [Google Scholar] [CrossRef]
- Wallbank, B.; Holmes, J.K.; Weingartshofer, A. Experimental differential cross sections for multiphoton free-free transitions. J. Phys. B At. Mol. Phys. 1987, 20, 6121–6138. [Google Scholar] [CrossRef]
- Wallbank, B.; Holmes, J.K. Differential cross sections for laser-assisted elastic electron scattering from argon. J. Phys. B At. Mol. Opt. Phys. 1994, 27, 5405–5418. [Google Scholar] [CrossRef]
- Musa, O.M.; Macdonald, A.; Tidswell, L.; Holmes, J.; Wallbank, B. Laser-induced free–free transitions in elastic electron scattering from CO2. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 175201. [Google Scholar] [CrossRef]
- Mason, N.J.; Newell, W.R. Simultaneous electron-photon excitation of the helium 23S state. J. Phys. B At. Mol. Phys. 1987, 20, L323–L325. [Google Scholar] [CrossRef]
- Wallbank, B.; Holmes, J.K.; Blanc, L.; Weingartshofer, A. Simultaneous off-shell excitation of He 23S by an electron and one or more photons. Eur. Phys. J. D 1988, 10, 467–472. [Google Scholar] [CrossRef]
- Wallbank, B.; Holmes, J.K.; Weingartshofer, A. Simultaneous electron-photon excitation of metastable states of rare-gas atoms. J. Phys. B At. Mol. Opt. Phys. 1989, 22, L615–L619. [Google Scholar] [CrossRef]
- Mason, N.J.; Newell, W.R. Simultaneous electron-photon excitation of the helium 23S state. J. Phys. B At. Mol. Opt. Phys. 1989, 22, 777–796. [Google Scholar] [CrossRef]
- Mason, N.J.; Newell, W.R. The polarisation dependence of the simultaneous electron-photon excitation cross section of the helium 23S state. J. Phys. B At. Mol. Opt. Phys. 1990, 23, L179–L182. [Google Scholar] [CrossRef]
- Wallbank, B.; Holmes, J.K.; Weingartshofer, A. Simultaneous electron-photon excitation of He 23S: An experimental investigation of the effects of laser intensity and polarisation. J. Phys. B At. Mol. Opt. Phys. 1990, 23, 2997–3005. [Google Scholar] [CrossRef]
- Luan, S.; Hippler, R.; Lutz, H.O. Simultaneous electron-photon excitation of helium (ħω=1.17 eV). J. Phys. B 1991, 24, 3241. [Google Scholar] [CrossRef]
- Wallbank, B.; Holmes, J.K.; Weingartshofer, A. Absorption and emission of radiation during electron excitation of the 2 1S and 2 1P states of helium. Phys. Rev. A 1989, 40, 5461–5463. [Google Scholar] [CrossRef]
- Wallbank, B.; Holmes, J.K.; Weingartshofer, A. Electron impact excitation of He 21P in the presence of a nonresonant laser field. Can. J. Phys. 1993, 71, 326–333. [Google Scholar] [CrossRef]
- Morimoto, Y.; Kanya, R.; Yamanouchi, K. Laser-assisted electron diffraction for femtosecond molecular imaging. J. Chem. Phys. 2014, 140, 64201. [Google Scholar] [CrossRef] [PubMed]
- Itatani, J.; Quéré, F.; Yudin, G.L.; Ivanov, M.Y.; Krausz, F.; Corkum, P.B. Attosecond Streak Camera. Phys. Rev. Lett. 2002, 88, 173903. [Google Scholar] [CrossRef] [PubMed]
- Scrinzi, A.; Kitzler, M.; Milosevic, N.; Krausz, F.; Brabec, T. Quantum Theory of Attosecond XUV Pulse Measurement by Laser Dressed Photoionization. Phys. Rev. Lett. 2002, 88, 173904. [Google Scholar]
- Baker, S.; Robinson, J.S.; Haworth, C.A.; Teng, H.; Smith, R.A.; Chirila, C.C.; Lein, M.; Tisch, J.W.G.; Marangos, J.P. Probing Proton Dynamics in Molecules on an Attosecond Time Scale. Science 2006, 312, 424–427. [Google Scholar] [CrossRef] [Green Version]
- Blaga, C.I.; Xu, J.; DiChiara, A.D.; Sistrunk, E.; Zhang, K.; Agostini, P.; Miller, T.A.; DiMauro, L.F.; Lin, C.D. Imaging ultrafast molecular dynamics with laser-induced electron diffraction. Nature 2012, 483, 194–197. [Google Scholar] [CrossRef]
- Kanya, R.; Morimoto, Y.; Yamanouchi, K. Apparatus for laser-assisted electron scattering in femtosecond intense laser fields. Rev. Sci. Instrum. 2011, 82, 123105. [Google Scholar] [CrossRef]
- Williamson, J.C.; Zewail, A.H. Ultrafast electron diffraction. Velocity mismatch and temporal resolution in crossed-beam experiments. Chem. Phys. Lett. 1993, 209, 10–16. [Google Scholar] [CrossRef]
- Toffoletto, F.; Leckey, R.; Riley, J. Design criteria for an angle resolved electron spectrometer of novel toroidal geometry. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 1985, 12, 282–297. [Google Scholar] [CrossRef]
- Ishida, K.; Morimoto, Y.; Kanya, R.; Yamanouchi, K. High-order multiphoton laser-assisted elastic electron scattering by Xe in a femtosecond near-infrared intense laser field: Plateau in energy spectra of scattered electrons. Phys. Rev. A 2017, 95, 023414. [Google Scholar] [CrossRef]
- Deharak, B.A.; Ladino, L.; Macadam, K.B.; Martin, N.L.S. High-energy electron-helium scattering in a Nd:YAG laser field. Phys. Rev. A 2011, 83, 022706. [Google Scholar] [CrossRef]
- Deharak, B.A.; Nosarzewski, B.; Siavashpouri, M.; Martin, N.L.S. Electron-helium scattering in a 1.17 eV laser field: The effect of polarization direction. Phys. Rev. A 2014, 90, 032709. [Google Scholar] [CrossRef]
- Deharak, A.B.; Kim, B.N.; Weaver, C.M.; Martin, N.L.S.; Siavashpouri, M.; Nosarzewski, B. Effects of polarization direction on laser-assisted free–free scattering. Plasma Sources Sci. Technol. 2016, 25, 35021. [Google Scholar] [CrossRef]
- Martin, N.L.S.; Deharak, B.A. Test of target independence for free-free scattering in a Nd:YAG laser field. Phys. Rev. A 2016, 93, 013403. [Google Scholar] [CrossRef]
- Martin, N.L.S.; Weaver, C.M.; Kim, B.N.; Deharak, B.A. Angular distribution of electrons elastically scattered from Ar in the presence of a 1.17 eV laser field. Phys. Rev. A 2019, 99, 032708. [Google Scholar] [CrossRef] [Green Version]
- Martin, N.L.S.; Kim, B.N.; Deharak, A.B.; Weaver, C.M. Free–free experiments: The search for dressed atom effects. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 134003. [Google Scholar] [CrossRef]
- Bishop, D.M. Aspects of non-Linear-optical calculations. Adv. Quantum Chem. 1995, 15, 1. [Google Scholar]
- Yamanouchi, K.; Sugue, M.; Takeo, H.; Matsumura, C.; Kuchitsu, K. Molecular structure and conformation of 1-chloropropane as determined by gas electron diffraction and microwave spectroscopy. J. Phys. Chem. 1984, 88, 2315–2320. [Google Scholar] [CrossRef]
- Hargittai, I.; Hargittai, M. Stereochemical Applications of Gas Phase Electron Diffraction, Part A.; Wiley-VCH Verlag GmbH: New York, NY, USA, 1988. [Google Scholar]
- Yamanouchi, K. Quantum Mechanics of Molecular Structures; Springer Science and Business Media LLC: Berlin, Germany, 2012. [Google Scholar]
- Srinivasan, R.; Lobastov, V.A.; Zewail, A.H.; Ruan, C.Y.; Ruan, C. Ultrafast Electron Diffraction (UED). A New Development for the 4D Determination of Transient Molecular Structures. Helv. Chim. Acta 2003, 34, 86. [Google Scholar] [CrossRef]
- Ihee, H.; Lobastov, V.A.; Gomez, U.M.; Goodson, B.M.; Srinivasan, R.; Ruan, C.Y.; Zewail, A.H. Direct Imaging of Transient Molecular Structures with Ultrafast Diffraction. Science 2001, 291, 458–462. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guehr, M.; Shen, X.; Li, R.; Vecchione, T.; Corbett, J.; Fry, A.; Hartmann, N.; Hast, C.; Hegazy, K.; Jobe, K.; et al. Diffractive Imaging of Coherent Nuclear Motion in Isolated Molecules. Phys. Rev. Lett. 2016, 117, 153002. [Google Scholar] [Green Version]
- Yang, J.; Zhu, X.; Wolf, T.J.A.; Li, Z.; Nunes, J.P.F.; Coffee, R.; Cryan, J.P.; Gühr, M.; Hegazy, K.; Heinz, T.F.; et al. Imaging CF3I conical intersection and photodissociation dynamics with ultrafast electron diffraction. Science 2018, 361, 64. [Google Scholar] [CrossRef] [PubMed]
- Kanya, R.; Morimoto, Y.; Yamanouchi, K. Laser-Assisted Electron Scattering and Diffraction in Ultrashort Intense Laser Fields. In Springer Series in Chemical Physics; Springer Science and Business Media LLC: Berlin, Germany, 2014; Volume 106, pp. 1–16. [Google Scholar]
- Morimoto, Y.; Kanya, R.; Yamanouchi, K. Laser-Assisted Electron Diffraction for Probing Femtosecond Nuclear Dynamics of Gas-Phase Molecules. In 19th International Conference on Ultrafast Phenomena; OSA Technical Digest (online), paper 09.Wed.C.2; Optical Society of America: Washington, DC, USA, 2014. [Google Scholar]
- Morino, Y.; Nakamura, Y.; Iijima, T. Mean square amplitudes and force constants of tetrahedral molecules. I. Carbon tetrachloride and germanium tetrachloride. J. Chem. Phys. 1960, 32, 643. [Google Scholar] [CrossRef]
- Zuo, T.; Bandrauk, A.; Corkum, P. Laser-induced electron diffraction: A new tool for probing ultrafast molecular dynamics. Chem. Phys. Lett. 1996, 259, 313–320. [Google Scholar] [CrossRef]
- Morishita, T.; Le, A.T.; Chen, Z.; Lin, C.D. Accurate Retrieval of Structural Information from Laser-Induced Photoelectron and High-Order Harmonic Spectra by Few-Cycle Laser Pulses. Phys. Rev. Lett. 2008, 100, 013903. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Le, A.T.; Morishita, T.; Lin, C.D. Quantitative rescattering theory for laser-induced high-energy plateau photoelectron spectra. Phys. Rev. A 2009, 79, 033409. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.D.; Le, A.T.; Chen, Z.; Morishita, T.; Lucchese, R. Strong-field rescattering physics—Self-imaging of a molecule by its own electrons. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 122001. [Google Scholar] [CrossRef]
- Meckel, M.; Comtois, D.; Zeidler, D.; Staudte, A.; Pavičić, D.; Bandulet, H.C.; Pépin, H.; Kieffer, J.C.; Dörner, R.; Villeneuve, D.M.; et al. Laser-Induced Electron Tunneling and Diffraction. Science 2008, 320, 1478. [Google Scholar] [CrossRef] [PubMed]
- Okunishi, M.; Niikura, H.; Lucchese, R.R.; Morishita, T.; Ueda, K. Extracting Electron-Ion Differential Scattering Cross Sections for Partially Aligned Molecules by Laser-Induced Rescattering Photoelectron Spectroscopy. Phys. Rev. Lett. 2011, 106, 063001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Blaga, C.I.; Xu, J.; Di Chiara, A.D.; Sistrunk, E.; Zhang, K.; Agostini, P.; Miller, T.A.; DiMauro, L.F.; Lin, C.D. Imaging ultrafast molecular dynamics with laser-induced electron diffraction. Nature 2012, 483, 194–197. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Blaga, C.I.; Zhang, K.; Lai, Y.H.; Lin, C.D.; Miller, T.A.; Agostini, P.; DiMauro, L.F. Diffraction using laser-driven broadband electron wave packets. Nat. Commun. 2014, 5, 4635. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pullen, M.G.; Wolter, B.; Le, A.T.; Baudisch, M.; Sclafani, M.; Pires, H.; Schröter, C.D.; Ullrich, J.; Moshammer, R.; Pfeifer, T.; et al. Influence of orbital symmetry on diffraction imaging with rescattering electron wave packets. Nat. Commun. 2016, 7, 11922. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pullen, M.G.; Wolter, B.; Le, A.T.; Baudisch, M.; Hemmer, M.; Senftleben, A.; Schröter, C.D.; Ullrich, J.; Moshammer, R.; Lin, C.D.; et al. Imaging an aligned polyatomic molecule with laser-induced electron diffraction. Nat. Commun. 2015, 6, 7262. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wolter, B.; Pullen, M.G.; Le, A.T.; Baudisch, M.; Doblhoff-Dier, K.; Senftleben, A.; Hemmer, M.; Schröter, C.D.; Ullrich, J.; Pfeifer, T.; et al. Ultrafast electron diffraction imaging of bond breaking in di-ionized acetylene. Science 2016, 354, 308–312. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Amini, K.; Sclafani, M.; Steinle, T.; Le, A.T.; Sanchez, A.; Müller, C.; Steinmetzer, J.; Yue, L.; Saavedra, J.R.M.; Hemmer, M.; et al. Imaging the Renner–Teller effect using laser-induced electron diffraction. Proc. Natl. Acad. Sci. USA 2019, 116, 8173–8177. [Google Scholar] [CrossRef]
- Fuest, H.; Lai, Y.H.; Blaga, C.I.; Suzuki, K.; Xu, J.; Rupp, P.; Li, H.; Wnuk, P.; Agostini, P.; Yamazaki, K.; et al. Diffractive Imaging of C60 Structural Deformations Induced by Intense Femtosecond Midinfrared Laser Fields. Phys. Rev. Lett. 2019, 122, 053002. [Google Scholar] [CrossRef]
- Nomura, Y.; Shirai, H.; Ishii, K.; Tsurumachi, N.; Voronin, A.A.; Zheltikov, A.M.; Fuji, T. Phase-stable sub-cycle mid-infrared conical emission from filamentation in gases. Opt. Express 2012, 20, 24741–24747. [Google Scholar] [CrossRef]
- Krogen, P.; Suchowski, H.; Liang, H.; Flemens, N.; Hong, K.H.; Kärtner, F.X.; Moses, J. Generation and multi-octave shaping of mid-infrared intense single-cycle pulses. Nat. Photonics 2017, 11, 222–226. [Google Scholar] [CrossRef]
- Elu, U.; Baudisch, M.; Pires, H.; Tani, F.; Frosz, M.H.; Köttig, F.; Ermolov, A.; Russell, P.S.; Biegert, J. High average power and single-cycle pulses from a mid-IR optical parametric chirped pulse amplifier. Optica 2017, 4, 1024. [Google Scholar] [CrossRef]
- Wang, P.; Li, Y.; Li, W.; Su, H.; Shao, B.; Li, S.; Wang, C.; Wang, D.; Zhao, R.; Peng, Y.; et al. 26 mJ/100 Hz CEP-stable near-single-cycle 4 μm laser based on OPCPA and hollow-core fiber compression. Opt. Lett. 2018, 43, 2197–2200. [Google Scholar] [CrossRef] [PubMed]
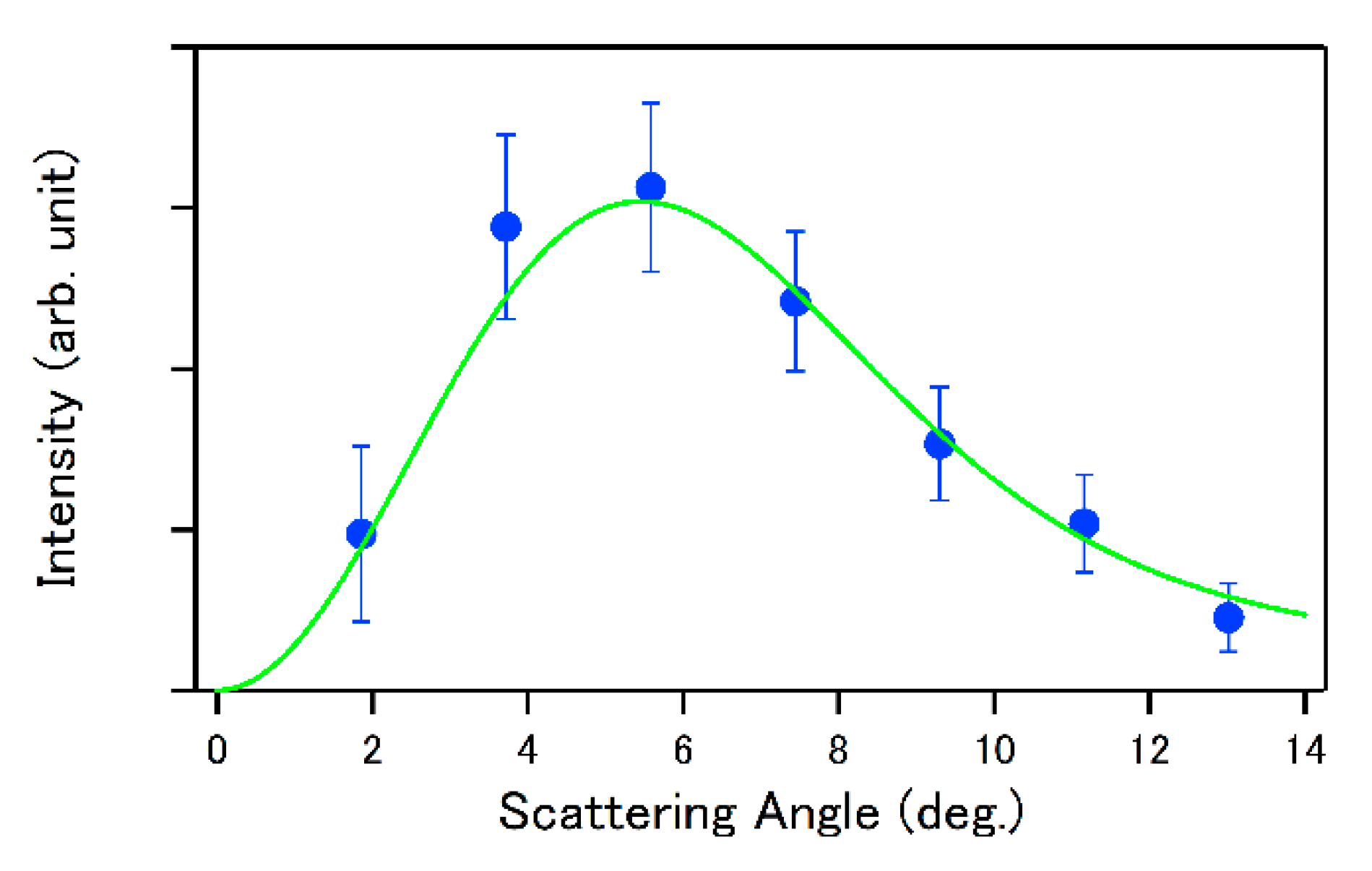
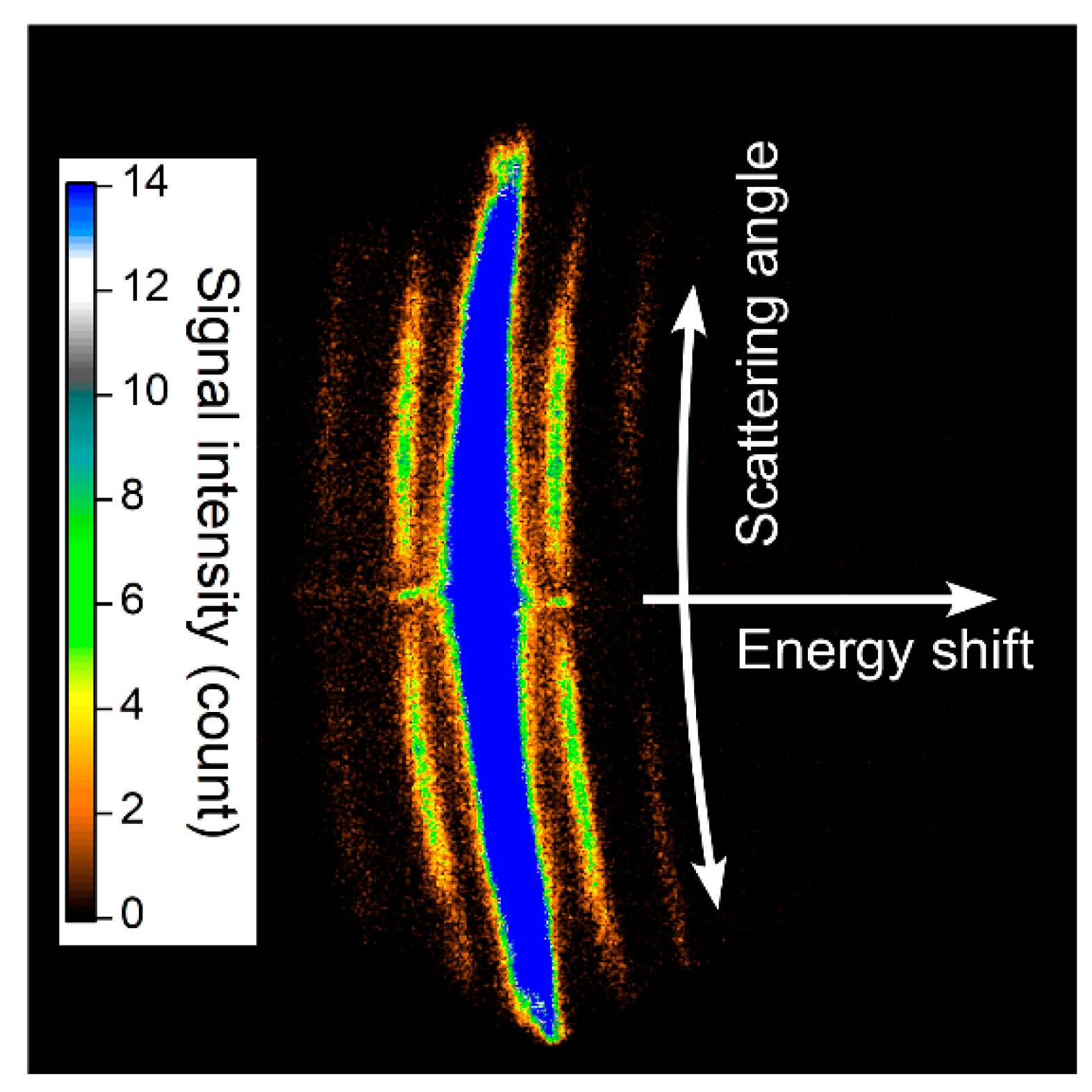
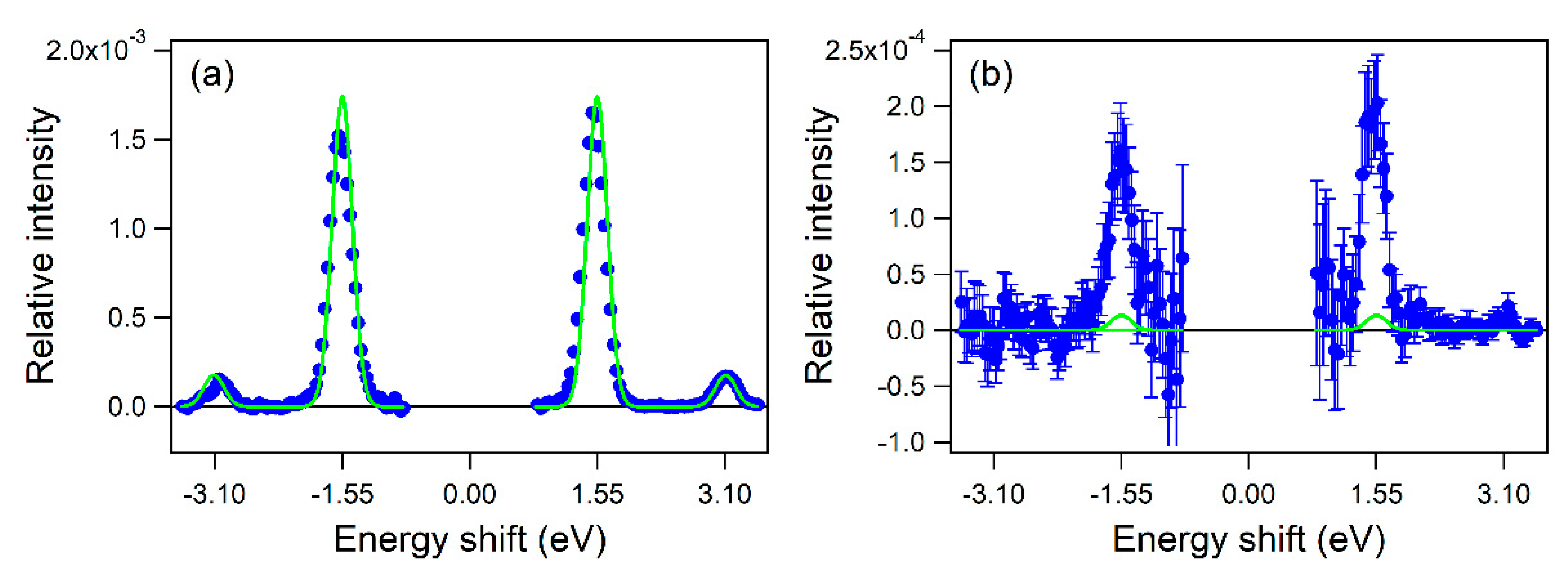
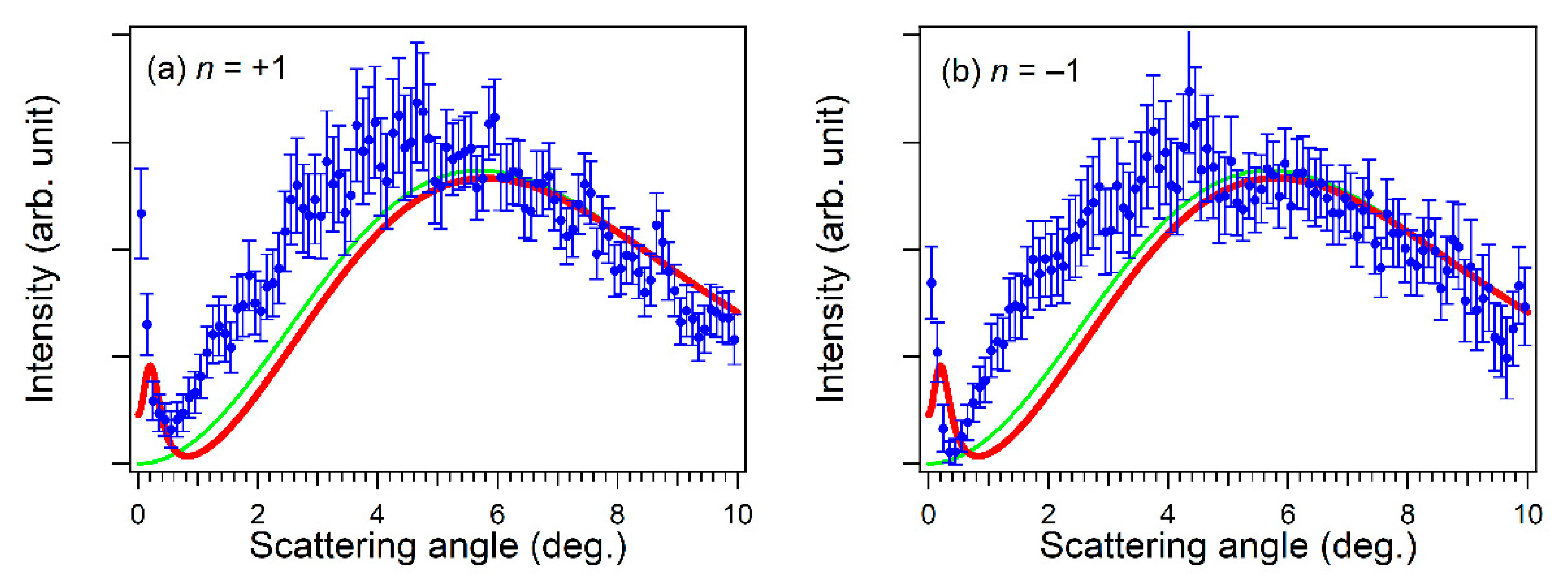


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanya, R.; Yamanouchi, K. Femtosecond Laser-Assisted Electron Scattering for Ultrafast Dynamics of Atoms and Molecules. Atoms 2019, 7, 85. https://doi.org/10.3390/atoms7030085
Kanya R, Yamanouchi K. Femtosecond Laser-Assisted Electron Scattering for Ultrafast Dynamics of Atoms and Molecules. Atoms. 2019; 7(3):85. https://doi.org/10.3390/atoms7030085
Chicago/Turabian StyleKanya, Reika, and Kaoru Yamanouchi. 2019. "Femtosecond Laser-Assisted Electron Scattering for Ultrafast Dynamics of Atoms and Molecules" Atoms 7, no. 3: 85. https://doi.org/10.3390/atoms7030085
APA StyleKanya, R., & Yamanouchi, K. (2019). Femtosecond Laser-Assisted Electron Scattering for Ultrafast Dynamics of Atoms and Molecules. Atoms, 7(3), 85. https://doi.org/10.3390/atoms7030085



