Electron-Impact Dissociation of Vibrationally-Excited Molecular Hydrogen into Neutral Fragments
Abstract
1. Introduction
2. Theory
2.1. Spheroidal Molecular CCC Method
2.2. Dissociative Excitation
2.3. Excitation-Radiative-Decay Dissociation
2.4. Constructing the Dissociation Cross Section
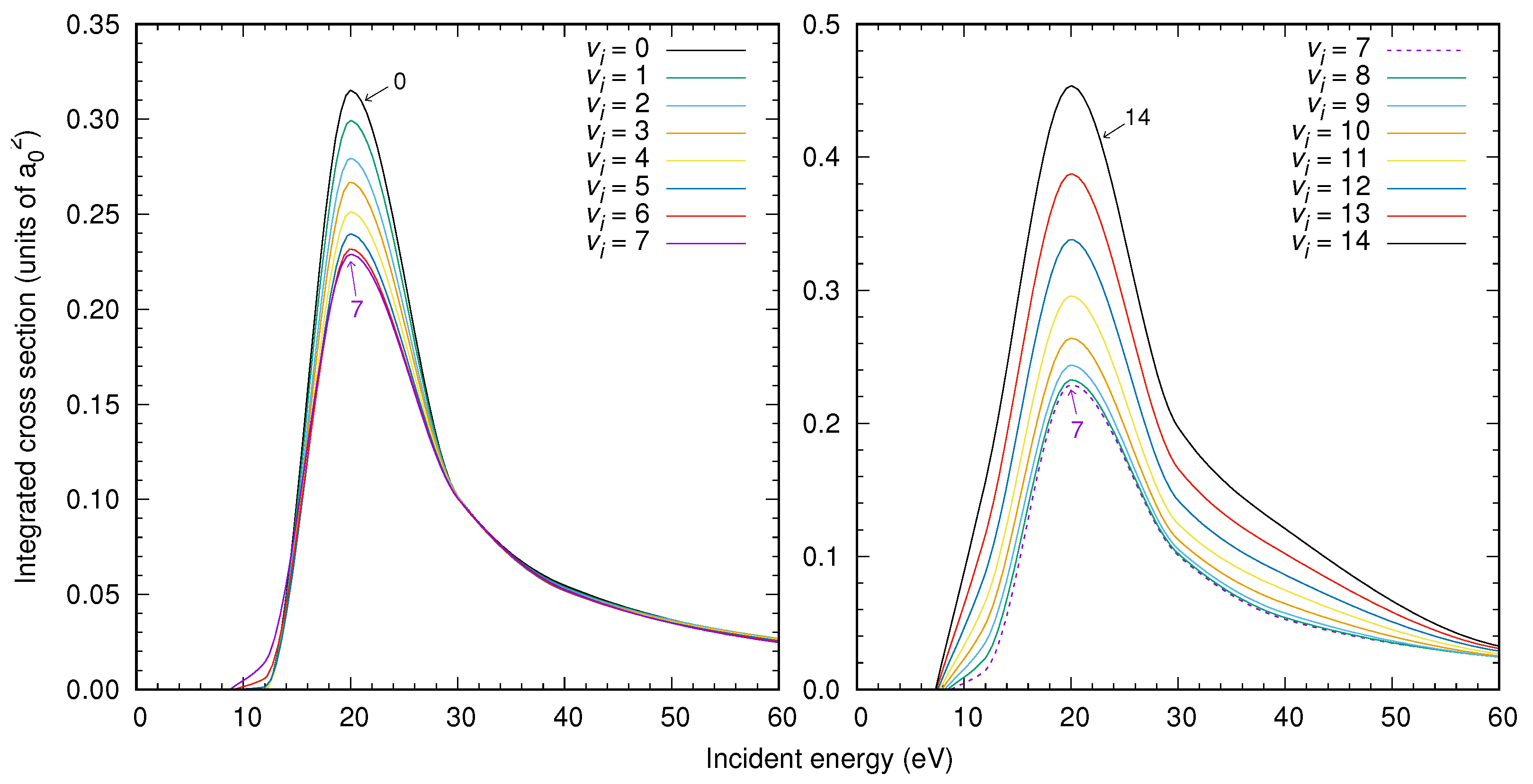
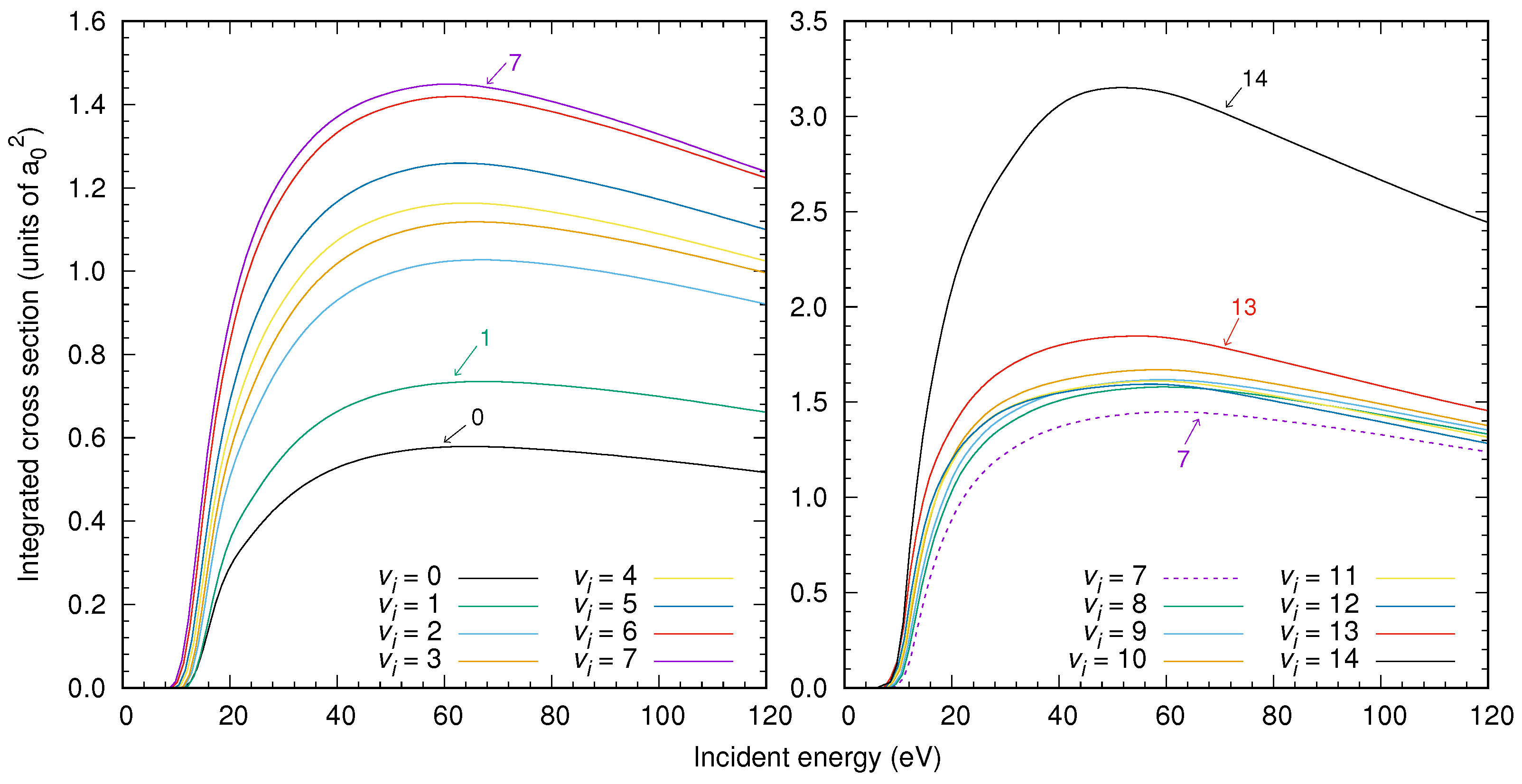
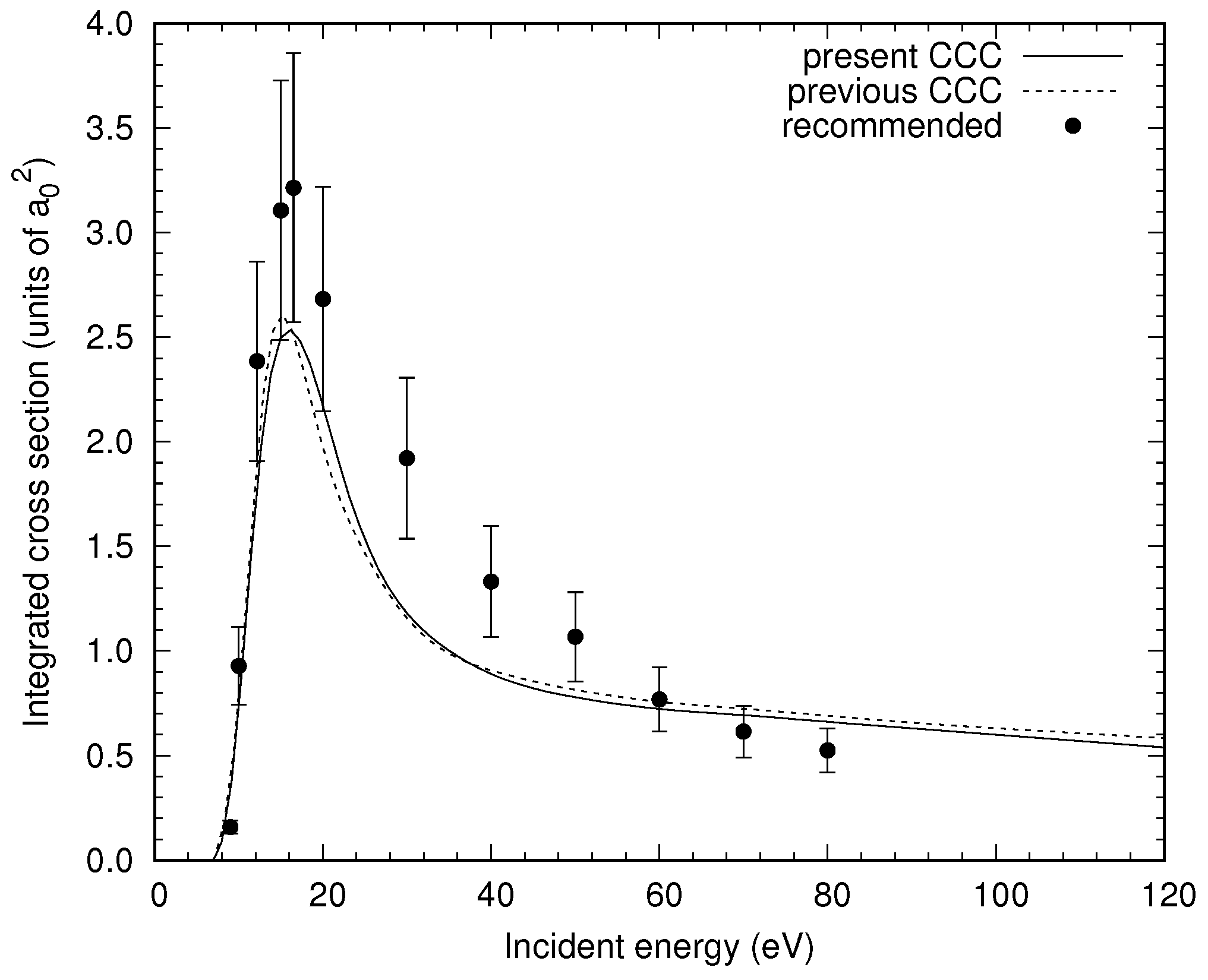
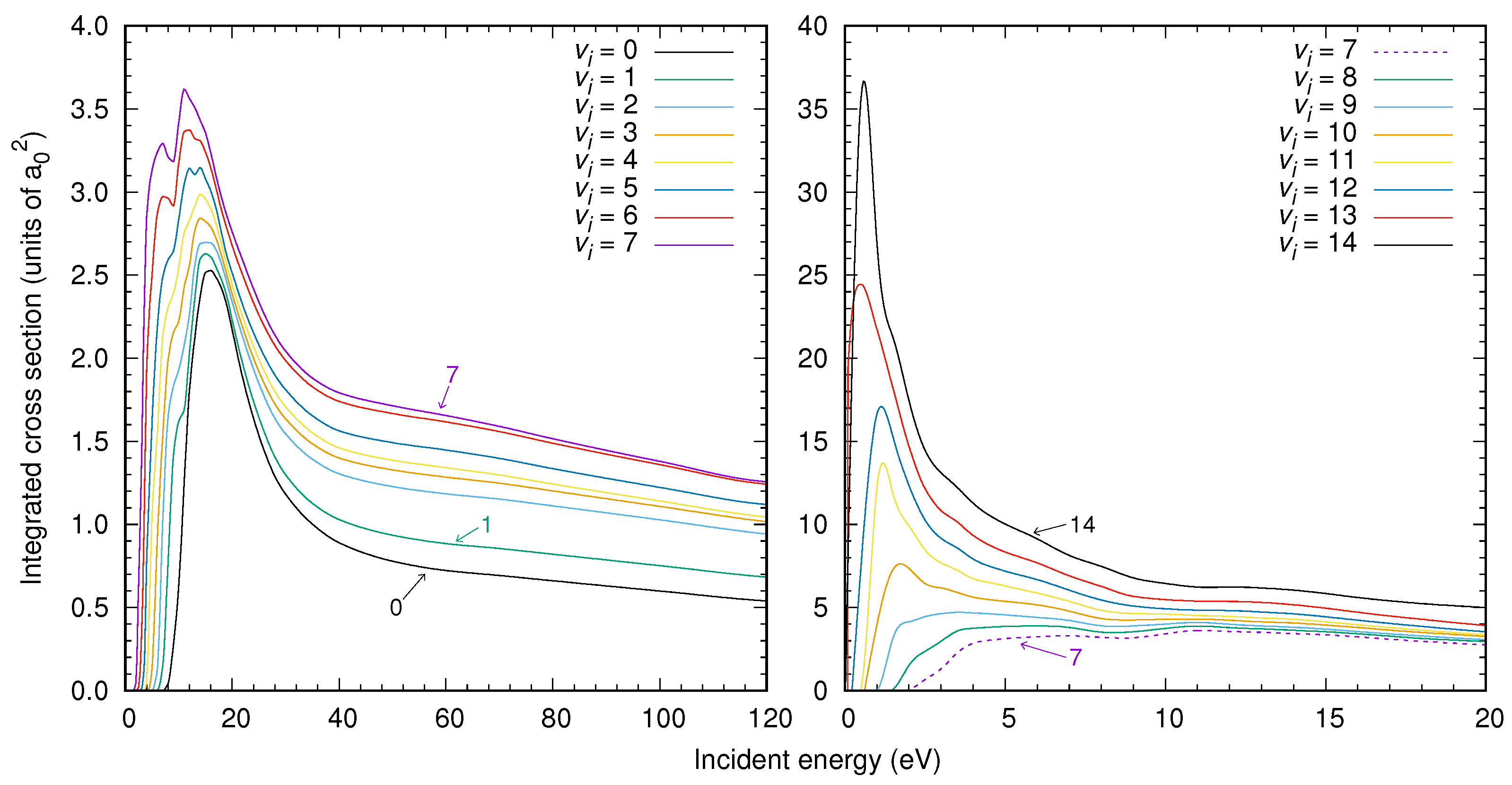
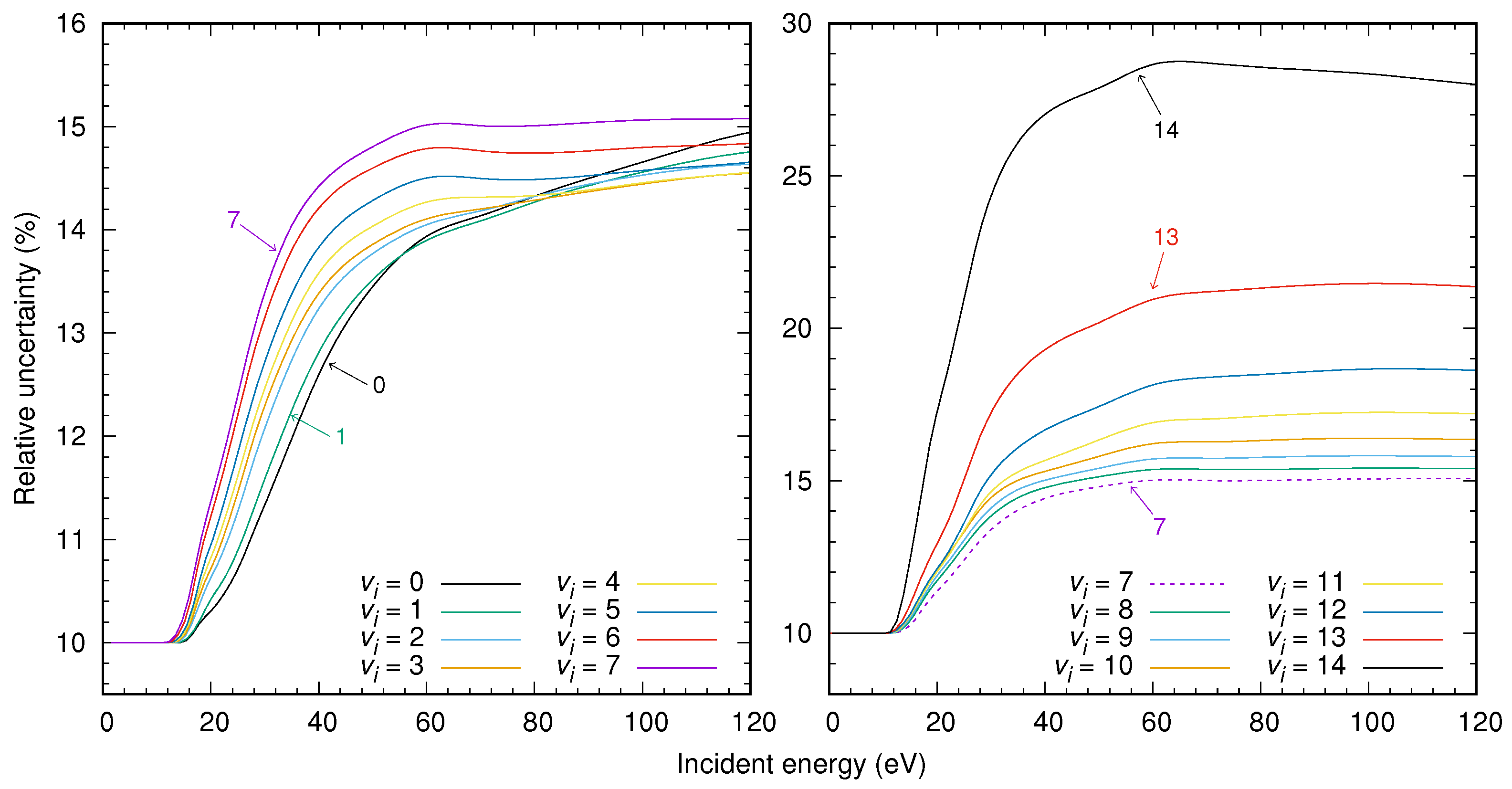
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Liu, X.; Ahmed, S.M.; Multari, R.A.; James, G.K.; Ajello, J.M. High-resolution electron-impact study of the far-ultraviolet emission spectrum of molecular hydrogen. Astrophys. J. Suppl. Ser. 1995, 101, 375–399. [Google Scholar] [CrossRef]
- Sawada, K.; Fujimoto, T. Effective ionization and dissociation hydrogen in plasma. J. Appl. Phys. 1995, 78, 2913–2924. [Google Scholar] [CrossRef]
- Jonin, C.; Liu, X.; Ajello, J.M.; James, G.K.; Abgrall, H. High resolution electron-impact emission spectrum of H2. I. Cross sections and emission yields 900–1200 Å. Astrophys. J. Suppl. Ser. 2000, 129, 247–266. [Google Scholar] [CrossRef]
- Yoon, J.S.; Song, M.Y.; Han, J.M.; Hwang, S.H.; Chang, W.S.; Lee, B.; Itikawa, Y. Cross Sections for Electron Collisions with Hydrogen Molecules. J. Phys. Chem. Ref. Data 2008, 37, 913–931. [Google Scholar] [CrossRef]
- Corrigan, S.J.B. Dissociation of Molecular Hydrogen by Electron Impact. J. Chem. Phys. 1965, 43, 4381. [Google Scholar] [CrossRef]
- Scarlett, L.H.; Tapley, J.K.; Fursa, D.V.; Zammit, M.C.; Savage, J.S.; Bray, I. Electron-impact dissociation of molecular hydrogen into neutral fragments. Eur. Phys. J. D 2018, 72, 34. [Google Scholar] [CrossRef]
- Zammit, M.C.; Savage, J.S.; Fursa, D.V.; Bray, I. Electron-impact excitation of molecular hydrogen. Phys. Rev. A 2017, 95, 022708. [Google Scholar] [CrossRef]
- Chung, S.; Lin, C.C. Application of the close-coupling method to excitation of electronic states and dissociation of H2 by electron impact. Phys. Rev. A 1978, 17, 1874–1891. [Google Scholar] [CrossRef]
- Borges, I.; Jalbert, G.; Bielschowsky, C.E. Non-Franck-Condon electron-imact dissociative-excitation cross sections of molecular hydrogen producing H(1s)+H(2l) through . Phys. Rev. A 1998, 57, 1025–1032. [Google Scholar] [CrossRef]
- Stibbe, D.T.; Tennyson, J. Near-threshold electron impact dissociation of H2 within the adiabatic nuclei approximation. New J. Phys. 1998, 1, 2. [Google Scholar] [CrossRef]
- Liu, X.; Shemansky, D.E.; Johnson, P.V.; Malone, C.P.; Khakoo, M.A.; Kanik, I. Electron and photon dissociation cross sections of the H2 singlet ungerade continua. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 105203. [Google Scholar] [CrossRef]
- Stibbe, D.T.; Tennyson, J. Rates for the electron impact dissociation of molecular hydrogen. Astrophys. J. 1999, 513, 147–150. [Google Scholar] [CrossRef]
- Tapley, J.K.; Scarlett, L.H.; Savage, J.S.; Fursa, D.V.; Zammit, M.C.; Bray, I. Electron-impact dissociative excitation of singlet states of molecular hydrogen. Phys. Rev. A 2018, 98, 032701. [Google Scholar] [CrossRef]
- Scarlett, L.H.; Tapley, J.K.; Savage, J.S.; Fursa, D.V.; Zammit, M.C.; Bray, I. Vibrational excitation of the H2 state via electron-impact excitation and radiative cascade. Plasma Sources Sci. Technol. 2019, 28, 025004. [Google Scholar] [CrossRef]
- Tapley, J.K.; Scarlett, L.H.; Savage, J.S.; Zammit, M.C.; Fursa, D.V.; Bray, I. Vibrationally resolved electron-impact excitation cross sections for singlet states of molecular hydrogen. J. Phys. B At. Mol. Phys. 2018, 51, 144007. [Google Scholar] [CrossRef]
- Zammit, M.C.; Fursa, D.V.; Savage, J.S.; Bray, I. Electron– and positron–molecule scattering: Development of the molecular convergent close-coupling method. J. Phys. B At. Mol. Opt. Phys. 2017, 50, 123001. [Google Scholar] [CrossRef]
- Lane, N.F. The theory of electron-molecule collisions. Rev. Mod. Phys. 1980, 52, 29–119. [Google Scholar] [CrossRef]
- Glass-Maujean, M.; Liu, X.; Shemansky, D.E. Analysis of Electron-Impact Excitation and Emission of the npσ1 and npπ1Πu Rydberg Series of H2. Astrophys. J. Suppl. Ser. 2009, 180, 38. [Google Scholar] [CrossRef]
- Trevisan, C.S.; Tennyson, J. Differential cross sections for near-threshold electron impact dissociation of molecular hydrogen. J. Phys. B At. Mol. Opt. Phys. 2001, 34, 2935–2949. [Google Scholar] [CrossRef]
- Trevisan, C.; Tennyson, J. Calculated rates for the electron impact dissociation of molecular hydrogen, deuterium and tritium. Plasma Phys. Control. Fusion 2002, 44, 1263–1276. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Scarlett, L.H.; Savage, J.S.; Fursa, D.V.; Zammit, M.C.; Bray, I. Electron-Impact Dissociation of Vibrationally-Excited Molecular Hydrogen into Neutral Fragments. Atoms 2019, 7, 75. https://doi.org/10.3390/atoms7030075
Scarlett LH, Savage JS, Fursa DV, Zammit MC, Bray I. Electron-Impact Dissociation of Vibrationally-Excited Molecular Hydrogen into Neutral Fragments. Atoms. 2019; 7(3):75. https://doi.org/10.3390/atoms7030075
Chicago/Turabian StyleScarlett, Liam H., Jeremy S. Savage, Dmitry V. Fursa, Mark C. Zammit, and Igor Bray. 2019. "Electron-Impact Dissociation of Vibrationally-Excited Molecular Hydrogen into Neutral Fragments" Atoms 7, no. 3: 75. https://doi.org/10.3390/atoms7030075
APA StyleScarlett, L. H., Savage, J. S., Fursa, D. V., Zammit, M. C., & Bray, I. (2019). Electron-Impact Dissociation of Vibrationally-Excited Molecular Hydrogen into Neutral Fragments. Atoms, 7(3), 75. https://doi.org/10.3390/atoms7030075





