1. Introduction
Over the past decades, it was suggested that the hydrohelium (helium hydride) cation HeH
can be present and observed in a number of astronomical environments, and particularly, in the planetary nebulae NGC 7027 [
1,
2,
3]. In the interstellar medium (ISM), it is the process of radiative association of He and H
or of He
and H that forms the ion [
4,
5]. However, only very recently, the presence of the ion was confirmed by Güsten et al. [
6] with the observation of the rotational ground-state transition of HeH
in the planetary nebula NGC 7027. These observations were made possible due to advances in terahertz spectroscopy [
7] and high-altitude observatories [
8]. Previously, a transition with a wavelength very similar to that of the
rotational transition was found by Liu et al. [
9]. However, further analysis suggested that it was actually caused by the CH molecule [
10].
HeH is easily formed in helium–hydrogen plasma, and in particular, in the hydrogen fusion reaction. The ion, with its isotopologues, plays an important role in the chemistry taking place in tokamaks, especially in the divertor region of the devices. Rovibrationally excited states, formed in collisions of HeH with electrons, can be used for plasma diagnostics. The other process involving the HeH isotopologues and electrons and taking place in the divertor and near walls of the reactors is the process of dissociative recombination. The process removes the ions from the plasma creating neutral atoms, which contribute to the damage of reactor walls.
There have been several experimental and theoretical studies [
11,
12,
13,
14,
15,
16] reporting cross sections for the dissociative recombination. Cross sections for vibrational excitation and de-excitation of the three lowest vibrational states of the ion by electron impact were also calculated previously [
17]. However, the presence of vibrational resonances in the collisional spectra was ignored in that study. Čurík and Greene [
18] have recently reported cross sections for rotational excitation of HeH
collisions, where the Rydberg series of rovibrational resonances were accounted for.
Data relevant to the other isotopologues HeD, HeH, and HeD could also be useful for plasma modeling and diagnostics in fusion reactors. In this respect, cross sections as well as rate coefficients for collisions of the HeH isotopologues with electrons are needed. To our knowledge, there is no such theoretical or experimental data available for the HeH isotopologues.
In a previous study [
19] (hereafter referred to as paper I), we reported cross sections and rate coefficients for vibrational excitation for transitions between the five lowest vibrational levels. In a further study [
20] (hereafter referred to as paper II), we presented similar data for rotational transitions in collisions of
HeH
with electrons. In the present study, as a follow-up of papers I and II, we determine cross sections and rate coefficients for vibrational and rotational (de-)excitation for collisions of the four stable HeH
isotopologues with electrons.
The rest of the article is organized in the following way. The next section briefly discusses the theoretical approach used in the present calculation. A detailed description of the approach is presented at length in papers I and II, so we restrict ourselves here only to underline its major ideas. In
Section 3 and
Section 4, the obtained rate coefficients for vibrational and rotational (de-)excitation are discussed and compared with the data available in the literature.
Section 5 concludes the study.
2. Theoretical Approach
Similarly to papers I and II, the present theoretical method uses the UK R-matrix code [
21,
22] with the Quantemol-N interface [
23] and some elements of the quantum defect theory (MQDT) [
24,
25,
26]. The same parameters (the basis and orbital spaces, the R-matrix size, etc.) as in Paper II were employed in the electron-scattering calculations. As a first step in the theoretical approach, the body-frame scattering matrix
is obtained numerically for a number of internuclear distances
R from
0.85 to
3.95 with a step of 0.05 bohr. At the second step, vibrational wave functions
for the four isotopologues are computed by solving the Schrödinger equation for vibrational motion using a DVR-type method [
27].
Energies for vibrational and rotational transitions for the four isotopologues are shown in
Table 1 and
Table 2 and compared with available data [
28,
29]. Note that unlike the present study, where the aug-cc-pVQZ basis is employed, in paper I, we used the cc-pVQZ basis to compute the potential energy curve (see Figure 2 of paper I). As a result, the obtained vibrational energies for the
HeH
ion are slightly different in the present study and paper I.
Scattering Matrix for Rovibrational Excitations in the HeH Molecule and Its Isotopologues
The next step in the treatment is the vibrational and rotational frame transformations. If we neglect the rotational structure of the ion, which corresponds to an experiment where cross sections for vibrational transitions
are averaged over all possible initial and summed over allowed final rotational states of the levels
v and
, the theoretical cross section is obtained from the following scattering matrix:
where the brackets imply an integration over the vibrational coordinates. As a second step, the rotational frame transformation is accomplished using the matrix elements
of Equation (
1), leading to the laboratory-frame scattering matrix
where
J is the total angular momentum of the
-HeH
system,
and
are the angular momenta with their projections on the molecular axis of the target before and after the rotational excitation of HeH
(and its isotopologues), and
and
are Clebsch–Gordan coefficients. A detailed derivation of Equation (
2) is given in Appendix A of paper II.
The matrices of Equations (
1) and (
2) are energy-independent and do not describe vibrational and rovibrational Rydberg resonances present in the collisional spectra. The actual scattering matrices
are obtained from those two matrices, applying the closed-channel elimination procedure [
24,
26] as discussed in paper I. The total energy
E of the system is the sum
of the relative kinetic energy
of a collision and the energy
of the initial state of the target.
3. Rate Coefficients and Cross Sections for Vibrational (De-)Excitation
The cross section for purely the vibrational transition
is [
30]
where
is the reduced mass of the electron-ion system.
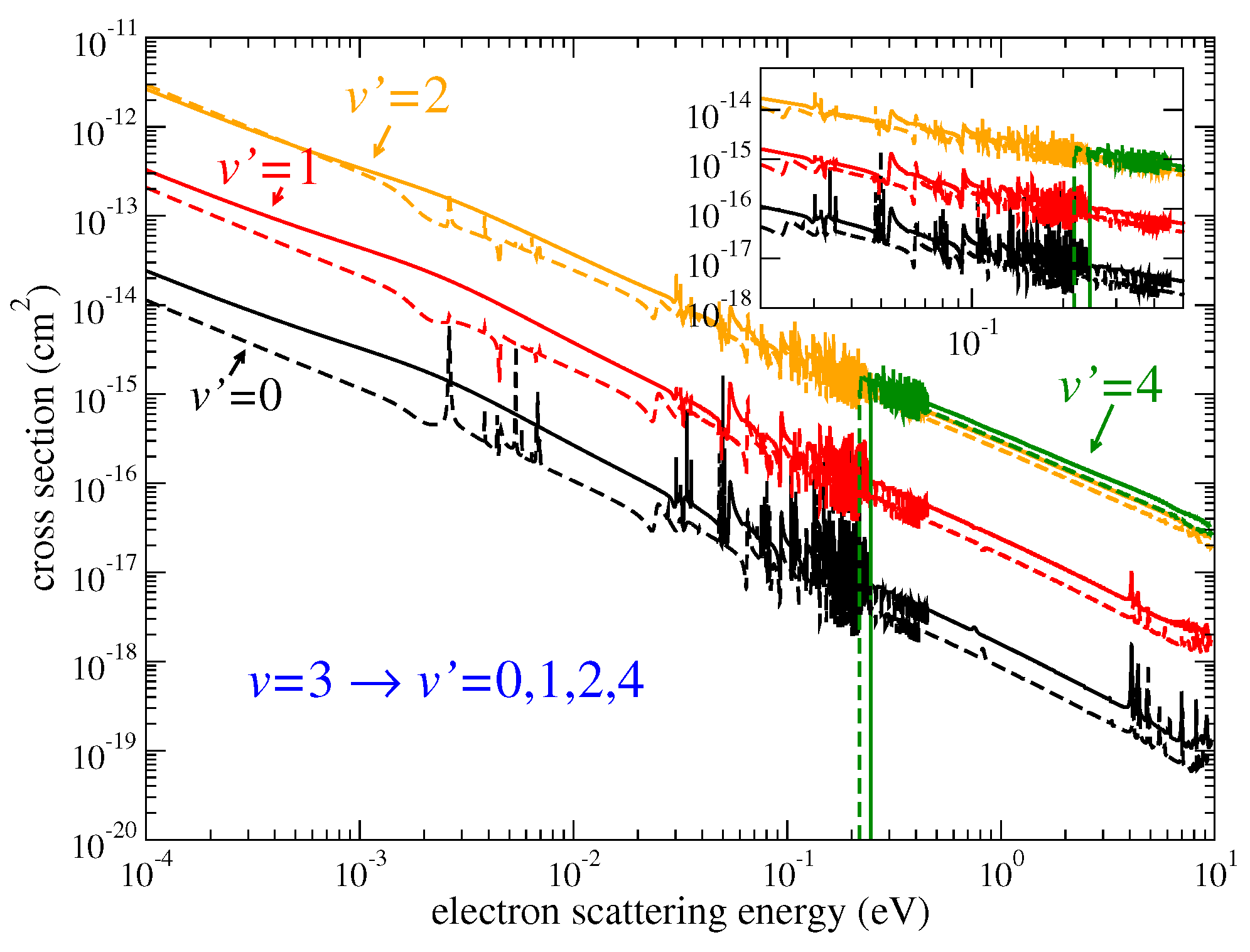
Figure 1 demonstrates, as examples, the cross sections of Equation (
3) for the
transitions of
HeH
(solid lines) and
HeD
(dashed lines). At very low scattering energies, below 0.001 eV, the de-excitation cross sections behave as
according to the Wigner threshold law [
31]. At higher energies, all the (de-)excitation cross sections vary significantly due to the presence of series of Rydberg resonances.
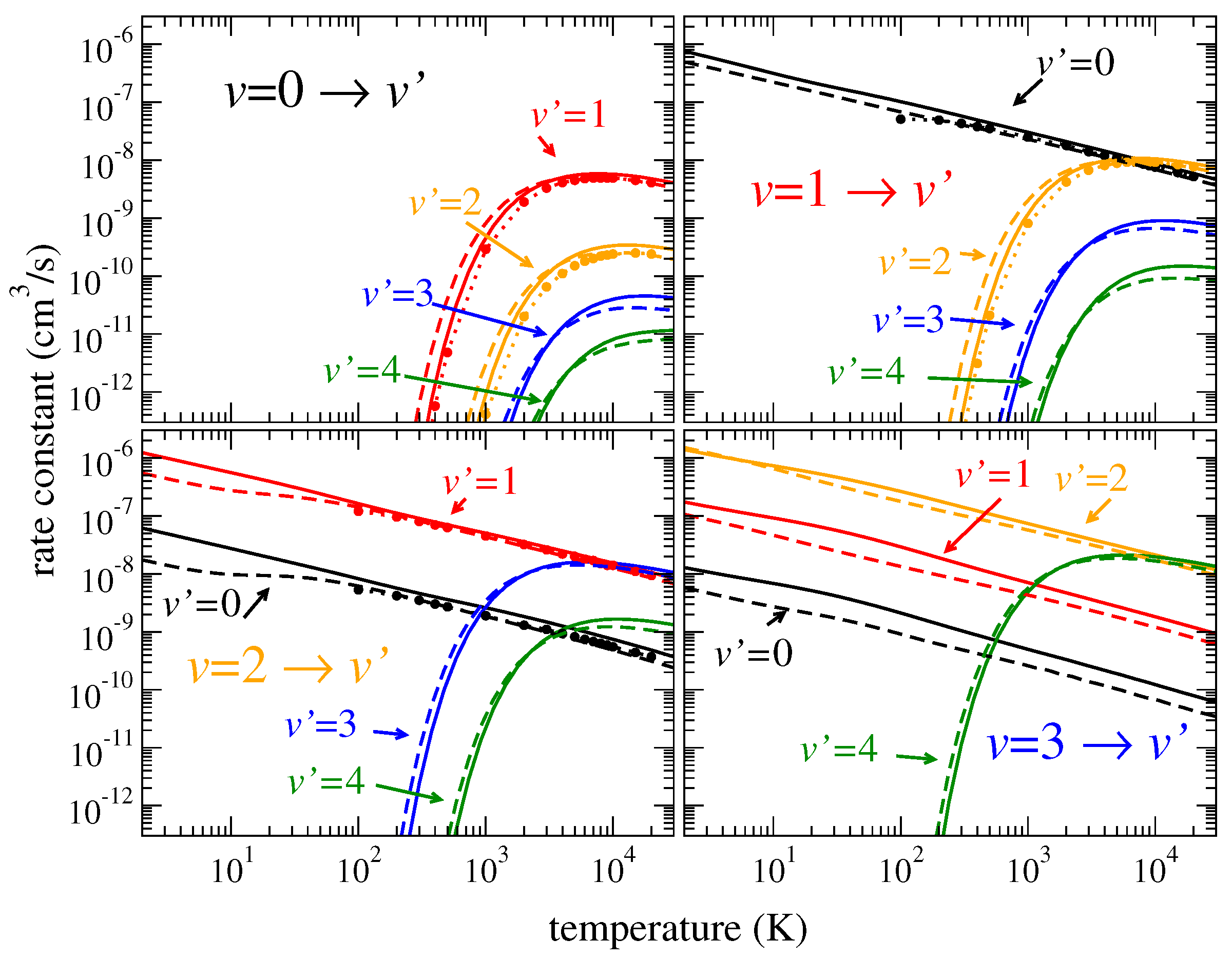
Figure 2 and
Figure 3 show thermally averaged rate coefficients (see Equation (13) of paper I) computed for transitions between the lowest vibrational levels for the four
HeH
isotopologues. The uncertainty of the rate coefficients for all transitions is about 5–30% for different temperatures. Due to the general
dependence of the cross sections, the calculated rate coefficients
behave as
as functions of temperature
T for de-excitation and as
for excitation transitions, where
is the excitation energy. Therefore, similarly to papers I and II, for convenience of use, the rate coefficients are fitted to the formula
where
are functions weakly dependent on temperature interpolated by a cubic polynomial
with
The coefficients
(
) are fitted for each pair of transitions
and given in
Table 3,
Table 4,
Table 5 and
Table 6. The numerical values of the coefficients
in the Tables are such that they give the rate coefficients in units of cm
·s
, with the temperature in fitting Equation (
5) being in kelvin.
4. Rate Coefficients and Cross Sections for Rotational (De-)Excitation
The inelastic cross section for the rotational excitation or de-excitation process
of a linear molecule by electron impact is obtained from the scattering matrix of Equation (
2)
where
is the Coulomb phase shift. The derivation of the above formula is given in paper II.
In the ground electronic state of
HeH
, the projection
of the electronic angular momentum on the molecular axis of the target is zero. Therefore, for scattering energies below the first excited electronic state
of
HeH
,
in Equation (
7).
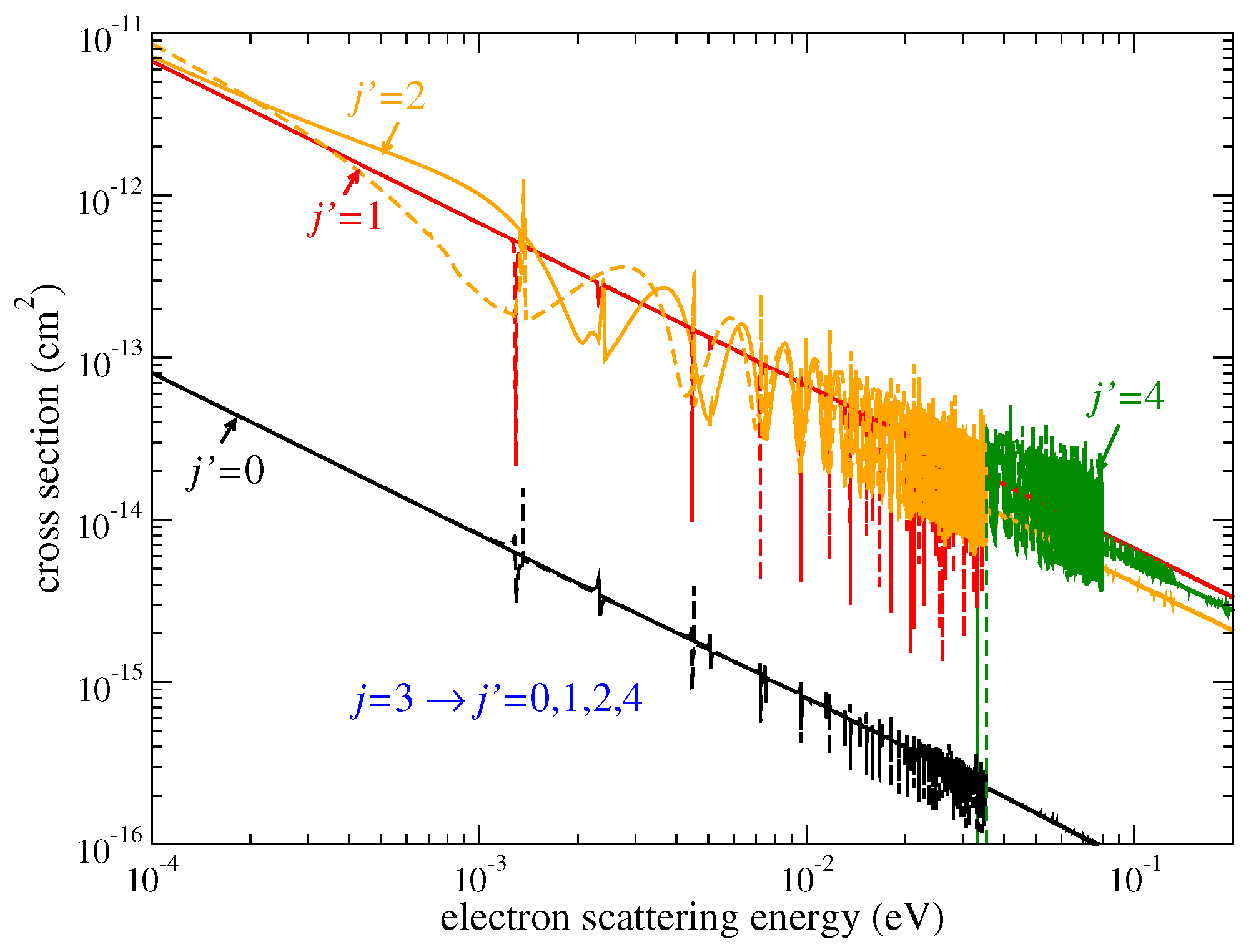
Figure 4 gives examples of the cross sections obtained with Equation (
7) for the
transitions of
HeH
and
HeH
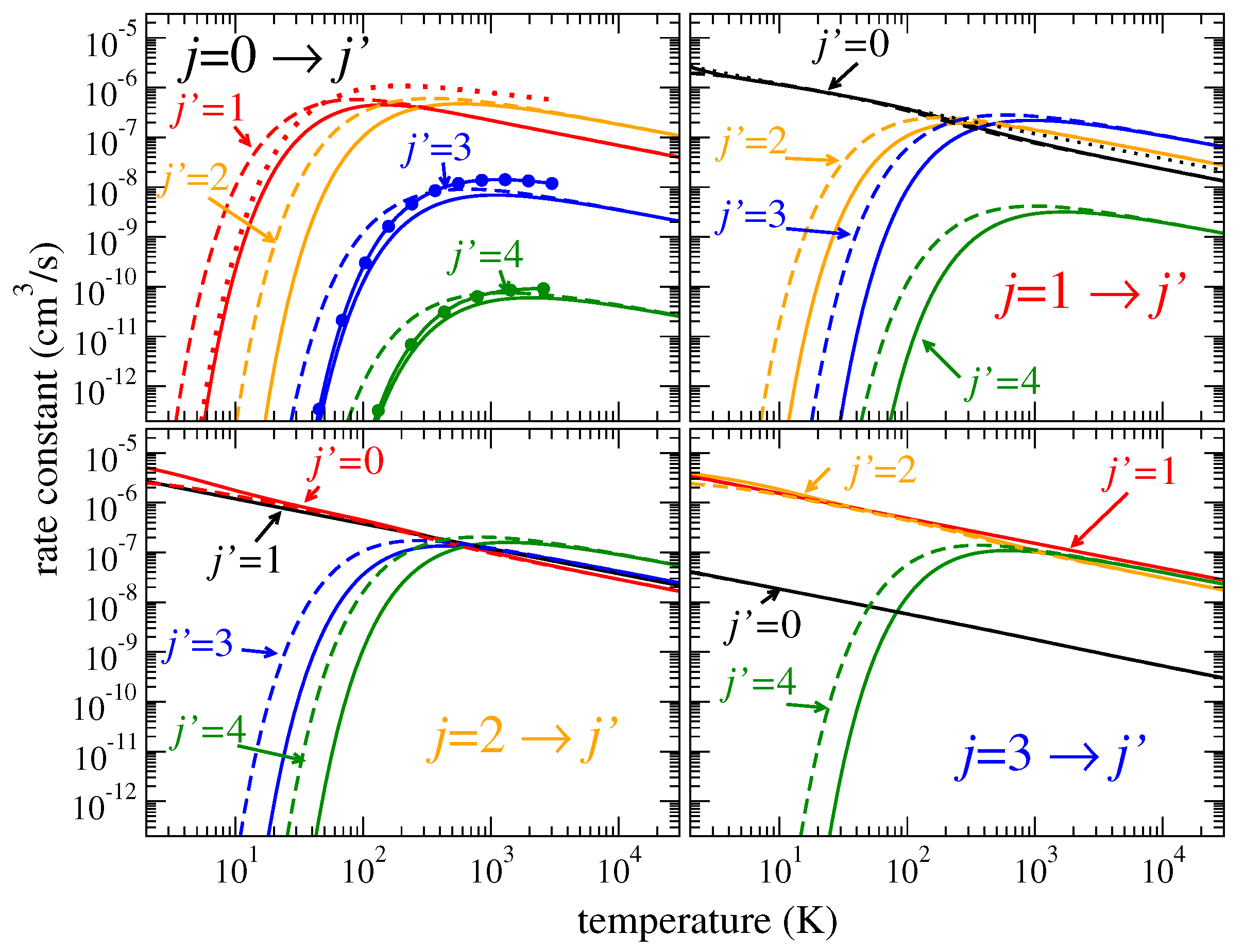
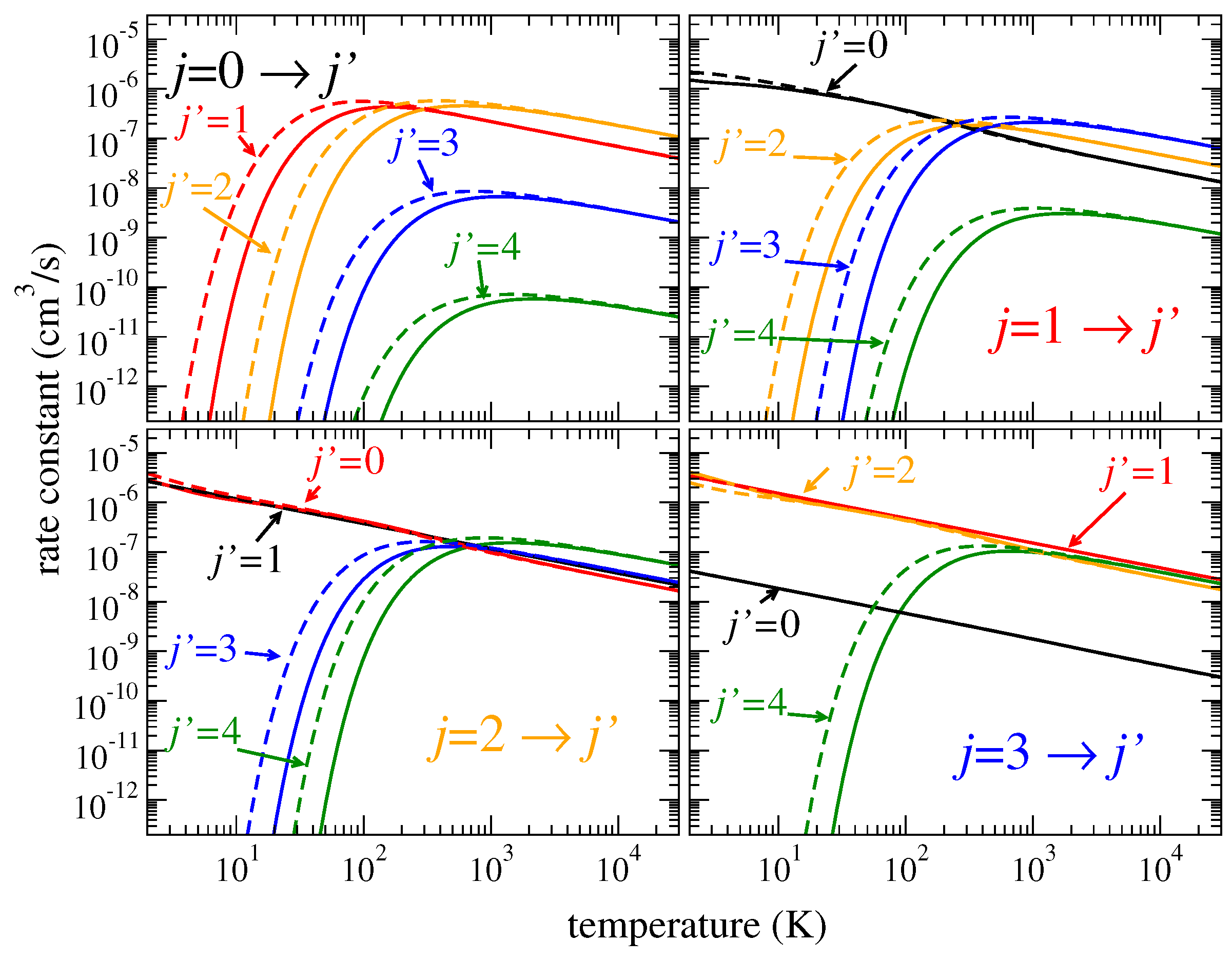
. The cross sections exhibit a strong resonant character for both molecular ions as well as for the two other isotopologues. These resonances are washed out when thermally-averaged rate coefficients are computed, leading to similar rate coefficients at high temperatures
T, as shown by solid lines in
Figure 5 and
Figure 6. Similar results are observed for
HeD
and
HeD
, shown in the figures by dashed lines. However, the thermally averaged coefficients at low temperatures are sensitive to exact positions and widths of the lowest resonances because the integral over thermal velocities at low temperatures
T is determined only by small collision energies,
. As a result, the rate coefficients for the
transitions, for example, in
Figure 5 and
Figure 6, are slightly different for different isotopologues.
In addition, the rotational rate coefficients behave approximately according to Equation (
4), where
should be replaced with the rotational threshold energy,
, and a quadratic polynomial is used in the fit. The probabilities for the direct
(
) and the inverse
(
) processes are related to each other by the relative degeneracy factor
The coefficients
(
) are fitted numerically for transitions
and are given in
Table 7,
Table 8,
Table 9 and
Table 10. Similarly to Tables in
Section 3, the coefficients
give the rate coefficients in Equation (
5) in units of cm
/s.
5. Conclusions
We presented cross sections and thermal rate coefficients for rotational and vibrational transitions in the stable isotopologues of the HeH
ion caused by electron impact. The differences observed in cross sections for the four isotopologues are due to different positions of vibrational and rotational levels of the target ion. The different positions of the levels produce Rydberg resonances in the collisional spectra that are situated at different energies. Different positions of individual resonances can significantly modify cross sections. This is especially important at low energies, as demonstrated in
Figure 1 and
Figure 4. Very different cross sections at low collision energies lead to very different thermal rate coefficients at low temperatures.
Because the overall coupling between different vibrational and rotational channels is the same for all isotopologues, generally, widths of the resonances are comparable for the four isotopologues. This results in thermally averaged rate coefficients that are very similar in magnitude to each other for the four isotopologues. The only essential effect on the rate coefficients is due to a higher density of rovibrational levels and, as a result, a higher density of resonances in the collisional spectra for heavier isotopologues. This effect is evident in
Figure 5 and
Figure 6 showing the coefficients for rotational excitation: For heavier isotopologues, the rotational excitation rate coefficients are, in general, higher. For vibrational transitions, the ratio of densities of vibrational resonances between different isotopologues is closer to unity compared to the rotational-level densities. Therefore, the isotope effect on the vibrational excitation coefficients is less important.
We extended our previous studies on HeH to its isotopologues HeD, HeH, and HeD. The obtained results are important for hydrogen–helium plasma modeling and diagnostics and could contribute to the search of the HeH isotopologues in astrophysical environments.