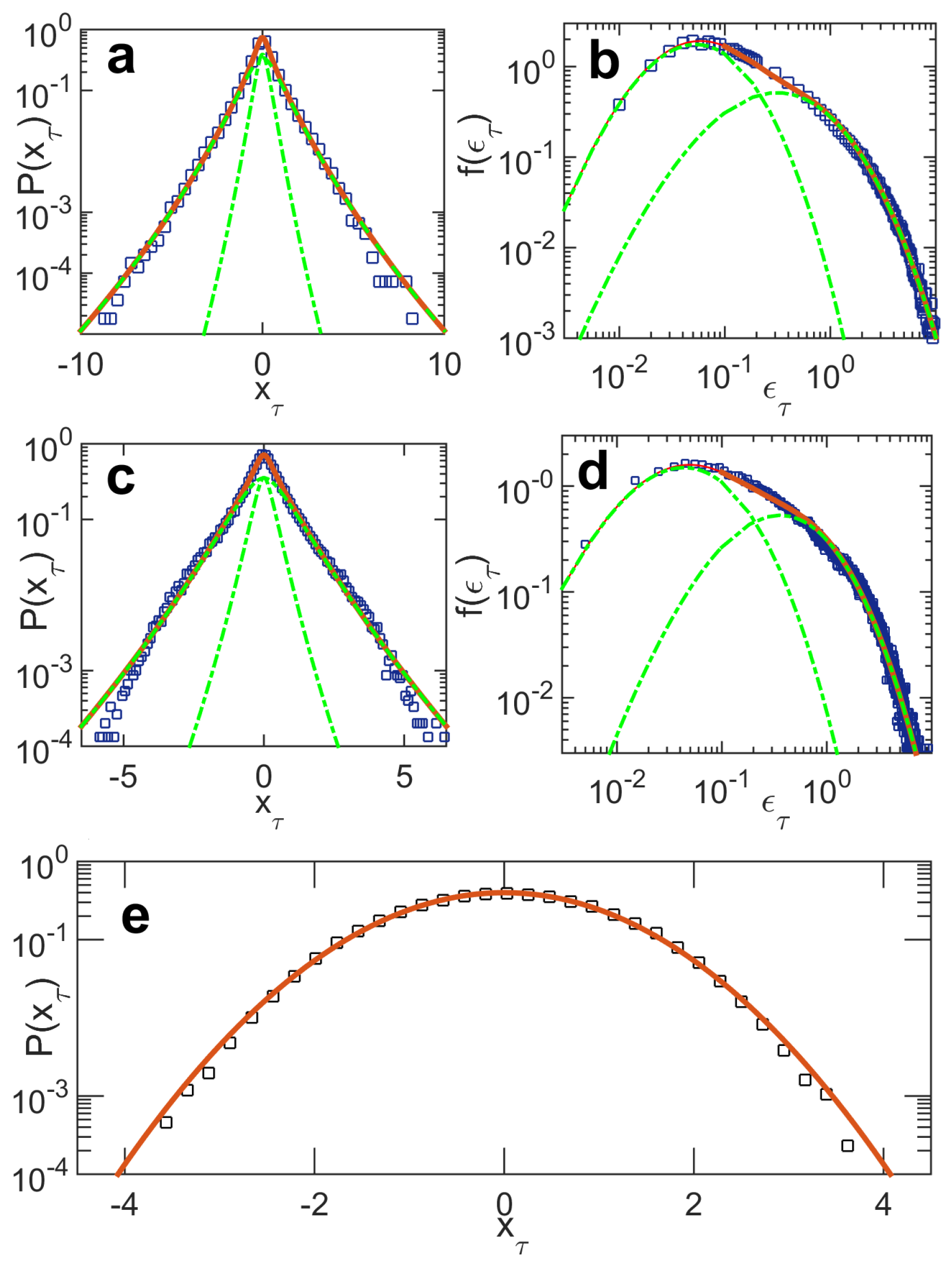
Our basic hypothesis is that the probability distribution of the experimental signal (see below) is a Gaussian at a local level (in time), with a slowly fluctuating variance
. This means that we can write the signal’s local equilibrium distribution as a conditional Gaussian:
. The marginal distribution
is then obtained by compounding this local Gaussian with a background distribution
of the fluctuating variance, thus
with
being determined by the underlying turbulent dynamics. There are two universality classes of such models [
15,
16]: In one class
has a power-law tail and in the other it shows a stretched-exponential behavior. Our experimental data is well fitted using the stretched-exponential class, and so we restrict the discussion to this case.
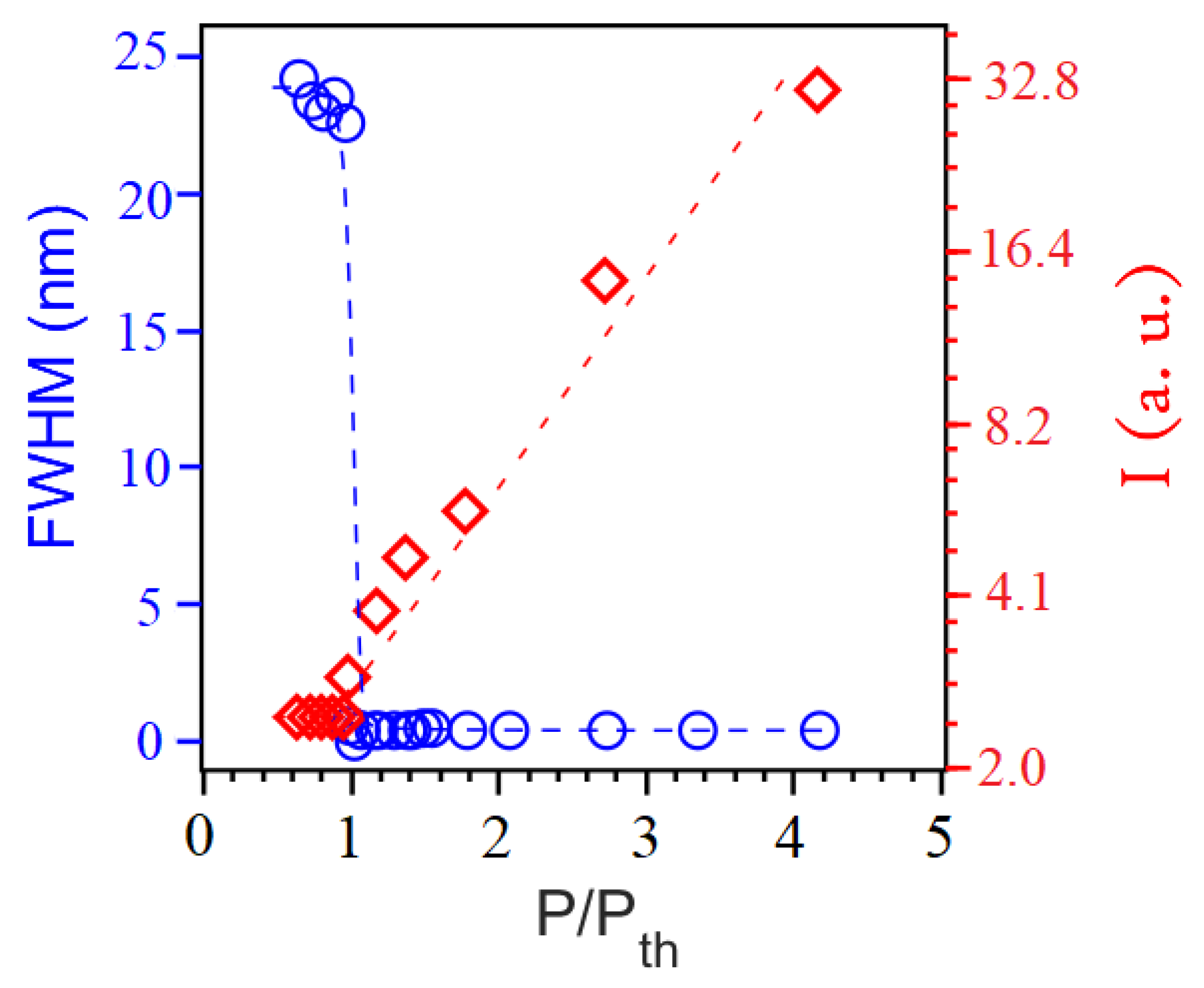
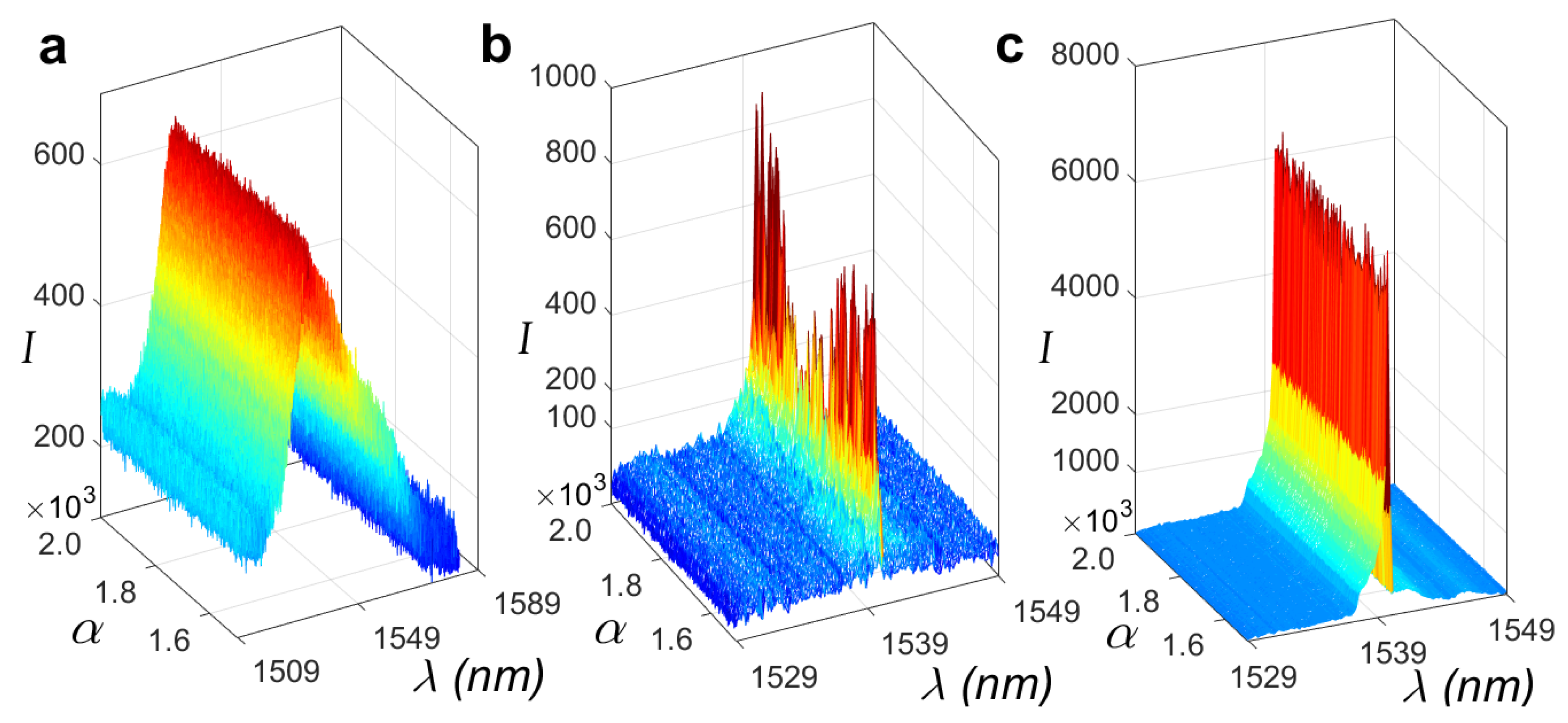
In fluid turbulence, the relevant statistical quantities (the signal) are the velocity increments between two points in the flow. By analogy, in photonic turbulence we may consider intensity increments between successive optical spectra,
with
(shortest separation time scale between the spectra
) and
k denotes the wavelength index. Thus, the object of our statistical analysis is the intensity increments between RL emission spectra
and
, always measured for the same wavelengths
k in the spectra
and
. In the prelasing regime (
), in which nonlinearities are irrelevant, the intensity increments are statistically independent and the probability distribution for a given wavelength,
,
, is a Gaussian. In contrast, when the excitation power is increased beyond the threshold, it has been shown in [
8] that nonlinearities give rise to a turbulent emission in which the Gaussian form of the intensity increments distribution remains valid only at a local level, with a slowly fluctuating variance
, for
. Therefore, the local conditional distribution at the shortest time scale,
, can be written for
as
The complex dynamics (intermittency) of the turbulent state is thus captured by the background density and deriving it from a suitable statistical model is our next step.
2.2.1. Stochastic Model (H-Theory)
One important feature of the hierarchical multiscale theory of complex systems, the H-Theory [
15,
16], is that it allows to obtain an exact expression for the background density
from the stationary solution of a set of stochastic differential equations that incorporates Kolmogorov’s hypothesis of turbulent cascades [
15,
16],
for
, where
N denotes the number of relevant intensity fluctuation time scales in the background variables. In our notation, the
N-th hierarchy is assigned to the shortest time scale
, that is,
. The variable
represents the fluctuating variance parameter at the respective scale in the hierarchy, with
as the largest-scale average,
and
denote positive constants, and
are independent Wiener processes. The first term in Equation (
5) describes the deterministic coupling between adjacent scales, which leads to the relaxation towards
, whilst the second term accounts for the non-linear couplings with the background variables at all scales, setting the ultimate source of intermittency. We remark that the form of these equations is dictated by the invariance under the scale transformation
, along with the positivity requirement
,
, and some constraints on the moments of the stationary distribution [
15,
16].
Under the assumption of large time scales separation,
, we write the density
at the shortest scale as
where the conditional probability distribution
arises from the stationary solution of Equation (
5) in the form of a gamma density,
with
. Remarkably, the multiple integral in Equation (
6) has an analytical representation in terms of a Meijer
G-function [
17] which, with the use of the notation
, is expressed as
where
and we have introduced the vector notation
and
Since the first lower index of the Meijer
G-function in Equation (
8) is null, the parameters in the top row are not present, as indicated by the dash.
Finally, by substituting Equation (
3) into the superposition integral (
4), we obtain
which, by using Equation (
8), allows the distribution of intensity increments at the shortest scale
to be obtained explicitly,
We remark that the large-
asymptotic limit of Equation (
10) has the form of a heavy-tailed modified stretched exponential [
17],
where
, thus displaying important deviations from the Gaussian density, as expected for the photonic turbulent behavior of the short-scale distribution of intensity increments.
We also comment that when the empirical data contains some internal structure indicating the presence of clusters of statistically independent samples, it is sometimes useful to employ a more general family of distributions given by a discrete statistical mixture of multiscale distributions,
where the statistical weights
satisfy
and each
is obtained from Equation (
10) for the same number
N of hierarchy scales and a specific set of internal parameters. In particular, in Reference [
8] we apply the statistical mixture of two components (
in Equation (
12)) to successfully explain all experimental results related to the turbulent laser emission in the RFL system.
2.2.2. Discrete Hierarquical Model
Although the dynamical stochastic model described above allows for a clear connection with fluid turbulence, it does not provide a direct interpretation of the discrete parameter
N, i.e., the number of levels or relevant scales in the model hierarchy. In other words, it is not always clear which structure should play the role of the turbulent eddies in the complex dynamical system described by the H-theory, particularly in the photonic context. In order to address this issue, we introduce below a discrete model that makes direct contact with the central limit theorem (CLT) and provides a simple interpretation for the number
N of hierarchical levels present in H-theory. A related approach, albeit restricted to the cases
and
of a two-dimensional random walk, can be found in Reference [
18].
We start by defining
X as a random variable, with
denoting a set of
M independent realizations of
X. We also define the random variable
Z via
, and let
. Then, the characteristic functions of
and
Z are related as follows:
In the standard form of the CLT, we consider
M to be a large number, so that
where
is the root-mean-square deviation of
X. This characteristic function implies that
is also Gaussian distributed, as expected from the CLT.
Let us now consider that
M is a discrete random variable with probability
. In this case, we may define a weighted averaged characteristic function,
Below we proceed by selecting from particular stationary solutions of well-known discrete stochastic processes. From these results, we will be able to make contact with the H-theory and the associated interpretation of the number of hierarchy scales N in the case of photonic turbulence in the RFL system.
(i) Poisson process ()
The Poisson process is described by the following master Equation [
19],
which represents an interaction-free evolution in discrete space, with
and
a positive parameter. The solution is given by
where
and the characteristic function is given by
. If we rescale
and take
, we recover the expected result of the CLT,
.
(ii) Pauli process ()
The master equation of the Pauli process is defined as [
19]
where
and
, with
being positive constants. The Pauli process contains dipole transitions [
19], and its stationary solution reads
, where
and
. The characteristic function is
Following the steps as in the previous case, if we rescale
and take
, we obtain
The corresponding distribution for the variable
Y is thus
which is a particular case of Equation (
10).
(iii) Negative binomial process ()
The negative binomial process is a generalization of the Pauli process that allows for the presence of bunches in the evolution of
[
19]. In this case, the stationary solution is
where
and the parameter
is the number of degrees of freedom. Notice that the binomial coefficient counts the number of partitions of
M among
states. The characteristic function reads
If we now rescale
and take
, we obtain
The corresponding distribution for the variable
Y is
which is also a particular case of Equation (
10). Notice that for
we recover the results of the Pauli process.
We are now in position to state the general result for
N arbitrary as follows. Consider a stochastic process with stationary distribution given by
where
and
. The integer parameter
N gives the order of the transitions induced by the interactions described by the evolution of
. In other words, there exists a non-vanishing coupling between
and
in the master equation. Observe that for
(no correlations) and
(dipole transitions) we recover the Poisson and negative binomial distributions, respectively. The corresponding distribution for the variable
Y can be expressed as
which reproduces the exact stationary solution (
10) of H-theory.
We can now interpret the parameter
N in the H-theory description of photonic turbulence. In this context, if we consider
to be a sum of
M independent sources that contribute to the observed intensity increments and admit that
M is proportional to the number of photons contributing to the photonic turbulent emission, then
N might be understood as giving the order of the transitions induced by the non-linearities in the medium. Therefore, for the conventional coherent light of a laser one has
, which implies a Gaussian distribution for the intensity increments. On the other hand, we may assign
for chaotic light and
for generic turbulent emission, which implies Equation (
10) for the corresponding intensity increments distribution, in agreement with the results on the RFL photonic turbulent state reported in [
8].