Testing Quantum Coherence in Stochastic Electrodynamics with Squeezed Schrödinger Cat States
Abstract
1. Introduction
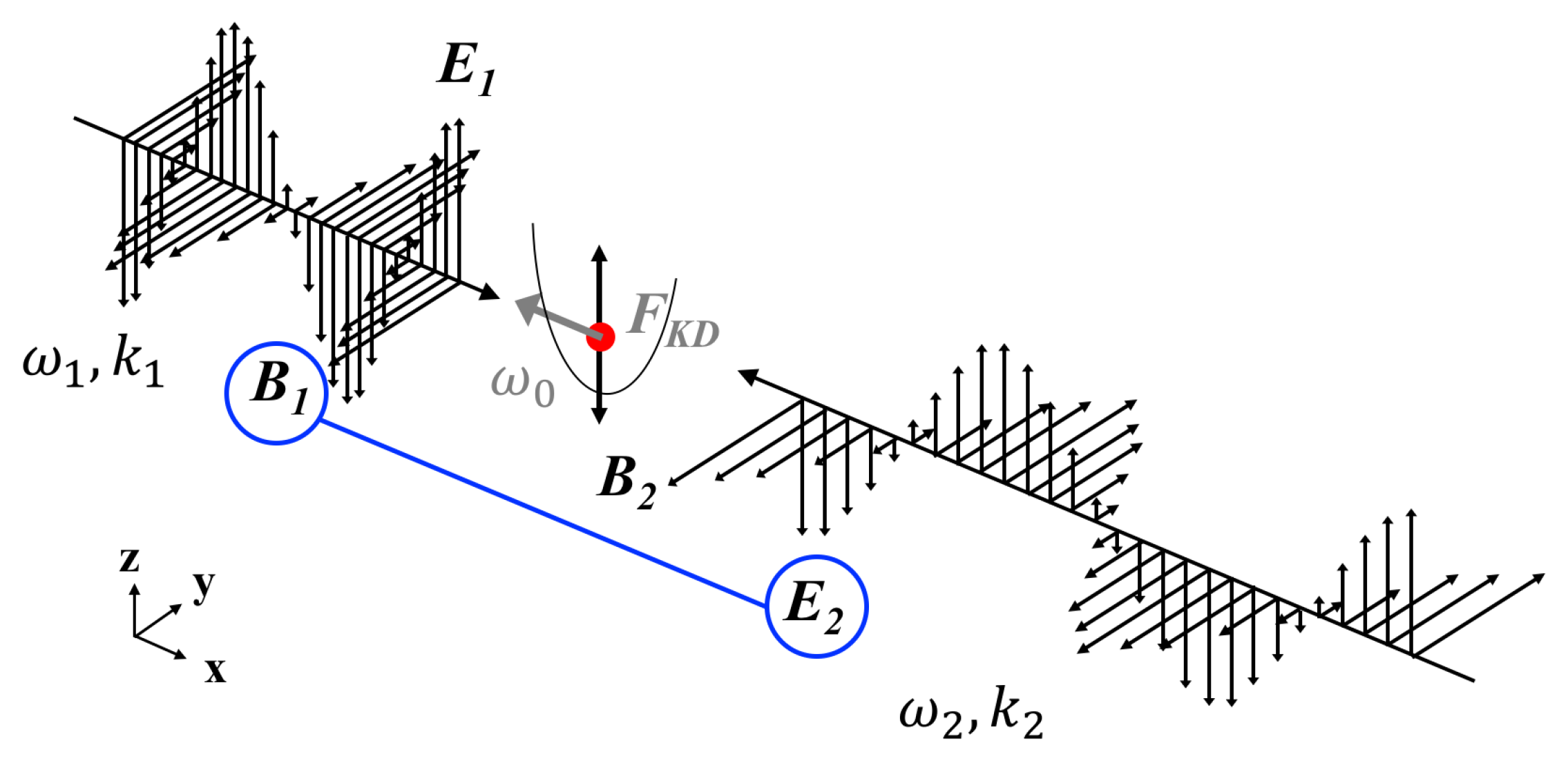
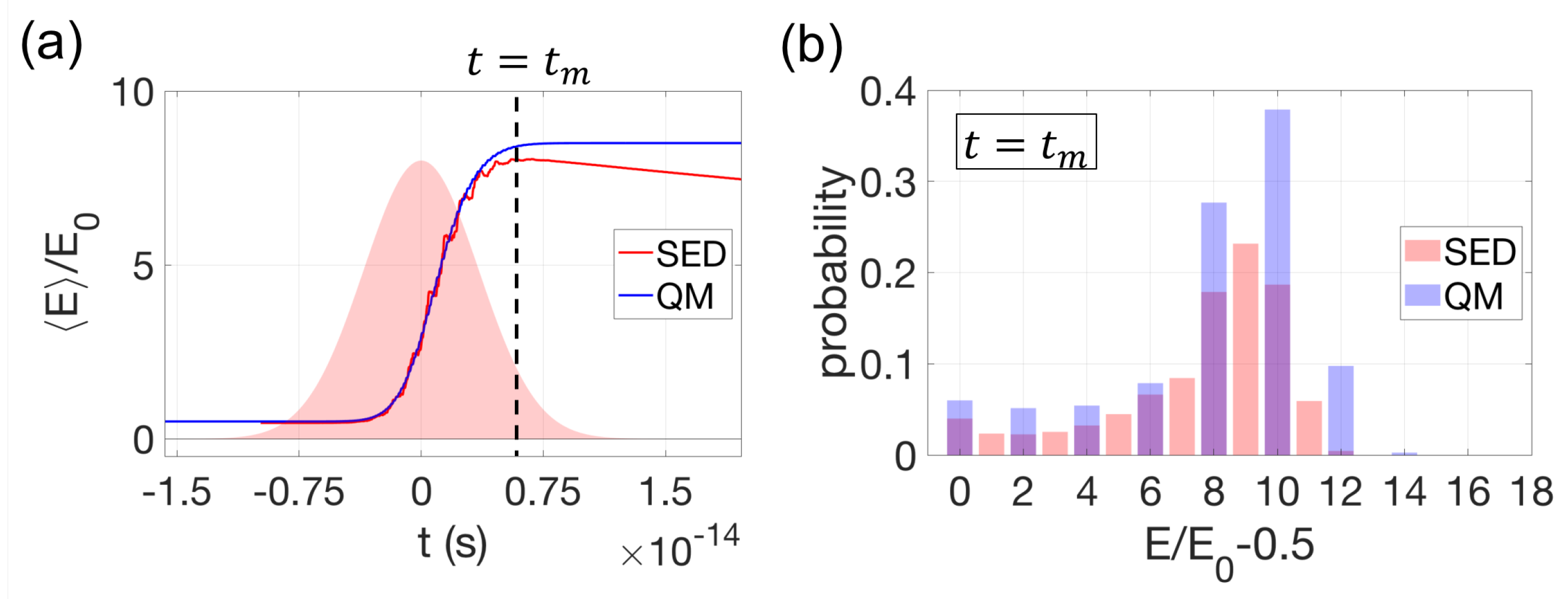
2. Kapitza–Dirac Force on Harmonic Oscillators
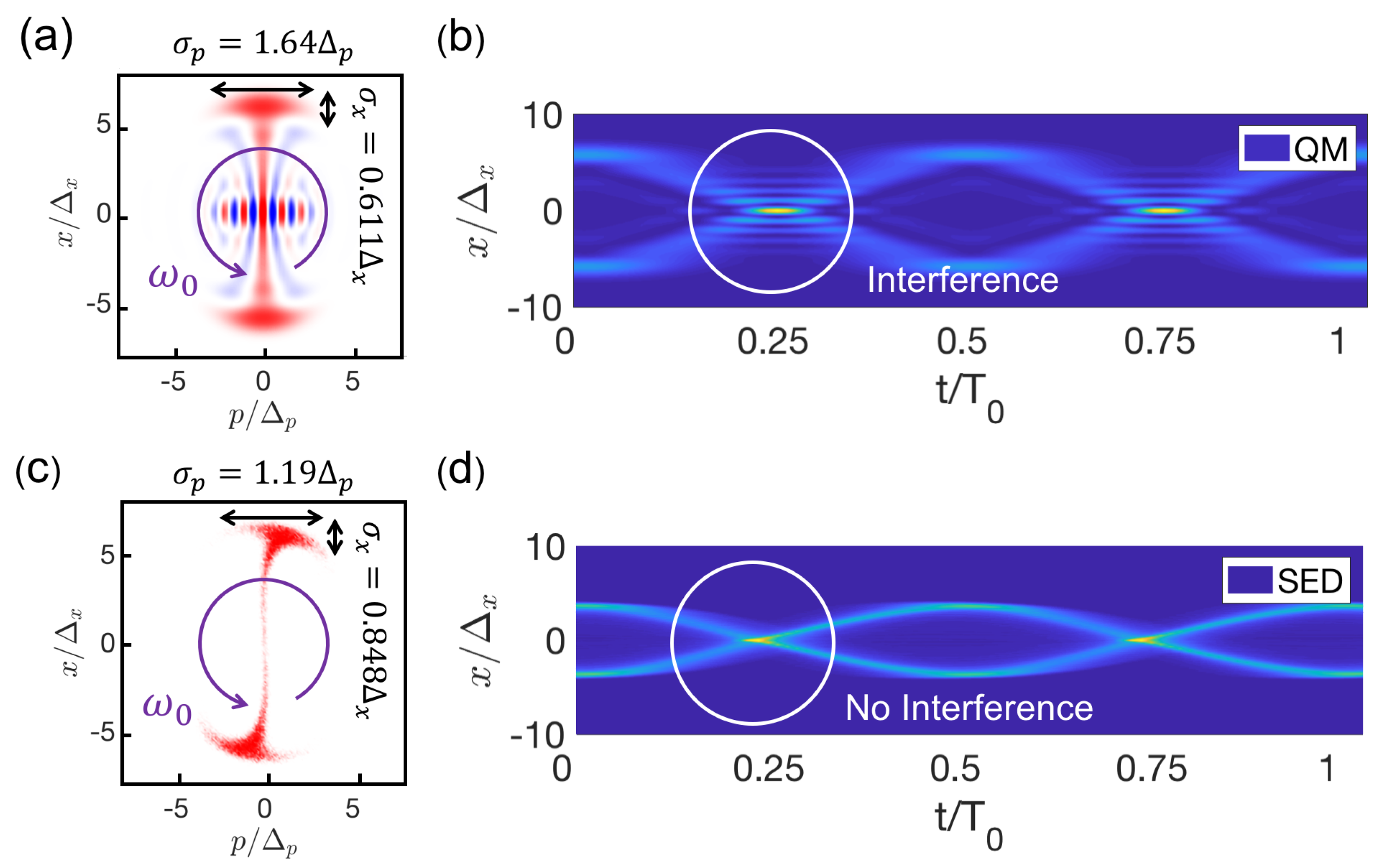
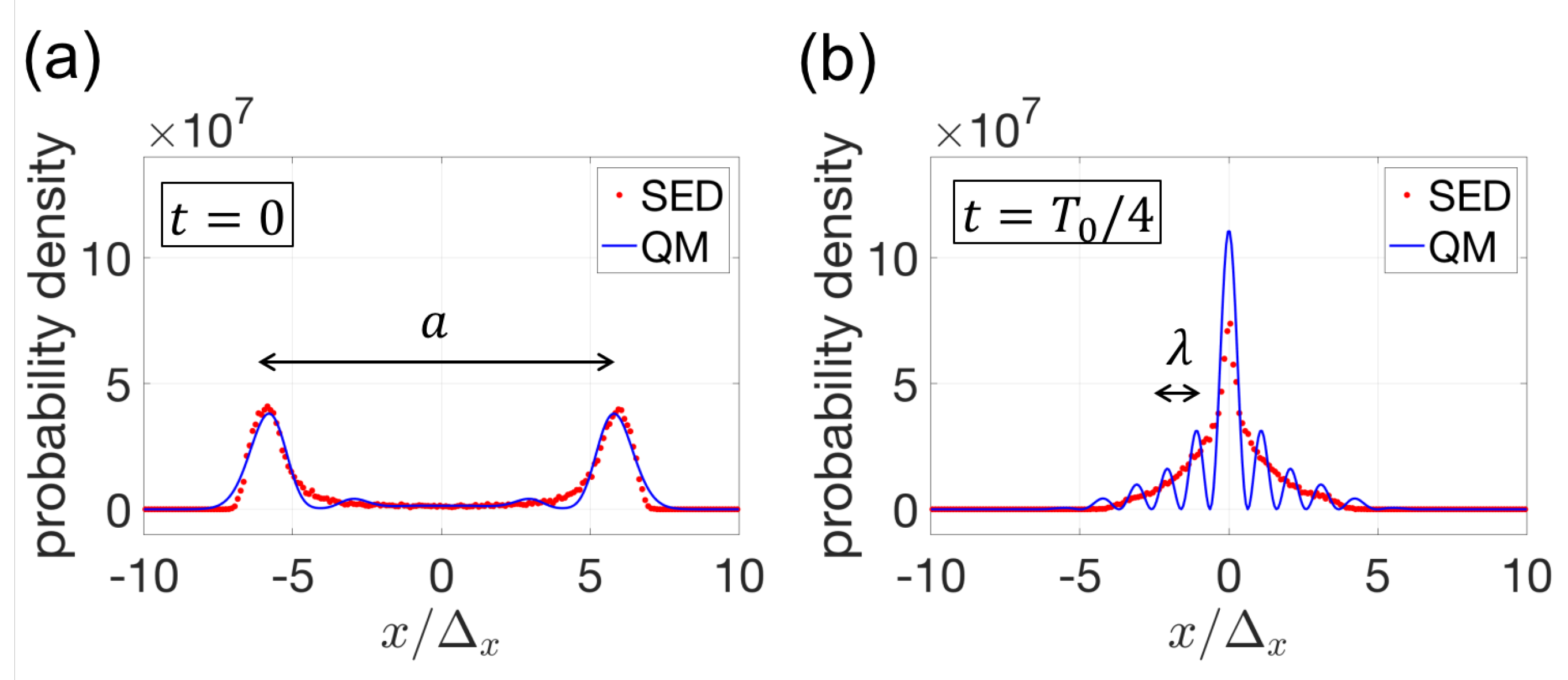
3. Generation of Squeezed Schrödinger Cat States
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Derivation of the Resonant Kapitza-Dirac Force
References
- De la Pe na, L.; Cetto, A.M. The Quantum Dice: An Introduction to Stochastic Electrodynamics; Springer: New York, NY, USA, 1996. [Google Scholar]
- De la Pe na, L.; Cetto, A.M.; Valdes-Hernandez, A. Emerging Quantum: The Physics Behind Quantum Mechanics; Springer: New York, NY, USA, 2015. [Google Scholar]
- Cavalleri, G.; Barbero, F.; Bertazzi, G.; Cesaroni, E.; Tonni, E.; Bosi, L.; Spavieri, G.; Gillies, G. Aquantitative assessment of stochastic electrodynamics with spin (SEDS): Physical principles and novel applications. Front. Phys. China 2010, 5, 107. [Google Scholar] [CrossRef]
- Milonni, P.W. The Quantum Vacuum: An Introduction to Quantum Electrodynamics; Academic Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Boyer, T.H. Random electrodynamics: The theory of classical electrodynamics with classical electromagnetic zero-point radiation. Phys. Rev. D 1975, 11, 790. [Google Scholar] [CrossRef]
- Boyer, T.H. Retarded van der Waals Forces at All Distances Derived from Classical Electrodynamics with Classical Electromagnetic Zero-Point Radiation. Phys. Rev. A 1973, 7, 1832. [Google Scholar] [CrossRef]
- Boyer, T.H. General connection between random electrodynamics and quantum electrodynamics for free electromagnetic fields and for dipole oscillator systems. Phys. Rev. D 1975, 11, 809–830. [Google Scholar] [CrossRef]
- Huang, W.C.; Batelaan, H.J. Dynamics Underlying the Gaussian Distribution of the Classical Harmonic Oscillator in Zero-Point Radiation. Comput. Methods Phys. 2013, 2013, 308538. [Google Scholar] [CrossRef]
- Boyer, T.H. Diamagnetism of a free particle in classical electron theory with classical electromagnetic zero-point radiation. Phys. Rev. A 1980, 21, 66–72. [Google Scholar] [CrossRef]
- Boyer, T.H. Understanding the Planck blackbody spectrum and Landau diamagnetism within classical electromagnetism. Eur. J. Phys. 2016, 37, 065102. [Google Scholar] [CrossRef]
- Boyer, T.H. Derivation of the blackbody radiation spectrum from the equivalence principle in classical physics with classical electromagnetic zero-point radiation. Phys. Rev. D 1984, 29, 1096. [Google Scholar] [CrossRef]
- Boyer, T.H. Scaling, scattering, and blackbody radiation in classical physics. Eur. J. Phys. 2017, 38, 045101. [Google Scholar] [CrossRef]
- Blanco, R.; Franca, H.M.; Santos, E. Classical interpretation of the Debye law for the specific heat of solids. Phys. Rev. A 1991, 43, 693. [Google Scholar] [CrossRef] [PubMed]
- Puthoff, H.E. Ground state of hydrogen as a zero-point-fluctuation-determined state. Phys. Rev. D 1987, 35, 3266–3269. [Google Scholar] [CrossRef]
- Cole, D.C.; Zou, Y. Quantum mechanical ground state of hydrogen obtained from classical electrodynamics. Phys. Lett. A 2003, 317, 14–20. [Google Scholar] [CrossRef]
- Nieuwenhuizen, T.M.; Liska, M.T.P. Simulation of the hydrogen ground state in stochastic electrodynamics. Phys. Scr. 2015, T165, 014006. [Google Scholar] [CrossRef]
- Nieuwenhuizen, T.M. On the stability of classical orbits of the hydrogen ground state in Stochastic Electrodynamics. Entropy 2016, 18, 135. [Google Scholar] [CrossRef]
- Huang, W.C.; Batelaan, H. Discrete excitation spectrum of a classical harmonic oscillator in zero-point radiation. Found. Phys. 2015, 45, 333–353. [Google Scholar] [CrossRef][Green Version]
- Bach, R.; Pope, D.; Liou, S.-H.; Batelaan, H. Controlled double-slit electron diffraction. New J. Phys. 2013, 15, 033018. [Google Scholar] [CrossRef]
- Avenda no, J.; de la Pe na, L. Dynamic electron control using light and nanostructure. Phys. Rev. E 2004, 72, 066605. [Google Scholar]
- Kracklauer, A.F. An Intutive Paragidm for Quantum Mechanics. Phys. Essays 1992, 5, 226. [Google Scholar] [CrossRef]
- Wolchover, N. Famous Experiment Dooms Alternative to Quantum Weirdness. Quanta Magazine, 11 October 2018. [Google Scholar]
- Couder, Y.; Fort, E. Single-particle diffraction and interference at a macroscopic scale. Phys. Rev. Lett. 2006, 97, 154101. [Google Scholar] [CrossRef]
- Andersen, A.; Madsen, J.; Reichelt, C.; Ahl, S.R.; Lautrup, B.; Ellegaard, C.; Levinsen, M.T.; Bohr, T. Double-slit experiment with single wave-driven particles and its relation to quantum mechanics. Phys. Rev. E 2015, 92, 013006. [Google Scholar] [CrossRef]
- Bohr, T.; Andersen, A.; Lautrup, B. Recent Advances in Fluid Dynamics with Environmental Applications; Springer: New York, NY, USA, 2016; pp. 335–349. [Google Scholar]
- Batelaan, H.; Jones, E.; Huang, W.C.; Bach, R. Momentum exchange in the electron double-slit experiment. J. Phys. Conf. Ser. 2016, 701, 012007. [Google Scholar] [CrossRef]
- Pucci, G.; Harris, D.M.; Faria, L.M.; Bush, J.W.M. Walking droplets interacting with single and double slits. J. Fluid Mech. 2018, 835, 1136–1156. [Google Scholar] [CrossRef]
- Kienzler, D.; Flühmann, C.; Negnevitsky, V.; Lo, H.-Y.; Marinelli, M.; Nadlinger, D.; Home, J.P. Observation of quantum interference between separated mechanical oscillator wave packets. Phys. Rev. Lett. 2016, 116, 140402. [Google Scholar] [CrossRef]
- Etesse, J.; Bouillard, M.; Kanseri, B.; Tualle-Brouri, R. Experimental generation of squeezed cat states with an operation allowing iterative growth. Phys. Rev. Lett. 2015, 114, 193602. [Google Scholar] [CrossRef]
- Huang, K.; le Jeannic, H.; Ruaudel, J.; Verma, V.B.; Shaw, M.D.; Marsili, F.; Nam, S.W.; Wu, E.; Zeng, H.; Jeong, Y.-C.; et al. Optical synthesis of large-amplitude squeezed coherent-state superpositions with minimal resources. J. Phys. Rev. Lett. 2015, 115, 023602. [Google Scholar] [CrossRef]
- Tonomura, A.; Endo, J.; Matsuda, T.; Kawasaki, T.; Ezawa, H. Demonstration of single-electron buildup of an interference pattern. Am. J. Phys. 1989, 57, 117. [Google Scholar] [CrossRef]
- Batelaan, H. Colloquium: Illuminating the Kapitza-Dirac effect with electron matter optics. Rev. Mod. Phys. 2007, 79, 929–941. [Google Scholar] [CrossRef]
- Sonnentag, P.; Hasselbach, F. Measurement of decoherence of electron waves and visualization of the quantum-classical transition. Phys. Rev. Lett. 2007, 98, 200402. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.C.-W.; Batelaan, H. Testing Quantum Coherence in Stochastic Electrodynamics with Squeezed Schrödinger Cat States. Atoms 2019, 7, 42. https://doi.org/10.3390/atoms7020042
Huang WC-W, Batelaan H. Testing Quantum Coherence in Stochastic Electrodynamics with Squeezed Schrödinger Cat States. Atoms. 2019; 7(2):42. https://doi.org/10.3390/atoms7020042
Chicago/Turabian StyleHuang, Wayne Cheng-Wei, and Herman Batelaan. 2019. "Testing Quantum Coherence in Stochastic Electrodynamics with Squeezed Schrödinger Cat States" Atoms 7, no. 2: 42. https://doi.org/10.3390/atoms7020042
APA StyleHuang, W. C.-W., & Batelaan, H. (2019). Testing Quantum Coherence in Stochastic Electrodynamics with Squeezed Schrödinger Cat States. Atoms, 7(2), 42. https://doi.org/10.3390/atoms7020042





