Radiative Transition Parameters in Atomic Lanthanum from Pseudo-Relativistic Hartree–Fock and Fully Relativistic Dirac–Hartree–Fock Calculations
Abstract
1. Introduction
2. Computational Methods Used
2.1. Pseudo-Relativistic Hartree–Fock Calculations
2.2. Fully Relativistic Multiconfiguration Dirac–Hartree–Fock Calculations
3. Results and Discussion
3.1. Radiative Lifetimes
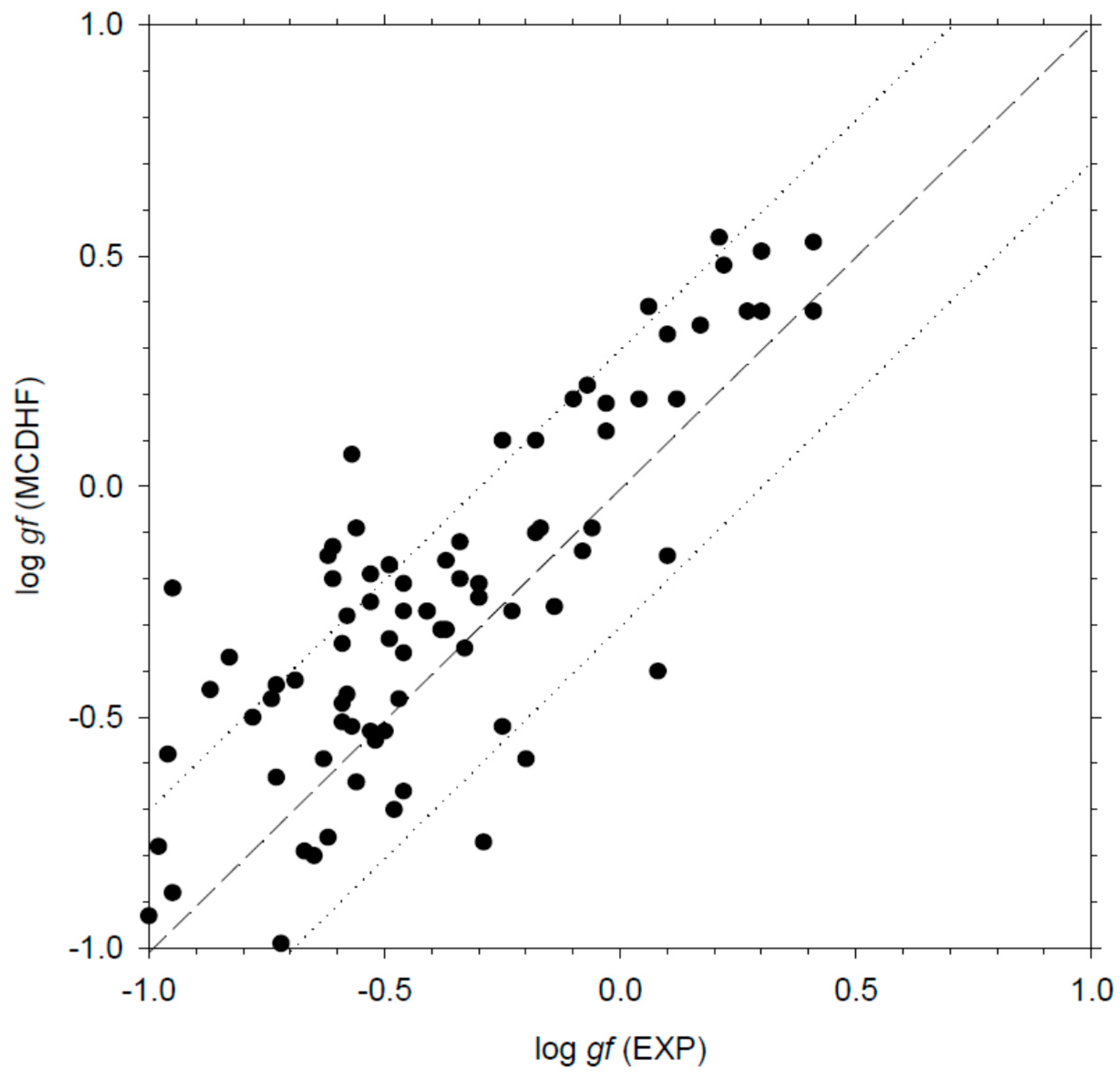
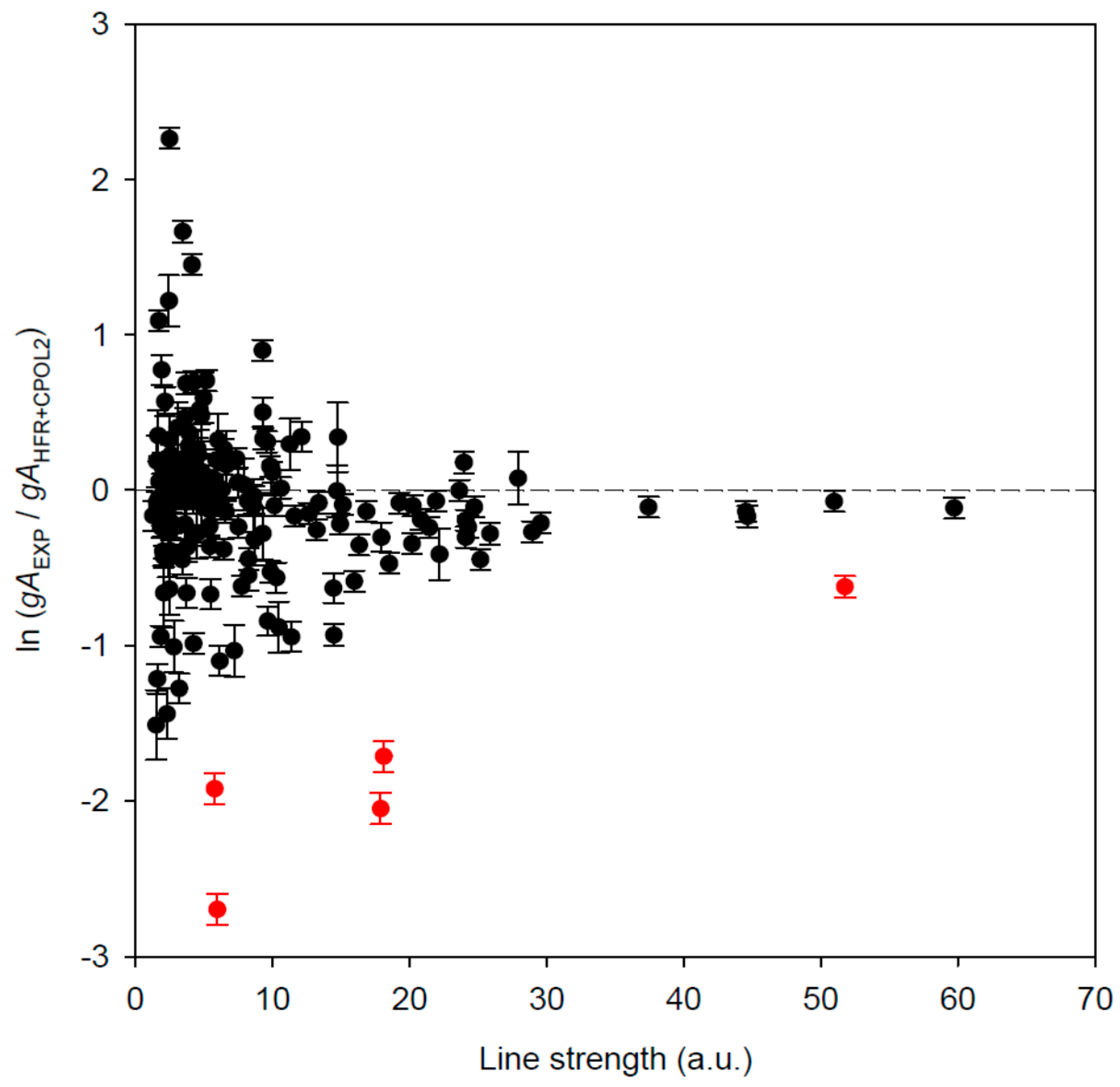
3.2. Oscillator Strengths and Transition Probabilities
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Biémont, E.; Quinet, P. Recent Advances in the Study of Lanthanide Atoms and Ions. Phys. Scr. 2003, 105, 38. [Google Scholar] [CrossRef]
- Wybourne, B.G. The fascination of the rare earths—Then, now and in the future. J. Alloys Compd. 2004, 380, 96–100. [Google Scholar] [CrossRef]
- Lawler, J.E.; Den Hartog, E.A.; Sneden, C. Spectroscopic Data for Neutral and Ionized Rare Earth Elements. AIP Conf. Proc. 2005, 771, 152–161. [Google Scholar]
- Sneden, C.; Lawler, J.E.; Cowan, J.J.; Ivans, I.I.; Den Hartog, E.A. New Rare Earth Element Abundance Distributions for the Sun and Five r-process-rich Very Metal-Poor Stars. Astrophys. J. Suppl. 2009, 182, 80. [Google Scholar] [CrossRef]
- Mumpower, M.R.; McLaughlin, G.C.; Surman, R. The Rare Earth Peak: An Overlooked r-process Diagnostic. Astrophys. J. 2012, 752, 117. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. Available online: http://physics.nist.gov/asd (accessed on 30 October 2018).
- Corliss, C.H.; Bozman, W.R. Experimental transition probabilities for spectral lines of seventy elements. Nat. Bur. Stand. Monogr. 1962, 53, 80–81. [Google Scholar]
- Kurucz, R.L. Including All the Lines. Can. J. Phys. 2011, 89, 417. [Google Scholar] [CrossRef]
- Hese, A. Level Crossing Experiments to Investigate the Hyperfine Structure and the Lifetime of the 5d6s6p z 2F5/2,7/2 States in the Lanthanum I Spectrum. Z. Phys. 1970, 236, 42. [Google Scholar] [CrossRef]
- Hese, A.; Buldt, G. Hyperfine Structure, Stark Effect and Lifetimes of the Excited 5d6s6p y 2D3/2,5/2 States of the Lanthanum I Spectrum. Z. Naturforsch. 1970, 25, 1537–1545. [Google Scholar]
- Hese, A.; Wiese, H.P. Investigation of the 5d6s6p z 2F Terms in the Lanthanum I Spectrum by Optical Double Resonance. Z. Angew. Phys. 1970, 30, 170. [Google Scholar]
- Bulos, B.R.; Glassman, A.J.; Gupta, R.; Moe, G.W. Measurement of the Lifetimes of the z 2F5/2, z 2D3/2, z 4G5/2, and y 2D3/2 States of Lanthanum. J. Opt. Soc. Am. 1978, 68, 842–845. [Google Scholar] [CrossRef]
- Penkin, N.P.; Gorshkov, V.N.; Komarovskii, V.A. Radiative lifetimes of excited La I levels. Opt. Spectrosc. 1985, 58, 840–841. [Google Scholar]
- Biémont, E.; Quinet, P.; Svanberg, S.; Xu, H.L. Lifetime measurements and calculations in La I. Eur. Phys. J. D. 2004, 30, 157–162. [Google Scholar] [CrossRef]
- Karaçoban, B.; Özdemir, L. Energies and Lifetimes for Some Excited Levels in La I. Acta Phys. Pol. A 2008, 113, 1609–1618. [Google Scholar] [CrossRef]
- Karaçoban, B.; Özdemir, L. Electric Dipole Transitions for La I (Z = 57). J. Quant. Spectrosc. Rad. Transf. 2008, 109, 1968–1985. [Google Scholar] [CrossRef]
- Froese-Fischer, C.F.; Brage, T.; Jönsson, P. Computational Atomic Structure—An MCHF Approach; Institute of Physics Publishing: Bristol, UK, 1997. [Google Scholar]
- Feng, Y.Y.; Zhang, W.; Kuang, B.; Ning, L.; Jiang, Z.; Dai, Z. Radiative Lifetime Measurements on Odd-Parity Levels of La I by Time-Resolved Laser Spectroscopy. J. Opt. Soc. Am. B 2011, 28, 543–546. [Google Scholar] [CrossRef]
- Feng, Y.Y.; Wang, Q.; Jiang, L.Y.; Jiang, Z.K.; Dai, Z. Radiative Lifetimes of Highly Excited Odd-Parity Levels of Neutral Lanthanum. Eur. Phys. J. D 2011, 65, 299–302. [Google Scholar] [CrossRef]
- Yarlagadda, S.; Mukund, S.; Nakhate, S.G. Radiative lifetime measurements in neutral lanthanum using time-resolved laser-induced fluorescence spectroscopy in supersonic free-jet. J. Opt. Soc. Am. B 2011, 28, 1928–1933. [Google Scholar] [CrossRef]
- Shang, X.; Tian, Y.; Wang, Q.; Fan, S.; Bai, W.; Dai, Z. Radiative lifetime measurements of some La I and La II levels by time-resolved laser spectroscopy. Mon. Not. R. Astron. Soc. 2014, 442, 138–141. [Google Scholar] [CrossRef]
- Den Hartog, E.A.; Palmer, A.J.; Lawler, J.E. Radiative lifetimes and transition probabilities of neutral lanthanum. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 155001. [Google Scholar] [CrossRef]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Quinet, P.; Palmeri, P.; Biémont, E.; McCurdy, M.M.; Rieger, G.; Pinnington, E.H.; Wickliffe, M.E.; Lawler, J.E. Experimental and theoretical lifetimes, branching fractions and oscillator strengths in Lu II. Mon. Not. R. Astron. Soc. 1999, 307, 934–940. [Google Scholar] [CrossRef]
- Quinet, P.; Palmeri, P.; Biémont, E.; Li, Z.S.; Zhang, Z.G.; Svanberg, S. Radiative lifetime measurements and transition probability calculations in lanthanide ions. J. Alloys Comp. 2002, 344, 255–259. [Google Scholar] [CrossRef]
- Quinet, P. An overview of the recent advances performed in the study of atomic structures and radiative processes in the lowest ionization stages of heavy elements. Can. J. Phys 2017, in press. [Google Scholar] [CrossRef]
- Fraga, S.; Karwowski, J.; Saxena, K.M.S. Handbook of Atomic Data; Elsevier: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Hibbert, A. Transitions in the Cadmium Sequence. Nucl. Instrum. Methods Phys. Res. 1982, 202, 323–327. [Google Scholar] [CrossRef]
- Hameed, S. Core Polarization Corrections to Oscillator Strengths and Singlet-Triplet Splittings in Alkaline Earth Atoms. J. Phys. B 1972, 5, 746. [Google Scholar] [CrossRef]
- Başar, G.; Gamper, B.; Güzelçimen, F.; Öztürk, I.K.; Binder, T.; Başar, G.; Kröger, S.; Windholz, L. New Even and Odd Parity Fine Structure Levels of La I Discovered by Means of Laser-Induced Fluorescence Spectroscopy. J. Quant. Spectrosc. Rad. Transfer. 2017, 187, 505–510. [Google Scholar] [CrossRef]
- Jönsson, P.; Gaigalas, G.; Bieron, J.; Froese Fischer, C.; Grant, I.P. New Version: GRASP2K Relativistic Atomic Structure Package. Comput. Phys. Commun. 2013, 184, 2197–2203. [Google Scholar] [CrossRef]
- Grant, I.P. Relativistic Quantum Theory of Atoms and Molecules. Theory and Computation; Springer: New York, NY, USA, 2007. [Google Scholar]
- Zhang, W.; Palmeri, P.; Quinet, P.; Biémont, E. Transition probabilities in Te II and Te III spectra. Astron. Astrophys. 2013, 551, A136. [Google Scholar] [CrossRef]
- Kramida, A. Critical evaluation of data on atomic energy levels, wavelengths, and transition probabilities. Fusion Sci. Technol. 2013, 63, 313–323. [Google Scholar] [CrossRef]
- Edlén, B. The refractive index of air. Metrologia 1966, 2, 71. [Google Scholar] [CrossRef]
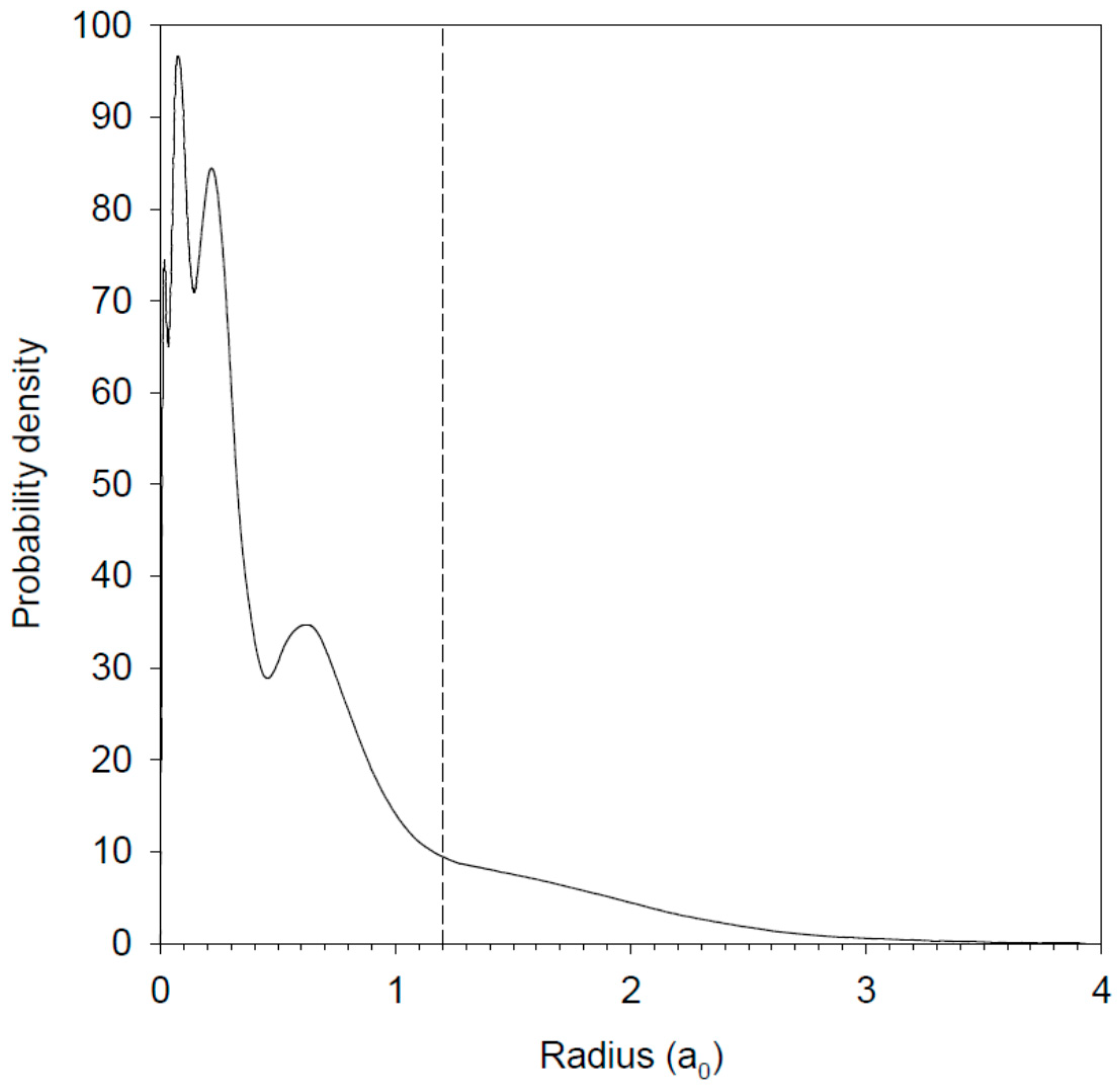
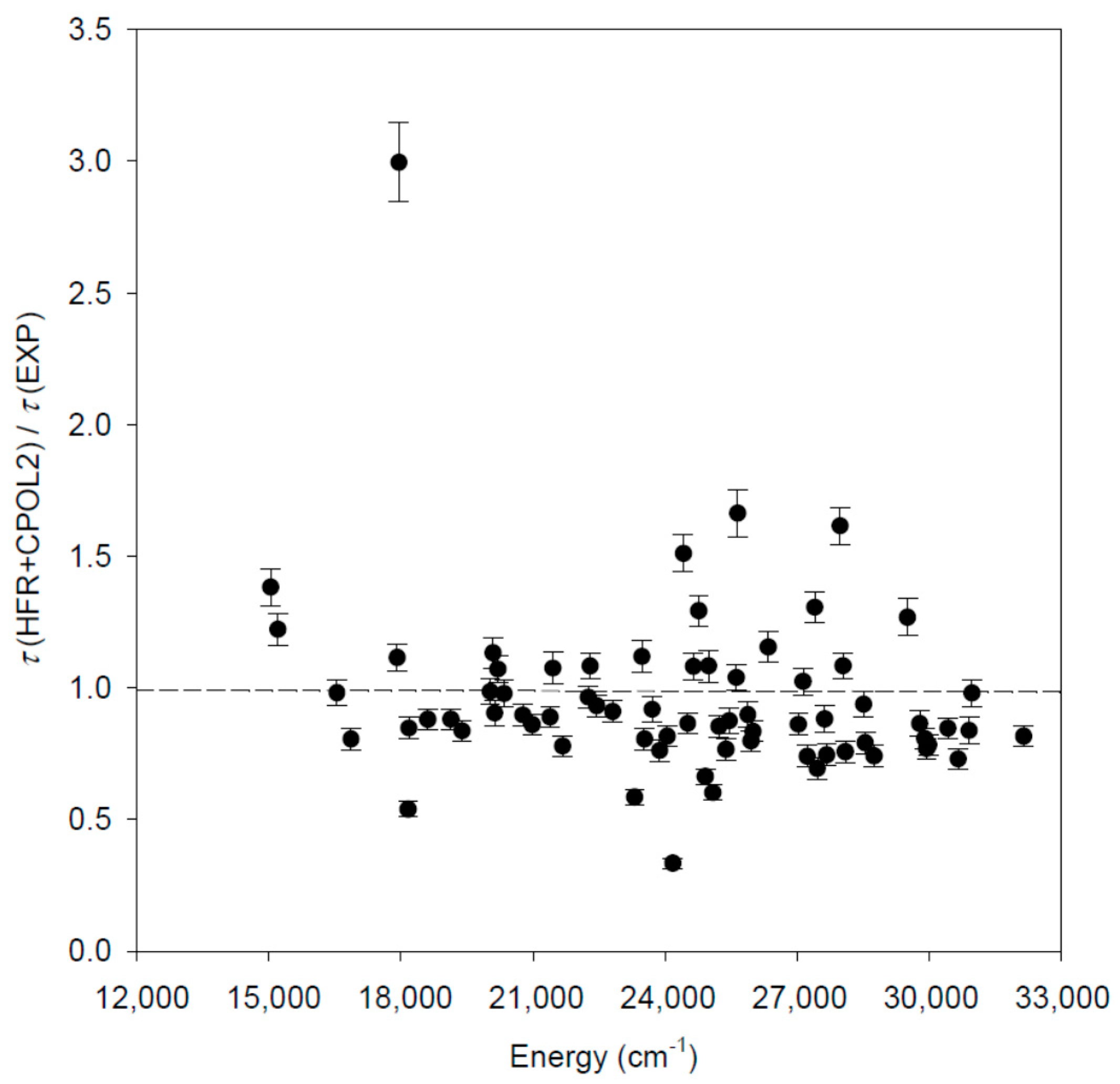
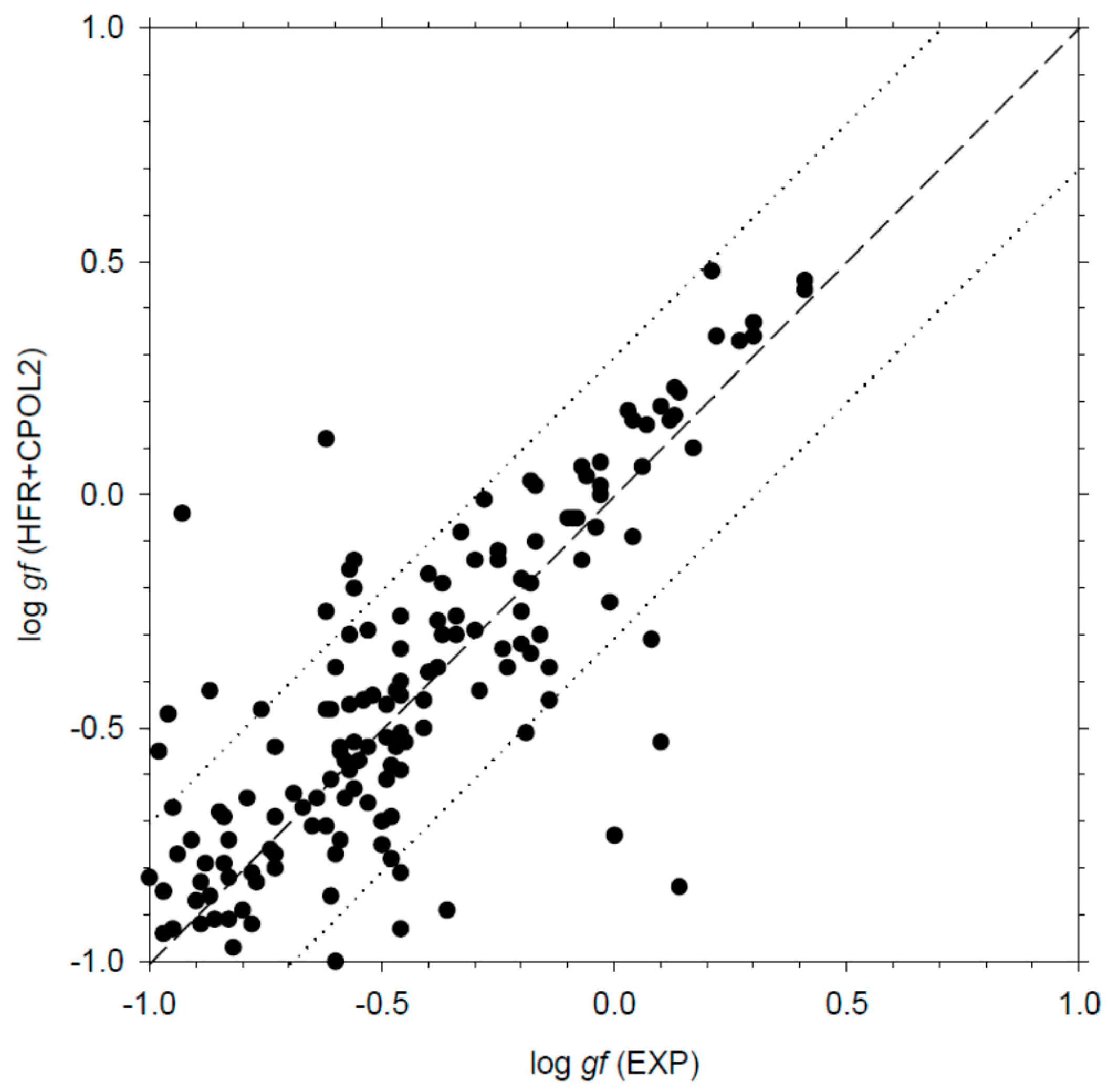
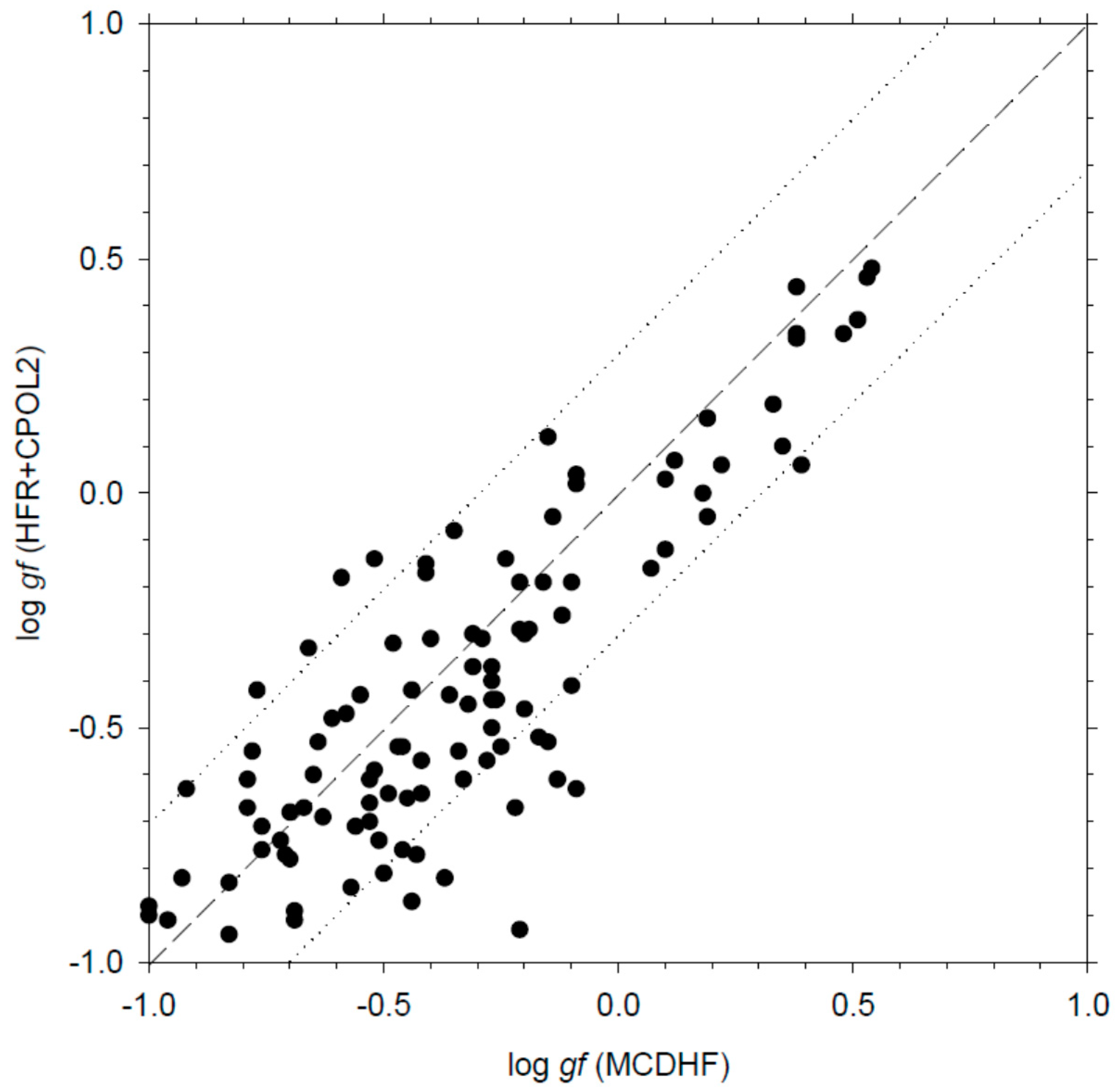
| Level a | This Work (ns) b | Experiment (ns) | |||||
|---|---|---|---|---|---|---|---|
| E (cm−1) | Designation | J | HFR-NOPOL | HFR+CPOL1 | HFR+CPOL2 | DH2015 c | Previous |
| 13,260.38 | 5d6s(3D)6p 4F° | 1.5 | 232 | 287 | 335 | 256.9 ± 12.3 f | |
| 13,631.04 | 5d6s(3D)6p ?° | 2.5 | 213 | 260 | 295 | 224.5 ± 13.8 f | |
| 14,095.69 | 5d6s(3D)6p 4D° | 0.5 | 119 | 149 | 179 | 220.9 ± 14.3 f | |
| 14,708.92 | 5d6s(3D)6p 4D° | 1.5 | 158 | 198 | 239 | 166.3 ± 9.3 f | |
| 14,804.08 | 5d6s(3D)6p 4F° | 2.5 | 194 | 236 | 270 | 257.9 ± 21.5 f | |
| 15,019.51 | 5d6s(3D)6p 4F° | 3.5 | 247 | 305 | 357 | 313.0 ± 17.8 f | |
| 15,031.64 | 5d6s(3D)6p ?° | 1.5 | 155 | 192 | 224 | 162 ± 8 | 183.7 ± 12.8 f |
| 15,196.83 | 4f6s2 2F° | 2.5 | 106 | 123 | 132 | 108 ± 5 | 127.0 ± 7.0 f |
| 15,219.89 | 5d6s(3D)6p ?° | 0.5 | 355 | 459 | 585 | 205.4 ± 16.9 f | |
| 15,503.64 | 5d6s(3D)6p 4D° | 2.5 | 106 | 132 | 158 | 131.8 ± 6.8 f | |
| 16,099.29 | 5d6s(3D)6p 4D° | 3.5 | 102 | 127 | 153 | 156.7 ± 14.2 f | |
| 16,280.26 | 6s26p ?° | 1.5 | 211 | 269 | 337 | 271.6 ± 19.2 f | |
| 16,538.39 | 4f6s2 2F° | 3.5 | 68.1 | 78.8 | 83.7 | 85.3 ± 4.3 | 112.9 ± 9.5 f |
| 16,856.80 | 5d2(3F)6p ?° | 2.5 | 34.6 | 40.6 | 42.2 | 52.4 ± 2.6 | 68.4 ± 5.1 f |
| 17,797.29 | 5d6s(3D)6p 4P° | 1.5 | 236 | 287 | 341 | 130.2 ± 11.5 f | |
| 17,910.17 | 5d2(3F)6p ?° | 3.5 | 44.4 | 52.0 | 54.5 | 48.9 ± 2.4 | 64.6 ± 2.7 f |
| 17,947.13 | 5d2(3F)6p 4G° | 2.5 | 115 | 138 | 154 | 51.4 ± 2.6 | 68.3 ± 3.1 f |
| 18,156.97 | 5d6s(3D)6p 4P° | 2.5 | 28.4 | 33.1 | 34.5 | 64.0 ± 3.2 | 68.4 ± 3.1 f |
| 18,172.35 | 5d2(3F)6p 2D° | 1.5 | 10.7 | 12.7 | 13.3 | 15.7 ± 0.8 | 17.7 ± 1.4 d |
| 18,603.92 | 5d2(3F)6p 4G° | 3.5 | 27.5 | 31.8 | 33.1 | 37.6 ± 1.9 | 54.8 ± 3.5 f |
| 19,129.31 | 5d2(3F)6p 4G° | 4.5 | 21.7 | 25.0 | 25.9 | 29.4 ± 1.5 | 46.0 ± 2.6 f |
| 19,379.40 | 5d2(3F)6p 2D° | 2.5 | 10.3 | 12.2 | 12.8 | 15.3 ± 0.8 | 17.2 ± 1.0 d |
| 15.9 ± 1.0 f | |||||||
| 20,018.99 | 5d6s(1D)6p ?° | 1.5 | 11.2 | 13.2 | 13.9 | 14.1 ± 0.7 | 17.0 ± 0.8 f |
| 20,082.98 | 5d2(3F)6p 4F° | 1.5 | 14.2 | 16.4 | 17.1 | 15.1 ± 0.8 | 17.5 ± 1.6 f |
| 20,117.38 | 5d2(3F)6p 4G° | 5.5 | 20.6 | 23.7 | 24.6 | 27.2 ± 1.4 | 32.0 ± 2.2 f |
| 20,197.34 | 5d6s(1D)6p ?° | 0.5 | 8.4 | 9.9 | 10.5 | 9.8 ± 0.5 | 17.2 ± 0.8 f |
| 20,338.25 | 5d2(3F)6p 4F° | 2.5 | 15.1 | 17.5 | 18.3 | 18.7 ± 0.9 | 20.0 ± 0.9 f |
| 20,763.21 | 5d2(3F)6p 4F° | 3.5 | 15.2 | 17.6 | 18.3 | 20.4 ± 1.0 | 25.8 ± 1.4 f |
| 20,972.17 | 5d2(3F)6p ?° | 2.5 | 17.9 | 21.0 | 22.1 | 25.7 ± 1.3 | 35.0 ± 3.5 f |
| 21,384.00 | 5d2(3F)6p 4F° | 4.5 | 14.6 | 17.0 | 17.7 | 19.9 ± 1.0 | 23.0 ± 2.1 f |
| 21,447.86 | 5d2(3F)6p ?° | 3.5 | 26.0 | 30.0 | 31.4 | 29.2 ± 1.5 | 34.1 ± 3.3 f |
| 21,662.51 | 5d2(3F)6p 2G° | 3.5 | 20.4 | 23.8 | 25.0 | 32.1 ± 1.6 | 39.8 ± 2.1 f |
| 22,246.64 | 5d2(3F)6p 4D° | 0.5 | 6.7 | 7.9 | 8.3 | 8.6 ± 0.4 | 10.1 ± 0.9 d |
| 9.6 ± 0.6 f | |||||||
| 22,285.77 | 5d2(3F)6p 2G° | 4.5 | 47.0 | 53.5 | 56.1 | 51.8 ± 2.6 | 73.4 ± 6.1 f |
| 22,439.36 | 5d2(3F)6p 4D° | 1.5 | 6.6 | 7.7 | 8.2 | 8.8 ± 0.4 | 10.2 ± 0.5 d |
| 9.5 ± 0.7 f | |||||||
| 22,804.25 | 5d2(3F)6p 4D° | 2.5 | 6.6 | 7.7 | 8.1 | 8.9 ± 0.4 | 10.7 ± 1.0 d |
| 10.4 ± 0.3 f | |||||||
| 23,221.10 | 5d6s(3D)6p ?° | 3.5 | 109 | 127 | 134 | 21.1 ± 1.1 | 22.0 ± 1.4 d |
| 27.5 ± 2.7 f | |||||||
| 23,260.92 | 5d2(3P)6p 2S° | 0.5 | 13.6 | 16.0 | 17.0 | 18.1 ± 1.5 f | |
| 23,303.26 | 5d2(3P)6p 4D° | 3.5 | 6.9 | 8.1 | 8.6 | 14.7 ± 0.7 | 16.1 ± 1.0 d |
| 16.5 ± 1.1 f | |||||||
| 23,466.84 | 4f5d(1G°)6s 2G° | 4.5 | 56.0 | 64.7 | 67.8 | 60.6 ± 3.0 | 67.9 ± 3.8 f |
| 23,528.45 | 5d2(3P)6p 4D° | 0.5 | 16.6 | 19.3 | 20.3 | 25.2 ± 1.3 | 27.8 ± 1.8 f |
| 23,704.81 | 5d2(3P)6p 4D° | 1.5 | 20.4 | 23.7 | 24.8 | 27.0 ± 1.4 | 31.2 ± 2.5 f |
| 23,874.95 | 5d6s(3D)6p ?° | 2.5 | 9.2 | 10.8 | 11.2 | 14.7 ± 0.7 | 16.2 ± 1.0 d |
| 14.7 ± 1.1 e | |||||||
| 24,046.10 | 5d2(3P)6p 4D° | 2.5 | 21.6 | 25.1 | 26.2 | 32.1 ± 1.6 | 16.1 ± 1.0 f |
| 24,088.54 | 4f5d(3H°)6s 4H° | 3.5 | 81.9 | 95.6 | 100.0 | 247 ± 12 e | |
| 207.5 ± 14.5 f | |||||||
| 24,173.83 | 4f5d(3F°)6s 4F° | 1.5 | 9.6 | 11.4 | 12.0 | 35.9 ± 1.8 | 37.7 ± 1.4 f |
| 24,409.68 | 4f5d(1G°)6s ?° | 3.5 | 17.9 | 20.7 | 21.6 | 14.3 ± 0.7 | 15.7 ± 0.7 d |
| 14.6 ± 1.2 e | |||||||
| 24,507.87 | 4f5d(3F°)6s 4F° | 2.5 | 13.5 | 15.9 | 16.7 | 19.3 ± 1.0 | 21.9 ± 1.0 d |
| 19.2 ± 1.5 e | |||||||
| 22.2 ± 1.9 f | |||||||
| 20.0 ± 0.8 g | |||||||
| 24,639.26 | 5d2(3P)6p 4S° | 1.5 | 13.9 | 16.4 | 17.3 | 16.0 ± 0.8 | 14.9 ± 0.9 e |
| 24,762.60 | 5d2(3P)6p? 2D°? | 1.5 | 11.3 | 13.2 | 13.7 | 10.6 ± 0.5 | 12.4 ± 1.1 f |
| 24,910.38 | 4f5d(1D°)6s? ?° | 1.5 | 16.8 | 19.4 | 20.3 | 30.6 ± 1.5 | 32.4 ± 1.8 f |
| 24,984.29 | 5d2(3P)6p? ?° | 2.5 | 19.1 | 22.3 | 23.4 | 21.6 ± 1.1 | 27.2 ± 1.9 f |
| 25,083.36 | 5d2(3P)6p 4D° | 3.5 | 9.5 | 11.0 | 11.5 | 19.1 ± 1.0 | 21.1 ± 0.9 d |
| 25,218.27 | 5d2(3P)6p ?° | 2.5 | 9.8 | 11.6 | 12.3 | 14.4 ± 0.7 | 15.7 ± 1.1 f |
| 25,380.27 | 4f5d(3F°)6s 4F° | 3.5 | 13.2 | 15.6 | 16.4 | 21.4 ± 1.1 | 23.2 ± 1.3 d |
| 25,453.95 | 5d6s(3D)6p ?° | 0.5 | 6.6 | 7.8 | 8.4 | 9.6 ± 0.5 | 19.4 ± 0.8 f |
| 25,616.95 | 5d2(3P)6p 4P° | 0.5 | 15.3 | 17.7 | 18.5 | 17.8 ± 0.9 | 17.6 ± 1.1 e |
| 25,643.00 | 5d2(3P)6p 4P° | 1.5 | 18.7 | 21.7 | 22.8 | 13.7 ± 0.7 | 16.2 ± 0.8 f |
| 25,874.52 | 5d2(1G)6p ?° | 5.5 | 46.4 | 53.0 | 55.4 | 61.7 ± 3.1 | |
| 25,950.32 | 5d2(3P)6p ?° | 1.5 | 7.6 | 8.9 | 9.5 | 11.9 ± 0.6 | 11.8 ± 0.9 e |
| 25,997.17 | 4f5d(3F°)6s 4F° | 4.5 | 14.1 | 16.8 | 17.7 | 21.2 ± 1.1 | 23.3 ± 1.5 d |
| 21.8 ± 0.9 f | |||||||
| 21.6 ± 1.0 g | |||||||
| 26,338.93 | 5d2(3P)6p 4P° | 2.5 | 15.9 | 18.5 | 19.3 | 16.7 ± 0.8 | 16.5 ± 1.2 e |
| 27,022.62 | 4f5d(3G°)6s 4G° | 2.5 | 13.7 | 16.3 | 16.8 | 19.5 ± 1.0 | 18.9 ± 1.4 e |
| 20.9 ± 1.3 f | |||||||
| 27,054.96 | 5d2(1G)6p ?° | 4.5 | 56.5 | 64.3 | 67.1 | 89.7 ± 4.4 g | |
| 27,132.44 | 5d2(1G)6p 2G° | 3.5 | 13.5 | 15.9 | 16.8 | 16.4 ± 0.8 | 16.6 ± 1.2 e |
| 27,225.26 | 5d2(3P)6p 2P° | 1.5 | 9.3 | 10.8 | 11.4 | 15.4 ± 0.8 | 17.1 ± 0.9 d |
| 27,393.04 | 5d2(1D)6p ?° | 2.5 | 13.1 | 15.6 | 16.2 | 12.4 ± 0.6 | 14.1 ± 0.6 d |
| 12.6 ± 0.8 e | |||||||
| 12.6 ± 0.6 g | |||||||
| 27,455.31 | 4f5d(3G°)6s 4G° | 3.5 | 11.1 | 13.2 | 13.6 | 19.6 ± 1.0 | 21.6 ± 1.6 d |
| 19.8 ± 1.4 e | |||||||
| 27,619.54 | 5d2(1G)6p 2G° | 4.5 | 10.9 | 12.7 | 13.4 | 12.7 ± 0.6 | 14.3 ± 1.1 e |
| 27,669.37 | 4f5d(3F°)6s 2F° | 2.5 | 9.6 | 11.1 | 11.7 | 15.7 ± 0.8 | 17.8 ± 0.9 d |
| 15.6 ± 0.7 g | |||||||
| 27,748.97 | 5d2(3P)6p 2P° | 0.5 | 10.7 | 12.6 | 13.3 | 27.0 ± 2.6 f | |
| 27,968.54 | 4f5d(3D°)6s ?° | 1.5 | 8.6 | 9.6 | 10.5 | 6.5 ± 0.3 | 9.5 ± 0.9 f |
| 28,039.45 | 5d6s(1D)6p ?° | 3.5 | 10.4 | 12.4 | 12.9 | 11.9 ± 0.6 | 13.0 ± 0.9 d |
| 11.9 ± 0.8 e | |||||||
| 28,089.17 | 4f5d(3G°)6s 4G° | 4.5 | 11.5 | 13.8 | 14.0 | 18.5 ± 0.9 | 21.8 ± 1.8 f |
| 28,506.41 | 5d6s(3D)6p ?° | 2.5 | 6.2 | 7.1 | 7.5 | 8.0 ± 0.4 | 7.9 ± 0.3 d |
| 7.9 ± 0.4 e | |||||||
| 28,543.08 | 4f5d(3F°)6s 2F° | 3.5 | 13.1 | 15.2 | 15.9 | 20.1 ± 1.0 | 21.7 ± 1.2 d |
| 19.7 ± 1.1 e | |||||||
| 28,743.24 | 4f5d(3G°)6s 4G° | 5.5 | 10.9 | 13.1 | 13.2 | 17.8 ± 0.9 | 23.8 ± 1.6 f |
| 28,893.51 | 4f5d(3D°)6s 4D° | 0.5 | 10.3 | 12.2 | 12.8 | 20.0 ± 1.7 f | |
| 28,971.84 | 4f5d(3D°)6s ?° | 1.5 | 9.9 | 11.5 | 12.0 | 17.2 ± 1.2 f | |
| 29,199.57 | 4f5d(3D°)6s ?° | 1.5 | 8.6 | 10.1 | 10.5 | 15.4 ± 0.8 e | |
| 29,466.67 | [4f5d(3G°)6s 2G°] | 3.5 | 12.2 | 14.2 | 14.7 | 28.3 ± 0.9 f | |
| 29,502.18 | 4f5d(3D°)6s ?° | 2.5 | 11.6 | 13.4 | 14.2 | 11.2 ± 0.6 | 10.4 ± 0.9 e |
| 29,564.70 | 4f5d(3P°)6s ?° | 0.5 | 10.1 | 11.8 | 12.6 | 16.9 ± 0.8 g | |
| 29,775.58 | 4f5d(3D°)6s ?° | 2.5 | 9.3 | 11.0 | 11.5 | 13.3 ± 0.7 | 12.3 ± 1.1 e |
| 29,894.91 | 4f5d(3D°)6s ?° | 3.5 | 10.3 | 12.2 | 12.6 | 15.6 ± 0.8 | 14.9 ± 0.8 e |
| 29,936.74 | 4f5d(3P°)6s ?° | 1.5 | 8.0 | 9.4 | 10.0 | 13.0 ± 0.7 | 12.5 ± 0.8 e |
| 29,985.46 | 4f5d(3P°)6s 4P° | 0.5 | 9.9 | 11.7 | 12.3 | 15.7 ± 0.8 | |
| 30,417.46 | 4f5d(3P°)6s 4P° | 1.5 | 9.3 | 10.9 | 11.6 | 13.7 ± 0.7 | 13.6 ± 0.9 e |
| 30,650.28 | [4f5d(3G°)6s 2G°] | 4.5 | 13.2 | 15.3 | 15.7 | 21.5 ± 1.1 | 20.8 ± 1.5 e |
| 30,788.45 | [4f5d(1F°)6s 2F°] | 2.5 | 9.4 | 10.9 | 11.4 | 14.4 ± 1.2 f | |
| 30,896.84 | 4f5d(3P°)6s 4P° | 2.5 | 8.8 | 10.4 | 10.9 | 13.0 ± 0.7 | 18.6 ± 1.7 f |
| 30,964.71 | [4f5d(1F°)6s 2F°] | 3.5 | 8.2 | 9.5 | 9.9 | 10.1 ± 0.5 | 11.9 ± 0.6 f |
| 31,477.22 | [5d2(1G)6p 2F°] | 2.5 | 5.9 | 6.7 | 7.0 | 8.7 ± 0.4 g | |
| 31,751.48 | [4f5d(3D°)6s 2D°] | 1.5 | 11.1 | 12.9 | 13.3 | 12.3 ± 0.8 g | |
| 32,140.55 | [5d2(1D)6p 2F°] | 3.5 | 5.2 | 5.9 | 6.2 | 7.6 ± 0.4 | 7.3 ± 0.5 e |
| Lower Level b | Upper Level b | This Work c | Experiment d | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ë (nm) a | E (cm−1) | J | E (cm−1) | J | log gf | gA (s−1) | Code | log gf | gA (s−1) |
| 317.5982 | 0.000 | 1.5 | 31,477.22 | 2.5° | −0.74 | 1.20 + 08 | E | ||
| 321.5810 | 1053.164 | 2.5 | 32,140.55 | 3.5° | −0.45 | 2.27 + 08 | E | −0.49 | 2.08 + 08 |
| 324.7034 | 0.000 | 1.5 | 30,788.45 | 2.5° | −0.99 | 6.54 + 07 | E | ||
| 334.2230 | 1053.164 | 2.5 | 30,964.71 | 3.5° | −0.37 | 2.55 + 08 | E | −0.14 | 4.32 + 08 |
| 336.2042 | 1053.164 | 2.5 | 30,788.45 | 2.5° | −0.88 | 7.74 + 07 | E | ||
| 340.4519 | 1053.164 | 2.5 | 30,417.46 | 1.5° | −0.94 | 6.60 + 07 | E | −1.01 | 5.60 + 07 |
| 342.3726 | 0.000 | 1.5 | 29,199.57 | 1.5° | −0.73 | 1.05 + 08 | E | ||
| 346.1184 | 1053.164 | 2.5 | 29,936.74 | 1.5° | −0.68 | 1.16 + 08 | E | −0.85 | 7.84 + 07 |
| 348.0605 | 1053.164 | 2.5 | 29,775.58 | 2.5° | −0.96 | 6.01 + 07 | E | ||
| 350.6980 | 0.000 | 1.5 | 28,506.41 | 2.5° | −0.87 | 7.23 + 07 | E | ||
| 357.4425 | 0.000 | 1.5 | 27,968.54 | 1.5° | −0.44 | 1.89 + 08 | E | −0.14 | 3.80 + 08 |
| 361.3074 | 0.000 | 1.5 | 27,669.37 | 2.5° | −0.54 | 1.47 + 08 | E | −0.73 | 9.42 + 07 |
| 363.6661 | 1053.164 | 2.5 | 28,543.08 | 3.5° | −0.77 | 8.58 + 07 | E | −0.94 | 5.76 + 07 |
| 364.1519 | 1053.164 | 2.5 | 28,506.41 | 2.5° | −0.10 | 4.03 + 08 | D | 0.04 | 5.46 + 08 |
| 370.4532 | 1053.164 | 2.5 | 28,039.45 | 3.5° | −0.80 | 7.65 + 07 | E | −0.46 | 1.66 + 08 |
| 378.6495 | 1053.164 | 2.5 | 27,455.31 | 3.5° | −0.70 | 9.34 + 07 | E | ||
| 385.2424 | 0.000 | 1.5 | 25,950.32 | 1.5° | −0.92 | 5.44 + 07 | E | −1.57 | 1.20 + 07 |
| 387.8879 | 4121.572 | 4.5 | 29,894.91 | 3.5° | −0.91 | 5.47 + 07 | E | −0.83 | 6.56 + 07 |
| 392.7551 | 0.000 | 1.5 | 25,453.95 | 0.5° | −0.30 | 2.14 + 08 | D | −0.37 | 1.86 + 08 |
| 399.4164 | 3010.002 | 2.5 | 28,039.45 | 3.5° | −0.36 | 1.84 + 08 | E | −1.19 | 2.72 + 07 |
| 401.5388 | 1053.164 | 2.5 | 25,950.32 | 1.5° | −0.18 | 2.71 + 08 | D | −0.20 | 2.60 + 08 |
| 404.3371 | 2668.188 | 1.5 | 27,393.04 | 2.5° | −0.40 | 1.60 + 08 | D | ||
| 406.0316 | 4121.572 | 4.5 | 28,743.24 | 5.5° | 0.34 | 8.76 + 08 | D+ | 0.22 | 6.72 + 08 |
| 406.4778 | 3494.526 | 3.5 | 28,089.17 | 4.5° | 0.18 | 6.09 + 08 | D+ | 0.03 | 4.32 + 08 |
| 407.9170 | 0.000 | 1.5 | 24,507.87 | 2.5° | −0.63 | 9.31 + 07 | E | −0.56 | 1.11 + 08 |
| 408.9610 | 3010.002 | 2.5 | 27,455.31 | 3.5° | −0.14 | 2.91 + 08 | D | −0.07 | 3.36 + 08 |
| 410.4870 | 2668.188 | 1.5 | 27,022.62 | 2.5° | −0.32 | 1.90 + 08 | D | −0.20 | 2.47 + 08 |
| 410.9481 | 1053.164 | 2.5 | 25,380.27 | 3.5° | −0.68 | 8.21 + 07 | E | −1.11 | 3.04 + 07 |
| 413.5538 | 0.000 | 1.5 | 24,173.83 | 1.5° | −0.60 | 9.77 + 07 | E | ||
| 413.7031 | 1053.164 | 2.5 | 25,218.27 | 2.5° | −0.53 | 1.15 + 08 | E | −0.53 | 1.15 + 08 |
| 414.3907 | 3494.526 | 3.5 | 27,619.54 | 4.5° | −0.83 | 5.70 + 07 | E | −0.77 | 6.60 + 07 |
| 416.0258 | 1053.164 | 2.5 | 25,083.36 | 3.5° | 0.12 | 5.10 + 08 | E | −0.62 | 9.20 + 07 |
| 416.3303 | 3010.002 | 2.5 | 27,022.62 | 2.5° | −0.94 | 4.43 + 07 | E | −0.97 | 4.08 + 07 |
| 417.1124 | 4121.572 | 4.5 | 28,089.17 | 4.5° | −0.82 | 5.81 + 07 | E | −1.00 | 3.79 + 07 |
| 417.2310 | 3494.526 | 3.5 | 27,455.31 | 3.5° | −0.79 | 6.26 + 07 | E | −0.84 | 5.52 + 07 |
| 417.7481 | 1053.164 | 2.5 | 24,984.29 | 2.5° | −0.70 | 7.69 + 07 | E | −0.73 | 7.08 + 07 |
| 418.7310 | 0.000 | 1.5 | 23,874.95 | 2.5° | 0.03 | 4.12 + 08 | D | −0.06 | 3.31 + 08 |
| 421.6542 | 1053.164 | 2.5 | 24,762.60 | 1.5° | −0.93 | 4.37 + 07 | E | −1.47 | 1.28 + 07 |
| 427.1148 | 7490.521 | 1.5 | 30,896.84 | 2.5° | −0.53 | 1.07 + 08 | E | −0.45 | 1.30 + 08 |
| 428.0256 | 1053.164 | 2.5 | 24,409.68 | 3.5° | −0.53 | 1.07 + 08 | E | 0.10 | 4.55 + 08 |
| 429.3445 | 7679.939 | 2.5 | 30,964.71 | 3.5° | −0.79 | 5.90 + 07 | E | −1.41 | 1.44 + 07 |
| 430.5996 | 7679.939 | 2.5 | 30,896.84 | 2.5° | −0.27 | 1.91 + 08 | D | −0.38 | 1.51 + 08 |
| 431.1725 | 7231.407 | 0.5 | 30,417.46 | 1.5° | −0.74 | 6.50 + 07 | E | −0.91 | 4.40 + 07 |
| 434.0720 | 8446.044 | 1.5 | 31,477.22 | 2.5° | −0.03 | 3.29 + 08 | D | ||
| 435.4793 | 9183.797 | 2.5 | 32,140.55 | 3.5° | 0.23 | 5.95 + 08 | D+ | 0.13 | 4.72 + 08 |
| 440.2640 | 9044.214 | 0.5 | 31,751.48 | 1.5° | −0.39 | 1.39 + 08 | D | ||
| 440.3015 | 7231.407 | 0.5 | 29,936.74 | 1.5° | −0.87 | 4.64 + 07 | E | −0.90 | 4.36 + 07 |
| 442.3905 | 8052.162 | 3.5 | 30,650.28 | 4.5° | 0.22 | 5.63 + 08 | D+ | 0.14 | 4.65 + 08 |
| 444.2675 | 3494.526 | 3.5 | 25,997.17 | 4.5° | −0.93 | 3.95 + 07 | E | −0.95 | 3.76 + 07 |
| 444.4197 | 7490.521 | 1.5 | 29,985.46 | 0.5° | −0.43 | 1.26 + 08 | D | −0.52 | 1.00 + 08 |
| 445.2149 | 7011.909 | 2.5 | 29,466.67 | 3.5° | 0.02 | 3.53 + 08 | D+ | ||
| 446.8965 | 3010.002 | 2.5 | 25,380.27 | 3.5° | −0.92 | 3.97 + 07 | E | −0.89 | 4.24 + 07 |
| 447.4538 | 8446.044 | 1.5 | 30,788.45 | 2.5° | −0.38 | 1.39 + 08 | D | ||
| 448.6053 | 7490.521 | 1.5 | 29,775.58 | 2.5° | −0.17 | 2.21 + 08 | E | −0.40 | 1.31 + 08 |
| 449.1748 | 7679.939 | 2.5 | 29,936.74 | 1.5° | −0.44 | 1.20 + 08 | D | −0.54 | 9.44 + 07 |
| 449.9040 | 9919.821 | 4.5 | 32,140.55 | 3.5° | −0.01 | 3.21 + 08 | E | −0.28 | 1.71 + 08 |
| 450.0206 | 7679.939 | 2.5 | 29,894.91 | 3.5° | 0.15 | 4.62 + 08 | D+ | 0.07 | 3.83 + 08 |
| 450.1565 | 3010.002 | 2.5 | 25,218.27 | 2.5° | −0.66 | 7.16 + 07 | E | −1.21 | 2.04 + 07 |
| 454.1773 | 7490.521 | 1.5 | 29,502.18 | 2.5° | −0.58 | 8.43 + 07 | E | −0.46 | 1.12 + 08 |
| 454.9498 | 3010.002 | 2.5 | 24,984.29 | 2.5° | −0.94 | 3.73 + 07 | E | −0.46 | 1.11 + 08 |
| 455.0164 | 2668.188 | 1.5 | 24,639.26 | 1.5° | −0.40 | 1.29 + 08 | E | −1.57 | 8.68 + 06 |
| 455.0766 | 7231.407 | 0.5 | 29,199.57 | 1.5° | −0.65 | 7.28 + 07 | E | ||
| 456.7904 | 3494.526 | 3.5 | 25,380.27 | 3.5° | −0.05 | 2.84 + 08 | D | −0.09 | 2.62 + 08 |
| 457.0023 | 4121.572 | 4.5 | 25,997.17 | 4.5° | 0.16 | 4.65 + 08 | D+ | 0.13 | 4.34 + 08 |
| 458.1197 | 7679.939 | 2.5 | 29,502.18 | 2.5° | −0.19 | 2.03 + 08 | E | −0.56 | 8.76 + 07 |
| 458.9890 | 9183.797 | 2.5 | 30,964.71 | 3.5° | −0.38 | 1.33 + 08 | D | ||
| 459.8436 | 7231.407 | 0.5 | 28,971.84 | 1.5° | −0.80 | 4.99 + 07 | E | ||
| 460.4237 | 9183.797 | 2.5 | 30,896.84 | 2.5° | −0.26 | 1.71 + 08 | E | −0.46 | 1.08 + 08 |
| 461.5064 | 7231.407 | 0.5 | 28,893.51 | 0.5° | −0.49 | 1.01 + 08 | D | ||
| 462.2072 | 3010.002 | 2.5 | 24,639.26 | 1.5° | −0.97 | 3.38 + 07 | E | ||
| 464.3129 | 7011.909 | 2.5 | 28,543.08 | 3.5° | −0.90 | 3.88 + 07 | E | −1.01 | 3.05 + 07 |
| 464.6335 | 9960.904 | 3.5 | 31,477.22 | 2.5° | −0.03 | 2.85 + 08 | D | ||
| 465.0322 | 3010.002 | 2.5 | 24,507.87 | 2.5° | −0.56 | 8.58 + 07 | E | −0.98 | 3.24 + 07 |
| 465.1874 | 8446.044 | 1.5 | 29,936.74 | 1.5° | −0.86 | 4.26 + 07 | E | −1.15 | 2.16 + 07 |
| 465.3905 | 7490.521 | 1.5 | 28,971.84 | 1.5° | −0.42 | 1.18 + 08 | D | ||
| 470.2641 | 4121.572 | 4.5 | 25,380.27 | 3.5° | −0.83 | 4.44 + 07 | E | −0.89 | 3.92 + 07 |
| 470.8186 | 9183.797 | 2.5 | 30,417.46 | 1.5° | −0.30 | 1.51 + 08 | E | −0.57 | 8.12 + 07 |
| 473.3826 | 8446.044 | 1.5 | 29,564.70 | 0.5° | −0.66 | 6.44 + 07 | E | ||
| 475.0419 | 9919.821 | 4.5 | 30,964.71 | 3.5° | −0.23 | 1.75 + 08 | E | −0.01 | 2.88 + 08 |
| 475.9711 | 9960.904 | 3.5 | 30,964.71 | 3.5° | −0.97 | 3.16 + 07 | E | −0.82 | 4.48 + 07 |
| 476.6891 | 0.000 | 1.5 | 20,972.17 | 2.5° | −0.46 | 1.02 + 08 | D | −0.62 | 7.08 + 07 |
| 477.0425 | 7011.909 | 2.5 | 27,968.54 | 1.5° | −0.51 | 9.04 + 07 | D | −0.46 | 1.02 + 08 |
| 479.9992 | 9960.904 | 3.5 | 30,788.45 | 2.5° | −0.33 | 1.35 + 08 | D | ||
| 481.7112 | 8446.044 | 1.5 | 29,199.57 | 1.5° | −0.52 | 8.77 + 07 | D | ||
| 481.7247 | 9183.797 | 2.5 | 29,936.74 | 1.5° | −0.86 | 3.96 + 07 | E | −0.61 | 7.00 + 07 |
| 483.9514 | 7011.909 | 2.5 | 27,669.37 | 2.5° | 0.02 | 3.01 + 08 | D+ | −0.03 | 2.63 + 08 |
| 485.0812 | 1053.164 | 2.5 | 21,662.51 | 3.5° | −0.46 | 9.76 + 07 | E | −0.76 | 4.96 + 07 |
| 485.4950 | 9183.797 | 2.5 | 29,775.58 | 2.5° | −0.34 | 1.30 + 08 | D | −0.24 | 1.62 + 08 |
| 487.0558 | 8446.044 | 1.5 | 28,971.84 | 1.5° | −0.73 | 5.21 + 07 | E | ||
| 487.8848 | 8052.162 | 3.5 | 28,543.08 | 3.5° | −0.10 | 2.21 + 08 | D | −0.17 | 1.90 + 08 |
| 488.7595 | 8052.162 | 3.5 | 28,506.41 | 2.5° | −0.15 | 1.97 + 08 | E | −0.56 | 7.68 + 07 |
| 490.1867 | 1053.164 | 2.5 | 21,447.86 | 3.5° | −0.87 | 3.77 + 07 | E | −0.87 | 3.76 + 07 |
| 492.0278 | 9183.797 | 2.5 | 29,502.18 | 2.5° | −0.75 | 4.93 + 07 | E | ||
| 494.5845 | 7011.909 | 2.5 | 27,225.26 | 1.5° | −0.79 | 4.44 + 07 | E | −0.88 | 3.64 + 07 |
| 494.9765 | 0.000 | 1.5 | 20,197.34 | 0.5° | −0.19 | 1.78 + 08 | D | −0.18 | 1.80 + 08 |
| 497.7952 | 0.000 | 1.5 | 20,082.98 | 1.5° | −0.94 | 3.07 + 07 | E | −1.35 | 1.20 + 07 |
| 500.1785 | 8052.162 | 3.5 | 28,039.45 | 3.5° | −0.50 | 8.39 + 07 | E | −0.19 | 1.70 + 08 |
| 504.6871 | 3494.526 | 3.5 | 23,303.26 | 3.5° | −0.40 | 1.04 + 08 | D | −0.46 | 9.04 + 07 |
| 505.0564 | 3010.002 | 2.5 | 22,804.25 | 2.5° | −0.29 | 1.34 + 08 | D | −0.30 | 1.30 + 08 |
| 505.6459 | 2668.188 | 1.5 | 22,439.36 | 1.5° | −0.43 | 9.74 + 07 | D | −0.46 | 9.04 + 07 |
| 510.6233 | 2668.188 | 1.5 | 22,246.64 | 0.5° | −0.05 | 2.30 + 08 | D+ | −0.08 | 2.10 + 08 |
| 511.4489 | 9919.821 | 4.5 | 29,466.67 | 3.5° | −0.76 | 4.47 + 07 | E | ||
| 514.5417 | 3010.002 | 2.5 | 22,439.36 | 1.5° | 0.16 | 3.67 + 08 | D+ | 0.12 | 3.28 + 08 |
| 515.2367 | 8052.162 | 3.5 | 27,455.31 | 3.5° | −0.77 | 4.28 + 07 | E | ||
| 515.8681 | 0.000 | 1.5 | 19,379.40 | 2.5° | −0.57 | 6.75 + 07 | D | −0.58 | 6.60 + 07 |
| 516.7783 | 4121.572 | 4.5 | 23,466.84 | 4.5° | −0.80 | 3.94 + 07 | E | −0.73 | 4.60 + 07 |
| 517.7296 | 3494.526 | 3.5 | 22,804.25 | 2.5° | 0.34 | 5.46 + 08 | C+ | 0.30 | 4.92 + 08 |
| 517.9119 | 8446.044 | 1.5 | 27,748.97 | 0.5° | −0.76 | 4.36 + 07 | E | ||
| 518.3910 | 1053.164 | 2.5 | 20,338.25 | 2.5° | −0.90 | 3.09 + 07 | E | −0.86 | 3.42 + 07 |
| 521.1854 | 4121.572 | 4.5 | 23,303.26 | 3.5° | 0.48 | 7.40 + 08 | E | 0.21 | 3.98 + 08 |
| 523.4274 | 4121.572 | 4.5 | 23,221.10 | 3.5° | −0.84 | 3.52 + 07 | E | 0.14 | 3.38 + 08 |
| 527.1174 | 1053.164 | 2.5 | 20,018.99 | 1.5° | 0.03 | 2.56 + 08 | E | −0.18 | 1.60 + 08 |
| 527.6413 | 8446.044 | 1.5 | 27,393.04 | 2.5° | −0.58 | 6.36 + 07 | D | −0.48 | 7.98 + 07 |
| 530.1974 | 9183.797 | 2.5 | 28,039.45 | 3.5° | −0.43 | 8.75 + 07 | D | ||
| 530.4012 | 7490.521 | 1.5 | 26,338.93 | 2.5° | −0.68 | 4.90 + 07 | E | −0.48 | 7.80 + 07 |
| 532.3555 | 8446.044 | 1.5 | 27,225.26 | 1.5° | −0.67 | 5.03 + 07 | E | −0.95 | 2.64 + 07 |
| 534.0705 | 7231.407 | 0.5 | 25,950.32 | 1.5° | −0.96 | 2.57 + 07 | E | ||
| 535.7856 | 7679.939 | 2.5 | 26,338.93 | 2.5° | −0.25 | 1.32 + 08 | D | −0.20 | 1.48 + 08 |
| 536.8136 | 9919.821 | 4.5 | 28,543.08 | 3.5° | −0.61 | 5.67 + 07 | D | ||
| 538.0005 | 9960.904 | 3.5 | 28,543.08 | 3.5° | −0.71 | 4.45 + 07 | E | −0.65 | 5.20 + 07 |
| 545.5142 | 1053.164 | 2.5 | 19,379.40 | 2.5° | 0.16 | 3.23 + 08 | D+ | 0.04 | 2.44 + 08 |
| 547.5155 | 9919.821 | 4.5 | 28,179.07 | 5.5° | −0.32 | 1.07 + 08 | D | ||
| 549.1060 | 7011.909 | 2.5 | 25,218.27 | 2.5° | −0.68 | 4.61 + 07 | E | −0.84 | 3.24 + 07 |
| 550.1337 | 0.000 | 1.5 | 18,172.35 | 1.5° | 0.07 | 2.61 + 08 | D+ | −0.03 | 2.05 + 08 |
| 550.2246 | 9919.821 | 4.5 | 28,089.17 | 4.5° | −0.77 | 3.74 + 07 | E | −0.60 | 5.60 + 07 |
| 551.5274 | 7490.521 | 1.5 | 25,616.95 | 0.5° | −0.45 | 7.79 + 07 | D | −0.61 | 5.32 + 07 |
| 551.7344 | 9919.821 | 4.5 | 28,039.45 | 3.5° | −0.72 | 4.18 + 07 | E | 0.00 | 2.21 + 08 |
| 552.9882 | 9960.904 | 3.5 | 28,039.45 | 3.5° | −0.24 | 1.25 + 08 | E | −0.62 | 5.20 + 07 |
| 554.1249 | 9183.797 | 2.5 | 27,225.26 | 1.5° | −0.14 | 1.57 + 08 | D | −0.25 | 1.22 + 08 |
| 554.4916 | 9719.439 | 1.5 | 27,748.97 | 0.5° | −0.43 | 8.07 + 07 | D | ||
| 556.5434 | 7679.939 | 2.5 | 25,643.00 | 1.5° | −0.32 | 1.02 + 08 | D | −0.46 | 7.44 + 07 |
| 556.9905 | 9183.797 | 2.5 | 27,132.44 | 3.5° | −0.49 | 6.91 + 07 | D | ||
| 558.5518 | 7011.909 | 2.5 | 24,910.38 | 1.5° | −0.94 | 2.46 + 07 | E | ||
| 558.8328 | 3494.526 | 3.5 | 21,384.00 | 4.5° | −0.61 | 5.27 + 07 | D | −0.49 | 6.90 + 07 |
| 563.1222 | 3010.002 | 2.5 | 20,763.21 | 3.5° | −0.50 | 6.71 + 07 | D | −0.41 | 8.16 + 07 |
| 564.5449 | 9960.904 | 3.5 | 27,669.37 | 2.5° | −0.71 | 4.09 + 07 | E | ||
| 564.8239 | 9919.821 | 4.5 | 27,619.54 | 4.5° | 0.44 | 5.73 + 08 | C+ | 0.41 | 5.33 + 08 |
| 565.4868 | 7231.407 | 0.5 | 24,910.38 | 1.5° | −0.48 | 6.90 + 07 | E | −0.96 | 2.28 + 07 |
| 565.6586 | 9719.439 | 1.5 | 27,393.04 | 2.5° | −0.64 | 4.73 + 07 | E | −0.64 | 4.80 + 07 |
| 565.7719 | 2668.188 | 1.5 | 20,338.25 | 2.5° | −0.64 | 4.72 + 07 | E | −0.58 | 5.52 + 07 |
| 567.1428 | 7011.909 | 2.5 | 24,639.26 | 1.5° | −0.89 | 2.70 + 07 | E | ||
| 570.2536 | 7231.407 | 0.5 | 24,762.60 | 1.5° | −0.84 | 2.95 + 07 | E | ||
| 571.4527 | 9960.904 | 3.5 | 27,455.31 | 3.5° | −0.55 | 5.79 + 07 | D | ||
| 571.4735 | 7490.521 | 1.5 | 24,984.29 | 2.5° | −0.78 | 3.41 + 07 | E | ||
| 573.4941 | 9960.904 | 3.5 | 27,393.04 | 2.5° | −0.88 | 2.64 + 07 | E | −0.36 | 8.94 + 07 |
| 574.0652 | 2668.188 | 1.5 | 20,082.98 | 1.5° | −0.07 | 1.71 + 08 | E | −0.33 | 9.52 + 07 |
| 574.4403 | 7679.939 | 2.5 | 25,083.36 | 3.5° | −0.31 | 9.91 + 07 | E | 0.08 | 2.44 + 08 |
| 576.9324 | 3010.002 | 2.5 | 20,338.25 | 2.5° | 0.01 | 2.03 + 08 | D+ | −0.03 | 1.87 + 08 |
| 577.7682 | 9719.439 | 1.5 | 27,022.62 | 2.5° | −0.96 | 2.22 + 07 | E | ||
| 578.8086 | 7490.521 | 1.5 | 24,762.60 | 1.5° | −0.33 | 9.40 + 07 | D | ||
| 578.9224 | 3494.526 | 3.5 | 20,763.21 | 3.5° | 0.19 | 3.09 + 08 | D+ | 0.10 | 2.48 + 08 |
| 579.1322 | 4121.572 | 4.5 | 21,384.00 | 4.5° | 0.37 | 4.65 + 08 | C | 0.30 | 3.93 + 08 |
| 580.8081 | 9919.821 | 4.5 | 27,132.44 | 3.5° | −0.40 | 7.82 + 07 | D | ||
| 582.1977 | 9960.904 | 3.5 | 27,132.44 | 3.5° | 0.10 | 2.46 + 08 | D+ | 0.17 | 2.94 + 08 |
| 582.3818 | 8052.162 | 3.5 | 25,218.27 | 2.5° | −0.37 | 8.40 + 07 | D | −0.40 | 7.86 + 07 |
| 582.5238 | 7011.909 | 2.5 | 24,173.83 | 1.5° | −0.48 | 6.52 + 07 | D | ||
| 582.7543 | 9183.797 | 2.5 | 26,338.93 | 2.5° | −0.37 | 8.47 + 07 | E | −0.60 | 4.92 + 07 |
| 584.8365 | 9960.904 | 3.5 | 27,054.96 | 4.5° | −0.17 | 1.33 + 08 | D | ||
| 585.2267 | 7679.939 | 2.5 | 24,762.60 | 1.5° | −0.43 | 7.29 + 07 | E | −0.87 | 2.64 + 07 |
| 585.5586 | 3010.002 | 2.5 | 20,082.98 | 1.5° | −0.80 | 3.07 + 07 | E | −0.78 | 3.24 + 07 |
| 586.9950 | 8052.162 | 3.5 | 25,083.36 | 3.5° | −0.89 | 2.51 + 07 | E | −1.16 | 1.33 + 07 |
| 587.4728 | 7490.521 | 1.5 | 24,507.87 | 2.5° | −0.53 | 5.77 + 07 | D | −0.49 | 6.18 + 07 |
| 590.4296 | 8052.162 | 3.5 | 24,984.29 | 2.5° | −0.89 | 2.49 + 07 | E | −1.01 | 1.86 + 07 |
| 593.0608 | 1053.164 | 2.5 | 17,910.17 | 3.5° | −0.57 | 5.08 + 07 | D | −0.55 | 5.36 + 07 |
| 593.0681 | 0.000 | 1.5 | 16,856.80 | 2.5° | −0.66 | 4.14 + 07 | E | −0.79 | 3.10 + 07 |
| 593.5285 | 3494.526 | 3.5 | 20,338.25 | 2.5° | −0.76 | 3.26 + 07 | E | −0.73 | 3.54 + 07 |
| 596.0586 | 8446.044 | 1.5 | 25,218.27 | 2.5° | −0.73 | 3.48 + 07 | E | −0.83 | 2.76 + 07 |
| 597.5723 | 7679.939 | 2.5 | 24,409.68 | 3.5° | −0.04 | 1.70 + 08 | E | −0.93 | 2.19 + 07 |
| 599.5495 | 13,631.04 | 2.5° | 30,305.61 | 2.5 | −0.73 | 3.43 + 07 | E | ||
| 600.7360 | 4121.572 | 4.5 | 20,763.21 | 3.5° | −0.82 | 2.82 + 07 | E | −0.83 | 2.80 + 07 |
| 601.7140 | 13,260.38 | 1.5° | 29,874.97 | 1.5 | −0.35 | 8.22 + 07 | D | ||
| 603.8588 | 7490.521 | 1.5 | 24,046.10 | 2.5° | −0.29 | 9.47 + 07 | E | −0.53 | 5.40 + 07 |
| 606.8711 | 7231.407 | 0.5 | 23,704.81 | 1.5° | −0.54 | 5.27 + 07 | D | −0.59 | 4.68 + 07 |
| 607.0418 | 15,219.89 | 0.5° | 31,688.66 | 1.5 | −0.99 | 1.86 + 07 | E | ||
| 607.5237 | 8052.162 | 3.5 | 24,507.87 | 2.5° | −0.91 | 2.23 + 07 | E | ||
| 610.8477 | 7679.939 | 2.5 | 24,046.10 | 2.5° | −0.30 | 9.01 + 07 | D | −0.34 | 8.16 + 07 |
| 612.1221 | 15,019.51 | 3.5° | 31,351.60 | 2.5 | −0.65 | 4.00 + 07 | D | ||
| 612.5770 | 15,031.64 | 1.5° | 31,351.60 | 2.5 | −0.93 | 2.09 + 07 | E | ||
| 613.4384 | 7231.407 | 0.5 | 23,528.45 | 0.5° | −0.54 | 5.08 + 07 | D | −0.59 | 4.60 + 07 |
| 614.2961 | 13,631.04 | 2.5° | 29,905.33 | 2.5 | −0.13 | 1.32 + 08 | D+ | ||
| 614.5306 | 15,019.51 | 3.5° | 31,287.59 | 3.5 | −0.61 | 4.32 + 07 | D | ||
| 616.4989 | 15,031.64 | 1.5° | 31,247.78 | 1.5 | −0.42 | 6.66 + 07 | D | ||
| 616.5693 | 7490.521 | 1.5 | 23,704.81 | 1.5° | −0.43 | 6.46 + 07 | D | −0.41 | 6.80 + 07 |
| 621.8210 | 9919.821 | 4.5 | 25,997.17 | 4.5° | −0.95 | 1.95 + 07 | E | ||
| 621.9456 | 14,095.69 | 0.5° | 30,169.82 | 1.5 | −0.62 | 4.12 + 07 | D | ||
| 623.4838 | 9183.797 | 2.5 | 25,218.27 | 2.5° | −0.80 | 2.72 + 07 | E | ||
| 624.9909 | 4121.572 | 4.5 | 20,117.38 | 5.5° | 0.46 | 4.95 + 08 | C+ | 0.41 | 4.42 + 08 |
| 626.6013 | 9919.821 | 4.5 | 25,874.52 | 5.5° | 0.06 | 1.94 + 08 | D+ | 0.06 | 1.94 + 08 |
| 627.8270 | 14,095.69 | 0.5° | 30,019.24 | 0.5 | −0.84 | 2.46 + 07 | E | ||
| 629.3556 | 3494.526 | 3.5 | 19,379.40 | 2.5° | −0.92 | 2.03 + 07 | E | −0.78 | 2.76 + 07 |
| 630.8216 | 15,503.64 | 2.5° | 31,351.60 | 2.5 | −0.19 | 1.07 + 08 | D | ||
| 631.7500 | 16,099.29 | 3.5° | 31,923.96 | 4.5 | −0.52 | 5.02 + 07 | D | ||
| 632.5908 | 1053.164 | 2.5 | 16,856.80 | 2.5° | −0.90 | 2.09 + 07 | E | −0.80 | 2.62 + 07 |
| 633.3798 | 15,503.64 | 2.5° | 31,287.59 | 3.5 | −0.59 | 4.28 + 07 | D | ||
| 635.6416 | 8446.044 | 1.5 | 24,173.83 | 1.5° | −0.45 | 5.82 + 07 | D | ||
| 637.5467 | 16,243.17 | 4.5° | 31,923.96 | 4.5 | −0.85 | 2.32 + 07 | E | ||
| 639.4227 | 3494.526 | 3.5 | 19,129.31 | 4.5° | 0.33 | 3.45 + 08 | C+ | 0.27 | 3.01 + 08 |
| 640.9845 | 14,708.92 | 1.5° | 30,305.61 | 2.5 | −0.83 | 2.41 + 07 | E | ||
| 641.0984 | 3010.002 | 2.5 | 18,603.92 | 3.5° | 0.06 | 1.85 + 08 | D+ | −0.07 | 1.37 + 08 |
| 642.6591 | 15,503.64 | 2.5° | 31,059.69 | 3.5 | −0.99 | 1.67 + 07 | E | ||
| 645.0317 | 9719.439 | 1.5 | 25,218.27 | 2.5° | −0.69 | 3.27 + 07 | D | ||
| 645.4502 | 2668.188 | 1.5 | 18,156.97 | 2.5° | −0.17 | 1.09 + 08 | E | −0.57 | 4.32 + 07 |
| 645.5984 | 1053.164 | 2.5 | 16,538.39 | 3.5° | −0.26 | 8.74 + 07 | D | −0.34 | 7.36 + 07 |
| 648.5531 | 8052.162 | 3.5 | 23,466.84 | 4.5° | −0.64 | 3.61 + 07 | D | −0.69 | 3.30 + 07 |
| 650.6187 | 14,804.08 | 2.5° | 30,169.82 | 1.5 | −0.38 | 6.60 + 07 | D | ||
| 652.3878 | 9183.797 | 2.5 | 24,507.87 | 2.5° | −0.85 | 2.24 + 07 | E | ||
| 652.9738 | 14,708.92 | 1.5° | 30,019.24 | 0.5 | −0.29 | 8.10 + 07 | D | ||
| 654.0084 | 15,019.51 | 3.5° | 30,305.61 | 2.5 | −0.23 | 9.16 + 07 | D | ||
| 656.5950 | 9183.797 | 2.5 | 24,409.68 | 3.5° | −0.87 | 2.06 + 07 | E | ||
| 657.8502 | 0.000 | 1.5 | 15,196.83 | 2.5° | −0.61 | 3.81 + 07 | D | −0.61 | 3.84 + 07 |
| 658.2197 | 16,099.29 | 3.5° | 31,287.59 | 3.5 | 0.08 | 1.84 + 08 | D+ | ||
| 660.0158 | 3010.002 | 2.5 | 18,156.97 | 2.5° | −0.93 | 1.82 + 07 | E | −1.02 | 1.47 + 07 |
| 660.7728 | 9044.214 | 0.5 | 24,173.83 | 1.5° | −0.68 | 3.16 + 07 | D | ||
| 660.8239 | 9960.904 | 3.5 | 25,089.35 | 4.5° | −0.16 | 1.06 + 08 | D+ | ||
| 661.6572 | 3494.526 | 3.5 | 18,603.92 | 3.5° | −0.76 | 2.62 + 07 | E | −0.74 | 2.78 + 07 |
| 663.3476 | 14,804.08 | 2.5° | 29,874.97 | 1.5 | −0.47 | 5.17 + 07 | D | ||
| 664.5148 | 16,243.17 | 4.5° | 31,287.59 | 3.5 | 0.18 | 2.30 + 08 | C+ | ||
| 666.1390 | 4121.572 | 4.5 | 19,129.31 | 4.5° | −0.74 | 2.71 + 07 | E | −0.59 | 3.90 + 07 |
| 667.6849 | 15,196.83 | 2.5° | 30,169.82 | 1.5 | −0.80 | 2.39 + 07 | E | ||
| 670.9481 | 3010.002 | 2.5 | 17,910.17 | 3.5° | −0.37 | 6.26 + 07 | D | −0.23 | 8.72 + 07 |
| 671.5948 | 15,019.51 | 3.5° | 29,905.33 | 2.5 | −0.67 | 3.18 + 07 | D | ||
| 674.8109 | 8446.044 | 1.5 | 23,260.92 | 0.5° | −0.84 | 2.12 + 07 | E | ||
| 682.3775 | 7011.909 | 2.5 | 21,662.51 | 3.5° | −0.78 | 2.36 + 07 | E | −0.48 | 4.72 + 07 |
| 691.6659 | 17,023.36 | 3.5 | 31,477.22 | 2.5° | −0.98 | 1.45 + 07 | E | ||
| 692.5240 | 7011.909 | 2.5 | 21,447.86 | 3.5° | −0.14 | 9.96 + 07 | D+ | −0.30 | 6.96 + 07 |
| 697.6842 | 9919.821 | 4.5 | 24,249.00 | 4.5° | −0.62 | 3.25 + 07 | D | ||
| 702.3688 | 8052.162 | 3.5 | 22,285.77 | 4.5° | −0.06 | 1.18 + 08 | D+ | −0.10 | 1.07 + 08 |
| 703.2039 | 9044.214 | 0.5 | 23,260.92 | 0.5° | −0.62 | 3.24 + 07 | D | ||
| 704.5963 | 2668.188 | 1.5 | 16,856.80 | 2.5° | −0.43 | 4.97 + 07 | D | −0.47 | 4.50 + 07 |
| 705.9527 | 17,947.13 | 2.5° | 32,108.48 | 3.5 | −0.74 | 2.41 + 07 | E | ||
| 707.6374 | 9960.904 | 3.5 | 24,088.54 | 3.5° | −0.71 | 2.61 + 07 | D | ||
| 712.7473 | 15,019.51 | 3.5° | 29,045.86 | 3.5 | −0.82 | 1.99 + 07 | E | ||
| 716.1216 | 7011.909 | 2.5 | 20,972.17 | 2.5° | −0.12 | 9.90 + 07 | D+ | −0.25 | 7.32 + 07 |
| 716.6031 | 14,804.08 | 2.5° | 28,754.96 | 2.5 | −0.97 | 1.39 + 07 | E | ||
| 723.1903 | 17,140.90 | 4.5 | 30,964.71 | 3.5° | −0.60 | 3.18 + 07 | D | ||
| 726.2753 | 17,023.36 | 3.5 | 30,788.45 | 2.5° | −0.25 | 7.17 + 07 | D | ||
| 734.5327 | 8052.162 | 3.5 | 21,662.51 | 3.5° | 0.02 | 1.29 + 08 | E | −0.17 | 8.24 + 07 |
| 737.9665 | 9919.821 | 4.5 | 23,466.84 | 4.5° | −0.30 | 6.11 + 07 | D | −0.16 | 8.60 + 07 |
| 738.2683 | 9719.439 | 1.5 | 23,260.92 | 0.5° | −0.58 | 3.22 + 07 | D | ||
| 739.6431 | 18,172.35 | 1.5° | 31,688.66 | 1.5 | −0.35 | 5.39 + 07 | D | ||
| 743.7636 | 17,910.17 | 3.5° | 31,351.60 | 2.5 | −0.67 | 2.59 + 07 | D | ||
| 745.8144 | 17,947.13 | 2.5° | 31,351.60 | 2.5 | −0.95 | 1.35 + 07 | E | ||
| 746.3028 | 8052.162 | 3.5 | 21,447.86 | 3.5° | −0.71 | 2.35 + 07 | E | −0.50 | 3.76 + 07 |
| 749.3930 | 17,947.13 | 2.5° | 31,287.59 | 3.5 | −0.39 | 4.83 + 07 | D | ||
| 750.9376 | 16,856.80 | 2.5° | 30,169.82 | 1.5 | −0.85 | 1.69 + 07 | E | ||
| 756.8598 | 17,910.17 | 3.5° | 31,119.02 | 2.5 | −0.83 | 1.71 + 07 | E | ||
| 763.6844 | 18,156.97 | 2.5° | 31,247.78 | 1.5 | −0.32 | 5.53 + 07 | D | ||
| 767.9457 | 16,856.80 | 2.5° | 29,874.97 | 1.5 | −0.44 | 4.07 + 07 | D | ||
| 781.2982 | 19,129.31 | 4.5° | 31,925.00 | 3.5 | −0.70 | 2.16 + 07 | D | ||
| 784.2407 | 18,603.92 | 3.5° | 31,351.60 | 2.5 | −0.36 | 4.69 + 07 | D | ||
| 790.3695 | 18,315.88 | 4.5 | 30,964.71 | 3.5° | −0.34 | 4.84 + 07 | D | ||
| 796.1502 | 17,797.29 | 1.5° | 30,354.28 | 2.5 | −0.91 | 1.28 + 07 | E | ||
| 796.8730 | 19,379.40 | 2.5° | 31,925.00 | 3.5 | −0.65 | 2.35 + 07 | D | ||
| 798.8150 | 18,603.92 | 3.5° | 31,119.02 | 2.5 | −0.56 | 2.85 + 07 | D | ||
| 800.1873 | 3010.002 | 2.5 | 15,503.64 | 2.5° | −0.95 | 1.16 + 07 | E | ||
| 802.8791 | 17,567.49 | 0.5° | 30,019.24 | 0.5 | −1.00 | 1.04 + 07 | E | ||
| 808.4499 | 9919.821 | 4.5 | 22,285.77 | 4.5° | −0.46 | 3.56 + 07 | D | −0.57 | 2.70 + 07 |
| 810.1920 | 18,310.92 | 5.5 | 30,650.28 | 4.5° | −0.33 | 4.71 + 07 | D | ||
| 811.0853 | 17,140.90 | 4.5 | 29,466.67 | 3.5° | −0.37 | 4.33 + 07 | D | ||
| 816.1092 | 13,747.276 | 4.5 | 25,997.17 | 4.5° | −0.98 | 1.05 + 07 | E | ||
| 824.7470 | 4121.572 | 4.5 | 16,243.17 | 4.5° | −0.75 | 1.76 + 07 | D | ||
| 832.4721 | 3494.526 | 3.5 | 15,503.64 | 2.5° | −0.63 | 2.24 + 07 | D | ||
| 833.4405 | 17,910.17 | 3.5° | 29,905.33 | 2.5 | −0.34 | 4.39 + 07 | D | ||
| 834.6542 | 4121.572 | 4.5 | 16,099.29 | 3.5° | −0.30 | 4.83 + 07 | D | ||
| 837.9660 | 19,129.31 | 4.5° | 31,059.69 | 3.5 | −0.09 | 7.73 + 07 | D+ | ||
| 846.7526 | 20,117.38 | 5.5° | 31,923.96 | 4.5 | 0.12 | 1.24 + 08 | C+ | ||
| 851.3598 | 9919.821 | 4.5 | 21,662.51 | 3.5° | −0.76 | 1.61 + 07 | D | ||
| 852.0643 | 18,172.35 | 1.5° | 29,905.33 | 2.5 | −0.78 | 1.54 + 07 | D | ||
| 854.3427 | 18,603.92 | 3.5° | 30,305.61 | 2.5 | −0.99 | 9.33 + 06 | E | ||
| 854.3488 | 9960.904 | 3.5 | 21,662.51 | 3.5° | −0.67 | 1.95 + 07 | D | −0.53 | 2.72 + 07 |
| 854.5451 | 3010.002 | 2.5 | 14,708.92 | 1.5° | −0.75 | 1.62 + 07 | D | ||
| 855.9080 | 19,379.40 | 2.5° | 31,059.69 | 3.5 | −0.66 | 1.97 + 07 | D | ||
| 863.3930 | 18,315.88 | 4.5 | 29,894.91 | 3.5° | −0.66 | 1.96 + 07 | D | ||
| 867.2120 | 9919.821 | 4.5 | 21,447.86 | 3.5° | −0.76 | 1.55 + 07 | E | −0.50 | 2.80 + 07 |
| 867.4419 | 3494.526 | 3.5 | 15,019.51 | 3.5° | −0.95 | 9.87 + 06 | E | ||
| 870.3136 | 9960.904 | 3.5 | 21,447.86 | 3.5° | −0.75 | 1.58 + 07 | D | ||
| 874.8416 | 2668.188 | 1.5 | 14,095.69 | 0.5° | −0.92 | 1.04 + 07 | E | ||
| 880.1268 | 20,392.60 | 0.5 | 31,751.48 | 1.5° | −0.73 | 1.60 + 07 | D | ||
| 881.8966 | 13,747.276 | 4.5 | 25,083.36 | 3.5° | −0.97 | 9.24 + 06 | E | ||
| 882.1670 | 20,018.99 | 1.5° | 31,351.60 | 2.5 | −0.70 | 1.72 + 07 | D | ||
| 882.5854 | 8052.162 | 3.5 | 19,379.40 | 2.5° | −0.53 | 2.54 + 07 | D | −0.56 | 2.34 + 07 |
| 895.6565 | 18,037.64 | 1.5 | 29,199.57 | 1.5° | −0.86 | 1.16 + 07 | E | ||
| 895.7760 | 7011.909 | 2.5 | 18,172.35 | 1.5° | −0.67 | 1.79 + 07 | D | −0.67 | 1.80 + 07 |
| 904.6930 | 20,197.34 | 0.5° | 31,247.78 | 1.5 | −0.81 | 1.25 + 07 | D | ||
| 907.9116 | 9960.904 | 3.5 | 20,972.17 | 2.5° | −0.42 | 3.05 + 07 | D | −0.29 | 4.14 + 07 |
| 908.9274 | 18,776.62 | 2.5 | 29,775.58 | 2.5° | −0.82 | 1.23 + 07 | D | ||
| 912.7555 | 20,972.17 | 2.5° | 31,925.00 | 3.5 | −0.98 | 8.30 + 06 | E | ||
| 915.7172 | 12,787.404 | 2.5 | 23,704.81 | 1.5° | −0.78 | 1.33 + 07 | D | ||
| 922.6653 | 9183.797 | 2.5 | 20,018.99 | 1.5° | −0.91 | 9.60 + 06 | E | ||
| 925.0058 | 13,238.323 | 3.5 | 24,046.10 | 2.5° | −0.59 | 2.02 + 07 | D | −0.57 | 2.10 + 07 |
| 932.8854 | 20,972.17 | 2.5° | 31,688.66 | 1.5 | −0.68 | 1.60 + 07 | D | ||
| 937.6175 | 13,747.276 | 4.5 | 24,409.68 | 3.5° | −0.59 | 1.94 + 07 | D | ||
| 948.5100 | 21,384.00 | 4.5° | 31,923.96 | 4.5 | 0.05 | 8.38 + 07 | C+ | ||
| 954.1972 | 21,447.86 | 3.5° | 31,925.00 | 3.5 | −0.70 | 1.46 + 07 | D | ||
| 957.0444 | 21,662.51 | 3.5° | 32,108.48 | 3.5 | −0.94 | 8.39 + 06 | E | ||
| 964.0855 | 17,023.36 | 3.5 | 27,393.04 | 2.5° | −0.33 | 3.34 + 07 | D | −0.18 | 4.74 + 07 |
| 970.9394 | 20,763.21 | 3.5° | 31,059.69 | 3.5 | −0.14 | 5.13 + 07 | D+ | ||
| 972.9114 | 20,972.17 | 2.5° | 31,247.78 | 1.5 | −0.85 | 1.00 + 07 | D | ||
| 973.7092 | 7679.939 | 2.5 | 17,947.13 | 2.5° | −0.85 | 9.90 + 06 | D | −0.97 | 7.50 + 06 |
| 974.1552 | 21,662.51 | 3.5° | 31,925.00 | 3.5 | −0.47 | 2.39 + 07 | D | ||
| 977.5166 | 18,315.88 | 4.5 | 28,543.08 | 3.5° | −0.74 | 1.27 + 07 | D | ||
| 980.4358 | 21,943.80 | 3.5 | 32,140.55 | 3.5° | −0.75 | 1.24 + 07 | D | ||
| 985.2573 | 20,972.17 | 2.5° | 31,119.02 | 2.5 | −0.33 | 3.20 + 07 | D+ | ||
| 991.1190 | 20,082.98 | 1.5° | 30,169.82 | 1.5 | −0.59 | 1.76 + 07 | D | ||
| 999.7999 | 17,023.36 | 3.5 | 27,022.62 | 2.5° | −0.86 | 9.30 + 06 | D | ||
| 1000.5724 | 17,140.90 | 4.5 | 27,132.44 | 3.5° | −0.07 | 5.64 + 07 | D+ | −0.04 | 6.08 + 07 |
| 1002.9997 | 20,338.25 | 2.5° | 30,305.61 | 2.5 | −0.59 | 1.69 + 07 | D | ||
| 1006.6821 | 18,037.64 | 1.5 | 27,968.54 | 1.5° | −0.98 | 6.93 + 06 | E | ||
| 1011.2194 | 20,018.99 | 1.5° | 29,905.33 | 2.5 | −0.77 | 1.10 + 07 | D | ||
| 1013.0834 | 18,310.92 | 5.5 | 28,179.07 | 5.5° | −0.85 | 9.24 + 06 | D | ||
| 1017.7700 | 22,285.77 | 4.5° | 32,108.48 | 3.5 | −0.74 | 1.18 + 07 | D | ||
| 1018.4625 | 12,430.609 | 1.5 | 22,246.64 | 0.5° | −0.70 | 1.28 + 07 | D | −0.62 | 1.54 + 07 |
| 1020.9630 | 20,082.98 | 1.5° | 29,874.97 | 1.5 | −0.90 | 8.08 + 06 | E | ||
| 1021.9890 | 21,969.32 | 2.5 | 31,751.48 | 1.5° | −0.34 | 2.90 + 07 | D+ | ||
| 1027.4898 | 18,776.62 | 2.5 | 28,506.41 | 2.5° | −0.48 | 2.08 + 07 | D | ||
| 1028.1470 | 18,315.88 | 4.5 | 28,039.45 | 3.5° | −0.36 | 2.74 + 07 | D | ||
| 1029.4429 | 18,037.64 | 1.5 | 27,748.97 | 0.5° | −0.98 | 6.59 + 06 | E | ||
| 1031.8059 | 21,662.51 | 3.5° | 31,351.60 | 2.5 | −0.87 | 8.44 + 06 | D | ||
| 1033.0277 | 20,197.34 | 0.5° | 29,874.97 | 1.5 | −0.85 | 8.77 + 06 | D | ||
| 1033.2348 | 21,384.00 | 4.5° | 31,059.69 | 3.5 | −0.75 | 1.11 + 07 | D | ||
| 1033.7188 | 21,447.86 | 3.5° | 31,119.02 | 2.5 | −0.33 | 2.95 + 07 | D+ | ||
| 1034.9172 | 9719.439 | 1.5 | 19,379.40 | 2.5° | −0.77 | 1.05 + 07 | D | ||
| 1035.7755 | 12,787.404 | 2.5 | 22,439.36 | 1.5° | −0.54 | 1.81 + 07 | D | −0.47 | 2.12 + 07 |
| 1037.1430 | 22,285.77 | 4.5° | 31,925.00 | 3.5 | −0.18 | 4.14 + 07 | D+ | ||
| 1044.9646 | 20,338.25 | 2.5° | 29,905.33 | 2.5 | −0.90 | 7.62 + 06 | E | ||
| 1045.0906 | 13,238.323 | 3.5 | 22,804.25 | 2.5° | −0.37 | 2.61 + 07 | D | −0.38 | 2.58 + 07 |
| 1046.1780 | 13,747.276 | 4.5 | 23,303.26 | 3.5° | −0.19 | 3.92 + 07 | D | −0.37 | 2.64 + 07 |
| 1048.2913 | 20,338.25 | 2.5° | 29,874.97 | 1.5 | −0.94 | 6.99 + 06 | E | ||
| 1048.6541 | 21,943.80 | 3.5 | 31,477.22 | 2.5° | −0.89 | 7.86 + 06 | D | ||
| 1051.4688 | 21,969.32 | 2.5 | 31,477.22 | 2.5° | −0.98 | 6.37 + 06 | E | ||
| 1057.1829 | 21,662.51 | 3.5° | 31,119.02 | 2.5 | −0.90 | 7.46 + 06 | D | ||
| 1063.8575 | 21,662.51 | 3.5° | 31,059.69 | 3.5 | −0.94 | 6.84 + 06 | E | ||
| 1073.9789 | 18,310.92 | 5.5 | 27,619.54 | 4.5° | 0.10 | 7.22 + 07 | C+ | ||
| 1093.5386 | 20,763.21 | 3.5° | 29,905.33 | 2.5 | −0.82 | 8.48 + 06 | D | ||
| 1093.8605 | 18,315.88 | 4.5 | 27,455.31 | 3.5° | −0.61 | 1.36 + 07 | D | ||
| 1096.1008 | 22,804.25 | 2.5° | 31,925.00 | 3.5 | −0.85 | 7.80 + 06 | D | ||
| 1110.6662 | 22,246.64 | 0.5° | 31,247.78 | 1.5 | −0.86 | 7.49 + 06 | D | ||
| 1115.9028 | 16,991.42 | 0.5 | 25,950.32 | 1.5° | −0.92 | 6.41 + 06 | D | ||
| 1121.7452 | 22,439.36 | 1.5° | 31,351.60 | 2.5 | −0.82 | 7.94 + 06 | D | ||
| 1128.6458 | 21,447.86 | 3.5° | 30,305.61 | 2.5 | −0.87 | 7.02 + 06 | D | ||
| 1139.4294 | 22,285.77 | 4.5° | 31,059.69 | 3.5 | −0.82 | 7.73 + 06 | D | ||
| 1143.9720 | 18,315.88 | 4.5 | 27,054.96 | 4.5° | −0.78 | 8.40 + 06 | D | ||
| 1144.6872 | 17,140.90 | 4.5 | 25,874.52 | 5.5° | −0.89 | 6.49 + 06 | D | ||
| 1145.6378 | 9183.797 | 2.5 | 17,910.17 | 3.5° | −0.86 | 7.05 + 06 | D | ||
| 1151.2147 | 9919.821 | 4.5 | 18,603.92 | 3.5° | −0.96 | 5.46 + 06 | E | ||
| 1151.8035 | 22,439.36 | 1.5° | 31,119.02 | 2.5 | −0.67 | 1.07 + 07 | D | ||
| 1154.5037 | 20,082.98 | 1.5° | 28,742.34 | 1.5 | −0.96 | 5.52 + 06 | E | ||
| 1159.6811 | 23,303.26 | 3.5° | 31,923.96 | 4.5 | −0.09 | 4.07 + 07 | C+ | ||
| 1182.0631 | 21,447.86 | 3.5° | 29,905.33 | 2.5 | −0.69 | 9.73 + 06 | D | ||
| 1183.2985 | 18,776.62 | 2.5 | 27,225.26 | 1.5° | −0.93 | 5.56 + 06 | D | ||
| 1187.7876 | 20,338.25 | 2.5° | 28,754.96 | 2.5 | −0.87 | 6.41 + 06 | D | ||
| 1202.3500 | 22,804.25 | 2.5° | 31,119.02 | 2.5 | −0.95 | 5.20 + 06 | D | ||
| 1207.0127 | 20,763.21 | 3.5° | 29,045.86 | 3.5 | −0.88 | 5.98 + 06 | D | ||
| 1210.9910 | 22,804.25 | 2.5° | 31,059.69 | 3.5 | −0.39 | 1.87 + 07 | D+ | ||
| 1245.3833 | 16,735.14 | 1.5 | 24,762.60 | 1.5° | −0.84 | 6.21 + 06 | D | ||
| 1251.1674 | 9919.821 | 4.5 | 17,910.17 | 3.5° | −0.69 | 8.60 + 06 | D | ||
| 1252.1106 | 23,303.26 | 3.5° | 31,287.59 | 3.5 | −0.62 | 1.03 + 07 | D | ||
| 1279.4518 | 23,874.95 | 2.5° | 31,688.66 | 1.5 | −0.47 | 1.39 + 07 | D | ||
| 1293.2303 | 22,439.36 | 1.5° | 30,169.82 | 1.5 | −0.89 | 5.13 + 06 | D | ||
| 1300.6688 | 18,310.92 | 5.5 | 25,997.17 | 4.5° | −0.96 | 4.32 + 06 | D | ||
| 1304.5776 | 17,099.38 | 2.5 | 24,762.60 | 1.5° | −0.68 | 8.17 + 06 | D | ||
| 1306.4272 | 12,430.609 | 1.5 | 20,082.98 | 1.5° | −0.65 | 8.66 + 06 | D | ||
| 1309.1039 | 13,747.276 | 4.5 | 21,384.00 | 4.5° | −0.19 | 2.52 + 07 | D+ | ||
| 1310.5444 | 22,246.64 | 0.5° | 29,874.97 | 1.5 | −0.92 | 4.68 + 06 | D | ||
| 1321.7602 | 18,310.92 | 5.5 | 25,874.52 | 5.5° | −0.53 | 1.12 + 07 | D | ||
| 1322.6731 | 21,943.80 | 3.5 | 29,502.18 | 2.5° | −0.91 | 4.69 + 06 | D | ||
| 1323.9928 | 12,787.404 | 2.5 | 20,338.25 | 2.5° | −0.60 | 9.62 + 06 | D | ||
| 1328.5602 | 13,238.323 | 3.5 | 20,763.21 | 3.5° | −0.40 | 1.49 + 07 | D+ | ||
| 1465.8062 | 24,088.54 | 3.5° | 30,908.86 | 2.5 | −0.59 | 7.89 + 06 | D | ||
| 1475.9447 | 18,315.88 | 4.5 | 25,089.35 | 4.5° | −0.80 | 4.82 + 06 | D | ||
| 1486.3792 | 25,414.63 | 2.5 | 32,140.55 | 3.5° | −0.84 | 4.33 + 06 | D | ||
| 1517.4482 | 23,466.84 | 4.5° | 30,055.05 | 3.5 | −0.90 | 3.64 + 06 | D | ||
| 1572.4612 | 23,221.10 | 3.5° | 29,578.82 | 2.5 | −0.64 | 6.16 + 06 | D | ||
| 1611.4542 | 17,099.38 | 2.5 | 23,303.26 | 3.5° | −0.70 | 5.14 + 06 | D | ||
| 1624.8588 | 24,249.00 | 4.5° | 30,401.70 | 3.5 | −0.50 | 7.92 + 06 | D+ | ||
| 1640.6878 | 24,841.42 | 5.5° | 30,934.76 | 4.5 | −0.36 | 1.07 + 07 | D+ | ||
| 1647.2380 | 16,735.14 | 1.5 | 22,804.25 | 2.5° | −0.96 | 2.66 + 06 | D | ||
| 1666.4281 | 21,969.32 | 2.5 | 27,968.54 | 1.5° | −0.96 | 2.62 + 06 | D | ||
| 1686.7932 | 25,997.17 | 4.5° | 31,923.96 | 4.5 | −0.62 | 5.57 + 06 | D | ||
| 1689.1713 | 25,558.80 | 1.5 | 31,477.22 | 2.5° | −0.83 | 3.48 + 06 | D | ||
| 1760.2624 | 25,380.27 | 3.5° | 31,059.69 | 3.5 | −0.82 | 3.27 + 06 | D | ||
| 1889.6931 | 25,997.17 | 4.5° | 31,287.59 | 3.5 | −0.89 | 2.40 + 06 | D | ||
| 2321.1898 | 17,140.90 | 4.5 | 21,447.86 | 3.5° | −0.55 | 3.50 + 06 | D+ | ||
| 2515.1319 | 18,310.92 | 5.5 | 22,285.77 | 4.5° | −0.42 | 4.05 + 06 | C+ | ||
| 2531.7177 | 17,023.36 | 3.5 | 20,972.17 | 2.5° | −1.00 | 1.04 + 06 | D | ||
| 2906.0572 | 27,619.54 | 4.5° | 31,059.69 | 3.5 | −0.95 | 8.95 + 05 | D | ||
| 2987.2656 | 18,315.88 | 4.5 | 21,662.51 | 3.5° | −0.93 | 8.68 + 05 | D | ||
| 3143.0848 | 28,743.24 | 5.5° | 31,923.96 | 4.5 | −0.54 | 1.96 + 06 | C+ | ||
| 3365.4959 | 28,089.17 | 4.5° | 31,059.69 | 3.5 | −0.82 | 8.99 + 05 | D+ | ||
| 4080.4865 | 27,455.31 | 3.5° | 29,905.33 | 2.5 | −0.94 | 4.59 + 05 | D+ | ||
| 4472.6128 | 29,905.33 | 2.5 | 32,140.55 | 3.5° | −0.97 | 3.57 + 05 | D+ | ||
| 7842.7216 | 30,650.28 | 4.5° | 31,925.00 | 3.5 | −0.86 | 1.48 + 05 | C+ | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gamrath, S.; Palmeri, P.; Quinet, P. Radiative Transition Parameters in Atomic Lanthanum from Pseudo-Relativistic Hartree–Fock and Fully Relativistic Dirac–Hartree–Fock Calculations. Atoms 2019, 7, 38. https://doi.org/10.3390/atoms7010038
Gamrath S, Palmeri P, Quinet P. Radiative Transition Parameters in Atomic Lanthanum from Pseudo-Relativistic Hartree–Fock and Fully Relativistic Dirac–Hartree–Fock Calculations. Atoms. 2019; 7(1):38. https://doi.org/10.3390/atoms7010038
Chicago/Turabian StyleGamrath, Sébastien, Patrick Palmeri, and Pascal Quinet. 2019. "Radiative Transition Parameters in Atomic Lanthanum from Pseudo-Relativistic Hartree–Fock and Fully Relativistic Dirac–Hartree–Fock Calculations" Atoms 7, no. 1: 38. https://doi.org/10.3390/atoms7010038
APA StyleGamrath, S., Palmeri, P., & Quinet, P. (2019). Radiative Transition Parameters in Atomic Lanthanum from Pseudo-Relativistic Hartree–Fock and Fully Relativistic Dirac–Hartree–Fock Calculations. Atoms, 7(1), 38. https://doi.org/10.3390/atoms7010038






