Abstract
Calculated radiative transition probabilities and oscillator strengths are reported for 392 lines of neutral lanthanum (La I) atom in the spectral range from the near ultraviolet to the mid infrared. They were obtained using two different theoretical methods based on the pseudo-relativistic Hartree–Fock (HFR) and the fully relativistic multiconfiguration Dirac–Hartree–Fock (MCDHF) approaches, both including the most important intravalence and core-valence electron correlations. The quality of these radiative parameters was assessed through detailed comparisons between the results obtained using different physical models and between our theoretical results and the experimental data, where available. Of the total number of La I lines listed in the present work, about 60% have gf- and gA-values determined for the first time.
1. Introduction
The determination of radiative parameters in lanthanide atoms and ions has been the subject of many experimental and theoretical studies over the past few decades. This is mainly due to the fact that the remarkably rich spectra corresponding to the first ionization stages of these elements provide useful information for the development of other scientific fields, such as astrophysics and the lighting industry, as mentioned in numerous papers (see e.g., [1,2,3,4,5]).
Neutral lanthanum, La I (Z = 57), is characterized by the 5d6s2 2D3/2 ground level, while, the lowest excited levels belong to many different configurations such as 5d6s2, 5d26s, 5d3, 4f6s6p, 5d27s, 5d6s7s, for the even parity, and 5d6s6p, 5d26p, 4f5d6s, 6s26p, 4f6s2, for the odd parity, according to the National Institute of Standards and Technology (NIST) database [6]. The overlap of these configurations is responsible for the strong mixing of most energy levels, which makes both experimental and theoretical analyses very difficult. This notably explains why the designation of some low-lying La I levels is still uncertain or even not yet assigned.
The first measurements of transition probabilities in La I were published by Corliss and Bozman [7] more than 55 years ago. These data, which are known to be of limited accuracy, were after all taken on by Kurucz in his database [8]. During the 1970s and 1980s, radiative lifetimes were obtained for a few levels using different experimental methods, i.e., the level-crossing and double resonance [9,10,11], the laser-induced fluorescence [12], and the pulse-electron delayed coincidence [13] techniques. More recently, radiative lifetime measurements were performed with the time-resolved laser-induced fluorescence technique for 20 odd-parity levels of La I between 18,172 and 28,506 cm−1 [14]. These results were compared with pseudo-relativistic Hartree–Fock (HFR) calculations and, although the agreement of theory with experiment was generally satisfactory, large discrepancies were found for some levels, emphasizing the difficulty to get a reliable theoretical model in such a heavy and complex neutral element. Theoretical lifetimes, transition probabilities and oscillator strengths in La I were also obtained by Karaçoban and Özdemir [15,16] who used the multiconfiguration Hartree–Fock (MCHF) method within the framework of Breit–Pauli relativistic corrections [17]. Finally, the laser-induced fluorescence (LIF) technique was used to measure, with an estimated accuracy of 5–10%, the radiative lifetimes for 32 levels in the range 23,874–37,982 cm−1 [18], 24 levels in the range 34,213–40,910 cm−1 [19], 63 levels in the range 13,260–30,965 cm−1 [20], 40 levels in the range 24,507–52,030 cm−1 [21], and 72 levels in the range 15,031–32,140 cm−1 [22]. The latter work was completed by Fourier transform spectroscopy measurements of branching fractions, which were combined with the experimental radiative lifetimes to yield transition probabilities for 315 lines in La I. This offers us a unique opportunity to test the reliability of new extensive theoretical models.
In the present paper, we report on moderately large-scale calculations of radiative decay rates in neutral lanthanum atom using two different methods, i.e., the pseudo-relativistic Hartree–Fock (HFR) and the fully relativistic multiconfiguration Dirac–Hartree–Fock (MCDHF) approaches. In both of them, the most important intravalence and core-valence electron interactions were considered. This allowed us to provide a set of oscillator strengths and transition probabilities for 392 strong La I spectral lines, in the wavelength range from 317 to 7843 nm, of which about 60% are given for the first time. The accuracy of these new radiative parameters was assessed through detailed comparisons between the results obtained in the present work using different physical models and between our theoretical results and the available experimental data.
2. Computational Methods Used
2.1. Pseudo-Relativistic Hartree–Fock Calculations
The first computational procedure used in the present work for modelling the atomic structure and calculating the radiative parameters in La I was the pseudo-relativistic Hartree–Fock (HFR) method, originally introduced by Cowan [23] and modified for taking core-polarization (CPOL) effects into account, giving rise to the so-called HFR+CPOL method [24,25,26]. Three different physical models were employed in the calculations.
In the first model (HFR-NOPOL), only intravalence correlation was considered by explicitly including the following 37 even- and 37 odd-parity configurations, namely 5d6s2, 5d26s, 5d27s, 5d26d, 5d3, 5d6p2, 5d6d2, 5d7s2, 5d6s6d, 5d6s7s, 5d6p7p, 5d6d7s, 4f25d, 4f26d, 4f26s, 4f27s, 4f5d6p, 4f5d7p, 4f6s6p, 4f6s7p, 4f6p6d, 4f6p7s, 4f6d7p, 4f7s7p, 6s26d, 6s27s, 6s6p2, 6s6d2, 6s7s2, 6s6p7p, 6s6d7s, 6p26d, 6p27s, 6p6d7p, 6p7s7p, 6d7s2, 7s6d2, and 5d26p, 5d27p, 5d6s6p, 5d6s7p, 5d6p6d, 5d6p7s, 5d6d7p, 5d7s7p, 4f3, 4f26p, 4f27p, 4f5d2, 4f6s2, 4f6p2, 4f6d2, 4f7s2, 4f5d6s, 4f5d7s, 4f5d6d, 4f6s6d, 4f6s7s, 4f6p7p, 4f6d7s, 6s26p, 6s27p1, 6s6p6d, 6s6p7s, 6s6d7p, 6s7s7p, 6p3, 6p27p, 6p6d2, 6p7s2, 6p6d7s, 6d27p, 6d7s7p, 7s27p, respectively. It is worth noting that these multiconfiguration expansions are considerably more extensive than those included in our previous HFR calculations published 15 years ago [14].
In the second model (HFR+CPOL1), the same set of configurations as the one given hereabove was explicitly considered in the computations. In addition, core-polarization effects were estimated by assuming a Xe-like La IV ionic core with the dipole polarizability value reported by Fraga et al. [27], i.e., αd = 9.50 a03, and a cut-off radius equal to the HFR average value <r> of the outermost core orbital (5p), i.e., rc = 1.80 a0.
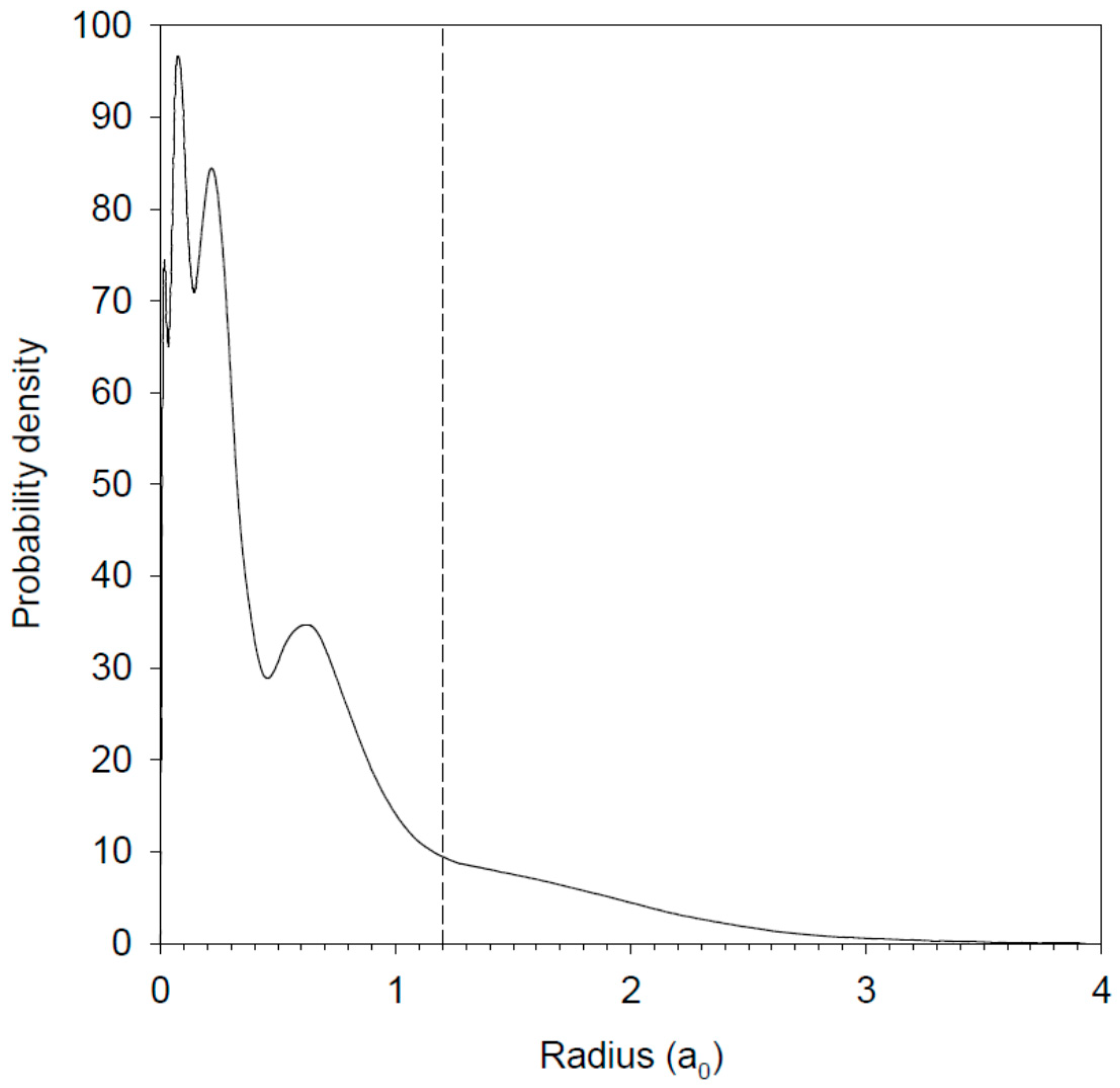
However, as mentioned, for example, in [28], the cut-off radius is not an unambiguously defined parameter. Therefore, the core-polarization contributions were also estimated in a third model (HFR+CPOL2), in which we used the same dipole polarizability as the one used in HFR+CPOL1 but with a different value of the cut-off radius, namely rc = 1.20 a0, representing the distance at which the total probability density of the ionic core orbitals falls to 10 per cent of its maximum value, as suggested in [29]. This is illustrated in Figure 1 which shows the calculated probability density of the La IV ionic core in the ground configuration of the lanthanum atom.
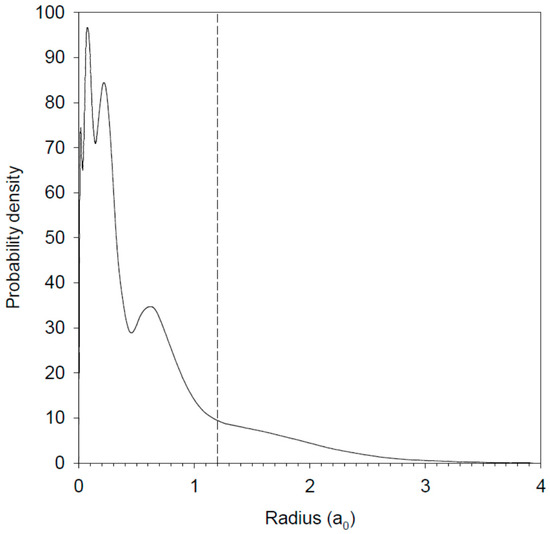
Figure 1.
Electron probability density (Pnl2) of the La IV ionic core in the ground configuration (5d6s2) of neutral lanthanum. The value of the cut-off radius used in the HFR+CPOL2 calculations (rc = 1.20 a0) is also shown in the figure. It represents the distance at which the electron probability density falls to 10 percent of its maximum value, as suggested in [29].
Furthermore, in each of these three models, the calculated eigenvalues of the Hamiltonian were optimized to the observed energy levels via a well-established least-squares fitting procedure [23] in which all the experimentally known levels included in the NIST compilation [6] up to 32,140 cm−1 were included, most of the level values above that limit being affected by dubious or unknown assignments. It is worth mentioning that the newly identified even-parity level at 25,558.774 cm−1 (J = 3/2) [30] was also incorporated in the fitting process. For this level, the leading component (52%) was found to be 5d3 2D3/2, according to our calculations. In this semi-empirical procedure, some radial energy parameters, such as the average energies, Slater integrals, spin-orbit parameters and effective interaction parameters, characterizing the 5d6s2, 5d26s, 5d27s, 5d26d, 5d3, 5d6s7s, 4f6s6p even-parity configurations, and the 5d26p, 5d6s6p, 4f6s2, 4f5d6s, 6s26p odd-parity configurations, were adjusted, giving rise to standard deviations of 129 cm−1 and 173 cm−1 for even and odd parities, respectively, whether for HFR-NOPOL, HFR+CPOL1 or HFR+CPOL2 models.
2.2. Fully Relativistic Multiconfiguration Dirac–Hartree–Fock Calculations
In order to assess the reliability of the pseudo-relativistic Hartree–Fock computations described above, another theoretical method used in our work was the one implemented in the GRASP2K computer package [31] which uses the fully relativistic multiconfiguration Dirac–Hartree–Fock (MCDHF) method [32].
In a first step, the 5d6s2, 5d26s, 5d27s, 5d26d, 5d3, 5d6s7s, 4f6s6p even-parity configurations, and the 5d26p, 5d27p, 5d6s6p, 5d6s7p, 6s26p, 6s27p, 4f5d2, 4f6s2 odd-parity configurations were chosen as multireference to optimize all the involved orbitals using the extended average level (EAL) option [31]. The valence-valence correlations were then taken into account by allowing single and double excitations from the multireference to 5d, 5f, 5g, 6s, 6p, 6d, 7s, 7p, 7d, 8s, 8p and 8d orbitals, giving rise to 20,265 CSFs. In this step, the additional 5f, 5g, 7d, 8s, 8p and 8d orbitals were first obtained by an EAL variational procedure, keeping frozen all the other orbitals, before re-optimizing all the orbitals together. Finally, the most important core-valence correlations were considered by including the 5p → 4f, 5s → 5d single excitations, and the 5p2 → 5d2, 5s2 → 4f2, 5s5p → 4f5d double excitations within the relativistic configuration interaction (RCI) approximation. This led to a total number of 84,314 CSFs. In addition, higher-order relativistic effects, such as the transverse-photon Breit interaction, together with the leading quantum electrodynamics (QED) corrections due to self-energy and vacuum polarization effects [32], were also incorporated in the calculations.
3. Results and Discussion
3.1. Radiative Lifetimes
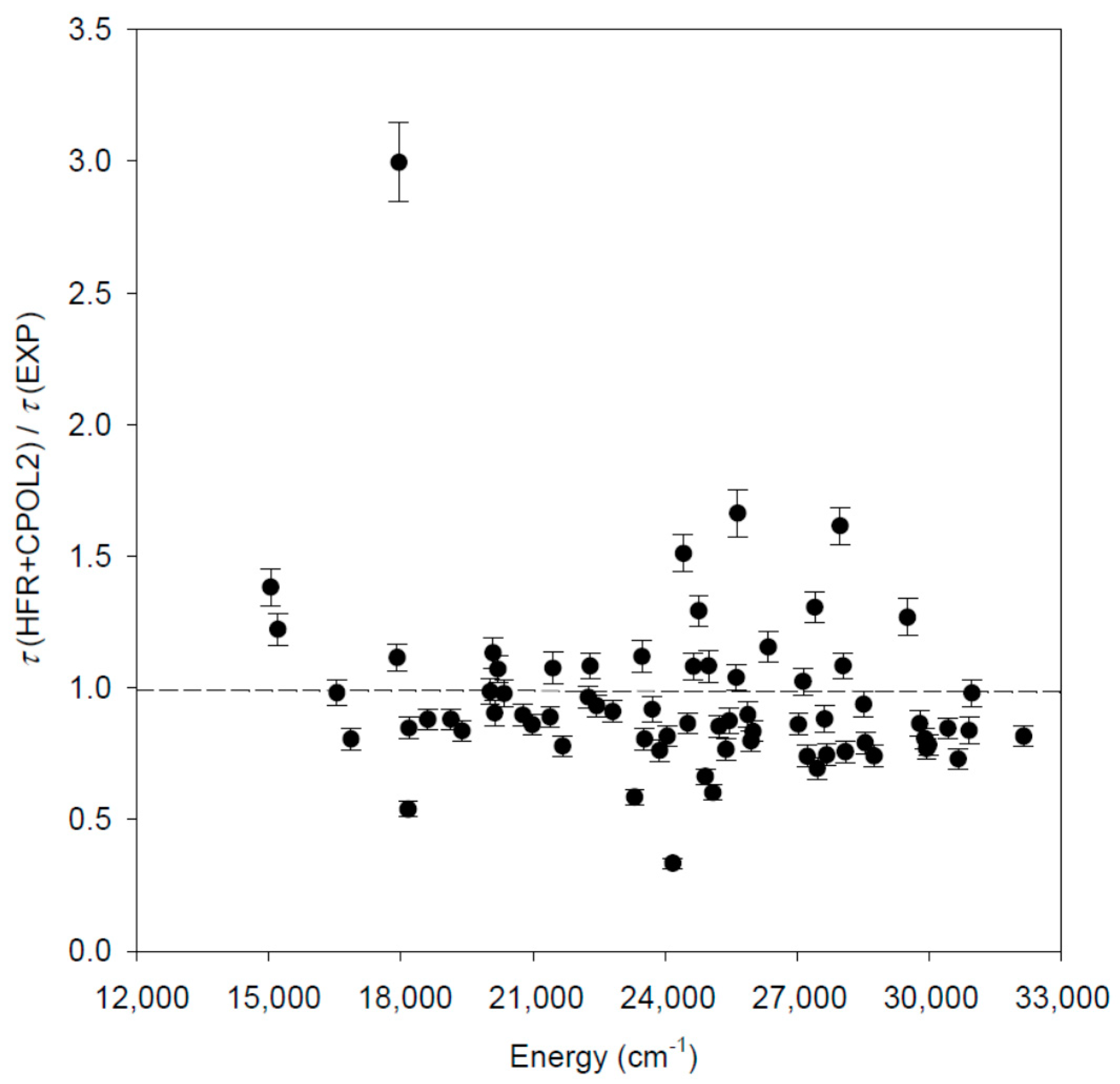
In Table 1, the calculated lifetime values, obtained using our three different HFR models, are compared with the available measurements performed by time-resolved laser-induced fluorescence spectroscopy (TR-LIF) for 96 odd-parity levels in La I. We note that the theoretical results are in satisfactory agreement with the most recent and the most accurate experimental data of Den Hartog et al. [22], if we except the three levels at 17,947.13, 23,221.10 and 24,173.83 cm−1 for which large discrepancies, exceeding a factor of 3, are observed. This can be explained by the poor representation of these levels in our theoretical models, as evidenced by the rather bad agreement we found when comparing the calculated HFR Landé g-factors, i.e., g ~ 1.06, 1.08, and 0.72, with the experimental values [6], i.e., g = 1.516, 0.781, and 0.806, respectively. It is interesting to notice however that, for the level at 24,173.83 cm−1, the lifetime computed by Karaçoban and Özdemir [15], i.e., ô = 6.04 ns, is in better agreement with our values (ranging from 9.6 to 12.0 ns) than with the experimental one (35.9 ns). When looking into more details, and when excluding the three levels mentioned above from the comparison, the mean ratios are found to be ô(HFR-NOPOL)/ô(EXP [22]) = 0.77 ± 0.18, ô(HFR+CPOL1)/ô(EXP [22]) = 0.90 ± 0.23, and ô(HFR+CPOL2)/ô(EXP [22]) = 0.94 ± 0.22, where the uncertainty corresponds to the standard deviation from the average. Firstly, as expected, it is clear that the core-valence correlations play a non-negligible role, the calculated lifetimes increasing by about 15% when including core-polarization contributions. Secondly, it appears that the HFR+CPOL2 model gives the best overall agreement with the experimental radiative lifetimes [22]. This agreement is also better than the one obtained when comparing the theoretical lifetimes calculated by Biémont et al. [14] (for 17 levels) and by Karaçoban and Özdemir [15] (for 37 levels) to the experimental measurements. Indeed, in these two cases, the mean ratios ô(THEORY)/ô(EXP [22]) are found to be equal to 0.98 ± 0.33 and 0.89 ± 0.47, respectively, the standard deviations (and therefore the scattering of results) being larger than the value obtained when using the HFR+CPOL2 model of the present work, which can thus be considered as the most reliable one. The comparison between the radiative lifetimes computed with the latter model and the TR-LIF experimental data of [22] is illustrated in Figure 2.

Table 1.
Comparison of the radiative lifetimes computed in the present work using three different HFR models with the most recent available experimental values for odd-parity levels in La I.
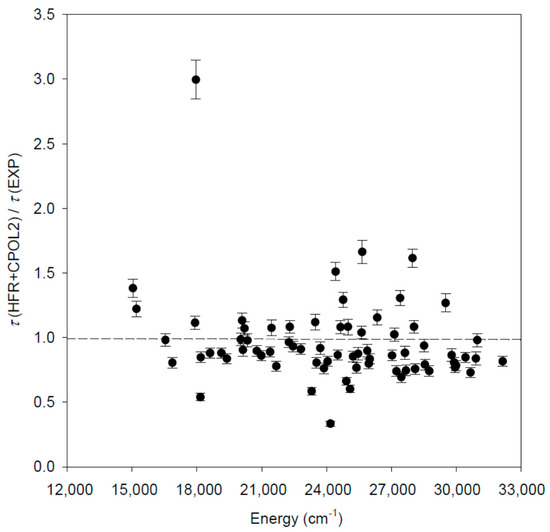
Figure 2.
Comparison between the radiative lifetimes (ô) computed in the present work using the HFR+CPOL2 model and the most recent laser-induced fluorescence experimental measurements [22]. The dashed line indicates unity.
Some other laser-induced fluorescence lifetime measurements were published before the work of Den Hartog et al. [22]. These data [14,18,20,21] are also reported in Table 1. The comparison between our HFR+CPOL2 calculated values with the latter gives the mean ratios ô(HFR+CPOL2)/ô(EXP [14]) = 0.81 ± 0.20, ô(HFR+CPOL2)/ô(EXP [18]) = 0.93 ± 0.24, ô(HFR+CPOL2)/ô(EXP [20]) = 0.91 ± 0.43, and ô(HFR+CPOL2)/ô(EXP [21]) = 0.88 ± 0.20, the larger scattering observed when using the experimental data of Yarlagadda et al. [20] being mainly due to the fact that many of the levels considered by these authors have rather long lifetimes (ô > 100 ns), which are more difficult to precisely determine both experimentally and theoretically.
Finally, let us note that the MCDHF lifetimes calculated in the present work are not listed in Table 1 because, for many levels (about 50%), either the identifications are rather difficult to unambiguously establish in the calculations (in particular for E > 26,000 cm−1), or most of the computed radiative decay rates are strongly affected by severe cancellation effects leading to very uncertain lifetimes (in particular for ô > 100 ns). It is useful to remind here that we have recently modified [33] the GRASP2K package to include the calculation of the cancellation factor (CF) as defined by Cowan [23]. Nevertheless, for clearly identified levels in our MCDHF calculations, it is interesting to point out that the theoretical lifetimes are generally slightly shorter than the experimental data of Den Hartog et al. [22], just like when compared to our HFR+CPOL2 results, the mean ratios being found to be ô(MCDHF)/ô(EXP [22]) = 0.85 ± 0.46 and ô(MCDHF)/ô(HFR+CPOL2) = 0.81 ± 0.43, respectively. This can be explained by the fact that core-valence interactions are taken into account more effectively by using the core-polarization corrections in the HFR method than by explicitly incorporating a limited set of core-excited configurations in the MCDHF model.
3.2. Oscillator Strengths and Transition Probabilities
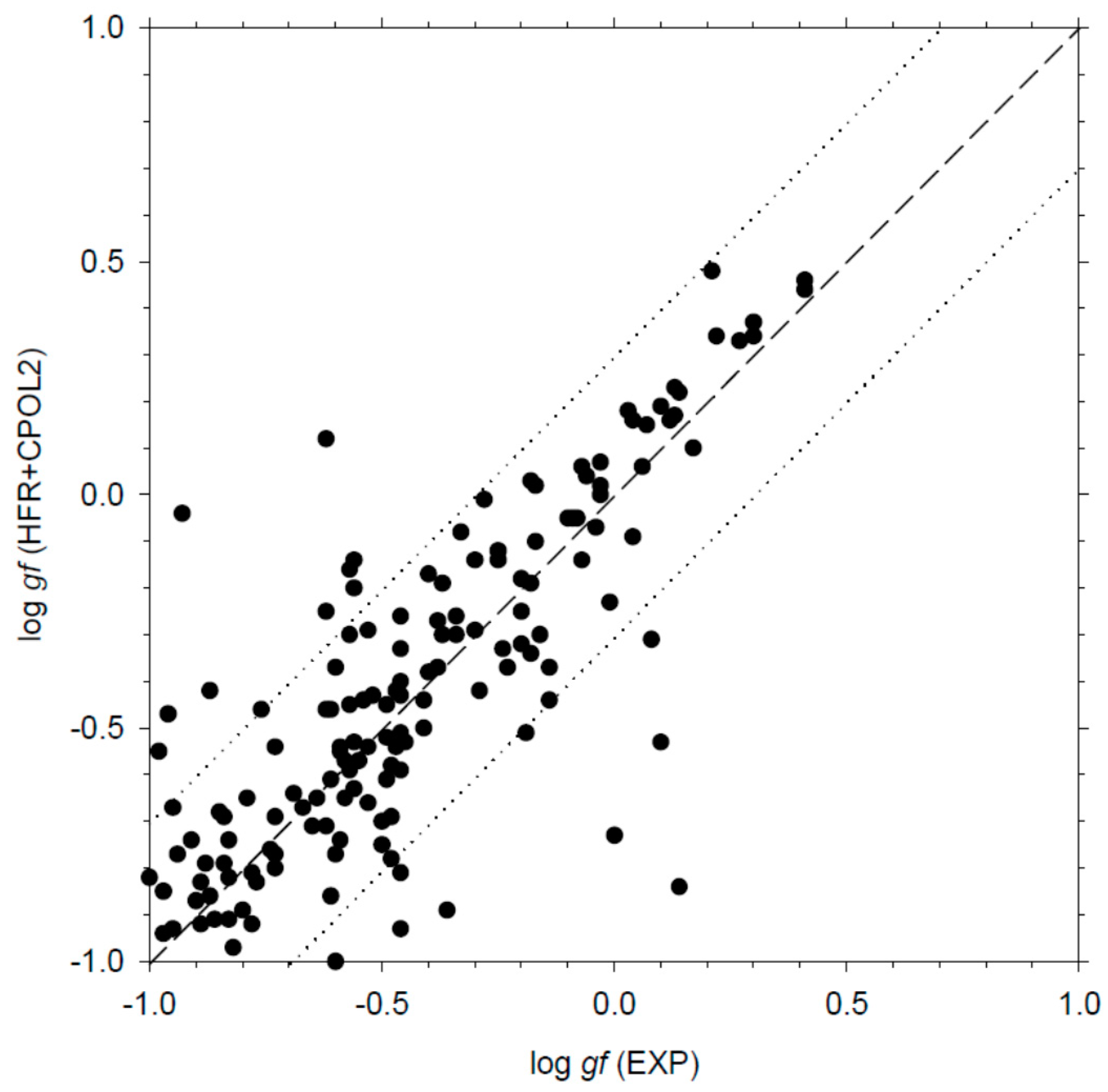
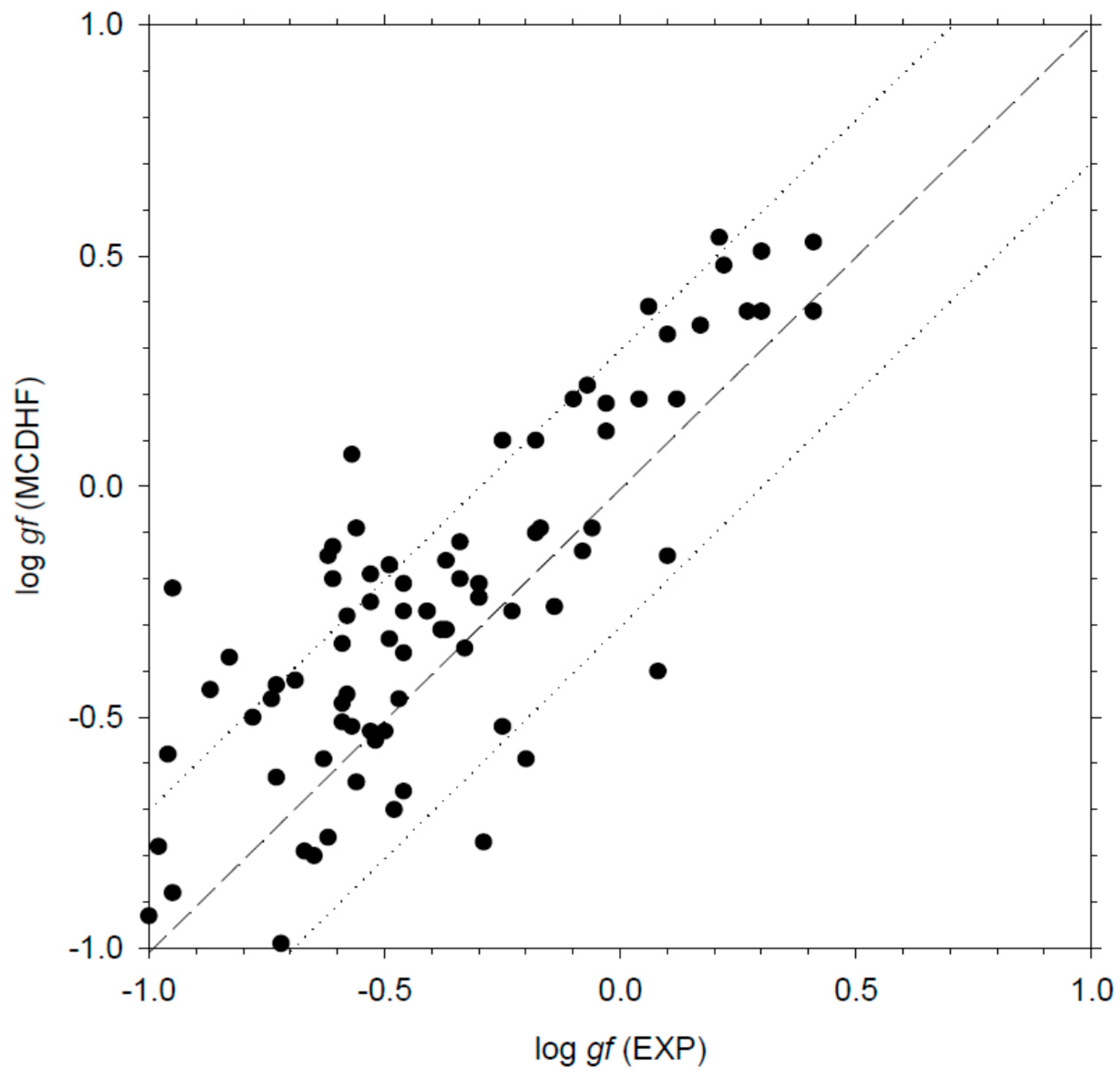
In Table 2, we give the oscillator strengths and transition probabilities computed in the present work using the HFR+CPOL2 model, and rescaled using the experimental wavelengths, for a set of 392 La I transitions with log gf-values greater than −1.0. These lines appear from the near-ultraviolet to the mid-infrared spectral regions, more precisely from 317 to 7843 nm. The experimental data recently published by Den Hartog et al. [22] are also reported for comparison in the table. There are 165 common transitions between this latter work and ours. For about three-quarter of these transitions, we note an agreement better than a factor of two between our calculated oscillator strengths and the experimental values while, for somewhat more than a half of the lines, the discrepancies between both sets of results do not exceed 25%. This is illustrated in Figure 3 where the HFR+CPOL2 and experimental log gf-values are compared. It appears also that the calculated transition rates obtained in the present work can be considered as much more reliable than the theoretical data reported by Karaçoban and Özdemir [16] and Kurucz [8], these latter data being found to disagree by more than a factor of 2 with the experimental oscillator strengths, as highlighted in Figure 2 and Figure 3 of [22].

Table 2.
Calculated oscillator strengths (log gf) and transition probabilities (gA) for spectral lines in La I. A + B stands for A × 10B. Experimental data are also given where available, for comparison.
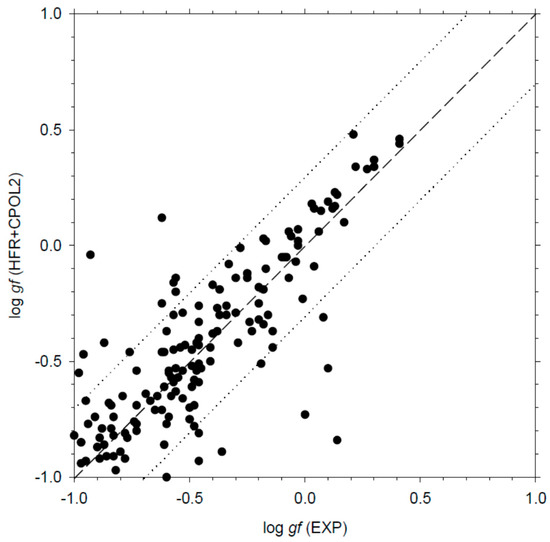
Figure 3.
Comparison between the oscillator strengths (log gf) computed in the present work using the HFR+CPOL2 model and the available experimental values [22]. The dashed line corresponds to a perfect agreement while the dotted lines correspond to a discrepancy of a factor of two on the gf-values.
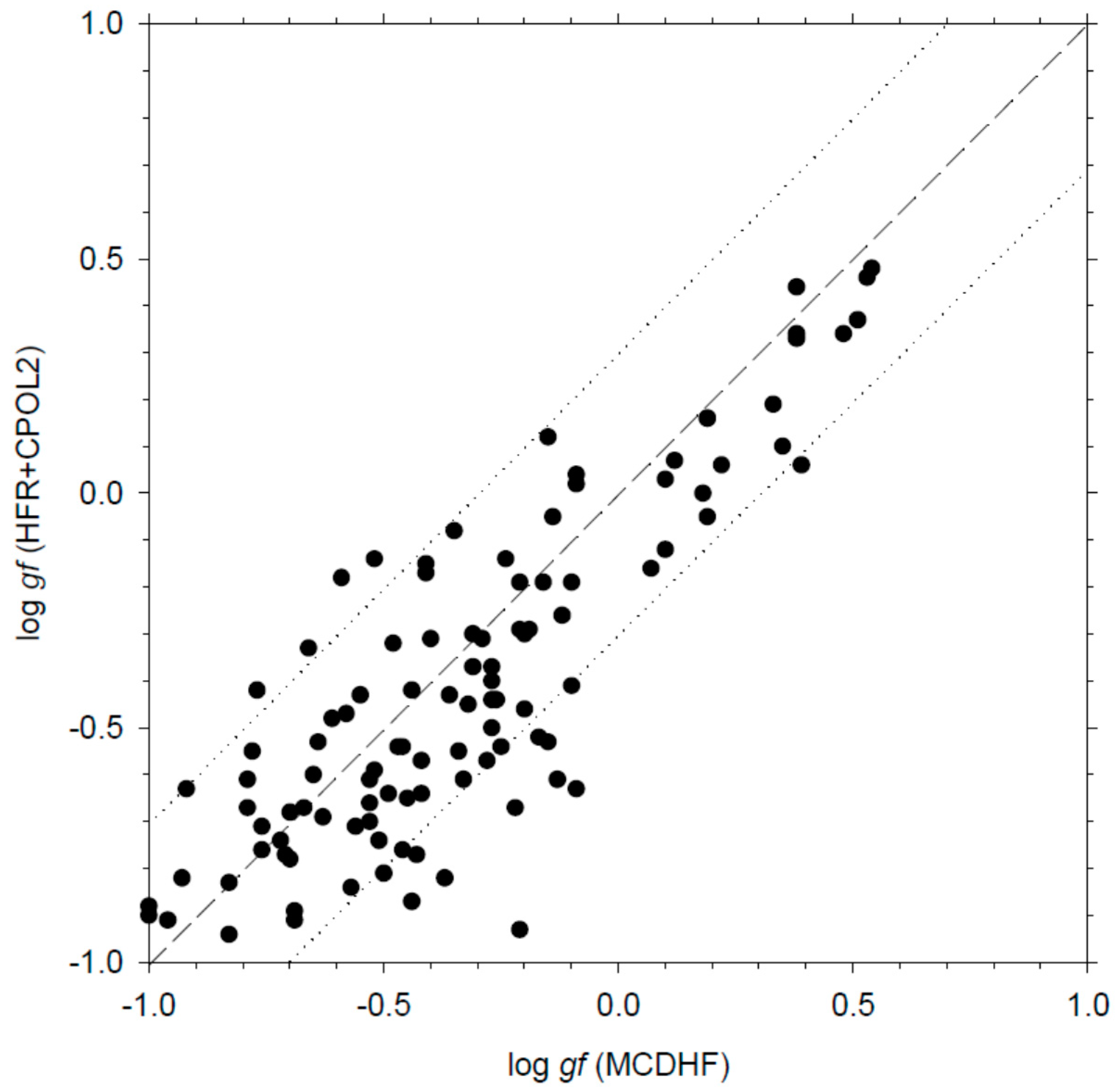
Another interesting comparison is the one between the results obtained with the HFR+CPOL2 model and those deduced from our MCDHF computations, as described in Section 2.2. Such a comparison is shown in Figure 4. In this case, the agreement between both sets of oscillator strengths is found to be good in view of the complexity of the La I atomic structure, the discrepancies not exceeding 30% for half of the transitions (within the limit log gf > −1) and being anyway not larger than a factor of two for 95% of the entire set of common lines. A comparable agreement is observed when comparing our MCDHF calculations to the experimental gf-values of Den Hartog et al. [22], as illustrated in Figure 5. It is however to be emphasized that, on average, the MCDHF oscillator strengths tend to be slightly larger (~10–15%) than the HFR+CPOL2 and the experimental data, for the same reason as the one discussed in Section 3.1.
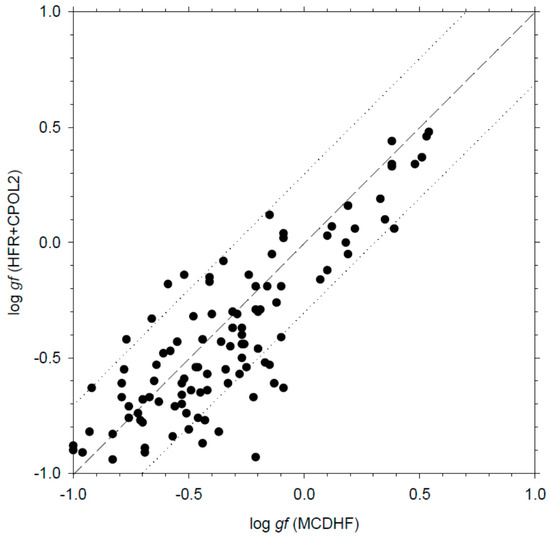
Figure 4.
Comparison between the oscillator strengths (log gf) computed in the present work using the HFR+CPOL2 and the MCDHF models. The dashed line corresponds to a perfect agreement while the dotted lines correspond to a discrepancy of a factor of two on the gf-values.
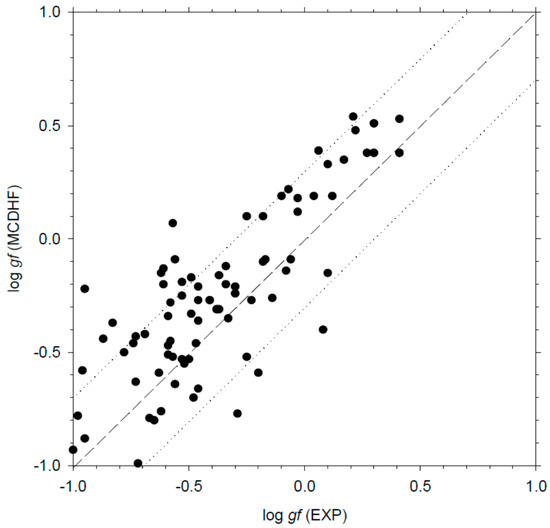
Figure 5.
Comparison between the oscillator strengths (log gf) computed in the present work using the MCDHF model and the available experimental values [22]. The dashed line corresponds to a perfect agreement while the dotted lines correspond to a discrepancy of a factor of two on the gf-values.
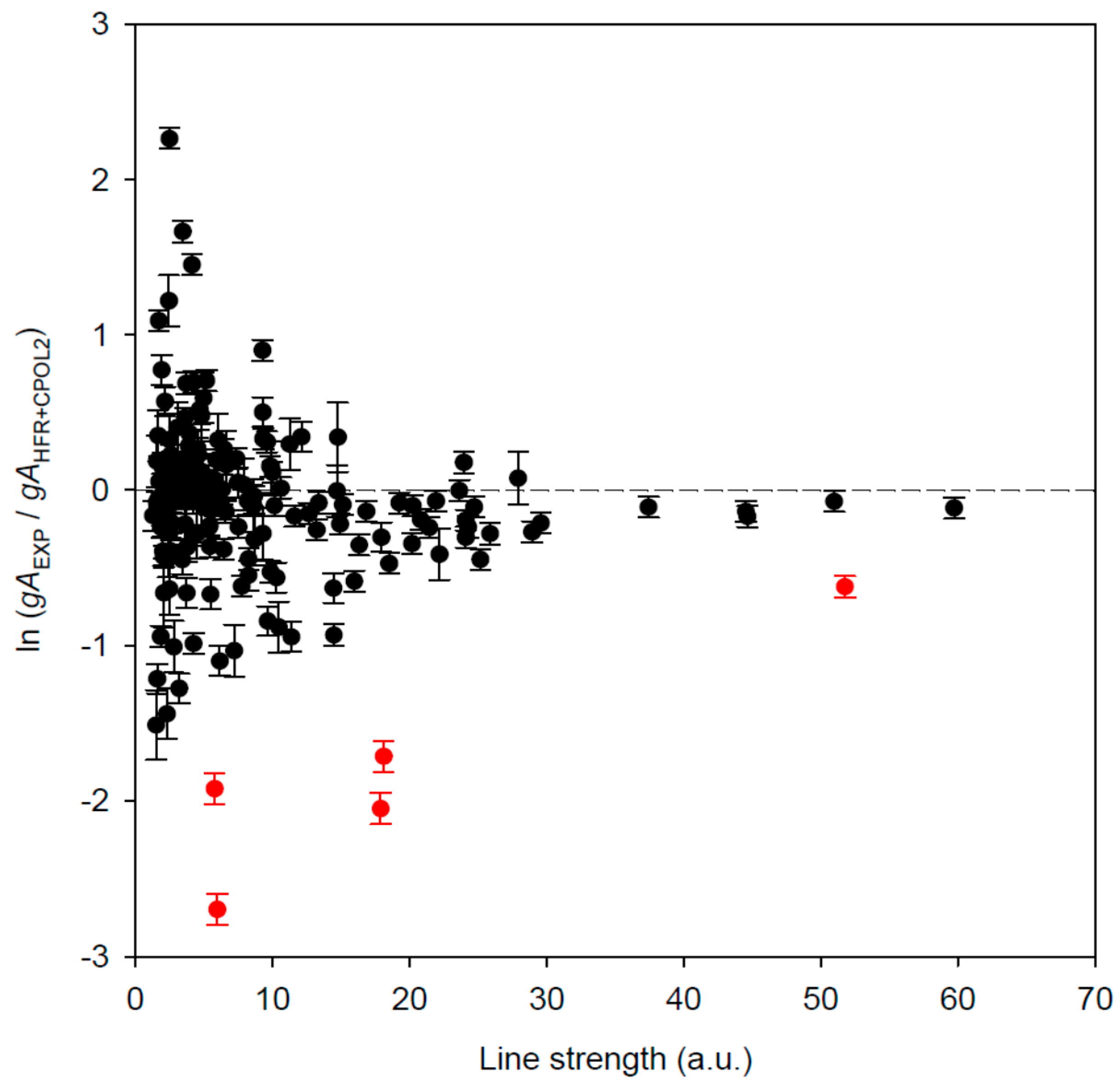
A more robust method of evaluating uncertainties in gf- and gA-values for each calculated transition, as described by Kramida [34], is to plot the differences between theoretical and reference data (i.e., the experimental transition probabilities of Den Hartog et al. [22] in the present work) against the theoretical line strengths (S). Such a plot is given in Figure 6 for the results reported in Table 2. From this figure, one can see that the entire range of calculated S-values can be divided into a few ranges, so that the average discrepancy is nearly constant in each range. Excluding a few outlying points shown in red in Figure 6, the root-mean-square deviations in the quantity ln(gAEXP/gAHFR+CPOL2) are 0.13, 0.28, 0.42, and 0.69 for S > 30 a.u., S = 15–30 a.u., S = 4.3–15 a.u., and S < 4.3 a.u., respectively. This corresponds to average relative deviations of 13%, 32%, 53%, and 98% for gA values. These estimates can be reliably extrapolated to calculated transitions for which there are no experimental data for comparison. Thus, a reliable estimate of uncertainty can be given for each calculated gA value of Table 2, even if there is no experimental data to compare with. From this evaluation, we found that among 227 transitions of Table 2 having no reference data, 8 calculated gA-values have an uncertainty of 13%, 19 have an uncertainty of 32%, 134 have an uncertainty of 53 %, and only 66 are affected by larger uncertainties. This allowed us to give an evaluation of the uncertainty for each computed transition rate reported in Table 2, using the same code letter as the one usually employed in the NIST database [6]. The five abnormally deviating points shown in red in Figure 6 are probably due to insufficient accuracy of the calculated wavefunctions for the levels involved in the corresponding transitions. This was actually highlighted when comparing the calculated and experimental Landé g-factors for each upper odd level of these transitions, i.e., 23,303.26 (J = 7/2), 24,409.68 (J = 7/2), 24,639.26 (J = 3/2), 25,083.36 (J = 7/2), and 28,039.45 (J = 7/2) cm−1, for which our g-values (g = 1.39, 1.34, 0.55, 1.22, and 1.04) showed rather large discrepancies with the experimental ones (g = 1.18, 1.16, 1.78, 1.38, and 1.14).
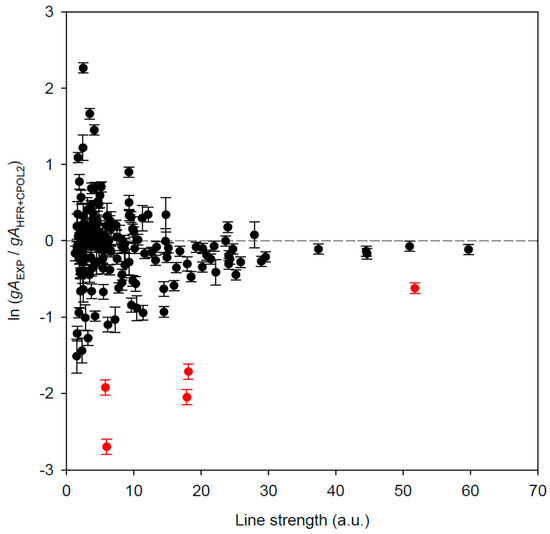
Figure 6.
Dependence of residuals (experiment-theory) on the line strength S (in atomic units) calculated in this work. The experimental gA-values (gAEXP), together with their error bars, originate from Den Hartog et al. [22] The red outlying points have been excluded from uncertainty evaluation (see text).
In summary, the oscillator strengths and transition probabilities computed in the present work using the HFR+CPOL2 model are expected to be accurate to within a factor of two for the vast majority of the La I spectral lines listed in Table 2 and even better than 30% for many of them. These new parameters thus represent the most reliable set of theoretical radiative rates produced up until now in lanthanum atom and can be considered as a valuable complement to the available experimental data [22], in particular in the infrared region where the latter are very sparse.
4. Conclusions
New oscillator strengths and transition probabilities for 392 spectral lines of neutral lanthanum are reported in this work. They were deduced from moderately large-scale pseudo-relativistic Hartree–Fock (HFR) calculations including the most important intravalence and core-valence configuration interaction effects. The accuracy of the results was estimated to be better than a factor of two for the entire set of transitions and likely within 30% for many of them. This was assessed from detailed comparisons between different theoretical models based on the HFR and the multiconfiguration Dirac–Hartree–Fock (MCDHF) methods, on the one hand, and between the theoretical results and the available experimental data, on the other hand. Among the La I lines listed in the present paper, about 60% have gf- and gA-values determined for the first time.
Author Contributions
All authors were equally involved in the calculations reported in the present paper as well as in the writing of the manuscript.
Funding
This research received no external funding.
Acknowledgments
P.P. and P.Q. are respectively Research Associate and Research Director of the Belgian National Fund for Scientific Research F.R.S.-FNRS. Financial support from this organization is acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Biémont, E.; Quinet, P. Recent Advances in the Study of Lanthanide Atoms and Ions. Phys. Scr. 2003, 105, 38. [Google Scholar] [CrossRef]
- Wybourne, B.G. The fascination of the rare earths—Then, now and in the future. J. Alloys Compd. 2004, 380, 96–100. [Google Scholar] [CrossRef]
- Lawler, J.E.; Den Hartog, E.A.; Sneden, C. Spectroscopic Data for Neutral and Ionized Rare Earth Elements. AIP Conf. Proc. 2005, 771, 152–161. [Google Scholar]
- Sneden, C.; Lawler, J.E.; Cowan, J.J.; Ivans, I.I.; Den Hartog, E.A. New Rare Earth Element Abundance Distributions for the Sun and Five r-process-rich Very Metal-Poor Stars. Astrophys. J. Suppl. 2009, 182, 80. [Google Scholar] [CrossRef]
- Mumpower, M.R.; McLaughlin, G.C.; Surman, R. The Rare Earth Peak: An Overlooked r-process Diagnostic. Astrophys. J. 2012, 752, 117. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. Available online: http://physics.nist.gov/asd (accessed on 30 October 2018).
- Corliss, C.H.; Bozman, W.R. Experimental transition probabilities for spectral lines of seventy elements. Nat. Bur. Stand. Monogr. 1962, 53, 80–81. [Google Scholar]
- Kurucz, R.L. Including All the Lines. Can. J. Phys. 2011, 89, 417. [Google Scholar] [CrossRef]
- Hese, A. Level Crossing Experiments to Investigate the Hyperfine Structure and the Lifetime of the 5d6s6p z 2F5/2,7/2 States in the Lanthanum I Spectrum. Z. Phys. 1970, 236, 42. [Google Scholar] [CrossRef]
- Hese, A.; Buldt, G. Hyperfine Structure, Stark Effect and Lifetimes of the Excited 5d6s6p y 2D3/2,5/2 States of the Lanthanum I Spectrum. Z. Naturforsch. 1970, 25, 1537–1545. [Google Scholar]
- Hese, A.; Wiese, H.P. Investigation of the 5d6s6p z 2F Terms in the Lanthanum I Spectrum by Optical Double Resonance. Z. Angew. Phys. 1970, 30, 170. [Google Scholar]
- Bulos, B.R.; Glassman, A.J.; Gupta, R.; Moe, G.W. Measurement of the Lifetimes of the z 2F5/2, z 2D3/2, z 4G5/2, and y 2D3/2 States of Lanthanum. J. Opt. Soc. Am. 1978, 68, 842–845. [Google Scholar] [CrossRef]
- Penkin, N.P.; Gorshkov, V.N.; Komarovskii, V.A. Radiative lifetimes of excited La I levels. Opt. Spectrosc. 1985, 58, 840–841. [Google Scholar]
- Biémont, E.; Quinet, P.; Svanberg, S.; Xu, H.L. Lifetime measurements and calculations in La I. Eur. Phys. J. D. 2004, 30, 157–162. [Google Scholar] [CrossRef]
- Karaçoban, B.; Özdemir, L. Energies and Lifetimes for Some Excited Levels in La I. Acta Phys. Pol. A 2008, 113, 1609–1618. [Google Scholar] [CrossRef]
- Karaçoban, B.; Özdemir, L. Electric Dipole Transitions for La I (Z = 57). J. Quant. Spectrosc. Rad. Transf. 2008, 109, 1968–1985. [Google Scholar] [CrossRef]
- Froese-Fischer, C.F.; Brage, T.; Jönsson, P. Computational Atomic Structure—An MCHF Approach; Institute of Physics Publishing: Bristol, UK, 1997. [Google Scholar]
- Feng, Y.Y.; Zhang, W.; Kuang, B.; Ning, L.; Jiang, Z.; Dai, Z. Radiative Lifetime Measurements on Odd-Parity Levels of La I by Time-Resolved Laser Spectroscopy. J. Opt. Soc. Am. B 2011, 28, 543–546. [Google Scholar] [CrossRef]
- Feng, Y.Y.; Wang, Q.; Jiang, L.Y.; Jiang, Z.K.; Dai, Z. Radiative Lifetimes of Highly Excited Odd-Parity Levels of Neutral Lanthanum. Eur. Phys. J. D 2011, 65, 299–302. [Google Scholar] [CrossRef]
- Yarlagadda, S.; Mukund, S.; Nakhate, S.G. Radiative lifetime measurements in neutral lanthanum using time-resolved laser-induced fluorescence spectroscopy in supersonic free-jet. J. Opt. Soc. Am. B 2011, 28, 1928–1933. [Google Scholar] [CrossRef]
- Shang, X.; Tian, Y.; Wang, Q.; Fan, S.; Bai, W.; Dai, Z. Radiative lifetime measurements of some La I and La II levels by time-resolved laser spectroscopy. Mon. Not. R. Astron. Soc. 2014, 442, 138–141. [Google Scholar] [CrossRef]
- Den Hartog, E.A.; Palmer, A.J.; Lawler, J.E. Radiative lifetimes and transition probabilities of neutral lanthanum. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 155001. [Google Scholar] [CrossRef]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Quinet, P.; Palmeri, P.; Biémont, E.; McCurdy, M.M.; Rieger, G.; Pinnington, E.H.; Wickliffe, M.E.; Lawler, J.E. Experimental and theoretical lifetimes, branching fractions and oscillator strengths in Lu II. Mon. Not. R. Astron. Soc. 1999, 307, 934–940. [Google Scholar] [CrossRef]
- Quinet, P.; Palmeri, P.; Biémont, E.; Li, Z.S.; Zhang, Z.G.; Svanberg, S. Radiative lifetime measurements and transition probability calculations in lanthanide ions. J. Alloys Comp. 2002, 344, 255–259. [Google Scholar] [CrossRef]
- Quinet, P. An overview of the recent advances performed in the study of atomic structures and radiative processes in the lowest ionization stages of heavy elements. Can. J. Phys 2017, in press. [Google Scholar] [CrossRef]
- Fraga, S.; Karwowski, J.; Saxena, K.M.S. Handbook of Atomic Data; Elsevier: Amsterdam, The Netherlands, 1976. [Google Scholar]
- Hibbert, A. Transitions in the Cadmium Sequence. Nucl. Instrum. Methods Phys. Res. 1982, 202, 323–327. [Google Scholar] [CrossRef]
- Hameed, S. Core Polarization Corrections to Oscillator Strengths and Singlet-Triplet Splittings in Alkaline Earth Atoms. J. Phys. B 1972, 5, 746. [Google Scholar] [CrossRef]
- Başar, G.; Gamper, B.; Güzelçimen, F.; Öztürk, I.K.; Binder, T.; Başar, G.; Kröger, S.; Windholz, L. New Even and Odd Parity Fine Structure Levels of La I Discovered by Means of Laser-Induced Fluorescence Spectroscopy. J. Quant. Spectrosc. Rad. Transfer. 2017, 187, 505–510. [Google Scholar] [CrossRef]
- Jönsson, P.; Gaigalas, G.; Bieron, J.; Froese Fischer, C.; Grant, I.P. New Version: GRASP2K Relativistic Atomic Structure Package. Comput. Phys. Commun. 2013, 184, 2197–2203. [Google Scholar] [CrossRef]
- Grant, I.P. Relativistic Quantum Theory of Atoms and Molecules. Theory and Computation; Springer: New York, NY, USA, 2007. [Google Scholar]
- Zhang, W.; Palmeri, P.; Quinet, P.; Biémont, E. Transition probabilities in Te II and Te III spectra. Astron. Astrophys. 2013, 551, A136. [Google Scholar] [CrossRef]
- Kramida, A. Critical evaluation of data on atomic energy levels, wavelengths, and transition probabilities. Fusion Sci. Technol. 2013, 63, 313–323. [Google Scholar] [CrossRef]
- Edlén, B. The refractive index of air. Metrologia 1966, 2, 71. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).