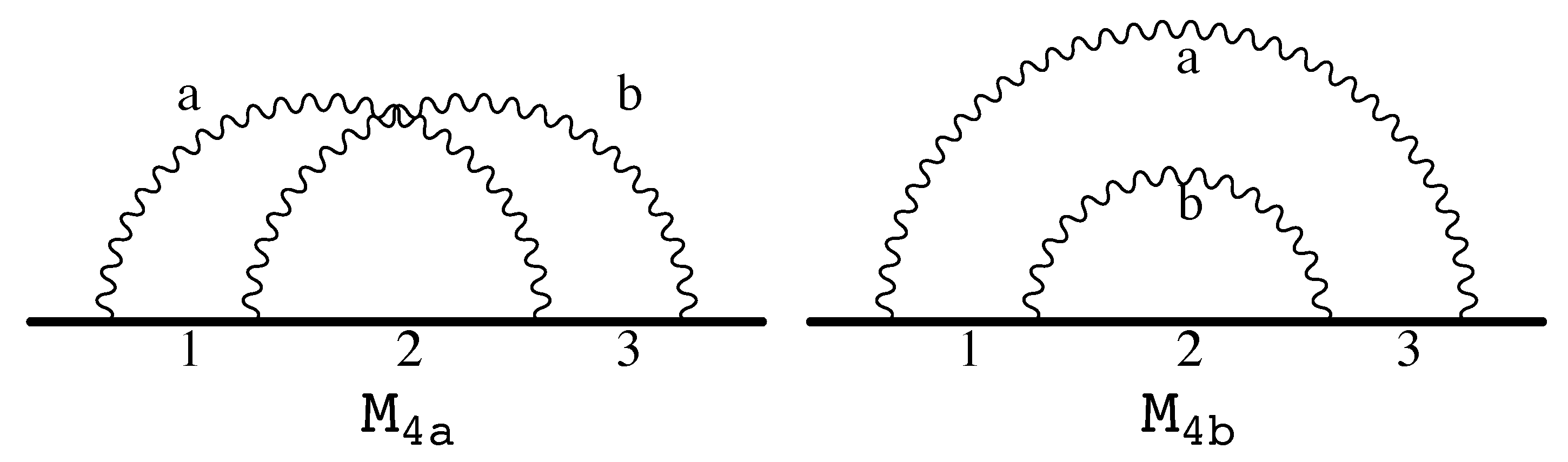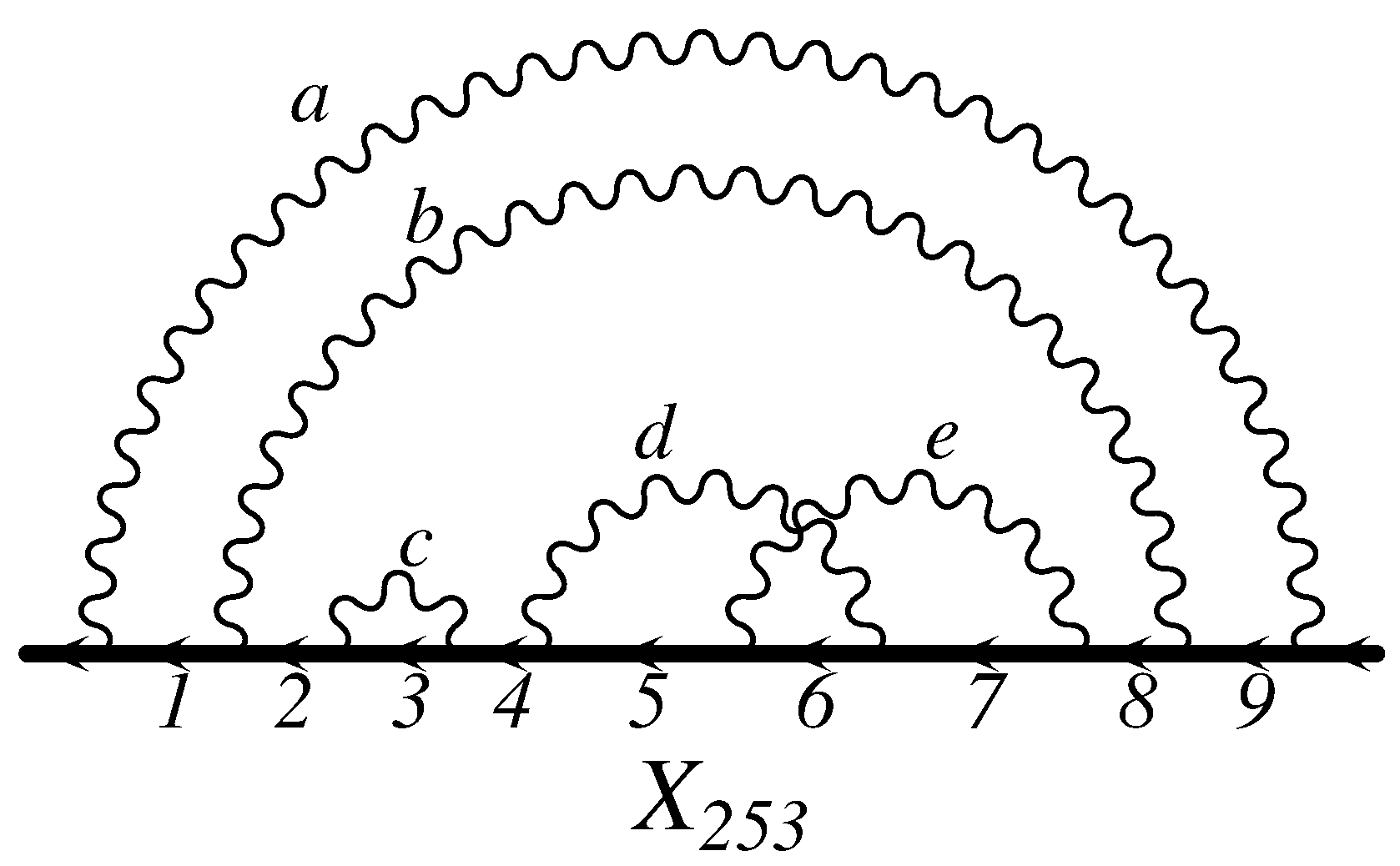1. Introduction
The anomalous magnetic moment of the electron was discovered in 1947 by P. Kusch and H. M. Foley [
1]. The Zeeman spectra of the gallium atom in a constant magnetic field were measured, and the gyromagnetic ratio (
g value) of the electron was determined. If the orbital
g value is assumed to be one as Dirac theory predicts, the spin
g value of the electron is determined to be
The
g value of the electron derived from the Dirac theory is exactly an integer two, and the difference between the measured
g value and Dirac’s two is called the anomalous magnetic moment of the electron:
This tiny 0.1% deviation of the electron
g, as well as the Lamb shift of the hydrogen atom discovered one year earlier [
2] were the achievements of the state-of-the-art improvements in the frequency measurements at that time.
Theory of charged particles and photons, named as quantum electrodynamics (QED), was also developed in the same era. It must be distinguished from its old version from the 1920s, which suffered from the divergence problem associated with perturbative calculation [
3,
4]. The new idea, renormalization, enables us to compute finite physical quantities from the perturbation theory of QED with high precision. J. Schwinger showed that the value of the anomalous magnetic moment of the electron
can be attributed to the one-loop effect of QED [
5]. Precision comparison between measurement and theory in 1947–1948 was the starting point of stringent tests of QED and the standard model of elementary particles. The very high precision achieved in testing
is a consequence of small values of the fine structure constant
and the small electron mass. The Lamb shift could not serve as the high precision test of QED since it depends on other quantities such as hadronic interactions and hadronic masses.
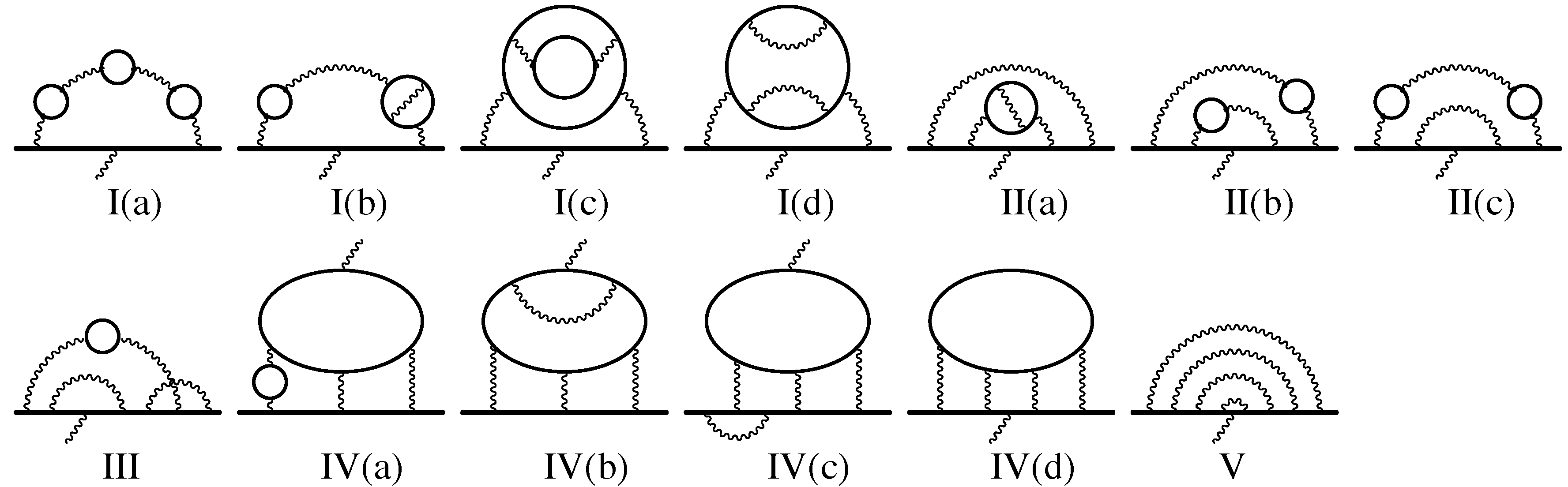
In this article, we review the current status of the theory of the electron anomalous magnetic moment, including the contribution of Feynman diagrams of QED up to the tenth-order perturbation theory. Of course, our starting points are Feynman diagrams and corresponding integrals. However, these integrals, usually defined in the momentum space, are not convenient for numerical integration. Thus, we transform them to forms accessible to numerical integration. Currently, the numerical integration method is the only way to approach the tenth-order QED Feynman diagrams. The numerical computation methods of QED have been given in several references: our approach is given in [
6,
7,
8,
9,
10,
11,
12], and alternatives are found in [
13,
14,
15]. In
Section 2, the contributions to
from all known sources are listed. In the subsequent sections, step-by-step instructions are given for the conversion of Feynman integrals to one accessible to numerical integration, working on the fourth-order diagrams as an example.
2. Summary of Contributions to
Before digging into the calculation method of a Feynman diagram, let us summarize the theoretical value of the electron anomalous magnetic moment
. The standard model contribution to
can be divided into three terms:
The QED contribution
involves the leptons, which are electron (
e), muon (
), and tau (
), and photons. The contribution involving the weak bosons (
) is categorized into
. The contribution from quarks or hadrons without a weak boson is denoted by
. Since the electron is much lighter than the weak bosons and hadrons, the QED contribution dominates over others:
and
amount to only 0.026 ppb [
16,
17,
18,
19] and 1.47 ppb [
20,
21,
22], respectively, of the whole contribution.
The QED contribution is further divided according to its lepton-mass dependence. Since the anomaly
is dimensionless, lepton-mass dependence appears in the form of the ratio between lepton masses. Thus, we may rewrite
where
,
, and
are masses of the electron, muon, and tau-lepton, respectively. The term
is independent of the lepton-mass ratios and universal for all lepton species.
Both mass-independent and mass-dependent terms can be calculated in a framework of the perturbation series expressed by Feynman diagrams. The expansion parameter of the perturbation series is the coupling constant of QED, namely the elementary charge e of leptons. Since it involves only even powers of e, the perturbation expansion is expressed in terms of the fine-structure constant , which is proportional to . Thus, a Feynman diagram with n-loops appears in the -order of the perturbation series of QED.
In SI units, the fine-structure constant
is defined as
where
ℏ is the Dirac constant, which is the Planck constant
h divided by
,
c is the speed of light, and
is the electric constant. As is well known, in the current SI system,
c and
are the defined constants. The new SI will be launched in May 2019, and the Planck constant
h and the elementary charge
e will become the defined constants, while the electric constant
will no longer be a defined constant.
In the natural units
, the fine-structure constant has a much simpler expression:
Hereafter, we shall use the natural units. Since the fine-structure constant
is a dimensionless constant, it has the same value regardless of the chosen units.
Since measurements find that
, we are lucky enough to have an effective perturbation series for QED calculation:
Because of the renormalizability of QED, every
is finite and calculable by using the Feynman-diagram techniques. The results of QED calculation are summarized in
Table 1. By now, all coefficients
up to the eighth-order have been found analytically [
5,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32]. They are consistent with numerical evaluations [
33,
34,
35]. The references quoted here are responsible only for the final stages of the calculation of each term, which were built upon much effort of many scientists over seventy years. Note that the mass-dependent terms of the sixth- and eighth-order terms,
,
, are not given in the closed forms. However, sufficiently higher order terms of the series expansion in a mass ratio were analytically obtained [
30,
31,
32]. Furthermore, the mass-independent eighth-order term
in [
26] is not fully analytic.
One of the recent achievements in the QED calculation is the near-analytic result of the eighth-order mass-independent term
obtained by S. Laporta [
26]. The Feynman integrals of the 891 eighth-order vertex diagrams are expressed in momentum space representation. They are decomposed into 334 master integrals (MI) according to the Laporta algorithm [
36]. These MIs are numerically evaluated with high precision, up to 9600 digits, using the difference equation and/or the differential equation methods. The numerical values are then fitted by using the PSLQ algorithm [
37,
38], which is a finder of integer relations, and the analytic expressions of the MIs are determined. The MIs for the eighth-order cannot be expressed only by the elementary functions. They contain harmonic polylogarithms and one-dimensional integrals of the products of elliptic integrals. The analytic expressions of several MIs related to the internal light-by-light scattering diagrams, shown as IV(d) of Figure 4, have not been determined yet. Thus, the result obtained by S. Laporta is near-analytic, but known up to 1100 digits.
The tenth-order terms have been calculated only numerically thus far [
35,
39,
40], though some small sets of diagrams are known analytically. An independent numerical double check has not been carried out yet. The mass-dependent term of the tenth-order was reported in [
39]. The mass-independent term,
, has been calculated continuously on supercomputers even after some results were published in [
40]. The latest numerical result
is consistent with
given in Equation (
16) of [
40] and supersedes it.
Obviously, the mass-dependent terms
and
depend on the lepton-mass ratios provided by [
41,
42], and they are used as input parameters. However, they are the only input parameters of QED calculation. Notably, the mass-independent contribution
is calculated without any input parameters. Principles, such as
gauge theory, Lorentz and CPT symmetries, and renormalizability determine
completely.
In order to obtain the theoretical prediction of
, however, we need the input parameter determined from measurements of the nature. QED itself cannot determine what the fine-structure constant
is. Its value can only be derived from measurements. The quantum Hall resistance, which is named as the von Klitzing constant
, used to be the best method to determine the value of
. However, the current best is to use atomic recoil measurements. A quotient of the Planck constant and the mass of an atom
X,
, can be precisely determined by using atom interferometry [
44]. Two quantum states of an atom are spatially separated by transferring momenta through Bloch oscillation of the optical lattice made of laser beams [
45]. The obtained quotient is converted to
through
where
is the Rydberg constant and
and
are the relative atomic masses of an atom
X and an electron, respectively, which is defined by
(
),
u being the unified atomic mass unit. All three are precisely known and found in the CODATA 2014 adjustment [
41].
is determined from the cyclotron frequency of an ion in the constant magnetic field.
is from the bound
g factor of the electron, and
is from hydrogen spectroscopy. To determine the values
and
from the measured quantities, one needs the QED corrections that have been obtained from many theoretical calculations [
41]. In this sense, the value of
determined from the quotient
is not perfectly independent of QED. However, the uncertainties due to QED corrections are sufficiently small, and the uncertainty from the quotient
dominates over others. Therefore,
can be regarded as an independent determination of QED.
Recently, two new measurements on the hydrogen spectra have been carried out, and new values of
have been reported. One is the 2S–4P transition by A. Beyer et al. [
46]. Their
is different from the CODATA adjusted value by 3.3
. Another is the 1S–3S transition by H. Fleurbaey et al., which reports a value of
consistent with CODATA [
47]. If we use the value of
from [
46], it increases the value of
by only
, which is within the uncertainty of
due to the
measurements. Thus, we use the CODATA2014 adjustment value for
. The values of
currently available are from the Rb atom [
48] and Cs atom [
49] measurements of
and are obtained as
Using them and hadronic and weak contributions to
as listed in
Table 2, we obtain the theoretical prediction of
as
where the uncertainties are due to the fine-structure constant
, numerical evaluation of the tenth-order QED, and the hadronic contribution in this order. Note that the uncertainty of QED is now smaller than that of hadrons.
The best measurement of
was performed at Harvard. Their result was [
50]
The differences between theory and measurement are
where the discrepancies are about 1.7
and 2.4
for
and
, respectively.
We can obtain one more value of
recalling that the theory of
depends almost exclusively on
. Equating the theoretical formula of
(
3) with the measurement (
14), we obtain
where the uncertainties are from the numerical evaluation of the tenth-order QED term, the hadronic contribution, and the measurement (
14). The differences in
from the atomic recoil determinations are
where the discrepancies are about 1.7
and 2.4
for
and
, respectively.
4. QED Diagrams without a Fermion Loop
4.1. Ward–Takahashi Sum
Let us focus on QED vertex diagrams without a fermion loop. For the higher order terms of the perturbation theory, the number of Feynman diagrams grows factorially with the loop order [
52]. Furthermore, as the order increases, the complexity of the integral derived from a Feynman diagram drastically increases. Reduction of the number of diagrams, if possible, is thus highly desirable. To achieve this goal, we combine vertex diagrams sharing the same quantum corrections and relate them to a self-energy diagram through the Ward–Takahashi identity:
where
is the “sum” of vertex diagrams that are obtained by inserting an external photon vertex in a fermion line of the self-energy diagram
in every possible way. Differentiating both sides with respect to
and taking a vanishing momentum transfer limit
, we obtain
This equation enables us to obtain the magnetic moment amplitude of the
-order diagram by projecting it out from the right-hand side of (
30). Although they are not explicitly written, photon momenta are imposed on a cut-off
, and a small mass
is given to a photon. These regularization parameters are safely removed after the finite amplitude is constructed.
The QED Feynman–Dyson rules introduced in many QED textbooks lead to a Feynman integral expressed in momentum space. Instead, we use the parametric Feynman–Dyson rules [
7,
9,
10] that enable us to write down the Feynman integral in terms of Feynman parameters without referring to the momentum representation at all. The Feynman integral derived from a
-order self-energy diagram can be expressed using Feynman parameters:
and
are assigned from the left to the right to
electron and
n photon propagators, respectively. All Feynman parameters are non-negative, and the sum of all is restricted to one. As an example, two self-energy-like diagrams of the fourth-order are shown in
Figure 6.
To illustrate the parametric Feynman–Dyson rules, we start with the Feynman–Dyson integral of the self-energy diagram
of the left pane of
Figure 6:
where
and
are the momenta of photon propagators
a and
b, respectively, and
are the momenta flowing on the electron propagators 1, 2, and 3. By introducing the Feynman parameters
and using the trick
the denominators of all propagators are combined as
The loop momenta
and
can be “diagonalized”, and Equation (
33) is rewritten as
where
and
The
U function is a “Jacobian” from the momentum space to the Feynman parameter space. After the shift of the loop momenta, the numerator of the integrand of (
31),
, is expressed as
where
’s are the linear combinations of the diagonalized loop momenta
and
and
’s are functions of Feynman parameters. Because of its definition in (
34),
G is obviously related to
as
More systematic derivation of
U and other functions of the Feynman parameters will be given in
Section 4.3, which is based on graph theory and is easily applicable to any higher order diagrams.
The right-hand side of (
30) for any order of the perturbation theory can be obtained by performing several manipulations on the Feynman parametric representation of a self-energy diagram
. They are expressed as
where
stands for integration variables over Feynman parameters subject to the constraint
. The function
U is a “Jacobian” for transformation from the momentum space to Feynman parametric space and
V is the combined denominators of all propagators of the diagram
. Explicit expressions of
U and
V will be determined later. The exact manipulations are given in [
7,
9,
10]. Briefly speaking, the procedure corresponding to the operator
is to insert an external photon vertex to one of the electron propagators of a self-energy diagram and to differentiate this electron propagator with respect to the momentum
q flowing in through the external photon vertex. The procedure corresponding to the operator
is to insert an external photon vertex to one of the electron propagators and to differentiate with respect to
q all other electron propagators to which an external photon vertex is not attached. The procedure corresponding to the operator
comes from the differentiation of the denominator function
V with respect to
. The operator
is defined by
, where
is the product of all numerators of the electron propagators of a self-energy diagram.
The procedures and their corresponding operators of
-matrices are explicitly constructed for the self-energy diagram
. There are three electron propagators in which an external photon vertex can be inserted. Thus, the
-operator consists of three terms:
where
is obtained by replacing the electron line factor
of
in (
36) by
:
is constructed by picking up two electron line factors:
where
can be obtained by replacing
and
of
by
and
, respectively. The coefficient
is defined in terms of
, which will be defined later in
Section 4.3, as
where
Since the denominator function
V contains the external momentum
p as given in (
34), the
-operator is trivially determined as
where
G is defined in (
34), and its explicit form is given in (
37). The explicit form of
-operator for
is given by
where
is obtained by replacing
of
by
.
4.2. Projection of Anomaly Contributions
We are now ready to extract the anomalous magnetic moment contribution paying attention to its Lorentz structure. After projection operators are applied to (
38) and (39), the magnetic moment amplitude has the form of
where the functions
,
,
,
are defined as
and the projection operators of
and
are given by
with
. Hereafter, we set
and the photon mass
, unless we need to distinguish
and
.
4.3. Building Blocks
We introduce the “correlation” functions
between two propagators
i and
j of the same diagram. The propagators
i and
j can be any of the electron or photon propagators. These
’s are the very basic building blocks of the Feynman parametric representation of a loop diagram. They are determined by and only by the topology of a loop diagram [
57,
58].
Let us introduce a chain diagram that is obtained when the external legs of a diagram are removed and no distinction is made between electron and photon propagators. Thus, chain diagrams of each order of the QED perturbation theory are identical to those of the scalar theory. A line between two nodes of a chain diagram is associated with a sum of several Feynman parameters belonging to it, and its direction is freely assigned. For a given chain diagram with n loops with , the numbers of nodes and lines are and , respectively. For , a chain diagram has no node, and it is just a circle. The number of topologically-distinguished chain diagrams at a given order of perturbation theory is quite small compared with those of Feynman diagrams. They are 1, 1, 2, 5, and 16 for the second-, fourth-, sixth-, eighth-, and tenth-order perturbation theory of QED.
A given n loop chain diagram has n independent closed circuits. In the case of a QED self-energy diagram without a fermion loop, independent closed circuits are easily identified. A closed circuit consists of a photon propagator and electron propagators that lie between the two vertices where this photon comes in and out. The direction of a closed circuit is chosen as the same as that of the electron propagators.
The diagrams and are reduced to the same chain diagram. For , the independent closed circuits and c consist of two lines and and two lines and , respectively. For , the independent circuits and consist of two lines and and two lines and , respectively.
The
loop matrix
for a chain diagram is defined as follows:
where
i indicates one of the independent chain circuits and
stands for a line number. The loop matrix
for
is
and the same for
. The
symmetric matrix
is derived from
such that
The Jacobian
U in (
38) and (39) is obtained as the determinant of the matrix
:
The correlation function
between two lines
and
of a chain diagram is defined by
where
is the inverse matrix of
.
The
between two propagators of a Feynman diagram is identical with
, where the propagator
i and
j are contained in the lines
and
, respectively. The scalar current
of an electron propagator introduced in (
36) is expressed using
as
The denominator function
V is given by
where
For
, we find
U,
in terms of Feynman parameters as
and for
,
It is easy to check that
U of (
58) and
G of (
37) with (
55) and (
59) are identical to those given in (
35).
Even for a higher order diagram, the construction of the loop matrix
is trivial. Once the loop matrix is formed, the building blocks of the Feynman parametric representation can be obtained. For instance, the loop matrix
of the tenth-order diagram
of
Figure 7 is found as
where the lines
are chosen as
and the closed circuits are numbered according to the lexicographical order of the contained photon propagators. With this matrix, Formulas (
52)–(
57) and (
43) lead to all necessary building blocks.
4.4. Integration over Loop Momenta
We perform integration over diagonalized loop momenta. In our formulation, this can be done by two steps, by which the loop momenta
appearing in (
36) should turn into “contractions”.
Firstly, all
’s in the numerator are replaced by the correlation functions. If a term of the numerator contains an odd number of
’s, it is dismissed after integration. Up to the sixth-order diagrams, the numerator contains 0, 2, or 4
’s. Therefore, the contraction rules of two
’s needed are
where the coefficient 4 represents the space-time dimension. The extension to the eighth- or tenth-order diagrams is straightforward.
Secondly, the powers of
V are changed according to the number of contractions of
’s. As is seen in (
47), the inverse power of
V starts with either
n or
. If the numerator originally contains
’s and is produced by
m contractions of
’s, the denominators change from
or
to
After applying the whole contraction procedures, the amplitude of the anomalous magnetic moment from the self-energy-like diagram
can be written in terms of the Feynman parameters as
For
, the unrenormalized amplitude
thus has the form:
and the explicit forms of the numerator functions are found to be
For
, the formal expression of the amplitude is the same as (
67). Because
for
, the numerator functions are much shorter and are given by
4.5. UV Renormalization by -Operation
Let us focus on the structure of UV divergence of an unrenormalized amplitude . Though the amplitude originates from a self-energy diagram, it does not suffer from an overall divergence associated with this -order self-energy diagram. This is because its UV divergence is dropped when the anomalous magnetic moment contribution is projected out from it. UV divergences of come from subdiagrams of a self-energy diagram , either self-energy or vertex, of a lower order than the .
As is discussed in
Section 3, the renormalization procedure we have to use is the on-shell renormalization condition. However, the on-shell renormalization is not suitable for numerical calculation of a Feynman integral. If we perform the on-shell renormalization for an unrenormalized amplitude, UV divergence can be canceled, but it brings new types of IR divergence into the integral. We, therefore, carry out the renormalization in two steps.
Our UV subtraction method is named as the
-operation, which is realized in practice as a simple power-counting rule. The form of a UV subtraction term is picked up by applying the
-operation to the unrenormalized amplitude of (
66), which is expressed with the auxiliary functions
U,
V,
,
, and
. The
-operation is also applied to these auxiliary functions. The resultant integral is written in the same Feynman parameter space of the unrenormalized amplitude, and point-wise UV subtraction is realized. With a little algebra on the Feynman parameters, the resultant integral for UV subtraction exactly decouples into the renormalization constant determined and the lower-order magnetic moment amplitude. This renormalization constant contains the same UV divergence of the on-shell renormalization constant, but it is free from IR divergence, unlike the on-shell one.
Let us examine the fourth-order cases. The diagram has a second-order vertex subdiagram consisting of the electron propagators 1 and 2 and the photon propagator a. To extract the UV divergent terms associated with this subdiagram, the -operation is applied to . The -operation in the Feynman parametric space is equivalent to taking the simultaneous limit of vanishing Feynman parameters of , , and , which form .
The
-operation on
and
U reflects the decoupling of subdiagram
and residual diagram
as
With these building blocks,
,
V, and
G can be formally written in the same form as (
55) and (
56).
We also need to apply the
-operation to the amplitude expression (
67). Among many terms of the numerator, only the terms explicitly proportional to
can survive. It is obvious if we recall that
is a Feynman parametric representation of the product of two loop momenta flowing in
. From (
67) and (
68), the
-operated amplitude becomes
After a little algebra on the integration variables of the Feynman parameters, the amplitude exactly decouples to lower order quantities as
where
is the term including the UV divergence of the second-order vertex renormalization constant
. The numbers in the parenthesis of
and
in (
72) indicate which electron propagators of the original diagram
are involved in them. The
is determined as the leading divergent component of
, and thus the remainder
, as well, such that
Note that
is completely free from UV divergence, but is IR divergent.
in (
72) is exactly the second-order anomalous magnetic moment and gives the Schwinger term
.
The diagram
has a second-order self-energy diagram
as a UV divergent subdiagram. The
-operated building blocks are
,
V, and
G are obtained in the same form of (
55) and (
56) with these building blocks.
Since the subdiagram
contains one electron propagator and no contraction occurs within
, the
-operated amplitude formally has the same form of
:
The numerator functions are obtained from (
69) by letting
and
. In addition to them,
and
in (
69) must be replaced by
and
, respectively. The latter part of the
-operation comes from the procedure of the wave-function renormalization. The numerator
of the self-energy diagram
is given by
The mass and wave-function renormalizations require that the term sandwiched between
and
of
is replaced by the mass and wave-function renormalization terms:
where
is the momentum flowing on the electron propagator adjacent to the self-energy diagram
and
and
are the mass and wave-function renormalization constants of the second-order. The replacement rules for the numerator functions by the
-operation:
are the consequence of multiplication of the adjacent momentum in front of the wave-function renormalization constant. For the
-operation of the higher order self-energy diagram, replacement rules are not so simple, but can be managed by changing the definition of
V and
slightly. Readers may consult [
8,
9,
10].
After change of variables and integration by parts, we find
where
is the second-order magnetic moment to which a two-point vertex is inserted and
is the UV divergent part of
:
Note that
is free from UV divergence.
4.6. Forest Formula
To extend the
-operation procedure for the UV renormalization to a higher order diagram, we need to handle multiple divergences occurring from many subdiagrams contained in it. Let us first list all divergent subdiagrams in a given self-energy diagram. For instance, the tenth-order self-energy diagram
shown in
Figure 7 has five UV divergent subdiagrams: three subdiagrams of a self-energy type,
, and
, and two subdiagrams of a vertex type,
and
. The
-operation renormalized amplitude of
is
formally given by
where the electron line numbers of the
-operation are shown as its subscripts to compactify the notation. To construct the UV subtraction terms, the product (
81) must be expanded, and the order of multiple
-operations must be changed according to the diagrammatic relations of subdiagrams.
The relation of subdiagrams and can be classified into three cases:
disjoint:
and do not share an electron propagator.
The operation exists, and and are commutable.
inclusion:
All electron propagators of are also components of .
The operation exists, and and are not commutable. must be applied first, and then, .
overlapping:
and partially share the same electron propagators.
The operations and are null.
Expanding the product (
81), we find that 23 UV subtraction terms are needed to make
free from UV divergence [
59]:
Note that this is a simple realization of Zimmermann’s forest formula [
59].
For instance, we can write down the fourth-order amplitudes free from UV divergences:
The term corresponding to
is not present, because the relationship between
and
of
is overlapping. The
-operation renormalized amplitude
is finite. Since the
-operation acts on the integrand, not on the integral, pointwise UV subtraction is realized in the Feynman parameter space. Thus,
is ready to go to numerical evaluation. We call it the finite amplitude and denote it as
without a prime. The amplitude
is also free from UV divergence. However, it still suffers from IR divergence. We need to remove it using a pointwise subtraction method.
4.7. IR Divergence
There are two kinds of origins of IR divergence arising in the unrenormalized magnetic moment amplitude
. Both are related to a self-energy subdiagram, but it is not the direct source of IR divergence. Suppose a self-energy-like diagram
has a self-energy subdiagram
. When the adjacent electron propagators of
become almost on-the-mass-shell, the residual diagram
yields IR divergence. Because we use the Ward–Takahashi sum for the magnetic moment amplitude, the self-energy subdiagram
may have two properties, either the self-mass
or the magnetic moment
[
11].
When the subdiagram behaves as a self-mass , the residual diagram is a magnetic moment amplitude with an insertion of a two-point vertex . This additional vertex increases the number of electron propagators and makes the IR behavior of the amplitude worse than the case without the insertion .
To avoid the IR divergence of this kind, we need to complete the mass renormalization with the on-shell condition. The UV divergent part of
has been already subtracted by the
-operation. To subtract the remaining part of the self-mass contribution, we introduce a new procedure, the residual mass renormalization
such that
where
When the subdiagram
yields the magnetic moment
, the IR behavior of the residual diagram
is similar to that of the vertex renormalization constant
that is obtained by replacing
by an electron-photon vertex. Thus, we introduce one more procedure, the
-subtraction, such that
where
The UV divergences arising in the IR subtraction terms (
85) and (
87) are removed by using the
-operation renormalization. Decoupled products of (
85) and (
87) are merged into the same Feynman parametric space of
by applying the technique to derive (
72) or (
79) inversely.
All IR divergences of the magnetic moment amplitude can be removed by the above two IR subtractions. For nested IR divergences appearing in a higher order diagram, we prepare the annotated forest formula and apply the - and/or -subtractions as needed. There are two types of relations between two self-energy subdiagrams and . Namely,
disjoint:
- (a)
One of the ’s is a magnetic moment, and another is a self-mass: .
- (b)
Both are self-masses: .
- (c)
Two ’s cannot simultaneously become magnetic moments: No double -subtractions.
inclusion:
- (a)
If is a magnetic moment, cannot be a self-mass: .
- (b)
Both S’s are self-masses: .
- (c)
is a self-mass, and is a magnetic moment: .
As an example, let us construct the IR subtraction terms for the tenth-order diagram
shown in
Figure 7. There are three self-energy subdiagrams
,
, and
. Because
in our definition, the residual mass renormalization for
is not needed. We find
The IR-subtraction terms for the unrenormalized amplitude
are produced first by using the multiple
and/or
-subtractions. Then, the UV divergences of these IR-subtraction terms are removed by using the
-operation described in
Section 4.5 and
Section 4.6. The latter part of the construction of the IR-subtraction terms is symbolically written as the application of
- and/or
-operations to the UV-free amplitude
.
In a similar fashion, we apply the
- and
-subtractions to
, and the finite amplitude
is obtained as
This is ready to go to numerical calculation. In fact, because of our definition of the
-operation, we have
and
. This simplifies the calculation of the physical contribution of
, especially for the higher order terms.
4.8. Residual Renormalization
The UV renormalization we have employed is not the standard on-shell renormalization. In addition, the
-operation renormalization, which is a simple power counting rule of contractions and Feynman parameters, violates the Ward–Takahashi identity between the renormalization constants:
We also artificially added IR subtraction terms in order to make the amplitude numerically calculable on a computer. The residual and finite renormalization procedure is to be introduced to obtain the physical contribution to
from the numerically-calculated finite amplitudes. During this process, the violation of the Ward–Takahashi identity of the renormalization constants is fixed. Then, the gauge invariance of the physical contribution to
is guaranteed. It is also used to check the IR cancellation in the physical contribution to
as stated by the Kinoshita–Lee–Nauenberg theorem [
57,
60].
Let us explicitly work out the fourth-order case. The standard renormalization procedure for the diagrams
and
can be expressed by using the finite amplitudes given in (
83) and (
90). We find
Thus, the physical contribution from the gauge-invariant set of the fourth-order becomes
where
is guaranteed to be finite because of the Ward–Takahashi identity. Thus, all three terms in the right-hand-side of (
94) are finite, and the physical contribution
is free from IR divergences. After numerical integration, the finite quantities in (
94) are found:
and we obtain
which is in agreement with the analytic result
.
As you can see from the derivation of it, an explicit recipe of the
-operation is not essential to derive the finite formula (
94). The on-shell mass renormalization is mandatory to make an integral free from IR divergence and available for numerical calculation. However, the separation of UV and residual terms of the vertex and wave-function renormalization constants can be arbitrary and is not necessarily the
-operation. For instance, S. Volkov used the separation such that the Ward–Takahashi identity holds [
15,
61]:
where
indicates that the electron-photon vertex is inserted in the electron propagator
i of the self-energy diagram
S and the sum is taken over all electron propagators of
S. Thus, no residual renormalization is required. In [
15,
61], this method is applied to numerical calculation of the eighth-order vertex diagrams without a fermion loop. The result is consistent with the previous numerical calculation formulated by using the
-operation [
39] and also the analytic calculation [
26].
5. Higher Order Calculation
For the higher order diagrams without a fermion loop, we have applied the same process described in
Section 4 to calculate the contributions to
. Because of the complexity and length of finite integrals of the higher orders, especially of the tenth-order, we automated many of the procedures described in
Section 4 [
10,
11].
The automatic code generator of the integrand of a given self-energy-like diagram without a fermion loop is called
gencodeN. It is applicable to any order self-energy-like diagrams up to tenth-order and is extendable to even higher orders. From one-line information representing a self-energy diagram
of the
-order, it generates the integrand of the finite amplitude
as a set of
FORTRAN programs. It can be numerically evaluated with multi-dimensional integration algorithm, such as VEGAS [
62]. The workflow of
gencodeN is the following:
The one-line input of self-energy-like diagrams
is given. It is a sequence of the names of photons attached to the electron propagators from left to right. For example, the tenth-order diagram
of
Figure 7 is represented by “
.”
The integrand of the unrenormalized magnetic amplitude is determined. More precisely, the numerator functions , and are determined in terms of the building blocks and the scalar currents.
The building blocks ’s and U are determined in terms of the Feynman parameters from the topology of .
The forest formula for UV divergences of is constructed. UV subtraction terms are then generated in terms of the building blocks.
The UV limit of the building blocks and U is taken for each UV subtraction term.
The annotated forest formula for IR divergences of is constructed. IR subtraction terms are then generated. The building blocks ’s and U of the UV subtraction terms that show the same decoupling of the subdiagrams are borrowed and used.
The integrand of the finite amplitude is constructed combining together all of the above.
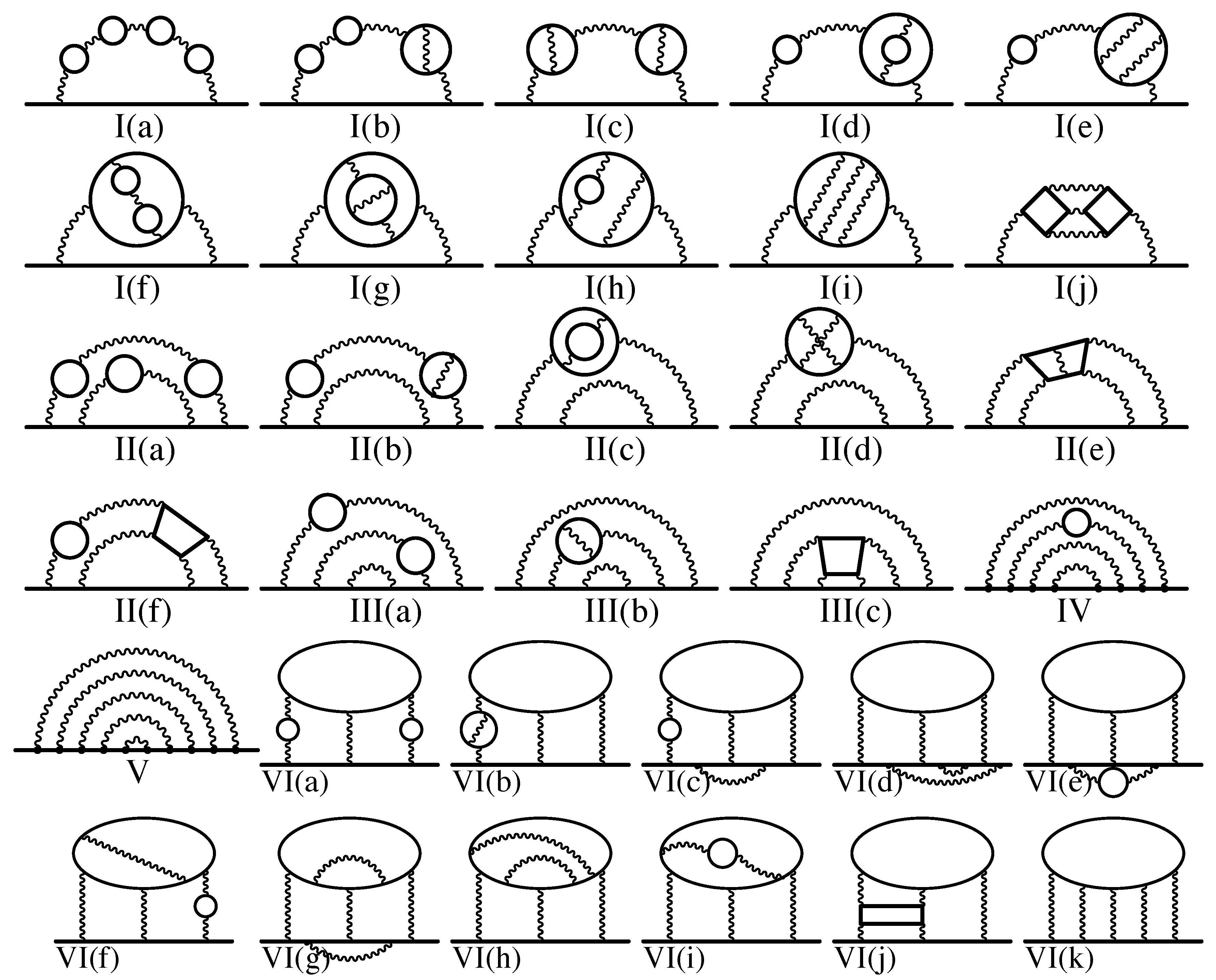
The 6354 vertex diagrams of Set V of the tenth-order as shown in
Figure 5 can be reduced to 389 self-energy-like subdiagrams. The 389 integrands, each consisting of about 100,000 lines of
FORTRAN code, are generated by
gencodeN running on a personal computer. While numerical integration of the 389 finite amplitudes of
are being carried out on supercomputers, the residual renormalization formula of the
-order is derived from the symbolic manipulation like (
94). Neither numerical calculation, nor difficult algebraic calculation are needed at this stage. For the tenth-order case, we obtain
The finite integrals
,
,
are obtained from the magnetic moment amplitudes, the sum of vertex and wave-function renormalization constants, and the mass renormalization constants, respectively, of the
-order diagrams without a fermion loop. An asterisk (∗) indicates that the quantity can be derived from diagrams having a two-point vertex insertion. For instance,
is the sum of finite parts of 24 diagrams, which are fourth-order vertices with a two-point vertex in one of four electron propagators. Some quantities appearing in (
99) are identical with those used in the lower order calculations such as the sixth- and eighth-order contributions. Agreement between the analytic results and the numerical results obtained by using these quantities is indirect, but strong evidence that they are correct.
Newly-evaluated ones specifically for the tenth-order are
,
, and
. The sixth- and fourth-order quantities are easily calculated. For
, we prepared another code generator
gencodeLBN similar to
gencodeN by changing projection operators. The 47 integrals for
were then numerically evaluated. The numerical values of all finite integrals in (
99) are listed in
Table 3. Many of them are borrowed from [
40]. The tenth-order finite magnetic moment amplitude is updated in this work as
in units of
. The factor two of each time-reversal-symmetric diagram is included in the numerical value of
. The improvement of the numerical value of
leads to a new tenth-order contribution
of (
8).