Abstract
Vibrational overtones in deeply-bound molecules are sensitive probes for variation of the proton-to-electron mass ratio . In nonpolar molecules, these overtones may be driven as two-photon transitions. Here, we present procedures for experiments with , including state-preparation through photoionization, a two-photon probe, and detection. We calculate transition dipole moments between all vibrational levels and those of the excited electronic state. Using these dipole moments, we calculate two-photon transition rates and AC-Stark-shift systematics for the overtones. We estimate other systematic effects and statistical precision. Two-photon vibrational transitions in provide multiple routes to improved searches for variation.
1. Introduction
Even simple molecules contain a rich set of internal degrees of freedom. When these internal states are controlled at the quantum level, they have many applications in fundamental physics [1,2] such as searches for new forces [3], the investigation of parity [4,5] and time-reversal [6,7] symmetries, or searches for time-variation of fundamental constants [8,9,10]. Experiments with molecular ions [6,11,12,13,14] are already at the forefront of these scientific questions, taking advantage of the long interrogation times allowed in trapped systems.
Because some degrees of freedom involve the motion of the nuclei themselves, molecules possess the potential to probe for changes in the proton mass relative to the electron mass. This mass ratio, , is predicted to change over time by several extensions to the standard model. Some models of quantum gravity include extra spatial dimensions or new scalar fields and suggest a drift in on cosmological timescales and continuing to the present day [15,16]. Ultralight dark matter could cause to oscillate at a frequency set by the mass of the dark matter particle [17,18]; topological dark matter could cause transient changes in [19]. Models typically predict that variation in should be approximately 40-times larger than corresponding changes in the fine structure constant [15].
Current limits on present-day variation in come from atomic clock experiments and find that [20]. The sensitivity to in these experiments is through the hyperfine structure of cesium. Linking the hyperfine frequency to the nuclear mass requires a model of the cesium nuclear magnetic moment [21]. The reliance on cesium clocks also means that atomic techniques are nearing their feasible limits, as the cesium microwave clock has been surpassed in stability by optical atomic clocks [22]. These optical clocks are based on electronic—not hyperfine—transitions, so they have little sensitivity to variation.
The vibration and rotation of molecules provide a model-independent means to search for variation in [8,9,10,23,24,25]. The current limit for a molecular experiment is , which is based on a rovibrational transition in SF and was conducted in a molecular beam [26]. Several proposals exist for next-generation searches in diatomic molecules [23,24,25,27,28,29,30,31,32,33,34]. In this manuscript, we provide additional support for the use of the molecule [31,32] in such a search. Much of the rationale for also applies to the isotopologue ; however, its higher mass changes the vibrational and rotational constants, so the particular values for the quantities we present would be different. We focus on the isotope because of its high natural abundance of 99.76%. The heteronuclear molecule is polar and would not have the advantages of a nonpolar molecule, such as intrinsic suppression of electric-field-related systematic effects.
Searches for a change in usually involve monitoring the energy difference between two energies with different dependence, . The fractional change in is then related to an absolute frequency shift through:
where we have defined the absolute sensitivity:
as the absolute frequency shift for a given fractional shift in . This quantity is sometimes called the absolute enhancement factor.
Both vibrational and rotational degrees of freedom have sensitivity to variation because both involve the nuclei moving. In general, vibrational sensitivity scales as and increases linearly with vibrational quantum number v. Rotational sensitivity scales as and increases as . Anharmonicity and centrifugal distortion reduce the sensitivity for higher vibrational or rotational states [35,36,37]. In general, vibrational transitions provide a favorable route to measure . They typically have much higher absolute frequencies compared to rotational transitions. Rotational changes are also constrained by selection rules to small , whereas it is possible to drive vibrational overtones with large .
The molecule is homonuclear and thus intrinsically nonpolar. Nuclear symmetry eliminates half the rotational states in any electronic manifold. The nuclei of are spin-zero, such that its ground state has only symmetric rotation states (see for example [35], Section V2c). The absence of opposite-parity states forbids electric-dipole () transitions between vibrational or rotational levels within the same electronic state. This absence suppresses many electric-field-related systematic effects without the need to average over multiple transitions [33,38]. However, this means that any transition between vibrational states within requires some higher-order process.
One option would be to use the electric quadrupole () coupling between states. The transition has been observed in the N nonpolar molecular ion [12]. Quadrupolar overtone transitions in have been proposed [32]. However, direct driving of such transitions is hampered by the very small quadrupole moments for large .
Alternatively, electric-dipole coupling to other excited electronic states provides a mechanism for driving two-photon transitions [28,30,39,40]. In this manuscript, we lay out potential experiments using such two-photon vibrational overtones. We calculate transition rates and systematic shifts for these experiments using existing spectroscopic data [41,42,43]. Many of these overtones are accessible with conventional laser technology. We find that the systematics for these experiments allow matching the molecular limit [26] in a trapped ensemble of multiple molecular ions. With fewer ions and a quantum-logic scheme, the system is capable of measurements several orders of magnitude below the present best limit.
2. Experimental Procedures
Despite the appealing properties of the two-photon transitions between vibrational states, there are experimental challenges with state preparation and detection. Because is nonpolar and has non-diagonal Franck–Condon factors, it is not amenable to state preparation by optical pumping [44,45,46]. For large numbers of molecules, as might be appropriate in preliminary investigations, one can create state-selected ions through photoionization. Detection of a transition can proceed by state-selective dissociation followed by analysis of the mass of the remaining ions. For small numbers of molecules, as might be appropriate in high-precision cases, one could pump and project molecules into an initial state by use of an auxiliary atomic ion and quantum control techniques [47]. Non-destructive detection could also rely on quantum logic [47,48,49,50].
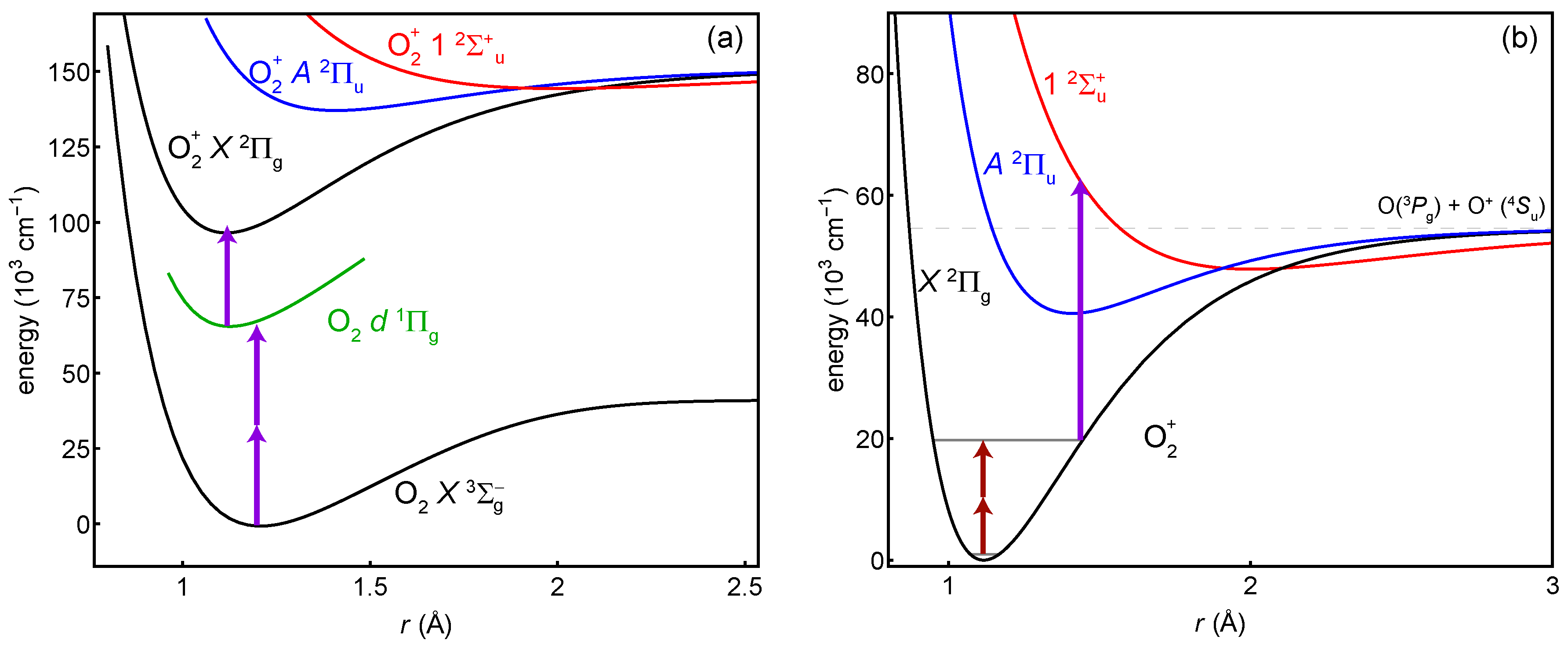
Here, we focus on spectroscopy procedures that are not limited in the number of ions probed. They are general enough to be used in a beam or trap. A trap with co-trapped atomic ions for cooling will be necessary for tests of variation, but initial measurements in a beam could begin narrowing the uncertainties in the transition frequencies. An overview of the procedure is shown in Figure 1. It takes place in three parts: (1) photoionization assisted by a resonance with a Rydberg state in the neutral (Figure 1a), (2) the two-photon vibrational transition (Figure 1b), and (3) selective dissociation of the excited vibrational state followed by measurement of any remaining ions’ masses (Figure 1b). The plotted example is for , but the techniques are general to many .
Figure 1.
General scheme of the proposed experiments. (a) The ion is prepared in its ground vibrational state by photoionization through the neutral Rydberg state with (2 + 1) photons at 301 nm. (b) Two photons drive the vibrational overtone, which is the spectroscopy transition. One photon dissociates any molecules in the excited vibrational state. The overtone shown is .
2.1. State Preparation: Resonance-Enhanced Multi-Photon Ionization
The electronic ground state of is of Hund’s case (a) and has two fine-structure manifolds with electronic angular momentum quantum numbers and . For reasons discussed in Section 4, systematic effects are more favorable in the rotational state [32]. Thus, the initial state for any experiment should be .
Much of the data about the molecule has been obtained through single-photon photoionization [42,43,51,52,53] while observing the kinetic energy of the photoelectron. The required vacuum or extreme ultraviolet radiation has been generated from four-wave mixing in gases [51,52] or a synchrotron light source [42,43,53]. While ionization into the molecule’s ground state with one photon would be possible, the 103-nm wavelength is challenging to produce. In general, one-photon ionization into excited rovibrational states would not be possible because of the poor Franck–Condon overlap of the neutral and ionic electronic ground states.
Instead, one can use a bound-to-bound resonance [54] in neutral with a more conventional laser source to reduce the number of resulting ionic states. In particular, Rydberg excited states can have very high Franck–Condon overlap with the ionic ground state [55]. In , such resonance-enhanced multi-photon ionization (REMPI) schemes have achieved near perfect vibrational selectivity [56,57,58,59,60]. With REMPI, a single laser can excite a unique rotational level in the neutral Rydberg state, but the ion’s rotational distributions will be governed by angular momentum propensities for the bound-to-continuum transition. The addition of a second laser in REMPI can enhance ionization into the rotational ground state, as has been demonstrated in the N molecule [61,62].
The Rydberg state provides a suitable resonant state for photoionization. It lies 66,380.15 cm−1 above the neutral ground state [59], such that it can be excited by two 301-nm photons. We use a frequency-doubled pulsed dye laser (the dye is a mix of Rhodamine 610 and 640) to drive the transition. The transition has a linewidth of approximately 2 cm [55,59].
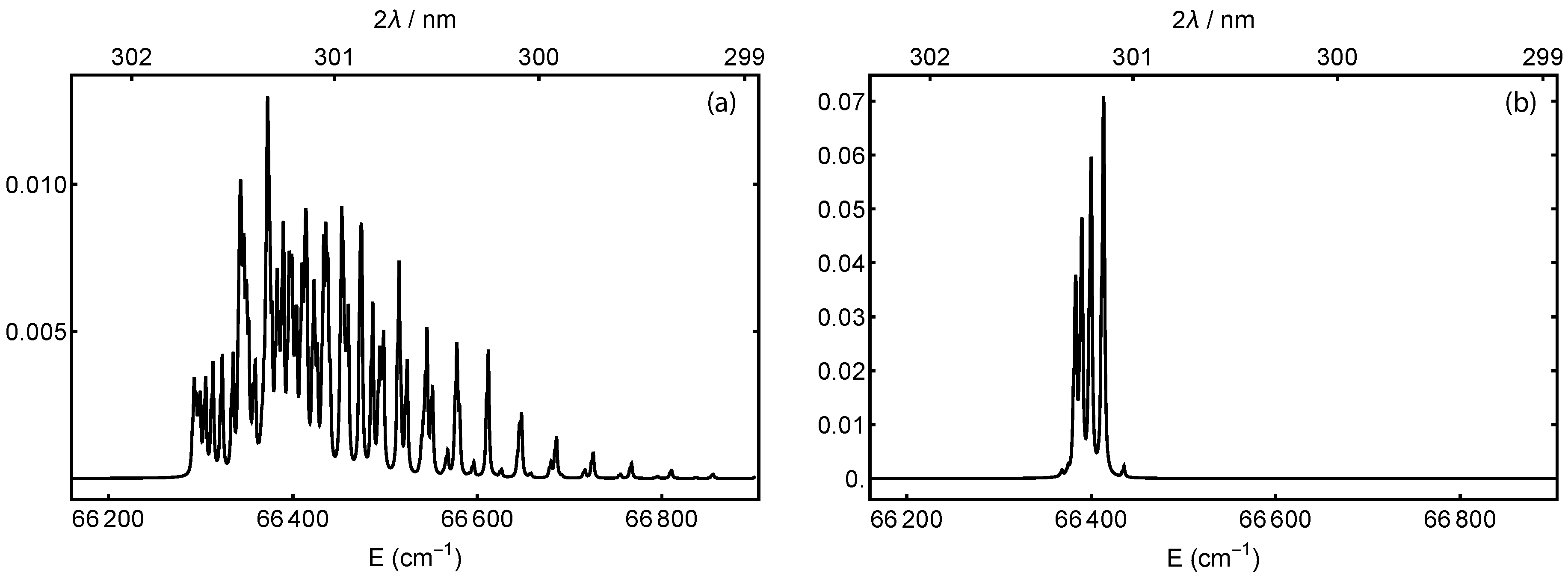
Figure 2 shows calculated excitation spectra for the transition, where the molecules remain in the ground vibrational state. The excitation has seven branches with . The work in [35], Equation V17, provides the fine-structure splitting and molecular constants for the triplet state. The O nuclei are spin-zero, such that only symmetric rotational states exist. For the ground state, these are the rotational states with odd-N ([35], Section V2c). The works in [55,59] provide the d-state constants. The figure includes two thermal initial rotational distributions [35]. Figure 2a is calculated at 300 K, which corresponds to an effusive beam or background gas. Because of the finite d-state linewidth, the peaks overlap such that a single laser frequency could excite to several different rotational states in d. Figure 2b is calculated at 5 K, which is an approximate temperature for a supersonically-expanded beam [59,63]. The lower temperature increases the population of the lower rotational states. Most of the remaining overlap comes from the triplet splitting of the ground state rather than any rotational difference in the Rydberg state.
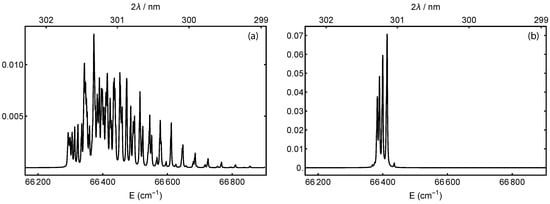
Figure 2.
Calculated two-photon excitation spectra from the neutral ground state to the Rydberg state, both in their ground vibrational state. The temperatures shown correspond to (a) an effusive beam at 300 K or (b) a supersonically-expanded one at 5 K. The traces are normalized such that the sum of all transitions is one; note the resulting scale change.
The ground state is 31,070 cm−1 above the state, such that a third photon from the 301-nm laser has sufficient energy to remove an electron. Although it also has enough energy to reach the first vibrationally-excited state of , the near diagonal Franck–Condon factors between the Rydberg and ionic states largely suppress any vibrational excitation. Ionization into the rotational state could be enhanced with a second laser of wavelength 323 nm, which would need to be tuned to have enough energy to ionize the molecule, but not enough to reach the state.
With only a single laser, the ionic rotational states are constrained by symmetry and angular momentum conservation [64,65]. Any change in the molecule’s angular momentum must come from one of three sources: the photoelectron with partial-wave orbital angular momentum l, the photoelectron’s spin of , or one unit of orbital angular momentum from the photon. The nature of the transition constrains l to be odd. The net orbital angular momentum transferred to the molecule can take values or . Including the photoelectron’s spin, the total angular momentum transferred to the molecule can take values or , such that the total angular momentum can change by . For example, orbital angular momentum transfers of or 2 would allow:
In general, many photoionization processes show a higher propensity for transitions with . Transitions with are somewhat less likely, and those with contribute very little. To say more about their relative probabilities in the transition would require either calculations with a model of the molecules’ orbitals or measurements of the relative strengths of each rotational transition.
The four prominent peaks in the low-temperature distribution of Figure 2b are excitations from to , in order from lowest to highest energy. The states can ionize into our target state with a transition. The state would require . The resonance for is 66,383.5 cm−1, which is two 301.280-nm photons. For , it is 66,390.2 cm−1, which is two 301.249-nm photons. In both cases, the peak is three overlapping transitions from the neutral’s triplet ground state and is broader to the low-energy side.
Photoionization is a useful state preparation technique for any number of molecular ions. With a single photoionization laser, some molecules will be in the wrong J state. For multiple-ion experiments, this simply eats into the signal. For single-ion experiments, one could reload the molecule until the state is achieved or could manipulate the rotational states with a quantum-projection scheme. The 50-GHz rotation constant [41] means that and are 151 GHz away, so a broadband/femtosecond laser would be required [66,67].
2.2. Probe: Two-Photon Transition
The potential is 54,600 cm−1 deep with approximately 55 vibrational levels [42]. In principle, two-photon transitions can be driven from to any . The transition frequency (for example, in hertz) for the vibrational overtone is:
Analysis of emission spectra [41] gives values for , including high-precision fine-structure and rotational constants, for . Pulsed-field-ionization photoelectron (PFI-PE) studies [42] give vibrational, fine-structure, and rotational constants up to . Uncertainties on the vibrational energies range from 1–150 GHz. Since all electric-dipole transitions within are forbidden, the two-photon transition is intrinsically narrow, with linewidths limited by the probe laser.
Driving the overtone will require a laser of wavelength . These wavelengths range from () to 418 () and beyond. Table 1 provides a list. The table also calculates the sensitivity to -variation , which grows linearly for low and peaks at .

Table 1.
Table of two-photon-transition information: the wavelength required to drive the transition, the absolute sensitivity of the transition to variation, estimates of photodissociation wavelength , and the calculated results for transition rates and electric-dipole-related systematics. These results are listed as the two-photon Rabi frequency (in terms of intensity I), the probe laser AC Stark shift (in terms of intensity and of Rabi frequency), the AC Stark shift from the trapping field (in terms of the mean-squared electric field), and the blackbody radiation shift at 300 K. The frequency shifts are normalized by the magnitude of the absolute sensitivity , so the numbers represent relative accuracy in , and the signs reflect the actual frequency shift.
Searches for drifts in consist of monitoring the transition frequency multiple times for a reasonable duration such as a year. Because the probe laser’s coherence time will be much less than a year, a second signal with different will be required, such as from an optical atomic clock or a second transition in (see Section 5.2). Fourier analysis of the measurements can probe for oscillations in with periods longer than twice the probe time. Sensitivity at shorter periods can be enhanced by use of dynamical decoupling pulse sequences ([68], Section VI). In such multipulse sensing sequences, the timing of pulses defines a filter in frequency space. By varying the timing, one can search at different oscillation frequencies.
2.3. Detection: Selective Dissociation
Detection of a successful transition to could be done by selective dissociation of that state [69,70,71,72] or energy-dependent chemical reaction such as charge transfer with a background gas [61,73], followed by observation of ion loss or the mass of any remaining ions. These are destructive and thus suitable for experiments with large numbers of ions, where the increased statistics justifies the experiment down time for reloading. For few- or single-ion experiments, as will be required at the highest precision, the more complex quantum-logic techniques [47,48,49,50] will be preferable.
The molecule has a relatively shallow bound state [41,74,75,76] that appears suitable for dissociation to . Its potential minimum is offset relative to such that many vibrational states have a good overlap with dissociating states.
Table 1 has a list of estimated dissociation laser wavelengths as a function of . This somewhat naive list simply finds the energy difference between the outer turning point of the potential and the inner turning point of . For the X potential, we use our own calculation (see Section 3.1); for the potential, we use a Morse approximation [35] based on coefficients in [76]. Photodissociation cross-sections are generally not so sensitive to wavelength, so other wavelengths should work as well. Figure 1b shows an example of the 238-nm dissociation of . For states with , the inner turning point of corresponds to a bound state, so a more in-depth look at photodissociation cross-sections—or a different detection scheme or dissociating state—is warranted.
The presence of atomic oxygen ions would thus signify a successful two-photon probe transition. The factor of two mass difference between and should be easy to resolve. In a radio frequency trap, the charge-to-mass ratio of the ions can be determined by their spatial distribution [61,77] (lighter ions are trapped more deeply) or by resonantly exciting the mass-dependent radial trap frequency [45,78,79]. Alternatively, ions in free space (either a beam or a rapidly-quenched trap) can be accelerated into a time-of-flight mass spectrometer [71,80,81,82,83]. Since the dissociation is itself destructive, the loss of the ions in the time-of-flight technique is not a concern. It is also fast and has a high signal-to-noise.
3. Transition Rates and Electric-Dipole-Related Systematics
The two-photon spectroscopy transition is enabled by electric-dipole coupling to excited electronic states. This coupling also creates a mechanism for systematic shifts from the driving laser, trapping field, and blackbody radiation. We estimate these rates and shifts by assuming the coupling is primarily through the state, which is the lowest energy state with the same spin multiplicity as the state. The large detuning of this state (the lowest vibrational states of X and A are 40,070 cm−1 = 1.20 PHz/c apart [41,42,43]) suppresses these systematic effects, but also increases the laser intensity required for the two-photon transition. We do not include other excited states because they have either a much larger detuning, much smaller Franck–Condon overlap (for example, the state), a different spin multiplicity (for example, the state), or the wrong center-of-inversion symmetry (g/u). We also neglect continuum transitions.
3.1. Calculating the Transition Dipole Moments
The perturbation-theory calculations for transition rates and systematic frequency shifts require electric dipole moments and energy differences between X and A vibrational states. The transition dipole moment between the states and is given by:
where d is the sum of all the charges’ electric dipole moments. We ignore rotation and fine-structure in this calculation. These splittings are of order 1 cm−1 for vibrational levels in the state [41,43] such that any change in the detuning is negligible. The calculations below involve sums over states, and the sum over the rotational and fine-structure states is effectively the identity.
We can separate the electronic and vibrational contributions [35,84] and write the transition dipole moment in terms of the vibrational wavefunctions, internuclear distance r, and the electronic transition dipole moment :
In general, is a function of the internuclear distance. In most cases, including here, this function varies slowly, and we may replace it with a constant evaluated at the r-centroid [35,84,85]:
The resulting transition dipole moment is given by:
The wavefunction-overlap integral in Equation (8) is the square-root of the Franck–Condon factor. Importantly—and unlike the Franck–Condon factor—it is a signed quantity that can interfere in a sum over vibrational states.
Calculated tables of X to A transition dipole moments and energies exist [85]; however, they only tabulate values up to the 21st vibrational state in each potential well. For some two-photon transitions, we found that contributions from higher-lying vibrational levels in the A potential were needed. We therefore calculated the terms ourselves.
As no recent experimental potentials were available, we performed our own Rydberg–Klein–Rees (RKR) calculation using the RKR1 2.0 program [86] with data from [42,43]. The state RKR, using the first 39 levels, was performed using a Dunham expansion to 19 terms in and . The state RKR, using the first 13 levels, was performed with a Dunham expansion to 11 terms in and seven terms in . The resulting potential for the A state was extended to long range by fitting for , , and coefficients using the last five RKR points. Using these potentials, the vibrational state energies and wavefunctions were generated using the program LEVEL 8.2 [87] with 0.001 angstrom resolution. Root-mean-squared residuals for the energies were 4 cm−1 for X and 3 cm−1 for A; all residuals were less than 10 cm−1. We then numerically calculated the wavefunction overlap integrals and r-centroids. We calculated the electronic transition dipole moment in the r-centroid approximation using the fit to theoretical values of found in [85].
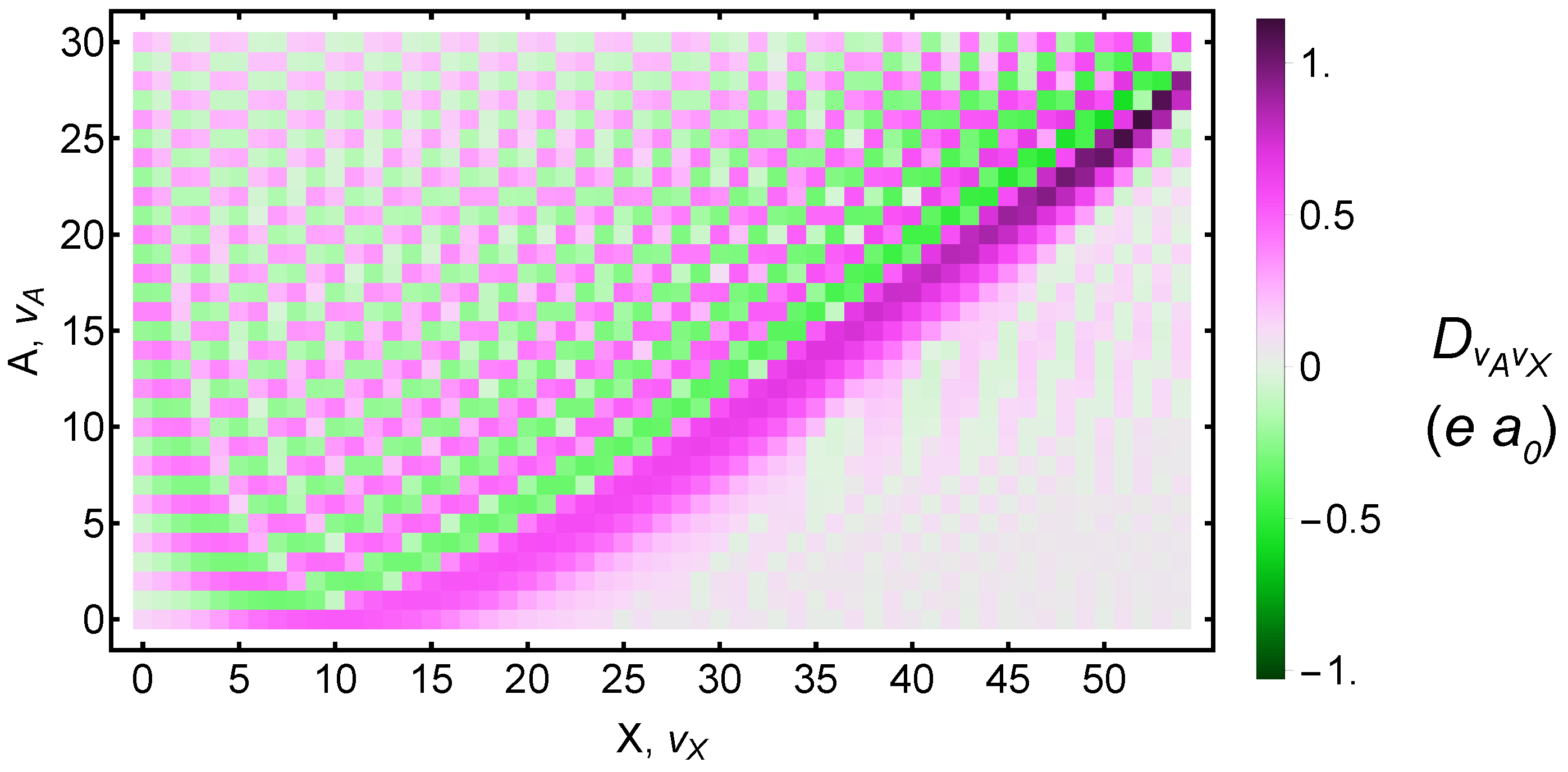
Figure 3 shows the transition dipole moment between each X and A vibrational state. In the Supplementary Materials accompanying this manuscript, we provide our RKR potentials; wavefunctions, energies, and rotational constants for 55 vibrational states within X and 31 states within A; as well as overlap integrals, energy differences, and transition dipole moments for all pairs of vibrational states.
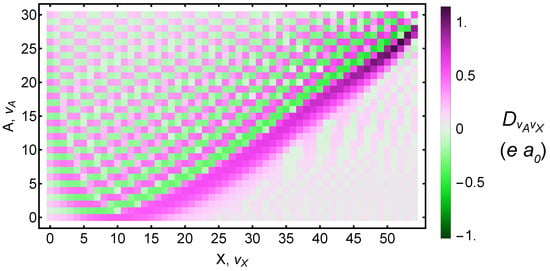
Figure 3.
Calculated transition dipole moments between and vibrational states. Both the electronic and vibrational contributions are included. Dipole moments are given in atomic units. Numeric values are available in the Supplementary Materials.
3.2. Transition Rate
The two-photon transition rate for the transition, stated as a Rabi frequency, is:
Here,
is the transition frequency (for example, in hertz) between the A and X vibrational states, is the laser frequency, which on resonance is or half the vibrational overtone frequency, and I is the laser intensity. The Rabi frequency is an angular frequency, but we state our results in terms of the actual frequency .
The signs of the dipole moments are important in the sum and cause the terms to interfere with each other. Some other references, such as [85], did not include the signs in their tables.
Table 1 lists the Rabi frequency in terms of laser intensity. It includes all two-photon transitions up to , which is the highest level for which spectroscopic data are available. Note that the potential overlaps with and the potential overlaps with . After accounting for fine-structure and rotational splittings, there may be some near-degeneracies among the X, A, and a states. These could provide alternate routes to -variation measurements [31]. For the purposes of the two-photon experiments, they could cause the eigenstates to mix such that new systematic effects creep in. Because both A and a states have ungerade symmetry, they should not mix with the gerade X state.
Achieving a reasonable transition probability requires either high intensity or long interrogation time. For example, a 1-W laser focused to a 150 waist has an intensity of . When resonant with the transition, that laser would produce a Rabi frequency of 1 Hz.
3.3. Stark Shifts
AC Stark shifts will be created by oscillating electric fields. Three main sources in this experiment are the probe laser itself, the trapping field of a radio frequency trap, and blackbody radiation. An electric field with the root-mean-squared (rms) value oscillating at frequency will shift the frequency of the state due to interactions with all vibrational states in :
The net shift on the overtone transition frequency is:
3.3.1. Probe Laser
For the probe laser, it is more useful to talk in terms of the intensity:
Both the Rabi frequency and AC Stark shift are proportional to the laser’s intensity, such that simple Rabi-style probes will have their Stark shifts increasing linearly with the transition rate. Table 1 lists the net AC Stark shift of the probe laser in terms of both the laser intensity and the transition Rabi frequency. In each case, we normalize the result by the absolute sensitivity (see Equation (2)) to show how it might affect a -variation measurement. We use the magnitude of to emphasize the sign of the shift on the actual frequency; the shift on is the opposite sign.
For the levels –23, the denominator in Equation (11) changes sign in the sum over . At the sign change, the denominator of one term can be considerably smaller than the others. It then dominates the sum and creates the non-monotonic behavior seen in the table. For example, the AC Stark shift of is dominated by the shift from . Although the probe laser’s detuning is still several terahertz, it is close enough to create the relatively large AC Stark shift.
The above example of a 1-W laser focused to 150 would produce a AC Stark shift on the transition. This is a fractional shift of in frequency and in . Thus, the probe laser’s AC Stark shift has the potential to be a major systematic effect. For lower-precision experiments with stable laser intensity, the Stark shift could be calibrated. Better would be to use a composite-pulse scheme such as hyper- and auto-balanced Ramsey spectroscopy [88,89,90,91]. Such schemes have suppressed AC Stark shifts by four orders of magnitude when used on the electric octupole () clock transition in Yb [90,92,93].
3.3.2. Trapping Fields
Experiments with longer probe times will require the ions to be held in place. In a radio frequency (rf) trap, the trapping field itself can produce an AC Stark shift. Since the rf trapping fields are much lower in frequency than any , we calculate the shift in the limit and tabulate the results in terms of in Table 1.
For a linear rf trap, the field is established by electrodes R away from the ions and oscillating at potentials . These produce an electric field [94]:
where is the mass-to-charge ratio of the trapped ion and are parameters in a Mathieu equation describing the ions’ motion (see for example [94,95]). These trapping parameters can be calibrated in place by use of the motional frequencies of the trapped ions. Typical values in our apparatus are and such that molecular ions would experience a field curvature of . Ions displaced 100 off the rf null—as might happen in a 3D crystal—would experience an electric field of . For the transition, this would lead to a shift of , which is a fractional shift of in frequency and in . As shown in Section 4.1, displacement off the rf null also produces a Doppler shift that is more of a concern.
3.3.3. Blackbody Radiation
The blackbody radiation (BBR) from the environment causes far off-resonant AC Stark shifts. To determine the shift of a given X-state vibrational level, we integrate over the continuous blackbody spectrum. At temperature T, the shift of level is given by [96,97]:
where:
The part of the integral is evaluated with the Cauchy principal value at the pole [96].
The net shift is calculated at 300 K and included in Table 1. At 300 K, the blackbody shift of the transition is , which is a fractional shift of in frequency and in . For other temperatures, the overall shift scales as [96]. For example, at 100 K, the shift would be -times smaller. For comparison, the Al and Lu atomic ions, which have the smallest blackbody shifts of any species in current or proposed atomic optical clocks, have room-temperature shifts [98] and [99]. Blackbody radiation will not be a major concern.
4. Additional Systematic Effects
4.1. Doppler Shifts
First-order Doppler shifts are highly suppressed when the ions are trapped [100]. Any possible first-order shift, such as the trap itself moving relative to the laser, can be monitored with counter-propagating probe beams [101]. Second-order Doppler shifts are a relativistic time-dilation effect. They arise from finite temperature and micromotion [94], which each cause a nonzero mean-squared velocity. The shift is equal to:
Co-trapped atomic ions can sympathetically cool the molecular motion to reduce any thermal Doppler shifts. For example, at the 0.5 mK theoretical Doppler-cooling limit of Be, the thermal motion has , such that the second-order Doppler shift would be ∼.
Excess micromotion, however, can produce significant shifts. A static electric field , for example from other ions or an uncompensated offset on the trap electrodes, can displace an ion off the trap’s rf null until balanced by the dynamic trapping field. When displaced to , the rf fields will drive the ion to have a velocity of [94], where and are the same Mathieu trap parameter and angular trap frequency used in Equation (14). This velocity gives a second-order Doppler shift [94] of:
For our typical parameters, the fractional frequency shift is or . An ion in a 3D crystal displaced 100 off the rf null would experience a fractional shift of in frequency and in . Here again, we have the potential for an important systematic effect. Any high-precision work will require ions to be close to the rf null with stray fields well compensated. For comparison, by use of sub-Doppler cooling in a well-compensated trap, an optical clock based on the ion (comparable in mass to ) has reduced the time-dilation frequency shift to [102].
4.2. Electric Quadrupole Shift
An electric quadrupole shift arises when a non-zero quadrupole electric field interacts with an electric quadrupole moment of the ion [103,104]. For example, Equation (14) shows that the ion trap itself produces a nonzero quadrupolar field. For an arbitrary molecular state , the shift scales as [103,104]. For states with or , the quadrupole moment is exactly zero, and so, the shift is also exactly zero. We thus choose to use the state in the manifold of .
4.3. Zeeman Shift
The diagonal matrix element for the Zeeman shift is [105,106]:
where B is the magnetic field, is the Bohr magneton, and and are the spin and orbital g-factors. For a state, . Since and is only a part-per-thousand larger than 2, the Zeeman shift in that state is suppressed by approximately . For , the shift would be 11 MHz /T (1.1 kHz /G). For transitions between the same (), the shift cancels. For transitions from to , the opposite transition could be probed and the two values averaged.
Higher-order Zeeman shifts from off-diagonal mixing with the fine-structure manifold should be largely suppressed because that manifold does not have a level. An intrinsic second-order Zeeman shift [107,108] arises from the Hamiltonian:
where the magnetic field is assumed to be in the z-direction. To estimate its size, if is of order the Bohr radius squared , then the shift should be of order Hz/T. A bias field of 1 mT would cause each energy level to shift around 15 mHz. Because the electronic state is unchanged, it is likely that the differential shift in the transition frequency would be much smaller.
Since the O nuclei are spin-zero, there are no Zeeman shifts from nuclear spin or hyperfine structure. Zeeman shifts of each energy level from nuclear rotation [32,109,110] are smaller by approximately . They should also largely cancel for transitions that do not change , J, and because the nuclear-rotation g factors should be comparable for the two vibrational states.
5. Prospects
5.1. Choice of State and Techniques
The molecule is amenable to many two-photon transitions, and there is not an obvious “best” choice. While the sensitivity increases to a maximum at , growing anharmonic effects make its sensitivity only 50% larger than that of . With a few exceptions like , the systematic effects are comparable. The growth of the blackbody shift is not a concern. For example, the shift at and 300 K means a temperature stability of only 1 K will provide an uncertainty on the BBR shift of .
The available laser technology should play a role. The 1063-nm wavelength for has multi-watt ytterbium-doped fiber amplifiers available. The transitions to are all within the range of a titanium-sapphire laser. Many transitions are available as diode lasers, some in tapered amplifiers. For dissociative detection, the UV lasers may be more challenging. For some species of co-trapped atomic ions, existing lasers could fill that role. For example, the 235-nm photoionization laser for Be is near the 238-nm wavelength to dissociate . Similarly, the 313 nm Be cooling laser could work for or 16 (323 nm or 351 nm). Lasers for Mg (280-nm cooling, 285-nm photoionization) would also work, but heavier ions’ wavelengths may be too long (for example, Ca at 397 nm). Since transitions to the continuum typically have smaller cross-sections than bound-to-bound transitions, pulsed lasers may be more appropriate. Actual calculations of photodissociation cross-sections would help in experimental preparations.
Of the systematic effects, the time-dilation and probe-laser AC Stark shifts pose the largest concerns. To achieve the ultimate accuracy will require a very well-compensated trap. Early experiments, however, need not have particularly good trap compensation or even confine the ions near the rf null. For example, the existing molecular-beam accuracy () could be matched with ions in a 3D crystal with approximately 45 radius (for our typical trap parameters above). Even achieving only requires compensation that keeps , which is straightforward in larger traps.
The AC Stark shift of the probe laser will typically be much larger than the target accuracy and thus must be compensated. For example, with for the transition, the probe light shift is in frequency and in . For a target accuracy of , this shift can be calibrated and the optical power kept stable to better than 2%. Reducing the Rabi frequency would reduce the shift, though it would require longer coherence times for the laser. Higher accuracy experiments should use a composite pulse sequence immune to the shift [88,89,90,91]. In [92], such a scheme yielded four orders of magnitude suppression of shifts of size and on the Yb octupole transition. Future work should evaluate whether these systematics-suppressing pulse sequences are compatible with dynamical-decoupling sequences [68] that would enable searches for faster oscillations in .
Because of the intrinsically narrow lines of these transitions, statistical uncertainty will average quickly to the systematic limits as long as the majority of the time can be spent probing the ions. In general, measuring N ions over time , where the linewidth is (for example in hertz) and the single probe time is , should yield a statistical uncertainty of [31]:
where we have assumed that the signal-to-noise is limited by quantum projection noise [111]. For example, with a 10-Hz linewidth, the transition could be measured with statistical precision .
In order to spend the majority of the time probing the ions, there is a trade-off in state preparation and detection schemes. Lower precision experiments that can use multiple ions in a 3D crystal can use the somewhat simpler, but destructive, dissociation and time-of-flight mass spectrometry detection scheme. Higher precision experiments in better-compensated traps will likely use quantum-logic detection schemes. Loading by REMPI is an efficient way to prepare the vibrational state of the ion. One-color REMPI uses one fewer laser, but at the expense of some ions in the wrong rotational state. This may be appropriate for multi-ion experiments, but at the cost of signal because not all molecules participate in the experiment. For fewer ions or higher efficiency, a second laser to enable REMPI will be preferred. With a quantum-logic detection scheme in place, it can also be used to prepare the initial state. Proposals exist to prepare different rotational states projectively [66,67], though an additional femtosecond laser would be required.
5.2. Reference Transitions
In order to detect any change in the transition frequency, and thus change in , measurements must be compared with a reference that has different . An obvious choice would be an optical atomic clock [22]. Because these are based on electronic transitions, they have very small . They are readily compared to the transitions by use of a frequency comb. It is possible that an atomic ion present in the same trap could provide the dual role of both clock and coolant/logic ion. Alternatively, a second transition in could be employed [112]. By the use of a co-trapped atomic ion or two optical transitions in the same molecule, both frequencies would be measured in the same electromagnetic environment, which could simplify evaluations of systematics. The cost of using for both frequencies is a smaller differential sensitivity to -variation.
For lower-precision experiments in the range, microwave or vapor-cell references would suffice. A frequency comb referred to either GPS or a local cesium clock could be used for any of the transitions. This was the approach taken with SF in [26]. Iodine vapor cells provide reference lines at room temperature for transitions to , with extensions to if the probe laser is doubled before the iodine cell [113]. Any sensitivity to variation in the microwave or vapor reference would need to be included in the net sensitivity. With the I vapor cell, most of the transition energy is an electronic transition from to , so is typically much smaller than in .
6. Conclusions
Two-photon vibrational transitions in provide multiple routes to improved searches for variation. We have presented experimental procedures capable of searching for with the highest precision achieved in molecules with prospects capable of improving current overall limits. The calculated transition dipole moments have allowed us to estimate the two-photon transition rates and electric-dipole-related systematic effects for each overtone. Additional systematic and statistical estimates show long-term promise at the level or better. Before embarking on a full time-variation experiment, additional spectroscopy is needed to reduce the transition uncertainties far below their current level of several gigahertz.
Supplementary Materials
The following are available online at http://www.mdpi.com/2218-2004/7/1/1/s1: RKR potentials; wavefunctions, energies, and rotational constants for 55 vibrational states within X and 31 states within A; overlap integrals, energy differences, and transition dipole moments for all pairs of vibrational states.
Author Contributions
A.F. conducted the formal analysis of the REMPI procedure. R.C. and D.H. conducted the formal analysis of the transition dipole moments. D.H. wrote the original draft. All authors participated in the formal analysis of experimental procedures and systematic effects as well as in reviewing and editing the manuscript.
Funding
This research was funded by the U.S. National Science Foundation Grants PHY-1255170 and PHY-1806223.
Conflicts of Interest
The authors declare no conflict of interest.
References
- DeMille, D.; Doyle, J.M.; Sushkov, A.O. Probing the frontiers of particle physics with tabletop-scale experiments. Science 2017, 357, 990–994. [Google Scholar] [CrossRef] [PubMed]
- Safronova, M.S.; Budker, D.; DeMille, D.; Jackson Kimball, D.F.; Derevianko, A.; Clark, C.W. Search for new physics with atoms and molecules. Rev. Mod. Phys. 2018, 90, 025008. [Google Scholar] [CrossRef]
- Salumbides, E.J.; Koelemeij, J.C.J.; Komasa, J.; Pachucki, K.; Eikema, K.S.E.; Ubachs, W. Bounds on fifth forces from precision measurements on molecules. Phys. Rev. D 2013, 87, 112008. [Google Scholar] [CrossRef]
- DeMille, D.; Cahn, S.B.; Murphree, D.; Rahmlow, D.A.; Kozlov, M.G. Using Molecules to Measure Nuclear Spin-Dependent Parity Violation. Phys. Rev. Lett. 2008, 100, 023003. [Google Scholar] [CrossRef]
- Quack, M.; Stohner, J.; Willeke, M. High-Resolution Spectroscopic Studies and Theory of Parity Violation in Chiral Molecules. Ann. Rev. Phys. Chem. 2008, 59, 741–769. [Google Scholar] [CrossRef] [PubMed]
- Cairncross, W.B.; Gresh, D.N.; Grau, M.; Cossel, K.C.; Roussy, T.S.; Ni, Y.; Zhou, Y.; Ye, J.; Cornell, E.A. Precision Measurement of the Electron’s Electric Dipole Moment Using Trapped Molecular Ions. Phys. Rev. Lett. 2017, 119, 153001. [Google Scholar] [CrossRef]
- ACME Collaboration; Andreev, V.; Ang, D.G.; DeMille, D.; Doyle, J.M.; Gabrielse, G.; Haefner, J.; Hutzler, N.R.; Lasner, Z.; Meisenhelder, C.; et al. Improved limit on the electric dipole moment of the electron. Nature 2018, 562, 355–360. [Google Scholar] [CrossRef]
- Carr, L.D.; DeMille, D.; Krems, R.V.; Ye, J. Cold and ultracold molecules: Science, technology, and applications. New J. Phys. 2009, 11, 055049. [Google Scholar] [CrossRef]
- Chin, C.; Flambaum, V.V.; Kozlov, M.G. Ultracold molecules: New probes on the variation of fundamental constants. New J. Phys. 2009, 11, 055048. [Google Scholar] [CrossRef]
- Jansen, P.; Bethlem, H.L.; Ubachs, W. Perspective: Tipping the scales: Search for drifting constants from molecular spectra. J. Chem. Phys. 2014, 140, 010901. [Google Scholar] [CrossRef]
- Bressel, U.; Borodin, A.; Shen, J.; Hansen, M.; Ernsting, I.; Schiller, S. Manipulation of Individual Hyperfine States in Cold Trapped Molecular Ions and Application to HD+ Frequency Metrology. Phys. Rev. Lett. 2012, 108, 183003. [Google Scholar] [CrossRef] [PubMed]
- Germann, M.; Tong, X.; Willitsch, S. Observation of electric-dipole-forbidden infrared transitions in cold molecular ions. Nat. Phys. 2014, 10, 820–824. [Google Scholar] [CrossRef]
- Biesheuvel, J.; Karr, J.; Hilico, L.; Eikema, K.S.E.; Ubachs, W.; Koelemeij, J.C.J. Probing QED and fundamental constants through laser spectroscopy of vibrational transitions in HD+. Nat. Commun. 2016, 7, 10385. [Google Scholar] [CrossRef] [PubMed]
- Calvin, A.T.; Brown, K.R. Spectroscopy of Molecular Ions in Coulomb Crystals. J. Phys. Chem. Lett. 2018, 9, 5797–5804. [Google Scholar] [CrossRef]
- Uzan, J.P. The fundamental constants and their variation: Observational and theoretical status. Rev. Mod. Phys. 2003, 75, 403–455. [Google Scholar] [CrossRef]
- Calmet, X.; Keller, M. Cosmological evolution of fundamental constants: From theory to experiment. Mod. Phys. Lett. A 2015, 30, 1540028. [Google Scholar] [CrossRef]
- Stadnik, Y.V.; Flambaum, V.V. Searching for Dark Matter and Variation of Fundamental Constants with Laser and Maser Interferometry. Phys. Rev. Lett. 2015, 114, 161301. [Google Scholar] [CrossRef]
- Arvanitaki, A.; Huang, J.; Van Tilburg, K. Searching for dilaton dark matter with atomic clocks. Phys. Rev. D 2015, 91, 015015. [Google Scholar] [CrossRef]
- Derevianko, A.; Pospelov, M. Hunting for topological dark matter with atomic clocks. Nat. Phys. 2014, 10, 933–936. [Google Scholar] [CrossRef]
- McGrew, W.F.; Zhang, X.; Leopardi, H.; Fasano, R.J.; Nicolodi, D.; Beloy, K.; Yao, J.; Sherman, J.A.; Schäffer, S.A.; Savory, J.; et al. Towards Adoption of an Optical Second: Verifying Optical Clocks at the SI Limit. arXiv, 2018; arXiv:1811.05885. [Google Scholar]
- Flambaum, V.V.; Tedesco, A.F. Dependence of nuclear magnetic moments on quark masses and limits on temporal variation of fundamental constants from atomic clock experiments. Phys. Rev. C 2006, 73, 055501. [Google Scholar] [CrossRef]
- Ludlow, A.D.; Boyd, M.M.; Ye, J.; Peik, E.; Schmidt, P.O. Optical atomic clocks. Rev. Mod. Phys. 2015, 87, 637–701. [Google Scholar] [CrossRef]
- Schiller, S.; Korobov, V. Tests of time independence of the electron and nuclear masses with ultracold molecules. Phys. Rev. A 2005, 71, 032505. [Google Scholar] [CrossRef]
- Chin, C.; Flambaum, V.V. Enhanced Sensitivity to Fundamental Constants in Ultracold Atomic and Molecular Systems near Feshbach Resonances. Phys. Rev. Lett. 2006, 96, 230801. [Google Scholar] [CrossRef]
- Flambaum, V.V.; Kozlov, M.G. Enhanced Sensitivity to the Time Variation of the Fine-Structure Constant and mp/me in Diatomic Molecules. Phys. Rev. Lett. 2007, 99, 150801. [Google Scholar] [CrossRef] [PubMed]
- Shelkovnikov, A.; Butcher, R.J.; Chardonnet, C.; Amy-Klein, A. Stability of the Proton-to-Electron Mass Ratio. Phys. Rev. Lett. 2008, 100, 150801. [Google Scholar] [CrossRef] [PubMed]
- DeMille, D.; Sainis, S.; Sage, J.; Bergeman, T.; Kotochigova, S.; Tiesinga, E. Enhanced Sensitivity to Variation of me/mp in Molecular Spectra. Phys. Rev. Lett. 2008, 100, 043202. [Google Scholar] [CrossRef] [PubMed]
- Zelevinsky, T.; Kotochigova, S.; Ye, J. Precision Test of Mass-Ratio Variations with Lattice-Confined Ultracold Molecules. Phys. Rev. Lett. 2008, 100, 043201. [Google Scholar] [CrossRef]
- Kajita, M.; Abe, M.; Hada, M.; Moriwaki, Y. Estimated accuracies of pure XH+ (X: Even isotopes of group II atoms) vibrational transition frequencies: Toward the test of the variance in mp/me. J. Phys. B 2011, 44, 025402. [Google Scholar] [CrossRef]
- Kajita, M.; Gopakumar, G.; Abe, M.; Hada, M.; Keller, M. Test of mp/me changes using vibrational transitions in . Phys. Rev. A 2014, 89, 032509. [Google Scholar] [CrossRef]
- Hanneke, D.; Carollo, R.A.; Lane, D.A. High sensitivity to variation in the proton-to-electron mass ratio in . Phys. Rev. A 2016, 94, 050101. [Google Scholar] [CrossRef]
- Kajita, M. Accuracy estimation for the transition frequencies targeting the search for the variation in the proton-electron mass ratio. Phys. Rev. A 2017, 95, 023418. [Google Scholar] [CrossRef]
- Kokish, M.G.; Stollenwerk, P.R.; Kajita, M.; Odom, B.C. Prospects for Polar Molecular Ion Optical Probe of Varying Proton-Electron Mass Ratio. arXiv, 2017; arXiv:1710.08589v3. [Google Scholar] [CrossRef]
- Stollenwerk, P.R.; Kokish, M.G.; de Oliveira-Filho, A.G.S.; Ornellas, F.R.; Odom, B.C. Optical Pumping of TeH+: Implications for the Search for Varying mp/me. Atoms 2018, 6, 53. [Google Scholar] [CrossRef]
- Herzberg, G. Molecular Spectra and Molecular Structure, Vol. I: Spectra of Diatomic Molecules; D. Van Nostrand Co.: New York, NY, USA, 1950. [Google Scholar]
- Beloy, K.; Kozlov, M.G.; Borschevsky, A.; Hauser, A.W.; Flambaum, V.V.; Schwerdtfeger, P. Rotational spectrum of the molecular ion NH+ as a probe for α and me/mp variation. Phys. Rev. A 2011, 83, 062514. [Google Scholar] [CrossRef]
- Pašteka, L.F.; Borschevsky, A.; Flambaum, V.V.; Schwerdtfeger, P. Search for the variation of fundamental constants: Strong enhancements in X2Π cations of dihalogens and hydrogen halides. Phys. Rev. A 2015, 92, 012103. [Google Scholar] [CrossRef]
- Schiller, S.; Bakalov, D.; Korobov, V.I. Simplest Molecules as Candidates for Precise Optical Clocks. Phys. Rev. Lett. 2014, 113, 023004. [Google Scholar] [CrossRef] [PubMed]
- Hilico, L.; Billy, N.; Grémaud, B.; Delande, D. Polarizabilities, light shifts and two-photon transition probabilities between J = 0 states of the and molecular ions. J. Phys. B 2001, 34, 491–507. [Google Scholar] [CrossRef]
- Karr, J.P. and HD+: Candidates for a molecular clock. J. Mol. Spectrosc. 2014, 300, 37–43. [Google Scholar] [CrossRef]
- Coxon, J.A.; Haley, M.P. Rotational Analysis of the A2Πu→X2Πg Second Negative Band System of . J. Mol. Spectrosc. 1984, 108, 119–136. [Google Scholar] [CrossRef]
- Song, Y.; Evans, M.; Ng, C.Y.; Hsu, C.W.; Jarvis, G.K. Rotationally resolved pulsed field ionization photoelectron bands of (X2Π1/2,3/2g,v+= 0–38) in the energy range of 12.05–18.15 eV. J. Chem. Phys. 1999, 111, 1905–1916. [Google Scholar] [CrossRef]
- Song, Y.; Evans, M.; Ng, C.Y.; Hsu, C.W.; Jarvis, G.K. Rotationally resolved pulsed-field ionization photoelectron bands of (A2Πu,v+= 0–12) in the energy range of 17.0–18.2 eV. J. Chem. Phys. 2000, 112, 1271–1278. [Google Scholar] [CrossRef]
- Staanum, P.F.; Højbjerre, K.; Skyt, P.S.; Hansen, A.K.; Drewsen, M. Rotational laser cooling of vibrationally and translationally cold molecular ions. Nat. Phys. 2010, 6, 271–274. [Google Scholar] [CrossRef]
- Schneider, T.; Roth, B.; Duncker, H.; Ernsting, I.; Schiller, S. All-optical preparation of molecular ions in the rovibrational ground state. Nat. Phys. 2010, 6, 275–278. [Google Scholar] [CrossRef]
- Lien, C.Y.; Seck, C.M.; Lin, Y.W.; Nguyen, J.H.; Tabor, D.A.; Odom, B.C. Broadband optical cooling of molecular rotors from room temperature to the ground state. Nat. Commun. 2014, 5, 4783. [Google Scholar] [CrossRef]
- Chou, C.; Kurz, C.; Hume, D.B.; Plessow, P.N.; Leibrandt, D.R.; Leibfried, D. Preparation and coherent manipulation of pure quantum states of a single molecular ion. Nature 2017, 545, 203–207. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, P.O.; Rosenband, T.; Langer, C.; Itano, W.M.; Bergquist, J.C.; Wineland, D.J. Spectroscopy Using Quantum Logic. Science 2005, 309, 749–752. [Google Scholar] [CrossRef]
- Mur-Petit, J.; García-Ripoll, J.J.; Pérez-Ríos, J.; Campos-Martínez, J.; Hernández, M.I.; Willitsch, S. Temperature-independent quantum logic for molecular spectroscopy. Phys. Rev. A 2012, 85, 022308. [Google Scholar] [CrossRef]
- Wolf, F.; Wan, Y.; Heip, J.C.; Gerbert, F.; Shi, C.; Schmidt, P.O. Non-destructive state detection for quantum logic spectroscopy of molecular ions. Nature 2016, 530, 457–460. [Google Scholar] [CrossRef]
- Kong, W.; Hepburn, J.W. Rotationally resolved threshold photoelectron spectroscopy of O2 using coherent XUV: Formation of vibrationally excited ions in the Franck–Condon gap. Can. J. Phys. 1994, 72, 1284–1293. [Google Scholar] [CrossRef]
- Merkt, F.; Signorell, R.; Palm, H.; Osterwalder, A.; Sommavilla, M. Towards resolving the hyperfine structure in ions by photoelectron spectroscopy. Mol. Phys. 1998, 95, 1045–1054. [Google Scholar] [CrossRef]
- Song, Y.; Evans, M.; Ng, C.Y.; Hsu, C.W.; Jarvis, G.K. Rotationally resolved pulsed field ionization photoelectron bands of (a4Πu,v+= 0–18) in the energy range of 16.0–18.0 eV. J. Chem. Phys. 2000, 112, 1306–1315. [Google Scholar] [CrossRef]
- Pratt, S.T. Excited-state molecular photoionization dynamics. Rep. Prog. Phys. 1995, 58, 821–883. [Google Scholar] [CrossRef]
- Morrill, J.S.; Ginter, M.L.; Lewis, B.R.; Gibson, S.T. The (X2Πg)nsσg1,3Πg Rydberg states of O2: Spectra, structures, and interactions. J. Chem. Phys. 1999, 111, 173–185. [Google Scholar] [CrossRef]
- Sur, A.; Ramana, C.V.; Colson, S.D. Optical spectra of the lowest Πg Rydberg states in O2. J. Chem. Phys. 1985, 83, 904–905. [Google Scholar] [CrossRef]
- Park, H.; Miller, P.J.; Chupka, W.A.; Colson, S.D. Production of vibrationally state-selected via newly discovered 4s–3d and 5s–4d Rydberg states of O2. J. Chem. Phys. 1988, 89, 3919–3921. [Google Scholar] [CrossRef]
- Ogorzalek Loo, R.; Marinelli, W.J.; Houston, P.L.; Arepalli, S.; Wiesenfeld, J.R.; Field, R.W. Multiphoton ionization of O2X3, a1Δg, and b1 via the two-photon resonant nsσg, ndσg, and ndπg Rydberg levels. J. Chem. Phys. 1989, 91, 5185–5200. [Google Scholar] [CrossRef]
- Sur, A.; Friedman, R.S.; Miller, P.J. Rotational dependence of the Rydberg-valence interactions in the 1Πg states of molecular oxygen. J. Chem. Phys. 1991, 94, 1705–1711. [Google Scholar] [CrossRef]
- Dochain, A.; Urbain, X. Production of a rovibrationally selected beam for dissociative recombination studies. EPJ Web Conf. 2015, 84, 05001. [Google Scholar] [CrossRef]
- Tong, X.; Winney, A.H.; Willitsch, S. Sympathetic Cooling of Molecular Ions in Selected Rotational and Vibrational States Produced by Threshold Photoionization. Phys. Rev. Lett. 2010, 105, 143001. [Google Scholar] [CrossRef]
- Tong, X.; Wild, D.; Willitsch, S. Collisional and radiative effects in the state-selective preparation of translationally cold molecular ions in ion traps. Phys. Rev. A 2011, 83, 023415. [Google Scholar] [CrossRef]
- Scoles, G.; Bassi, D.; Buck, U.; Laine, D.C. (Eds.) Atomic and Molecular Beam Methods; Oxford University Press: New York, NY, USA, 1988; Volume 1. [Google Scholar]
- Xie, J.; Zare, R.N. Selection rules for the photoionization of diatomic molecules. J. Chem. Phys. 1990, 93, 3033–3038. [Google Scholar] [CrossRef]
- Germann, M.; Willitsch, S. Fine- and hyperfine-structure effects in molecular photoionization. I. General theory and direct photoionization. J. Chem. Phys. 2016, 145, 044314. [Google Scholar] [CrossRef] [PubMed]
- Leibfried, D. Quantum state preparation and control of single molecular ions. New J. Phys. 2012, 14, 023029. [Google Scholar] [CrossRef]
- Ding, S.; Matsukevich, D.N. Quantum logic for the control and manipulation of molecular ions using a frequency comb. New J. Phys. 2012, 14, 023028. [Google Scholar] [CrossRef]
- Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Bertelsen, A.; Jørgensen, S.; Drewsen, M. The rotational temperature of polar molecular ions in Coulomb crystals. J. Phys. B 2006, 39, L83–L89. [Google Scholar] [CrossRef]
- Roth, B.; Koelemeij, J.C.J.; Daerr, H.; Schiller, S. Rovibrational spectroscopy of trapped molecular hydrogen ions at millikelvin temperatures. Phys. Rev. A 2006, 74, 040501. [Google Scholar] [CrossRef]
- Seck, C.M.; Hohenstein, E.G.; Lien, C.Y.; Stollenwerk, P.R.; Odom, B.C. Rotational state analysis of AlH+ by two-photon dissociation. J. Mol. Spectrosc. 2014, 300, 108–111. [Google Scholar] [CrossRef]
- Ni, K.K.; Loh, H.; Grau, M.; Cossel, K.C.; Ye, J.; Cornell, E.A. State-specific detection of trapped HfF+ by photodissociation. J. Mol. Spectrosc. 2014, 300, 12–15. [Google Scholar] [CrossRef]
- Schlemmer, S.; Kuhn, T.; Lescop, E.; Gerlich, D. Laser excited in a 22-pole ion trap: Experimental studies of rotational relaxation processes. Int. J. Mass Spectrom. 1999, 185, 589–602. [Google Scholar] [CrossRef]
- Akahori, T.; Morioka, Y.; Tanaka, T.; Yoshii, H.; Hayaishi, T.; Ito, K. High resolution threshold photoelectron spectrum of oxygen in the 12–19 eV region. J. Chem. Phys. 1997, 107, 4875–4880. [Google Scholar] [CrossRef]
- Fedorov, D.G.; Gordon, M.S.; Song, Y.; Ng, C.Y. Theoretical study of spin-orbit coupling constants for (A2Π3/2,1/2u,v+= 0–17 and a4Π5/2,3/2,1/2,-1/2u,v+= 0–25). J. Chem. Phys. 2001, 115, 7393–7400. [Google Scholar] [CrossRef]
- Liu, H.; Shi, D.; Sun, J.; Zhu, Z. Accurate theoretical investigations of the 20 Λ-S and 58 Ω states of cation including spin–orbit coupling effect. Mol. Phys. 2015, 113, 120–136. [Google Scholar] [CrossRef]
- Zhang, C.B.; Offenberg, D.; Roth, B.; Wilson, M.A.; Schiller, S. Molecular-dynamics simulations of cold single-species and multispecies ion ensembles in a linear Paul trap. Phys. Rev. A 2007, 76, 012719. [Google Scholar] [CrossRef]
- Baba, T.; Waki, I. Cooling and Mass-Analysis of Molecules Using Laser-Cooled Atoms. Jpn. J. Appl. Phys. 1996, 35, L1134–L1137. [Google Scholar] [CrossRef]
- Baba, T.; Waki, I. Spectral shape of in situ mass spectra of sympathetically cooled molecular ions. J. Appl. Phys. 2002, 92, 4109–4116. [Google Scholar] [CrossRef]
- Schowalter, S.J.; Chen, K.; Rellergert, W.G.; Sullivan, S.T.; Hudson, E.R. An integrated ion trap and time-of-flight mass spectrometer for chemical and photo- reaction dynamics studies. Rev. Sci. Instrum. 2012, 83, 043103. [Google Scholar] [CrossRef]
- Deb, N.; Pollum, L.L.; Smith, A.D.; Keller, M.; Rennick, C.J.; Heazlewood, B.R.; Softley, T.P. Coulomb crystal mass spectrometry in a digital ion trap. Phys. Rev. A 2015, 91, 033408. [Google Scholar] [CrossRef]
- Schneider, C.; Schowalter, S.J.; Yu, P.; Hudson, E.R. Electronics of an ion trap with integrated time-of-flight mass spectrometer. Int. J. Mass Spectrom. 2016, 394, 1–8. [Google Scholar] [CrossRef]
- Schmid, P.C.; Greenberg, J.; Miller, M.I.; Loeffler, K.; Lewandowski, H.J. An ion trap time-of-flight mass spectrometer with high mass resolution for cold trapped ion experiments. Rev. Mod. Phys. 2017, 88, 123107. [Google Scholar] [CrossRef] [PubMed]
- Lefebvre-Brion, H.; Field, R.W. The Spectra and Dynamics of Diatomic Molecules; Elsevier: San Diego, CA, USA, 2004. [Google Scholar]
- Gilmore, F.R.; Laher, R.R.; Espy, P.J. Franck–Condon Factors, r-Centroids, Electronic Transition Moments, and Einstein Coefficients for Many Nitrogen and Oxygen Band Systems. J. Phys. Chem. Ref. Data 1992, 21, 1005–1107. [Google Scholar] [CrossRef]
- Le Roy, R.J. RKR1: A computer program implementing the first-order RKR method for determining diatomic molecule potential energy functions. J. Quant. Spectrosc. Radiat. Transf. 2017, 186, 158–166. [Google Scholar] [CrossRef]
- Le Roy, R.J. LEVEL: A Computer Program for Solving the Radial Schrödinger Equation for Bound and Quasibound Levels. J. Quant. Spectrosc. Radiat. Transf. 2017, 186, 167–178. [Google Scholar] [CrossRef]
- Yudin, V.I.; Taichenachev, A.V.; Oates, C.W.; Barber, Z.W.; Lemke, N.D.; Ludlow, A.D.; Sterr, U.; Lisdat, C.; Riehle, F. Hyper-Ramsey spectroscopy of optical clock transitions. Phys. Rev. A 2010, 82, 011804. [Google Scholar] [CrossRef]
- Yudin, V.I.; Taichenachev, A.V.; Basalaev, M.Y.; Zanon-Willette, T.; Pollock, J.W.; Shuker, M.; Donley, E.A.; Kitching, J. Generalized Autobalanced Ramsey Spectroscopy of Clock Transitions. Phys. Rev. Appl. 2018, 9, 054034. [Google Scholar] [CrossRef]
- Sanner, C.; Huntemann, N.; Lange, R.; Tamm, C.; Peik, E. Autobalanced Ramsey Spectroscopy. Phys. Rev. Lett. 2018, 120, 053602. [Google Scholar] [CrossRef] [PubMed]
- Zanon-Willette, T.; Lefevre, R.; Metzdorff, R.; Sillitoe, N.; Almonacil, S.; Minissale, M.; de Clercq, E.; Taichenachev, A.V.; Yudin, V.I.; Arimondo, E. Composite laser-pulses spectroscopy for high-accuracy optical clocks: A review of recent progress and perspectives. Rep. Prog. Phys. 2018, 81, 094401. [Google Scholar] [CrossRef]
- Huntemann, N.; Lipphardt, B.; Okhapkin, M.; Tamm, C.; Peik, E.; Taichenachev, A.V.; Yudin, V.I. Generalized Ramsey Excitation Scheme with Suppressed Light Shift. Phys. Rev. Lett. 2012, 109, 213002. [Google Scholar] [CrossRef]
- Huntemann, N.; Sanner, C.; Lipphardt, B.; Tamm, C.; Peik, E. Single-Ion Atomic Clock with 3 × 10-18 Systematic Uncertainty. Phys. Rev. Lett. 2016, 116, 063001. [Google Scholar] [CrossRef]
- Berkeland, D.J.; Miller, J.D.; Bergquist, J.C.; Itano, W.M.; Wineland, D.J. Minimization of ion micromotion in a Paul trap. J. Appl. Phys. 1998, 83, 5025–5033. [Google Scholar] [CrossRef]
- Wineland, D.J.; Monroe, C.; Itano, W.M.; Leibfried, D.; King, B.E.; Meekhof, D.M. Experimental Issues in Coherent Quantum-State Manipulation of Trapped Atomic Ions. J. Res. Natl. Inst. Stand. Technol. 1998, 103, 259–328. [Google Scholar] [CrossRef] [PubMed]
- Farley, J.W.; Wing, W.H. Accurate calculation of dynamic Stark shifts and depopulation rates of Rydberg energy levels induced by blackbody radiation. Hydrogen, helium, and alkali-metal atoms. Phys. Rev. A 1981, 23, 2397–2424. [Google Scholar] [CrossRef]
- Porsev, S.G.; Derevianko, A. Multipolar theory of blackbody radiation shift of atomic energy levels and its implications for optical lattice clocks. Phys. Rev. A 2006, 74, 020502. [Google Scholar] [CrossRef]
- Rosenband, T.; Itano, W.M.; Schmidt, P.O.; Hume, D.B.; Koelemeij, J.C.J.; Bergquist, J.C.; Wineland, D.J. Blackbody radiation shift of the 27Al+1S0→3P0 transition. arXiv, 2006; arXiv:physics/0611125. [Google Scholar]
- Arnold, K.J.; Kaewuam, R.; Roy, A.; Tan, T.R.; Barrett, M.D. Blackbody radiation shift assessment for a lutetium ion clock. Nat. Commun. 2018, 9, 1650. [Google Scholar] [CrossRef] [PubMed]
- Dicke, R.H. The Effect of Collisions upon the Doppler Width of Spectral Lines. Phys. Rev. 1953, 89, 472–473. [Google Scholar] [CrossRef]
- Rosenband, T.; Hume, D.B.; Schmidt, P.O.; Chou, C.W.; Brusch, A.; Lorini, L.; Oskay, W.H.; Drullinger, R.E.; Fortier, T.M.; Stalnaker, J.E.; et al. Frequency Ratio of Al+ and Hg+ Single-Ion Optical Clocks; Metrology at the 17th Decimal Place. Science 2008, 319, 1808–1812. [Google Scholar] [CrossRef]
- Chen, J.S.; Brewer, S.M.; Chou, C.W.; Wineland, D.J.; Leibrandt, D.R.; Hume, D.B. Sympathetic Ground State Cooling and Time-Dilation Shifts in an 27Al+ Optical Clock. Phys. Rev. Lett. 2017, 118, 053002. [Google Scholar] [CrossRef]
- Itano, W.M. External-Field Shifts of the 199Hg+ Optical Frequency Standard. J. Res. Natl. Inst. Stand. Technol. 2000, 105, 829–837. [Google Scholar] [CrossRef]
- Bakalov, D.; Schiller, S. The electric quadrupole moment of molecular hydrogen ions and their potential for a molecular ion clock. Appl. Phys. B 2014, 114, 213–230. [Google Scholar] [CrossRef]
- Schadee, A. On the Zeeman effect in electronic transitions of diatomic molecules. J. Quant. Spectrosc. Radiat. Transf. 1978, 19, 517–531. [Google Scholar] [CrossRef]
- Berdyugina, S.V.; Solanki, S.K. The molecular Zeeman effect and diagnostics of solar and stellar magnetic fields. Astron. Astrophys. 2002, 385, 701–715. [Google Scholar] [CrossRef]
- Schiff, L.I.; Snyder, H. Theory of the Quadratic Zeeman Effect. Phys. Rev. 1939, 55, 59–63. [Google Scholar] [CrossRef]
- Garstang, R.H. Atoms in high magnetic fields (white dwarfs). Rep. Prog. Phys. 1977, 40, 105–154. [Google Scholar] [CrossRef]
- Townes, C.H.; Schawlow, A.L. Microwave Spectroscopy; Dover: Mineola, NY, USA, 1975. [Google Scholar]
- Brown, J.; Carrington, A. Rotational Spectroscopy of Diatomic Molecules; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Itano, W.M.; Bergquist, J.C.; Bollinger, J.J.; Gilligan, J.M.; Heinzen, D.J.; Moore, F.L.; Raizen, M.G.; Wineland, D.J. Quantum projection noise: Population fluctuations in two-level systems. Phys. Rev. A 1993, 47, 3554–3570. [Google Scholar] [CrossRef] [PubMed]
- Kajita, M. Search for the Variation in (mp/me) Using Two Vibrational Transition Frequencies of Molecular Ions. J. Phys. Soc. Jpn. 2017, 86, 133301. [Google Scholar] [CrossRef]
- Gerstenkorn, S.; Luc, P. Atlas du Spectre d’Absorption de la Molecule d’Iode, 14 800–20 000 cm−1; CNRS: Paris, France, 1978. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).