1. Introduction
Entanglement is of interest not only as a basic feature of quantum theory, but also for applications in quantum optics including quantum cryptography [
1], quantum imaging [
2], quantum spectroscopy [
3,
4], and metrology [
5], among others. The strong correlations implied by entanglement have long been of interest in connection with quantum interference effects [
6] and various classically counterintuitive experimental results, and there have been many investigations of entanglement with suitable experiments and associated theoretical analyses.
Entanglement contains some of the surprising features of quantum theory and demonstrates correlations stronger than are possible in classical physics. Different approaches were taken in the past, such as the introduction of hidden parameters, to explain these observations. However, it was shown that such hidden parameters are inconsistent with quantum theory and experiment. As we show in this paper, the explicit consideration of vacuum quantum fields allows an intuitive description of quantum-optical effects in spontaneous parametric down-conversion that are typically explained by entanglement.
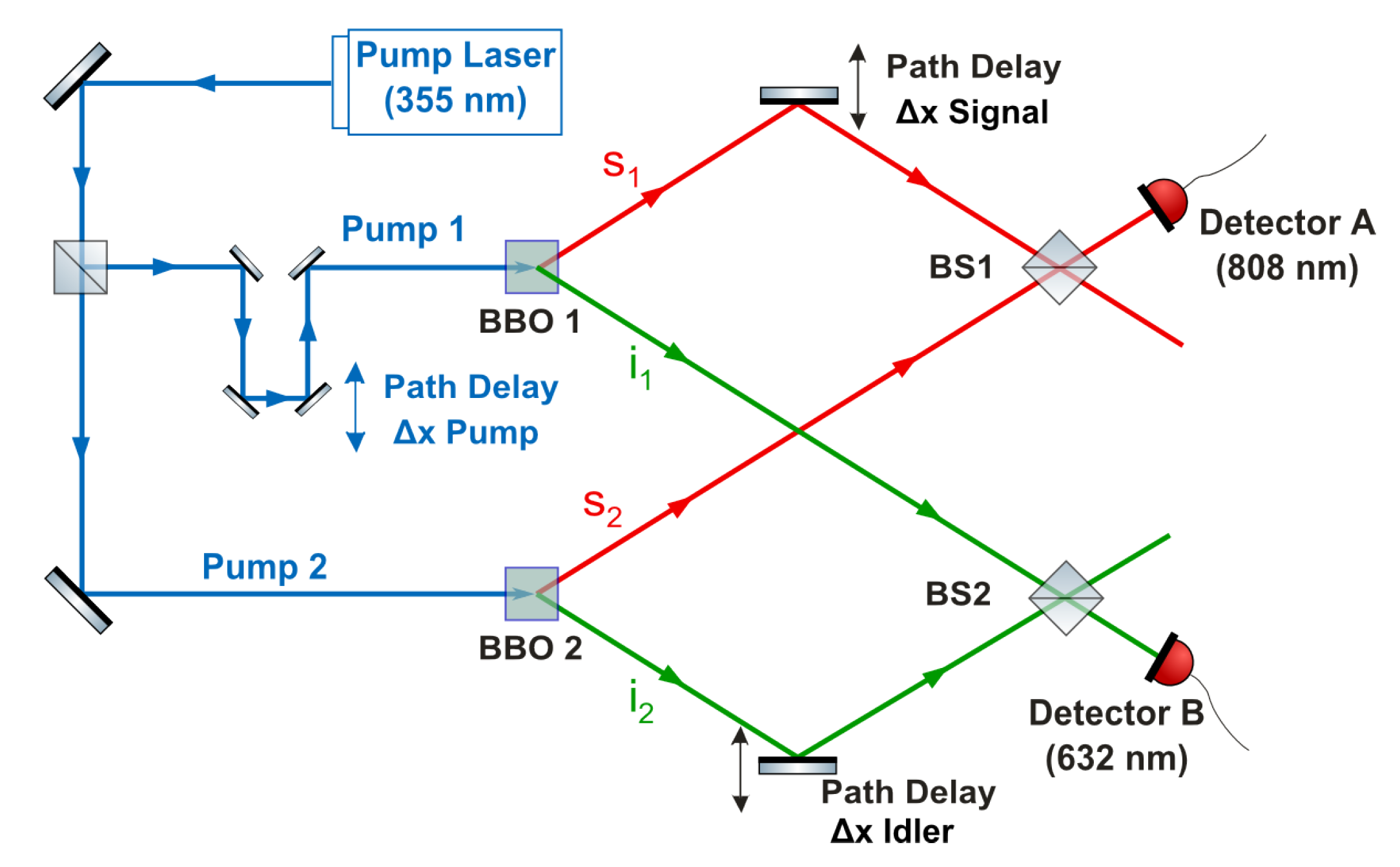
Spontaneous parametric down-conversion (SPDC) has been one of the most useful tools in quantum-optical investigations of entanglement. In this paper we revisit SPDC from a perspective somewhat different from much of the previous work on the subject. For this purpose, we investigated the interference of two biphotons generated in two parallel, pumped down-conversion crystals as in [
7], but with no further coupling, as in [
8,
9]. Our experimental results are in agreement with the earlier work (but with much greater interference visibility), but it seems worthwhile to describe and analyze them from the perspectives taken in our recently-reported work [
7,
10] and to formulate in more detail the analyses outlined in that work. In doing so, the question arises as to the extent to which the experimental results we show can be understood in a classical, stochastic treatment of the vacuum field. We discuss the difficulties posed by such an intuitive approach to the signal and idler vacuum fields, which can nevertheless account for some of the effects observed in SPDC [
11].
In analyzing our earlier experiments, we considered in particular the role of vacuum fields and complementarity in different SPDC setups. SPDC is especially interesting in this regard because the down-converted photons result from nonlinear mixing of the pump field with the vacuum fields at the crystals, and therefore, the statistical properties of the generated signal and idler fields reflect those of the vacuum fields involved in the three-wave mixing process. It has been demonstrated that, in spite of the random character of these vacuum fields, a phase memory effect could be observed if the same vacuum mode takes part in the down-conversion in two crystals [
9,
12]. Using an extended version of this experiment with three down-conversion crystals, it was shown that the absence of correlations between the vacuum fields at different crystals results in an incoherent background photon count. However, this effect of the different vacuum field modes taking part in the down-conversion could be completely overcome, and almost perfect coherence could be observed, in the stimulated process with coherent laser radiation, distinct from the pump laser, fed into a previously open vacuum mode [
7].
We begin in the following section by describing the experiment with two down-conversion crystals. In this experiment, there are a total of four open vacuum entrances, two at each crystal, involved in the three-wave-mixing processes generating the two down-converted biphotons. No first-order coherence is observed between the single-photon signal and idler fields, but high-visibility interference is observed when photons are counted in coincidence, consistent with complementarity and the absence of which-path information (
Section 3). In
Section 4, a Heisenberg picture analysis of these results is presented. In this description, there is no first-order coherence observed between the single-photon signal and idler fields because the vacuum fields at the four open entrances are uncorrelated, whereas second-order, “intensity” correlations of these vacuum fields result in the observed interference effect when photons are counted in coincidence. The same formalism is then used in
Section 5 to describe the Hong–Ou–Mandel (HOM) dip [
13], where we show that this consequence of entanglement and quantum interference can again be explained equivalently in terms of non-vanishing intensity correlations of the vacuum fields. The vacuum signal and idler fields in both the two-crystal experiment and the HOM effect make explicit contributions not only to the generation of the signal and idler photons, but also to the photon coincidence counting rate. In
Section 6, we discuss further the simplified Heisenberg picture theory employed in
Section 4 and
Section 5 and its relation to a more complete SPDC theory.
Section 7 addresses the question of the extent to which the vacuum field in these experiments can be regarded as a classical stochastic field. Our results are summarized and discussed further in
Section 8.
4. Theoretical Description
The interaction Hamiltonian describing the down-conversion process in a single crystal is
when the pump is treated as a classically-prescribed, undepleted, and spatially-uniform field of frequency
.
and
are the photon annihilation operators for the signal and idler fields satisfying the energy conservation (
) and phase-matching (
) conditions, and
C is proportional to the pump amplitude and the nonlinear susceptibility. To lowest order in
C,
in spontaneous parametric down-conversion generates an entangled field state [
9,
14] that is a linear superposition of the vacuum state
and the two-photon state
consisting of a single-signal photon and a single-idler photon. In the Heisenberg picture, the positive frequency (photon annihilation) parts of the signal and idler electric field operators may be expressed, to lowest order in
C, as
and
and
are the photon annihilation operators for the signal and idler vacuum fields, respectively, in the absence of the pump field. The functions
and
include the spatial dependence of the corresponding electric fields, which are polarized according to type I phase matching in the experiments described in the preceding sections.
D, which is proportional to
C, is determined by the solution of the Heisenberg equations of motion that follow from the Hamiltonian with the interaction (
1). The specific forms of
,
, and
D will not be needed for our purposes.
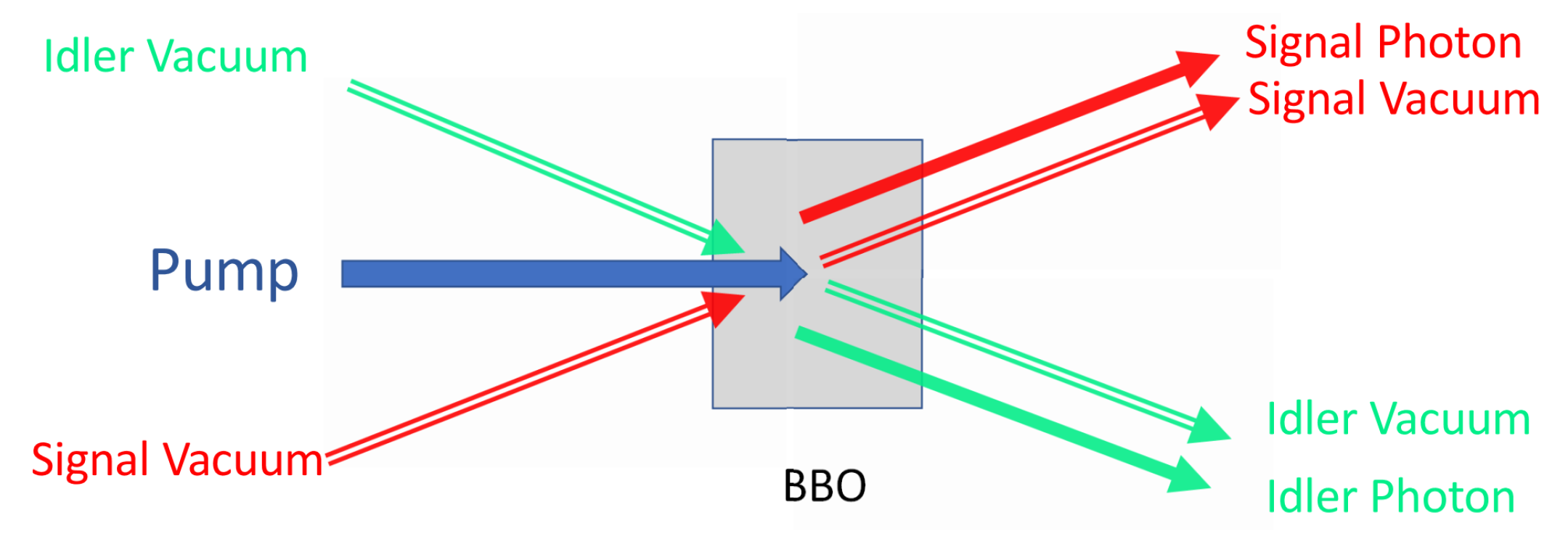
As illustrated in
Figure 5, the signal field
in our simplified Heisenberg picture analysis has two contributions: (i) the vacuum field in the signal mode and (ii) the field generated by the mixing in the crystal of the pump field with the vacuum field in the idler mode. Likewise, the idler field
consists of the vacuum field in the idler mode plus the field generated by the mixing in the crystal of the pump field with the vacuum field in the signal mode.
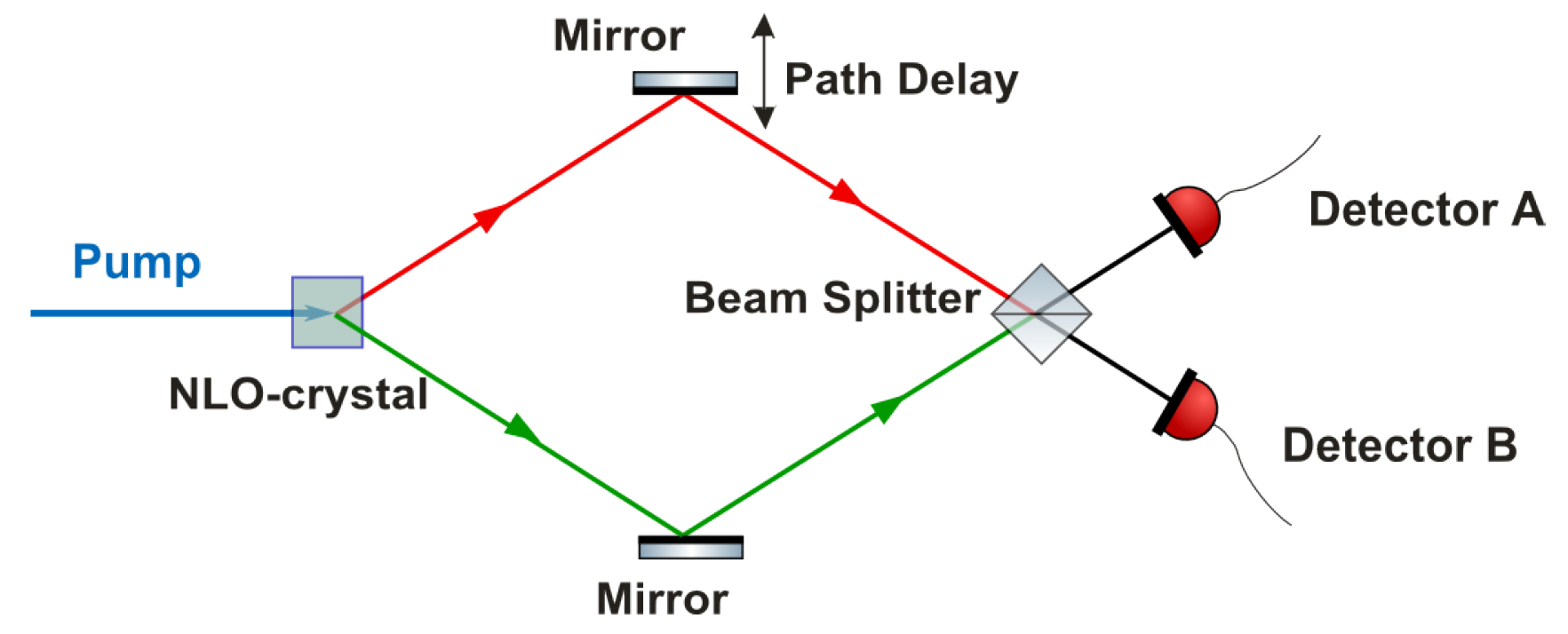
For the two-crystal configuration of interest here,
where the subscripts s 1, s2, i1, and i2 refer to the modes indicated in
Figure 1. The two crystals are assumed to be identical, in which case
and
are proportional to the complex amplitudes of the pump fields at BBO1 and BBO2, respectively.
The coincidence rate may be obtained simply from the superposition of probability amplitudes. Suppose first that
. There are two (indistinguishable) ways by which a signal photon can be counted at A in coincidence with an idler photon at B. Referring to
Figure 1, these are (i) a signal photon s1 is counted at A and an idler photon i1 at B, and (ii) a signal photon s2 is counted at A and an idler photon i2 at B. In Process (i), the signal field undergoes a reflection and a phase delay
, and the idler field is transmitted through the lower beam splitter in
Figure 1. The amplitude for Path (i) is therefore proportional to
, where
r and
t are respectively the amplitude reflection and transmission coefficients of the beam splitters, which are assumed to be identical. In Process (ii), the signal field is transmitted through the upper beam splitter in
Figure 1, the idler field undergoes a reflection and a phase delay
, and the probability for this path is therefore proportional to
. The total probability amplitude for a signal photon to be counted at A in coincidence with an idler photon at B is therefore proportional to
, and the coincidence counting rate is proportional to
,
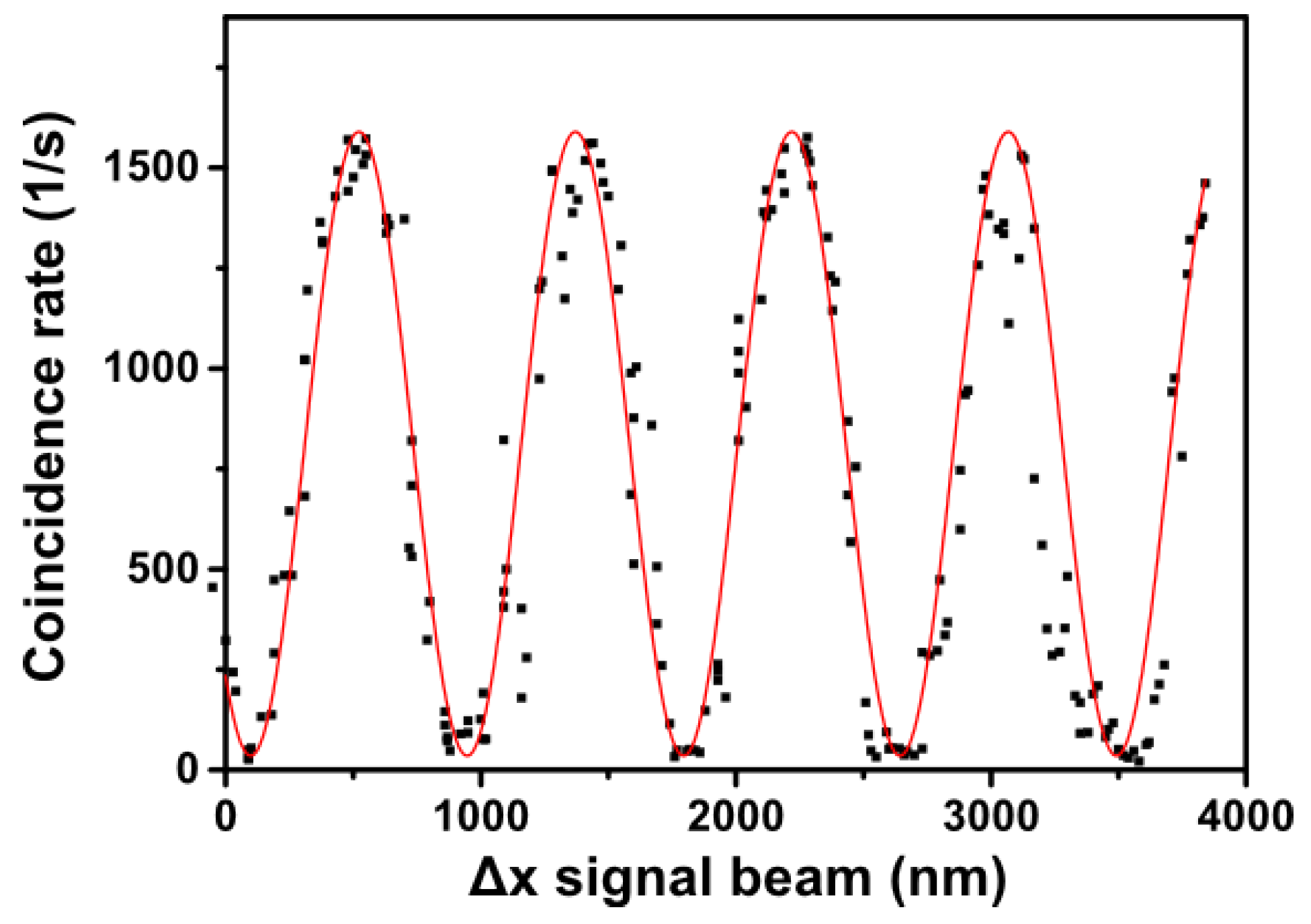
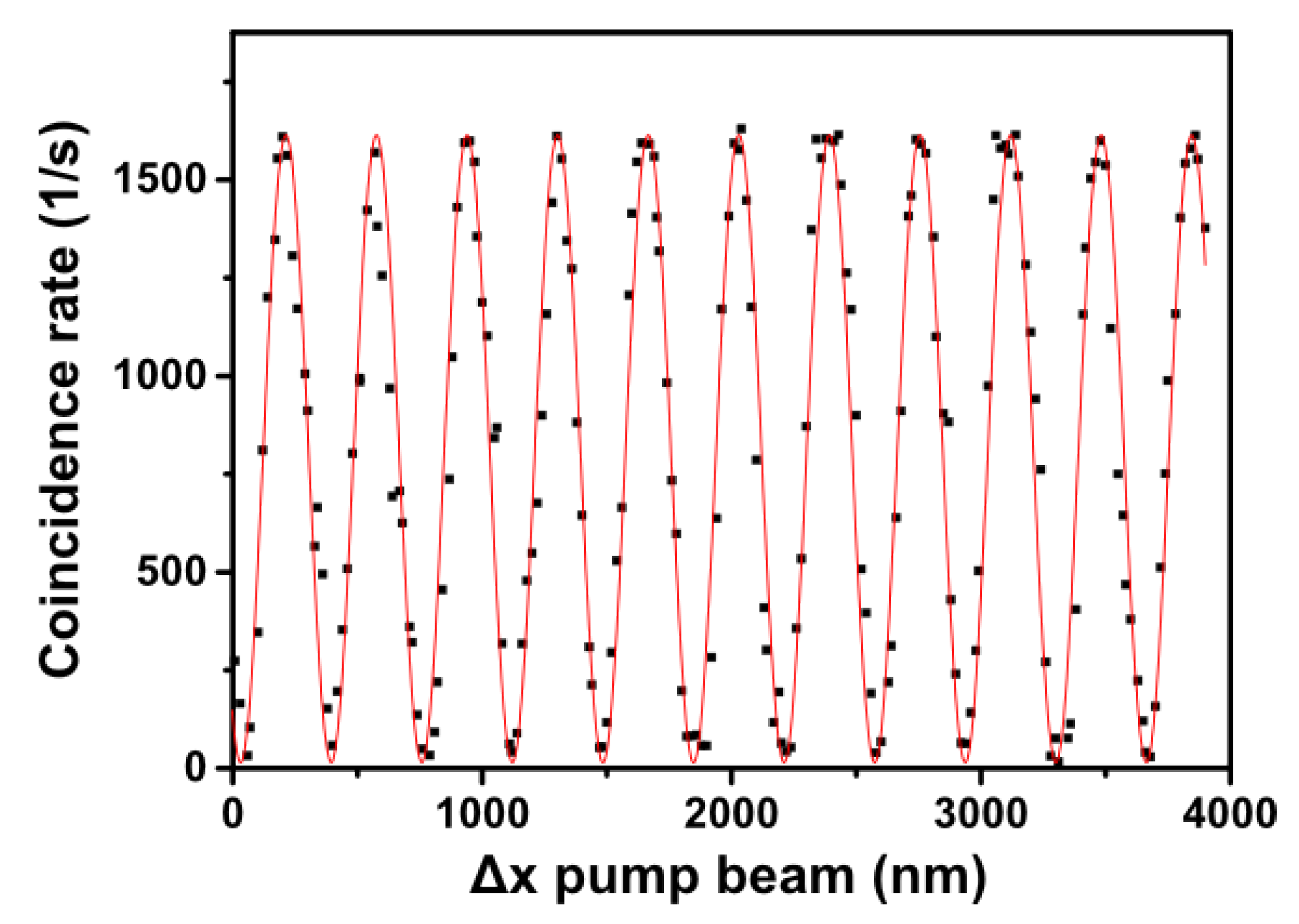
. This implies the variation of the measured coincidence rate with signal path delay shown in
Figure 3, with the oscillation period determined by the signal path delay (
) and therefore the 808-nm signal wavelength.
If
, which would be the case if, for example, the pump amplitudes at the two crystals were different, the coincidence rate
as discussed above will be proportional to
. Writing
, we have
and a coincidence-rate “visibility”:
We similarly define a contrast, or “distinguishability”,
It follows that
which is a special case of the more general expression
of complementarity [
15,
16,
17,
18,
19]. The inequality in our case would apply if we did not make the implicit assumption that the pump fields at the two crystals are mutually coherent.
First-order perturbation theory with the interaction Hamiltonian (
4), assuming an initial state
with no photons in the modes s1,i1,s2,i2 (
Figure 1), gives
Here,
is the state with one photon in each of the modes
and
, etc. The factor
K need not be specified, nor will it be necessary to normalize
for our purposes. As discussed in [
8], the “entanglement with the vacuum” described by the state (
9) implies the observed two-photon coincidence rate. In terms of interfering probability amplitudes as discussed above, the amplitude to count (annihilate) a signal photon
at Detector A in coincidence with an idler photon
at Detector B, including the phase delay
, is proportional to
, where the vacuum state of the field is denoted by
Similarly, the amplitude to count a signal photon at Detector A in coincidence with an idler photon at Detector B is proportional to , and the rate for counting a signal photon at A in coincidence with an idler photon at B is therefore proportional to . This simple argument emphasizes the role played by entanglement with the vacuum field: to explain the observed coincidence rate, we must include the vacuum states and , as well as the two-photon states and in describing the state of the field.
We now turn to a simplified Heisenberg picture analysis that exhibits explicitly the role of the vacuum fields, as opposed to the vacuum states, participating in the downconversion at the two crystals. The rate for counting a signal photon at Detector A in coincidence with an idler photon at Detector B may be taken to be proportional to [
20,
21]
where
and
are the positive-frequency parts of the electric field operators at Detectors A and B,
,
are their Hermitian conjugates, and
is again the vacuum field state. As in the preceding discussion, we treat A and B as effectively point detectors, since as a practical matter, the spatial integration over detector volumes only introduces a complication of no interest for our purposes here. We therefore ignore entirely the spatial variations of the electric fields, except, of course, for the path delays described by
and
. Then, to calculate the dependence of
on these path delays, we can effectively take, to first-order in
D,
and
which are obvious extensions of (
2) and (
3).
Suppose first that only the crystal BBO1 is pumped. Since
, and the photon operators for different modes commute,
i.e., the signal and idler fields in SPDC are uncorrelated [
7]. The signal-idler photon coincidence rate is found similarly; to second-order in D,
The dependence of this signal-idler coincidence rate on only the vacuum idler field reflects the fact that a signal photon at Detector A, produced by the mixing of the vacuum idler field with the pump field at BBO1, is accompanied by its partner idler photon at Detector B. Since
, we can also write
in the form
which can be interpreted in the same way as (
15), except that now, the roles of the signal and idler fields are switched. The fact that we can write
in terms of either signal or idler vacuum expectation values simply reflects the fact that signal and idler photons are generated in (biphoton) pairs.
For the experiment of
Figure 1 in which both crystals are pumped, we obtain, from (
11)–(
13),
to lowest order in
D, where again,
. Equivalently, since
,
Since all the vacuum expectation values in (
16) and (
17)
, we obtain again
:
The generalization to non-identical crystals or pump fields is straightforward and of course reproduces the complementarity relation (
8).
In the derivation of
based on probability amplitudes, the
term resulted from the interference of the amplitudes for the two indistinguishable processes (i) and (ii). Obviously, the interference here is similar to the interference of two probability amplitudes in the two-slit experiment with single photons, with the difference that
describes the counting of two photons (signal and idler) in coincidence. The complementarity relation (
8) applies to both examples. In the classical description of the two-slit experiment, for example, the visibility of interference fringes is reduced when the difference in the field intensities incident on the two slits is increased. In the experiment of
Figure 1, the visibility (
6) is reduced when the distinguishability of the processes (i) and (ii) is increased.
In the Heisenberg picture calculation, the role of the vacuum fields taking part in SPDC is explicit in Expression (
16). The vacuum fields incident on BBO1 and BBO2 are associated with
and
, respectively, and the last term on the right-hand side of (
16) is non-vanishing because these fields have quantum fluctuations and zero-point energy, e.g.,
. This suggests an interpretation along the lines of the classical theory of stochastic electrodynamics, which we discuss in
Section 7.
6. Remarks on the Simplified Theory
The theoretical approach we have taken accounts for the experimental results described in
Section 3, as well as the HOM dip, and as discussed in
Section 4, it is consistent with the basic notions of complementarity, which-path information, and the interference of probability amplitudes. It also accounts for the main results of earlier experiments involving three crystals, induced coherence, and stimulated down-conversion [
7,
10,
12]. In addition to the assumption of monochromatic pump and signal and idler fields, the applicability of this simplified theory relies on the assumption that the SPDC rate of generation of biphotons is very small. Consider, for example, the approximate solution for the signal photon annihilation operator
implied by (
2):
Since vacuum-field signal and idler field operators satisfy
,
, (
24) implies the incorrect equal-time commutation relation
In a more complete theory in which the down-conversion efficiency is not necessarily small,
is related to
and
by a Bogoliubov transformation [
22]:
and likewise for
, and the correct commutation relations
are satisfied. To better appreciate the approximation (
24) (and the corresponding approximation for
), consider first the expectation value of the number of signal photons implied by (
26):
Next, consider the expectation value of the square of the number of signal photons implied by (
26):
Now, if, as in the experiments described earlier, the probability of generating more than one biphoton in the measurement interval is very small, we can assume that
, i.e., that there is at most a single signal-idler pair generated during the measurement interval. This means that (
28) should be well approximated by (
27), which in turn implies that
and
. Comparison of (
24) and (
26) then implies that
. The simplified theory is therefore accurate as long as, with high probability, there is at most a single biphoton during the measurement interval, and we therefore require that
.
The relation (
25) in our simplified theory does not invalidate our calculations because we have not required
anywhere in these calculations. We have, however, used the commutation relation
in writing (
17), for instance, but this is perfectly consistent within the simplified theory, since, from (
12) and (
13),
for all values of
r and
t.
7. Classical Stochastic Theory of Vacuum Fields
Signal-idler intensity correlations in single-crystal SPDC have been shown to follow from a theory in which the incoming vacuum signal fields are treated as classical stochastic fields [
11]. We now re-examine such an approach, following the same lines as the simplified theory we have used in treating these correlations with quantized fields. Our approach will be semiclassical in the sense that the fields are treated classically, while the photodetection is described by replacing normally-ordered field correlation functions such as
in the quantized-field theory by
, where
denotes an average over an appropriate classical ensemble. This approach is justified for our purposes by the fact that the main features of photoelectric detection do not require field quantization [
23]. The same approach is in fact implicit in the part of the work of [
11] that relates to the classical stochastic description of the vacuum fields.
For a single vacuum mode of frequency
, the positive-frequency part of the classical stochastic field is assumed, as in the completely classical theory of stochastic electrodynamics [
24,
25], to have the form
such that
is a fixed constant and
is a random variable having a uniform probability distribution on the interval
. The appropriate averaging
is then an average over the phase distribution, and it is assumed that the randomly-varying phases of different modes are uncorrelated. We can fix the values of the
’s such that the average energy density per mode in the classical stochastic theory is the same as the corresponding quantized-field vacuum expectation value, which for our purposes is proportional to
Since
this requires
for each field mode in the stochastic theory. As in the preceding calculations, it will suffice for our purposes to ignore any explicit consideration of the spatial dependence of the fields.
The classical counterparts of the quantized fields (
12) and (
13) are
and
where
, and
are uncorrelated random variables, uniformly distributed on
.
Suppose first that only the crystal BBO1 in
Figure 1 is pumped. The fields at A and B are uncorrelated because of their random and uncorrelated phases, and this is consistent with the quantized-field theory. For the signal-idler coincidence rate, we obtain
in the stochastic theory. If we ignore the first,
D-independent term and replace each
in the remaining term by
as in (
33), we obtain
in agreement with the result (
16) obtained in the quantized-field theory. In the case that both crystals in
Figure 1 are pumped, we obtain, similarly,
where again
. If we again ignore the
D-independent term and replace every
by
, we obtain
in agreement with the result (
18) derived in the quantized-field theory.
D, which was introduced in
Section 4, is proportional to the lowest (second-) order nonlinear susceptibility, the pump-field amplitude, and the interaction time of the fields in the crystals, and it has been assumed for simplicity that it is the same for each crystal. In most SPDC experiments,
, as we have assumed, so that the generation of multiple biphotons during the interaction time is negligible. (The assumption that the generation of multiple biphotons during the interaction time is negligible is also made in the more detailed, multimode analysis of Hong and Mandel [
26].) As shown in
Section 6,
is in fact required for the validity of our simplified theory.
The
D-independent terms we have ignored in obtaining (
37) and (
39) arise from the signal and idler vacuum fields that are present even in the absence of any pump field or crystals. In free space without any crystals, for example, (
30) implies that
, i.e., a photodetector would respond to a vacuum field in free space without any sources. It would make sense, therefore, to argue that the physically meaningful, measurable intensity should be defined by subtracting out the source-free contribution in the classical stochastic treatment of the vacuum field [
11,
27]. In the calculation of
, it might be argued similarly that the
D-independent terms in (
34) and (
35) are unphysical and should be dropped. A problem with such an argument, however, is that those terms contribute to the
D-dependent terms in
, and without them, the stochastic theory does not reproduce results such as (
37) or (
39) that are consistent with the quantized-field theory and with the experiment, as discussed earlier. In other words, the
D-independent terms are required if we are to obtain interference effects that appear naturally in the quantized-field theory. Thus, while a classical stochastic approach to the vacuum field can yield results that mimic those found in the quantized-field theory, such an approach appears to be fundamentally inconsistent.
In the quantized-field theory, there are also, of course, D-independent operators in the expressions for and , and they do contribute explicitly to . However, in the quantized-field theory, these operators do not give rise to measurable effects in the absence of any sources, nor do they give rise to D-independent terms in . Unlike the intensity in the absence of any sources, for example, in the quantized-field theory: a photodetector does not respond to a source-free, vacuum field.