Mixed-State Ionic Beams: An Effective Tool for Collision Dynamics Investigations
Abstract
:1. Introduction
2. Production of Metastable States
3. Lifetimes of Metastable States
4. Mixed-State Ionic Beams—Content Determination
4.1.
4.2.
5. Case Studies: Results and Discussion
5.1. Doubly and Triply Excited Li-Like States
5.2. Doubly Excited He-Like States
6. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| APAPES | Atomic Physics with Accelerators: Projectile Electron Spectroscopy |
| AOCC | Atomic Orbital Close Coupling |
| ZAPS | Zero-degree Auger Projectile Spectroscopy |
| TANDEM | The two-stage (tandem) Van de Graaff accelerator |
| FPS | Foil Post-Stripping |
| FTS | Foil Terminal Stripping |
| GPS | Gas Post-Stripping |
| GTS | Gas Terminal Stripping |
| RTE | Resonant Transfer and Excitation |
References
- Beyer, H.F.; Shevelko, P. Introduction to the Physics of Highly Charged Ions; Series in Atomic and Molecular Physics; Institute of Physics Publishing: Bristol, UK; Philadelphia, PA, USA, 2003. [Google Scholar]
- Currell, F.J. The Physics of Multiply and Highly Charged Ions. Volume 1. Sources, Applications and Fundamental Processes; Series in Atomic and Molecular Physics; Springer-Science+Business Media: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Janev, R.K. Atomic and Molecular Processes in Fusion Edge Plasmas; Springer Science+Business Media, LLC: New York, NY, USA, 1995. [Google Scholar]
- Stolterfoht, N.; Dubois, R.D.; Rivarola, R.D. Electron Emission in Heavy Ion-Atom Collisions; Springer Series on Atoms and Plasmas; Springer: Berlin, Germany, 1997. [Google Scholar]
- Itikawa, Y. Molecular Processes in Plasmas; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2007. [Google Scholar]
- Müller, A. Electron-ion collisions: Fundamental processes in the focus of applied research. Adv. At. Mol. Opt. Phys. 2008, 55, 293–417. [Google Scholar]
- V. Shevelko, H.T. Atomic Processes in Basic and Applied Physics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2012. [Google Scholar]
- Janev, R.K.; Winter, H. State-selective electron capture in atom-highly charged ion collisions. Phys. Rep. 1985, 117, 265–387. [Google Scholar] [CrossRef]
- Summers, H.P.; Dickson, W.J. Applications of Recombination. In Recombination of Atomic Ions; Graham, W.G., Fritsch, W., Hahn, Y., Tanis, J., Eds.; NATO Advanced Study Institute Series B: Physics; Plenum Publishing Corporation: New York, NY, USA, 1992; Volume 296, pp. 31–48. [Google Scholar]
- Kunze, H.J. Introduction to Plasma Spectroscopy, Springer Series on Atomic, Optical, and Plasma Physics; Springer: Berlin, Germany, 2009. [Google Scholar]
- Tallents, G.J. An Introduction to the Atomic and Radiation Physics of Plasmas; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Becker, R.L.; Ford, A.L.; Reading, J.F. Multiple-vacancy production in the independent-Fermi-particle model. Phys. Rev. A 1984, 29, 3111–3121. [Google Scholar] [CrossRef] [Green Version]
- Stolterfoht, N. Electron Correlation Processes in Energetic Ion-Atom Collisions. In Spectroscopy and Collisions of Few-Electron Ions; Ivascu, M., Florescu, V., Zoran, V., Eds.; World Scientific: Singapore; London, UK, 1989; p. 342. [Google Scholar]
- Stolterfoht, N. Dynamics of Electron Correlation Processes in Atoms and Atomic Collisions. Phys. Scr. 1990, 42, 192–204. [Google Scholar] [CrossRef]
- Mcguire, J. Multiple-Electron Excitation, Ionization, and Transfer in High-Velocity Atomic and Molecular Collisions. Adv. At. Mol. Opt. Phys. 1991, 29, 217–323. [Google Scholar]
- Zouros, T.J.M. Resonant Transfer and Excitation Associated with Auger Electron Emission. In Recombination of Atomic Ions; Graham, W.G., Fritsch, W., Hahn, Y., Tanis, J., Eds.; NATO Advanced Study Institute Series B: Physics; Plenum Publishing Corporation: New York, NY, USA, 1992; Volume 296, pp. 271–300. [Google Scholar]
- Lee, D.H.; Zouros, T.J.M.; Sanders, J.M.; Richard, P.; Anthony, J.M.; Wang, Y.D.; McGuire, J.H. K-shell Ionization of O4+ and C2+ ions in fast collisions with H2 and He targets. Phys. Rev. A 1992, 46, 1374–1387. [Google Scholar] [CrossRef] [PubMed]
- Montenegro, E.C.; Meyerhof, W.E.; McGuire, J.H. Role of two–center electron-electron interaction in projectile electron excitation and loss. Adv. At. Mol. Opt. Phys. 1994, 34, 249–300. [Google Scholar]
- Zouros, T.J.M. Excitation and ionization in fast ion-atom collisions due to projectile electron–target electron interactions. In Applications of Particle and Laser Beams in Materials Technology; Misailides, P., Ed.; NATO Advanced Study Institute Series E: Applied Sciences; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1995; Volume 283, pp. 37–52. [Google Scholar]
- Zouros, T.J.M. Projectile-Electron—Target-Electron Interactions: Exposing the Dynamic Role of Electrons in Fast Ion-Atom Collisions. Comments At. Mol. Phys. 1996, 32, 291–313. [Google Scholar]
- Zouros, T.J.M.; Benis, E.P.; Gorczyca, T.W. Large-angle elastic resonant and non-resonant scattering of electrons from B3+(1s2) and B4+(1s) ions: Comparison of experiment and theory. Phys. Rev. A 2003, 68, R010701. [Google Scholar] [CrossRef]
- Benis, E.P.; Zouros, T.J.M.; Gorczyca, T.W.; González, A.D.; Richard, P. Elastic resonant and non-resonant differential scattering of quasi-free electrons from B4+(1s) and B3+(1s2) ions. Phys. Rev. A 2004, 69, 052718. [Google Scholar]
- Stolterfoht, N. High resolution Auger spectroscopy in energetic ion atom collisions. Phys. Rep. 1987, 146, 315–424. [Google Scholar] [CrossRef]
- Zouros, T.J.M.; Lee, D.H. Zero Degree Auger Electron Spectroscopy of Projectile Ions. In Accelerator-Based Atomic Physics Techniques and Applications; Shafroth, S.M., Austin, J.C., Eds.; American Institute of Physics: Woodbury, NY, USA, 1997; Chapter 13; pp. 426–479. [Google Scholar]
- Mack, M.; Niehaus, A. Radiative and Auger decay channels in K-Shell excited Li-like ions (Z = 6–8). Nucl. Instrum. Methods Phys. Res. B 1987, 23, 109–115. [Google Scholar] [CrossRef]
- Lee, D.H.; Richard, P.; Sanders, J.M.; Zouros, T.J.M.; Shinpaugh, J.L.; Varghese, S.L. Electron Capture and Excitation Studied by State-Resolved KLL Auger Measurement in 0.25-2 MeV/u F7+(1s21S,1s2s3S) + H2/He Collisions. Nucl. Instrum. Methods Phys. Res. B 1991, 56/57, 99–103. [Google Scholar] [CrossRef]
- Tanis, J.A.; Landers, A.L.; Pole, D.J.; Alnaser, A.S.; Hossain, S.; Kirchner, T. Evidence for Pauli Exchange Leading to Excited-State Enhancement in Electron Transfer. Phys. Rev. Lett. 2004, 92, 133201. [Google Scholar] [CrossRef] [PubMed]
- Mack, M.; Niehaus, A. Double electron capture by He-like ions: Collision energy dependence of the reaction window. Nucl. Instrum. Methods Phys. Res. B 1987, 23, 116–119. [Google Scholar] [CrossRef]
- Zouros, T.J.M.; Lee, D.H.; Richard, P. Projectile 1s→2p Excitation Due to Electron-Electron Interaction in Collisions of F6+ and O5+ Ions with He and H2 Targets. Phys. Rev. Lett. 1989, 62, 2261–2264. [Google Scholar] [CrossRef] [PubMed]
- Zouros, T.J.M.; Lee, D.H.; Sanders, J.M.; Shinpaugh, J.L.; Tipping, T.N.; Varghese, S.L.; Richard, P. High Resolution Studies of Electron Capture and Excitation by 0∘ Projectile Electron Spectroscopy. Nucl. Instrum. Methods Phys. Res. B 1989, 40/41, 17. [Google Scholar] [CrossRef]
- Zouros, T.J.M.; Lee, D.H.; Richard, P.; Sanders, J.M.; Shinpaugh, J.L.; Varghese, S.L.; Karim, K.R.; Bhalla, C.P. State-Selective Observation of Resonance Transfer-Excitation (RTE) in Collisions of F6+ with He and H2 Targets. Phys. Rev. A 1989, 40, 6246. [Google Scholar] [CrossRef]
- Graham, W.G.; Fritsch, W.; Hahn, Y.; Tanis, J. (Eds.) Recombination of Atomic Ions; NATO Advanced Study Institute Series B: Physics; Plenum Publishing Corporation: New York, NY, USA, 1992; Volume 296. [Google Scholar]
- Lee, D.H.; Richard, P.; Sanders, J.M.; Zouros, T.J.M.; Shinpaugh, J.L.; Varghese, S.L. KLL resonant transfer and excitation to F6+(1s2l2l′) intermediate states. Phys. Rev. A 1991, 44, 1636–1643. [Google Scholar] [CrossRef] [PubMed]
- Benis, E.P.; Zouros, T.J.M.; Gorczyca, T.W.; Zamkov, M.; Richard, P. Isoelectronic study of triply excited Li-like states. J. Phys. B 2003, 36, L341–L348. [Google Scholar] [CrossRef]
- Závodszky, P.A.; Aliabadi, H.; Bhalla, C.P.; Richard, P.; Tóth, G.; Tanis, J.A. Superelastic scattering of electrons from highly charged ions with inner shell vacancies. Phys. Rev. Lett. 2001, 87, 033202. [Google Scholar] [CrossRef] [PubMed]
- Alnaser, A.S.; Landers, A.L.; Pole, D.J.; Hossain, S.; Haija, O.A.; Gorczyca, T.W.; Tanis, J.A.; Knutson, H. Supereleastic scattering of electrons from metastable He-like C4+ and O6+ ions. Phys. Rev. A 2002, 65, 042709. [Google Scholar] [CrossRef]
- Borovik, A., Jr.; Müller, A.; Schippers, S.; Bray, I.; Fursa, D. Electron impact ionization of ground-state and metastable Li+ ions. J. Phys. B 2009, 42, 025203. [Google Scholar] [CrossRef]
- Renwick, A.C.; Bray, I.; Fursa, D.V.; Jacobi, J.; Knopp, H.; Schippers, S.; Müller, A. Electron-impact ionization of B3+ ions. J. Phys. B 2009, 42, 175203. [Google Scholar] [CrossRef]
- Schlummer, T.; Marchuk, O.; Schultz, D.; Bertschinger, G.; Biel, W.; Reiter, D.; Textor-Team, T. Comparison of effective rate coefficients for high energy charge-exchange with measurements of the Rydberg series of Ar16+ at the tokamak TEXTOR. J. Phys. B 2015, 48, 144033. [Google Scholar] [CrossRef]
- Cui, Z.; Morita, S.; Zhou, H.; Ding, X.; Sun, P.; Kobayashi, M.; Cui, X.; Xu, Y.; Huang, X.; Shi, Z.; et al. Enhancement of edge impurity transport with ECRH in the HL-2A tokamak. Nucl. Fusion 2013, 53, 093001. [Google Scholar] [CrossRef]
- Liu, L.; Jakimovski, D.; Wang, J.G.; Janev, R.K. Electron capture and excitation in H+-He (1s2s; 1,3 S) collisions. J. Phys. B 2012, 45, 225203. [Google Scholar] [CrossRef]
- Trassinelli, M.; Prigent, C.; Lamour, E.; Mezdari, F.; Merot, J.; Reuschl, R.; Rozet, J.P.; Steydli, S.; Vernhet, D. Investigation of slow collisions for (quasi) symmetric heavy systems: what can be extracted from high resolution x-ray spectra. J. Phys. B 2012, 45, 085202. [Google Scholar] [CrossRef] [Green Version]
- Nandi, T.; Oswal, M.; Kumar, S.; Jhingan, A.; Abhilash, S.; Karmakar, S. Radiative resonant energy transfer: A new excitation process of beam-foil interaction. J. Quant. Spectrosc. Radiat. Transf. 2012, 113, 783–788. [Google Scholar] [CrossRef]
- Lin, Y.C.; Ho, Y. Quantum entanglement for two electrons in the excited states of helium-like systems. Can. J. Phys. 2014, 93, 646–653. [Google Scholar] [CrossRef]
- Betz, H.D. Charge States and Charge-Changing Cross Sections of Fast Heavy Ions Penetrating Through Gaseous and Solid Media. Rev. Mod. Phys. 1972, 44, 465–539. [Google Scholar] [CrossRef]
- Sayer, R. Semi-empirical formulas for heavy-ion stripping data. Rev. Phys. Appl. 1977, 12, 1543–1546. [Google Scholar] [CrossRef]
- Rozet, J.; StÃphan, C.; Vernhet, D. ETACHA: A program for calculating charge states at {GANIL} energies. Nucl. Instrum. Methods Phys. Res. B 1996, 107, 67–70. [Google Scholar] [CrossRef]
- Dmitriev, I.S.; Nikolaev, V.S. Semi-empirical method for the calculation of the equilibrium distribution of charges in a fast-ion beam. Sov. Phys. JETP 1965, 20, 409–415. [Google Scholar]
- Shima, K.; Kuno, N.; Yamanouchi, M.; Tawara, H. Equilibrium Charge Fractions of Ions of Z = 4–92 Emerging From A Carbon Foil. At. Data Nucl. Data Tables 1992, 51, 173–241. [Google Scholar] [CrossRef]
- Schiwietz, G.; Grande, P. Improved charge-state formulas. Nucl. Instrum. Methods Phys. Res. B 2001, 175–177, 125–131. [Google Scholar] [CrossRef]
- Asimakopoulou, E.M. TARDIS (Transmitted chARge DIStribution); Technical Report; Institute of Nuclear and Particle Physics and Department of Physics, University of Athens: Athens, Greece, 2014. [Google Scholar]
- Hvelplund, P. Energy Loss and Straggling of 100–500-keV 90Th, 82Pb, 80Hg and 64Gd in H2. Phys. Rev. A 1975, 11, 1921–1927. [Google Scholar] [CrossRef]
- Andersen, L.H.; Bolbo, J.; Kvistgaard, P. State-selective dielectronic-recombination measurements for He- and Li-like carbon and oxygen ions. Phys. Rev. A 1990, 41, 1293–1302. [Google Scholar] [CrossRef] [PubMed]
- Andersen, L.H.; Pan, G.Y.; Schmidt, H.T.; Badnell, N.R.; Pindzola, M.S. Absolute measurements and calculaitons of Dielectronic Recombination with metastable He- N, F, and Si ions. Phys. Rev. A 1992, 45, 7868–7875. [Google Scholar] [CrossRef] [PubMed]
- Andersen, L.H.; Hvelplund, P.; Knudsen, H.; Kvistgaard, P. State-selective Dielectronic-Recombination measurements for He-like Oxygen ions in an electron cooler. Phys. Rev. Lett. 1989, 62, 2656. [Google Scholar] [CrossRef] [PubMed]
- Kilgus, G.; Habs, D.; Schwalm, D.; Wolf, A.; Schuch, R.; Badnell, N.R. Dielectronic recombination from ground state of heliumlike carbon ions. Phys. Rev. A 1993, 47, 4859. [Google Scholar] [CrossRef] [PubMed]
- Benis, E.P.; Zamkov, M.; Richard, P.; Zouros, T.J.M. Comparison of two experimental techniques for the determination of the 1s2s3S metastable beam fraction in energetic B3+ions. Nucl. Instrum. Methods Phys. Res. B 2003, 205, 517–521. [Google Scholar] [CrossRef]
- Strohschein, D.; Röhrbein, D.; Kirchner, T.; Fritzsche, S.; Baran, J.; Tanis, J.A. Nonstatistical enhancement of the 1s2s2p4P state in electron transfer in 0.5–1.0-MeV/u C4,5+ + He and Ne collisions. Phys. Rev. A 2008, 77, 022706. [Google Scholar] [CrossRef]
- Benis, E.P.; Zouros, T.J.M. Determination of the 1s2ℓ2ℓ′ state production ratios 4Po/2P, 2D/2P and 2P+/2P- from fast (1s2,1s2s3S) mixed-state He-like ion beams in collisions with H2 targets. J. Phys. B 2016, 49, 235202. [Google Scholar] [CrossRef]
- Schiebel, U.; Doyle, B.L.; Macdonald, J.R.; Ellsworth, L.D. Projectile K x rays from Si12+ ions in the 1s2s 3S1 metastable state incident on helium gas. Phys. Rev. A 1977, 16, 1089. [Google Scholar] [CrossRef]
- Terasawa, M.; Gray, T.J.; Hagmann, S.; Hall, J.; Newcomb, J.; Pepmiller, P.; Richard, P. Electron capture by and electron excitation of two-electron fluorine ions incident on helium. Phys. Rev. A 1983, 27, 2868–2875. [Google Scholar] [CrossRef]
- Zamkov, M.; Aliabadi, H.; Benis, E.P.; Richard, P.; Tawara, H.; Zouros, T.J.M. Energy dependence of the metastable fraction in B3+(1s21S,1s2s3S) beams produced in collisions with solid and gas targets. Phys. Rev. A 2001, 64, 052702. [Google Scholar] [CrossRef]
- Zamkov, M.; Benis, E.P.; Richard, P.; Zouros, T.J.M. Fraction of metastable 1s2s3S ions in fast He-like beams (Z = 5–9) produced in collisions with carbon foils. Phys. Rev. A 2002, 65, 062706. [Google Scholar] [CrossRef]
- Benis, E.P.; Zamkov, M.; Richard, P.; Zouros, T.J.M. Technique for the determination of the 1s2s 3S metastable fraction in two-electron ion beams. Phys. Rev. A 2002, 65, 064701. [Google Scholar] [CrossRef]
- Lamour, E.; Gervais, B.; Rozet, J.P.; Vernhet, D. Production and transport of long-lifetime excited states in preequilibrium ion-solid collisions. Phys. Rev. A 2006, 73, 042715. [Google Scholar] [CrossRef]
- Drake, G.W.F.; Victor, G.A.; Dalgarno, A. Two-Photon Decay of the Singlet and Triplet Metastable States of Helium-like Ions. Phys. Rev. 1969, 180, 25–32. [Google Scholar] [CrossRef] [Green Version]
- Drake, G.W.F. Theory of Relativistic Magnetic Dipole Transitions: Lifetime of the Metastable 23S State of the Heliumlike Ions. Phys. Rev. A 1971, 3, 908–915. [Google Scholar] [CrossRef]
- Fischer, C.F.; Gaigalas, G. Note on the 2s 2 1 S 0 -2s2p 3 P 1 intercombination line of B II and C III. Phys. Scr. 1997, 56, 436. [Google Scholar] [CrossRef]
- Fischer, C.F. Multiconfiguration Dirac-Hartree-Fock Calculations for Be-like Intercombination Lines Revisited. Phys. Scr. 2000, 62, 458. [Google Scholar] [CrossRef]
- Madesis, I.; Dimitriou, A.; Laoutaris, A.; Lagoyannis, A.; Axiotis, M.; Mertzimekis, T.; Andrianis, M.; Harissopulos, S.; Benis, E.P.; Sulik, B.; et al. Atomic Physics with Accelerators: Projectile Electron Spectroscopy (APAPES). J. Phys: Conf. Ser. 2015, 583, 012014. [Google Scholar] [CrossRef]
- Turner, B.R.; Rutherford, J.A.; Compton, D.M.J. Abundance of Excited Ions in O+ and O2+ Ion Beams. J. Chem. Phys. 1968, 48, 1602–1608. [Google Scholar] [CrossRef]
- Pedersen, E.H. Metastable-Atom Population of Fast, Neutral Helium Beams. Phys. Rev. Lett. 1979, 42, 440–443. [Google Scholar] [CrossRef]
- Meyer, F.; Havener, C.; Phaneuf, R.; Swenson, J.; Shafroth, S.; Stolterfoht, N. Evidence for correlated double-electron capture in slow collisions of multicharged ions with He and H2. Nucl. Instrum. Methods Phys. Res. B 1987, 24–25, 106–110. [Google Scholar] [CrossRef]
- Müller, A.; Borovik, A.; Buhr, T.; Hellhund, J.; Holste, K.; Kilcoyne, A.L.D.; Klumpp, S.; Martins, M.; Ricz, S.; Viefhaus, J.; Schippers, S. Near-K-edge single, double, and triple photoionization of C+ ions. Phys. Rev. A 2018, 97, 013409. [Google Scholar] [CrossRef]
- Cocke, C.L.; Varghese, S.L.; Curnutte, B. Yields of K-vacancy-bearing metastable states following foil excitation. Phys. Rev. A 1977, 15, 874. [Google Scholar] [CrossRef]
- Welton, R.F.; Moran, T.F.; Thomas, E.W. Metastable state abundances in multiply charged ion beams. J. Phys. B 1991, 24, 3815. [Google Scholar] [CrossRef]
- Bliek, F.W.; Hoekstra, R.; Bannister, M.E.; Havener, C.C. Low-energy electron capture by C4+ ions from atomic hydrogen. Phys. Rev. A 1997, 56, 426. [Google Scholar] [CrossRef]
- Müller, A.; Borovik, A.; Huber, K.; Schippers, S.; Fursa, D.V.; Bray, I. Double-K-vacancy states in electron- impact single ionization of metastable two-electron N5+(1s2s3S1) ions. Phys. Rev. A 2014, 90, 010701. [Google Scholar] [CrossRef]
- Meyerhof, W.E. K-Vacancy Sharing in Near-Symmetric Heavy-Ion Collisions. Phys. Rev. Lett. 1973, 31, 1341–1344. [Google Scholar] [CrossRef]
- Benis, E.P.; Doukas, S.; Zouros, T.J.M. Evidence for the non-statistical population of the 1s2s2p4P metastable state by electron capture in 4 MeV collisions of B3+(1s2s3S) with H2 targets. Nucl. Instrum. Methods Phys. Res. B 2016, 369, 83–86. [Google Scholar] [CrossRef]
- Doerfert, J.; Träbert, E.; Wolf, A.; Schwalm, D.; Uwira, O. Precision Measurement of the Electric Dipole Intercombination Rate in C2+. Phys. Rev. Lett. 1997, 78, 4355–4358. [Google Scholar] [CrossRef]
- Träbert, E.; Wolf, A.; Gwinner, G. Measurement of EUV intercombination transition rates in Be-like ions at a heavy-ion storage ring. Phys. Lett. A 2002, 295, 44–49. [Google Scholar] [CrossRef]
- Müller, A.; Schippers, S.; Phaneuf, R.A.; Kilcoyne, A.L.D.; Bräuning, H.; Schlachter, A.S.; Lu, M.; McLaughlin, B.M. Fine-structure resolved photoionization of metastable Be-like ions C III, N IV, and O V. J. Phys. Conf. Ser. 2007, 58, 383–386. [Google Scholar] [CrossRef]
- Stolterfoht, N.; Miller, P.D.; Krause, H.F.; Yamazaki, Y.; Swenson, J.K.; Bruch, R.; Dittner, P.F.; Pepmiller, P.L.; Datz, S. Surgery of fast, highly charged ions studied by zero-degree Auger spectroscopy. Nucl. Instrum. Methods Phys. Res. B 1987, 24/25, 168–172. [Google Scholar] [CrossRef]
- Scully, S.W.J.; Aguilar, A.; Emmons, E.D.; Phaneuf, R.A.; Halka, M.; Leitner, D.; Levin, J.C.; Lubell, M.S.; Püttner, R.; Schlachter, A.S.; et al. K-shell photoionization of Be-like carbon ions: experiment and theory for C2+. J. Phys. B 2005, 38, 1967–1975. [Google Scholar] [CrossRef]
- Shorman, M.M.A.; Gharaibeh, M.F.; Bizau, J.M.; Cubaynes, D.; Guilbaud, S.; Hassan, N.E.; Miron, C.; Nicolas, C.; Robert, E.; Sakho, I.; et al. K-shell photoionization of Be-like and Li-like ions of atomic nitrogen: experiment and theory. J. Phys. B 2013, 46, 195701. [Google Scholar] [CrossRef]
- Müller, A.; Schippers, S.; Phaneuf, R.A.; Scully, S.W.J.; Aguilar, A.; Cisneros, C.; Gharaibeh, M.F.; Schlachter, A.S.; McLaughlin, B.M. K-shell photoionization of Be-like boron (B+) ions: experiment and theory. J. Phys. B 2014, 47, 135201. [Google Scholar] [CrossRef]
- McLaughlin, B.M.; Bizau, J.M.; Cubaynes, D.; Guilbaud, S.; Douix, S.; Shorman, M.M.A.; Ghazaly, M.O.A.E.; Sakho, I.; Gharaibeh, M.F. K-shell photoionization of O4+ and O5+ ions: experiment and theory. MNRAS 2017, 465, 4690–4702. [Google Scholar] [CrossRef]
- Benis, E.P.; Madesis, I.; Laoutaris, A.; Nanos, S.; Zouros, T.J.M. Experimental determination of the effective solid angle of long-lived projectile states in zero-degree Auger projectile spectroscopy. J. Electron Spectrosc. Relat. Phenom. 2018, 222, 31–39. [Google Scholar] [CrossRef]
- Doukas, S.; Madesis, I.; Dimitriou, A.; Laoutaris, A.; Zouros, T.J.M.; Benis, E.P. Determination of the solid angle and response function of a hemispherical spectrograph with injection lens for Auger electrons emitted from long lived projectile states. Rev. Sci. Instrum. 2015, 86, 043111. [Google Scholar] [CrossRef] [PubMed]
- Benis, E.; Doukas, S.; Zouros, T.; Indelicato, P.; Parente, F.; Martins, C.; Santos, J.; Marques, J. Evaluation of the effective solid angle of a hemispherical deflector analyser with injection lens for metastable Auger projectile states. Nucl. Instrum. Methods Phys. Res. B 2015, 365, 457–461. [Google Scholar] [CrossRef]
- SIMION 8.1.3.4; Scientific Instrument Services, Inc.: Ringoes, NJ, USA, 2017; Available online: http://www.simion.com (accessed on 01 April 2017).
- Zamkov, M.; Aliabadi, H.; Benis, E.P.; Richard, P.; Tawara, H.; Zouros, T.J.M. Absolute cross sections and decay rates for the triply excited B2+(2s2p22D) resonance in electron–metastable-ion collisions. Phys. Rev. A 2002, 65, 032705. [Google Scholar] [CrossRef]
- Zouros, T.J.M.; Benis, E.P.; Gorczyca, T.W.; González, A.D.; Zamkov, M.; Richard, P. Differential electron scattering from positive ions measured by zero-degree ion-atom spectroscopy. Nucl. Instrum. Methods Phys. Res. B 2003, 205, 508–516. [Google Scholar] [CrossRef]
- Schneider, D.; Bruch, R.; Butscher, W.; Schwarz, W.H.E. Prompt and time-delayed electron decay-in-flight spectra of gas-excited carbon ions. Phys. Rev. A 1981, 24, 1223–1236. [Google Scholar] [CrossRef]
- Zouros, T.J.M.; Sulik, B.; Gulyás, L.; Tökési, K. Selective enhancement of 1s2s2p4PJ metastable states populated by cascades in single-electron transfer collisions of F7+(1s2/1s2s3S) ions with He and H2 targets. Phys. Rev. A 2008, 77, 050701. [Google Scholar] [CrossRef]
- Lamour, E.; Fainstein, P.D.; Galassi, M.; Prigent, C.; Ramirez, C.A.; Rivarola, R.D.; Rozet, J.P.; Trassinelli, M.; Vernhet, D. Extension of charge-state-distribution calculations for ion-solid collisions towards low velocities and many-electron ions. Phys. Rev. A 2015, 92, 042703. [Google Scholar] [CrossRef]
- Gao, J.W.; Wu, Y.; Sisourat, N.; Wang, J.G.; Dubois, A. Single- and double-electron transfer in low- and intermediate-energy C4+ + He collisions. Phys. Rev. A 2017, 96, 052703. [Google Scholar] [CrossRef]
- Gao, J.W.; Wu, Y.; Wang, J.G.; Sisourat, N.; Dubois, A. State-selective electron transfer in He++He collisions at intermediate energies. Phys. Rev. A 2018, 97, 052709. [Google Scholar] [CrossRef]
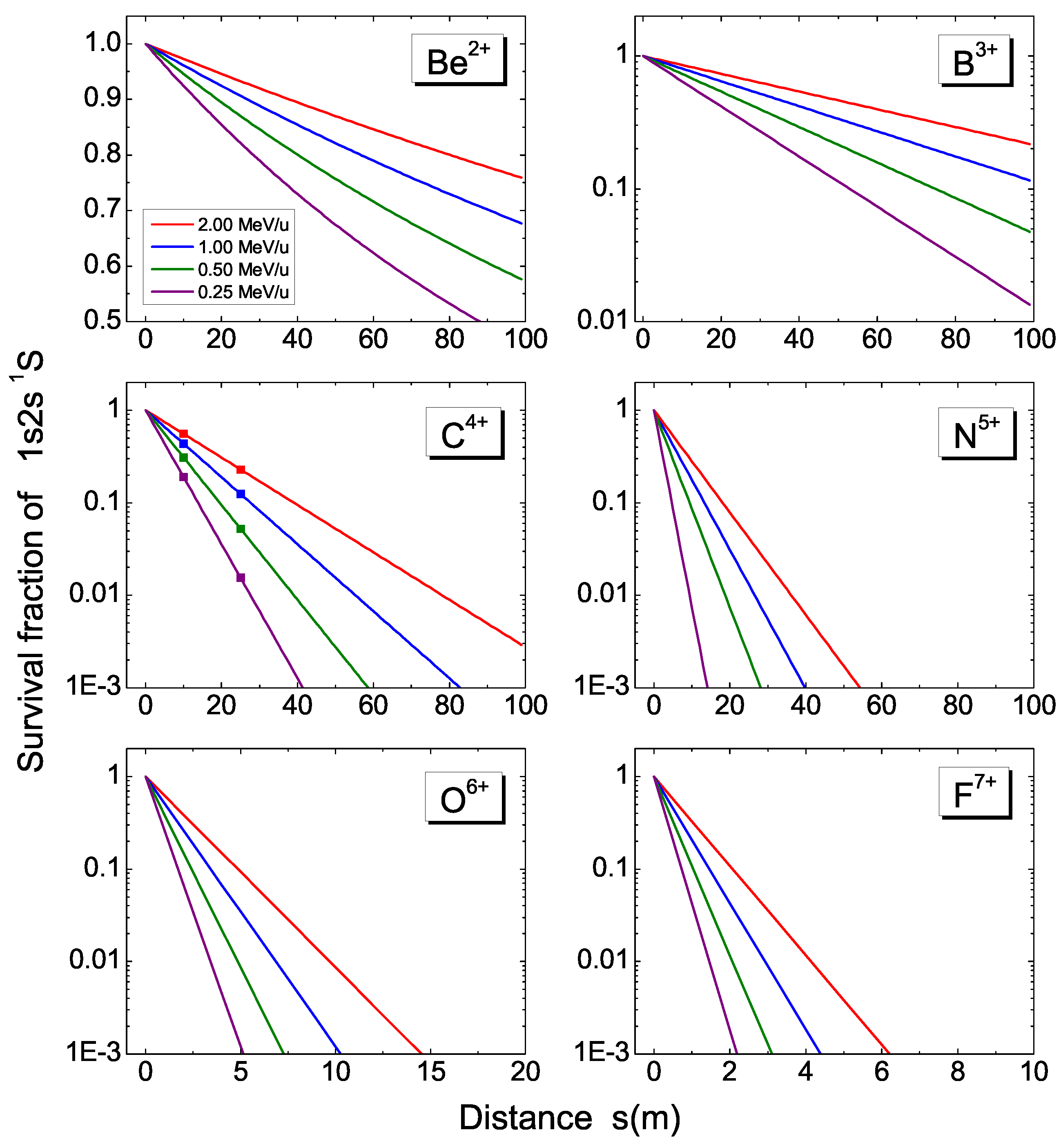
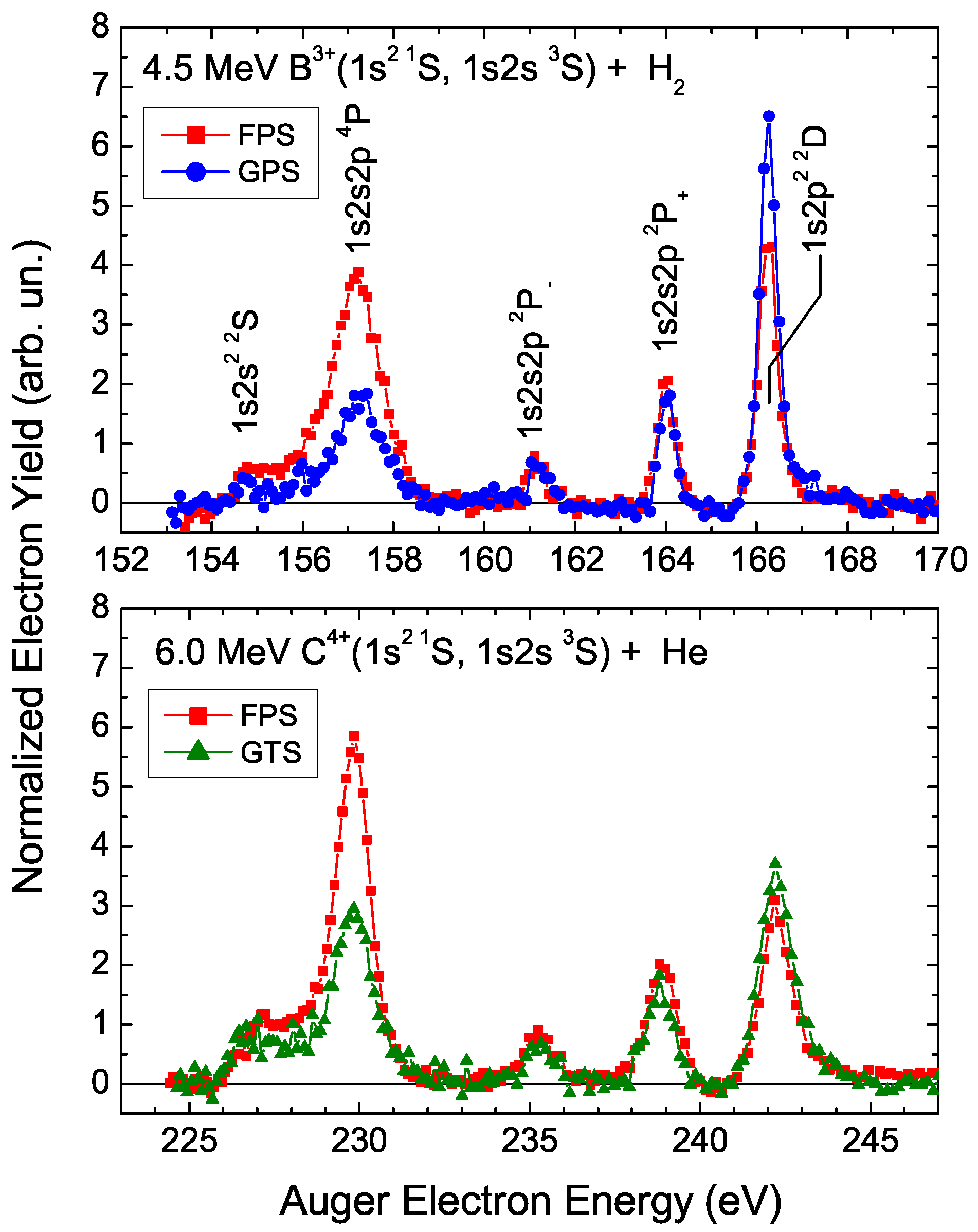
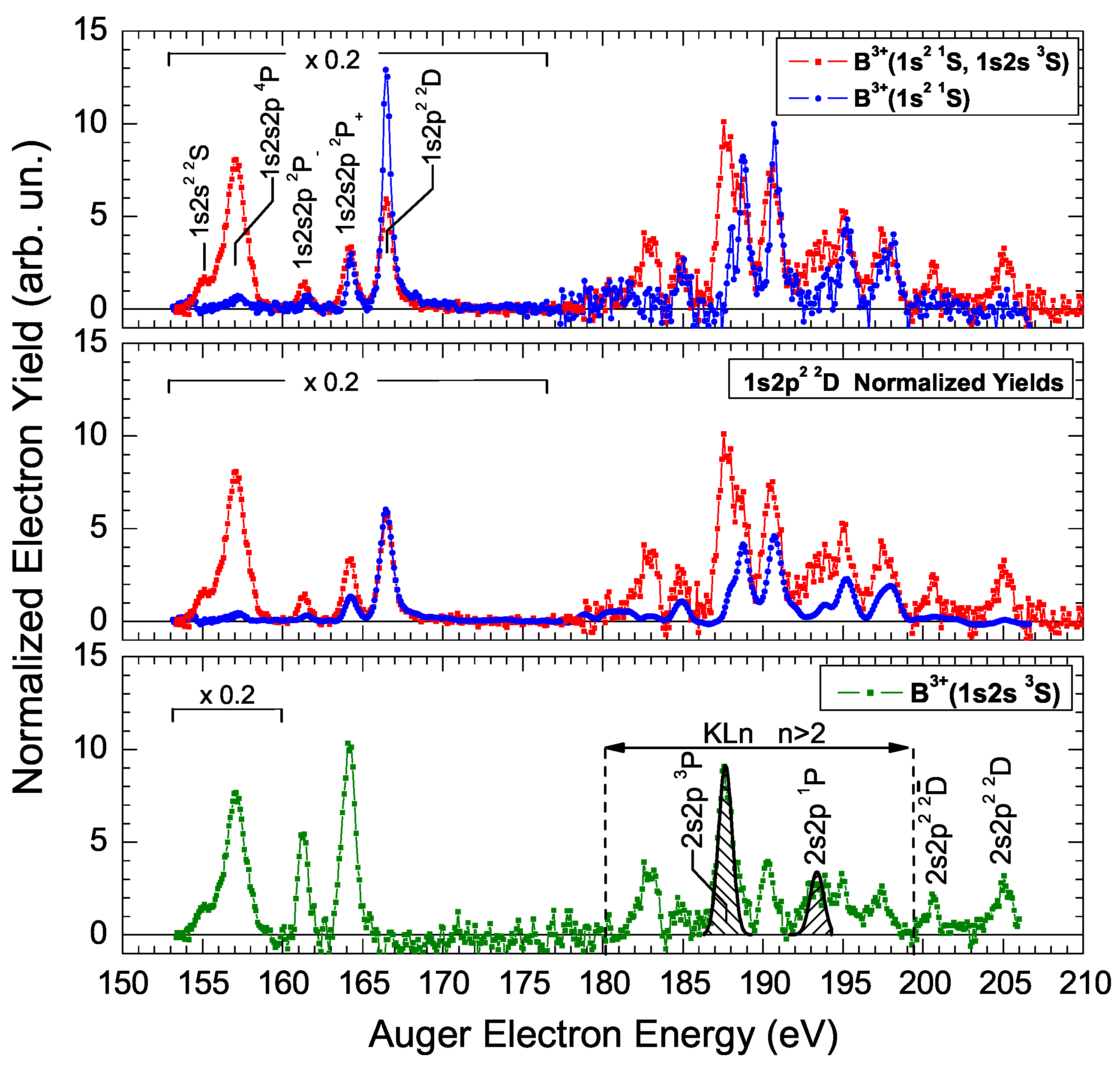
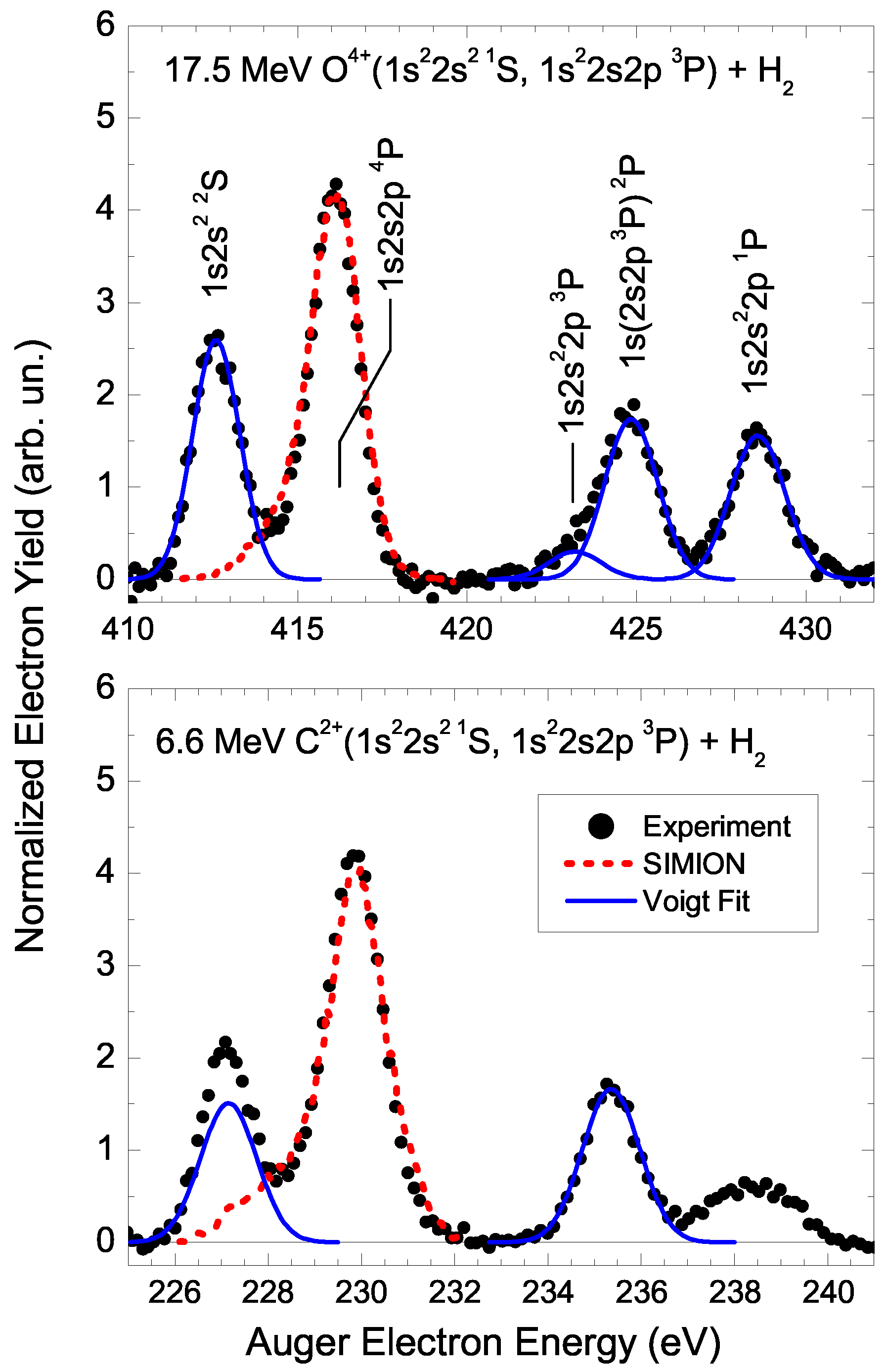
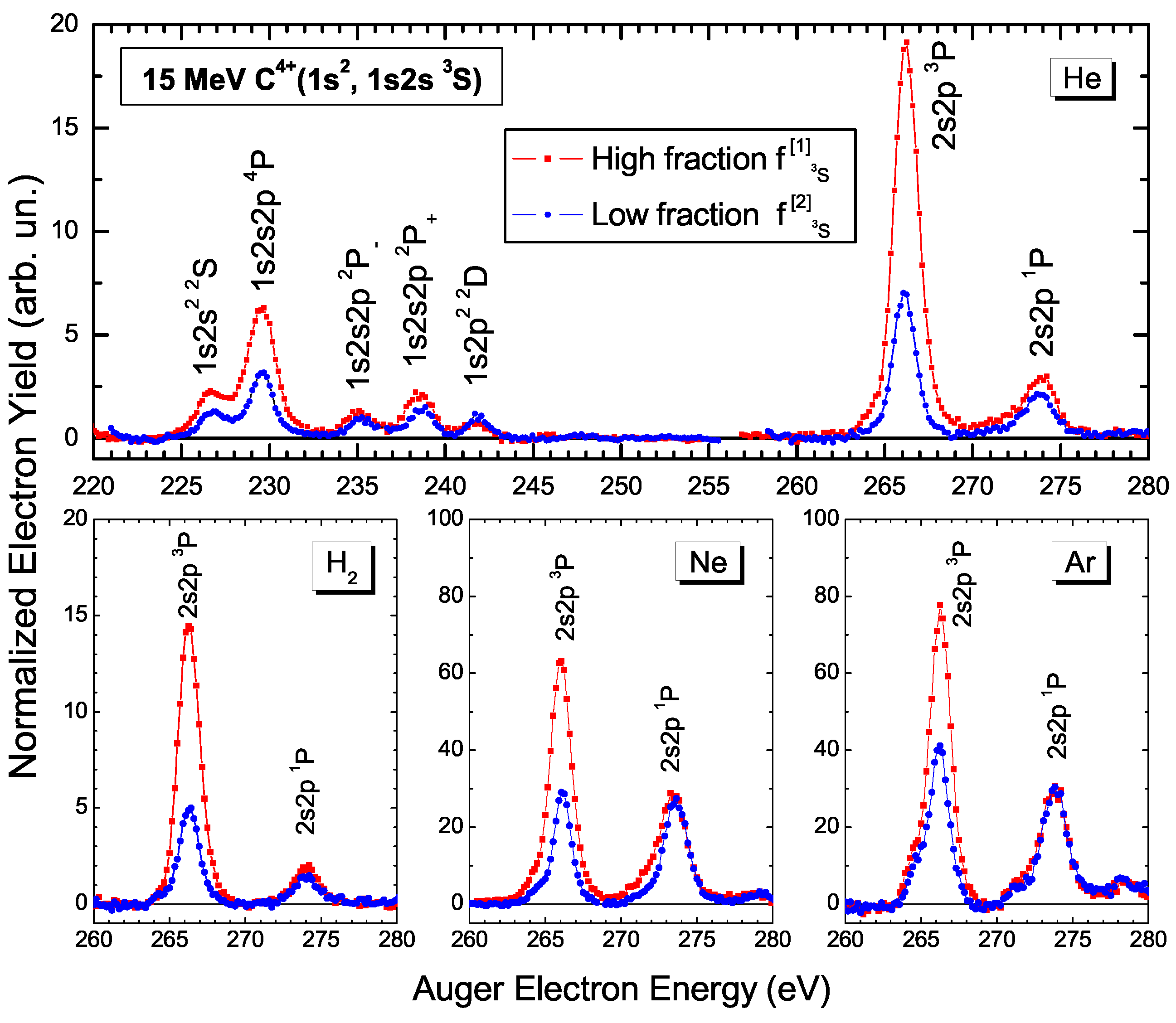
| 3 | - | ||
| 4 | - | ||
| 5 | |||
| 6 | |||
| 7 | |||
| 8 | |||
| 9 | |||
| 10 |
| Stripping | Incident | Stripping Energy | Final Energy | |
|---|---|---|---|---|
| Method | Ion | MeV | MeV | % |
| FPS | B | 4.5 | 4.5 | 42 (10) |
| GPS | B | 4.5 | 4.5 | 18 (5) |
| FPS | C | 6.0 | 6.0 | 16 (3) |
| GTS | C | 1.2 | 6.0 | 7 (2) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benis, E.P.; Madesis, I.; Laoutaris, A.; Nanos, S.; Zouros, T.J.M. Mixed-State Ionic Beams: An Effective Tool for Collision Dynamics Investigations. Atoms 2018, 6, 66. https://doi.org/10.3390/atoms6040066
Benis EP, Madesis I, Laoutaris A, Nanos S, Zouros TJM. Mixed-State Ionic Beams: An Effective Tool for Collision Dynamics Investigations. Atoms. 2018; 6(4):66. https://doi.org/10.3390/atoms6040066
Chicago/Turabian StyleBenis, Emmanouil P., Ioannis Madesis, Angelos Laoutaris, Stefanos Nanos, and Theo J. M. Zouros. 2018. "Mixed-State Ionic Beams: An Effective Tool for Collision Dynamics Investigations" Atoms 6, no. 4: 66. https://doi.org/10.3390/atoms6040066
APA StyleBenis, E. P., Madesis, I., Laoutaris, A., Nanos, S., & Zouros, T. J. M. (2018). Mixed-State Ionic Beams: An Effective Tool for Collision Dynamics Investigations. Atoms, 6(4), 66. https://doi.org/10.3390/atoms6040066







