Collision Strengths and Effective Collision Strengths for Allowed Transitions among the n ≤ 5 Degenerate Levels of Atomic Hydrogen
Abstract
1. Introduction
2. Theory
2.1. Close-Coupling Method
2.2. Born Approximation
2.3. The Choice of for Bethe–Born Approximation
3. Energy Levels
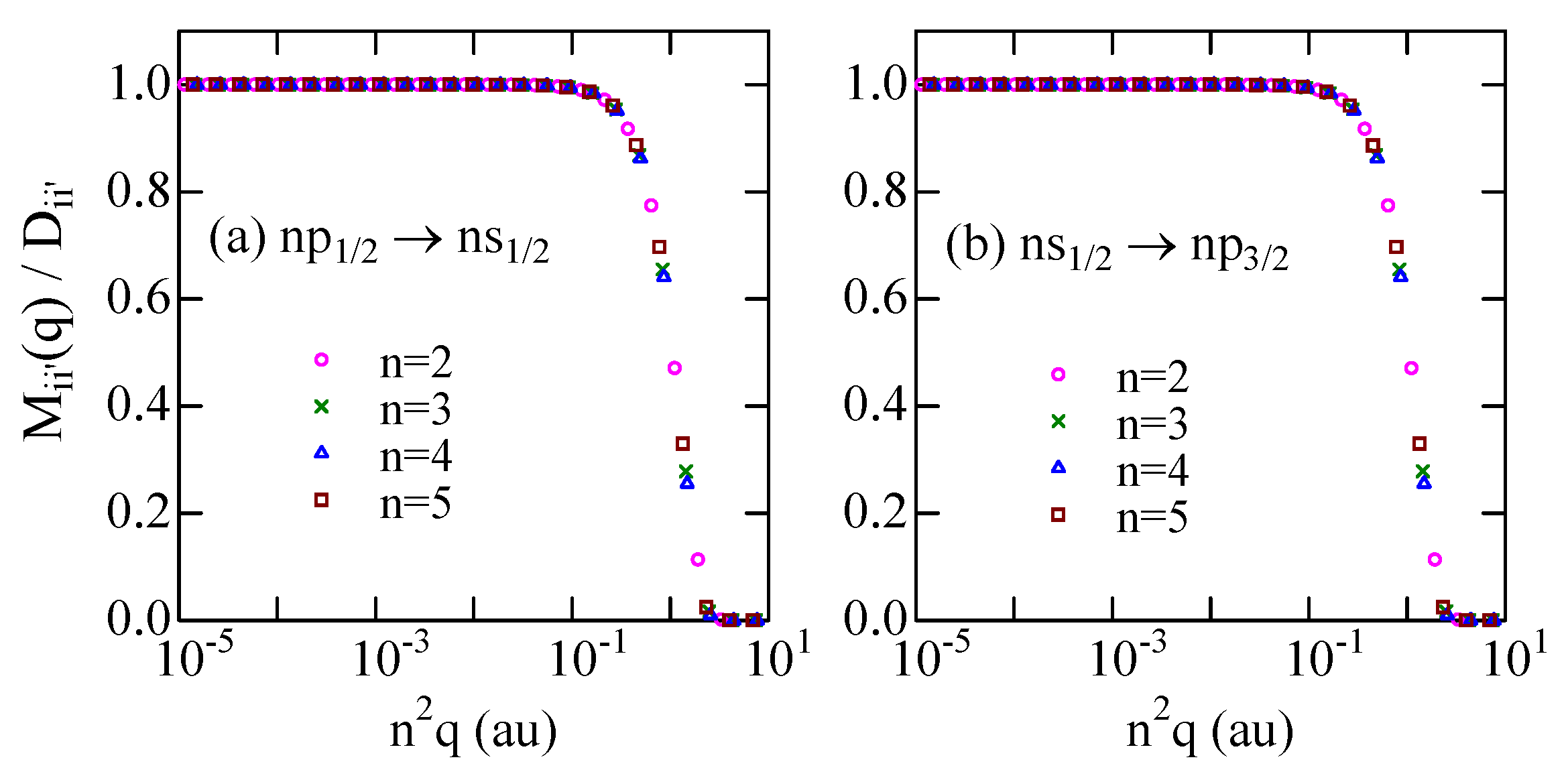
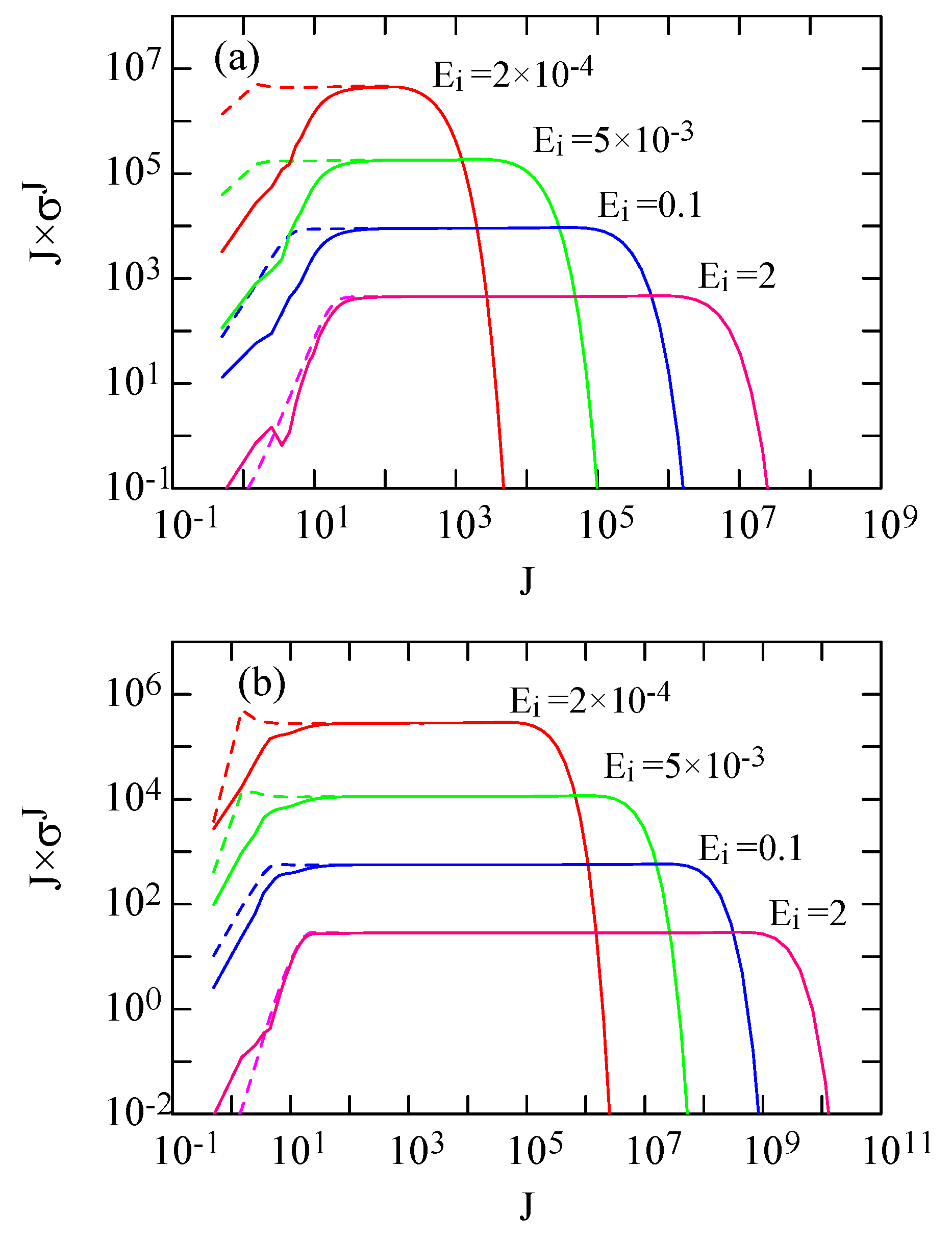
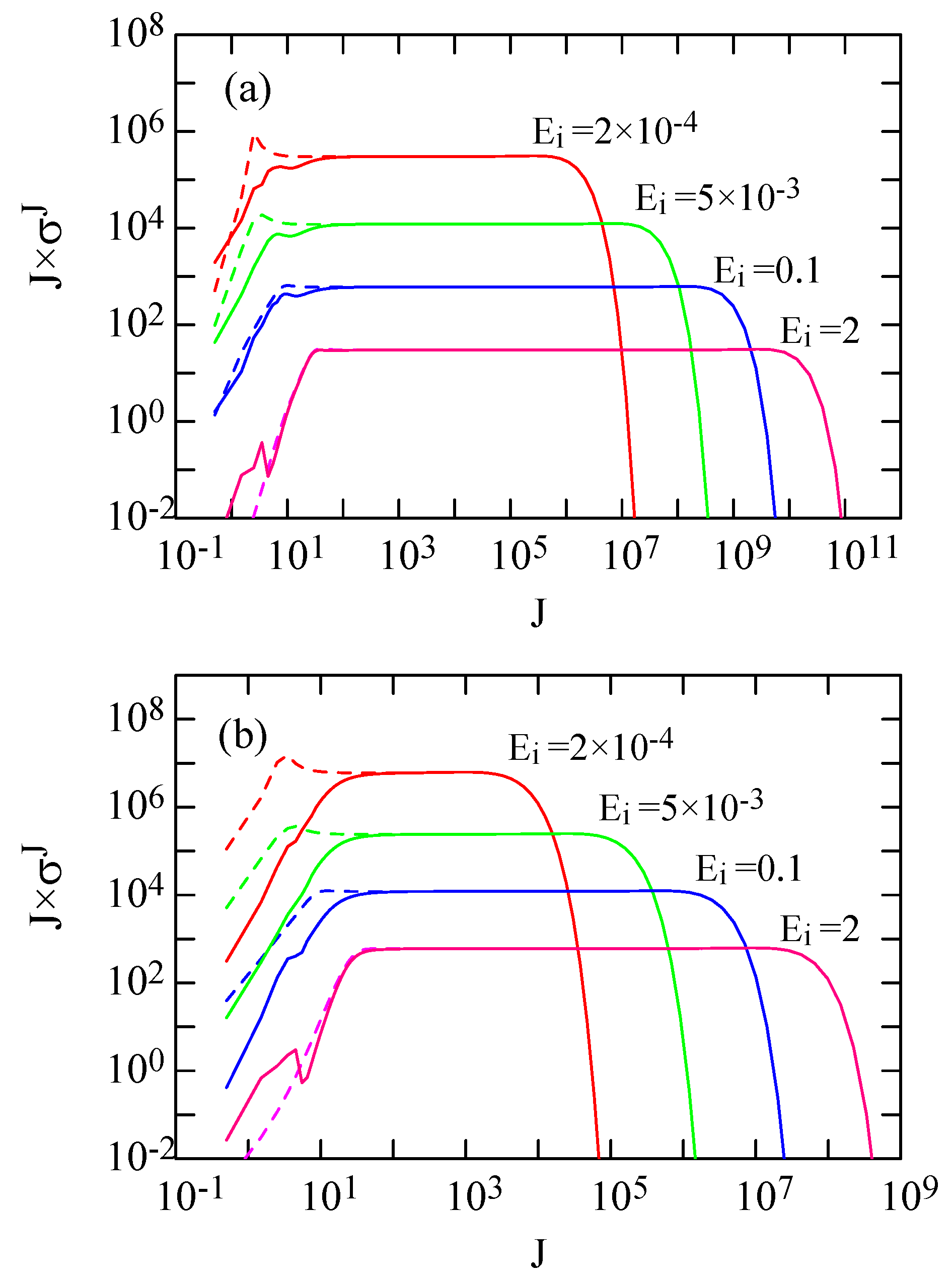
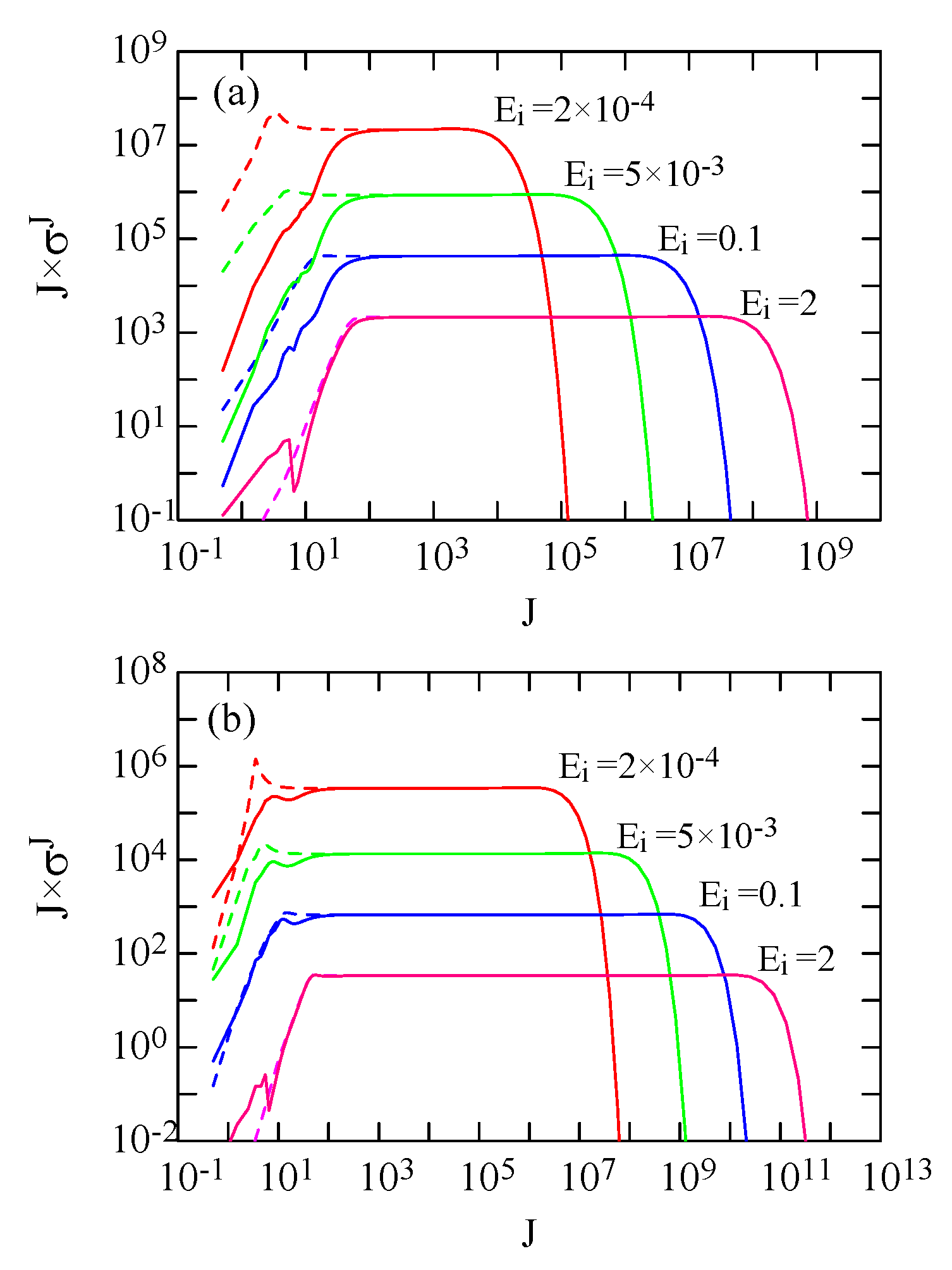
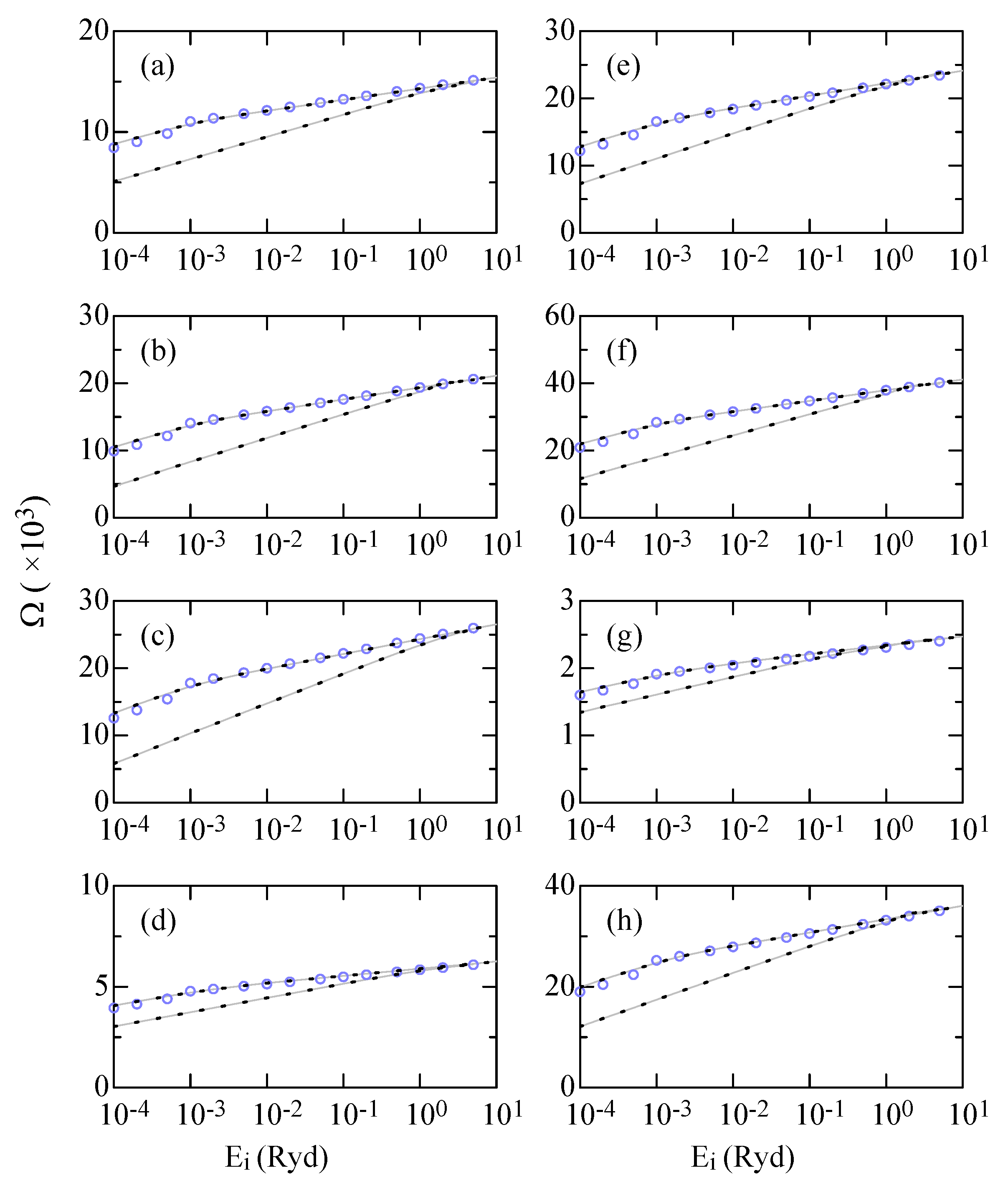
4. Partial Cross Sections and Collision Strengths
5. Effective Collision Strengths
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Kramida, A.E. A critical compilation of experimental data on spectral lines and energy levels of hydrogen, deuterium, and tritium. Atomic Data Nucl. Data Tables 2010, 96, 586–644. [Google Scholar] [CrossRef]
- Wiese, W.L.; Fuhr, J.R. Accurate atomic transition probabilities for hydrogen, helium, and lithium. J. Phys. Chem. Ref. Data 2009, 38, 565–720. [Google Scholar] [CrossRef]
- Anderson, H.; Ballance, C.P.; Badnell, N.R.; Summers, H.P. An R-matrix with pseudostates approach to the electron-impact excitation of H I for diagnostic applications in fusion plasmas. J. Phys. B 2000, 33, 1255. [Google Scholar] [CrossRef]
- Benda, J.; Houfek, K. Converged and consistent high-resolution low-energy electron-hydrogen scattering. I. Data below n = 4 threshold for applications in stellar physics. Atomic Data Nucl. Data Tables 2018, 119, 303–313. [Google Scholar] [CrossRef]
- Aggarwal, K.M.; Berrington, K.A.; Burke, P.G.; Kingston, A.E.; Pathak, A. Electron collision cross sections at low energies for all transitions between the n = 1, 2, 3, 4 and 5 levels of atomic hydrogen. J. Phys. B 1991, 24, 1385–1410. [Google Scholar] [CrossRef]
- Henry, R.J.W. Excitation of atomic positive ions by electron impact. Phys. Rep. 1981, 6, 1–91. [Google Scholar] [CrossRef]
- Anderson, H.; Ballance, C.P.; Badnell, N.R.; Summers, H.P. Corrigendum: An R-matrix with pseudostates approach to the electron-impact excitation of H I for diagnostic applications in fusion plasmas. J. Phys. B 2002, 35, 1613. [Google Scholar] [CrossRef]
- Lavrov, B.P.; Pipa, A.V. Account of the fine structure of hydrogen atom levels in the effective emission cross sections of Balmer lines excited by electron impact in gases and plasma. Opt. Spectrosc. 2002, 92, 647–657. [Google Scholar] [CrossRef]
- Wünderlich, D.; Dietrich, S.; Fantz, U. Application of a collisional radiative model to atomic hydrogen for diagnostic purposes. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 62–71. [Google Scholar] [CrossRef]
- Hamada, K.; Aggarwal, K.M.; Akita, K.; Igarashi, A.; Keenan, F.P.; Nakazaki, S. Effective collision strengths for optically allowed transitions among degenerate levels of hydrogenic ions with 2 ≤ Z ≤ 30. Atomic Data Nucl. Data Tables 2010, 96, 481–530. [Google Scholar] [CrossRef]
- Gu, M.F. The flexible atomic code. Can. J. Phys. 2008, 86, 675–689. [Google Scholar] [CrossRef]
- Lawson, K.D.; Aggarwal, K.M.; Coffey, I.H.; Keenan, F.P.; O’Mullane, M.G.; JET-EFDA Contributors. Population modelling of the He II energy levels in tokamak plasmas. I : Collisional excitation model. J. Phys. B 2018, 51. submitted. [Google Scholar]
- Igarashi, A.; Horiguchi, Y.; Ohsaki, A.; Nakazaki, S. Electron-impact excitations between the n = 2 fine-structure levels of hydrogenic ions. J. Phys. Soc. Jpn. 2003, 72, 307–312. [Google Scholar] [CrossRef]
- Igarashi, A.; Ohsaki, A.; Nakazaki, S. Electron-exchange effect in electron-impact excitation of the n = 2 fine-structure levels of hydrogenic ions. J. Phys. Soc. Jpn. 2005, 74, 321–325. [Google Scholar] [CrossRef]
- Aggarwal, K.M.; Igarashi, A.; Keenan, F.P.; Nakazaki, S. Radiative rates and electron impact excitation rates for transitions in He II. Atoms 2017, 5, 19. [Google Scholar] [CrossRef]
- Alder, K.; Bohr, A.; Huus, T.; Mottelson, B.; Winther, A. Study of nuclear structure by electromagnetic excitation with accelerated ions. Rev. Mod. Phys. 1956, 28, 432–542. [Google Scholar] [CrossRef]
- Alder, K.; Bohr, A.; Huus, T.; Mottelson, B.; Winther, A. Errata: Study of nuclear structure by electromagnetic excitation with accelerated ions. Rev. Mod. Phys. 1958, 30, 353. [Google Scholar] [CrossRef]

| a | |||
| Level | H | D | |
| 2 | 2p | 0.000000 + 0 | 0.000000 + 0 |
| 2s | 3.215489 − 7 | 3.219711 − 7 | |
| 2p | 3.334219 − 6 | 3.335129 − 6 | |
| 3 | 3p | 0.000000 + 0 | 0.000000 + 0 |
| 3s | 9.571226 − 8 | 9.583735 − 8 | |
| 3d | 9.862969 − 7 | 9.865650 − 7 | |
| 3p | 9.879176 − 7 | 9.881873 − 7 | |
| 3d | 1.315595 − 6 | 1.315953 − 6 | |
| 4 | 4p | 0.000000 + 0 | 0.00000 + 0 |
| 4s | 4.045105 − 8 | 4.050383 − 8 | |
| 4d | 4.160819 − 7 | 4.161950 − 7 | |
| 4p | 4.167772 − 7 | 4.168910 − 7 | |
| 4f | 5.547586 − 7 | 5.549094 − 7 | |
| 4d | 5.550046 − 7 | 5.551556 − 7 | |
| 4f | 6.242196 − 7 | 6.243893 − 7 | |
| 5 | 5p | 0.000000 + 0 | 0.000000 + 0 |
| 5s | 2.072911 − 8 | 2.075613 − 8 | |
| 5d | 2.130304 − 7 | 2.130883 − 7 | |
| 5p | 2.133897 − 7 | 2.134479 − 7 | |
| 5f | 2.840319 − 7 | 2.841091 − 7 | |
| 5d | 2.841589 − 7 | 2.842362 − 7 | |
| 5g | 3.195295 − 7 | 3.196164 − 7 | |
| 5f | 3.195959 − 7 | 3.196829 − 7 | |
| 5g | 3.408679 − 7 | 3.409606 − 7 | |
| b | |||
| Index | Level | H | D |
| 1 | 1s | 0.000 000 000 000 | 0.000 000 000 000 |
| 2 | 2p | 0.749 598 426 021 | 0.749 802 385 029 |
| 3 | 2s | 0.749 598 747 570 | 0.749 802 707 000 |
| 4 | 2p | 0.749 601 760 240 | 0.749 805 720 158 |
| 5 | 3p | 0.888 414 397 520 | 0.888 656 128 310 |
| 6 | 3s | 0.888 414 493 232 | 0.888 656 224 147 |
| 7 | 3d | 0.888 415 383 817 | 0.888 657 114 875 |
| 8 | 3p | 0.888 415 385 438 | 0.888 657 116 497 |
| 9 | 3d | 0.888 415 713 115 | 0.888 657 444 263 |
| 10 | 4p | 0.936 999 852 243 | 0.937 254 802 720 |
| 11 | 4s | 0.936 999 892 694 | 0.937 254 843 224 |
| 12 | 4d | 0.937 000 268 325 | 0.937 255 218 915 |
| 13 | 4p | 0.937 000 269 020 | 0.937 255 219 611 |
| 14 | 4f | 0.937 000 407 002 | 0.937 255 357 629 |
| 15 | 4d | 0.937 000 407 248 | 0.937 255 357 876 |
| 16 | 4f | 0.937 000 476 463 | 0.937 255 427 109 |
| 17 | 5p | 0.959 487 919 100 | 0.959 748 987 500 |
| 18 | 5s | 0.959 487 939 829 | 0.959 749 008 256 |
| 19 | 5d | 0.959 488 132 130 | 0.959 749 200 588 |
| 20 | 5p | 0.959 488 132 490 | 0.959 749 200 948 |
| 21 | 5f | 0.959 488 203 132 | 0.959 749 271 609 |
| 22 | 5d | 0.959 488 203 259 | 0.959 749 271 736 |
| 23 | 5g | 0.959 488 238 630 | 0.959 749 307 116 |
| 24 | 5f | 0.959 488 238 696 | 0.959 749 307 183 |
| 25 | 5g | 0.959 488 259 968 | 0.959 749 328 461 |
| (Ryd) | Transition | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| i | 2: 2p | 3: 2s | 5: 3p | 5: 3p | 6: 3s | 7: 3d | 8: 3p | 10: 4p | 10: 4p |
| 3: 2s | 4: 2p | 6: 3s | 7: 3d | 8: 3p | 8: 3p | 9: 3d | 11: 4s | 12: 4d | |
| 1.0 − 04 | 2.328 + 2 | 3.172 + 2 | 1.462 + 3 | 1.201 + 3 | 1.756 + 3 | 7.185 + 2 | 2.673 + 3 | 5.089 + 3 | 4.691 + 3 |
| 2.0 − 04 | 2.692 + 2 | 3.463 + 2 | 1.670 + 3 | 1.324 + 3 | 2.026 + 3 | 7.708 + 2 | 3.122 + 3 | 5.759 + 3 | 5.747 + 3 |
| 5.0 − 04 | 3.120 + 2 | 4.039 + 2 | 1.927 + 3 | 1.654 + 3 | 2.549 + 3 | 8.435 + 2 | 3.753 + 3 | 6.637 + 3 | 7.238 + 3 |
| 1.0 − 03 | 3.438 + 2 | 4.674 + 2 | 2.131 + 3 | 1.919 + 3 | 2.979 + 3 | 8.862 + 2 | 4.204 + 3 | 7.308 + 3 | 8.314 + 3 |
| 2.0 − 03 | 3.854 + 2 | 5.397 + 2 | 2.335 + 3 | 2.172 + 3 | 3.384 + 3 | 9.386 + 2 | 4.642 + 3 | 7.976 + 3 | 9.383 + 3 |
| 5.0 − 03 | 4.316 + 2 | 6.697 + 2 | 2.598 + 3 | 2.573 + 3 | 3.896 + 3 | 1.012 + 3 | 5.246 + 3 | 8.855 + 3 | 1.078 + 4 |
| 1.0 − 02 | 4.559 + 2 | 6.971 + 2 | 2.800 + 3 | 2.748 + 3 | 4.311 + 3 | 1.067 + 3 | 5.693 + 3 | 9.517 + 3 | 1.185 + 4 |
| 2.0 − 02 | 4.877 + 2 | 7.758 + 2 | 3.000 + 3 | 3.000 + 3 | 4.711 + 3 | 1.114 + 3 | 6.140 + 3 | 1.018 + 4 | 1.292 + 4 |
| 5.0 − 02 | 5.313 + 2 | 8.852 + 2 | 3.259 + 3 | 3.368 + 3 | 5.233 + 3 | 1.174 + 3 | 6.735 + 3 | 1.106 + 4 | 1.432 + 4 |
| 1.0 − 01 | 5.736 + 2 | 9.148 + 2 | 3.459 + 3 | 3.578 + 3 | 5.632 + 3 | 1.222 + 3 | 7.247 + 3 | 1.172 + 4 | 1.538 + 4 |
| 2.0 − 01 | 6.063 + 2 | 9.805 + 2 | 3.655 + 3 | 3.824 + 3 | 6.024 + 3 | 1.270 + 3 | 7.619 + 3 | 1.238 + 4 | 1.642 + 4 |
| 5.0 − 01 | 6.471 + 2 | 1.080 + 3 | 3.909 + 3 | 4.125 + 3 | 6.529 + 3 | 1.331 + 3 | 8.161 + 3 | 1.324 + 4 | 1.778 + 4 |
| 1.0 + 00 | 6.742 + 2 | 1.133 + 3 | 4.081 + 3 | 4.368 + 3 | 6.875 + 3 | 1.350 + 3 | 8.523 + 3 | 1.385 + 4 | 1.872 + 4 |
| 2.0 + 00 | 6.891 + 2 | 1.180 + 3 | 4.236 + 3 | 4.587 + 3 | 7.184 + 3 | 1.381 + 3 | 8.910 + 3 | 1.437 + 4 | 1.998 + 4 |
| 5.0 + 00 | 7.165 + 2 | 1.235 + 3 | 4.412 + 3 | 4.714 + 3 | 7.534 + 3 | 1.444 + 3 | 9.206 + 3 | 1.496 + 4 | 2.053 + 4 |
| 1.0 + 01 | 7.378 + 2 | 1.261 + 3 | 4.541 + 3 | 4.863 + 3 | 7.799 + 3 | 1.448 + 3 | 9.477 + 3 | 1.541 + 4 | 2.114 + 4 |
| 2.0 + 01 | 7.543 + 2 | 1.294 + 3 | 4.641 + 3 | 4.987 + 3 | 7.995 + 3 | 1.473 + 3 | 9.702 + 3 | 1.574 + 4 | 2.167 + 4 |
| 5.0 + 01 | 7.764 + 2 | 1.338 + 3 | 4.771 + 3 | 5.153 + 3 | 8.260 + 3 | 1.506 + 3 | 9.995 + 3 | 1.618 + 4 | 2.237 + 4 |
| 1.0 + 02 | 7.929 + 2 | 1.371 + 3 | 4.872 + 3 | 5.278 + 3 | 8.459 + 3 | 1.530 + 3 | 1.022 + 4 | 1.651 + 4 | 2.291 + 4 |
| i | 11: 4s | 12: 4d | 12: 4d | 13: 4p | 14: 4f | 15: 4d | 17: 5p | 17: 5p | 18: 5s |
| 13: 4p | 13: 4p | 14: 4f | 15: 4d | 15: 4d | 16: 4f | 18: 5s | 19: 5d | 20: 5p | |
| 1.0 − 04 | 5.816 + 3 | 3.030 + 3 | 7.301 + 3 | 1.163 + 4 | 1.341 + 3 | 1.210 + 4 | 1.318 + 4 | 1.338 + 4 | 1.543 + 4 |
| 2.0 − 04 | 7.134 + 3 | 3.242 + 3 | 8.439 + 3 | 1.360 + 4 | 1.426 + 3 | 1.372 + 4 | 1.485 + 4 | 1.632 + 4 | 1.882 + 4 |
| 5.0 − 04 | 8.935 + 3 | 3.523 + 3 | 9.944 + 3 | 1.617 + 4 | 1.527 + 3 | 1.581 + 4 | 1.707 + 4 | 2.023 + 4 | 2.327 + 4 |
| 1.0 − 03 | 1.033 + 4 | 3.736 + 3 | 1.104 + 4 | 1.804 + 4 | 1.608 + 3 | 1.743 + 4 | 1.874 + 4 | 2.328 + 4 | 2.664 + 4 |
| 2.0 − 03 | 1.163 + 4 | 3.952 + 3 | 1.217 + 4 | 1.998 + 4 | 1.688 + 3 | 1.904 + 4 | 2.040 + 4 | 2.619 + 4 | 3.005 + 4 |
| 5.0 − 03 | 1.342 + 4 | 4.232 + 3 | 1.366 + 4 | 2.253 + 4 | 1.790 + 3 | 2.114 + 4 | 2.259 + 4 | 3.006 + 4 | 3.447 + 4 |
| 1.0 − 02 | 1.475 + 4 | 4.449 + 3 | 1.478 + 4 | 2.447 + 4 | 1.870 + 3 | 2.275 + 4 | 2.426 + 4 | 3.297 + 4 | 3.782 + 4 |
| 2.0 − 02 | 1.608 + 4 | 4.658 + 3 | 1.590 + 4 | 2.638 + 4 | 1.946 + 3 | 2.434 + 4 | 2.591 + 4 | 3.589 + 4 | 4.113 + 4 |
| 5.0 − 02 | 1.784 + 4 | 4.937 + 3 | 1.737 + 4 | 2.890 + 4 | 2.050 + 3 | 2.643 + 4 | 2.810 + 4 | 3.973 + 4 | 4.552 + 4 |
| 1.0 − 01 | 1.917 + 4 | 5.149 + 3 | 1.847 + 4 | 3.080 + 4 | 2.128 + 3 | 2.802 + 4 | 2.976 + 4 | 4.260 + 4 | 4.882 + 4 |
| 2.0 − 01 | 2.050 + 4 | 5.358 + 3 | 1.955 + 4 | 3.267 + 4 | 2.196 + 3 | 2.956 + 4 | 3.140 + 4 | 4.548 + 4 | 5.211 + 4 |
| 5.0 − 01 | 2.221 + 4 | 5.616 + 3 | 2.089 + 4 | 3.512 + 4 | 2.273 + 3 | 3.147 + 4 | 3.355 + 4 | 4.924 + 4 | 5.647 + 4 |
| 1.0 + 00 | 2.342 + 4 | 5.789 + 3 | 2.180 + 4 | 3.681 + 4 | 2.324 + 3 | 3.275 + 4 | 3.510 + 4 | 5.188 + 4 | 5.954 + 4 |
| 2.0 + 00 | 2.457 + 4 | 5.943 + 3 | 2.265 + 4 | 3.924 + 4 | 2.391 + 3 | 3.451 + 4 | 3.644 + 4 | 5.456 + 4 | 6.282 + 4 |
| 5.0 + 00 | 2.585 + 4 | 6.117 + 3 | 2.381 + 4 | 3.990 + 4 | 2.437 + 3 | 3.535 + 4 | 3.794 + 4 | 5.675 + 4 | 6.602 + 4 |
| 1.0 + 01 | 2.653 + 4 | 6.258 + 3 | 2.412 + 4 | 4.113 + 4 | 2.473 + 3 | 3.606 + 4 | 3.906 + 4 | 5.867 + 4 | 6.742 + 4 |
| 2.0 + 01 | 2.720 + 4 | 6.364 + 3 | 2.467 + 4 | 4.209 + 4 | 2.514 + 3 | 3.685 + 4 | 3.989 + 4 | 6.012 + 4 | 6.907 + 4 |
| 5.0 + 01 | 2.808 + 4 | 6.506 + 3 | 2.541 + 4 | 4.335 + 4 | 2.567 + 3 | 3.791 + 4 | 4.100 + 4 | 6.204 + 4 | 7.127 + 4 |
| 1.0 + 02 | 2.875 + 4 | 6.612 + 3 | 2.597 + 4 | 4.431 + 4 | 2.606 + 3 | 3.871 + 4 | 4.182 + 4 | 6.351 + 4 | 7.294 + 4 |
| i | 19: 5d | 19: 5d | 20: 5p | 21: 5f | 21: 5f | 22: 5d | 23: 5g | 24: 5f | |
| 20: 5p | 21: 5f | 22: 5d | 22: 5d | 23: 5g | 24: 5f | 24: 5f | 25: 5g | ||
| 1.0 − 04 | 8.346 + 3 | 2.564 + 4 | 3.257 + 4 | 4.626 + 3 | 2.574 + 4 | 4.290 + 4 | 2.184 + 3 | 3.652 + 4 | |
| 2.0 − 04 | 8.925 + 3 | 2.992 + 4 | 3.825 + 4 | 4.908 + 3 | 2.886 + 4 | 4.843 + 4 | 2.307 + 3 | 4.064 + 4 | |
| 5.0 − 04 | 9.696 + 3 | 3.518 + 4 | 4.505 + 4 | 5.289 + 3 | 3.319 + 4 | 5.613 + 4 | 2.454 + 3 | 4.618 + 4 | |
| 1.0 − 03 | 1.028 + 4 | 3.923 + 4 | 5.038 + 4 | 5.579 + 3 | 3.642 + 4 | 6.190 + 4 | 2.574 + 3 | 5.034 + 4 | |
| 2.0 − 03 | 1.086 + 4 | 4.326 + 4 | 5.567 + 4 | 5.856 + 3 | 3.965 + 4 | 6.761 + 4 | 2.695 + 3 | 5.449 + 4 | |
| 5.0 − 03 | 1.162 + 4 | 4.855 + 4 | 6.261 + 4 | 6.235 + 3 | 4.388 + 4 | 7.515 + 4 | 2.851 + 3 | 6.000 + 4 | |
| 1.0 − 02 | 1.221 + 4 | 5.256 + 4 | 6.785 + 4 | 6.530 + 3 | 4.712 + 4 | 8.086 + 4 | 2.964 + 3 | 6.417 + 4 | |
| 2.0 − 02 | 1.279 + 4 | 5.656 + 4 | 7.308 + 4 | 6.811 + 3 | 5.027 + 4 | 8.652 + 4 | 3.085 + 3 | 6.830 + 4 | |
| 5.0 − 02 | 1.356 + 4 | 6.179 + 4 | 7.996 + 4 | 7.187 + 3 | 5.449 + 4 | 9.407 + 4 | 3.234 + 3 | 7.375 + 4 | |
| 1.0 − 01 | 1.415 + 4 | 6.575 + 4 | 8.515 + 4 | 7.468 + 3 | 5.766 + 4 | 9.971 + 4 | 3.341 + 3 | 7.785 + 4 | |
| 2.0 − 01 | 1.472 + 4 | 6.970 + 4 | 9.037 + 4 | 7.746 + 3 | 6.073 + 4 | 1.053 + 5 | 3.435 + 3 | 8.184 + 4 | |
| 5.0 − 01 | 1.546 + 4 | 7.474 + 4 | 9.715 + 4 | 8.080 + 3 | 6.456 + 4 | 1.126 + 5 | 3.545 + 3 | 8.677 + 4 | |
| 1.0 + 00 | 1.595 + 4 | 7.827 + 4 | 1.019 + 5 | 8.306 + 3 | 6.707 + 4 | 1.176 + 5 | 3.619 + 3 | 9.002 + 4 | |
| 2.0 + 00 | 1.639 + 4 | 8.126 + 4 | 1.060 + 5 | 8.507 + 3 | 6.963 + 4 | 1.219 + 5 | 3.753 + 3 | 9.284 + 4 | |
| 5.0 + 00 | 1.688 + 4 | 8.461 + 4 | 1.106 + 5 | 8.734 + 3 | 7.172 + 4 | 1.266 + 5 | 3.794 + 3 | 9.607 + 4 | |
| 1.0 + 01 | 1.725 + 4 | 8.714 + 4 | 1.140 + 5 | 8.906 + 3 | 7.359 + 4 | 1.302 + 5 | 3.838 + 3 | 9.847 + 4 | |
| 2.0 + 01 | 1.755 + 4 | 8.913 + 4 | 1.167 + 5 | 9.049 + 3 | 7.517 + 4 | 1.331 + 5 | 3.897 + 3 | 1.005 + 5 | |
| 5.0 + 01 | 1.793 + 4 | 9.180 + 4 | 1.201 + 5 | 9.236 + 3 | 7.731 + 4 | 1.368 + 5 | 3.975 + 3 | 1.033 + 5 | |
| 1.0 + 02 | 1.822 + 4 | 9.377 + 4 | 1.227 + 5 | 9.379 + 3 | 7.891 + 4 | 1.397 + 5 | 4.035 + 3 | 1.054 + 5 | |
| (K) | Transition | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| i | 2: 2p | 3: 2s | 5: 3p | 5: 3p | 6: 3s | 7: 3d | 8: 3p | 10: 4p | 10: 4p |
| 3: 2s | 4: 2p | 6: 3s | 7: 3d | 8: 3p | 8: 3p | 9: 3d | 11: 4s | 12: 4d | |
| 3.00 | 4.100 + 2 | 6.121 + 2 | 2.500 + 3 | 2.403 + 3 | 3.713 + 3 | 9.859 + 2 | 5.021 + 3 | 8.526 + 3 | 1.026 + 4 |
| 3.33 | 4.447 + 2 | 6.862 + 2 | 2.719 + 3 | 2.672 + 3 | 4.150 + 3 | 1.042 + 3 | 5.513 + 3 | 9.254 + 3 | 1.143 + 4 |
| 3.66 | 4.802 + 2 | 7.611 + 2 | 2.938 + 3 | 2.944 + 3 | 4.588 + 3 | 1.096 + 3 | 6.010 + 3 | 9.982 + 3 | 1.260 + 4 |
| 4.00 | 5.188 + 2 | 8.327 + 2 | 3.162 + 3 | 3.222 + 3 | 5.037 + 3 | 1.151 + 3 | 6.525 + 3 | 1.073 + 4 | 1.380 + 4 |
| 4.33 | 5.567 + 2 | 9.003 + 2 | 3.378 + 3 | 3.486 + 3 | 5.470 + 3 | 1.203 + 3 | 7.011 + 3 | 1.146 + 4 | 1.495 + 4 |
| 4.66 | 5.931 + 2 | 9.697 + 2 | 3.590 + 3 | 3.746 + 3 | 5.896 + 3 | 1.253 + 3 | 7.476 + 3 | 1.217 + 4 | 1.609 + 4 |
| 5.00 | 6.272 + 2 | 1.040 + 3 | 3.801 + 3 | 4.011 + 3 | 6.316 + 3 | 1.298 + 3 | 7.932 + 3 | 1.289 + 4 | 1.726 + 4 |
| 5.33 | 6.556 + 2 | 1.102 + 3 | 3.990 + 3 | 4.250 + 3 | 6.695 + 3 | 1.338 + 3 | 8.345 + 3 | 1.354 + 4 | 1.835 + 4 |
| 5.66 | 6.809 + 2 | 1.156 + 3 | 4.164 + 3 | 4.453 + 3 | 7.042 + 3 | 1.377 + 3 | 8.712 + 3 | 1.413 + 4 | 1.930 + 4 |
| 6.00 | 7.051 + 2 | 1.204 + 3 | 4.325 + 3 | 4.634 + 3 | 7.366 + 3 | 1.411 + 3 | 9.045 + 3 | 1.468 + 4 | 2.012 + 4 |
| 6.33 | 7.268 + 2 | 1.244 + 3 | 4.466 + 3 | 4.792 + 3 | 7.647 + 3 | 1.439 + 3 | 9.337 + 3 | 1.515 + 4 | 2.082 + 4 |
| 6.66 | 7.471 + 2 | 1.282 + 3 | 4.592 + 3 | 4.940 + 3 | 7.901 + 3 | 1.466 + 3 | 9.608 + 3 | 1.558 + 4 | 2.146 + 4 |
| 7.00 | 7.666 + 2 | 1.320 + 3 | 4.712 + 3 | 5.084 + 3 | 8.142 + 3 | 1.493 + 3 | 9.871 + 3 | 1.598 + 4 | 2.208 + 4 |
| i | 11: 4s | 12: 4d | 12: 4d | 13: 4p | 14: 4f | 15: 4d | 17: 5p | 17: 5p | 18: 5s |
| 13: 4p | 13: 4p | 14: 4f | 15: 4d | 15: 4d | 16: 4f | 18: 5s | 19: 5d | 20: 5p | |
| 3.00 | 1.276 + 4 | 4.128 + 3 | 1.311 + 4 | 2.159 + 4 | 1.751 + 3 | 2.036 + 4 | 2.177 + 4 | 2.862 + 4 | 3.282 + 4 |
| 3.33 | 1.422 + 4 | 4.361 + 3 | 1.433 + 4 | 2.370 + 4 | 1.837 + 3 | 2.211 + 4 | 2.360 + 4 | 3.182 + 4 | 3.648 + 4 |
| 3.66 | 1.568 + 4 | 4.594 + 3 | 1.556 + 4 | 2.580 + 4 | 1.923 + 3 | 2.385 + 4 | 2.541 + 4 | 3.501 + 4 | 4.012 + 4 |
| 4.00 | 1.718 + 4 | 4.832 + 3 | 1.681 + 4 | 2.795 + 4 | 2.010 + 3 | 2.564 + 4 | 2.728 + 4 | 3.828 + 4 | 4.387 + 4 |
| 4.33 | 1.864 + 4 | 5.062 + 3 | 1.801 + 4 | 3.003 + 4 | 2.091 + 3 | 2.736 + 4 | 2.909 + 4 | 4.145 + 4 | 4.750 + 4 |
| 4.66 | 2.007 + 4 | 5.285 + 3 | 1.917 + 4 | 3.208 + 4 | 2.166 + 3 | 2.902 + 4 | 3.088 + 4 | 4.458 + 4 | 5.110 + 4 |
| 5.00 | 2.151 + 4 | 5.502 + 3 | 2.031 + 4 | 3.419 + 4 | 2.237 + 3 | 3.069 + 4 | 3.268 + 4 | 4.774 + 4 | 5.477 + 4 |
| 5.33 | 2.284 + 4 | 5.695 + 3 | 2.136 + 4 | 3.617 + 4 | 2.301 + 3 | 3.224 + 4 | 3.432 + 4 | 5.062 + 4 | 5.822 + 4 |
| 5.66 | 2.406 + 4 | 5.870 + 3 | 2.231 + 4 | 3.786 + 4 | 2.358 + 3 | 3.358 + 4 | 3.581 + 4 | 5.322 + 4 | 6.136 + 4 |
| 6.00 | 2.516 + 4 | 6.034 + 3 | 2.315 + 4 | 3.931 + 4 | 2.410 + 3 | 3.471 + 4 | 3.720 + 4 | 5.558 + 4 | 6.410 + 4 |
| 6.33 | 2.608 + 4 | 6.177 + 3 | 2.384 + 4 | 4.055 + 4 | 2.457 + 3 | 3.568 + 4 | 3.840 + 4 | 5.760 + 4 | 6.636 + 4 |
| 6.66 | 2.691 + 4 | 6.308 + 3 | 2.448 + 4 | 4.170 + 4 | 2.502 + 3 | 3.659 + 4 | 3.948 + 4 | 5.944 + 4 | 6.839 + 4 |
| 7.00 | 2.770 + 4 | 6.433 + 3 | 2.512 + 4 | 4.282 + 4 | 2.546 + 3 | 3.749 + 4 | 4.049 + 4 | 6.119 + 4 | 7.035 + 4 |
| i | 19: 5d | 19: 5d | 20: 5p | 21: 5f | 21: 5f | 22: 5d | 23: 5g | 24: 5f | |
| 20: 5p | 21: 5f | 22: 5d | 22: 5d | 23: 5g | 24: 5f | 24: 5f | 25: 5g | ||
| 3.00 | 1.134 + 4 | 4.657 + 4 | 6.001 + 4 | 6.097 + 3 | 4.230 + 4 | 7.234 + 4 | 2.791 + 3 | 5.795 + 4 | |
| 3.33 | 1.198 + 4 | 5.096 + 4 | 6.576 + 4 | 6.411 + 3 | 4.581 + 4 | 7.859 + 4 | 2.920 + 3 | 6.250 + 4 | |
| 3.66 | 1.262 + 4 | 5.534 + 4 | 7.149 + 4 | 6.724 + 3 | 4.931 + 4 | 8.483 + 4 | 3.046 + 3 | 6.704 + 4 | |
| 4.00 | 1.328 + 4 | 5.982 + 4 | 7.738 + 4 | 7.044 + 3 | 5.290 + 4 | 9.124 + 4 | 3.172 + 3 | 7.168 + 4 | |
| 4.33 | 1.391 + 4 | 6.415 + 4 | 8.309 + 4 | 7.350 + 3 | 5.633 + 4 | 9.743 + 4 | 3.287 + 3 | 7.613 + 4 | |
| 4.66 | 1.453 + 4 | 6.841 + 4 | 8.874 + 4 | 7.645 + 3 | 5.964 + 4 | 1.035 + 5 | 3.393 + 3 | 8.042 + 4 | |
| 5.00 | 1.514 + 4 | 7.262 + 4 | 9.436 + 4 | 7.930 + 3 | 6.288 + 4 | 1.095 + 5 | 3.498 + 3 | 8.455 + 4 | |
| 5.33 | 1.569 + 4 | 7.639 + 4 | 9.943 + 4 | 8.183 + 3 | 6.576 + 4 | 1.149 + 5 | 3.598 + 3 | 8.819 + 4 | |
| 5.66 | 1.618 + 4 | 7.980 + 4 | 1.040 + 5 | 8.411 + 3 | 6.829 + 4 | 1.198 + 5 | 3.684 + 3 | 9.146 + 4 | |
| 6.00 | 1.664 + 4 | 8.296 + 4 | 1.084 + 5 | 8.625 + 3 | 7.060 + 4 | 1.243 + 5 | 3.756 + 3 | 9.451 + 4 | |
| 6.33 | 1.704 + 4 | 8.571 + 4 | 1.120 + 5 | 8.813 + 3 | 7.264 + 4 | 1.282 + 5 | 3.819 + 3 | 9.720 + 4 | |
| 6.66 | 1.741 + 4 | 8.821 + 4 | 1.154 + 5 | 8.988 + 3 | 7.455 + 4 | 1.318 + 5 | 3.882 + 3 | 9.970 + 4 | |
| 7.00 | 1.776 + 4 | 9.059 + 4 | 1.186 + 5 | 9.154 + 3 | 7.641 + 4 | 1.352 + 5 | 3.946 + 3 | 1.021 + 5 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aggarwal, K.M.; Owada, R.; Igarashi, A. Collision Strengths and Effective Collision Strengths for Allowed Transitions among the n ≤ 5 Degenerate Levels of Atomic Hydrogen. Atoms 2018, 6, 37. https://doi.org/10.3390/atoms6030037
Aggarwal KM, Owada R, Igarashi A. Collision Strengths and Effective Collision Strengths for Allowed Transitions among the n ≤ 5 Degenerate Levels of Atomic Hydrogen. Atoms. 2018; 6(3):37. https://doi.org/10.3390/atoms6030037
Chicago/Turabian StyleAggarwal, Kanti M., Ryu Owada, and Akinori Igarashi. 2018. "Collision Strengths and Effective Collision Strengths for Allowed Transitions among the n ≤ 5 Degenerate Levels of Atomic Hydrogen" Atoms 6, no. 3: 37. https://doi.org/10.3390/atoms6030037
APA StyleAggarwal, K. M., Owada, R., & Igarashi, A. (2018). Collision Strengths and Effective Collision Strengths for Allowed Transitions among the n ≤ 5 Degenerate Levels of Atomic Hydrogen. Atoms, 6(3), 37. https://doi.org/10.3390/atoms6030037






