Matrix Methods for Solving Hartree-Fock Equations in Atomic Structure Calculations and Line Broadening
Abstract
:1. Introduction
2. The Hartree-Fock Method for Atomic Structure Calculations
- (1)
- Assume a wavefunction for the state of interest (hydrogenic is good enough for this step).
- (2)
- Determine a mean-Coulomb field acting on electron i based on the wavefunctions of the other electron.
- (3)
- Solve the one-electron Schrödinger equation for electron i in its mean-Coulomb field to generate a new set of wavefunctions.
- (4)
- Repeat steps (2) and (3) until convergence is achieved.
3. Finite Difference Matrix to Solve the Schrödinger Equation for One-Electron Atom
4. Matrix Form of the Hartree-Fock Equation
5. Extension to Free-Electron Wavefunctions
6. Application to Spectral Line Broadening
6.1. Atomic Structure
6.2. Electron-Atom Collisions
7. Summary
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Falcon, R.E.; Rochau, G.A.; Bailey, J.E.; Gomez, T.A.; Montgomery, M.H.; Winget, D.E.; Nagayama, T. Laboratory Measurements of White Dwarf Photospheric Spectral Lines: Hβ. Astrophys. J. 2015, 806, 214. [Google Scholar] [CrossRef]
- Nagayama, T.; Bailey, J.E.; Mancini, R.C.; Iglesias, C.A.; Hansen, S.B.; Blancard, C.; Chung, H.K.; Colgan, J.; Cosse, P.; Faussurier, G.; et al. Model uncertainties of local-thermodynamic-equilibrium K-shell spectroscopy. High Energy Density Phys. 2016, 20, 17–22. [Google Scholar] [CrossRef]
- Bergeron, P.; Saffer, R.A.; Liebert, J. A spectroscopic determination of the mass distribution of DA white dwarfs. Astrophys. J. 1992, 394, 228–247. [Google Scholar] [CrossRef]
- Seaton, M.J. Atomic data for opacity calculations. XIII - Line profiles for transitions in hydrogenic ions. J. Phys. B 1990, 23, 3255–3296. [Google Scholar] [CrossRef]
- Bethe, H.A.; Salpeter, E.E. Quantum Mechanics of One- and Two-Electron Atoms; Academic Press: New York, NY, USA, 1957. [Google Scholar]
- Moiseiwitsch, B.L.; Smith, S.J. Electron Impact Excitation of Atoms. Rev. Mod. Phys. 1968, 40, 238–353. [Google Scholar] [CrossRef]
- Mott, N.; Massey, H. The Theory of Atomic Collisions; The International Series of Monographs on Physics; Clarendon Press: London, UK, 1965. [Google Scholar]
- Madison, D.H.; Bray, I.; McCarthy, I.E. Exact second-order distorted-wave calculation for hydrogen including second-order exchange. J. Phys. B 1991, 24, 3861–3888. [Google Scholar] [CrossRef]
- Gomez, T.A. Improving Calculations of the Interaction Between Atoms and Plasma Particles and Its Effect on Spectral Line Shapes. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 2017. [Google Scholar]
- Gunderson, M.A.; Junkel-Vives, G.C.; Hooper, C.F. A comparison of a second-order quantum mechanical and an all-order semi-classical electron broadening model. J. Quant. Spectrosc. Radiat. Transf. 2001, 71, 373–382. [Google Scholar] [CrossRef]
- Alexiou, S.; Poquérusse, A. Standard line broadening impact theory for hydrogen including penetrating collisions. Phys. Rev. E 2005, 72, 046404. [Google Scholar] [CrossRef] [PubMed]
- Gomez, T.A.; Nagayama, T.; Kilcrease, D.P.; Montgomery, M.H.; Winget, D.E. Effect of higher-order multipole moments on the Stark line shape. Phys. Rev. A 2016, 94, 022501. [Google Scholar] [CrossRef]
- Woltz, L.A.; Hooper, C.F., Jr. Full Coulomb calculation of Stark broadening in laser-produced plasmas. Phys. Rev. A 1984, 30, 468–473. [Google Scholar] [CrossRef]
- Junkel, G.C.; Gunderson, M.A.; Hooper, C.F., Jr.; Haynes, D.A., Jr. Full Coulomb calculation of Stark broadened spectra from multielectron ions: A focus on the dense plasma line shift. Phys. Rev. E 2000, 62, 5584–5593. [Google Scholar] [CrossRef]
- Griem, H.R.; Ralchenko, Y.V.; Bray, I. Stark broadening of the B III 2s-2p lines. Phys. Rev. E 1997, 56, 7186–7192. [Google Scholar] [CrossRef]
- Griem, H.R.; Ralchenko, Y.V. Electron collisional broadening of isolated lines from multiply-ionized atoms. J. Quant. Spec. Radiat. Transf. 2000, 65, 287–296. [Google Scholar] [CrossRef]
- Ralchenko, Y.V.; Griem, H.R.; Bray, I. Electron-impact broadening of the 3s-3p lines in low-Z Li-like ions. J. Quant. Spec. Radiat. Transf. 2003, 81, 371–384. [Google Scholar] [CrossRef]
- Glenzer, S.; Uzelac, N.I.; Kunze, H.J. Stark broadening of spectral lines along the isoelectronic sequence of Li. Phys. Rev. A 1992, 45, 8795–8802. [Google Scholar] [CrossRef] [PubMed]
- Glenzer, S.; Kunze, H.J. Stark broadening of resonance transitions in B III. Phys. Rev. A 1996, 53, 2225–2229. [Google Scholar] [CrossRef] [PubMed]
- Alexiou, S.; Dimitrijević, M.; Sahal-Brechot, S.; Stambulchik, E.; Duan, B.; González-Herrero, D.; Gigosos, M. The Second Workshop on Lineshape Code Comparison: Isolated Lines. Atoms 2014, 2, 157–177. [Google Scholar] [CrossRef]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; Los Alamos Series in Basic and Applied Sciences; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Fontes, C.J.; Zhang, H.L.; Jr, J.A.; Clark, R.E.H.; Kilcrease, D.P.; Colgan, J.; Cunningham, R.T.; Hakel, P.; Magee, N.H.; Sherrill, M.E. The Los Alamos suite of relativistic atomic physics codes. J. Phys. B 2015, 48, 144014. [Google Scholar] [CrossRef]
- Hartree, D.R. The Wave Mechanics of an Atom with a Non-Coulomb Central Field. Part I. Theory and Methods. Proc. Camb. Philos. Soc. 1928, 24, 89. [Google Scholar] [CrossRef]
- Fock, V. Näherungsmethode zur Lösung des quantenmechanischen Mehrkörperproblems. Z. Phys. 1930, 61, 126–148. [Google Scholar] [CrossRef]
- Grant, I.P. Relativistic Quantum Theory of Atoms and Molecules; Springer Series on Atomic, Optical, and Plasma Physics; Springer Science+Business Media, LLC: Berlin, Germany, 2007; Volume 40, ISBN 978-0-387-34671-7. [Google Scholar]
- Talman, J.D.; Shadwick, W.F. Optimized effective atomic central potential. Phys. Rev. A 1976, 14, 36–40. [Google Scholar] [CrossRef]
- Shiozaki, T.; Hirata, S. Grid-based numerical Hartree-Fock solutions of polyatomic molecules. Phys. Rev. A 2007, 76, 040503. [Google Scholar] [CrossRef]
- Beck, T.L. Real-space mesh techniques in density-functional theory. Rev. Mod. Phys. 2000, 72, 1041–1080. [Google Scholar] [CrossRef]
- Chow, P.C. Computer Solutions to the Schrödinger Equation. Am. J. Phys. 1972, 40, 730–734. [Google Scholar] [CrossRef]
- Pillai, M.; Goglio, J.; Walker, T.G. Matrix Numerov Method for solving Schrödinger’s equation. Am. J. Phys. 2012, 80, 1017–1019. [Google Scholar] [CrossRef]
- Anderson, E.; Bai, Z.; Bischof, C.; Blackford, S.; Demmel, J.; Dongarra, J.; Du Croz, J.; Greenbaum, A.; Hammarling, S.; McKenney, A.; et al. LAPACK Users’ Guide; SIAM: Warrendale, PA, USA, 1999. [Google Scholar]
- Sharma, C.S. On the Hartree-Fock equations for helium with non-orthogonal orbitals. J. Phys. B 1968, 1, 1023. [Google Scholar] [CrossRef]
- Kramida, A.; Yu, R.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (Ver. 5.5.2); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2018. Available online: https://physics.nist.gov/asd (accessed on 16 April 2015).
- Morton, D.C.; Wu, Q.X.; Drake, G.W.F. Energy levels for the stable isotopes of atomic helium (He-4 I and He-3 I). Can. J. Phys. 2006, 84, 83–105. [Google Scholar] [CrossRef]
- Slater, J.C. A Simplification of the Hartree-Fock Method. Phys. Rev. 1951, 81, 385–390. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, 1133–1138. [Google Scholar] [CrossRef]
- Baranger, M. General Impact Theory of Pressure Broadening. Phys. Rev. 1958, 112, 855–865. [Google Scholar] [CrossRef]
- Fano, U. Pressure Broadening as a Prototype of Relaxation. Phys. Rev. 1963, 131, 259–268. [Google Scholar] [CrossRef]
- Kingston, A.E.; Walters, H.R.J. Electron scattering by atomic hydrogen - The distorted-wave second Born approximation. J. Phys. B 1980, 13, 4633–4662. [Google Scholar] [CrossRef]
- Bray, I. Convergent close-coupling method for the calculation of electron scattering on hydrogenlike targets. Phys. Rev. A 1994, 49, 1066–1082. [Google Scholar] [CrossRef] [PubMed]
- Bray, I.; Stelbovics, A.T. Calculation of Electron Scattering on Hydrogenic Targets. Adv. Atom. Mol. Opt. Phys. 1995, 35, 209–254. [Google Scholar] [CrossRef]
- Seaton, M.J.; Yan, Y.; Mihalas, D.; Pradhan, A.K. Opacities for Stellar Envelopes. Mon. Not. R. Astron. Soc. 1994, 266, 805. [Google Scholar] [CrossRef]
- Gomez, T.A.; Nagayama, T.; Kilcrease, D.P.; Fontes, C.J.; Hansen, S.B.; Montgomery, M.H.; Winget, D.E. Penetrating Collisions by Electrons and its Effect on Electron Broadening. 2018; in preparation. [Google Scholar]
- Fourth SLSP Workshop, In Proceedings of the Fourth Spectral Line Shape in Plasmas Code Comparison Workshop, Baden, Austria, 20–24 March 2017. Available online: http://plasma-gate.weizmann.ac.il/projects/slsp/slsp4/ (accessed on 20 March 2018).
| 1 | |
| 2 | This method fails to capture some correlation effects because the potential in which the electron is moving is defined to be a mean field of the other electrons, which is to say that it does not account for the strong repulsion when the two electrons are close to each other. |
| 3 | If the two wavefunctions are assumed to be orthogonal, then these terms vanish. |
| 4 | In fact, radial solutions of three-electron problems can be solved on a laptop with the help of sparse matrix eigenvalue solvers. Any system larger than this would require the use of a supercomputer. |
| 5 | |
| 6 | This may be a dangerous approximation because some (non-negligible) processes need to be considered when orthogonality is not guaranteed. |
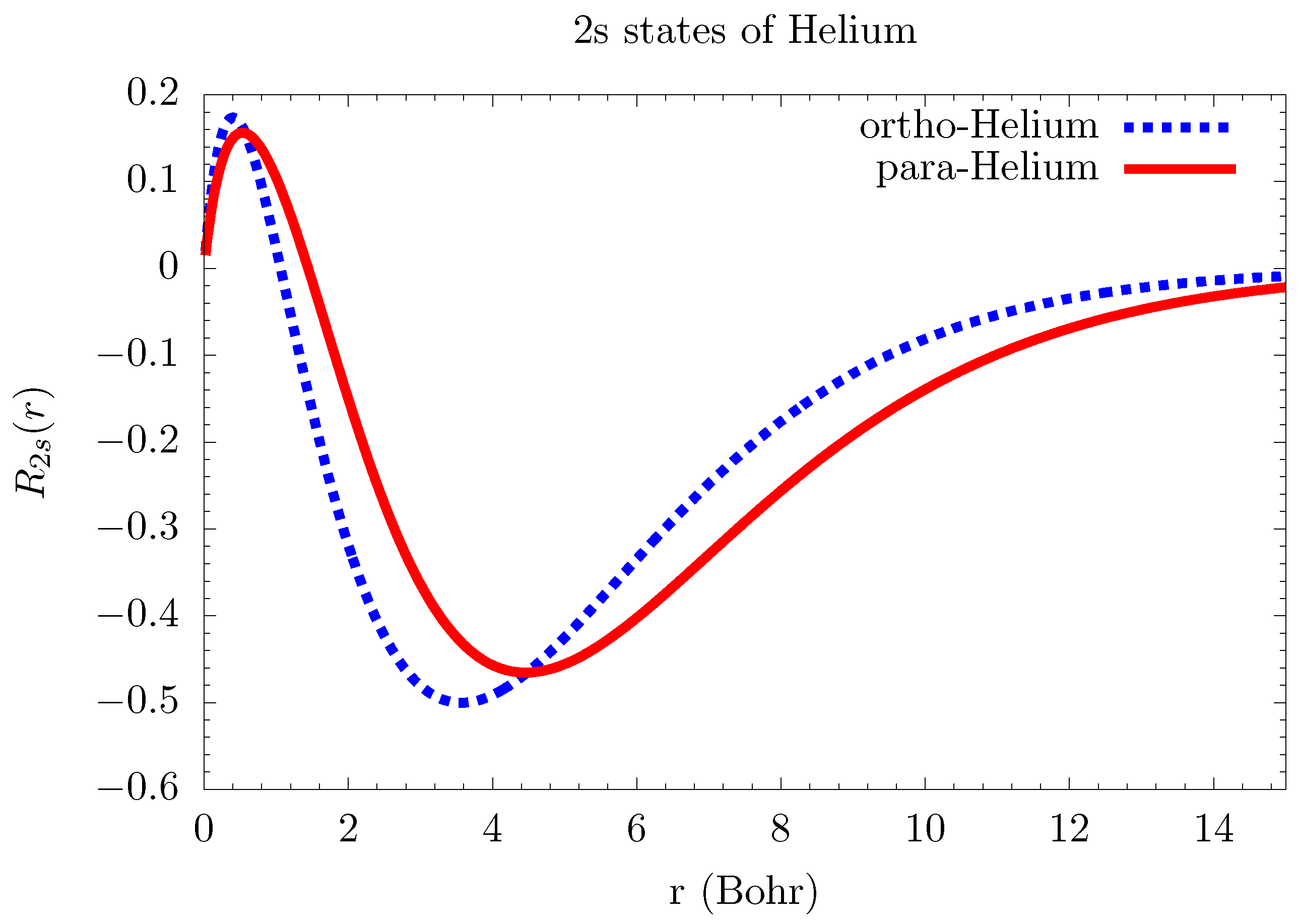
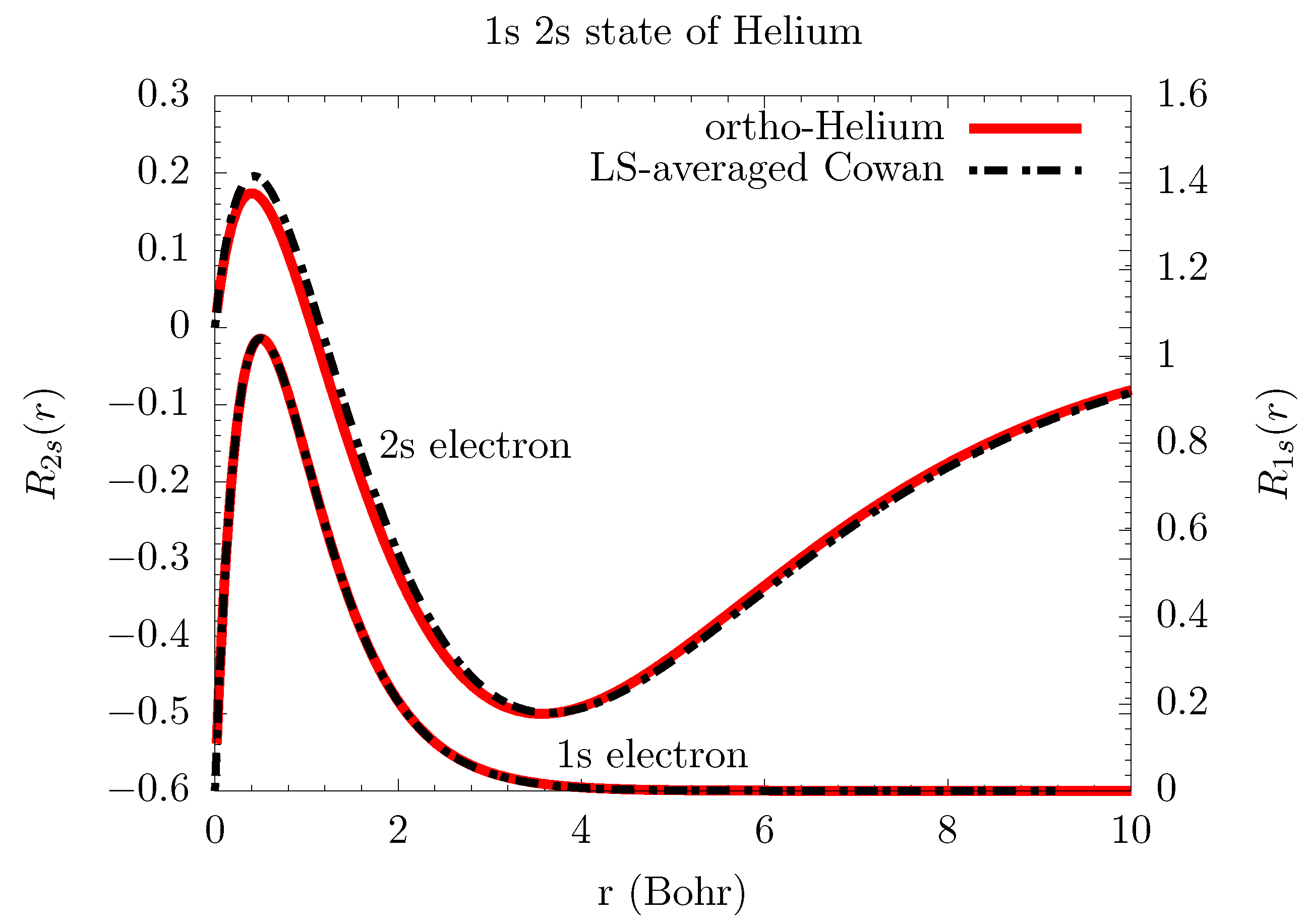
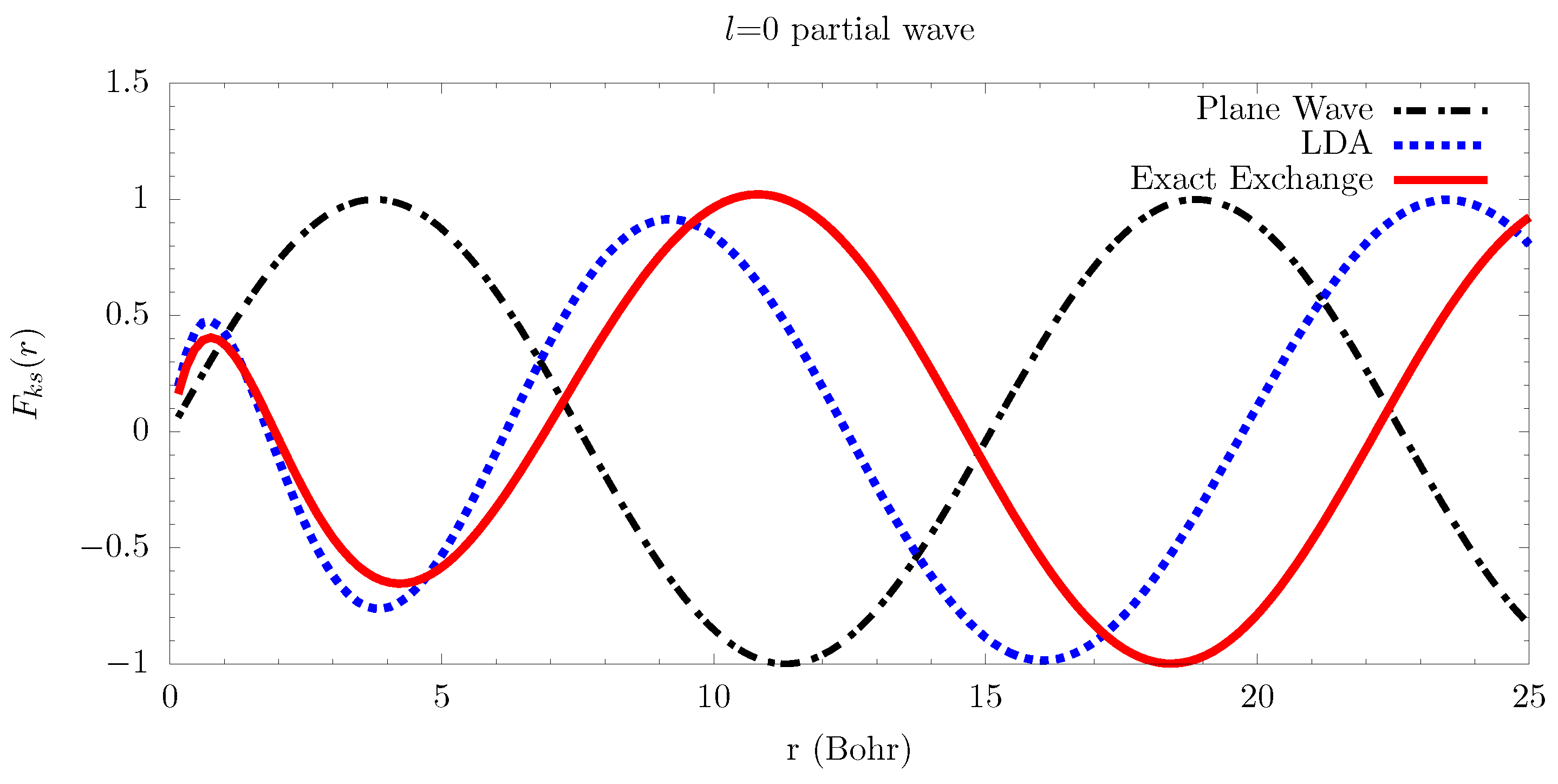
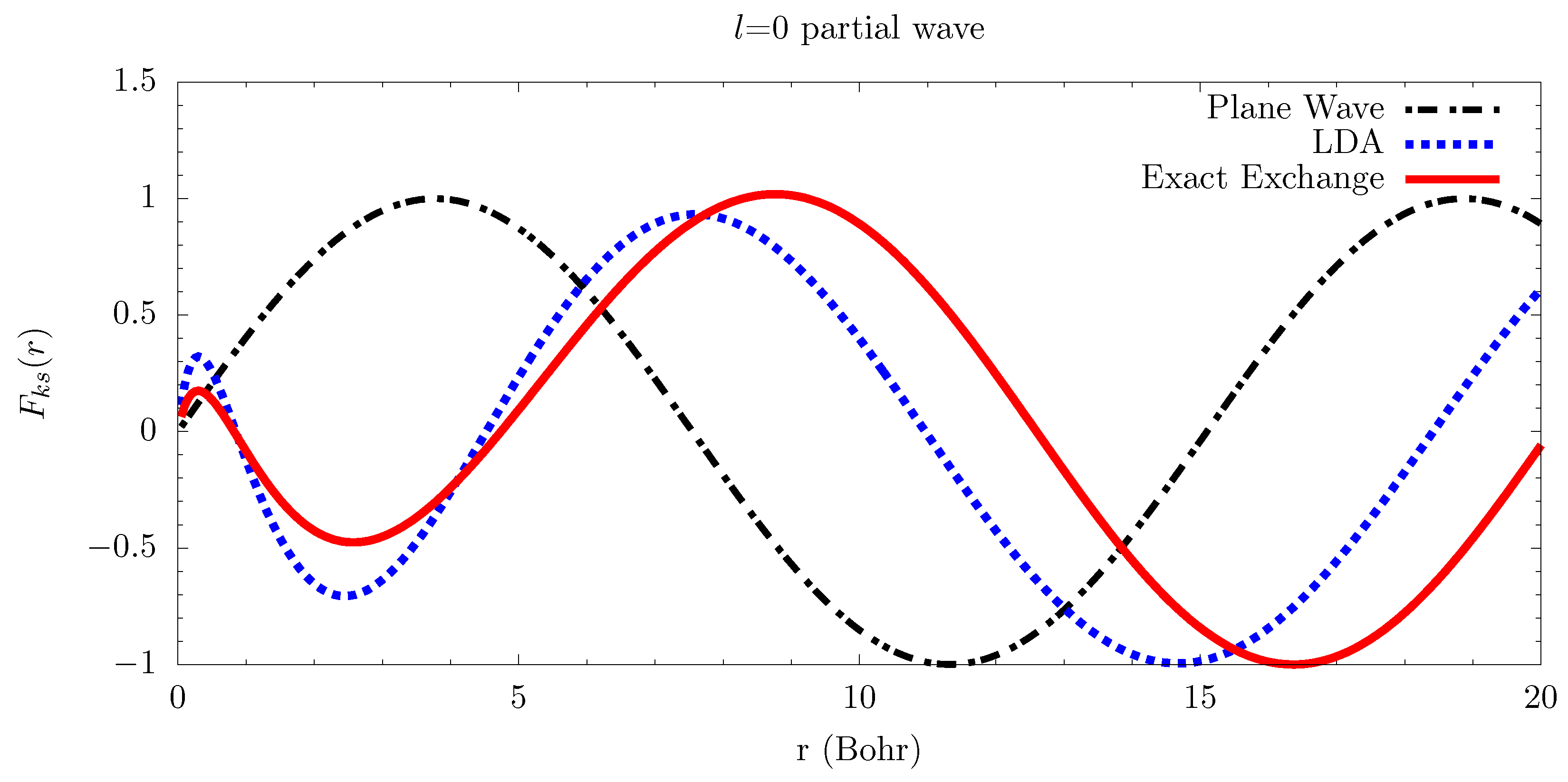
| n | Exact | ||||
|---|---|---|---|---|---|
| 1 | −0.94427 | −0.99019 | −0.99751 | −0.99937 | −1.00000 |
| 2 | −0.24621 | −0.24938 | −0.24984 | −0.24996 | −0.25000 |
| 3 | −0.11035 | −0.11098 | −0.11108 | −0.11110 | −0.11111 |
| 4 | −0.06218 | −0.06237 | −0.06240 | −0.06241 | −0.06250 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gomez, T.; Nagayama, T.; Fontes, C.; Kilcrease, D.; Hansen, S.; Montgomery, M.; Winget, D. Matrix Methods for Solving Hartree-Fock Equations in Atomic Structure Calculations and Line Broadening. Atoms 2018, 6, 22. https://doi.org/10.3390/atoms6020022
Gomez T, Nagayama T, Fontes C, Kilcrease D, Hansen S, Montgomery M, Winget D. Matrix Methods for Solving Hartree-Fock Equations in Atomic Structure Calculations and Line Broadening. Atoms. 2018; 6(2):22. https://doi.org/10.3390/atoms6020022
Chicago/Turabian StyleGomez, Thomas, Taisuke Nagayama, Chris Fontes, Dave Kilcrease, Stephanie Hansen, Mike Montgomery, and Don Winget. 2018. "Matrix Methods for Solving Hartree-Fock Equations in Atomic Structure Calculations and Line Broadening" Atoms 6, no. 2: 22. https://doi.org/10.3390/atoms6020022
APA StyleGomez, T., Nagayama, T., Fontes, C., Kilcrease, D., Hansen, S., Montgomery, M., & Winget, D. (2018). Matrix Methods for Solving Hartree-Fock Equations in Atomic Structure Calculations and Line Broadening. Atoms, 6(2), 22. https://doi.org/10.3390/atoms6020022





