Quantum and Semiclassical Stark Widths for Ar VII Spectral Lines
Abstract
1. Introduction
2. Outline of the Theory and Computational Procedure
2.1. Quantum Mechanical Formalism
2.2. Semiclassical Perturbation Method
3. Results and Discussions
3.1. Atomic Structure and Electron Scattering Data
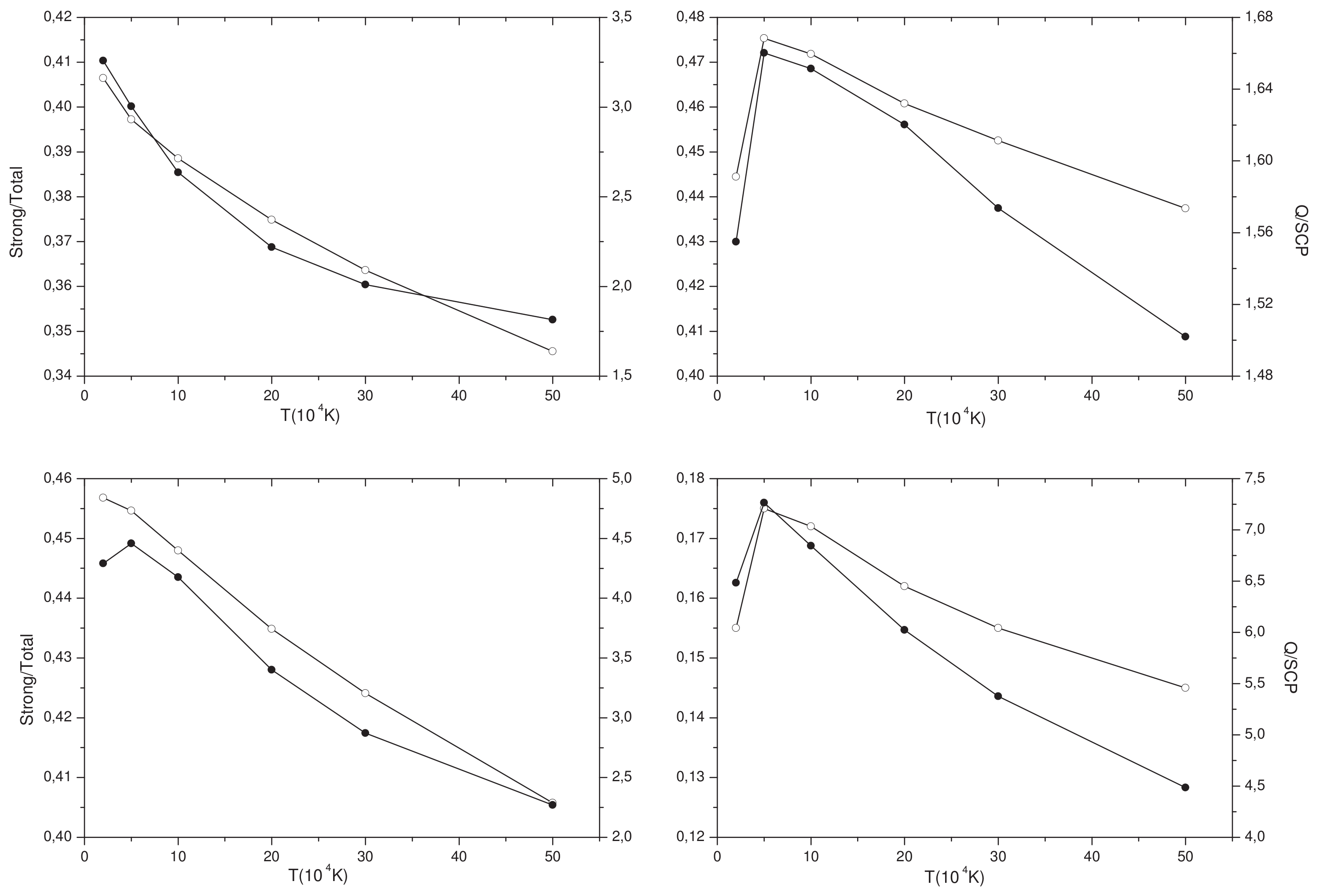
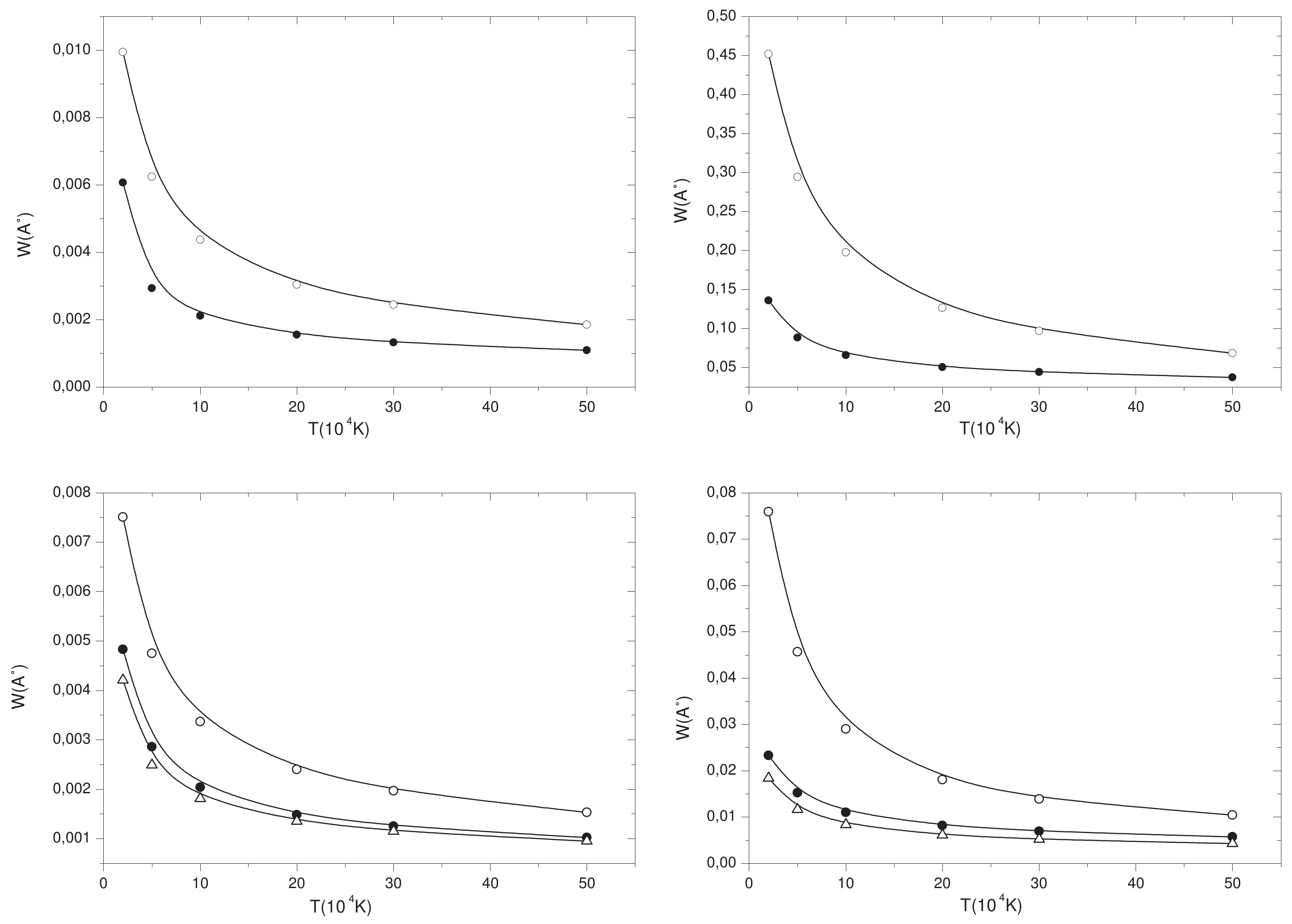
3.2. Line Broadening Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dimitrijević, M.S. Stark broadening in astrophysics (applications of Belgrade school results and collaboration with former Soviet republics. Astron. Astrophys. Trans. 2003, 22, 389–412. [Google Scholar] [CrossRef]
- Popović, L.Č.; Simić, S.; Milovanović, N.; Dimitrijević, M.S. Stark Broadening Effect in Stellar Atmospheres: Nd II Lines. Astrophys. J. Suppl. Ser. 2001, 135, 109–114. [Google Scholar] [CrossRef]
- Dimitrijević, M.S.; Ryabchikova, T.; Simić, Z.; Popović, L.Č.; Dačić, M. The influence of Stark broadening on Cr II spectral line shapes in stellar atmospheres. Astron. Astrophys. 2007, 469, 681–686. [Google Scholar] [CrossRef][Green Version]
- Rauch, T.; Ziegler, M.; Werner, K.; Kruk, J.W.; Oliveira, C.M.; Putte, D.V.; Mignani, R.P.; Kerber, F. High-resolution FUSE and HST ultraviolet spectroscopy of the white dwarf central star of Sh 2-216. Astron. Astrophys. 2007, 470, 317–329. [Google Scholar] [CrossRef]
- Werner, K.; Rauch, T.; Kruk, J.W. Discovery of photospheric argon in very hot central stars of planetary nebulae and white dwarfs. Astron. Astrophys. 2007, 466, 317–322. [Google Scholar] [CrossRef]
- Djurović, S.; Mar, S.; Peláez, R.J.; Aparicio, J.A. Stark broadening of ultraviolet Ar III spectral lines. Mon. Not. R. Astron. Soc. 2011, 414, 1389–1396. [Google Scholar] [CrossRef]
- Elabidi, H.; Ben Nessib, N.; Sahal-Bréchot, S. Quantum mechanical calculations of the electron-impact broadening of spectral lines for intermediate coupling. J. Phys. B 2004, 37, 63–71. [Google Scholar] [CrossRef]
- Elabidi, H.; Ben Nessib, N.; Cornille, M.; Dubau, J.; Sahal-Bréchot, S. Electron impact broadening of spectral lines in Be-like ions: Quantum calculations. J. Phys. B 2008, 41, 025702. [Google Scholar] [CrossRef]
- Elabidi, H.; Sahal-Bréchot, S.; Ben Nessib, N. Quantum Stark broadening of 3s-3p spectral lines in Li-like ions; Z-scaling and comparison with semi-classical perturbation theory. Eur. Phys. J. D 2009, 54, 51–64. [Google Scholar] [CrossRef]
- Elabidi, H.; Sahal-Bréchot, S. Checking the dependence on the upper level ionization potential of electron impact widths using quantum calculations. Eur. Phys. J. D 2011, 61, 285–290. [Google Scholar] [CrossRef]
- Elabidi, H.; Sahal-Bréchot, S.; Dimitrijević, M.S. Quantum Stark broadening of Ar XV lines. Strong collision and quadrupolar potential contributions. Adv. Res. Space 2014, 54, 1184–1189. [Google Scholar] [CrossRef]
- Dimitrijević, M.S.; Valjarević, A.; Sahal-Bréchot, S. Semiclassical Stark broadening parameters of Ar VII spectral lines. Atoms 2017, 5, 27. [Google Scholar] [CrossRef]
- Bates, D.R.; Damgaard, A. The calculation of the absolute strengths of spectral lines. Phil. Trans. R. Soc. Lond. A 1949, 242, 101–122. [Google Scholar] [CrossRef]
- Eissner, W.; Jones, M.; Nussbaumer, H. Techniques for the calculation of atomic structures and radiative data including relativistic corrections. Comput. Phys. Commun. 1974, 8, 270–306. [Google Scholar] [CrossRef]
- Bethe, H.A.; Salpeter, E.E. Quantum Mechanics of One- and Two-Electron Atoms; Springer: Berlin/Göttingen, Germany, 1957. [Google Scholar]
- Eissner, W. The UCL distorted wave code. Comput. Phys. Commun. 1998, 114, 295–341. [Google Scholar] [CrossRef]
- Saraph, H.E. Fine structure cross sections from reactance matrices. Comput. Phys. Commun. 1972, 4, 256–268. [Google Scholar] [CrossRef]
- Sahal-Bréchot, S. Impact Theory of the Broadening and Shift of Spectral Lines due to Electrons and Ions in a Plasma. Astron. Astrophys. 1969, 1, 91–123. [Google Scholar]
- Sahal-Bréchot, S. Impact Theory of the Broadening and Shift of Spectral Lines due to Electrons and Ions in a Plasma (Continued). Astron. Astrophys. 1969, 2, 322–354. [Google Scholar]
- Fleurier, C.; Sahal-Bréchot, S.; Chapelle, J. Stark profiles of some ion lines of alkaline earth elements. J. Quant. Spectrosc. Radiat. Transfer 1977, 17, 595–603. [Google Scholar]
- Sahal-Bréchot, S.; Dimitrijević, M.S.; Ben Nessib, N. Widths and Shifts of Isolated Lines of Neutral and Ionized Atoms Perturbed by Collisions with Electrons and Ions: An Outline of the Semiclassical Perturbation Method and of the Approximations Used for the Calculations. Atoms 2014, 2, 225–252. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (Version 5.5.1); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015. Available online: http://physics.nist.gov/asd (accessed on 8 November 2017).
- Saloman, E.B. Energy Levels and Observed Spectral Lines of Ionized Argon, Ar II through Ar XVIII. J. Phys. Chem. Ref. Data 2010, 39, 033101. [Google Scholar] [CrossRef]
- Froese Fischer, C.; Tachiev, G.; Irimia, A. Relativistic energy levels, lifetimes, and transition probabilities for the sodium-like to argon-like sequences. At. Data Nucl. Data Tables 2006, 92, 607–812. [Google Scholar] [CrossRef]
- Fernández-Menchero, L.; Del Zanna, G.; Badnell, N.R. R-matrix electron-impact excitation data for the Mg-like iso-electronic sequence. Astron. Astrophys. 2014, 572, A115. [Google Scholar] [CrossRef]
- Christensen, R.B.; Norcross, D.W.; Pradhan, A.K. Electron-impact excitation of ions in the magnesium sequence. II. SV, ArVII, CaIX, CrXIII, and NiXVII. Phys. Rev. A 1986, 34, 4704–4715. [Google Scholar] [CrossRef]
- Del Zanna, G.; Dere, K.P.; Young, P.R.; Landi, E.; Mason, H.E. CHIANTI—An atomic database for emission lines. Astron. Astrophys. 2015, 582, A56. [Google Scholar] [CrossRef]
- Burgess, A.; Sheorey, V.B. Electron impact excitation of the resonance lines of alkali-like positive ions. J. Phys. B 1974, 7, 2403–2416. [Google Scholar] [CrossRef]
- Chidichimo, M.C.; Haig, S.P. Electron-impact excitation of quadrupole-allowed transitions in positive ions. Phys. Rev. A 1989, 39, 4991–4997. [Google Scholar] [CrossRef]
- Chidichimo, M.C. Electron-impact excitation of electric octupole transitions in positive ions: Asymptotic behavior of the sum over partial-collision strengths. Phys. Rev. A 1992, 45, 1690–1700. [Google Scholar] [CrossRef] [PubMed]
- Hamdi, R.; Ben Nessib, N.; Dimitrijević, M.S.; Sahal-Bréchot, S. Stark broadening of Pb IV lines. Mon. Not. R. Astron. Soc. 2013, 431, 1039–1047. [Google Scholar] [CrossRef]
- Hamdi, R.; Ben Nessib, N.; Sahal-Bréchot, S.; Dimitrijević, M.S. Stark widths of Ar III spectral lines in the atmospeheres of subdwarfs B stars. Adv. Res. Space 2014, 54, 1223–1230. [Google Scholar] [CrossRef]
- Hamdi, R.; Ben Nessib, N.; Sahal-Bréchot, S.; Dimitrijević, M.S. Stark widths of Ar II spectral lines in the atmospeheres of subdwarfs B stars. Atoms 2017, 5, 26. [Google Scholar] [CrossRef]
- Sahal-Bréchot, S.; Dimitrijević, M.S.; Moreau, N. STARK-B Database. Observatory of Paris, LERMA and Astronomical Observatory of Belgrade. 2017. Available online: http://stark-b.obspm.fr (accessed on 8 November 2017).
| i | Conf. | Level | E | NIST | MCHF | AS2014 | (%) |
|---|---|---|---|---|---|---|---|
| 1 | 0.0 | 0.0 | 0.0 | 0.0 | − | ||
| 2 | 110,717 | 113,101 | 112,817.66 | 112,070 | 2.1 | ||
| 3 | 111,488 | 113,906 | 113,632.14 | 112,889 | 2.1 | ||
| 4 | 113,088 | 115,590 | 115,324.84 | 114,593 | 2.2 | ||
| 5 | 172,878 | 170,722 | 170,598.08 | 173,751 | 1.3 | ||
| 6 | 263,439 | 264,749 | 264,797.88 | 264,530 | 0.5 | ||
| 7 | 271,494 | 269,836 | 269,688.15 | 270,704 | 0.6 | ||
| 8 | 272,341 | 270,777 | 270,667.14 | 271,641 | 0.6 | ||
| 9 | 273,971 | 272,562 | 272,474.76 | 273,432 | 0.5 | ||
| 10 | 325,254 | 324,104 | 324,950.35 | 326,054 | 0.4 | ||
| 11 | 325,335 | 324,141 | 324,966.00 | 326,141 | 0.4 | ||
| 12 | 325,456 | 324,205 | 325,056.68 | 326,273 | 0.4 | ||
| 13 | 333,116 | 316,717 | 317,014.73 | 320,974 * | 5.2 | ||
| 14 | 384,031 | 370,294 | 371,275.29 | 377,167 | 3.7 | ||
| 15 | 443,952 | 443,362 | 444,508.36 | 444,677 | 0.1 | ||
| 16 | 444,892 | 444,780 | 445,556.29 | 445,701 | 0.0 | ||
| 17 | 446,051 | 446,011 | 446,849.87 | 446,969 | 0.0 | ||
| 18 | 450,025 | 450,477 | 450,808.06 | 451352 | 0.1 | ||
| 19 | 474,314 | 472,282 | 473,009.27 | 475,022 | 0.4 | ||
| 20 | 474,956 | 472,875 | 473,782.67 | 475,699 | 0.4 | ||
| 21 | 475,497 | 473,810 | 474,466.36 | 476,301 | 0.4 | ||
| 22 | 477,133 | 475,217 | 475,932.22 | 477,901 | 0.4 | ||
| 23 | 477,515 | 475,585 | 476,306.50 | 478,313 | 0.4 | ||
| 24 | 477,753 | 475,762 | 476,474.91 | 478,560 | 0.4 | ||
| 25 | 513,685 | 514,076 | 508,971.69 | 511,372 | 0.1 | ||
| 26 | 521,897 | 510,268 | 514,890.47 | 515,169 * | 2.3 | ||
| 27 | 527,518 | 517,105 | 517,788.24 | 524,282 | 2.0 | ||
| 28 | 529,866 | 528,910 | 526,205.45 | 523,618 | 0.2 | ||
| 29 | 567,050 | 563,880 | 568,040.66 | 565,087 | 0.6 | ||
| 30 | 567,287 | 564,418 | 568,275.74 | 565,295 | 0.5 | ||
| 31 | 567,811 | 564,728 | 568,944.94 | 565,840 | 0.5 | ||
| 32 | 576,576 | 569,797 | 570,403.78 | 568,205 | 0.2 | ||
| 33 | 635,209 | 634,605 | 635,580.25 | 632,497 | 0.1 | ||
| 34 | 635,241 | 634,639 | 635,659.10 | 632,562 | 0.1 | ||
| 35 | 635,290 | 634,701 | 635,749.02 | 632,659 | 0.1 | ||
| 36 | 639,087 | 635,295 | 636,353.38 | 633,443 | 0.6 | ||
| 37 | 713,912 | 715,747 | − | 717,638 | 0.3 | ||
| 38 | 719,473 | 714,794 | − | 717,997 | 0.7 |
| AS2014) | SST | SST | S | |||
|---|---|---|---|---|---|---|
| 5.968 × | 7.13 × | 1.65 × | 2.160 × | 5.820 × | 0.000638 | |
| 8.114 × | 8.30 × | 8.21 × | 1.221 × | 1.270 × | 2.325423 | |
| 1.854 × | 2.97 × | 2.39 × | 6.018 × | 7.780 × | 0.013038 | |
| 3.748 × | 6.18 × | 6.07 × | 1.243 × | 2.020 × | 0.027216 | |
| 3.719 × | 4.00 × | 3.98 × | 3.400 × | 3.380 × | 1.235825 | |
| 7.249 × | 6.94 × | 6.93 × | 4.245 × | 4.280 × | 0.873472 | |
| 7.818 × | 1.72 × | 1.02 × | 1.205 × | 1.590 × | 0.000402 | |
| 2.492 × | 2.40 × | 2.35 × | 4.291 × | 4.250 × | 0.874104 | |
| 1.842 × | 1.77 × | 1.74 × | 3.202 × | 3.180 × | 0.655396 | |
| 2.976 × | 2.85 × | 2.84 × | 5.278 × | 5.310 × | 1.090986 | |
| 1.274 × | 1.33 × | 3.65 × | 5.793 × | 1.670 × | 0.000192 | |
| 1.877 × | 1.80 × | 1.77 × | 5.329 × | 5.270 × | 1.079810 | |
| 5.481 × | 5.24 × | 5.22 × | 1.587 × | 1.590 × | 3.248175 | |
| 4.965 × | 8.35 × | 7.11 × | 3.642 × | 5.240 × | 0.011859 | |
| 5.993 × | 5.86 × | 5.92 × | 5.857 × | 5.980 × | 0.898754 | |
| 4.449 × | 4.35 × | 4.40 × | 4.379 × | 4.480 × | 0.674448 | |
| 2.906 × | 2.84 × | 2.88 × | 2.904 × | 2.980 × | 0.045058 | |
| 5.117 × | 5.88 × | 1.52 × | 9.913 × | 2.950 × | 0.000214 | |
| 8.015 × | 7.84 × | 7.92 × | 1.314 × | 1.340 × | 2.022700 | |
| 2.618 × | 2.56 × | 2.60 × | 4.356 × | 4.480 × | 0.675718 | |
| 7.418 × | 7.91 × | 1.15 × | 2.392 × | 3.710 × | 0.000517 | |
| 1.048 × | 1.02 × | 1.04 × | 2.439 × | 2.510 × | 3.781547 | |
| 4.347 × | 9.07 × | 5.79 × | 1.327 × | 2.030 × | 0.000197 | |
| 8.643 × | 6.98 × | 6.97 × | 5.047 × | 4.840 × | 1.036879 | |
| 9.459 × | 9.90 × | 1.40 × | 9.546 × | 1.590 × | 0.001153 | |
| 4.427 × | 4.77 × | 4.47 × | 4.521 × | 5.130 × | 0.000055 | |
| 2.085 × | 1.90 × | 1.88 × | 3.506 × | 3.540 × | 5.466647 |
| Ry | Ry | Ry | ||||
|---|---|---|---|---|---|---|
| Present | DW86 | Present | DW86 | Present | DW86 | |
| 8.901 × | 9.29 × | 4.523 × | 4.54 × | 2.067 × | 2.01 × | |
| 2.936 × | 2.87 × | 1.652 × | 1.46 × | 9.202 × | 7.08 × | |
| 4.430 × | 4.64 × | 2.251 × | 2.26 × | 1.029 × | 1.00 × | |
| 8.841 × | 8.60 × | 9.848 × | 1.03 × | 1.006 × | 1.21 × | |
| 4.208 × | 3.57 × | 4.712 × | 3.48 × | 5.067 × | 3.17 × | |
| 5.400 × | 1.06× | 2.900 × | 5.40 × | 1.200 × | 2.33 × | |
| 1.560× | 2.81× | 8.400 × | 1.30× | 3.300 × | 4.64 × | |
| 4.102 × | 5.74 × | 4.449 × | 5.38 × | 4.785 × | 4.80 × | |
| 2.239 × | 2.39 × | 1.051 × | 1.10 × | 4.603 × | 4.73 × | |
| 3.731 × | 3.99 × | 1.752 × | 1.84 × | 7.671 × | 7.87 × | |
| 5.222 × | 5.58 × | 2.452 × | 2.57 × | 1.074 × | 1.10 × | |
| 3.460× | 1.28 × | 1.030× | 1.10 × | 5.800 × | 8.06 × | |
| 5.431 × | 7.40 × | 6.408 × | 8.03 × | 7.164 × | 8.46 × | |
| 6.257 × | 9.55 × | 3.113 × | 5.28 × | 1.475 × | 3.03 × | |
| 3.621 × | 2.98 × | 3.562 × | 2.79 × | 3.553 × | 2.50 × | |
| 1.103 × | 1.19 × | 5.152 × | 5.09 × | 2.222 × | 2.13 × | |
| 2.860 × | 2.77 × | 1.381 × | 1.40 × | 5.991 × | 6.05 × | |
| 5.657 × | 2.09 × | 2.784 × | 2.95 × | 1.210 × | 1.27 × | |
| 3.379 × | 3.32 × | 3.796 × | 4.05 × | 3.867 × | 4.70 × | |
| 4.773 × | 6.85 × | 2.338 × | 6.45 × | 1.012 × | 3.57 × | |
| 2.744 × | 2.75 × | 3.272 × | 3.43 × | 3.563 × | 4.10 × | |
| 2.286 × | 4.89 × | 1.027 × | 1.23 × | 4.178 × | 5.19 × | |
| 5.517 × | 6.10 × | 5.424 × | 5.58 × | 5.713 × | 5.14 × | |
| 1.746 × | 1.68 × | 8.200 × | 9.19× | 3.490× | 3.75× | |
| 9.861 × | 1.25 × | 4.171 × | 4.77 × | 1.639 × | 1.85 × | |
| 8.916 × | 7.87 × | 8.398 × | 6.89 × | 8.177 × | 5.96 × | |
| 3.383 × | 3.61 × | 1.603 × | 1.55 × | 7.172 × | 6.55 × | |
| 1.349 × | 1.43 × | 9.775 × | 1.19 × | 7.539 × | 1.10 × | |
| 3.379 × | 3.51 × | 3.926 × | 4.27 × | 4.410 × | 4.89 × | |
| 2.556 × | 2.67 × | 2.857 × | 3.12 × | 2.904 × | 3.60 × | |
| 4.186 × | 4.06 × | 4.695 × | 4.81 × | 4.780 × | 5.63 × | |
| 2.088 × | 2.17 × | 2.467 × | 2.66 × | 2.677 × | 3.15 × | |
| 6.232 × | 6.04 × | 7.416 × | 7.47 × | 8.072 × | 9.00 × | |
| 1.428 × | 1.90 × | 1.231 × | 1.28 × | 1.202 × | 1.09 × | |
| 6.369 × | 6.50 × | 3.504 × | 4.24 × | 2.005 × | 2.75 × | |
| 3.305 × | 3.80 × | 1.675 × | 1.49 × | 9.606 × | 6.27 × | |
| 5.693 × | 6.08 × | 2.671 × | 2.61 × | 1.169 × | 1.10 × | |
| 2.318 × | 2.89 × | 1.793 × | 2.75 × | 1.471 × | 2.74 × | |
| 6.345 × | 7.20 × | 3.119 × | 7.70 × | 1.355 × | 4.21 × | |
| 4.238 × | 4.63 × | 4.751 × | 5.46 × | 4.835 × | 6.23 × | |
| 1.261 × | 1.27 × | 1.414 × | 1.52 × | 1.439 × | 1.76 × | |
| 2.468 × | 2.79 × | 2.679 × | 2.93 × | 2.979 × | 3.16 × | |
| 2.208 × | 2.29 × | 2.581 × | 2.75 × | 2.795 × | 3.23 × | |
| 1.165 × | 1.07 × | 1.382 × | 1.32 × | 1.501 × | 1.62 × | |
| 1.042 × | 1.01 × | 4.917 × | 5.27 × | 2.094 × | 2.16 × | |
| 4.929 × | 6.27 × | 2.100 × | 2.39 × | 8.410 × | 9.45 × | |
| 6.396 × | 6.54 × | 6.502 × | 7.69 × | 6.069 × | 8.82 × | |
| 1.214 × | 1.21 × | 6.841 × | 8.61 × | 3.973 × | 5.89 × | |
| 3.337 × | 2.99 × | 1.671 × | 1.68 × | 7.776 × | 7.31 × | |
| 1.169 × | 1.34 × | 8.954 × | 1.27 × | 7.004 × | 1.27 × | |
| 4.295 × | 4.18 × | 1.955 × | 1.84 × | 8.514 × | 7.74 × | |
| 7.151 × | 6.94 × | 3.279 × | 3.04 × | 1.459 × | 1.25 × | |
| 9.742 × | 9.63 × | 4.322 × | 4.18 × | 1.770 × | 1.69 × | |
| 3.939 × | 4.46 × | 4.478 × | 5.32 × | 4.587 × | 6.12 × | |
| 1.653 × | 1.64 × | 1.990 × | 2.06 × | 2.181 × | 2.54 × | |
| Transition | T | Q (Å) | ||||
|---|---|---|---|---|---|---|
| 2 | 2.684 × | 2.380 × | 0.966 | 0.288 | 1.13 | |
| 5 | 1.872 × | 1.500 × | 0.937 | 0.287 | 1.25 | |
| 3s2 −3s3p | 10 | 1.453 × | 1.070 × | 0.891 | 0.286 | 1.36 |
| Å | 20 | 1.135 × | 7.640 × | 0.789 | 0.282 | 1.49 |
| 30 | 9.875 × | 6.360 × | 0.706 | 0.276 | 1.55 | |
| 50 | 8.322 × | 5.160 × | 0.605 | 0.267 | 1.61 | |
| 2 | 9.941 × | 6.070 × | 0.897 | 0.575 | 1.64 | |
| 5 | 6.242 × | 2.930 × | 0.827 | 0.361 | 2.13 | |
| 3s2 −3s4p | 10 | 4.370 × | 2.110 × | 0.766 | 0.357 | 2.07 |
| Å | 20 | 3.038 × | 1.550 × | 0.689 | 0.345 | 1.96 |
| 30 | 2.445 × | 1.320 × | 0.641 | 0.334 | 1.85 | |
| 50 | 1.848 × | 1.090 × | 0.588 | 0.319 | 1.70 | |
| 2 | 6.322 × | 9.750 × | 0.944 | 0.155 | 6.48 | |
| 5 | 3.923 × | 5.400 × | 0.767 | 0.175 | 7.26 | |
| 3s3p −3s4s | 10 | 2.676 × | 3.190 × | 0.616 | 0.172 | 6.84 |
| Å | 20 | 1.759 × | 2.920 × | 0.472 | 0.162 | 6.02 |
| 30 | 1.344 × | 2.500 × | 0.401 | 0.155 | 5.38 | |
| 50 | 9.332 × | 2.080 × | 0.328 | 0.145 | 4.49 | |
| 2 | 4.517 × | 1.360 × | 0.792 | 0.193 | 3.32 | |
| 5 | 2.942 × | 8.840 × | 0.595 | 0.189 | 3.33 | |
| 3s4p −3s5s | 10 | 1.975 × | 6.570 × | 0.458 | 0.179 | 3.01 |
| Å | 20 | 1.266 × | 5.050 × | 0.359 | 0.166 | 2.51 |
| 30 | 9.671 × | 4.400 × | 0.315 | 0.156 | 2.20 | |
| 50 | 6.843 × | 3.740 × | 0.274 | 0.144 | 1.83 | |
| 2 | 1.910 × | 4.150 × | 0.859 | 0.361 | 4.60 | |
| 5 | 1.355 × | 2.650 × | 0.809 | 0.356 | 5.11 | |
| 3s3d −3s4p | 10 | 1.011 × | 1.930 × | 0.737 | 0.346 | 5.24 |
| Å | 20 | 6.854 × | 1.430 × | 0.661 | 0.335 | 4.79 |
| 30 | 5.206 × | 1.210 × | 0.611 | 0.323 | 4.30 | |
| 50 | 3.602 × | 1.010 × | 0.561 | 0.307 | 3.57 | |
| 2 | 1.779 × | 8.070 × | 0.825 | 0.085 | 2.20 | |
| 5 | 1.119 × | 4.750 × | 0.559 | 0.092 | 2.36 | |
| 3s3p −3s5s | 10 | 7.845 × | 3.520 × | 0.400 | 0.087 | 2.23 |
| Å | 20 | 5.460 × | 2.710 × | 0.282 | 0.081 | 2.01 |
| 30 | 4.390 × | 2.360 × | 0.229 | 0.076 | 1.86 | |
| 50 | 3.303 × | 2.000 × | 0.177 | 0.069 | 1.65 |
| Transition | T | Q (Å) | ||||
|---|---|---|---|---|---|---|
| 0.2 | 2.684 × | 2.380 × | 0.966 | 0.288 | 1.13 | |
| 0.5 | 1.872 × | 1.500 × | 0.937 | 0.287 | 1.25 | |
| 1 | 1.453 × | 1.070 × | 0.891 | 0.286 | 1.36 | |
| 2 | 1.135 × | 7.640 × | 0.789 | 0.282 | 1.49 | |
| 3s2 −3s3p | 3 | 9.875 × | 6.360 × | 0.706 | 0.276 | 1.55 |
| Å | 5 | 8.322 × | 5.160 × | 0.605 | 0.267 | 1.61 |
| 7.5 | 7.271 × | 4.430 × | 0.537 | 0.255 | 1.64 | |
| 10 | 6.593 × | 4.020 × | 0.494 | 0.245 | 1.64 | |
| 15 | 5.699 × | 3.530 × | 0.444 | 0.232 | 1.61 | |
| 30 | 4.284 × | 2.890 × | 0.389 | 0.211 | 1.48 | |
| 50 | 3.327 × | 2.530 × | 0.366 | 0.199 | 1.32 |
| Transition | T | Q | ||||||
|---|---|---|---|---|---|---|---|---|
| 2 | 7.510 × | 4.83 × | 4.21 × | 1.55 | 0.889 | 0.444 | 1.77 | |
| 5 | 4.748 × | 2.86 × | 2.49 × | 1.66 | 0.877 | 0.475 | 1.90 | |
| 3s3p −3s4d | 10 | 3.369 × | 2.04 × | 1.81 × | 1.65 | 0.861 | 0.472 | 1.85 |
| Å | 20 | 2.389 × | 1.48 × | 1.35 × | 1.62 | 0.823 | 0.461 | 1.77 |
| 30 | 1.967 × | 1.25 × | 1.15 × | 1.47 | 0.798 | 0.453 | 1.70 | |
| 50 | 1.532 × | 1.02 × | 9.51 × | 1.50 | 0.764 | 0.437 | 1.61 | |
| 2 | 1.613 × | 3.76 × | 3.09 × | 4.29 | 0.901 | 0.457 | 5.22 | |
| 5 | 1.061 × | 2.38 × | 1.99 × | 4.46 | 0.873 | 0.455 | 5.33 | |
| 3s4p −3s4d | 10 | 7.141 × | 1.71 × | 1.45 × | 4.18 | 0.824 | 0.448 | 4.92 |
| Å | 20 | 4.285 × | 1.26 × | 1.08 × | 3.40 | 0.767 | 0.435 | 3.97 |
| 30 | 3.073 × | 1.07 × | 9.27 × | 2.87 | 0.740 | 0.424 | 3.31 | |
| 50 | 2.013 × | 8.87 × | 7.77 × | 2.27 | 0.705 | 0.406 | 2.59 | |
| 2 | 7.585 × | 2.33 × | 1.84 × | 3.26 | 0.928 | 0.406 | 4.12 | |
| 5 | 4.562 × | 1.52 × | 1.16 × | 3.00 | 0.878 | 0.397 | 3.93 | |
| 3s3d −3s4p | 10 | 2.896 × | 1.10 × | 8.35 × | 2.64 | 0.809 | 0.389 | 3.47 |
| Å | 20 | 1.806 × | 8.14 × | 6.12 × | 2.22 | 0.723 | 0.375 | 2.95 |
| 30 | 1.389 × | 6.91 × | 5.18 × | 2.01 | 0.675 | 0.364 | 2.68 | |
| 50 | 1.040 × | 5.73 × | 4.27 × | 1.82 | 0.625 | 0.346 | 2.43 | |
| 2 | 7.605 × | 5.36 × | 5.34 × | 1.42 | 0.942 | 0.337 | 1.42 | |
| 5 | 5.453 × | 3.44 × | 3.33 × | 1.59 | 0.863 | 0.331 | 1.64 | |
| 3s4s −3s4p | 10 | 4.272 × | 2.49 × | 2.40 × | 1.72 | 0.757 | 0.326 | 1.78 |
| Å | 20 | 3.336 × | 1.85 × | 1.79 × | 1.80 | 0.632 | 0.309 | 1.86 |
| 30 | 2.871 × | 1.59 × | 1.53 × | 1.81 | 0.577 | 0.298 | 1.88 | |
| 50 | 2.350 × | 1.33 × | 1.28 × | 1.77 | 0.518 | 0.281 | 1.84 | |
| 2 | 1.396 × | 8.72 × | 5.06 × | 1.56 | 0.996 | 0.358 | 2.75 | |
| 5 | 8.893 × | 5.35 × | 2.68 × | 1.66 | 0.947 | 0.368 | 3.30 | |
| 3s3p −3s4s | 10 | 6.351 × | 3.80 × | 1.91 × | 1.67 | 0.860 | 0.368 | 3.31 |
| Å | 20 | 4.549 × | 2.78 × | 1.41 × | 1.64 | 0.750 | 0.358 | 3.21 |
| 30 | 3.742 × | 2.35 × | 1.21 × | 1.59 | 0.690 | 0.349 | 3.08 | |
| 50 | 2.915 × | 1.94 × | 1.01 × | 1.50 | 0.626 | 0.333 | 2.87 | |
| 2 | 5.727 × | 1.69 × | 9.11 × | 3.39 | 0.986 | 0.334 | 6.24 | |
| 5 | 2.896 × | 9.92 × | 5.85 × | 2.92 | 0.961 | 0.363 | 4.91 | |
| 3s3p −3s3d | 10 | 1.708 × | 7.02 × | 4.17 × | 2.43 | 0.921 | 0.362 | 4.06 |
| Å | 20 | 1.022 × | 5.02 × | 2.96 × | 2.04 | 0.830 | 0.357 | 3.43 |
| 30 | 7.755 × | 4.18 × | 2.45 × | 1.86 | 0.764 | 0.353 | 3.14 | |
| 50 | 5.734 × | 3.37 × | 1.95 × | 1.70 | 0.684 | 0.343 | 2.92 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aloui, R.; Elabidi, H.; Sahal-Bréchot, S.; Dimitrijević, M.S. Quantum and Semiclassical Stark Widths for Ar VII Spectral Lines. Atoms 2018, 6, 20. https://doi.org/10.3390/atoms6020020
Aloui R, Elabidi H, Sahal-Bréchot S, Dimitrijević MS. Quantum and Semiclassical Stark Widths for Ar VII Spectral Lines. Atoms. 2018; 6(2):20. https://doi.org/10.3390/atoms6020020
Chicago/Turabian StyleAloui, Rihab, Haykel Elabidi, Sylvie Sahal-Bréchot, and Milan S. Dimitrijević. 2018. "Quantum and Semiclassical Stark Widths for Ar VII Spectral Lines" Atoms 6, no. 2: 20. https://doi.org/10.3390/atoms6020020
APA StyleAloui, R., Elabidi, H., Sahal-Bréchot, S., & Dimitrijević, M. S. (2018). Quantum and Semiclassical Stark Widths for Ar VII Spectral Lines. Atoms, 6(2), 20. https://doi.org/10.3390/atoms6020020









