Doppler Broadening of Spectral Line Shapes in Relativistic Plasmas
Abstract
:1. Introduction
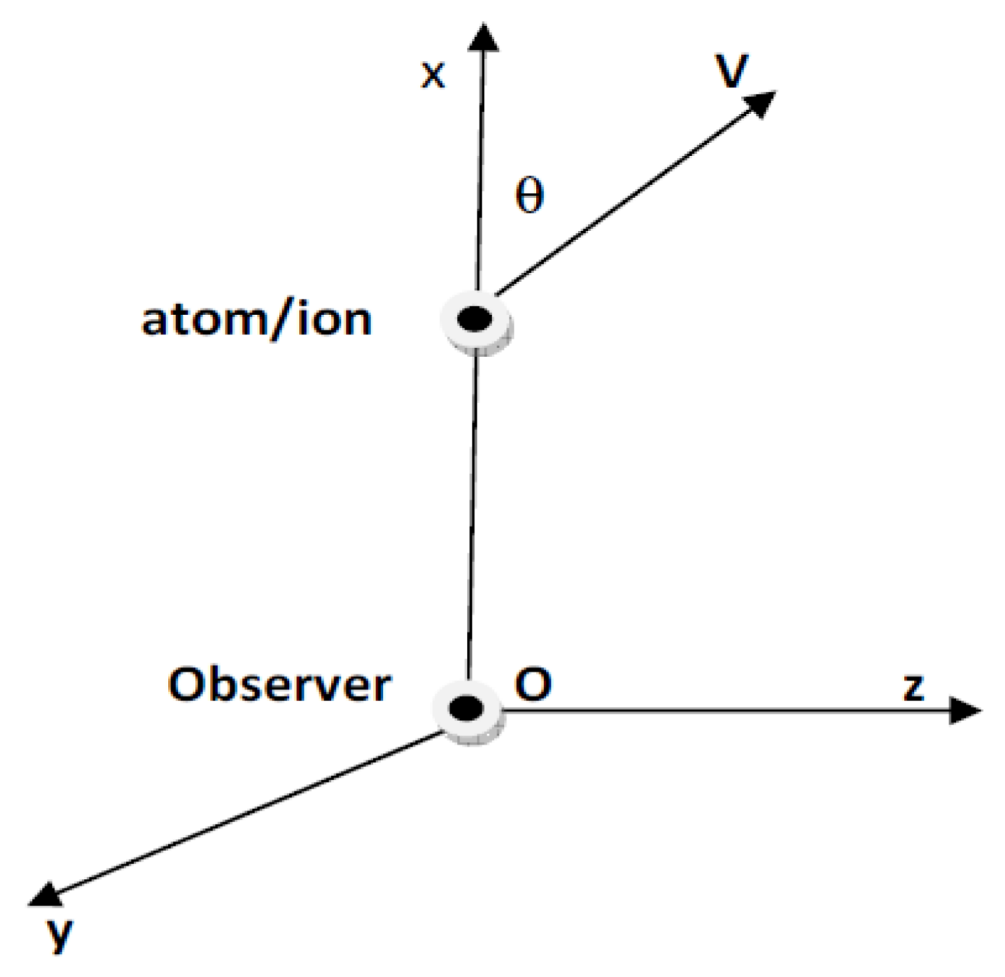
2. Doppler Broadening
2.1. Classical Doppler Broadening: Non Relativistic Case
2.2. Relativistic Doppler Broadening
3. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Huang, Y.-S. Formulation of relativistic Doppler-broadened absorption line profile. Europhys. Lett. 2012, 97, 23001. [Google Scholar] [CrossRef]
- Huang, Y.-S. Formulation of the classical and the relativistic Doppler effect by a systematic method. Can. J. Phys. 2004, 82, 957–964. [Google Scholar] [CrossRef]
- Kichenassamy, S.; Krikorian, R.; Nikogosian, A. The relativistic Doppler broadening of the line absorption profile. J. Quant. Spectrosc. Radiat. Transf. 1982, 27, 653–655. [Google Scholar] [CrossRef]
- McKinley, J.M. Relativistic transformations of light power. Am. J. Phys. 1979, 47, 602–605. [Google Scholar] [CrossRef]
- Haines, M.G.; LePell, P.D.; Coverdale, C.A.; Jones, B.; Deeney, C.; Apruzese, J.P. Ion Viscous Heating in a Magnetohydrodynamically Unstable Z Pinch at Over 2 × 109 Kelvin. Phys. Rev. Lett. 2006, 96, 075003. [Google Scholar] [CrossRef] [PubMed]
- Jackson, J.D. Special Theory of Relativity. In Classical Electrodynamics, 3rd ed.; John Wiley: New York, NY, USA, 1962; Chapter 11; pp. 360–364. [Google Scholar]
- Zenitani, S. Loading relativistic Maxwell distributions in particle simulations. Phys. Plamas 2015, 22, 042116. [Google Scholar] [CrossRef]
- Stehlé, C.; Gilles, D.; Demura, A.V. Asymmetry of Stark profiles: The microfield point of view. Eur. Phys. J. D 2000, 12, 355–367. [Google Scholar] [CrossRef]
- Schwartz, L. Théorie des Distributions; Editions Hernmann: Paris, France, 1967. [Google Scholar]
- Huang, Y.-S.; Chiue, J.-H.; Huang, Y.-C.; Hsiung, T.-C. Relativistic formulation for the Doppler-broadened line profile. Phys. Rev. A 2010, 82, 010102(R). [Google Scholar] [CrossRef]
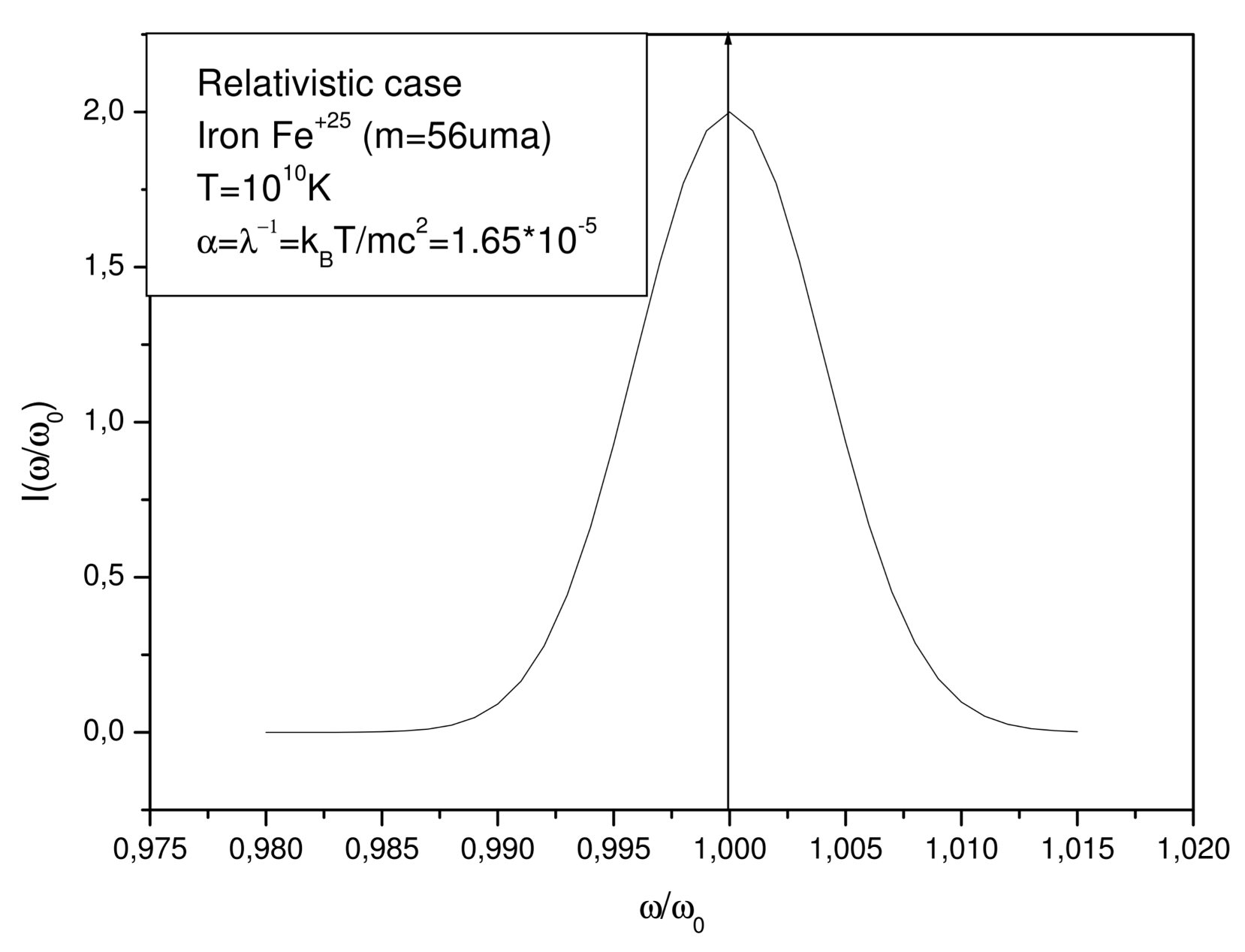
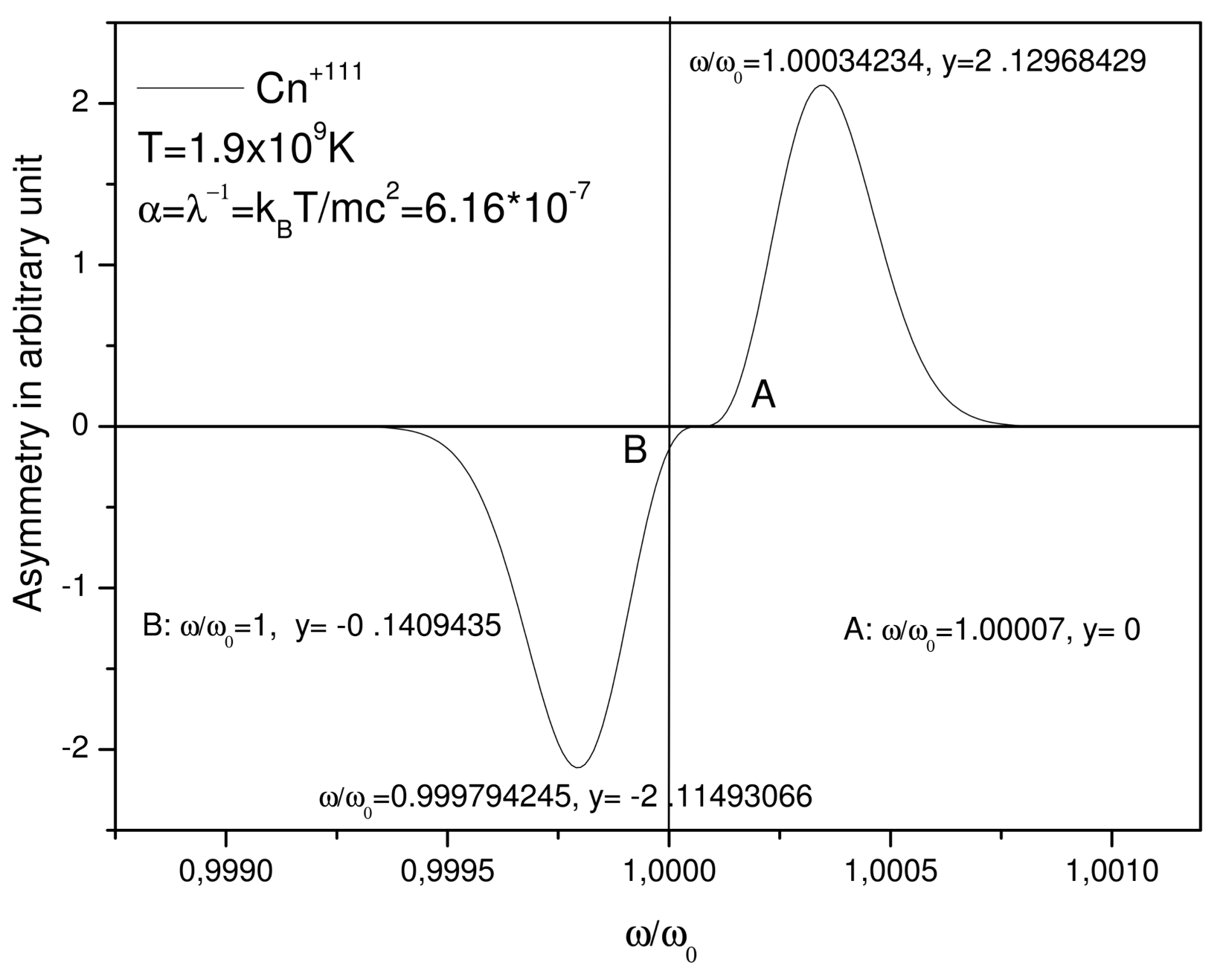
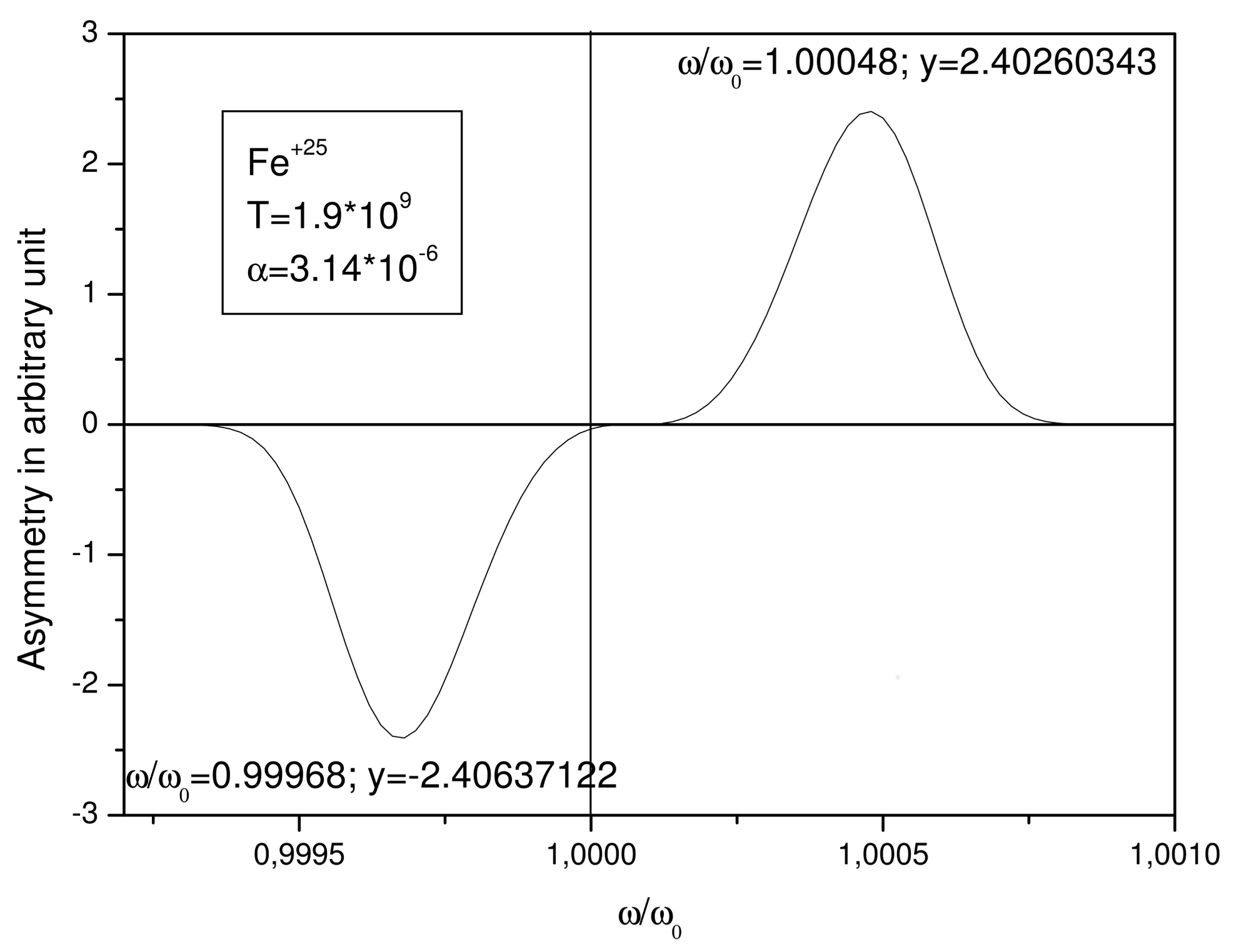
| T = 10 K, Fe | T = 8.5 × 10 K, W | T = 1.5 × 10 K, Fm | T = 1.9 × 10 K, Cn | |
|---|---|---|---|---|
| 0.99955 | 0.99925 | 0.99915 | 0.99905 | |
| 1.00045 | 1.00075 | 1.00085 | 1.00095 | |
| 1.0802 | 1. 0303 | 1. 0195 | 0.95715 | |
| 1.0807 | 1. 0313 | 1. 0206 | 0.95849 | |
| 0.030 | 0.051 | 0.056 | 0.060 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meftah, M.T.; Gossa, H.; Touati, K.A.; Chenini, K.; Naam, A. Doppler Broadening of Spectral Line Shapes in Relativistic Plasmas. Atoms 2018, 6, 16. https://doi.org/10.3390/atoms6020016
Meftah MT, Gossa H, Touati KA, Chenini K, Naam A. Doppler Broadening of Spectral Line Shapes in Relativistic Plasmas. Atoms. 2018; 6(2):16. https://doi.org/10.3390/atoms6020016
Chicago/Turabian StyleMeftah, Mohammed Tayeb, Hadda Gossa, Kamel Ahmed Touati, Keltoum Chenini, and Amel Naam. 2018. "Doppler Broadening of Spectral Line Shapes in Relativistic Plasmas" Atoms 6, no. 2: 16. https://doi.org/10.3390/atoms6020016
APA StyleMeftah, M. T., Gossa, H., Touati, K. A., Chenini, K., & Naam, A. (2018). Doppler Broadening of Spectral Line Shapes in Relativistic Plasmas. Atoms, 6(2), 16. https://doi.org/10.3390/atoms6020016




