Stark Broadening of Cr III Spectral Lines: DO White Dwarfs
Abstract
1. Introduction
2. The Modified Semiempirical Method
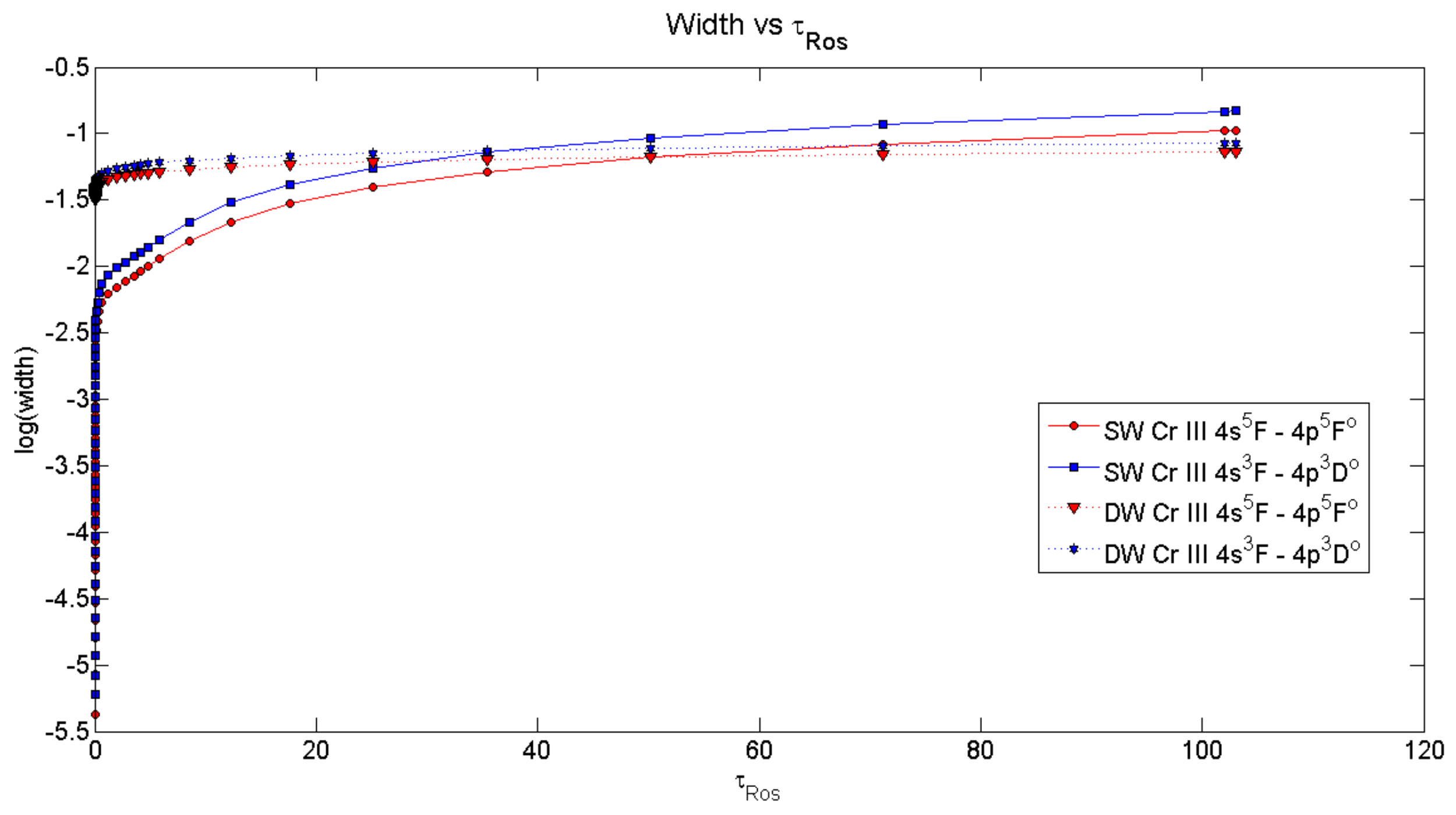
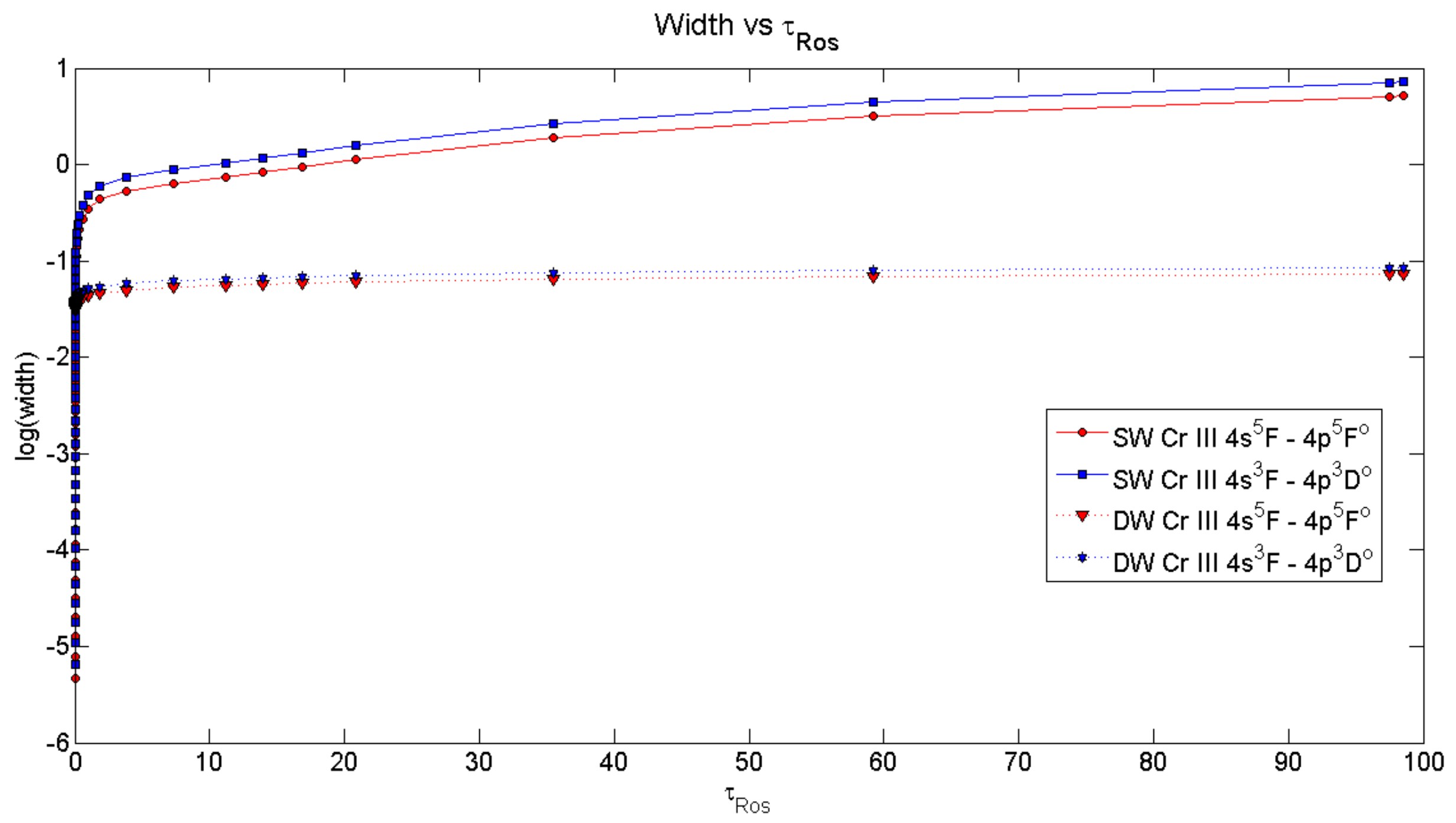
3. Results and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Underhill, A.B. The Ultraviolet Spectrum of Eta Canis Majoris, B5 Ia. Astrophys. J. Suppl. Ser. 1974, 27, 359–389. [Google Scholar] [CrossRef]
- Underhill, A.B. Line Identifications in the Ultraviolet Spectra of Tau Herculis (B5 IV) and Zeta Draconis (B6 III). Astrophys. J. Suppl. Ser. 1974, 34, 309–380. [Google Scholar] [CrossRef]
- Fahey, R.P.; Fischel, D.; Sparks, W. Intensity Changes in the UV Spectrum of Beta Cephei. NASCP 1982, 2238, 442–445. [Google Scholar]
- Bauer, W.H.; Bennett, P.D. An Atlas of Far-ultraviolet Spectra of the Zeta Aurigae Binary 31 Cygni with Line Identifications. Astrophys. J. Suppl. Ser. 2014, 211, 27. [Google Scholar] [CrossRef]
- Johansson, S. On regularities in complex spectra of iron group elements and their dominance in stellar spectra. Phys. Scr. 1987, 36, 99–106. [Google Scholar] [CrossRef]
- Swings, J.P.; Klutz, M.; Peytremann, E.; Vreux, J.M. Fe III lines in the ultraviolet spectra of early B stars. Astron. Astrophys. Suppl. Ser. 1976, 25, 193–212. [Google Scholar]
- Cowley, C.R.; Frey, M. On the completeness of the analysis of third and fourth spectra of the iron group, and the spectra of early B stars. Nucl. Instrum. Methods Phys. Res. B 1988, 31, 214–221. [Google Scholar] [CrossRef]
- Smillie, D.G.; Pickering, J.C.; Smith, P.L. Reference ultraviolet wavelengths of Cr III measured by Fourier transform spectrometry. Mon. Not. R. Astron. Soc. 2008, 390, 733–740. [Google Scholar] [CrossRef]
- Adelman, S.J.; Philip, A.G.D. Elemental abundances of field horizontal branch stars—IV. HD 74721, 86986 and 93329. Mon. Not. R. Astron. Soc. 1996, 280, 285–290. [Google Scholar] [CrossRef][Green Version]
- Caliskan, H.; Adelman, S.J. Elemental abundance analyses with DAO spectrograms—XVII. The superficially normal early A stars 2 Lyncis, omicron Ursa Majoris and phi Aquilae. Mon. Not. R. Astron. Soc. 1997, 288, 501–511. [Google Scholar] [CrossRef]
- Adelman, S.J. Elemental abundance analyses with DAO spectrograms. VII—The late normal B stars Pi Ceti, 134 Tauri, 21 Aquilae, and Nu Capricorni and the use of RETICON spectra. Mon. Not. R. Astron. Soc. 1991, 252, 116–131. [Google Scholar] [CrossRef]
- Cowley, C.R.; Ryabchikova, T.; Kupka, F.; Bord, D.J.; Mathys, G.; Bidelman, W.P. Abundances in Przybylski’s star. Mon. Not. R. Astron. Soc. 2000, 317, 299–309. [Google Scholar] [CrossRef]
- Schevchenko, V.S. V380 Ori: An Ae/Be Herbig star at an early stage of its envelope formation-emission lines of metals. Astron. Rep. 1994, 38, 505–519. [Google Scholar]
- Andrievsky, S.M.; Kovtyukh, V.V.; Usenko, I.A. The chemical composition of the s-Cepheids. 1: Alpha Ursae Minoris (Polaris) and HR 7308 (V 473 Lyrae): Unique Cepheids of the Galaxy. Astron. Astrophys. 1994, 281, 465–470. [Google Scholar]
- Goswami, A.; Rao, N.K.; Lambert, D.L. Emission-line spectra of XX Ophiuchi in 1996 and 1997. Observatory 2001, 121, 97–107. [Google Scholar]
- Merrill, P.W. The Spectrum of XX Ophiuchi in 1949 and 1950. Astrophys. J. 1951, 114, 37–46. [Google Scholar] [CrossRef]
- Babel, J.; Lanz, T. Stratification of chemical elements in the atmosphere of the AP star 53 Camelopardalis. Astron. Astrophys. 1992, 263, 232–240. [Google Scholar]
- Dimitrijević, M.S.; Ryabchikova, T.; Simić, Z.; Popović, L.Č.; Dačić, M. The Influence of Stark broadening on Cr II spectral line shapes in stellar atmospheres. Astron. Astrophys. 2007, 469, 681–686. [Google Scholar] [CrossRef][Green Version]
- Popović, L.Č.; Dimitrijević, M.S.; Tankosić, D. The stark broadening effect in hot star atmospheres: Au I and Au II lines. Astron. Astrophys. Suppl. Ser. 1999, 139, 617–623. [Google Scholar] [CrossRef]
- Tankosić, D.; Popović, L.Č.; Dimitrijević, M.S. The electron-impact broadening parameters for Co III spectral lines. Astron. Astrophys. 2003, 399, 795–797. [Google Scholar] [CrossRef]
- Simić, Z.; Dimitrijević, M.S.; Popović, L.Č.; Dačić, M. Importance of collisions with charged particles for stellar UV line shapes: Cd III. Astron. Astrophys. 2004, 417, 375–380. [Google Scholar]
- Simić, Z.; Dimitrijević, M.S.; Popović, L.Č.; Dačić, M. Stark broadening parameters for Cu III, Zn III and Se III lines in laboratory and stellar plasma. MNRAS 2006, 423, 766–773. [Google Scholar] [CrossRef]
- Dufour, P.; Ben Nessib, N.; Sahal-Bréchot, S.; Dimitrijević, M.S. Stark Broadening of Carbon and Oxygen Lines in Hot DQ White Dwarf Stars: Recent Results and Applications. Baltic Astron. 2011, 20, 511–515. [Google Scholar] [CrossRef]
- Larbi-Terzi, N.; Sahal-Bréchot, S.; Ben Nessib, N.; Dimitrijević, M.S. Stark-broadening calculations of singly ionized carbon spectral lines. New Astron. 2012, 12, 187–191. [Google Scholar] [CrossRef]
- Simi′c, Z.; Dimitrijevi′c, M.S.; Sahal-Bréchot, S. Stark broadening of resonant Cr II 3d5-3d44p spectral lines. Mon. Not. R. Astron. Soc. 2013, 432, 2247–2251. [Google Scholar] [CrossRef]
- Dimitrijević, M.S.; Simić, Z.; Kovačević, A.; Valjarević, A.; Sahal-Bréchot, S. Stark broadening of Xe VIII spectral lines. Mon. Not. R. Astron. Soc. 2015, 454, 1736–1741. [Google Scholar] [CrossRef]
- Majlinger, Z.; Simić, Z.; Dimitrijević, M.S. Stark broadening of Zr IV spectral lines in the atmospheres of chemically peculiar stars. Mon. Not. R. Astron. Soc. 2017, 470, 1911–1918. [Google Scholar] [CrossRef]
- Gianninas, A.; Hermes, J.J.; Brown, W.R.; Dufour, P.; Barber, S.D.; Kilic Mukremin, B.; Kenyon, S.J.; Harrold, S.T. SDSS J074511.56+194926.5: Discovery of a Metal-rich and Tidally Distorted Extremely Low Mass White Dwarf. Astrophys. J. 2014, 781, 104. [Google Scholar] [CrossRef]
- Dufour, P.; Bergeron, P.; Schmidt, G.D.; Liebert, J.; Harris, H.C.; Knapp, G.R.; Anderson, S.F.; Schneider, D.P. Model Atmosphere Analysis of the Weakly Magnetic DZ White Dwarf G165-7. Astrophys. J. 2006, 651, 1112–1119. [Google Scholar] [CrossRef][Green Version]
- Klein, B.; Jura, M.; Koester, D.; Zuckerman, B.; Melis, C. Chemical Abundances in the Externally Polluted White Dwarf GD 40: Evidence of a Rocky Extrasolar Minor Planet. Astrophys. J. 2010, 709, 950–962. [Google Scholar] [CrossRef]
- Rauch, T.; Ziegler, M.; Werner, K.; Kruk, J.W.; Oliveira, C.M.; Vande Putte, D.; Mignani, R.P.; Kerber, F. High-resolution FUSE and HST ultraviolet spectroscopy of the white dwarf central star of Sh 2-216. Astron. Astrophys. 2007, 470, 317–329. [Google Scholar] [CrossRef]
- Dimitrijević, M.S.; Ryabchikova, T.; Popović, L.Č.; Shulyak, D.; Khan, S. On the Influence of Stark broadening on Cr I lines in stellar atmospheres. Astron. Astrophys. 2005, 435, 1191–1198. [Google Scholar] [CrossRef]
- Sahal-Bréchot, S. Impact theory of the broadening and shift of spectral lines due to electrons and ions in a plasma. Astron. Astrophys. 1969, 1, 91–123. [Google Scholar]
- Sahal-Bréchot, S. Impact theory of the broadening and shift of spectral lines due to electrons and ions in a plasma (continued). Astron. Astrophys. 1969, 2, 322–354. [Google Scholar]
- Sahal-Bréchot, S.; Dimitrijević, M.S.; Ben Nessib, N. Widths and Shifts of Isolated Lines of Neutral and Ionized Atoms Perturbed by Collisions With Electrons and Ions: An Outline of the Semiclassical Perturbation (SCP) Method and of the Approximations Used for the Calculations. Atoms 2014, 2, 225–252. [Google Scholar] [CrossRef]
- Lakićević, I.S. Estimated Stark widths and shifts of neutral atom and singly charged ion resonance lines. Astrophys. J. 1951, 121, 37–41. [Google Scholar]
- Kurucz, R.L. ATLAS9 Stellar Atmosphere Programs and 2 km s-1 grid, Kurucz CD-ROM No. 13; Smithsonian Astrophysical Observatory: Cambridge, MA, USA, 1993; pp. 13, 22–23. [Google Scholar]
- Dimitrijević, M.S.; Simić, Z.; Sahal-Bréchot, S. On the Stark broadening of Cr VI spectral lines in astrophysical plasmas. J. Phys. Conf. Ser. 2017, 810, 012021. [Google Scholar] [CrossRef]
- Rathore, B.A.; Lakićević, I.S.; Ćuk, M.; Purić, J. Measurement of the Stark widths and shifts of Cr II 4s4D-4p4Fo spectral lines. Phys. Rev. A 1984, 28, 2264–2268. [Google Scholar]
- Aguilera, J.A.; Aragón, C.; Manrique, J. Experimental Stark widths and shifts of Cr II spectral lines. Mon. Not. R. Astron. Soc. 2014, 438, 841–845. [Google Scholar] [CrossRef]
- Dimitrijević, M.S.; Konjević, N. Stark widths of doubly- and triply-ionized atom lines. J. Quant. Spectrosc. Radiat. Transf. 1980, 24, 451–459. [Google Scholar] [CrossRef]
- Dimitrijević, M.S.; Kršljanin, V. Electron-impact shifts of ion lines—Modified semiempirical approach. Astron. Astrophys. 1986, 165, 269–274. [Google Scholar]
- Dimitrijević, M.S.; Popović, L.Č. Modified Semiempirical Method. J. Appl. Spectrosc. 2001, 68, 893–901. [Google Scholar] [CrossRef]
- Griem, H.R. Semiempirical Formulas for the Electron-Impact Widths and Shifts of Isolated Ion Lines in Plasmas. Phys. Rev. 1968, 165, 258–266. [Google Scholar] [CrossRef]
- Sugar, J.; Corliss, C. Atomic Energy Levels of the Iron-Period Elements: Potassium through Nickel. J. Phys. Chem. Ref. Data 1985, 14 (Suppl. 2), 1–664. [Google Scholar]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database; Version 5.3; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015. [Google Scholar]
- Bates, D.R.; Damgaard, A. The Calculation of the Absolute Strengths of Spectral Lines. Phil. Trans. R. Soc. Lond. A 1949, 242, 101–122. [Google Scholar] [CrossRef]
- Hamdi, R.; Ben Nessib, N.; Milovanović, N.; Popović, L.Č.; Dimitrijević, M.S.; Sahal-Bréchot, S. Atomic data and electron-impact broadening effect in DO white dwarf atmospheres: SiVI. Mon. Not. R. Astron. Soc. 2008, 387, 871–882. [Google Scholar] [CrossRef]
- Chayer, P.; Vennes, S.; Dupuis, J.; Kruk, J.W. Abundance of Elements beyond the Iron Group in Cool DO White Dwarfs. Astrophys. J. Lett. 2005, 630, 169–172. [Google Scholar] [CrossRef]
- Wesemael, F. Atmospheres for hot, high-gravity stars. II. Pure helium models. Astrophys. J. Suppl. Ser. 1981, 45, 177–257. [Google Scholar] [CrossRef]
- Seaton, M.J. Atomic data for opacity calculations. I—General description. J. Phys. B 1987, 20, 6363–6378. [Google Scholar] [CrossRef]
- Sahal-Bréchot, S.; Dimitrijević, M.S.; Moreau, N. STARK-B Database, Observatory of Paris, LERMA and Astronomical Observatory of Belgrade. Available online: http://stark-b.obspm.fr (accesed on 1 February 2018).
- Sahal-Bréchot, S.; Dimitrijević, M.S.; Moreau, N.; Ben Nessib, N. The STARK-B database VAMDC node: A repository for spectral line broadening and shifts due to collisions with charged particles. Phys. Scr. 2015, 50, 054008. [Google Scholar] [CrossRef]
- Dubernet, M.L.; Boudon, V.; Culhane, J.L.; Dimitrijevic, M.S.; Fazliev, A.Z.; Joblin, C.; Kupka, F.; Leto, G.; Le Sidaner, P.; Loboda, P.A.; et al. Virtual atomic and molecular data centre. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 2151–2159. [Google Scholar] [CrossRef]
- Dubernet, M.L.; Antony, B.K.; Ba, Y.A.; Babikov, Y.L.; Bartschat, K.; Boudon, V.; Braams, B.J.; Chung, H.-K.; Daniel, F.; Delahaye, F.; et al. The virtual atomic and molecular data centre (VAMDC) consortium. J. Phys. B 2016, 49, 074003. [Google Scholar] [CrossRef]
| Transition | T (K) | FWHM (Å) |
|---|---|---|
| CrIII 3d(F)4sF–3d(F)4pFo | 5000 | 0.723E-01 |
| 10,000 | 0.511E-01 | |
| = 2121.8 Å | 20,000 | 0.361E-01 |
| 3kT/2E = 0.234 | 40,000 | 0.256E-01 |
| 80,000 | 0.181E-01 | |
| CrIII 3d(F)4sF–3d(F)4pGo | 5000 | 0.791E-01 |
| 10,000 | 0.559E-01 | |
| = 2241.9 Å | 20,000 | 0.396E-01 |
| 3kT/2E = 0.234 | 40,000 | 0.280E-01 |
| 80,000 | 0.198E-01 | |
| CrIII 3d(F)4sF–3d(F)4pDo | 5000 | 0.732E-01 |
| 10,000 | 0.518E-01 | |
| = 2138.2 Å | 20,000 | 0.366E-01 |
| 3kT/2E = 0.234 | 40,000 | 0.259E-01 |
| 80,000 | 0.183E-01 | |
| CrIII 3d(F)4sF–3d(F)4pFo | 5000 | 0.850E-01 |
| 10,000 | 0.601E-01 | |
| = 2235.6 Å | 20,000 | 0.425E-01 |
| 3kT/2E = 0.258 | 40,000 | 0.301E-01 |
| 80,000 | 0.213E-01 | |
| CrIII 3d(F)4sF–3d(F)4pGo | 5000 | 0.905E-01 |
| 10,000 | 0.640E-01 | |
| = 2321.9 Å | 20,000 | 0.453E-01 |
| 3kT/2E = 0.258 | 40,000 | 0.320E-01 |
| 80,000 | 0.226E-01 | |
| CrIII 3d(F)4sF–3d(F)4pDo | 5000 | 0.101 |
| 10,000 | 0.715E-01 | |
| = 2478.9 Å | 20,000 | 0.505E-01 |
| 3kT/2E = 0.258 | 40,000 | 0.357E-01 |
| 80,000 | 0.253E-01 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimitrijević, M.S.; Chougule, A. Stark Broadening of Cr III Spectral Lines: DO White Dwarfs. Atoms 2018, 6, 15. https://doi.org/10.3390/atoms6020015
Dimitrijević MS, Chougule A. Stark Broadening of Cr III Spectral Lines: DO White Dwarfs. Atoms. 2018; 6(2):15. https://doi.org/10.3390/atoms6020015
Chicago/Turabian StyleDimitrijević, Milan S., and Abhishek Chougule. 2018. "Stark Broadening of Cr III Spectral Lines: DO White Dwarfs" Atoms 6, no. 2: 15. https://doi.org/10.3390/atoms6020015
APA StyleDimitrijević, M. S., & Chougule, A. (2018). Stark Broadening of Cr III Spectral Lines: DO White Dwarfs. Atoms, 6(2), 15. https://doi.org/10.3390/atoms6020015






