1. Introduction
It is well known that atomic physics experiments can reveal some properties of nuclei—see, e.g., [
1] and the references therein. For example, observations of isotope shifts were used for determining nuclear sizes; the corresponding results obtained under the assumption of the spherical nuclear shapes for the uniform charge distribution can even be found in textbooks on quantum mechanics—see, e.g., Flügge [
2]. Further results, obtained under the assumption of the spherical nuclear shapes, but for Gaussian and the so-called exponential charge distributions, can be found in [
3]. We note that the Lamb shift calculations are usually performed under the assumption of the spherical nuclear shapes—see, e.g., [
4], where such calculations were done for Gaussian and Lorentzian (called “dipole” in [
4]) charge distributions.
However, many different atomic nuclei have non-spherical shapes, e.g. (though not limited to), oblate or prolate ellipsoid of revolution (spheroid)—see, e.g., [
5,
6,
7] and the references therein. (Below, for brevity, we use the term “ellipsoid” for the ellipsoid of revolution.)
In the present paper we analytically calculate the shift of spectral lines of hydrogenlike ions for ellipsoid-shaped nuclei for the uniform charge distribution. In this situation the contribution to the shift originates not only from the part of the ionic (“atomic”) wave function inside the nucleus, as was the case for spherical nuclei, but also from the modification of the ionic wave function outside the nucleus—distinct from the case of spherical nuclei. Here and below, by ionic wave function we mean the wave function of the bound charged lepton, e.g., electron or muon.
We show that the allowance for the ellipsoidal nuclear shape can change the shift of spectral lines of muonic ions by several times compared to the corresponding shift for spherical nuclei. This can serve as an additional method for the experimental determination of the quadrupole moment of nuclei and of the standard beta-parameter (whose definition will be reminded in the next section) related to the quadrupole moment.
2. Analytical Results
We consider a hydrogenlike ion consisting of the oblate or prolate ellipsoid-shaped nucleus of charge Z and a charged lepton, such as electron or muon. Here and below, we use atomic units ħ = e = m
e = 1, unless specified to the contrary. The ellipsoid has the size 2a in the equatorial plane and the size 2c along the axis of symmetry. The potential outside the nucleus is usually approximated in the following way
where
is one of Legendre polynomials. The coefficient β is related to the quadrupole moment D of the ellipsoid as follows:
where
(see, e.g., [
8]).
Motion in the potential from Equation (1) is not a unique feature of nuclear physics. The same type of potential arises in the problem of a hydrogenic atom with a point-like nucleus in the field of a high-frequency electromagnetic radiation, as shown in [
9,
10]. One of the most important results from [
10] was that the corresponding Hamiltonian possesses symmetry higher than the geometrical (axial) symmetry: in addition to the conservation of the projection of the angular momentum on the axis of symmetry (which follows from the geometrical symmetry), there is an additional conserved (approximately) quantity—the square of the angular momentum. It was also noted in [
10] that this problem from atomic physics has a well-known celestial analogy: the motion of a satellite in the gravitational field of an oblate planet (e.g., the Earth). Interestingly enough, the latter problem from celestial mechanics is mathematically equivalent (approximately) to the motion of a satellite in the field of two stationary planets (or stars) separated by a purely imaginary (!) distance—see, e.g., [
11]. Thus, the potential from Equation (1) is responsible for rich physics in various research areas.
The quantum manifestation of the higher than geometrical symmetry of the Hamiltonian with the potential (1) is that spherical wave functions of the unperturbed Hamiltonian (i.e., for β = 0) turned out to be the correct eigenfunctions of the zeroth order of the perturbed Hamiltonian (i.e., for nonzero β), as shown in [
9]. Therefore, despite the degeneracy of the states of the unperturbed Hamiltonian, the first nonvanishing energy correction turned out to be the same as obtained by the perturbation theory for nondegenerate states [
9]. According to formulas derived in [
9], the first nonvanishing energy correction can be represented in the following form for nonzero values of the quantum number L:
where μ is the reduced mass of the pair “nucleus—charged lepton”. In atomic units, the value of μ is close to unity if the lepton is an electron or about 200 if the lepton is a muon.
For L = 0, the corresponding result obtained in [
9] can be represented as follows
1:
For nonzero values of L, after averaging the energy correction E(2)nLM from Equation (5) over the M-sublevels, it vanishes. Therefore, the average of M energy correction of the second order is only E(2)n00 given by Equation (6).
Thus, the contribution to the energy shift due to the non-spherical potential
outside the nucleus is relevant only to L = 0 levels and is equal to
where for obtaining the utmost right side for Equation (7) we used Equations (3) and (4).
Now we proceed to calculating the energy shift due to the non-spherical potential
inside the nucleus. First we remind the corresponding result for the spherical nucleus presented, e.g., in [
2]. The potential inside the spherical nucleus of the radius R had the form
By calculating the mean value of the perturbation:
the energy shift for the levels of L = 0 was found to be
while the shift of the levels of non-zero values of L was zero (see, e.g., [
2]), the latter being due to the fact that for non-zero values of L, the wave function of the bound lepton is zero at the origin.
The potential inside the ellipsoid-shape nucleus of the same volume V as the sphere of the radius R can be represented in the form
where ρ and z are the cylindrical coordinates (the z-axis being the symmetry axis of the ellipsoid) and
Equation (12) was obtained by equating the volume of the ellipsoid 4πa
2c/3 to the volume of the sphere 4πR
3/3 of the radius R. In spherical polar coordinates, Equation (11) can be rewritten as follows:
where θ is the polar angle.
By calculating the mean value of the perturbation:
similarly to the situation with the spherical nucleus, we find that the energy shift is non-zero only for the levels of L = 0 and is equal to
By combining this contribution to the energy shift due to the non-spherical potential
inside the nucleus with the corresponding contribution to the energy shift due to the non-spherical potential
outside the nucleus (given by Equation (7)), we obtain the following total shift for the levels of L = 0:
where R was defined in Equation (12).
It is instructive to calculate the ratio of the shift from Equation (16) to the corresponding shift for the spherical nucleus from Equation (10):
By substituting Equation (4) into Equation (3), the parameter β, entering Equation (1) for the potential and characterizing the degree of non-sphericity of the nucleus, can be represented in the form:
(obviously, since c/a formally can take values from 0 to ∞, the parameter β formally can take values from −2/5 to ∞). Therefore, the “ellipticity” parameter c/a can be expressed through the parameter β as follows:
On substituting Equation (19) in Equation (17), we obtain the following final formula for the dependence of the above ratio on the parameter β:
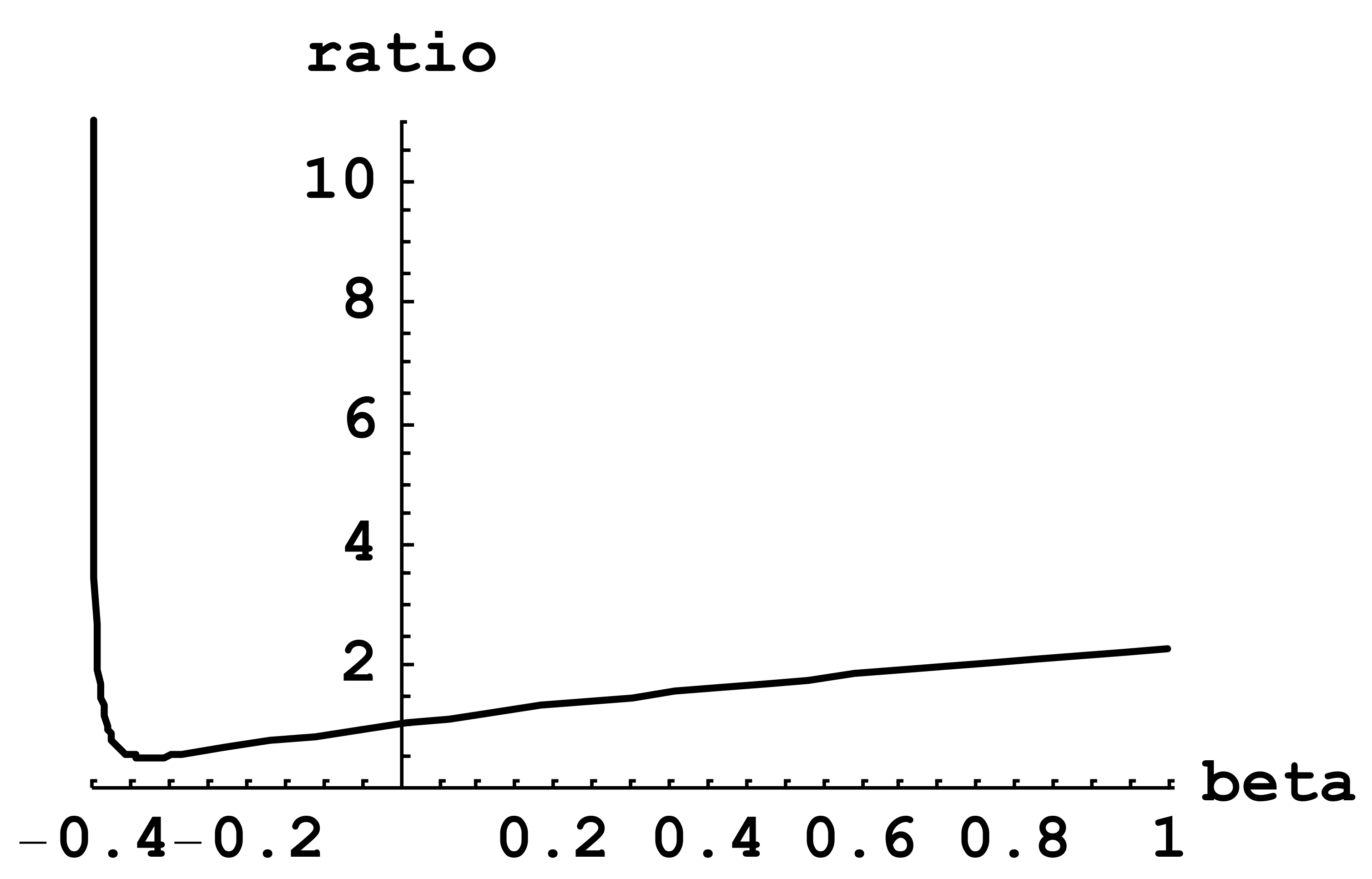
Figure 1 shows the dependence of this ratio on parameter β.
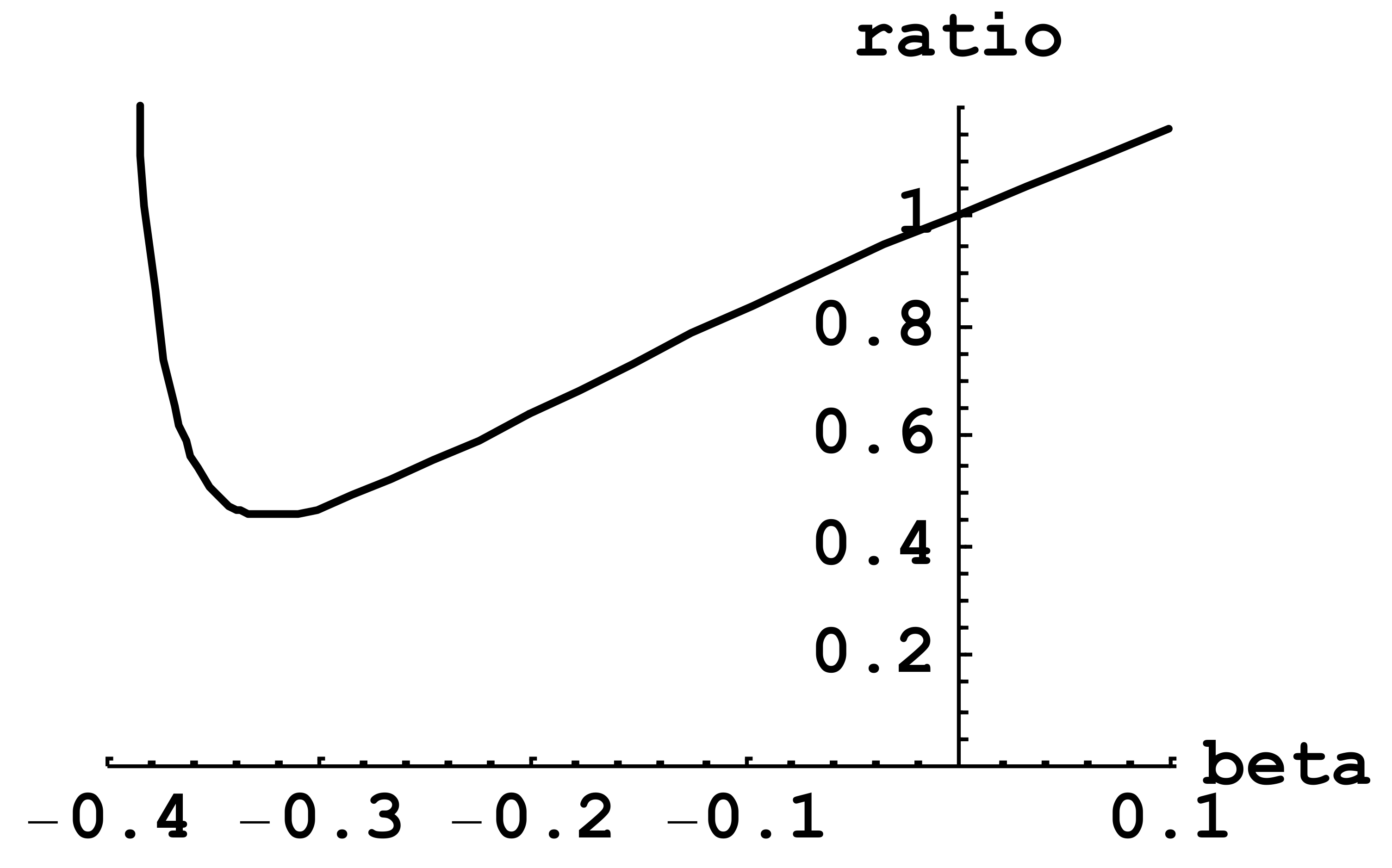
Figure 2 shows the magnified part of this dependence around its minimum equal to 0.454, corresponding to β = −0.322.
It is seen that the allowance for the ellipsoidal nuclear shape can indeed change the energy shift of muonic ions
by several times compared to the corresponding shift for spherical nuclei. This energy shift and its change compared to the spherical nucleus should be possible to detect by observing the shift of the Lyman spectral lines of muonic ions. It is important to note that since the spectral lines of the Lyman series correspond to the radiative transitions from the upper level nP to the lower (ground) level 1S and only the lower level energy gets shifted by ΔE
tot presented in Equation (16), then the shift S of the Lyman lines
in the frequency scale is
where R was defined in Equation (12). Since ΔE
tot(n = 1) is positive for any β (see
Figure 1), then S is always negative for any β, so the shift of the Lyman lines
in the wavelength scale is
always red for any β.
Thus, by measuring the shift S of the Lyman lines of a muonic ion and knowing the nuclear volume V or the average nuclear radius R = [3V/4π]
1/3, it is possible to use Equation (21) (or
Figure 1) to determine the experimental value of the parameter β and thus the experimental value of the nuclear quadrupole moment D connected to β. For the latter purpose, the expression for D in Equation (4) can be rewritten as follows;
As for the coefficient in front of the square brackets in Equation (21), here is a practical formula for it:
This formula yields the above coefficient in the frequency unit of s
–1.
In the above derivations for the simplicity of formulas, we disregarded the change of the wave function of the bound muon across the nucleus. This is valid if the ratio of the nuclear size R
0(a.u.) = 2.6 × 10
−5A
1/3 (A being the atomic number) to the characteristic size of the muonic cloud r
0(a.u.) = 1/(μZ) (in the ground state) is relatively small:
Since typically A = (2 − 3)Z, Equation (22) can be rewritten as
and it is satisfied if Z < Z
max ~ 40.
It should be emphasized that we disregarded the change of the wave function of the bound muon across the nucleus just to get the message across in the simplest form. The change of the wave function of the bound muon across the nucleus (resulting in corrections of the order of R0/r0) can be taken into account in future publications.
3. Comparison with Competing Effects and Numerical Examples
Since the energy shift due to an ellipsoid-shape nucleus can be of the order of several times greater than the energy shift due to the spherical nucleus ΔE
insidesphere (as demonstrated in
Section 2, with ΔE
insidesphere being presented in Equation (10)), it is sufficient to show that the energy shift due to the spherical nucleus significantly exceeds the competing effects. One of these effects is the fine structure splitting:
where j is the quantum number of the total angular momentum and α is the fine structure constant (1/α ~ 137).
First of all, the nuclear-shape-caused shift of the Lyman lines is due to the shift of the ground level (
n = 1), for which there is no fine structure splitting. Second, even if we compare ΔE
insidesphere(
n) with ΔE
fs(
n) for
n > 1, we get
for A > 1, i.e., for any nucleus heavier than the hydrogen nucleus. Since the fine structure splitting is the relativistic effect, this comparison also justifies our employment of the nonrelativistic wave functions in
Section 2. In other words, the allowance for the relativistic effects would introduce relative corrections to the primary shift-effect under consideration ~ [α/(μR
0)]
2, where R
0(a.u.) = 2.6 × 10
−5A
1/3, so that the relative correction for muonic ions is ~1/A
2/3 and thus is insignificant for A >> 1.
The next comparison is with the natural width γ. It is proportional to μZ4. By scaling the natural width data from the NIST database to muonic ions, we find the following:
Ly-alpha line:
so that the latter ratio is much greater than unity for any A.
Ly-beta line:
so that the latter ratio is much greater than unity for any A.
Ly-gamma line:
so that the latter ratio is much greater than unity for any A.
Thus, the nuclear-shape-caused shift of the Lyman lines exceeds the natural width by several orders of magnitude for any nucleus.
Finally, we estimate the ratio of the nuclear-shape-caused shift of the Lyman lines in the frequency scale to their unperturbed frequency ω
0(n), where
in atomic units. The purpose of the comparison is to make sure that this shift exceeds the spectral resolution and thus can be observed. For this estimate we again use the shift due to the spherical nucleus: if the shift can be resolved for the spherical nucleus, then it could be resolved for the ellipsoid-shaped nucleus since for the latter the shift is of the order of several times greater than for the former.
According to Equation (21), the frequency shift of Lyman lines of muonic ions caused by the spherical nucleus (c = a) is
so that for the ratio we obtain:
Consequently, for ellipsoid-shaped nuclei the corresponding estimate can be represented in the form
Below we present numerical values of S
min/ω
0(n) for the muonic Lyman lines for several nuclei that are listed, e.g., in [
5] as known to be oblate (β < 0).
206C14 (oblate in the nuclear ground state):
4214Si28 (oblate in the nuclear ground state):
126C6 (oblate in the 1st excited 2+ nuclear state):
2814Si14 (oblate in the 1st excited 2+ nuclear state):
3416S18 (oblate in the 1st excited 2+ nuclear state):
3618Ar18 (oblate in the 1st excited 2+ nuclear state):
Thus, for all of the above examples, the relative shift of the muonic Lyman lines caused by ellipsoid-shaped nuclei is sufficiently large to be detected by spectrometers.