Abstract
In this contribution, we present results of bound state transition modeling using the cut-off Coulomb model potential. The cut-off Coulomb potential has proven itself as a model potential for the dense hydrogen plasma. The main aim of our investigation include further steps of improvement of the usage of model potential. The results deal with partially ionized dense hydrogen plasma. The presented results covers , and , where the comparison with the experimental data should take place, and the theoretical values for comparison. Since the model was successfully applied on continuous photoabsorption of dense hydrogen plasma in the broad area of temperatures and densities, it is expected to combine both continuous and bound-bound photoabsorption within single quantum mechanical model with the same success.
1. Introduction
The problems of plasma opacity, energy transport and radiative transfer under moderate and strong non-ideality are of interest in theoretical and experimental research [1,2,3,4]. The strong coupling and density effects in plasma radiation were the subject of numerous experimental and theoretical studies in the last decades. Here, we keep in mind the plasma of the inner layers of the solar atmosphere, as well as of partially ionized layers of other stellar atmospheres—for example, the atmospheres of DA white dwarfs with effective temperatures between 4500 K and 30,000 K.
In this paper, we presented a new model way of describing atomic photo-absorption processes in dense, strongly ionized hydrogen plasmas, which is based on the approximation of the cut-off Coulomb potential. By now, this approximation has been used in order to describe transport properties of dense plasmas (e.g., [1,5,6]), but it was clear that it could be applied to some absorption processes in non-ideal plasmas too [3,7,8,9]. This topic itself, and the search for more consistent models of screening and more realistic potentials in plasmas is still continuing and is very real (e.g., [10,11,12,13] and references therein).
The neutral hydrogen acts as an absorber in plasma, and its concentration determination is essential in order to calculate the absorption coefficients. The neutral hydrogen concentration from experimental data from [14] is used, and, since the result presented here is in the area where the Saha equation is valid, the neutral concentrations using the Saha equation with the ionization potential correction is possible. Since this is related to the further step, bound level broadening mechanism, the procedure was not elaborated here. In addition, the emitter, neutral hydrogen, interacts with other plasma species such as electrons and ions. In such a way, the theoretical hydrogen plasma model results as well as NIST database values act as a limiting case for verification of solutions, in the case when plasma influence is small or diminishes, e.g., in later case.
In order to calculate the total absorption coefficient, the same broadening mechanism for the bound state levels should be applied. Up until now, the continuous absorption processes were calculated with the help of parametric broadening for the bound-free absorption [7]. The broadening processes play a more important role in bound-bound processes, and, as such, the more realistic theoretical model of broadening of bound state levels or a result of adequate molecular dynamics (MD) simulations should be used. Only in such a case could the total absorption coefficients, obtained within the same broadening model, be compared with real experimental data. This work is in progress.
A first step in extending of the model with additional processes is the bound state transition processes inclusion. The bound state transition processes are stated as the most important goal in the development of the self containing model, capable of describing optical as well as dynamical characteristics of dense hydrogen plasma. The characteristics of the bound state transitions in plasma diagnostics are well known, an almost mandatory method [15]. The usage of the hydrogen lines as a probing method for the plasma characteristics is also well known and widely used in plasmas of moderate and small non-ideality [16]. In accordance with that previously mentioned, the continuation of research of the presented approach is the inclusion of the bound-bound photo absorption process using the same model potential. The investigated process is the bound-bound i.e., photo absorption processes:
where n and l are the principal and the orbital quantum number of hydrogen-atom excited states, hydrogen atom in its initial state is presented by , its final state by , and presents absorbed photon energy.
2. Theory
2.1. The Approximation of the Cut-Off Coulomb Potential
The absorption processes (1) in astrophysical plasma are considered here as a result of radiative transition in the whole system “electron–ion pair (atom) + the neighborhood”, namely: , where and denote the rest of the considered plasma. However, as it is well known, many-body processes can sometimes be simplified by their transformation to the corresponding single-particle processes in an adequately chosen model potential.
As an adequate model potential for hydrogen plasma with such density, we choose, as in [3,5], the screening cut-off Coulomb potential, which satisfies above conditions, and can be presented in the form:
where the cut-off radius is defined by relation (3), as it is illustrated by Figure 1a. Here, e is the modulus of the electron charge, r—distance from the ion, and cut-off radius —the characteristic screening length of the considered plasma. Namely, within this model, it is assumed that quantity
is the mean potential energy of an electron in the considered hydrogen plasma.
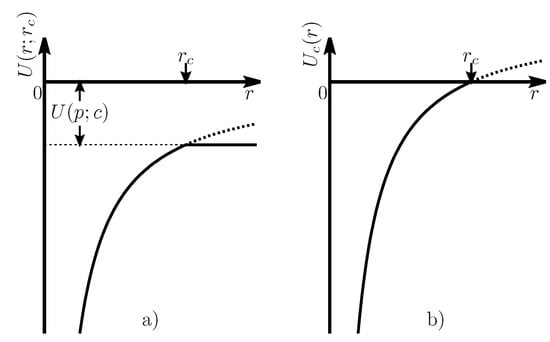
Figure 1.
Behaviour of the potentials and , where is the cut-off parameter. In (a) the potetntial goes to the mean potential energy of an electron in the considered hydrogen plasma , and in (b), the value of is taken as zero energy, i.e., , in the more applicable form used here.
As in [3,5,8], we will take the value as the zero of energy. After that, the potential Equation (2) is transformed to the form
which is illustrated by Figure 1b. Here, e is the modulus of the electron charge, r—distance from the ion, and cut-off radius —the characteristic screening length of the considered plasma.
It is important that the cut-off radius can be determined as a given function of and T, using two characteristic lengths:
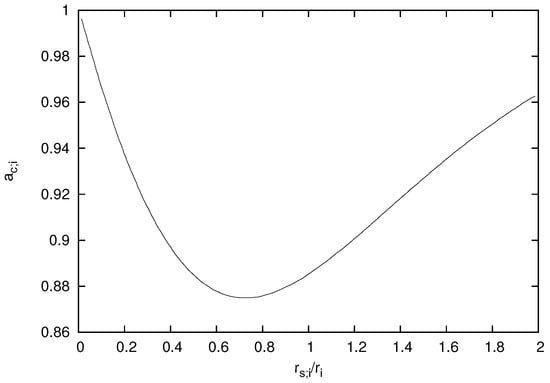
namely, taking that and we can directly determine the factor as a function of ratio , on the basis of the data about the mean potential energy of the electron in the single ionized plasma from [12]. The behavior of in a wide region of values of is presented in Figure 2.
2.2. The Calculated Quantities
In accordance with that, the behavior of the dipole matrix element is investigated here. It is given by
where the wave functions and are initial and final state wave functions obtained within the model of cut-off Coulomb potential, for the calculations of the plasma characteristics, or the theoretical hydrogen ones in order to additionally check the model.
For the calculation of oscillator strength, we use expressions from [17,18,19]
where is the Rydberg constant, in the same units as the frequency of the transition . The calculated data are presented in Table 1.

Table 1.
The oscillator strength values for the ”short”, , , and ”long” pulse, , , from [14], as well as a theoretical hydrogen case calculated by code from [18], and NIST spectral database values [30].
Our future plan is to include broadening processes and make it possible to directly compare data with the experimental ones (e.g., the data from [14]). In continuation, some of the bound-bound theoretical aspects are shown.
The total absorption cross section of the line could be linked with the dipole moment directly with the help of relation
It should be noted that the absorption line profile is needed in order to apply the obtained results to the absorption calculations:
Here, is the spectral line profile and could be obtained, for instance, as a result of a molecular dynamics (MD) simulations [20,21,22] or as a result of theoretical modeling and spectral line data [23,24,25,26,27]. The lineshape is normalized to unity area, e.g.,
The line profile is a convolution of the broadening of the initial and final state energy levels, e.g.,
Here, and are energy level broadening shapes of the initial and final states.
From here, the absorption coefficient could be calculated
Here, is the concentration of hydrogen in initial level . The broadening of the levels should be considered separately in order to use the same broadening profiles for the calculation of the bound-free transition continuous photo absorption.
There are a few steps to be carried out, and the first to be taken into account is to use a parametric level and line broadening model. The second one is to use a theoretical model for spectral line broadening and try to deconvolve level broadening values, and the final step should be the usage of the MD code [20,21,22]. A candidate for the coupling of the MD code is LAMMPS, which is capable of simulating a large scale molecular dynamics simulations, and it also could include particular interaction potential as well as all relevant processes of interest not included in the initial code as an additional module. The broadening parameters could be calculated from average energy and particle distributions and their temporal distributions, or, as an iterative procedure, a more real plasma potential could be obtained [20,21,28,29]. In the former case, the solutions would not necessary to be described as a set of analytical functions. Since there are more steps, we did not elaborate on the ideas until we obtained some initial results.
3. Results and Discussion
The convergence toward theoretical values for hydrogen is examined and proven for the bound-bound transitions that could appear in the investigated area of electron concentrations and temperatures, [31]. Since the initial results have proven that the model potential could be used for the bound-bound state transition calculations, further investigation was completed.
The next step towards the application of the model results is a calculation of the oscillator strength values for the plasma parameters denoted as ”short”, with , and ”long” pulse, with , from [14]. The radius , given by Equation (5), Wigner–Seitz and cut-off radius as well as atom concentrations given by the Saha equation are , , , for short and , , , for long pulse.
The essential quality of the presented approach is that the values are calculated with the help of wave functions that are obtained as a completely analytical solution in the frame of the presented model. The influence of the numerical procedure is minimized, and, as a consequence, the possibility of introducing the numerical artifacts into the solution is also minimized.
Since the convergence towards the theoretical, unperturbed Coulomb potential is investigated in [31], and the results of the presented calculations converge uniformly towards theoretical values, it is expected that the presented model could obtain good data in a wider variety of plasma parameters than shown here.
There is a need to introduce the broadening mechanism for the energy levels in the presented approach. There is a possibility to couple the presented model calculations with the MD code in order to obtain a consistent model for the broadening of the bound levels. Those results influence the bound-free and bound-bound absorption profiles and are essential for the hydrogen plasma optical properties calculation in the frame of the cut-off Coulomb potential model approach.
4. Conclusions
The presented results are a step forward towards inclusion of the entire photo-absorption processes for hydrogen atoms in plasma within the frame of the cut-off Coulomb potential model. One of the benefits of the presented results is a completely quantum mechanical solution for the cut-off Coulomb model potential, obtained from wave functions that are analytical and represented with the help of special functions, e.g., the influence of additional numerical source of errors is minimized as much as possible. Along with this, the solutions converge towards theoretical pure Coulomb potential ones as the cut-off radius converges to infinity, e.g., the influence of plasma diminishes. Further steps in application of the presented results, the inclusion of the bound-bound transition processes within the continuous absorption model, as well as its application in the analysis of the spectral absorption processes is to be carried out. In order to make such calculations, it is needed to include the models for the bound state level broadening. Our plan is to present the results obtained during this investigation in a database that can be accessed directly through http://servo.aob.rs as a web service, similar to the existing databases [26,27,32].
Acknowledgments
The authors are thankful to the Ministry of Education, Science and Technological Development of the Republic of Serbia for the support of this work within the projects 176002 and III44002. We acknowledge the contribution of the late Dr A. A. Mihajlov, who participated in the initial discussions and preparation of this paper
Author Contributions
N. M. S. have adopted the cut-off Coulomb potential model for the optical plasma characteistics; N. M. S. developed the code and performed the calculations; M. S. D., Z. J. S. and V. A. S. analysed the data; N. M. S., V. A. S. and M. S. D. wrote the paper; M. S. D., V. A. S. and Z. J. S. have edited the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fortov, V.E.; Iakubov, I.T. The Physics of Non-Ideal Plasma; World Scientific: Singapore, 1999. [Google Scholar]
- Rogers, F.J.; Iglesias, C.A. Opacity of stellar matter. Space Sci. Rev. 1998, 85, 61–70. [Google Scholar] [CrossRef]
- Mihajlov, A.A.; Sakan, N.M.; Srećković, V.A.; Vitel, Y. Modeling of continuous absorption of electromagnetic radiation in dense partially ionized plasmas. J. Phys. A 2011, 44, 095502. [Google Scholar] [CrossRef]
- Mihajlov, A.A.; Ignjatović, L.M.; Srećković, V.A.; Dimitrijević, M.S.; Metropoulos, A. The non-symmetric ion-atom radiative processes in the stellar atmospheres. Mon. Not. R. Astron. Soc. 2013, 431, 589–599. [Google Scholar] [CrossRef]
- Mihajlov, A.A.; Djordjević, D.; Popović, M.M.; Meyer, T.; Luft, M.; Kraeft, W.D. Determination of the Electrical Conductivity of a Plasma on the Basis of the Coulomb cut-off Potential Model. Contrib. Plasma Phys. 1989, 29, 441–446. [Google Scholar] [CrossRef]
- Ignjatović, L.M.; Srećković, V.A.; Dimitrijević, M.S. The Screening Characteristics of the Dense Astrophysical Plasmas: The Three-Component Systems. Atoms 2017, 5, 42. [Google Scholar] [CrossRef]
- Mihajlov, A.A.; Sakan, N.M.; Srećković, V.A.; Vitel, Y. Modeling of the Continuous Absorption of Electromagnetic Radiation in Dense Hydrogen Plasma. Balt. Astron. 2011, 20, 604–608. [Google Scholar] [CrossRef]
- Mihajlov, A.A.; Srećković, V.A.; Sakan, N.M. Inverse Bremsstrahlung in Astrophysical Plasmas: The Absorption Coefficients and Gaunt Factors. J. Astrophys. Astron. 2015, 36, 635–642. [Google Scholar] [CrossRef]
- Sakan, N.M.; Srećković, V.A.; Mihajlov, A.A. The application of the cut-off Coulomb potential for the calculation of a continuous spectra of dense hydrogen plasma. Mem. Soc. Astron. Ital. Suppl. 2005, 7, 221–224. [Google Scholar]
- Mihajlov, A.A.; Vitel, Y.; Ignjatović, L.M. The new screening characteristics of strongly non-ideal and dusty plasmas. Part 1: Single-component systems. High Temp. 2008, 46, 737–745. [Google Scholar] [CrossRef]
- Mihajlov, A.A.; Vitel, Y.; Ignjatović, L.M. The new screening characteristics of strongly non-ideal and dusty plasmas. Part 2: Two-component systems. High Temp. 2009, 47, 1–12. [Google Scholar] [CrossRef]
- Mihajlov, A.; Vitel, Y.; Ignjatović, L.M. The new screening characteristics of strongly non-ideal and dusty plasmas. Part 3: Properties and applications. High Temp. 2009, 47, 147–157. [Google Scholar] [CrossRef]
- Demura, A. Physical models of plasma microfield. Int. J. Spectrosc. 2009, 2010, 671073. [Google Scholar] [CrossRef]
- Vitel, Y.; Gavrilova, T.; D’yachkov, L.; Kurilenkov, Y.K. Spectra of dense pure hydrogen plasma in Balmer area. J. Quant. Spectrosc. Radiat. Transf. 2004, 83, 387–405. [Google Scholar] [CrossRef]
- Griem, H.R. Principles of Plasma Spectroscopy; Cambridge University Press: Cambridge, UK, 2005; Volume 2. [Google Scholar]
- Konjević, N.; Ivković, M.; Sakan, N. Hydrogen Balmer lines for low electron number density plasma diagnostics. Spectrochim. Acta B 2012, 76, 16–26. [Google Scholar] [CrossRef]
- Sobelman, I.I. Atomic spectra and radiative transitions. In Springer Series in Chemical Physics; Springer: Berlin, Germany, 1979. [Google Scholar]
- Hoang-Binh, D. A program to compute exact hydrogenic radial integrals, oscillator strengths, and Einstein coefficients, for principal quantum numbers up to n ≈ 1000. Comput. Phys. Commun. 2005, 166, 191–196. [Google Scholar] [CrossRef]
- Hilborn, R.C. Einstein coefficients, cross sections, f values, dipole moments, and all that. Am. J. Phys. 1982, 50, 982–986. [Google Scholar] [CrossRef]
- Stambulchik, E.; Maron, Y. Plasma line broadening and computer simulations: A mini-review. High Energ. Dens. Phys. 2010, 6, 9–14. [Google Scholar] [CrossRef]
- Stambulchik, E.; Fisher, D.; Maron, Y.; Griem, H.; Alexiou, S. Correlation effects and their influence on line broadening in plasmas: Application to Hα. High Energ. Dens. Phys. 2007, 3, 272–277. [Google Scholar] [CrossRef]
- Talin, B.; Dufour, E.; Calisti, A.; Gigosos, M.A.; Gonzalez, M.A.; Gaztelurrutia, T.D.R.; Dufty, J.W. Molecular dynamics simulation for modeling plasma spectroscopy. J. Phys. A 2003, 36, 6049. [Google Scholar] [CrossRef]
- Ferri, S.; Calisti, A.; Mossé, C.; Rosato, J.; Talin, B.; Alexiou, S.; Gigosos, M.A.; González, M.A.; González-Herrero, D.; Lara, N.; et al. Ion Dynamics Effect on Stark-Broadened Line Shapes: A Cross-Comparison of Various Models. Atoms 2014, 2, 299–318. [Google Scholar] [CrossRef]
- Calisti, A.; Demura, A.V.; Gigosos, M.A.; González-Herrero, D.; Iglesias, C.A.; Lisitsa, V.S.; Stambulchik, E. Influence of microfield directionality on line shapes. Atoms 2014, 2, 259–276. [Google Scholar] [CrossRef]
- Alexiou, S.; Dimitrijević, M.S.; Sahal-Brechot, S.; Stambulchik, E.; Duan, B.; González-Herrero, D.; Gigosos, M.A. The second workshop on lineshape code comparison: Isolated lines. Atoms 2014, 2, 157–177. [Google Scholar] [CrossRef]
- Marinković, B.P.; Jevremović, D.; Srećković, V.A.; Vujčić, V.; Ignjatović, L.M.; Dimitrijević, M.S.; Mason, N.J. BEAMDB and MolD—Databases for atomic and molecular collisional and radiative processes: Belgrade nodes of VAMDC. Eur. Phys. J. D 2017, 71, 158. [Google Scholar] [CrossRef]
- Srećković, V.A.; Ignjatović, L.M.; Jevremović, D.; Vujčić, V.; Dimitrijević, M.S. Radiative and Collisional Molecular Data and Virtual Laboratory Astrophysics. Atoms 2017, 5, 31. [Google Scholar] [CrossRef]
- Sadykova, S.; Ebeling, W.; Valuev, I.; Sokolov, I. Electric Microfield Distributions in Li + Plasma With Account of the Ion Structure. Contrib. Plasma Phys. 2009, 49, 76–89. [Google Scholar] [CrossRef]
- Calisti, A.; Ferri, S.; Mossé, C.; Talin, B.; Gigosos, M.; González, M. Microfields in hot dense hydrogen plasmas. High Energ. Dens. Phys. 2011, 7, 197–202. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (Ver. 5.5); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2017. Available online: https://physics.nist.gov/asd (accessed on 30 October 2017).
- Sakan, N.M. The Calculation of the Photo Absorption Processes in Dense Hydrogen Plasma with the Help of Cut-Off Coulomb Potential Model. J. Phys. Conf. Ser. 2010, 257, 012036. [Google Scholar] [CrossRef]
- Sahal-Bréchot, S.; Dimitrijević, M.; Moreau, N.; Nessib, N.B. The STARK-B database VAMDC node: A repository for spectral line broadening and shifts due to collisions with charged particles. Phys. Scr. 2015, 90, 054008. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).