Oriented Polar Molecules in a Solid Inert-Gas Matrix: A Proposed Method for Measuring the Electric Dipole Moment of the Electron
Abstract
1. Introduction
2. Components for the EDM Method
2.1. Inert-Gas Solids
2.2. The Study of Molecules Trapped in an Inert-Gas Solid
2.3. Oriented Polar Molecules within an Inert-Gas Lattice
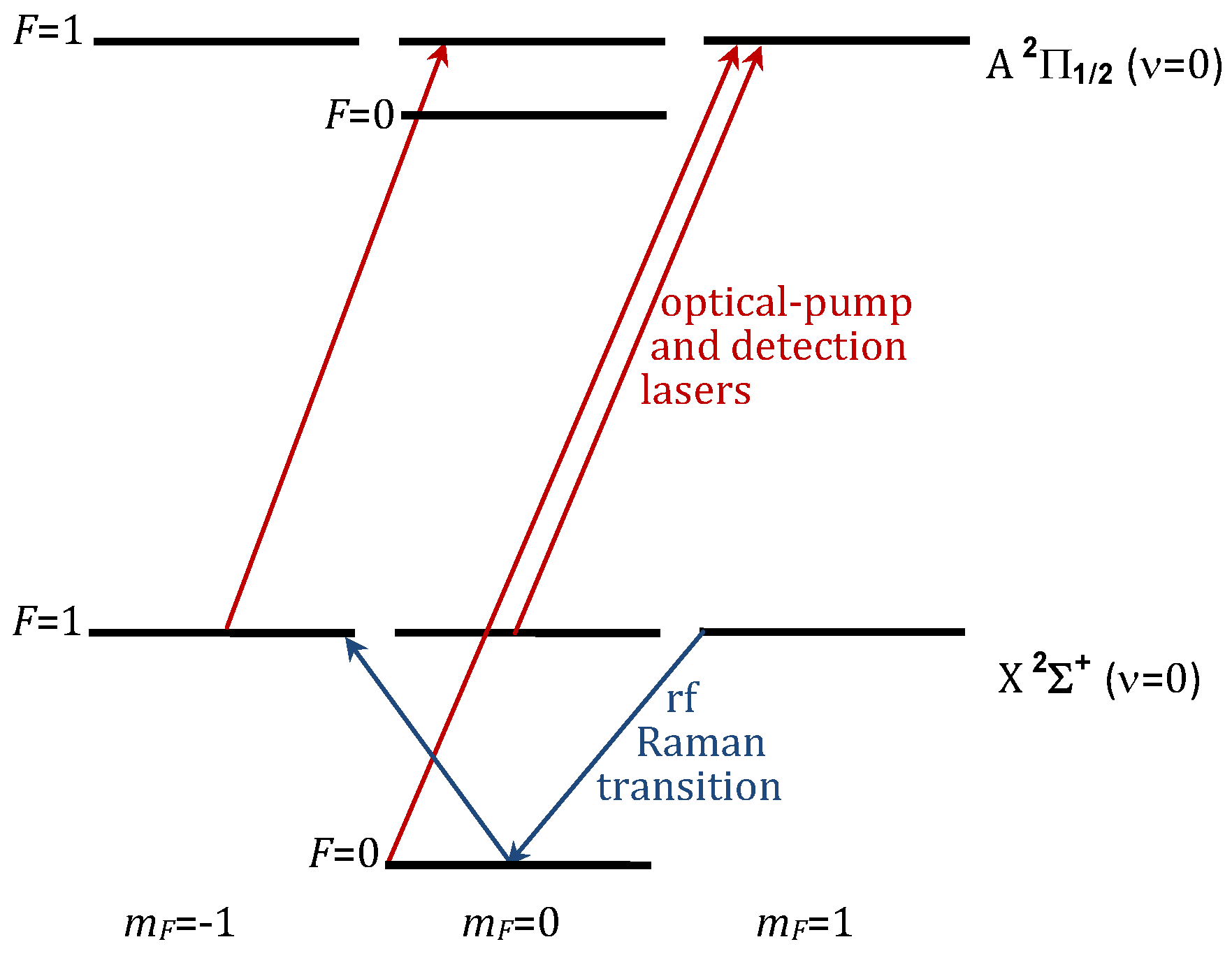
2.4. Choice of Polar Molecule
2.5. The Time Sequence for EDM
2.6. Orientation without an Electric Field
3. Potential Advantages of the EDM Method
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pospelov, M.; Ritz, A. CKM benchmarks for electron electric dipole moment experiments. Phys. Rev. D 2014, 89, 056006. [Google Scholar] [CrossRef]
- Pospelov, M.E.; Khriplovich, I.B. Electric dipole moment of the W boson and the electron in the Kobayashi-Maskawa model. Yad. Fiz. 1991, 53, 1030–1033. [Google Scholar]
- Booth, M. The electric dipole moment of the W and electron in the standard model. arXiv, 1993; arXiv:hep-ph/9301293. [Google Scholar]
- Ibrahim, T.; Itani, A.; Nath, P. Electron electric dipole moment as a sensitive probe of PeV scale physics. Phys. Rev. D 2014, 90, 055006. [Google Scholar] [CrossRef]
- McKeen, D.; Pospelov, M.; Ritz, A. Electric dipole moment signatures of PeV-scale superpartners. Phys. Rev. D 2013, 87, 113002. [Google Scholar] [CrossRef]
- Baron, J.; Campbell, W.C.; DeMille, D.; Doyle, J.M.; Gabrielse, G.; Gurevich, Y.V.; Hess, P.W.; Hutzler, N.R.; Kirilov, E.; Kozyryev, I.; et al. Order of magnitude smaller limit on the electric dipole moment of the electron. Science 2014, 343, 269. [Google Scholar] [PubMed]
- Cairncross, W.B.; Gresh, D.N.; Grau, M.; Cossel, K.C.; Roussy, T.S.; Ni, Y.; Zhou, Y.; Ye, J.; Cornell, E.A. A precision measurement of the electron’s electric dipole moment using trapped molecular ions. Phys. Rev. Lett. 2017, 119, 153001. [Google Scholar] [CrossRef] [PubMed]
- Leanhardt, A.E.; Bohn, J.L.; Loh, H.; Maletinsky, P.; Meyer, E.R.; Sinclair, L.C.; Stutz, R.P.; Cornell, E.A. High-resolution spectroscopy on trapped molecular ions in rotating electric fields: A new approach for measuring the electron electric dipole moment. J. Mol. Spectrosc. 2011, 270, 1–25. [Google Scholar] [CrossRef]
- Tarbutt, M.R.; Sauer, B.E.; Hudson, J.J.; Hinds, E.A. Design for a fountain of YbF molecules to measure the electron’s electric dipole moment. New J. Phys. 2013, 15, 053034. [Google Scholar] [CrossRef]
- Hunter, L.R.; Peck, S.K.; Greenspon, A.S.; Alam, S.S.; DeMille, D. Prospects for laser cooling TlF. Phys. Rev. A 2012, 85, 012511. [Google Scholar] [CrossRef]
- Arndt, M.; Kanorsky, S.I.; Weis, A.; Hänsch, T.W. Long electronic spin relaxation times of Cs atoms in solid 4He. Phys. Rev. Lett. 1995, 74, 1359. [Google Scholar] [CrossRef] [PubMed]
- Kanorsky, S.I.; Lang, S.; Lücke, S.; Ross, S.B.; Hänsch, T.W.; Weis, A. Millihertz magnetic resonance spectroscopy of Cs atoms in body-centered-cubic 4He. Phys. Rev. A 1996, 54, R1010–R1013. [Google Scholar] [CrossRef] [PubMed]
- Kanagin, A.N.; Regmi, S.K.; Pathak, P.; Weinstein, J.D. Optical pumping of rubidium atoms frozen in solid argon. Phys. Rev. A 2013, 88, 063404. [Google Scholar] [CrossRef]
- Park, Y.; Kang, H.; Kang, H. Brute force orientation of matrix-isolated molecules: Reversible reorientation of formaldehyde in an argon matrix toward perfect alignment. Angew. Chem. 2017, 56, 1046–1049. [Google Scholar] [CrossRef] [PubMed]
- Shin, S.; Kim, Y.; Moon, E.; Lee, D.H.; Kang, H.; Kang, H. Generation of strong electric fields in an ice film capacitor. J. Chem. Phys. 2013, 139, 074201. [Google Scholar] [CrossRef] [PubMed]
- Lemeshko, M.; Krems, R.V.; Doyle, J.M.; Kais, S. Manipulation of molecules with electromagnetic fields. Mol. Phys. 2013, 111, 1648. [Google Scholar] [CrossRef]
- Flygare, W.H. Molecular rotation in the solid state. Theory of rotation of trapped molecules in rare gas lattices. J. Chem. Phys. 1963, 39, 2263. [Google Scholar] [CrossRef]
- Kiljunen, T.; Schmidt, B.; Schwentner, N. Aligning and orienting molecules trapped in octahedral crystal fields. Phys. Rev. A 2005, 72, 053415. [Google Scholar] [CrossRef]
- Heidenreich, B.J.; Elliott, O.T.; Charney, N.D.; Virgien, K.A.; Bridges, A.W.; McKeon, M.A.; Peck, S.K.; Krause, D.; Gordon, J.E.; Hunter, L.R.; et al. Limit on the electron electric dipole moment in gadolinium-iron garnet. Phys. Rev. Lett. 2005, 95, 253004. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.J.; Liu, C.-Y.; Lamoreaux, S.K.; Visser, G.; Kunkler, B.; Matlashov, A.N.; Long, J.C.; Reddy, T.G. New experimental limit on the electric dipole moment of the electron in a paramagnetic insulator. Phys. Rev. D 2015, 91, 102004. [Google Scholar] [CrossRef]
- Lamoreaux, S.K. Solid-state systems for the electron electric dipole moment and other fundamental measurements. Phys. Rev. A 2002, 66, 022109. [Google Scholar] [CrossRef]
- Hudson, J.J.; Kara, D.M.; Smallman, I.J.; Sauer, B.E.; Tarbutt, M.R.; Hinds, E.A. Improved measurement of the shape of the electron. Nature 2011, 473, 493–496. [Google Scholar] [CrossRef] [PubMed]
- Kozlov, M.G.; Derevianko, A. Proposal for a sensitive search for the electric dipole moment of the electron with matrix-isolated radicals. Phys. Rev. Lett. 2006, 97, 063001. [Google Scholar] [CrossRef] [PubMed]
- Kara, D.M.; Smallman, I.J.; Hudson, J.J.; Sauer, B.E.; Tarbutt, M.R.; Hinds, E.A. Measurement of the electron’s electric dipole moment using YbF molecules: Methods and data analysis. New J. Phys. 2012, 14, 103051. [Google Scholar] [CrossRef]
- Weis, A.; Kanorsky, S.; Lang, S.; Hänsch, T.W. Can atoms trapped in solid helium be used to search for physics beyond the standard model? In Atomic Physics Methods in Modern Research; Springer: Berlin, Germany, 1997; pp. 57–75. [Google Scholar]
- Nataraj, H.S.; Sahoo, B.K.; Das, B.P.; Mukherjee, D. Intrinsic electric dipole moments of paramagnetic atoms: rubidium and cesium. Phys. Rev. Lett. 2008, 101, 033002. [Google Scholar] [CrossRef] [PubMed]
- Zhong, M.; Hedges, M.P.; Ahlefeldt, R.L.; Bartholomew, J.G.; Beavan, S.E.; Wittig, S.M.; Longdell, J.J.; Sellars, M.J. Optically addressable nuclear spins in a solid with a six-hour coherence time. Nature 2015, 517, 177–180. [Google Scholar] [CrossRef] [PubMed]
- Pollack, G.L. The solid state of rare gases. Rev. Mod. Phys. 1964, 36, 748. [Google Scholar] [CrossRef]
- Endoh, Y.; Shirane, G.; Skalyo, J. Lattice dynamics of solid neon at 6.5 and 23.7 K. Phys. Rev. B 1975, 11, 1681. [Google Scholar] [CrossRef]
- Berne, A.; Boato, G.; De Paz, M. Experiments on solid argon. Il Nuovo Cimento B 1966, 46, 182–209. [Google Scholar] [CrossRef]
- Eshchenko, D.G.; Storchak, V.G.; Brewer, J.H.; Morris, G.D.; Cottrell, S.P.; Cox, S.F.J. Excess electron transport and delayed muonium formation in condensed rare gases. Phys. Rev. B 2002, 66, 035105. [Google Scholar] [CrossRef]
- Mann, D.E. Infrared spectra of HCl, DCl, HBr, and DBr in solid rare-gas matrices. J. Chem. Phys. 1966, 44, 3453. [Google Scholar] [CrossRef]
- Van Zee, R.J.; Seely, M.L.; Weltner, W. YbH and YbD molecules: ESR and optical spectroscopy in argon matrices at 4 K. J. Chem. Phys. 1977, 67, 861. [Google Scholar] [CrossRef]
- Dubost, H. Infrared absorption spectra of carbon monoxide in rare gas matrices. Chem. Phys. 1976, 12, 139–151. [Google Scholar] [CrossRef]
- Knight, L.B., Jr.; Wise, M.B. The generation and ESR investigation of the BeF radical in rare gas matrices. J. Chem. Phys. 1980, 73, 4198. [Google Scholar] [CrossRef]
- Mason, M.G. Mid- and far-infrared spectra of HF and DF in rare-gas matrices. J. Chem. Phys. 1971, 54, 3491. [Google Scholar] [CrossRef]
- Lang, V.I.; Winn, J.S. Matrix-isolated OCS: The high resolution infrared spectra of a cryogenically solvated linear molecule. J. Chem. Phys. 1991, 94, 5270. [Google Scholar] [CrossRef]
- Kiljunen, T.; Schmidt, B. Alignment and orientation of molecules in matrices. Anal. Control Ultrafast Photoinduced React. 2007, 87, 337. [Google Scholar]
- Kiljunen, T.; Schmidt, B.; Schwentner, N. Time-dependent alignment of molecules trapped in octahedral crystal fields. J. Chem. Phys. 2006, 124, 164502. [Google Scholar] [CrossRef] [PubMed]
- Knight, L.B. ESR investigations of H2O+, HDO+, D2O+, and H217O+ isolated in neon matrices at 4 K. J. Chem. Phys. 1983, 78, 5940. [Google Scholar] [CrossRef]
- Tarbutt, M.R.; Hudson, J.J.; Sauer, B.E.; Hinds, E.A.; Ryzhov, V.A.; Ryabov, V.L.; Ezhov, V.F. A jet beam source of cold YbF radicals. J. Phys. B At. Mol. Opt. Phys. 2002, 35, 5013–5022. [Google Scholar] [CrossRef]
- Hutzler, N.R.; Parsons, M.F.; Gurevich, Y.V.; Hess, P.W.; Petrik, E.; Spaun, B.; Vutha, A.C.; DeMille, D.; Gabrielse, G.; Doyle, J.M. A cryogenic beam of refractory, chemically reactive molecules with expansion cooling. Phys. Chem. Chem. Phys. 2011, 13, 18976–18985. [Google Scholar] [CrossRef] [PubMed]
- West, E.; Baron, J.; Hutzler, N.; Ang, D.; Haefner, J.; Lasner, Z.; Panda, C.; West, A.; DeMille, D.; Gabrielse, G.; et al. Improved Thermochemical Beam Source of ThO for Measuring the Electric Dipole Moment of the Electron. Proceedings of APS Division of Atomic and Molecular Physics Meeting 2017, Sacramento, CA, USA, 5–9 June 2017. [Google Scholar]
- Abe, M.; Gopakumar, G.; Hada, M.; Das, B.P.; Tatewaki, H.; Mukherjee, D. Application of relativistic coupled-cluster theory to the effective electric field in YbF. Phys. Rev. A 2014, 90, 022501. [Google Scholar] [CrossRef]
- Prasannaa, V.S.; Vutha, A.C.; Abe, M.; Das, B.P. Mercury monohalides: Suitability for electron electric dipole moment searches. Phys. Rev. Lett. 2015, 114, 183001. [Google Scholar] [CrossRef] [PubMed]
- Sasmal, S.; Pathak, H.; Nayak, M.K.; Vaval, N.; Pal, S. Relativistic coupled-cluster study of RaF as a candidate for the parity- and time-reversal-violating interaction. Phys. Rev. A 2016, 93, 062506. [Google Scholar] [CrossRef]
- Lee, J.; Meyer, E.R.; Paudel, R.; Bohn, J.L.; Leanhardt, A.E. An electron electric dipole moment search in the X 3Δ1 ground state of tungsten carbide molecules. J. Mod. Opt. 2009, 56, 2005–2012. [Google Scholar] [CrossRef]
- Jacobs, J.P.; Klipstein, W.M.; Lamoreaux, S.K.; Heckel, B.R.; Fortson, E.N. Limit on the electric-dipole moment of 199Hg using synchronous optical pumping. Phys. Rev. A 1995, 52, 3521. [Google Scholar] [CrossRef] [PubMed]
- DeMille, D.; Bay, F.; Bickman, S.; Kawall, D.; Hunter, L.; Krause, D.; Maxwell, S.; Ulmer, K. Search for the electric dipole moment of the electron using metastable PbO. In Proceedings of the Conference on Art and Symmetry in Experimental Physics: Festschrift Commins (Eugene D), Berkeley, CA, USA, 20–21 May 2001. [Google Scholar]
- Eckel, S.; Hamilton, P.; Kirilov, E.; Smith, H.W.; DeMille, D. Search for the electron electric dipole moment using Ω-doublet levels in PbO. Phys. Rev. A 2013, 87, 052130. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vutha, A.C.; Horbatsch, M.; Hessels, E.A. Oriented Polar Molecules in a Solid Inert-Gas Matrix: A Proposed Method for Measuring the Electric Dipole Moment of the Electron. Atoms 2018, 6, 3. https://doi.org/10.3390/atoms6010003
Vutha AC, Horbatsch M, Hessels EA. Oriented Polar Molecules in a Solid Inert-Gas Matrix: A Proposed Method for Measuring the Electric Dipole Moment of the Electron. Atoms. 2018; 6(1):3. https://doi.org/10.3390/atoms6010003
Chicago/Turabian StyleVutha, A. C., M. Horbatsch, and E. A. Hessels. 2018. "Oriented Polar Molecules in a Solid Inert-Gas Matrix: A Proposed Method for Measuring the Electric Dipole Moment of the Electron" Atoms 6, no. 1: 3. https://doi.org/10.3390/atoms6010003
APA StyleVutha, A. C., Horbatsch, M., & Hessels, E. A. (2018). Oriented Polar Molecules in a Solid Inert-Gas Matrix: A Proposed Method for Measuring the Electric Dipole Moment of the Electron. Atoms, 6(1), 3. https://doi.org/10.3390/atoms6010003





