A New Analysis of Stark and Zeeman Effects on Hydrogen Lines in Magnetized DA White Dwarfs

Abstract

White dwarfs with magnetic field strengths larger than 10 T are understood to represent more than 10% of the total population of white dwarfs. The presence of such strong magnetic fields is clearly indicated by the Zeeman triplet structure visible on absorption lines. In this work, we discuss the line broadening mechanisms and focus on the sensitivity of hydrogen lines on the magnetic field. We perform new calculations in conditions relevant to magnetized DA stellar atmospheres using models inspired from magnetic fusion plasma spectroscopy. A white dwarf spectrum from the Sloan Digital Sky Survey (SDSS) database is analyzed. An effective temperature is provided by an adjustment of the background radiation with a Planck function, and the magnetic field is inferred from absorption lines presenting a Zeeman triplet structure. An order-of-magnitude estimate for the electron density is also performed from Stark broadening analysis.

1. Introduction

White dwarfs—the end products of stellar evolution—occupy a key position in astrophysical theory. Their properties provide clues to the physical processes that take place during the evolutionary stages near the end of stellar lifetimes. With an understanding of white dwarf magnetic fields, one can indicate the formation or the existence of centered or non-centered dipoles of these magnetic fields [1]. However, only 10% of white dwarfs are thought to carry strong magnetic fields. Most of them have so far only been analyzed by visual comparison of the observation with relatively simple models of the radiation transport in a magnetized stellar atmosphere [2,3]. Some of them have been analyzed by using the least squares minimization scheme to find the best fit for magnetic field geometry [1,4]. Studies of white dwarf atmospheres have shown that the majority of white dwarfs have an atmosphere of pure hydrogen as a result of gravitational setting, which removes helium and heavier elements from the atmosphere and moves them towards inner layers [5,6]. These atmospheres can be considered as hydrogen plasmas, which are similar to some created in laboratory. Such white dwarfs are classified as of DA type due to the strong hydrogen absorption lines they present. The electron density in a white dwarf atmosphere is high enough (up to ${10}^{17}$ cm${}^{-3}$, and higher) so that the line shapes are dominated by Stark broadening, and hence can serve as a probe for the electron density $N_e$. A noticeable feature of magnetized DA white dwarfs is that their absorption lines exhibit a Zeeman triplet structure, which stems from the perturbation of the atomic energy levels due to the magnetic field. The design of a line shape model accounting for both Stark broadening and Zeeman splitting is not straightforward, because these two effects do not act as additive perturbations. Previous investigations in low-density (tokamak edge) magnetized plasma conditions have indicated an alteration of the broadening of each Zeeman component due to the change of the atomic energy level structure (degeneracy removal) in response to an external magnetic field [7,8]. This issue also concerns magnetized white dwarfs with spectra exhibiting Zeeman splitting. In this work, we report on the current status of the design of a line shape model accounting for Stark and Zeeman effects simultaneously, for applications to white dwarf atmosphere analysis. We perform new Stark–Zeeman line shape calculations. The applicability of spectroscopy as a diagnostic means is illustrated through the analysis of a white dwarf spectrum obtained from the Sloan Digital Sky Survey (SDSS) database.

2. Stark Line Shape Modeling

In a plasma, the energy levels of atomic species (either neutral atoms or multicharged ions) emitting line radiation is perturbed by the microscopic electric field, which results in a broadening of spectral lines. The spectral profile of an atomic line is proportional to the Fourier transform of the dipole autocorrelation function $C\left(t\right)$ [9]

$$L\left(\omega \right)=\frac{1}{\pi }\mathrm{Re}{\int }_0^{\infty }dtC\left(t\right)e^{i\omega t},$$

(1)

$$C\left(t\right)=\sum _{\overrightarrow{ϵ}}\langle \langle \overrightarrow{d}·\overrightarrow{ϵ}|\left\{\widehat{U}\left(t\right)\right\}|\rho \overrightarrow{d}·\overrightarrow{ϵ}\rangle \rangle ,$$

(2)

where $\{\dots \}$ is the average over plasma particles, $\rho$ is the atomic density operator, and $\overrightarrow{d}·\overrightarrow{ϵ}$ is the projection of the atomic dipole operator into the polarization plane. The double bracket notation $\langle \langle \dots |\dots \rangle \rangle$ is used for the scalar product in the Liouville space which is formed by the tensor product $\mathcal{H}\otimes {\mathcal{H}}^{*}$ between the atomic state space $\mathcal{H}$ and its dual ${\mathcal{H}}^{*}$. The evolution operator $\widehat{U}\left(t\right)$ obeys the time-dependent Schrödinger equation in the Liouville space

$$i\frac{d\widehat{U}\left(t\right)}{dt}\left(t\right)=[{\widehat{L}}_0+\widehat{V}\left(t\right)]\widehat{U}\left(t\right),$$

(3)

which is also called the Liouville equation. ${\widehat{L}}_0$ is the energy superoperator and $\widehat{V}=-\widehat{\overrightarrow{d}}·\overrightarrow{E}$ is the interaction superoperator corresponding to the Stark perturbation. The action of a superoperator $\widehat{A}$ on an operator X is defined by $\widehat{A}X=[A,X]/\hslash$, where A is the related operator and $[,]$ is the commutator. In a plasma, the electric field is caused by the electrons and the ions and the corresponding Stark perturbation decomposes into two parts

$$\widehat{V}=\widehat{\overrightarrow{d}}·\overrightarrow{E}=-\widehat{\overrightarrow{d}}·{\overrightarrow{E}}_i-\widehat{\overrightarrow{d}}·{\overrightarrow{E}}_e,$$

(4)

where the e and i subscripts correspond to the electrons and ions, respectively. In the framework of the so-called “standard model”, the ions are assumed motionless and a constant electric field is used for their contribution, while the electron contribution is described within a collisional picture by a relaxation (“collision”) operator ${\widehat{K}}_e$, that is through the formal substitution $-\widehat{\overrightarrow{d}}·{\overrightarrow{E}}_e\to -i{\widehat{K}}_e$. In this way, the Liouville equation has the exponential solution $\widehat{U}\left(t\right)=exp[-i({\widehat{L}}_0-\widehat{\overrightarrow{d}}.{\overrightarrow{E}}_i-i{\widehat{K}}_e)]t$ and the line shape function is obtained from a matrix inversion

$$L\left(\omega \right)=-\frac{1}{\pi }\mathrm{Im}\sum _{\overrightarrow{ϵ}}\int d^3{E}_{i}W({\overrightarrow{E}}_i)\langle \langle \overrightarrow{d}·\overrightarrow{ϵ}|{(\omega -{\widehat{L}}_0+\widehat{\overrightarrow{d}}.{\overrightarrow{E}}_i+i{\widehat{K}}_e)}^{-1}|\rho \overrightarrow{d}·\overrightarrow{ϵ}\rangle \rangle$$

(5)

The integral is performed over the ionic electric field ${\overrightarrow{E}}_i$ and involves its probability density function $W({\overrightarrow{E}}_i)$. This integration can be performed numerically by using a discretization scheme or by Monte Carlo method. The standard model is convenient for numerical applications due to the structure of Equation (5), which can be interpreted as a sum of complex Lorentzian functions after decomposition of the Liouville double brackets onto a basis is done. The static ion approximation holds at conditions such that the collision time $r_0/v_i$ ($r_0$ and $v_i$ being the mean interparticle distance and the thermal ion velocity, respectively) is much larger than the characteristic time for dipole decorrelation (also called “time of interest”). Extensions of the standard model accounting for ion dynamics effects can be set up through suitable modifications; e.g., by formally adding a non-Hermitian contribution to $L_0$ (Model Microfield Method [10,11], Frequency Fluctuation Model [12,13]). The ion dynamics leads to an additional broadening, which can be important especially at low densities, high temperatures, or for lines with a low upper principal quantum number. Simulations involving a numerical integration of the Liouville Equation (3) and not referring to Equation (5) can also be performed, but they become time-consuming if the atomic system is complex [7,14,15].

For hydrogen lines, the electron collision operator can be evaluated using the Griem–Kolb–Shen model [16], which provides an analytical expression for the contribution of weak collisions based on the time-dependent perturbation series. Such weak collisions involve an impact parameter larger than the Weisskopf radius $b_W=\hslash n^2/m_{e}v$ (n being the principal quantum number and v being the velocity), and they give a dominant contribution to the Stark broadening due to electrons. The strong collision contribution is usually estimated using a Lorentz model, assuming complete interruption of the wave train. Extensions to the Griem–Kolb–Shen model, accounting for “static” perturbations due to the electrons (especially present in the line wings), can be devised through the use of kinetic theory techniques (such as the “unified theory” [17,18,19]) and they lead to a frequency-dependent collision operator. In white dwarf atmospheres, the plasma is partially ionized and there can be a significant additional broadening caused by collisions with neutrals, either due to resonant interactions or to van der Waals interactions. This broadening is also described with a collision operator ${\widehat{K}}_0$, and it is added to ${\widehat{K}}_e$. Simple models can be found in [9].

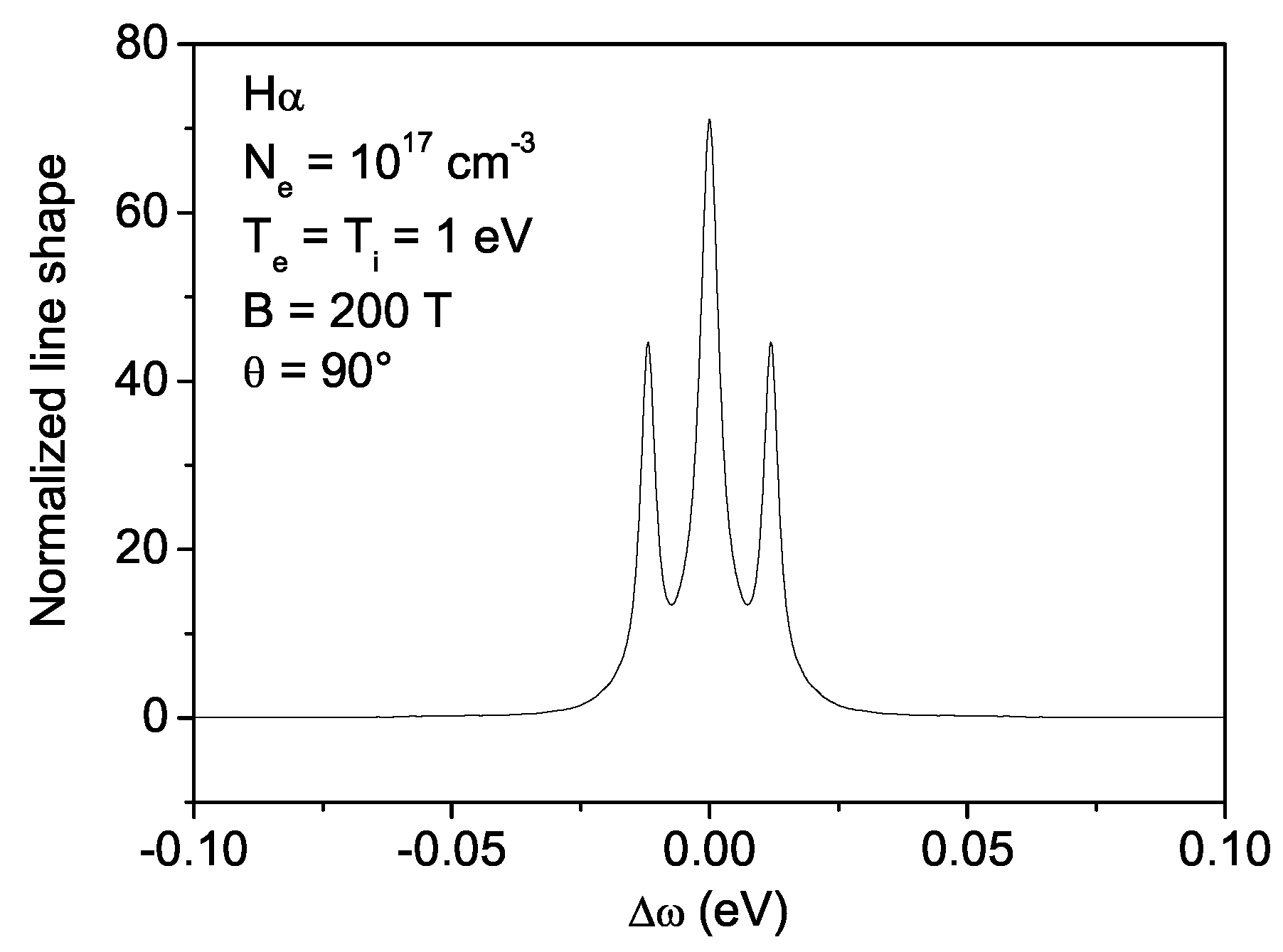
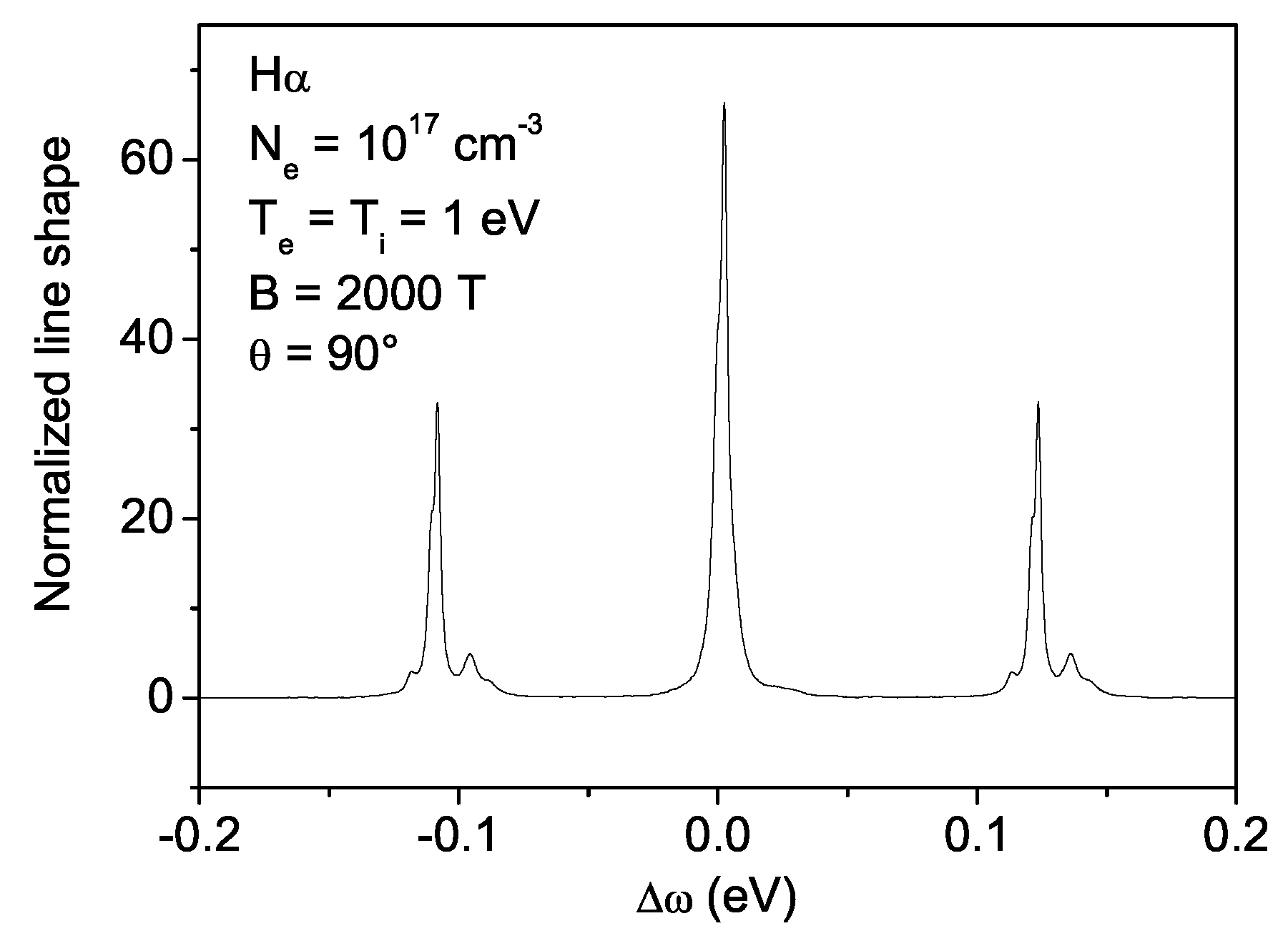
3. Zeeman Effect in Magnetized White Dwarfs

In the presence of a magnetic field, the atomic Hamiltonian and the corresponding Liouvillian ${\widehat{L}}_0$ contain an additional term due to the coupling with the field. Observations of white dwarf spectra have indicated that the magnetic field can attain values larger than 100 T, which renders the Zeeman effect visible on spectra. A description of this effect in line shape modeling requires the following substitution be done in the Liouville Equation (3):

$${\widehat{L}}_0\to {\widehat{L}}_0-\widehat{\overrightarrow{\mu }}·\overrightarrow{B},$$

(6)

where $\widehat{\overrightarrow{\mu }}$ is the magnetic moment expressed in the Liouville space. We do not consider the weak (“anomalous”) Zeeman effect that perturbs fine structure lines, because it is negligible in white dwarf spectra due to high density and strong magnetic fields. If the standard model is used, the same substitution as Equation (6) must be done in the line shape formula (5). An illustration of the Zeeman effect in white dwarf atmosphere conditions is shown in Figure 1. The H$\alpha$ line shape has been calculated assuming an electron density of ${10}^{17}$ cm${}^{-3}$, a temperature of 1 eV, and a magnetic field of 200 T. An observation direction perpendicular to the magnetic field has been assumed. The line shape exhibits a clean Zeeman triplet structure. The splitting is proportional to the magnetic field, and hence can be used to estimate the magnetic field in white dwarfs. In some white dwarfs, the magnetic field can be sufficiently large so that the quadratic Zeeman effect becomes visible in spectra. This effect can be retained through an additional term in the Hamiltonian which is proportional to $B^2$. This term stems from the expansion of the quantity ${(\overrightarrow{p}+e\overrightarrow{A})}^2$ present in the kinetic energy to the second order in the vector potential $\overrightarrow{A}$. Algebraic manipulations lead to the following expression for the quadratic Zeeman effect Hamiltonian:

$$V_{Z2}=\frac{e^2{B}^2{r}_{\perp }^2}{8m_e},$$

(7)

where ${\overrightarrow{r}}_{\perp }$ stands for the atomic electron position operator projected onto the plane perpendicular to $\overrightarrow{B}$. A similar relation holds for the corresponding superoperator in the Liouville space. The quadratic Zeeman effect is illustrated in Figure 2. A calculation of H$\alpha$ at the same plasma conditions as above, assuming a magnetic field of 2000 T, is shown. Note the asymmetry of the spectrum and the presence of more components.

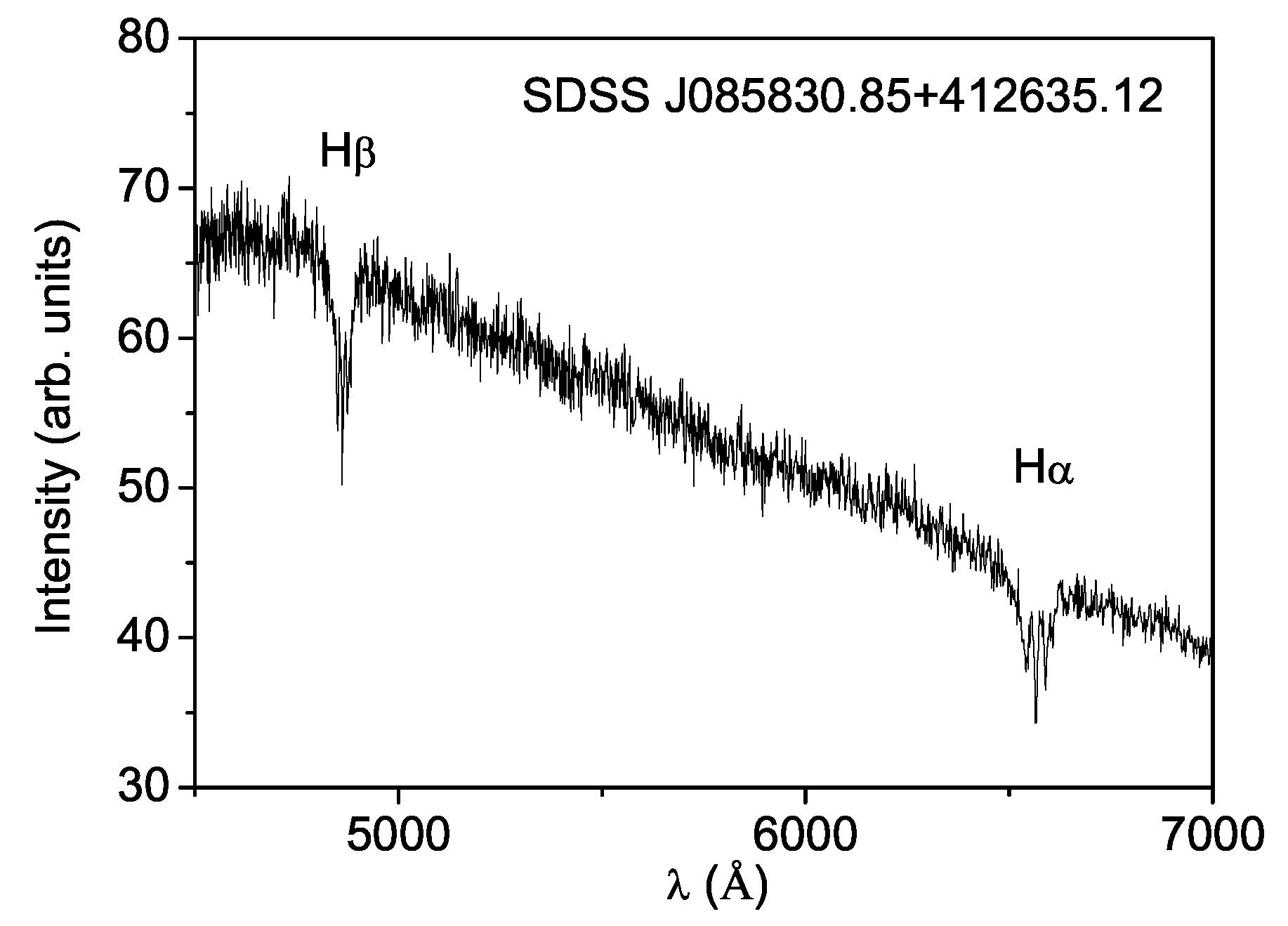
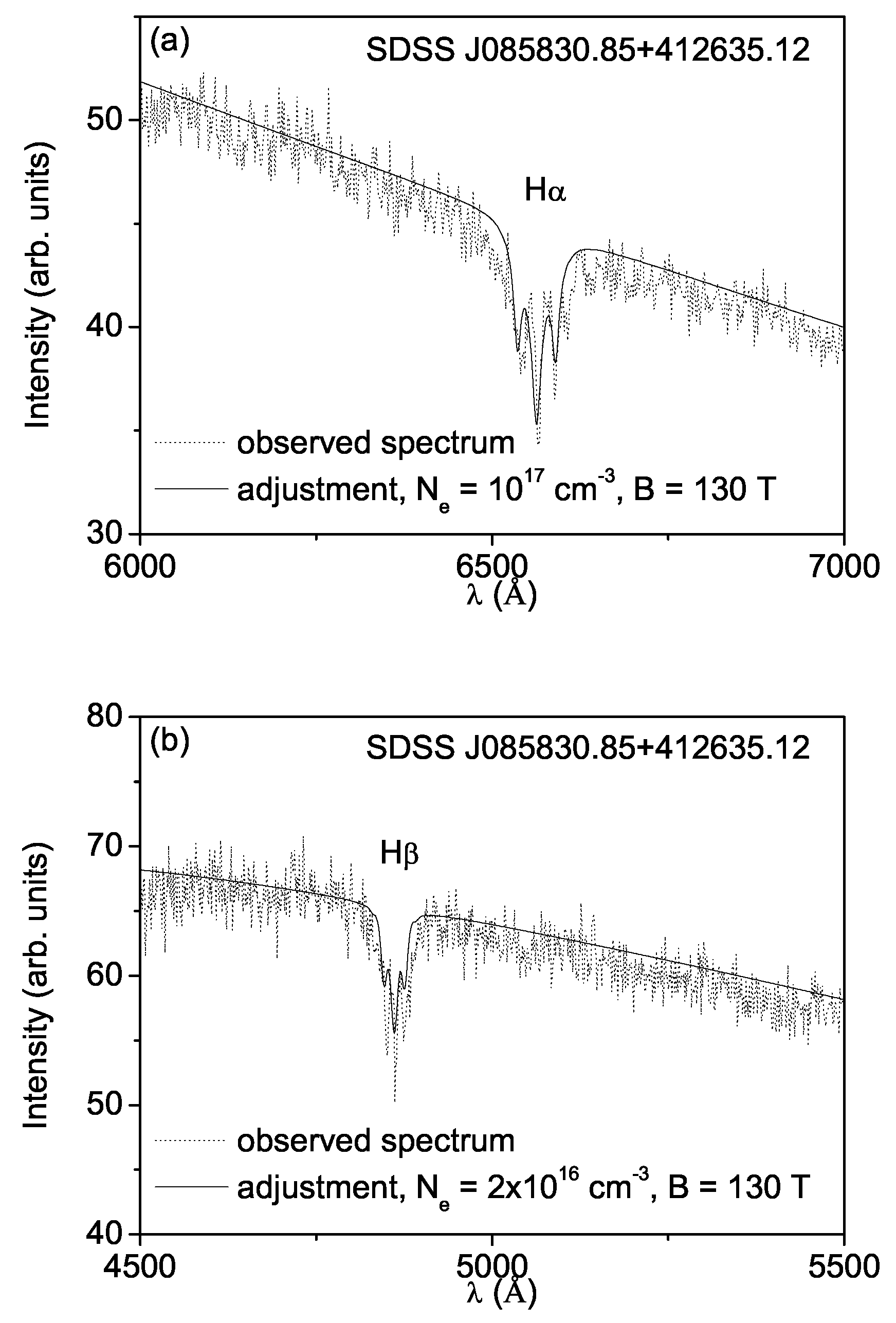
4. White Dwarf Spectrum Analysis

In this section, we illustrate the applicability of spectroscopy as a diagnostic means for the characterization of white dwarf atmosphere. A large amount of spectra presenting Zeeman splitting are available on the SDSS database (www.sdss.org) [1,4]. Figure 3 shows an example of such a spectrum. We have performed a fitting of the H$\alpha$ and H$\beta$ absorption lines using an exponential attenuation model (Beer-Lambert formula) assuming a homogeneous atmosphere slab, leaving the product $N_2\times L$ between absorber density $N_2$ and thickness L as an adjustable parameter. The temperature that enters the formula (through the electron collision operator and the microfield probability density function) is estimated from adjustment of the background radiation with a Planck function, assuming local thermodynamic equilibrium. Figure 4 shows the fitting result. The effective temperature is around 7000 K. In order to get a reasonable adjustment on each of these lines, we had to assume different values for the electronic density and the $N_{2}L$ parameter: $N_e=5\times {10}^{17}$ cm${}^{-3}$ and $N_{2}L=5\times {10}^{17}$ m${}^{-2}$ for H$\alpha$, $N_e=2\times {10}^{16}$ cm${}^{-3}$ and $N_{2}L=2\times {10}^{18}$ m${}^{-2}$ for H$\beta$. A value of 130 T for the magnetic was found in both cases. These results can be used as a first order-of-magnitude estimate. The necessity of using different values for densities stems from inaccuracies intrinsic to the model (e.g., due to the neglect of self-emission), and this indicates that a further refinement is required.

5. Conclusions

According to observations, a significant proportion of white dwarfs have a strong magnetic field, sufficiently so that the absorption lines present a Zeeman triplet structure. In this work, we have done new calculations of Stark–Zeeman hydrogen line shapes in preparation for the development of a model. Specific issues such as the quadratic Zeeman effect need to be investigated further. The applicability of spectroscopy as a diagnostic means for magnetized white dwarf atmospheres has been illustrated through adjustments performed on a spectrum from the Sloan Digital Sky Survey (SDSS) database. It is found that line width adjustments provide an order of magnitude for the electron density and the magnetic field in the atmosphere. An extension of the work to the accounting for plasma non-homogeneity is presently ongoing. Comparisons to other white dwarf spectra analyses, such as in [1,4], will be done.