Two-Photon Collective Atomic Recoil Lasing
Abstract
:1. Introduction
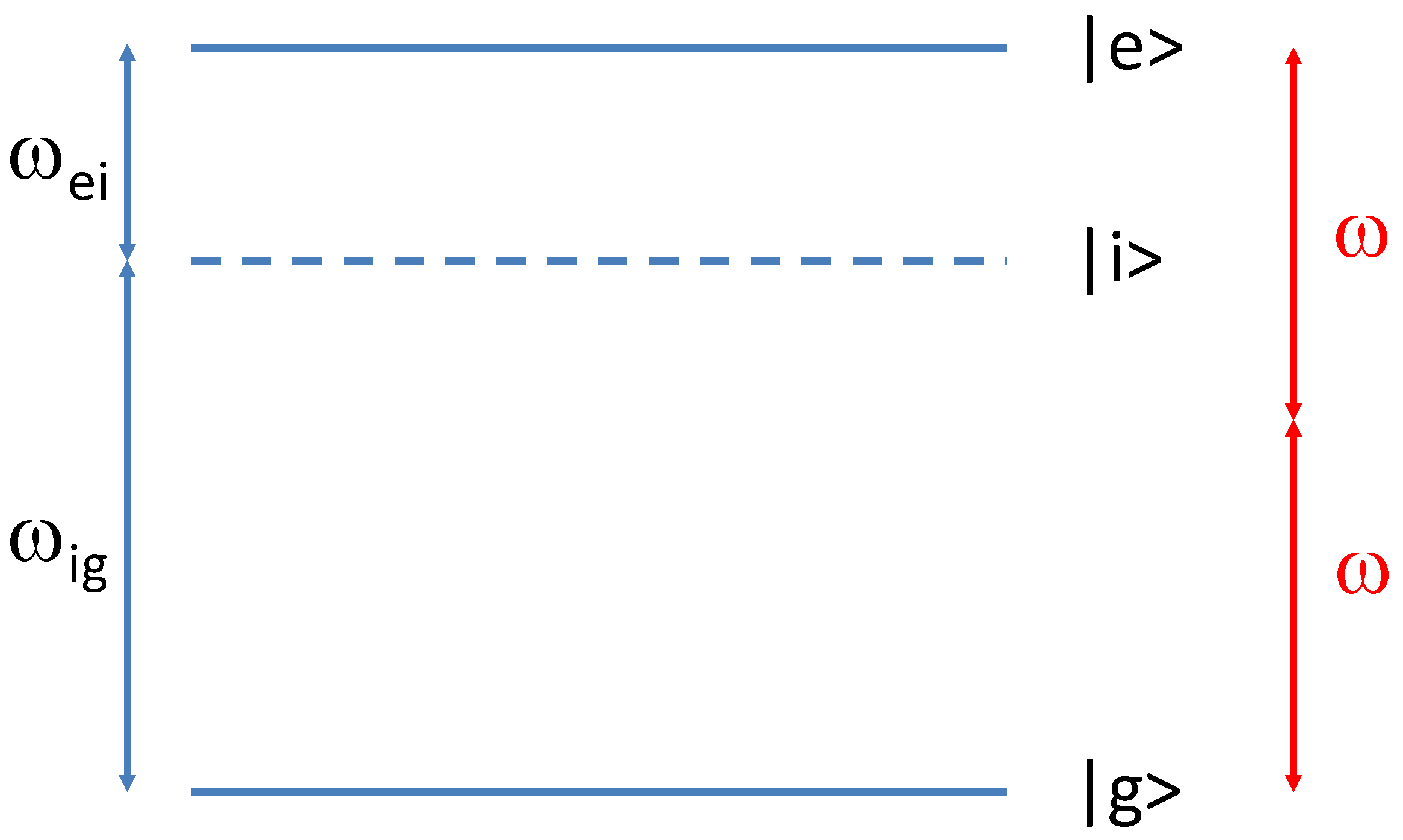
2. Model
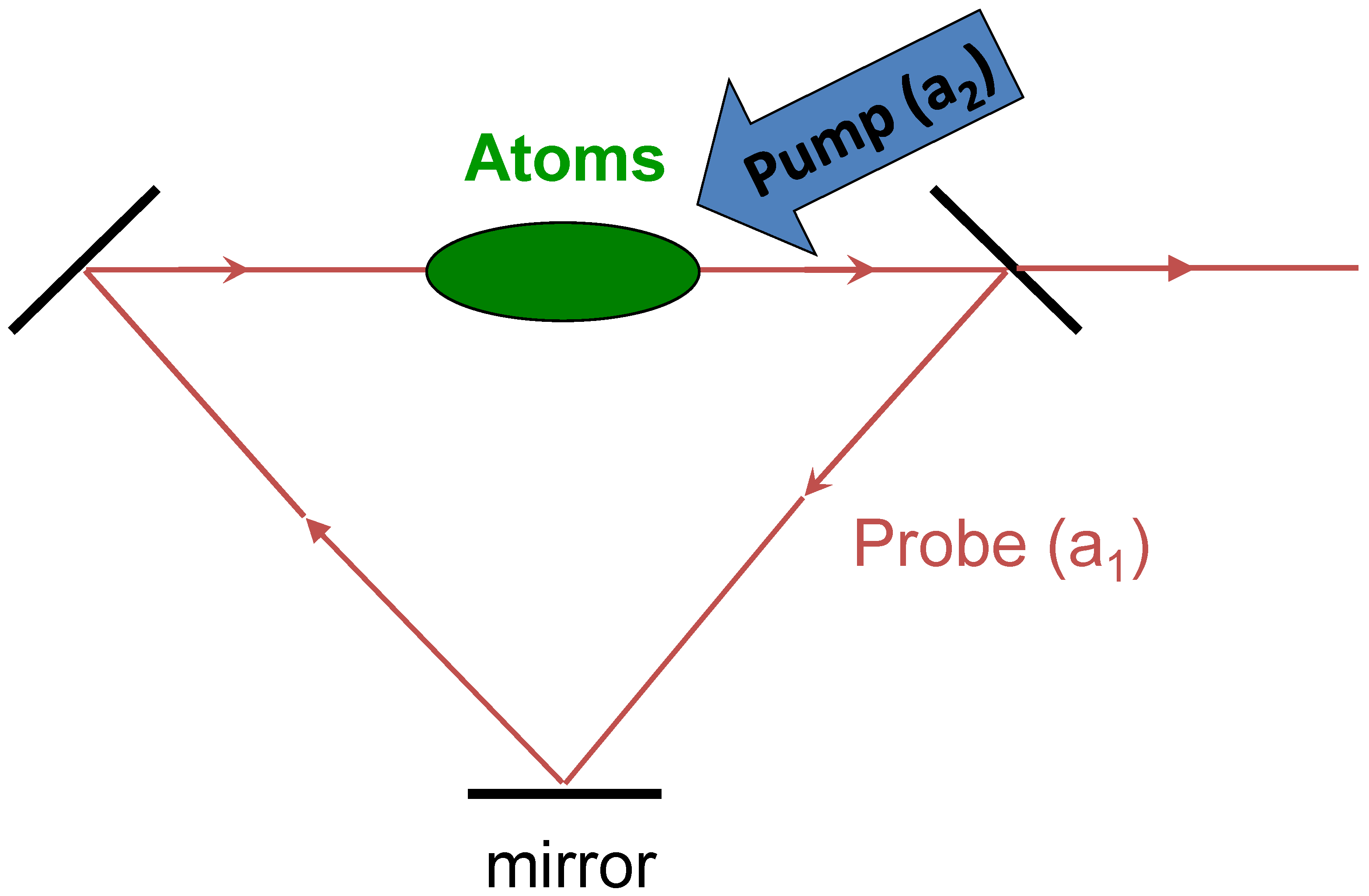
2.1. The Three-Level Atom
2.2. The Two-Photon Approximation
2.3. Atomic Motion
2.4. Cavity Field Evolution
3. Two-Photon CARL with Weak and Strong Excitation
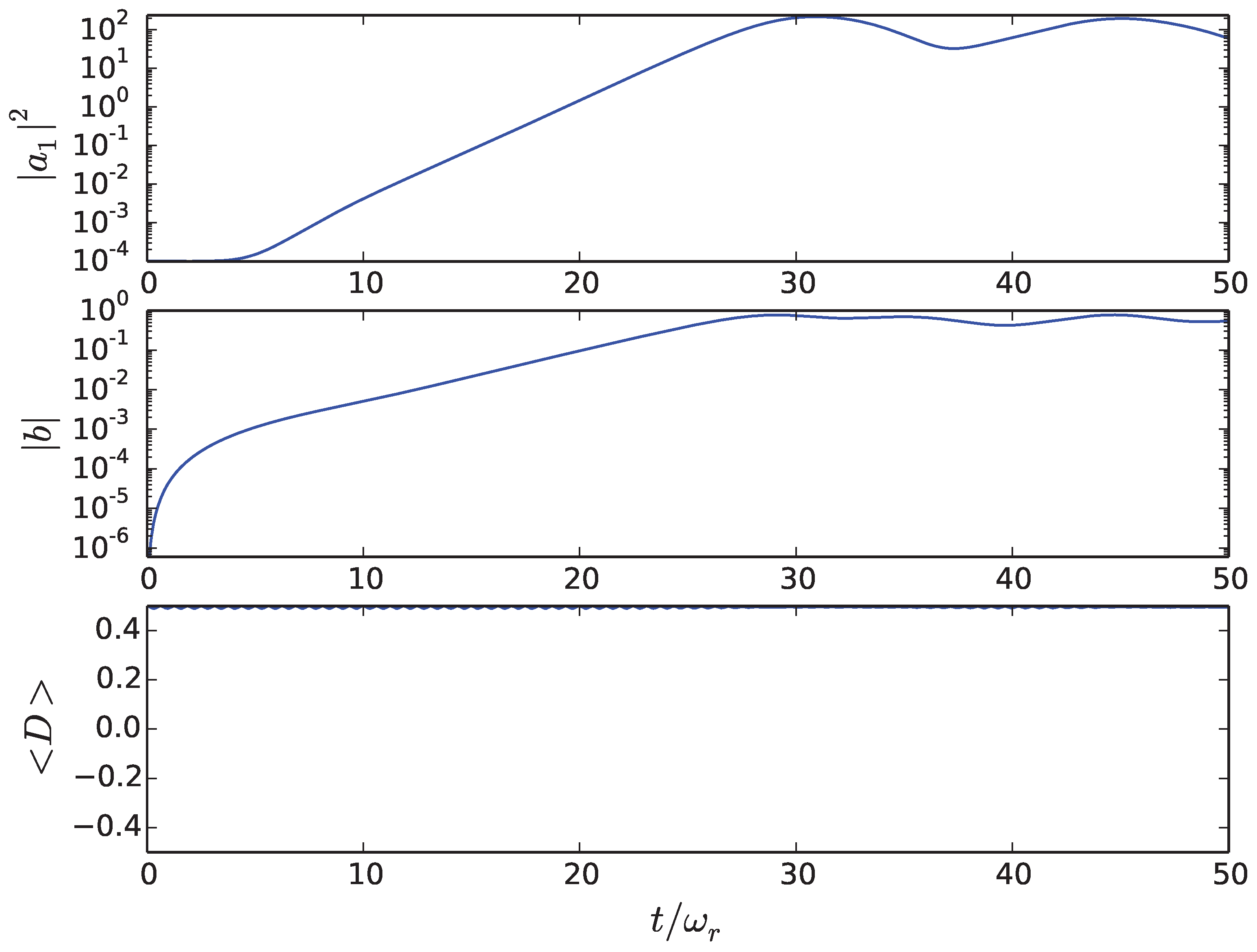
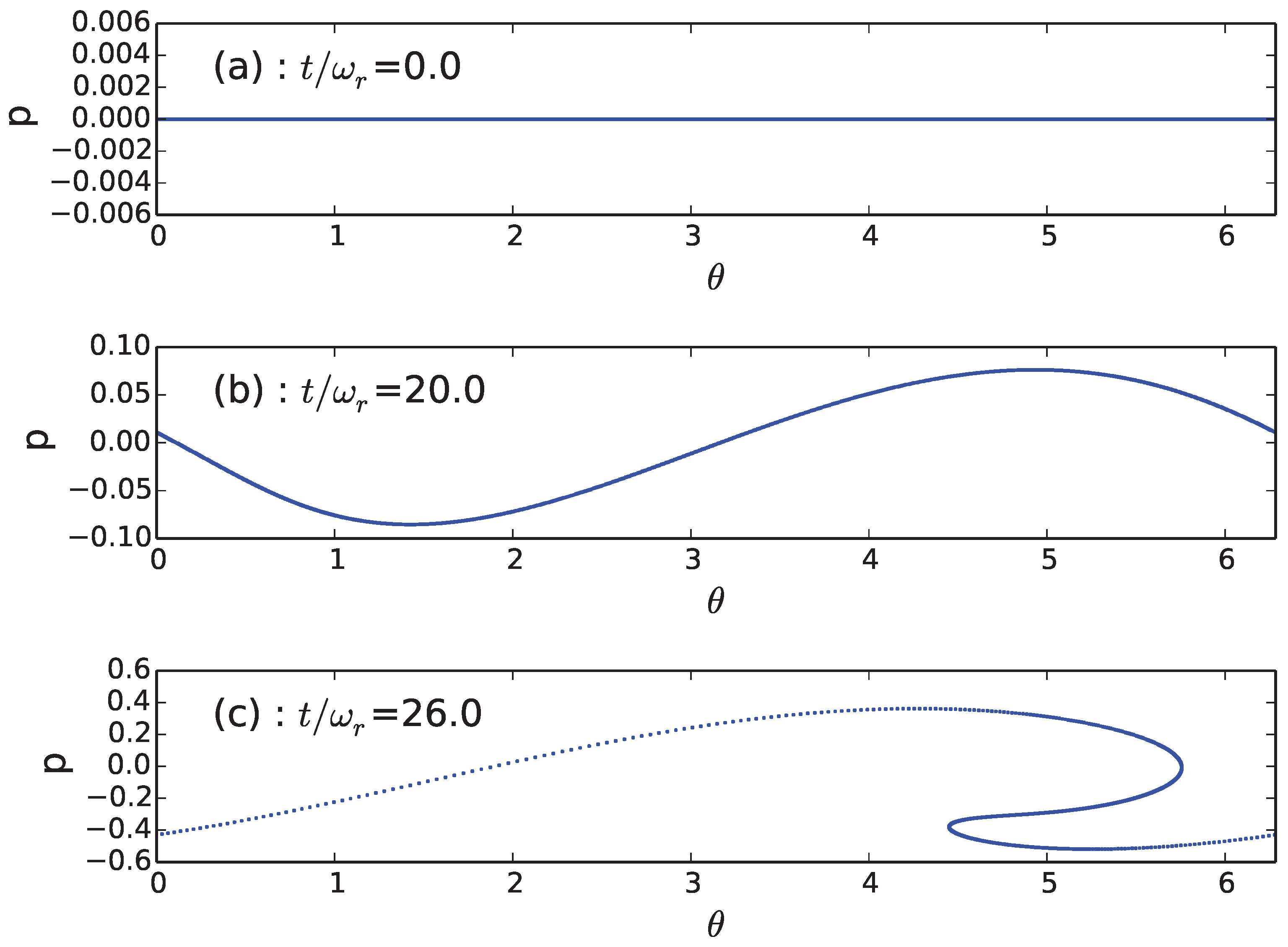
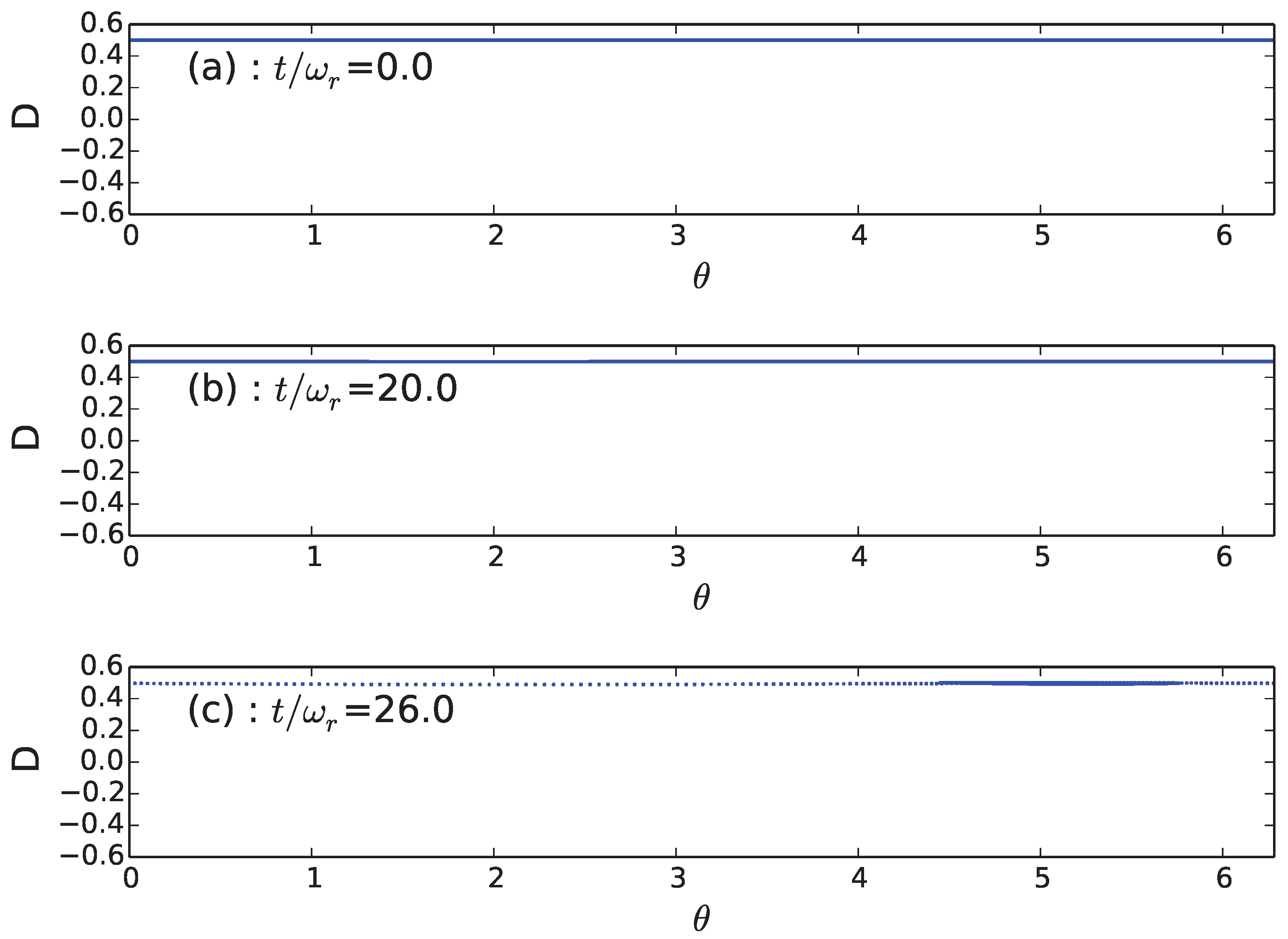
4. Strong Excitation
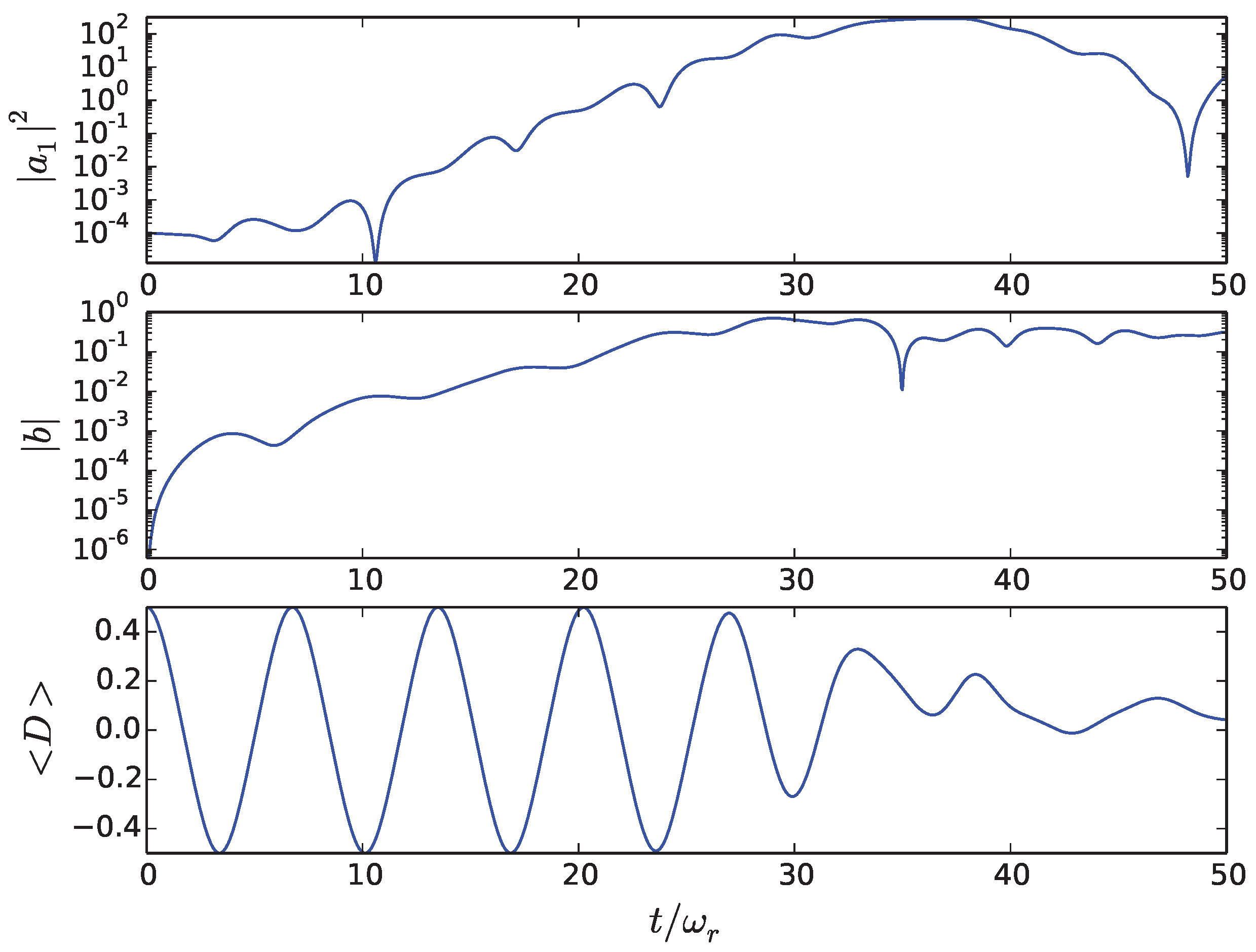
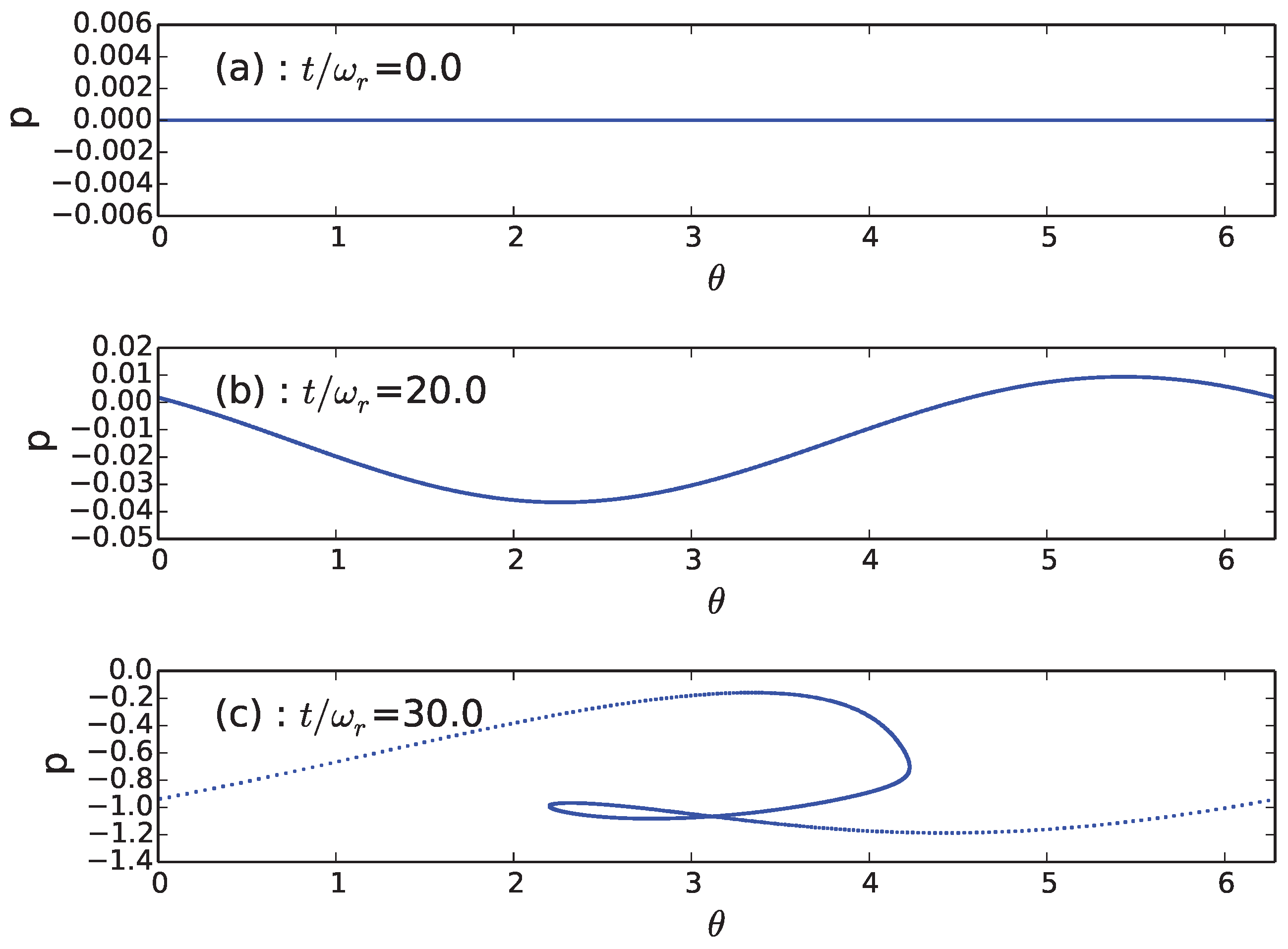
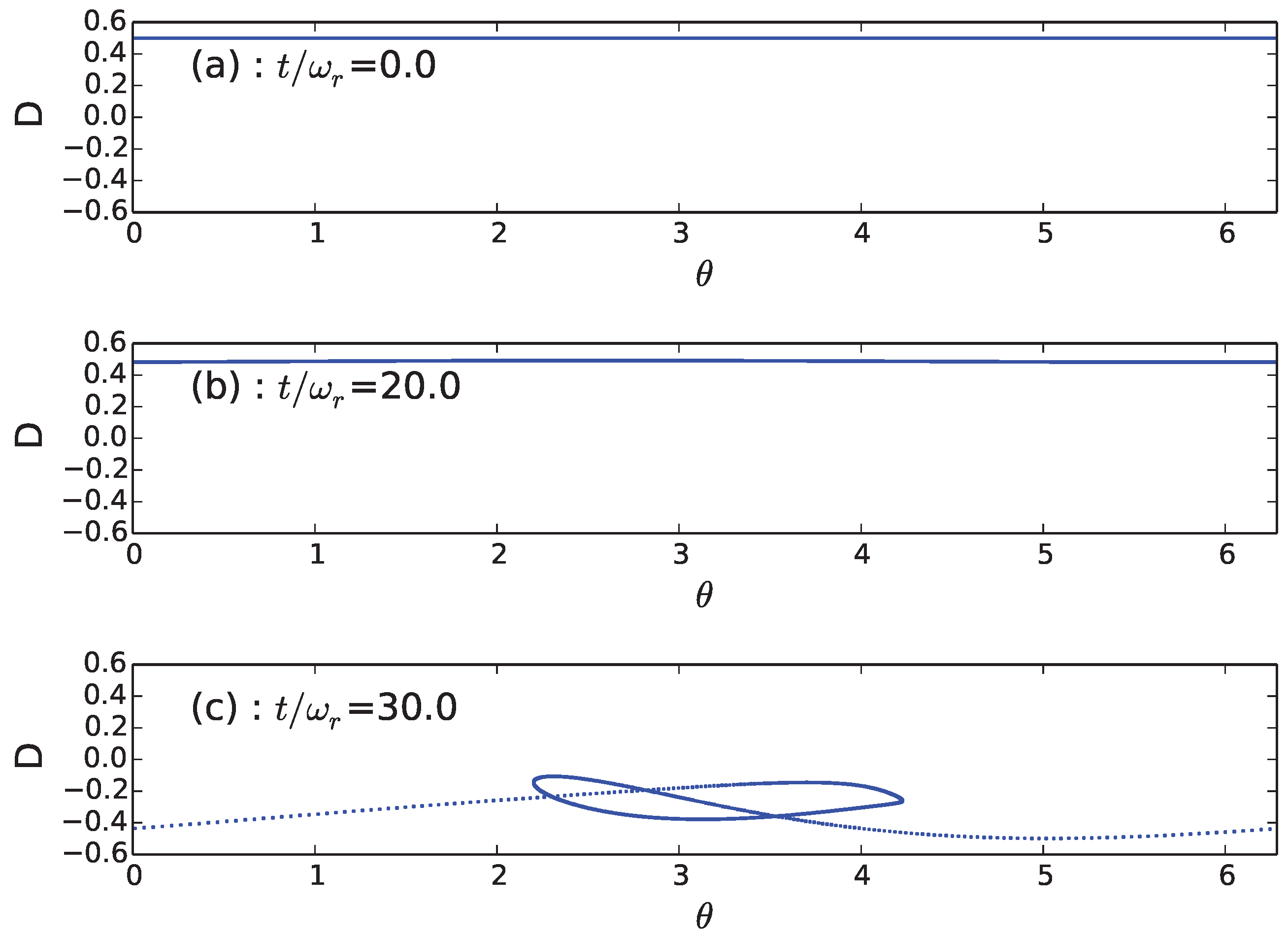
5. Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Bonifacio, R.; de Salvo, L. Collective atomic recoil laser (CARL) optical gain without inversion by collective atomic recoil and self-bunching of two-level atoms. Nucl. Instrum. Meth. Phys. Res. A 1994, 341, 360–362. [Google Scholar] [CrossRef]
- Bonifacio, R; de Salvo Souza, L.; Narducci, L.; D’Angelo, E.J. Exponential gain and self-bunching in a collective atomic recoil laser. Phys. Rev. A 1994, 50, 1716–1724. [Google Scholar]
- Inouye, S.; Chikkatur, A.P.; Stamper-Kurn, D.M.; Stenger, J.; Pritchard, D.E.; Ketterle, W. Superradiant Rayleigh scattering from a Bose-Einstein condensate. Science 1999, 285, 571–574. [Google Scholar] [CrossRef]
- Moore, M.G.; Meystre, P. Theory of superradiant scattering of laser light from Bose-Einstein condensates. Phys. Rev. Lett. 1999, 83, 5202–5205. [Google Scholar] [CrossRef]
- Gangl, M.; Ritsch, H. Cold atoms in a high-Q ring cavity. Phys. Rev. A 2000, 61, 043405. [Google Scholar] [CrossRef]
- Piovella, N.; Gatelli, M.; Bonifacio, R. Quantum effects in the collective light scattering by coherent atomic recoil in a Bose–Einstein condensate. Opt. Commun. 2001, 194, 167–173. [Google Scholar] [CrossRef]
- Schneble, D.; Torii, Y.; Boyd, M.; Streed, E.W.; Pritchard, D.E.; Ketterle, W. The onset of matter–wave amplification in a superradiant Bose–Einstein condensate. Science 2003, 300, 475–478. [Google Scholar] [CrossRef] [PubMed]
- Kruse, D.; von Cube, C.; Zimmermann, C.; Courteille, Ph.W. Observation of lasing mediated by collective atomic recoil. Phys. Rev. Lett. 2003, 91, 183601. [Google Scholar] [CrossRef] [PubMed]
- Nagorny, B.; Elsässer, Th.; Hemmerich, A. Collective atomic motion in an optical lattice formed inside a high finesse cavity. Phys. Rev. Lett. 2003, 91, 153003. [Google Scholar] [CrossRef] [PubMed]
- Yoshikawa, Y.; Torii, Y.; Kuga, T. Superradiant light scattering from thermal atomic vapors. Phys. Rev. Lett. 2005, 94, 083602. [Google Scholar] [CrossRef] [PubMed]
- Von Cube, C.; Slama, S.; Kruse, D.; Zimmermann, C.; Courteille, Ph.W.; Robb, G.R.M.; Piovella, N.; Bonifacio, R. Self-Synchronization and Dissipation-Induced Threshold in Collective Atomic Recoil Lasing. Phys. Rev. Lett. 2004, 93, 083601. [Google Scholar] [CrossRef] [PubMed]
- Fallani, L.; Fort, C.; Piovella, N.; Cola, M.M.; Cataliotti, F.S.; Inguscio, M.; Bonifacio, R. Collective atomic recoil in a moving Bose–Einstein condensate: From superradiance to Bragg scattering. Phys. Rev. A 2005, 71, 033612. [Google Scholar] [CrossRef]
- Asboth, J.K.; Domokos, P.; Ritsch, H.; Vukics, A. Self–organization of atoms in a cavity field: Threshold, bistability, and scaling laws. Phys. Rev. A 2005, 72, 053417. [Google Scholar] [CrossRef]
- Nagy, D.; Asboth, J.K.; Domokos, P.; Ritsch, H. Self–organization of a laser–driven cold gas in a ring cavity. Europhys. Lett. 2006, 74, 254. [Google Scholar] [CrossRef]
- Slama, S.; Bux, S.; Krenz, G.; Zimmermann, C.; Courteille, Ph.W. Superradiant Rayleigh scattering and collective atomic recoil lasing in a ring cavity. Phys. Rev. Lett. 2007, 98, 053603. [Google Scholar] [CrossRef] [PubMed]
- Keeling, J.; Bhaseen, M.J.; Simons, B.D. Collective dynamics of Bose–Einstein condensates in optical cavities. Phys. Rev. Lett. 2010, 105, 043001. [Google Scholar] [CrossRef]
- Bux, S.; Gnahm, C.; Maier, R.A.W.; Zimmermann, C.; Courteille, Ph.W. Cavity–Controlled Collective Scattering at the Recoil Limit. Phys. Rev. Lett. 2011, 106, 203601. [Google Scholar] [CrossRef]
- Greenberg, J.A.; Schmittberger, B.L.; Gauthier, D.J. Bunching–induced optical nonlinearity and instability in cold atoms. Opt. Express 2011, 19, 22535. [Google Scholar] [CrossRef] [PubMed]
- Schmittberger, B.L.; Gauthier, D.J. Enhancing light–atom interactions via atomic bunching. Phys. Rev. A 2014, 90, 013813. [Google Scholar] [CrossRef]
- Kessler, H.; Klinder, J.; Wolke, M.; Hemmerich, A. Steering matter wave superradiance with an ultranarrow–band optical cavity. Phys. Rev. Lett. 2014, 113, 070404. [Google Scholar] [CrossRef] [PubMed]
- Keeling, J.; Bhaseen, M.J.; Simons, B.D. Fermionic Superradiance in a Transversely Pumped Optical Cavity. Phys. Rev. Lett. 2014, 112, 143002. [Google Scholar] [CrossRef]
- Fernández-Vidal, S.; de Chiara, G.; Larson, J.; Morigi, G. Quantum ground state of self–organized atomic crystals in optical resonators. Phys. Rev. A 2010, 81, 043407. [Google Scholar] [CrossRef]
- Schmidt, D.; Tomczyk, H.; Slama, S.; Zimmermann, C. Dynamical Instability of a Bose–Einstein Condensate in an Optical Ring Resonator. Phys. Rev. Lett. 2014, 112, 115302. [Google Scholar] [CrossRef] [PubMed]
- Domokos, P.; Ritsch, H. Collective cooling and self–organization of atoms in a cavity. Phys. Rev. Lett. 2002, 89, 253003. [Google Scholar] [CrossRef] [PubMed]
- Chan, H.W.; Black, A.T.; Vuletic, V. Observation of collective–emission–induced cooling of atoms in an optical cavity. Phys. Rev. Lett. 2003, 90, 63003. [Google Scholar] [CrossRef] [PubMed]
- Black, A.T.; Chan, H.W.; Vuletic, V. Observation of collective friction forces due to spatial self–organization of atoms: From Rayleigh to Bragg scattering. Phys. Rev. Lett. 2003, 91, 203001. [Google Scholar] [CrossRef] [PubMed]
- Muradyan, G.A.; Wang, Y.; Williams, W.; Saffman, M. Absolute instability and pattern formation in cold atomic vapors. Nonlinear Guided Waves Top. Meet. Tech. Dig. 2005. [Google Scholar] [CrossRef]
- Saffman, M.; Wang, Y. Collective focusing and modulational instability of light and cold atoms. In Dissipative Solitons: From Optics to Biology and Medicine; Springer: Berlin, Germany, 2008. [Google Scholar]
- Tesio, E.; Robb, G.R.M.; Ackemann, T.; Firth, W.J.; Oppo, G.-L. Spontaneous optomechanical pattern formation in cold atoms. Phys. Rev. A 2012, 86, 031801. [Google Scholar] [CrossRef]
- Tesio, E.; Robb, G.R.M.; Ackemann, T.; Firth, W.J.; Oppo, G.-L. Kinetic theory for transverse optomechanical instabilities. Phys. Rev. Lett. 2012, 112, 043901. [Google Scholar] [CrossRef] [PubMed]
- Labeyrie, G.; Tesio, E.; Gomes, P.M.; Oppo, G.-L.; Firth, W.J.; Robb, G.R.M.; Arnold, A.S.; Kaiser, R.; Ackemann, T. Optomechanical self-structuring in a cold atomic gas. Nat. Phot. 2014, 8, 321–325. [Google Scholar] [CrossRef]
- Robb, G.R.M.; Tesio, E.; Oppo, G.-L.; Firth, W.J.; Ackemann, T.; Bonifacio, R. Quantum Threshold for Optomechanical Self-Structuring in a Bose-Einstein Condensate. Phys. Rev. Lett. 2015, 114, 173903. [Google Scholar] [CrossRef]
- Brennecke, F.; Ritter, S.; Donner, T.; Esslinger, T. Cavity optomechanics with a Bose–Einstein condensate. Science 2008, 322, 235–238. [Google Scholar] [CrossRef]
- Baumann, K.; Guerlin, C.; Brennecke, F.; Esslinger, T. Dicke quantum phase transition with a superfluid gas in an optical cavity. Nature 2010, 464, 1301–1306. [Google Scholar] [CrossRef]
- Botter, T.; Brooks, D.W.C.; Schreppler, S.; Brahms, N.; Stamper-Kurn, D.M. Optical readout of the quantum collective motion of an array of atomic ensembles. Phys. Rev. Lett. 2013, 110, 153001. [Google Scholar] [CrossRef] [PubMed]
- Ritsch, H.; Domokos, P.; Brenneke, F.; Esslinger, T. Cold atoms in cavity-generated dynamical optical potentials. Rev. Mod. Phys. 2013, 85, 553–601. [Google Scholar] [CrossRef]
- Bonifacio, R.; de Salvo, L. Analytical theory of the collective atomic recoil laser in the FEL limit. Appl. Phys. B 1995, 60, S233–S239. [Google Scholar]
- Katori, H.; Takamoto, M.; Pal’chikov, V.G.; Ovsiannikov, V.D. Ultrastable Optical Clock with Neutral Atoms in an Engineered Light Shift Trap. Phys. Rev. Lett. 2003, 91, 173005. [Google Scholar] [CrossRef] [PubMed]
- Ludlow, A.D.; Hinkley, N.M.; Sherman, J.A.; Phillips, N.B.; Schioppo, M.; Lemke, N.D.; Beloy, K.P.; Pizzocaro, M.; Oates, C.W. An atomic clock with 10‒18 instability. Science 2013, 341, 1215–1218. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
McKelvie, J.A.; Robb, G.R.M. Two-Photon Collective Atomic Recoil Lasing. Atoms 2015, 3, 495-508. https://doi.org/10.3390/atoms3040495
McKelvie JA, Robb GRM. Two-Photon Collective Atomic Recoil Lasing. Atoms. 2015; 3(4):495-508. https://doi.org/10.3390/atoms3040495
Chicago/Turabian StyleMcKelvie, James A., and Gordon R.M. Robb. 2015. "Two-Photon Collective Atomic Recoil Lasing" Atoms 3, no. 4: 495-508. https://doi.org/10.3390/atoms3040495
APA StyleMcKelvie, J. A., & Robb, G. R. M. (2015). Two-Photon Collective Atomic Recoil Lasing. Atoms, 3(4), 495-508. https://doi.org/10.3390/atoms3040495




