Electron Impact Excitation and Dielectronic Recombination of Highly Charged Tungsten Ions

Abstract

Electron impact excitation (EIE) and dielectronic recombination (DR) of tungsten ions are basic atomic processes in nuclear fusion plasmas of the International Thermonuclear Experimental Reactor (ITER) tokamak. Detailed investigation of such processes is essential for modeling and diagnosing future fusion experiments performed on the ITER. In the present work, we studied total and partial electron-impact excitation (EIE) and DR cross-sections of highly charged tungsten ions by using the multiconfiguration Dirac–Fock method. The degrees of linear polarization of the subsequent X-ray emissions from unequally-populated magnetic sub-levels of these ions were estimated. It is found that the degrees of linear polarization of the same transition lines, but populated respectively by the EIE and DR processes, are very different, which makes diagnosis of the formation mechanism of X-ray emissions possible. In addition, with the help of the flexible atomic code on the basis of the relativistic configuration interaction method, DR rate coefficients of highly charged W${}^{37+}$ to W${}^{46+}$ ions are also studied, because of the importance in the ionization equilibrium of tungsten plasmas under running conditions of the ITER.

1. Introduction

Owing to its physical properties of high melting temperature, excellent thermal conductivity, low sputtering rate and low affinity for tritium [1,2], tungsten has been used as a plasma-facing material in several magnetic confinement fusion facilities [3,4,5,6] and is planned to be used in the divertor region having the highest heat load in the International Thermonuclear Experimental Reactor (ITER) tokamak [7]. However, inevitably, tungsten appears as an intrinsic impurity in fusion plasmas, which results in some severe problems due to its high radiation efficiency. The radiated X-ray emissions from excited tungsten lead to substantial plasma cooling that has to be well controlled in order to maintain conditions for nuclear fusions [8,9,10,11,12,13]. Therefore, it is important to know the atomic properties of tungsten in plasma under the conditions ranging from the cold temperature (≃ 1 eV) of near-wall plasma to the approximate 20 keV electron temperature expected in the plasma core region. X-ray emissions from highly charged tungsten ions can be used as diagnostic probes to reflect the information on the fusion plasmas. W${}^{46+}$–W${}^{42+}$ ions are arranged in a filled M-shell structure that are expected to be present over a wide range of electron temperatures in plasmas. The radiated X-rays from strong M-band ($nf$ → $3d$) atomic transitions have great significance in that they are suitable for fusion plasma modeling and diagnostics, since the radiations involving the 3d subshell are very intense [13]. Because of that, these charge states of tungsten are selected to study X-ray polarization in the present work.

Up to now, the atomic properties of tungsten have been extensively studied experimentally by using plasma devices, beams and trapped ions and theoretically by atomic structure and scattering calculations. For example, charge state distribution in plasmas, X-ray emission spectra and transition properties following electron-impact excitation (EIE) and ionization, as well as dielectronic recombination (DR) processes have been performed. An overview of the photoionization, electron-impact ionization, as well as electron-ion recombination of low to moderately-charged tungsten ions was reported very recently, together with a critical assessment of the methods and results [14]. Extreme-ultraviolet (EUV) spectra from a variety of tungsten ions have been recorded at the electron beam ion trap and the Axially Symmetric Divertor EXperiment (ASDEX) Upgrade tokamak facilities [15,16,17,18,19,20,21]. The majority of these spectra have been identified and assigned to $nf$ → $3d$ ($n=$ 4, 5, 6) and $4d$ → $3p$ atomic transitions mostly by performing fully-relativistic ab initio calculations [22,23,24,25]. Besides atomic structure and spectra, the dynamical processes of tungsten ions were also investigated for the purpose of X-ray diagnostics and simulation, such as electron-impact ionization [26], electron-impact excitation [27,28] and dielectronic recombination [29]. However, to the best of our knowledge, there are few work about the linear polarization of tungsten X-ray emissions in ITER fusion plasmas. Since angle-resolved observables, such as linear polarization and angular distribution, are much more sensitive to various atomic effects and physical variables than the total (angle-averaged) decay rates of X-ray emissions, the angle-resolved studies of X-rays have been used to extract a variety of physical effects in the last few decades [30,31,32,33,34,35,36]. For those strong X-ray emissions from tungsten ions, they are hardly affected by the radiative damping caused by additional atomic excitation processes [27] and, thus, are relatively clean atomic radiations, which could be used to study the angle-resolved observables to reveal the population mechanism of excited levels [37,38] and perhaps to reflect plasma conditions. In the present work, linear polarization of tungsten X-ray emissions from strong $nf$ → $3d$ (n = 4, 5, 6) radiative transitions following electron-impact excitation and resonant electron capture (REC) of W${}^{42+}$ to W${}^{46+}$ ions is studied theoretically.

Moreover, DR has been known as one of the important recombination processes, which plays dominant roles in the ionization equilibrium of various plasmas. Triggered by this, much work on the DR process and the rate coefficients of tungsten ions has been done, both theoretically and experimentally [39,40,41,42,43,44,45,46,47,48,49,50]. For example, the Atomic Data and Analysis Structure (ADAS) database is currently used for modeling plasmas in the community [7,42,51,52]. The computations of DR rate coefficients from the ADAS are based on the generalized collisional-radiative framework [53] and the semiempirical Burgess formulas [54]. Although many experiments on spectral emissions from tungsten have been carried out, especially at the ASDEX Upgrade tokamak [2,3,4,7,17,51], the first measurement on DR rate coefficients of tungsten ions was performed just recently for W${}^{20+}$ using the technique of the electron-ion merged beam at the heavy ion storage ring [39]. A big discrepancy with a factor of four was found between the measured and calculated rate coefficients from the ADAS database, which was attributed to the neglect of DR-associated fine-structure excitations of W${}^{20+}$ in the calculations [39]. Further intermediate-coupling calculations with all important single-electron excitations reduced the discrepancy to a factor of three at an electron temperature of 1 eV and to a much better 50%–30% among 100–300 eV [42]. Very recently, other theoretical methods, such as the configuration-average distorted-wave method [41], the statistical theory of resonant multielectron recombination [43,44] and the Breit–Wigner partitioned method [40], were further developed to calculate DR rate coefficients. These methods could produce results that agree reasonably well with the experimental findings. Apart from DR, radiative recombination (RR) is another non-negligible recombination process in which the fusion community is interested. For example, Trzhaskovskaya et al. calculated in great detail RR cross-sections and rate coefficients, as well as radiated power loss rate coefficients for a wide range of tungsten ions W${}^{14+}$–W${}^{71+}$ [55,56,57,58]. With the purpose of assisting the simulation of the ionization equilibrium of tungsten plasmas, DR rate coefficients of W${}^{37+}$ to W${}^{46+}$ ions are studied, as well, in the present work.

The paper is structured as follows. In the next section, theoretical methods for calculating partial EIE and DR cross-sections, linear polarization of X-ray emissions and DR rate coefficients are described. In Section 3, we discuss the calculated partial cross-sections and DR rate coefficients and especially compare the linear polarization of X-rays for both cases of EIE and DR. Finally, a few conclusions of the present work are given in Section 4.

2. Theoretical Background

2.1. Electron Impact Excitation and Dielectronic Recombination Cross-Sections

In the present work, a recently-developed computational code, REIE06 [38,59], is utilized to calculate electron-impact excitation cross-sections that is based on the fully-relativistic distorted-wave (RDW) method. In this method, the partial electron-impact excitation cross-section from an initial ${\beta }_i{J}_i{M}_i$ state to a final ${\beta }_f{J}_f{M}_f$ state of ions is given by [60,61]:

$$\begin{array}{cc}{\sigma }_{{\epsilon }_i}({\beta }_i{J}_i{M}_i-{\beta }_f{J}_f{M}_f)=& \frac{2\pi a_0^2}{k_i^2}·\sum _{l_i,l_i^{{}^{\prime }},j_i,j_i^{{}^{\prime }},m_{s_i},l_f,j_f,m_f}\sum _{J,J^{{}^{\prime }},M}{i}^{(l_i-l_{i^{{}^{\prime }}})}{\left[(2l_i+1)(2l_i^{{}^{\prime }}+1)\right]}^{1/2}\hfill \\ & \times exp[i({\delta }_{{\kappa }_i}-{\delta }_{{\kappa }_{i^{{}^{\prime }}}})]C(l_i\frac{1}{2}{m}_{l_i}{m}_{s_i};j_i{m}_i)C(l_i^{{}^{\prime }}\frac{1}{2}{m}_{l_i^{{}^{\prime }}}{m}_{s_i};j_i^{{}^{\prime }}{m}_i)\hfill \\ & \times C(J_i{j}_i{M}_i{m}_i;JM)C(J_i{j}_i^{{}^{\prime }}{M}_i{m}_i;J^{{}^{\prime }}M)C(J_f{j}_f{M}_f{m}_f;JM)\hfill \\ \mathrm{(1)}& & \times C(J_f{j}_f{M}_f{m}_f;J^{{}^{\prime }}M)R({\gamma }_i,{\gamma }_f)R({\gamma }_i^{{}^{\prime }},{\gamma }_f^{{}^{\prime }}).\hfill \end{array}$$

Here, the subscripts i and f refer to the initial and final states, respectively; ${\epsilon }_i$ is the incident electron energy in the Rydberg; $a_0$ is the Bohr radius; $Cs$ are Clebsch–Gordan coefficients; ${\gamma }_i={\epsilon }_i{l}_i{j}_i{\beta }_i{J}_{i}JM$ and ${\gamma }_f={\epsilon }_f{l}_f{j}_f{\beta }_f{J}_{f}JM$; J and M represent the total angular momentum and its z component for the impact system, i.e., target ion plus free electron; β represents all additional quantum numbers required to specify the initial and final states of the target ion in addition to its total angular momentum J and z component M; $m_{s_i},l_i,j_i,m_{l_i}$ and $m_i$ are the spin, orbital angular momentum, total angular momentum and its z component quantum numbers, respectively, for the incident electron $e_i$; ${\delta }_{{\kappa }_i}$ is the phase factor for the continuum electron; κ is the relativistic quantum number, which is related to the orbital and total angular momentum l and j; $k_i$ is the relativistic wave number of the incident electron and given by $k_i^2={\epsilon }_i(1+{\alpha }^2{\epsilon }_i/4)$ with the fine-structure constant α. R’s denote the electron-impact excitation matrix elements, which can be represented as:

$$\begin{array}{c}\hfill R({\gamma }_i,{\gamma }_f)=\langle {\Psi }_{{\gamma }_f}|\sum _{p,q,p<q}^{\text{N}+1}(V_{Coul}+V_{Breit})|{\Psi }_{{\gamma }_i}\rangle ,\end{array}$$

(2)

in which, besides the leading Coulomb interaction, the Breit interaction is also taken into account; ${\Psi }_{{\gamma }_i}$ and ${\Psi }_{{\gamma }_f}$ are the antisymmetric $N+1$ electron wavefunctions for the initial and final states of the impact system. In the present calculations, the target state wavefunctions are generated with the use of the atomic structure package GRASP92 [62] based on the multiconfiguration Dirac–Fock (MCDF) method, and the continuum electron wavefunctions are produced with the component COWF of the RATIP package [63] by solving the coupled Dirac equation in which the exchange effect between the bound and continuum electrons is considered. To obtain accurate atomic energy levels and wavefunctions of the initial and final states, the contribution of the quantum electrodynamics effect has been taken into account. Additionally, the partial-waves of the free electron up to κ = 50 are included to ensure convergence of cross-sections in the present calculation.

For initially randomly-orientated target ions, the case of interest here, one can average over initial magnetic sub-levels $M_i$ of the target ion and then obtain the cross-section for electron-impact excitation to a specific final magnetic sub-level $M_f$,

$$\begin{array}{c}\hfill {\sigma }_{{\epsilon }_i}({\beta }_i{J}_i-{\beta }_f{J}_f{M}_f)=\frac{1}{2J_i+1}\sum _{M_i}{\sigma }_{{\epsilon }_i}({\beta }_i{J}_i{M}_i-{\beta }_f{J}_f{M}_f).\end{array}$$

(3)

The same excited state populated in the electron-impact excitation process perhaps can also be produced in the dielectronic recombination process. In this case, we are interested in the resonant capture cross-section from an initial state i to an final state i, which can be given as follows if the capture electrons are spin-unpolarized: [61]

$$\begin{array}{cc}{\sigma }_{{\epsilon }_i}^{cap}({\beta }_i{J}_i{M}_i-{\beta }_f{J}_f{M}_f)=& \frac{2\pi a_0^2}{k_{i^2}}·\sum _{l_i,l_i^{{}^{\prime }},j_i,j_i^{{}^{\prime }},m_{s_i}}{i}^{(l_i-l_i^{{}^{\prime }})}{\left[(2l_i+1)(2l_i^{{}^{\prime }}+1)\right]}^{1/2}exp[i({\delta }_{{\kappa }_i}-{\delta }_{{\kappa }_i^{{}^{\prime }}})]\hfill \\ & \times C(l_i\frac{1}{2}0m_{s_i};j_i{m}_i)C(l_i^{{}^{\prime }}\frac{1}{2}0m_{s_i};j_i^{{}^{\prime }}{m}_i)C(J_i{j}_i{M}_i{m}_i;J_f{M}_f)\hfill \\ \mathrm{(4)}& & \times C(J_i{j}_i^{{}^{\prime }}{M}_i{m}_i;J_f{M}_f)R({\gamma }_f,{\gamma }_i)R({\gamma }_f^{{}^{\prime }},{\gamma }_i^{{}^{\prime }})\delta ({\epsilon }_i-{\epsilon }_{if}),\hfill \end{array}$$

where the delta function $\delta ({\epsilon }_i-{\epsilon }_{if})$ guarantees the resonance condition of the dielectronic recombination; R’s denote the resonant capture matrix elements. Similarly, the partial resonant capture cross-section from an initial level to a particular final magnetic substate can be easily obtained by using the same route as in the case of the electron impact excitation.

2.2. Degree of Linear Polarization of Radiated X-ray Emissions

Experimentally, the degree of linear polarization for radiated X-ray emissions is defined as follows if the scattered electron is not detected [64]:

$$\begin{array}{c}\hfill P=\frac{I_{\parallel }-I_{\perp }}{I_{\parallel }+I_{\perp }},\end{array}$$

(5)

where $I_{\parallel }$ and $I_{\perp }$ denote the intensities of emitted X-ray photons with the electric vectors parallel and perpendicular to the direction of the incident electron, respectively.

In order to calculate the degree of linear polarization, we use the density matrix theory [65,66] to derive its computational formula, the particular form of which actually depends on the total angular momentum of the initial and final atomic levels related to radiated X-ray emissions. Take the $J_i=1\to J_f=0$ and $J_i=3/2\to J_f=1/2$ radiative transitions of our interest for example; the degree of linear polarization for corresponding X-ray emissions is given by [37,67]:

$$\begin{array}{c}\hfill P=\frac{{\sigma }_0-{\sigma }_1}{{\sigma }_0+{\sigma }_1},\end{array}$$

(6)

$$\begin{array}{c}\hfill P=\frac{3({\sigma }_{1/2}-{\sigma }_{3/2})}{5{\sigma }_{1/2}+3{\sigma }_{3/2}}.\end{array}$$

(7)

If we assume that the electron-impact excitation process is the dominant mechanism for populating upper magnetic substates, ${\sigma }_0$ and ${\sigma }_1$ denote the partial cross-sections for electron-impact excitation from the ground level to the magnetic substates $M_f$ = 0 and $M_f$ = 1 of the excited level, respectively. In contrast, if the dielectronic recombination process is the leading population mechanism for upper magnetic substates, ${\sigma }_0$ and ${\sigma }_1$ are the partial capture cross-sections from the ground level to the magnetic substates $M_f$ = 0 and $M_f$ = 1 of the resonant doubly-excited level, respectively. Furthermore, ${\sigma }_{1/2}$ and ${\sigma }_{3/2}$ have similar meaning in both cases of electron-impact excitation and dielectronic recombination.

2.3. Dielectronic Recombination Rate Coefficients

Apart from degree of linear polarization of X-ray emissions following electron-impact excitation and dielectronic recombination, DR rate coefficients of tungsten ions are also studied in the present work. In the isolated-resonance approximation, if we assume that the electron velocity obeys the Maxwellian distribution in plasmas, DR rate coefficients can be given by [68]:

$$\begin{array}{c}\hfill {\alpha }^{DR}\left(k{T}_e\right)={\left(\frac{2\pi {\hslash }^2}{m_{e}k{T}_e}\right)}^{3/2}\frac{g_j}{2g_i}{A}_{ji}^a{B}_{j,f}^{r}exp\left(-\frac{E_{ij}}{k{T}_e}\right).\end{array}$$

(8)

Here, $k{T}_e$ is the electron temperature, ℏ is the reduced Planck’s constant, $m_e$ is the electron mass, $g_i$ and $g_j$ denote the statistical weights of the initial and intermediate ionic states, respectively, and $E_{ij}$ represents the resonance energy. Moreover, $B_{j,f}^r$ refers to the so-called radiative branching ratio and is defined in terms of the Auger decay rate $A_{ji}^a$ and the radiative decay rate $A_{jf}^r$ as follows:

$$\begin{array}{c}\hfill B_{j,f}^r=\frac{A_{jf}^r}{{\sum }_{f^{\prime }}{A}_{j{f}^{\prime }}^r+{\sum }_{i^{\prime }}{A}_{j{i}^{\prime }}^a},\end{array}$$

(9)

where the summations over $f^{\prime }$ and $i^{\prime }$ run through all of the possible radiative and Auger final states, respectively. The Auger and radiative decay rates are given respectively by:

$$\begin{array}{c}\hfill A_{ji}^a=\frac{2\pi }{\hslash }|\langle {\Psi }_{i{\epsilon }_i}|\sum _{p,q,p<q}(V_{\mathrm{Coul}}+V_{\mathrm{Breit}})|{\Psi }_j\rangle {|}^2,\end{array}$$

(10)

$$\begin{array}{c}\hfill A_{jf}^r=\frac{4e^2\omega }{3c^3{g}_j\hslash }|\langle {\Psi }_f|T^{\left(t\right)}|{\Psi }_j\rangle {|}^2.\end{array}$$

(11)

Here, ${\Psi }_{i{\epsilon }_i}$ denotes the atomic state function (ASF) of the combined system consisting of the initial bound state i and a free electron with kinetic energy ${\epsilon }_i$; ${\Psi }_j$ and ${\Psi }_f$ the ASFs of the bound states j and f, respectively; $V_{\mathrm{Coul}}$ and $V_{\mathrm{Breit}}$ the Coulomb and Breit operators; and the summation runs over all pairs of electrons. Moreover, e and c have their usual meaning; ω denotes the photon energy; $T^{\left(t\right)}$ represents the radiative tensor operator with the multipoles t; and in the present calculations, we consider just dominant electric-dipole (E1) transitions, i.e., $t=1$. As seen from Equations (8) and (9), the computation of DR rate coefficients can be traced back to the Auger $A_{ji}^a$ and the radiative $A_{jf}^r$ decay rates of associated DR process. In order to calculate these decay rates, we here use the flexible atomic code (FAC) that is based on the relativistic configuration-interaction method [69,70]. In this method, an atomic state function is approximated by a linear combination of configuration state functions (CSFs) with the same symmetries. In addition, the CSFs are constructed as antisymmetrized products of a common basis set of orthonormal orbits that is optimized with regards to the Dirac–Coulomb Hamiltonian.

3. Results and Discussion

In the present work, we studied the linear polarization of X-ray emissions from unequally-populated magnetic sub-levels following the EIE and REC of highly charged tungsten ions. To do this, we firstly calculated the corresponding total and magnetic sub-level cross-sections. In addition, DR rate coefficients of highly charged tungsten ions have been also studied due to the importance in modeling the ionization equilibrium of tungsten plasmas.

3.1. Excitation Energies and Electron-Impact Excitation Cross-Sections

To ensure the validity of our results, the presently calculated transition energies for the $3d$ → $nf$ (n = 4, 5, 6) excitations of W${}^{46+}$–W${}^{42+}$ ions are given in Table 1 together with other available theoretical and experimental results [71,72,73]. A good agreement among them has been found within the experimental errors. The relative differences are expected to be less than 0.07% for W${}^{46+}$ and 0.17% for W${}^{45+}$. For other lower charged tungsten ions, the deviations are also kept within 0.3%. For example, the present energy is 2111.59 eV for the $3d_{5/2}$ → $4f_{7/2}$ excitation of W${}^{46+}$, compared to the experimental result $2112.2\pm 3.0$ eV and other theoretical values 2112.57 eV and 2110.20 eV. For illustrating further the reliability of the present calculations, in addition, total EIE cross-sections for the $3d_{5/2}$ → $4f_{7/2}$ and $3d_{3/2}$ → $4f_{5/2}$ excitations of W${}^{46+}$ ions are plotted in Figure 1 compared to the previous RDW results from Das et al. [72] and Zhang et al. [74], as well as the relativistic R-matrix results from Ballance et al. [27]. In all of these calculations, the contribution of the Breit interaction is taken into account, which has been proven to be very important [32,36,37,75]. As seen from the figure, the present cross-sections are a little bit smaller than other ones. Nevertheless, the results from different calculations are in good accord with each other, especially for the $3d_{5/2}$ → $4f_{7/2}$ excitation. Since the subsequent radiative transitions from these two excited levels to the ground state have the largest decay rates, the resonant contribution to these two excitations remains very small, and thus, the effect of the radiative damping caused by resonant excitations is negligible, as demonstrated in [27]. Under such an analysis, the discrepancy among different curves could be attributed mostly to the treatment of bound-state wavefunctions and energy levels before and after electron-impact excitation, i.e., atomic configurations considered to expand the relevant atomic state functions.

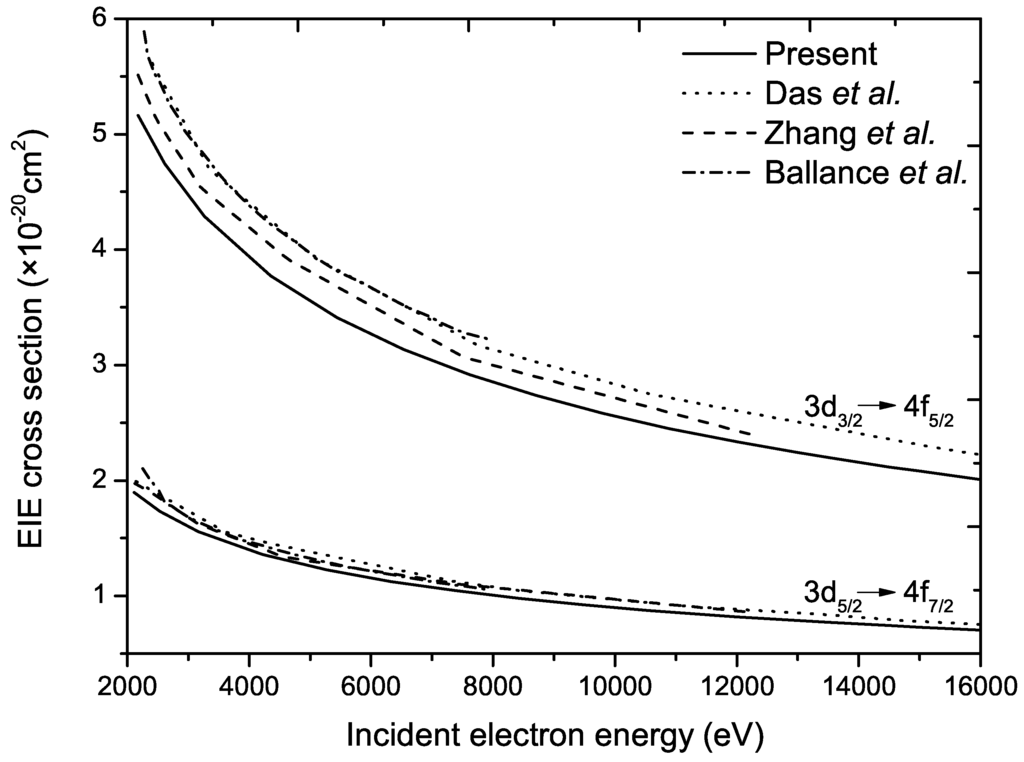
Figure 1. The presently calculated total cross-sections for the $3d_{5/2}$→$4f_{7/2}$ and $3d_{3/2}$→$4f_{5/2}$ electron-impact excitations of W${}^{46+}$ ions as a function of incident electron energy together with other available results from Das et al. [72], Zhang et al. [74] and Ballance et al. [27].

Figure 1. The presently calculated total cross-sections for the $3d_{5/2}$→$4f_{7/2}$ and $3d_{3/2}$→$4f_{5/2}$ electron-impact excitations of W${}^{46+}$ ions as a function of incident electron energy together with other available results from Das et al. [72], Zhang et al. [74] and Ballance et al. [27].

Table 1. The presently calculated excitation energies (eV) for electron-impact excitations $3d$ → $nf$ (n = 4, 5, 6) of W${}^{46+}$–W${}^{42+}$ ions together with other available theoretical and experimental results. Note that closed inner-subshells have been omitted from the upper and lower levels for the sake of brevity. Experimental errors are given in the parenthesis.

Ions	Upper Level → Lower level	Present	Theo. [71]	Theo. [72]	Exp. [73]
W${}^{46+}$	${(3d_{5/2}^{-1}4f_{7/2})}_{J=1}$→${(3d^{10})}_{J=0}$	2111.59	2112.57	$2110.20$	$2112.2(3)$
	${(3d_{3/2}^{-1}4f_{5/2})}_{J=1}$→${(3d^{10})}_{J=0}$	2179.97	2181.36	$2178.88$	$2179.7(4)$
	${(3d_{5/2}^{-1}5f_{7/2})}_{J=1}$→${(3d^{10})}_{J=0}$	2814.39		$2812.61$	2816.1(3)
	${(3d_{3/2}^{-1}5f_{5/2})}_{J=1}$→${(3d^{10})}_{J=0}$	2876.70		$2874.99$	2878.2(3)
	${(3d_{5/2}^{-1}6f_{7/2})}_{J=1}$→${(3d^{10})}_{J=0}$	3194.47		$3193.12$	3196.8(3)
	${(3d_{3/2}^{-1}6f_{5/2})}_{J=1}$→${(3d^{10})}_{J=0}$	3257.73		$3256.57$	3259.9(3)
W${}^{45+}$	${(3d_{5/2}^{-1}4s4f_{7/2})}_{J=3/2}$→${(3d^{10}4s)}_{J=1/2}$	2098.36	2094.9	$2097.57$	2094.8(5)
	${(3d_{3/2}^{-1}4s4f_{5/2})}_{J=3/2}$→${(3d^{10}4s)}_{J=1/2}$	2166.84	2169.8	$2166.07$
	${(3d_{5/2}^{-1}4s5f_{7/2})}_{J=3/2}$→${(3d^{10}4s)}_{J=1/2}$	2782.97	2783.1	$2781.62$
	${(3d_{3/2}^{-1}4s5f_{5/2})}_{J=3/2}$→${(3d^{10}4s)}_{J=1/2}$	2843.69	2844.7	$2843.41$
	${(3d_{5/2}^{-1}4s6f_{7/2})}_{J=3/2}$→${(3d^{10}4s)}_{J=1/2}$	3149.21	3151.9	$3149.69$
	${(3d_{3/2}^{-1}4s6f_{5/2})}_{J=3/2}$→${(3d^{10}4s)}_{J=1/2}$	3211.78	3214.7	$3212.49$	$3215.8(5)$
W${}^{44+}$	${(3d_{5/2}^{-1}4f_{7/2})}_{J=1}$→${(3d^{10}4s^2)}_{J=0}$	2085.38	2082.6	$2084.35$	2082.2(4)
	${(3d_{3/2}^{-1}4f_{5/2})}_{J=1}$→${(3d^{10}4s^2)}_{J=0}$	2152.70	2159.0	$2152.04$
	${(3d_{5/2}^{-1}5f_{7/2})}_{J=1}$→${(3d^{10}4s^2)}_{J=0}$	2751.51	2750.2	$2749.98$	2750.3(10)
	${(3d_{3/2}^{-1}5f_{5/2})}_{J=1}$→${(3d^{10}4s^2)}_{J=0}$	2813.45	2811.6
	${(3d_{5/2}^{-1}6f_{7/2})}_{J=1}$→${(3d^{10}4s^2)}_{J=0}$	3104.45	3107.9	$3105.54$	3107.8(5)
	${(3d_{3/2}^{-1}6f_{5/2})}_{J=1}$→${(3d^{10}4s^2)}_{J=0}$	3167.36	3171.0	$3168.62$	3171.2(6)
W${}^{43+}$	${(3d_{5/2}^{-1}4p_{1/2}4f_{7/2})}_{J=3/2}$→${(3d^{10}4p_{1/2})}_{J=1/2}$	2067.96
	${(3d_{3/2}^{-1}4p_{1/2}4f_{5/2})}_{J=3/2}$→${(3d^{10}4p_{1/2})}_{J=1/2}$	2136.12	2140.3
	${(3d_{5/2}^{-1}4p_{1/2}5f_{7/2})}_{J=3/2}$→${(3d^{10}4p_{1/2})}_{J=1/2}$	2715.49	2718.1
	${(3d_{3/2}^{-1}4p_{1/2}5f_{5/2})}_{J=3/2}$→${(3d^{10}4p_{1/2})}_{J=1/2}$	2780.92	2781.1
	${(3d_{5/2}^{-1}4p_{1/2}6f_{7/2})}_{J=3/2}$→${(3d^{10}4p_{1/2})}_{J=1/2}$	3060.51	3062.1
	${(3d_{3/2}^{-1}4p_{1/2}6f_{5/2})}_{J=3/2}$→${(3d^{10}4p_{1/2})}_{J=1/2}$	3124.77	3126.7
W${}^{42+}$	${(3d_{5/2}^{-1}4p_{1/2}^{2}4f_{7/2})}_{J=1}$→${(3d^{10}4p_{1/2}^2)}_{J=0}$	2054.00
	${(3d_{3/2}^{-1}4p_{1/2}^{2}4f_{5/2})}_{J=1}$→${(3d^{10}4p_{1/2}^2)}_{J=0}$	2119.98
	${(3d_{5/2}^{-1}4p_{1/2}^{2}5f_{7/2})}_{J=1}$→${(3d^{10}4p_{1/2}^2)}_{J=0}$	2683.09
	${(3d_{3/2}^{-1}4p_{1/2}^{2}5f_{5/2})}_{J=1}$→${(3d^{10}4p_{1/2}^2)}_{J=0}$	2748.89
	${(3d_{5/2}^{-1}4p_{1/2}^{2}6f_{7/2})}_{J=1}$→${(3d^{10}4p_{1/2}^2)}_{J=0}$	3016.27
	${(3d_{3/2}^{-1}4p_{1/2}^{2}6f_{5/2})}_{J=1}$→${(3d^{10}4p_{1/2}^2)}_{J=0}$	3080.31

Table 1. The presently calculated excitation energies (eV) for electron-impact excitations $3d$ → $nf$ (n = 4, 5, 6) of W${}^{46+}$–W${}^{42+}$ ions together with other available theoretical and experimental results. Note that closed inner-subshells have been omitted from the upper and lower levels for the sake of brevity. Experimental errors are given in the parenthesis.

Ions	Upper Level → Lower level	Present	Theo. [71]	Theo. [72]	Exp. [73]
W${}^{46+}$	${(3d_{5/2}^{-1}4f_{7/2})}_{J=1}$→${(3d^{10})}_{J=0}$	2111.59	2112.57	$2110.20$	$2112.2(3)$
	${(3d_{3/2}^{-1}4f_{5/2})}_{J=1}$→${(3d^{10})}_{J=0}$	2179.97	2181.36	$2178.88$	$2179.7(4)$
	${(3d_{5/2}^{-1}5f_{7/2})}_{J=1}$→${(3d^{10})}_{J=0}$	2814.39		$2812.61$	2816.1(3)
	${(3d_{3/2}^{-1}5f_{5/2})}_{J=1}$→${(3d^{10})}_{J=0}$	2876.70		$2874.99$	2878.2(3)
	${(3d_{5/2}^{-1}6f_{7/2})}_{J=1}$→${(3d^{10})}_{J=0}$	3194.47		$3193.12$	3196.8(3)
	${(3d_{3/2}^{-1}6f_{5/2})}_{J=1}$→${(3d^{10})}_{J=0}$	3257.73		$3256.57$	3259.9(3)
W${}^{45+}$	${(3d_{5/2}^{-1}4s4f_{7/2})}_{J=3/2}$→${(3d^{10}4s)}_{J=1/2}$	2098.36	2094.9	$2097.57$	2094.8(5)
	${(3d_{3/2}^{-1}4s4f_{5/2})}_{J=3/2}$→${(3d^{10}4s)}_{J=1/2}$	2166.84	2169.8	$2166.07$
	${(3d_{5/2}^{-1}4s5f_{7/2})}_{J=3/2}$→${(3d^{10}4s)}_{J=1/2}$	2782.97	2783.1	$2781.62$
	${(3d_{3/2}^{-1}4s5f_{5/2})}_{J=3/2}$→${(3d^{10}4s)}_{J=1/2}$	2843.69	2844.7	$2843.41$
	${(3d_{5/2}^{-1}4s6f_{7/2})}_{J=3/2}$→${(3d^{10}4s)}_{J=1/2}$	3149.21	3151.9	$3149.69$
	${(3d_{3/2}^{-1}4s6f_{5/2})}_{J=3/2}$→${(3d^{10}4s)}_{J=1/2}$	3211.78	3214.7	$3212.49$	$3215.8(5)$
W${}^{44+}$	${(3d_{5/2}^{-1}4f_{7/2})}_{J=1}$→${(3d^{10}4s^2)}_{J=0}$	2085.38	2082.6	$2084.35$	2082.2(4)
	${(3d_{3/2}^{-1}4f_{5/2})}_{J=1}$→${(3d^{10}4s^2)}_{J=0}$	2152.70	2159.0	$2152.04$
	${(3d_{5/2}^{-1}5f_{7/2})}_{J=1}$→${(3d^{10}4s^2)}_{J=0}$	2751.51	2750.2	$2749.98$	2750.3(10)
	${(3d_{3/2}^{-1}5f_{5/2})}_{J=1}$→${(3d^{10}4s^2)}_{J=0}$	2813.45	2811.6
	${(3d_{5/2}^{-1}6f_{7/2})}_{J=1}$→${(3d^{10}4s^2)}_{J=0}$	3104.45	3107.9	$3105.54$	3107.8(5)
	${(3d_{3/2}^{-1}6f_{5/2})}_{J=1}$→${(3d^{10}4s^2)}_{J=0}$	3167.36	3171.0	$3168.62$	3171.2(6)
W${}^{43+}$	${(3d_{5/2}^{-1}4p_{1/2}4f_{7/2})}_{J=3/2}$→${(3d^{10}4p_{1/2})}_{J=1/2}$	2067.96
	${(3d_{3/2}^{-1}4p_{1/2}4f_{5/2})}_{J=3/2}$→${(3d^{10}4p_{1/2})}_{J=1/2}$	2136.12	2140.3
	${(3d_{5/2}^{-1}4p_{1/2}5f_{7/2})}_{J=3/2}$→${(3d^{10}4p_{1/2})}_{J=1/2}$	2715.49	2718.1
	${(3d_{3/2}^{-1}4p_{1/2}5f_{5/2})}_{J=3/2}$→${(3d^{10}4p_{1/2})}_{J=1/2}$	2780.92	2781.1
	${(3d_{5/2}^{-1}4p_{1/2}6f_{7/2})}_{J=3/2}$→${(3d^{10}4p_{1/2})}_{J=1/2}$	3060.51	3062.1
	${(3d_{3/2}^{-1}4p_{1/2}6f_{5/2})}_{J=3/2}$→${(3d^{10}4p_{1/2})}_{J=1/2}$	3124.77	3126.7
W${}^{42+}$	${(3d_{5/2}^{-1}4p_{1/2}^{2}4f_{7/2})}_{J=1}$→${(3d^{10}4p_{1/2}^2)}_{J=0}$	2054.00
	${(3d_{3/2}^{-1}4p_{1/2}^{2}4f_{5/2})}_{J=1}$→${(3d^{10}4p_{1/2}^2)}_{J=0}$	2119.98
	${(3d_{5/2}^{-1}4p_{1/2}^{2}5f_{7/2})}_{J=1}$→${(3d^{10}4p_{1/2}^2)}_{J=0}$	2683.09
	${(3d_{3/2}^{-1}4p_{1/2}^{2}5f_{5/2})}_{J=1}$→${(3d^{10}4p_{1/2}^2)}_{J=0}$	2748.89
	${(3d_{5/2}^{-1}4p_{1/2}^{2}6f_{7/2})}_{J=1}$→${(3d^{10}4p_{1/2}^2)}_{J=0}$	3016.27
	${(3d_{3/2}^{-1}4p_{1/2}^{2}6f_{5/2})}_{J=1}$→${(3d^{10}4p_{1/2}^2)}_{J=0}$	3080.31

Up to now, we are ready to study electron-impact excitation of highly charged tungsten ions. In this part, we focus on the excitations $3d_{3/2}$ → $n{f}_{5/2}$ and $3d_{5/2}$ → $n{f}_{7/2}$ (n = 4, 5, 6) of W${}^{46+}$–W${}^{42+}$ ions that can subsequently give rise to very strong X-ray emissions. Since W${}^{42+,44+,46+}$ ions have a similar shell structure and this is also true for W${}^{43+,45+}$ ions, only W${}^{43+}$ and W${}^{42+}$ ions are taken here as examples. In Figure 2, the calculated total and magnetic sub-level cross-sections for the excitations $3d$ → $nf$ (n = 4, 5, 6) of W${}^{42+}$ and W${}^{43+}$ ions are given as a function of incident electron energy. Take the excitations $3d_{3/2}$ → $4f_{5/2}$ and $3d_{5/2}$ → $4f_{7/2}$ of W${}^{42+}$ for example; the total cross-sections decrease with increasing incident electron energy, and it behaves more sensitively to less-energetic electron collisions than to energetic ones. With respect to the magnetic sub-levels, the partial cross-sections for electron-impact excitation to the $M_f=0$ substate are significantly larger than the ones to the $M_f=\pm 1$ states. This indicates that the magnetic sub-level $M_f=0$ is preferentially populated in the electron-impact excitation process. Similarly, the same characteristics can be summarized for the $3d$ → $5f$ and $3d$ → $6f$ excitations. In addition, for W${}^{43+}$ ions, the cross-sections for electron-impact excitations to the $M_f$ = $\pm 1/2$ substates are larger than the ones to the $M_f$ = $\pm 3/2$ and $M_f$ = $\mp 1/2$ substates, and the magnetic sub-level cross-sections for the $M_f$ = $\mp 1/2$ substates are much smaller at all given incident electron energies. Since the magnetic sub-level cross-sections for excitation to the $M_f$ = $\mp 3/2$ substates are negligibly smaller than others by four orders of magnitude, they are not plotted in the figure.

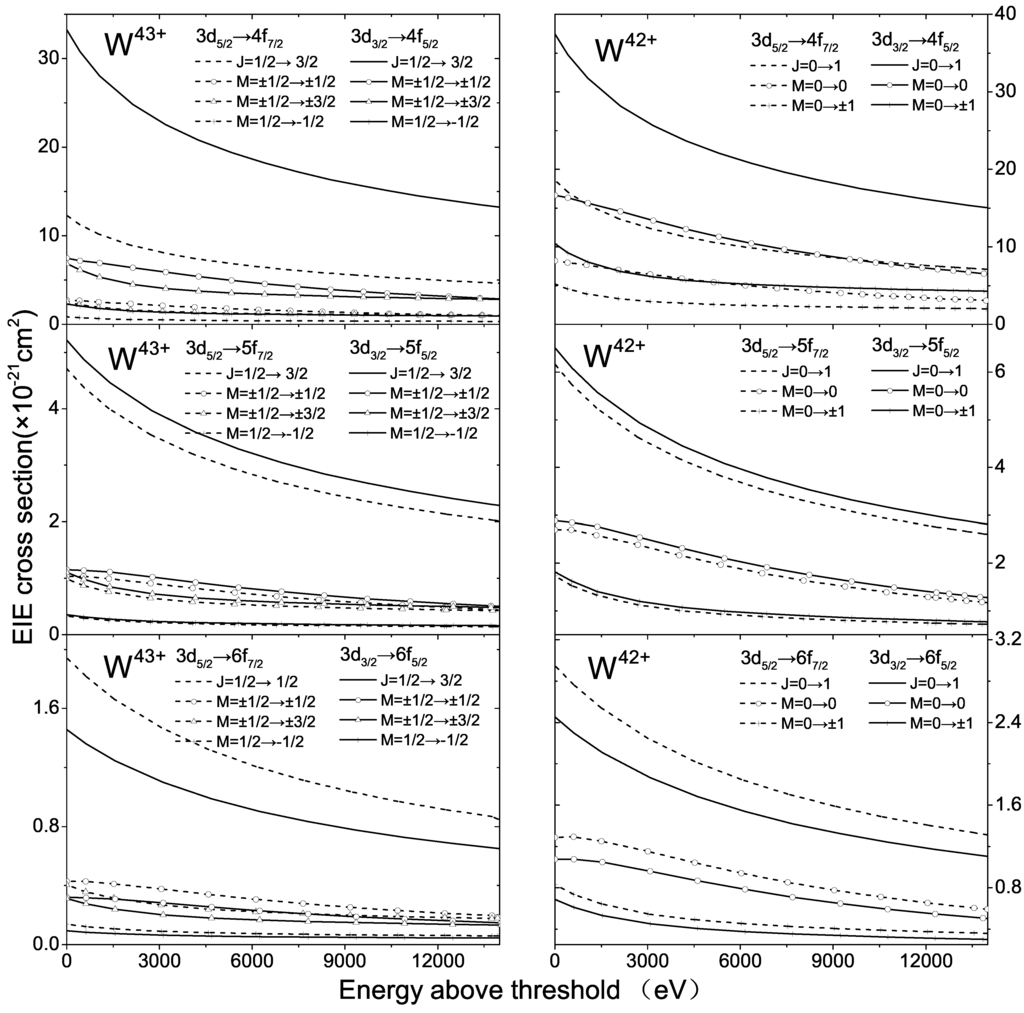
Figure 2. The presently calculated total and magnetic sub-level cross-sections for electron-impact excitations $3d_{3/2}$ → $n{f}_{5/2}$ and $3d_{5/2}$ → $n{f}_{7/2}$ (n = 4, 5, 6) of W${}^{43+}$ (left panel) and W${}^{42+}$ (right panel) ions as a function of incident electron energy.

Figure 2. The presently calculated total and magnetic sub-level cross-sections for electron-impact excitations $3d_{3/2}$ → $n{f}_{5/2}$ and $3d_{5/2}$ → $n{f}_{7/2}$ (n = 4, 5, 6) of W${}^{43+}$ (left panel) and W${}^{42+}$ (right panel) ions as a function of incident electron energy.

3.2. Resonant Energies and Resonant Electron Capture Cross-Sections

Besides the electron-impact excitation processes, the resonant electron capture can also populate those excited levels that subsequently give rise to the same X-ray emissions. In Table 2, for W${}^{45+}$–W${}^{42+}$ final ions, we identify some of possible population processes and show the associated resonant energies, as well as total and magnetic sub-level REC cross-sections. As seen from the table, only the doubly-excited $3d^{-1}4lnf$ ($l=s,p;n=5,6$) levels are considered compared to the case of the electron-impact excitations. The $3d^{-1}4s4f$ and $3d^{-1}4p4f$ excited levels are not included, since they are not auto-ionizing states of W${}^{45+}$–W${}^{42+}$ final ions. For a given n ($n=5,6$), the $n{f}_{5/2}$ resonant energies are greater than the $n{f}_{7/2}$ ones, and the differences are approximately 63 eV and 65 eV for each n, respectively. Moreover, ${\sigma }_{M=i\to f}$ in the table represents magnetic sub-level cross-sections for REC to the $M_f$ final substate from the $M_i$ initial substate. The same as in electron-impact excitation, the magnetic sub-levels here are not populated statistically. Note that the REC channels with $|M_i-M_f|>1$ are forbidden due to selection rules of angular momentum as shown by ${\sigma }_{M=\pm 1/2\to \mp 1}=0$ and ${\sigma }_{M=0\to \pm 3/2}=0$. Finally, the resonant electron capture processes give rise to larger total and magnetic sub-level cross-sections, compared to the case of electron-impact excitations at almost all given incident electron energies.

Table 2. The presently calculated resonant energies (eV), as well as total and magnetic sub-level cross-sections (${10}^{-20}$ cm${}^2$) for resonant $nf$ ($n=5,6$) electron captures of final W${}^{45+}$–W${}^{42+}$ ions. Note that closed inner-subshells have been omitted from the initial and final levels for the sake of brevity.

Ions	Initial Level → Final Level	$\Delta E$	Magnetic Sub-level CS${\sigma }_{M=i\to f}$			Total CS
W${}^{45+}$			${\sigma }_{0\to \pm 1/2}$	${\sigma }_{0\to \pm 3/2}$
	${(3d^{10})}_{J=0}$→${(3d_{5/2}^{-1}4s5f_{7/2})}_{J=3/2}$	363.89	21.1	0		42.2
	${(3d^{10})}_{J=0}$→${(3d_{3/2}^{-1}4s5f_{5/2})}_{J=3/2}$	425.39	28.0	0		56.0
	${(3d^{10})}_{J=0}$→${(3d_{5/2}^{-1}4s6f_{7/2})}_{J=3/2}$	732.42	5.12	0		10.2
	${(3d^{10})}_{J=0}$→${(3d_{3/2}^{-1}4s6f_{5/2})}_{J=3/2}$	794.99	5.97	0		11.9
W${}^{44+}$			${\sigma }_{\pm 1/2\to 0}$	${\sigma }_{\pm 1/2\to \mp 1}$	${\sigma }_{\pm 1/2\to \pm 1}$
	${(3d^{10}4s)}_{J=1/2}$→${(3d_{5/2}^{-1}5f_{7/2})}_{J=1}$	398.44	11.8	0	0.26	12.1
	${(3d^{10}4s)}_{J=1/2}$→${(3d_{3/2}^{-1}5f_{5/2})}_{J=1}$	460.17	12.9	0	1.19	14.1
	${(3d^{10}4s)}_{J=1/2}$→${(3d_{5/2}^{-1}6f_{7/2})}_{J=1}$	754.40	3.02	0	0.10	3.12
	${(3d^{10}4s)}_{J=1/2}$→${(3d_{3/2}^{-1}6f_{5/2})}_{J=1}$	817.30	2.79	0	0.34	3.16
W${}^{43+}$			${\sigma }_{0\to \pm 1/2}$	${\sigma }_{0\to \pm 3/2}$
	${(3d^{10}4s^2)}_{J=0}$→${(3d_{5/2}^{-1}4p_{1/2}5f_{7/2})}_{J=3/2}$	513.23	1.06	0		2.12
	${(3d^{10}4s^2)}_{J=0}$→${(3d_{3/2}^{-1}4p_{1/2}5f_{5/2})}_{J=3/2}$	575.84	0.64	0		1.28
	${(3d^{10}4s^2)}_{J=0}$→${(3d_{5/2}^{-1}4p_{1/2}6f_{7/2})}_{J=3/2}$	856.78	0.10	0		0.20
	${(3d^{10}4s^2)}_{J=0}$→${(3d_{3/2}^{-1}4p_{1/2}6f_{5/2})}_{J=3/2}$	921.03	0.01	0		0.02
W${}^{42+}$			${\sigma }_{\pm 1/2\to 0}$	${\sigma }_{\pm 1/2\to \mp 1}$	${\sigma }_{\pm 1/2\to \pm 1}$
	${(3d^{10}4p_{1/2})}_{J=1/2}$→${(3d_{5/2}^{-1}4p_{1/2}^{2}5f_{7/2})}_{J=1}$	536.81	2.53	0	1.11	3.64
	${(3d^{10}4p_{1/2})}_{J=1/2}$→${(3d_{3/2}^{-1}4p_{1/2}^{2}5f_{5/2})}_{J=1}$	598.89	3.00	0	2.08	5.08
	${(3d^{10}4p_{1/2})}_{J=1/2}$→${(3d_{5/2}^{-1}4p_{1/2}^{2}6f_{7/2})}_{J=1}$	868.14	0.69	0	0.56	1.24
	${(3d^{10}4p_{1/2})}_{J=1/2}$→${(3d_{3/2}^{-1}4p_{1/2}^{2}6f_{5/2})}_{J=1}$	931.56	0.68	0	0.85	1.53

Table 2. The presently calculated resonant energies (eV), as well as total and magnetic sub-level cross-sections (${10}^{-20}$ cm${}^2$) for resonant $nf$ ($n=5,6$) electron captures of final W${}^{45+}$–W${}^{42+}$ ions. Note that closed inner-subshells have been omitted from the initial and final levels for the sake of brevity.

Ions	Initial Level → Final Level	$\Delta E$	Magnetic Sub-level CS${\sigma }_{M=i\to f}$			Total CS
W${}^{45+}$			${\sigma }_{0\to \pm 1/2}$	${\sigma }_{0\to \pm 3/2}$
	${(3d^{10})}_{J=0}$→${(3d_{5/2}^{-1}4s5f_{7/2})}_{J=3/2}$	363.89	21.1	0		42.2
	${(3d^{10})}_{J=0}$→${(3d_{3/2}^{-1}4s5f_{5/2})}_{J=3/2}$	425.39	28.0	0		56.0
	${(3d^{10})}_{J=0}$→${(3d_{5/2}^{-1}4s6f_{7/2})}_{J=3/2}$	732.42	5.12	0		10.2
	${(3d^{10})}_{J=0}$→${(3d_{3/2}^{-1}4s6f_{5/2})}_{J=3/2}$	794.99	5.97	0		11.9
W${}^{44+}$			${\sigma }_{\pm 1/2\to 0}$	${\sigma }_{\pm 1/2\to \mp 1}$	${\sigma }_{\pm 1/2\to \pm 1}$
	${(3d^{10}4s)}_{J=1/2}$→${(3d_{5/2}^{-1}5f_{7/2})}_{J=1}$	398.44	11.8	0	0.26	12.1
	${(3d^{10}4s)}_{J=1/2}$→${(3d_{3/2}^{-1}5f_{5/2})}_{J=1}$	460.17	12.9	0	1.19	14.1
	${(3d^{10}4s)}_{J=1/2}$→${(3d_{5/2}^{-1}6f_{7/2})}_{J=1}$	754.40	3.02	0	0.10	3.12
	${(3d^{10}4s)}_{J=1/2}$→${(3d_{3/2}^{-1}6f_{5/2})}_{J=1}$	817.30	2.79	0	0.34	3.16
W${}^{43+}$			${\sigma }_{0\to \pm 1/2}$	${\sigma }_{0\to \pm 3/2}$
	${(3d^{10}4s^2)}_{J=0}$→${(3d_{5/2}^{-1}4p_{1/2}5f_{7/2})}_{J=3/2}$	513.23	1.06	0		2.12
	${(3d^{10}4s^2)}_{J=0}$→${(3d_{3/2}^{-1}4p_{1/2}5f_{5/2})}_{J=3/2}$	575.84	0.64	0		1.28
	${(3d^{10}4s^2)}_{J=0}$→${(3d_{5/2}^{-1}4p_{1/2}6f_{7/2})}_{J=3/2}$	856.78	0.10	0		0.20
	${(3d^{10}4s^2)}_{J=0}$→${(3d_{3/2}^{-1}4p_{1/2}6f_{5/2})}_{J=3/2}$	921.03	0.01	0		0.02
W${}^{42+}$			${\sigma }_{\pm 1/2\to 0}$	${\sigma }_{\pm 1/2\to \mp 1}$	${\sigma }_{\pm 1/2\to \pm 1}$
	${(3d^{10}4p_{1/2})}_{J=1/2}$→${(3d_{5/2}^{-1}4p_{1/2}^{2}5f_{7/2})}_{J=1}$	536.81	2.53	0	1.11	3.64
	${(3d^{10}4p_{1/2})}_{J=1/2}$→${(3d_{3/2}^{-1}4p_{1/2}^{2}5f_{5/2})}_{J=1}$	598.89	3.00	0	2.08	5.08
	${(3d^{10}4p_{1/2})}_{J=1/2}$→${(3d_{5/2}^{-1}4p_{1/2}^{2}6f_{7/2})}_{J=1}$	868.14	0.69	0	0.56	1.24
	${(3d^{10}4p_{1/2})}_{J=1/2}$→${(3d_{3/2}^{-1}4p_{1/2}^{2}6f_{5/2})}_{J=1}$	931.56	0.68	0	0.85	1.53

3.3. Degrees of Linear Polarization of Subsequently Radiated X-Ray Emissions

Once we obtain the magnetic sub-level cross-sections (i.e., the relative populations) of excited levels, the degree of linear polarization of X-ray emissions radiated from these levels can be calculated by using Equations (6) and (7). In Figure 3, we show the degrees of linear polarization of X-ray emissions following the $3d$ → $nf$ ($n=4,5,6$) electron-impact excitations of W${}^{43+}$ and W${}^{42+}$ ions just as examples. Again, the results for W${}^{46+}$–W${}^{44+}$ ions are not given here owing to very similar characteristics shown in the figure. As seen clearly, the X-ray emissions are strongly linearly polarized and possess positive degrees of polarization, which means that these X-rays are preferentially emitted perpendicular to the direction of incident electrons. Besides, these X-ray emissions have very similar polarization behaviors with respect to incident electron energy. As the incident electrons move more energetically, at first, the X-ray emissions become more linearly polarized up to a maximum degree at approximately 2.5-times their excitation thresholds, and then, a depolarization of X-ray emissions occurs at higher electron energies. For example, such a maximum degree reaches 0.20 and 0.37 for the $3d_{5/2}$ → $4f_{7/2}$ excitations of W${}^{43+}$ and W${}^{42+}$ ions, respectively.

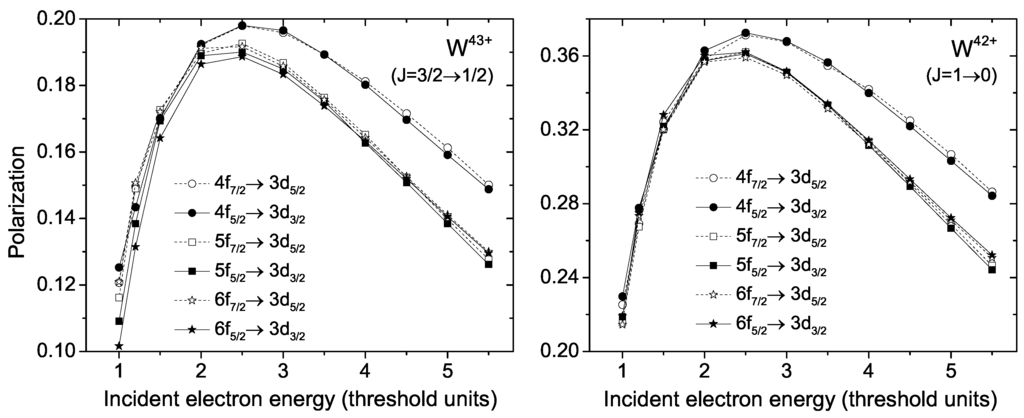
Figure 3. The presently calculated degrees of linear polarization of X-ray emissions following electron-impact excitations $3d$ → $nf$ ($n=4,5,6$) of W${}^{43+}$ (left panel) and W${}^{42+}$ (right panel) ions as a function of incident electron energy.

Figure 3. The presently calculated degrees of linear polarization of X-ray emissions following electron-impact excitations $3d$ → $nf$ ($n=4,5,6$) of W${}^{43+}$ (left panel) and W${}^{42+}$ (right panel) ions as a function of incident electron energy.

Besides degrees of linear polarization of X-ray emissions following the electron-impact excitation, linear polarizations of X-ray emissions following the resonant electron capture are also studied, as shown in Table 3. It has been found that the degrees of linear polarization of these X-rays are totally different for different charged tungsten ions, compared to the case of the electron-impact excitations. For W${}^{45+}$ and W${}^{43+}$ ions, the degrees of linear polarization of all involved X-ray emissions give rise to exactly 0.6, since the cross-section ${\sigma }_{0\to \pm 3/2}$ for resonant electron capture to the $M_f$ = 3/2 magnetic substate is equal to zero, as discussed above. However, for W${}^{44+}$ and W${}^{42+}$ ions, they show different stories of interest. For example, the X-ray emissions from W${}^{44+}$ ions exhibit an extremely strong degree of linear polarization that reaches above 0.9. In contrast, much lesser, but still strong linearly polarized X-ray emissions are obtained for W${}^{42+}$ tungsten ions. Moreover, the linear polarizations of the $n{f}_{7/2}$ → $3d_{5/2}$ (n = 5, 6) X-ray emissions are obviously stronger than the ones of the $n{f}_{5/2}$ → $3d_{3/2}$ emissions in the case of W${}^{42+}$ and W${}^{44+}$ ions.

Table 3. The presently calculated degrees of linear polarization of X-ray emissions following resonant $nf$ ($n=5,6$) electron captures of final W${}^{45+}$–W${}^{42+}$ ions. Note that closed inner-subshells have been omitted from the initial and final levels of the radiative transitions for the sake of brevity.

Ions	Transitions	Polarization
W${}^{45+}$	${(3d_{5/2}^{-1}4s5f_{7/2})}_{J=3/2}$ → ${(3d^{10}4s)}_{J=1/2}$	0.60
	${(3d_{3/2}^{-1}4s5f_{5/2})}_{J=3/2}$ → ${(3d^{10}4s)}_{J=1/2}$	0.60
	${(3d_{5/2}^{-1}4s6f_{7/2})}_{J=3/2}$ → ${(3d^{10}4s)}_{J=1/2}$	0.60
	${(3d_{3/2}^{-1}4s6f_{5/2})}_{J=3/2}$ → ${(3d^{10}4s)}_{J=1/2}$	0.60
W${}^{44+}$	${(3d_{5/2}^{-1}4s^{2}5f_{7/2})}_{J=1}$ → ${(3d^{10}4s^2)}_{J=0}$	0.98
	${(3d_{3/2}^{-1}4s^{2}5f_{5/2})}_{J=1}$ → ${(3d^{10}4s^2)}_{J=0}$	0.91
	${(3d_{5/2}^{-1}4s^{2}6f_{7/2})}_{J=1}$ → ${(3d^{10}4s^2)}_{J=0}$	0.97
	${(3d_{3/2}^{-1}4s^{2}6f_{5/2})}_{J=1}$ → ${(3d^{10}4s^2)}_{J=0}$	0.89
W${}^{43+}$	${(3d_{5/2}^{-1}4s^{2}4p_{1/2}5f_{7/2})}_{J=3/2}$ → ${(3d^{10}4s^{2}4p_{1/2})}_{J=1/2}$	0.60
	${(3d_{3/2}^{-1}4s^{2}4p_{1/2}5f_{5/2})}_{J=3/2}$ → ${(3d^{10}4s^{2}4p_{1/2})}_{J=1/2}$	0.60
	${(3d_{5/2}^{-1}4s^{2}4p_{1/2}6f_{7/2})}_{J=3/2}$ → ${(3d^{10}4s^{2}4p_{1/2})}_{J=1/2}$	0.60
	${(3d_{3/2}^{-1}4s^{2}4p_{1/2}6f_{5/2})}_{J=3/2}$ → ${(3d^{10}4s^{2}4p_{1/2})}_{J=1/2}$	0.60
W${}^{42+}$	${(3d_{5/2}^{-1}4s^{2}4p_{1/2}^{2}5f_{7/2})}_{J=1}$ → ${(3d^{10}4s^{2}4p_{1/2}^2)}_{J=0}$	0.64
	${(3d_{3/2}^{-1}4s^{2}4p_{1/2}^{2}5f_{5/2})}_{J=1}$ → ${(3d^{10}4s^{2}4p_{1/2}^2)}_{J=0}$	0.49
	${(3d_{5/2}^{-1}4s^{2}4p_{1/2}^{2}6f_{7/2})}_{J=1}$ → ${(3d^{10}4s^{2}4p_{1/2}^2)}_{J=0}$	0.42
	${(3d_{3/2}^{-1}4s^{2}4p_{1/2}^{2}6f_{5/2})}_{J=1}$ → ${(3d^{10}4s^{2}4p_{1/2}^2)}_{J=0}$	0.23

Table 3. The presently calculated degrees of linear polarization of X-ray emissions following resonant $nf$ ($n=5,6$) electron captures of final W${}^{45+}$–W${}^{42+}$ ions. Note that closed inner-subshells have been omitted from the initial and final levels of the radiative transitions for the sake of brevity.

Ions	Transitions	Polarization
W${}^{45+}$	${(3d_{5/2}^{-1}4s5f_{7/2})}_{J=3/2}$ → ${(3d^{10}4s)}_{J=1/2}$	0.60
	${(3d_{3/2}^{-1}4s5f_{5/2})}_{J=3/2}$ → ${(3d^{10}4s)}_{J=1/2}$	0.60
	${(3d_{5/2}^{-1}4s6f_{7/2})}_{J=3/2}$ → ${(3d^{10}4s)}_{J=1/2}$	0.60
	${(3d_{3/2}^{-1}4s6f_{5/2})}_{J=3/2}$ → ${(3d^{10}4s)}_{J=1/2}$	0.60
W${}^{44+}$	${(3d_{5/2}^{-1}4s^{2}5f_{7/2})}_{J=1}$ → ${(3d^{10}4s^2)}_{J=0}$	0.98
	${(3d_{3/2}^{-1}4s^{2}5f_{5/2})}_{J=1}$ → ${(3d^{10}4s^2)}_{J=0}$	0.91
	${(3d_{5/2}^{-1}4s^{2}6f_{7/2})}_{J=1}$ → ${(3d^{10}4s^2)}_{J=0}$	0.97
	${(3d_{3/2}^{-1}4s^{2}6f_{5/2})}_{J=1}$ → ${(3d^{10}4s^2)}_{J=0}$	0.89
W${}^{43+}$	${(3d_{5/2}^{-1}4s^{2}4p_{1/2}5f_{7/2})}_{J=3/2}$ → ${(3d^{10}4s^{2}4p_{1/2})}_{J=1/2}$	0.60
	${(3d_{3/2}^{-1}4s^{2}4p_{1/2}5f_{5/2})}_{J=3/2}$ → ${(3d^{10}4s^{2}4p_{1/2})}_{J=1/2}$	0.60
	${(3d_{5/2}^{-1}4s^{2}4p_{1/2}6f_{7/2})}_{J=3/2}$ → ${(3d^{10}4s^{2}4p_{1/2})}_{J=1/2}$	0.60
	${(3d_{3/2}^{-1}4s^{2}4p_{1/2}6f_{5/2})}_{J=3/2}$ → ${(3d^{10}4s^{2}4p_{1/2})}_{J=1/2}$	0.60
W${}^{42+}$	${(3d_{5/2}^{-1}4s^{2}4p_{1/2}^{2}5f_{7/2})}_{J=1}$ → ${(3d^{10}4s^{2}4p_{1/2}^2)}_{J=0}$	0.64
	${(3d_{3/2}^{-1}4s^{2}4p_{1/2}^{2}5f_{5/2})}_{J=1}$ → ${(3d^{10}4s^{2}4p_{1/2}^2)}_{J=0}$	0.49
	${(3d_{5/2}^{-1}4s^{2}4p_{1/2}^{2}6f_{7/2})}_{J=1}$ → ${(3d^{10}4s^{2}4p_{1/2}^2)}_{J=0}$	0.42
	${(3d_{3/2}^{-1}4s^{2}4p_{1/2}^{2}6f_{5/2})}_{J=1}$ → ${(3d^{10}4s^{2}4p_{1/2}^2)}_{J=0}$	0.23

Such huge differences in linear polarization of X-ray emissions following electron-impact excitation and resonant electron capture processes provide us a new possibility of distinguishing and identifying the population mechanism of these emissions. Further, particular plasma conditions can be also assessed by measuring linear polarization of associated X-ray emissions. For instance, electron-impact excitation would play very important roles in hot and dense plasmas, while resonant electron capture would dominate in low density plasmas that are cooled and recombining by capturing free electrons.

3.4. Dielectronic Recombination Rate Coefficients

Another part of the present work is the calculations of DR rate coefficients for highly charged tungsten ions with the purpose of tungsten plasma modeling. Before discussing these rate coefficients, we start with the comparison of DR cross-sections as shown in Figure 4 for the $3d^{10}+e^{-}\to 3d^{9}4l4l^{\prime }\to 3d^{10}4l^{″}+h\nu$ processes of W${}^{46+}$ ions to illustrate the reliability of the present calculations. A very good agreement between the present cross-sections and other available results [29] was found, especially at high electron energies. As seen from the figure, in the given electron energy range, there are many DR channels with different cross-sections, which all contribute to associated DR rate coefficients. Moreover, we also compared total DR rate coefficients of W${}^{37+}$ ions, as shown in Figure 5, with other available results from the ADAS database [76], which is being used currently for the modeling and diagnosis of the tokamak plasmas in the fusion community. The OPEN-ADAS data are scaled from the ADPAK by adjusting empirically the recombination rates to match measurements of radiated power in the ASDEX Upgrade, while the ADAS-Type B rate coefficients are obtained from another ADAS formulation for DR, i.e., Burgess Type B [51,52,53]. As seen from the figure, the present DR rate coefficients match the OPEN-ADAS data very well at high electron temperatures, while at low ones, the three sets of rate coefficients differ from each other. Furthermore, the present rate coefficients are similar in tendency to the results of the ADAS-Type B, but with a factor of two difference in magnitude at the electron temperatures above 2 eV. Much smaller total rate coefficients of the ADAS-Type B at low temperatures result from the omission of some configurations in the calculations [76].

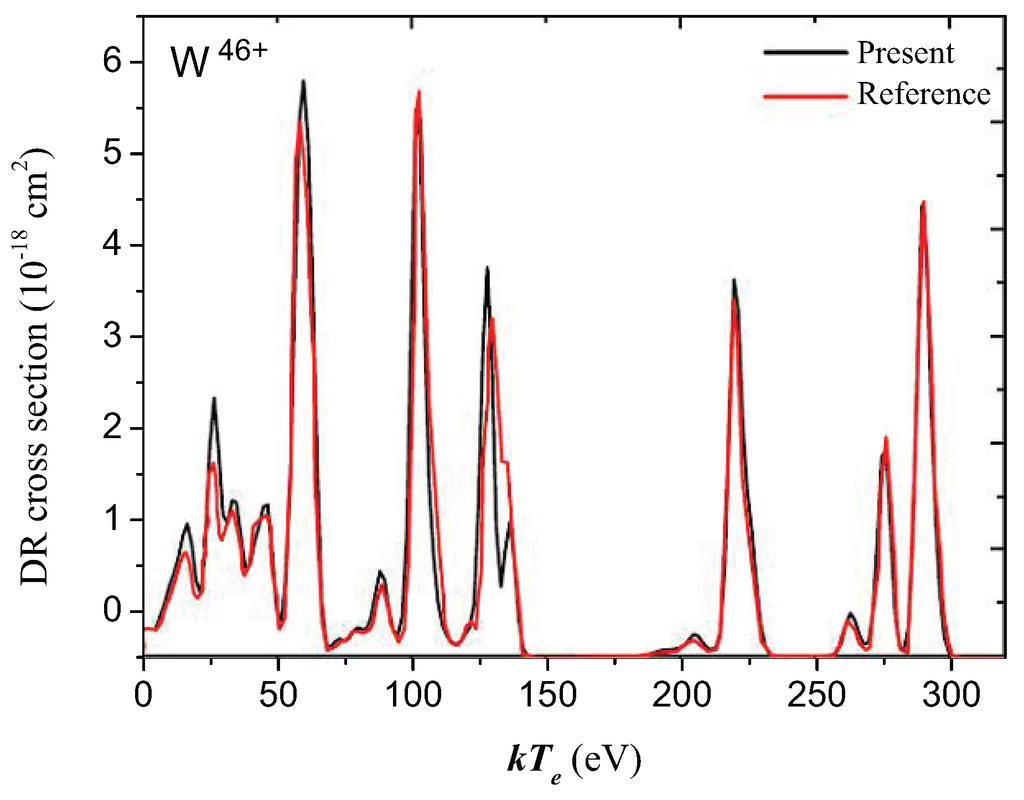
Figure 4. The presently calculated DR cross-sections for the $3d^{10}+e^{-}\to 3d^{9}4l4l^{\prime }\to 3d^{10}4l^{″}+h\nu$ processes of W${}^{46+}$ ions as a function of electron energy $k{T}_e$ together with other available results [29].

Figure 4. The presently calculated DR cross-sections for the $3d^{10}+e^{-}\to 3d^{9}4l4l^{\prime }\to 3d^{10}4l^{″}+h\nu$ processes of W${}^{46+}$ ions as a function of electron energy $k{T}_e$ together with other available results [29].

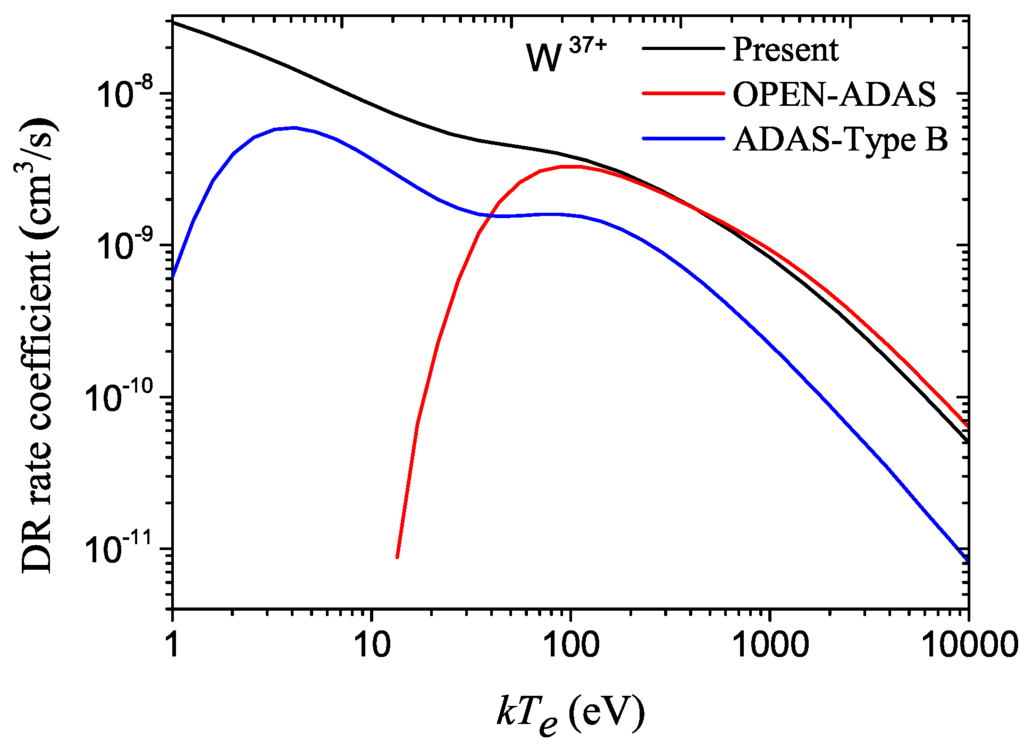
Figure 5. The presently calculated total DR rate coefficients of W${}^{37+}$ ions as a function of electron energy $k{T}_e$, compared to available ones from the ADAS database [76].

Figure 5. The presently calculated total DR rate coefficients of W${}^{37+}$ ions as a function of electron energy $k{T}_e$, compared to available ones from the ADAS database [76].

In this part, we calculate total DR rate coefficients of W${}^{46+}$–W${}^{37+}$ ions (calculations on W${}^{40+}$ ions are currently underway). As an example, total DR rate coefficients of W${}^{39+}$ ions are displayed in Figure 6 together with their partial contributions, as associated with the $3s$, $3p$, $3d$, $4s$ and $4p$ subshell excitations as a function of electron temperature. This charge state W${}^{39+}$ is inferred to be dominant at around 2 keV in modeling ITER plasmas [51]. The calculations of total DR rate coefficients require the summation, in principle, over an infinite number of individual level-by-level DR channels. To do this, we first calculate individual configuration-by-configuration rate coefficients, which could be achieved by performing the statistical summation over all corresponding level-by-level rate coefficients. Since the initial configuration is well defined for potentially considered DR process, the intermediate (doubly excited) and final configurations should be specified explicitly. In the case of W${}^{39+}$, we consider the following doubly-excited configurations, ([Ne]${(3s^{2}3p^{6}3d^{10}4s^{2}4p^5)}^{-1}nl{n}^{{}^{\prime }}{l}^{{}^{\prime }}{)}^{**}$ with n = 4–8, l = 0–4, $n^{{}^{\prime }}$ = 4–20 and $l^{{}^{\prime }}$ = 0–12, as well as the final configurations ([Ne]${(3s^{2}3p^{6}3d^{10}4s^{2}4p^5)}^{-1}{n}^{{}^{″}}{l}^{{}^{″}}{n}^{{}^{\prime }}{l}^{{}^{\prime }}{)}^{*}$ with $n^{{}^{″}}$ = 3–7 and $l^{{}^{″}}$ = 0–4 from the subsequently radiative decays. The excitations from K and L shells are not taken into account in the present calculations due to their negligible contribution to total DR rate coefficients [77]. The contributions from higher-$n^{{}^{\prime }}$ states are extrapolated up to $n^{{}^{\prime }}$ = 1000 using the empirical ${\left(n^{{}^{\prime }}\right)}^{-3}$ scaling [78]. These rate coefficients are calculated for electron temperatures from 1 eV to $5\times {10}^4$ eV, which is a critical range for thermonuclear fusion plasmas [79]. As seen clearly from this figure, excitations from the $4p$ subshell dominate total DR rate coefficients in the whole region of electron temperature. With respect to excitations from the $3l$ subshells, it is found that the DR rate coefficients for $3d$ subshell excitation are the largest and that the partial rate coefficients decrease with the decreasing l quantum number. This characteristics is similar to the case of Sn${}^{12+}$ [77] and Pd${}^{19+}$ [80] ions. For electron temperatures lower than 100 eV, excitations from the $3l$ subshells are much less significant than from the $4l$ subshells, and thus, the contributions to total DR rate coefficients can be neglected. However, as the electron temperature increases, the $3l$ subshell excitations become more important and consequently start to compete with the $4l$ excitations. Regarding excitations from the $4l$ subshells, DR rate coefficients for the $4p$ excitation are the largest, while the contribution from the $4s$ excitation cannot be neglected. For the rest of the tungsten ions discussed above, we use the same procedures as W${}^{39+}$ ions, and very similar characteristics are summarized; thus, only total DR rate coefficients are given for them for the sake of brevity, as shown in Figure 7.

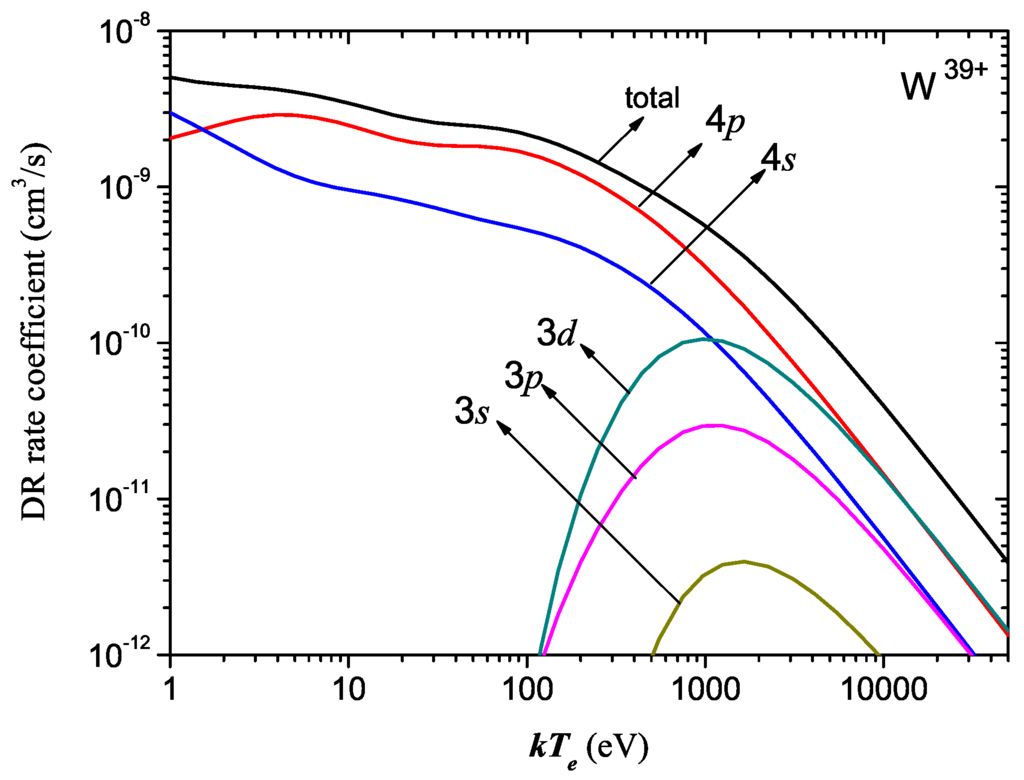
Figure 6. The presently calculated total and partial DR rate coefficients of W${}^{39+}$ ions as a function of electron temperature $k{T}_e$. This charge state W${}^{39+}$ is inferred to be dominant at around 2 keV in modeling International Thermonuclear Experimental Reactor (ITER) plasmas [51].

Figure 6. The presently calculated total and partial DR rate coefficients of W${}^{39+}$ ions as a function of electron temperature $k{T}_e$. This charge state W${}^{39+}$ is inferred to be dominant at around 2 keV in modeling International Thermonuclear Experimental Reactor (ITER) plasmas [51].

To facilitate the applications of DR rate coefficients, one can use the following semiempirical fitting formula (in cm${}^3$·s${}^{-1}$) [81]:

$$\begin{array}{c}\hfill {\alpha }^{DR}(k{T}_e)=(k{T}_e{)}^{-3/2}\sum _i^6{A}_i{e}^{-B_i/k{T}_e}.\end{array}$$

(12)

Here, $A_i$ and $B_i$ are fitting parameters that can be obtained by fitting the calculated DR rate coefficients. For example, these parameters for total DR rate coefficients of W${}^{46+}$–W${}^{37+}$ ions are listed in Table 4, which can be utilized to reproduce the presently calculated total rate coefficients with discrepancies of less than 1% for electron temperatures above 5 eV. However, one should be very careful to use the fitted data at temperatures below 5 eV, since DR rate coefficients are very sensitive to the resonance energies in that region.

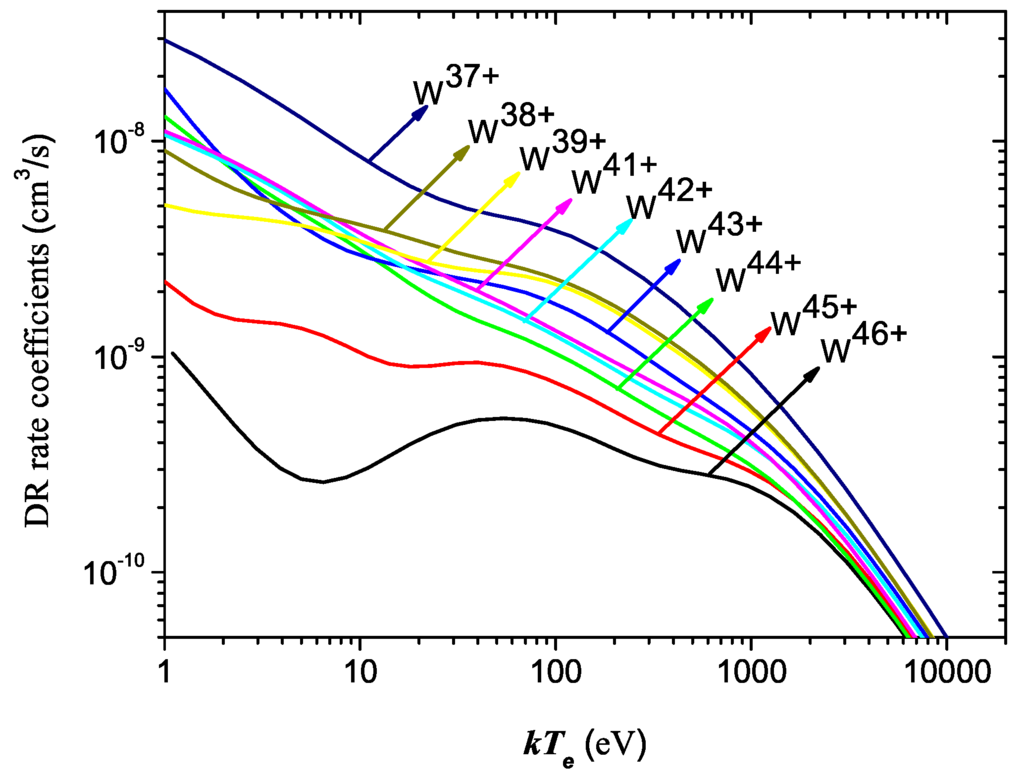
Figure 7. The presently calculated total DR rate coefficients of W${}^{46+}$–W${}^{37+}$ ions as a function of electron temperature $k{T}_e$.

Figure 7. The presently calculated total DR rate coefficients of W${}^{46+}$–W${}^{37+}$ ions as a function of electron temperature $k{T}_e$.

Table 4. Fitting parameters for the presently calculated total DR rate coefficients of W${}^{46+}$–W${}^{37+}$ ions. Numbers in brackets denote powers of 10.

Fitting	W${}^{46+}$	W${}^{45+}$	W${}^{44+}$	W${}^{43+}$	W${}^{42+}$	W${}^{41+}$	W${}^{39+}$	W${}^{38+}$	W${}^{37+}$
$A_1$	1.4543[−8]	2.6717[−7]	1.1569[−6]	4.1371[−7]	1.6944[−6]	1.6014[−7]	6.0746[−7]	1.9070[−7]	3.9007[−7]
$B_1$	8.3243[0]	7.0342[0]	9.0374[1]	7.7850[0]	1.1615[2]	5.0613[0]	3.3713[1]	6.5731[0]	5.1508[0]
$A_2$	1.9915[−7]	4.0559[−7]	7.4592[−6]	1.6914[−6]	4.4742[−6]	4.8517[−6]	1.7700[−7]	7.7977[−7]	1.2141[−6]
$B_2$	4.2241[1]	3.2974[1]	7.1384[2]	5.9659[1]	3.4936[2]	3.3090[2]	6.9936[0]	3.2360[1]	3.5521[1]
$A_3$	6.7361[−7]	2.6009[−6]	2.5384[−7]	4.3113[−6]	6.2817[−7]	1.6915[−6]	5.7629[−6]	2.9429[−6]	5.0545[−6]
$B_3$	1.0717[2]	1.0912[2]	2.2324[1]	1.8934[2]	4.0746[1]	1.0235[2]	2.2787[2]	1.0602[2]	1.0896[2]
$A_4$	1.7027[−6]	5.9321[−6]	1.0583[−7]	9.6379[−6]	1.7999[−5]	1.2484[−5]	2.9373[−6]	6.7028[−6]	1.0545[−5]
$B_4$	2.7908[2]	2.7452[2]	3.8774[0]	5.9801[2]	2.1950[3]	9.1731[2]	9.8938[1]	2.5447[2]	2.4496[2]
$A_5$	2.0410[−5]	2.1212[−5]	2.3367[−6]	2.8462[−5]	1.7095[−7]	1.4246[−5]	2.2508[−5]	1.2033[−5]	1.5455[−5]
$B_5$	2.0661[3]	9.0060[2]	2.1982[2]	1.7244[3]	5.6003[0]	1.9728[3]	1.7514[3]	6.7877[2]	6.4479[2]
$A_6$	8.3537[−6]	4.9140[−5]	2.0007[−5]		1.4323[−5]	5.2788[−7]	1.1814[−5]	1.9456[−5]	2.1248[−5]
$B_6$	9.7091[2]	1.9984[3]	1.9094[3]		1.0829[3]	3.1933[1]	6.5898[2]	1.7055[3]	1.6974[3]

Table 4. Fitting parameters for the presently calculated total DR rate coefficients of W${}^{46+}$–W${}^{37+}$ ions. Numbers in brackets denote powers of 10.

Fitting	W${}^{46+}$	W${}^{45+}$	W${}^{44+}$	W${}^{43+}$	W${}^{42+}$	W${}^{41+}$	W${}^{39+}$	W${}^{38+}$	W${}^{37+}$
$A_1$	1.4543[−8]	2.6717[−7]	1.1569[−6]	4.1371[−7]	1.6944[−6]	1.6014[−7]	6.0746[−7]	1.9070[−7]	3.9007[−7]
$B_1$	8.3243[0]	7.0342[0]	9.0374[1]	7.7850[0]	1.1615[2]	5.0613[0]	3.3713[1]	6.5731[0]	5.1508[0]
$A_2$	1.9915[−7]	4.0559[−7]	7.4592[−6]	1.6914[−6]	4.4742[−6]	4.8517[−6]	1.7700[−7]	7.7977[−7]	1.2141[−6]
$B_2$	4.2241[1]	3.2974[1]	7.1384[2]	5.9659[1]	3.4936[2]	3.3090[2]	6.9936[0]	3.2360[1]	3.5521[1]
$A_3$	6.7361[−7]	2.6009[−6]	2.5384[−7]	4.3113[−6]	6.2817[−7]	1.6915[−6]	5.7629[−6]	2.9429[−6]	5.0545[−6]
$B_3$	1.0717[2]	1.0912[2]	2.2324[1]	1.8934[2]	4.0746[1]	1.0235[2]	2.2787[2]	1.0602[2]	1.0896[2]
$A_4$	1.7027[−6]	5.9321[−6]	1.0583[−7]	9.6379[−6]	1.7999[−5]	1.2484[−5]	2.9373[−6]	6.7028[−6]	1.0545[−5]
$B_4$	2.7908[2]	2.7452[2]	3.8774[0]	5.9801[2]	2.1950[3]	9.1731[2]	9.8938[1]	2.5447[2]	2.4496[2]
$A_5$	2.0410[−5]	2.1212[−5]	2.3367[−6]	2.8462[−5]	1.7095[−7]	1.4246[−5]	2.2508[−5]	1.2033[−5]	1.5455[−5]
$B_5$	2.0661[3]	9.0060[2]	2.1982[2]	1.7244[3]	5.6003[0]	1.9728[3]	1.7514[3]	6.7877[2]	6.4479[2]
$A_6$	8.3537[−6]	4.9140[−5]	2.0007[−5]		1.4323[−5]	5.2788[−7]	1.1814[−5]	1.9456[−5]	2.1248[−5]
$B_6$	9.7091[2]	1.9984[3]	1.9094[3]		1.0829[3]	3.1933[1]	6.5898[2]	1.7055[3]	1.6974[3]

4. Conclusions

The degrees of linear polarization of radiated X-ray emissions following electron-impact excitation and resonant electron capture of highly charged tungsten ions have been studied. Special attention has been focused on the strong $nf\to 3d(n=4,5,6)$ M-band spectra of W${}^{46+}$–W${}^{42+}$ ions. In order to do this, total and magnetic sub-level cross-sections for the associated excitations were discussed in much detail. It has been found that the linear polarizations of those X-rays behave very variously for different population mechanisms, even for identical transition lines. Such big differences in linear polarization of X-ray emissions following electron-impact excitation and resonant electron capture processes provide us a new possibility of distinguishing and identifying the population mechanism of these emissions. In addition, with the purpose of assisting the study and simulation of the ionization equilibrium of tungsten plasmas, DR rate coefficients of highly charged W${}^{37+}$ to W${}^{46+}$ ions are also estimated and discussed. To facilitate applications of those DR rate coefficients, a semiempirical fitting to them has been performed.