Detailed Analysis of Configuration Interaction and Calculation of Radiative Transition Rates in Seven Times Ionized Tungsten (W VIII)
Abstract
:1. Introduction
2. Available Atomic Data in W VIII
3. Configuration Interaction Analysis
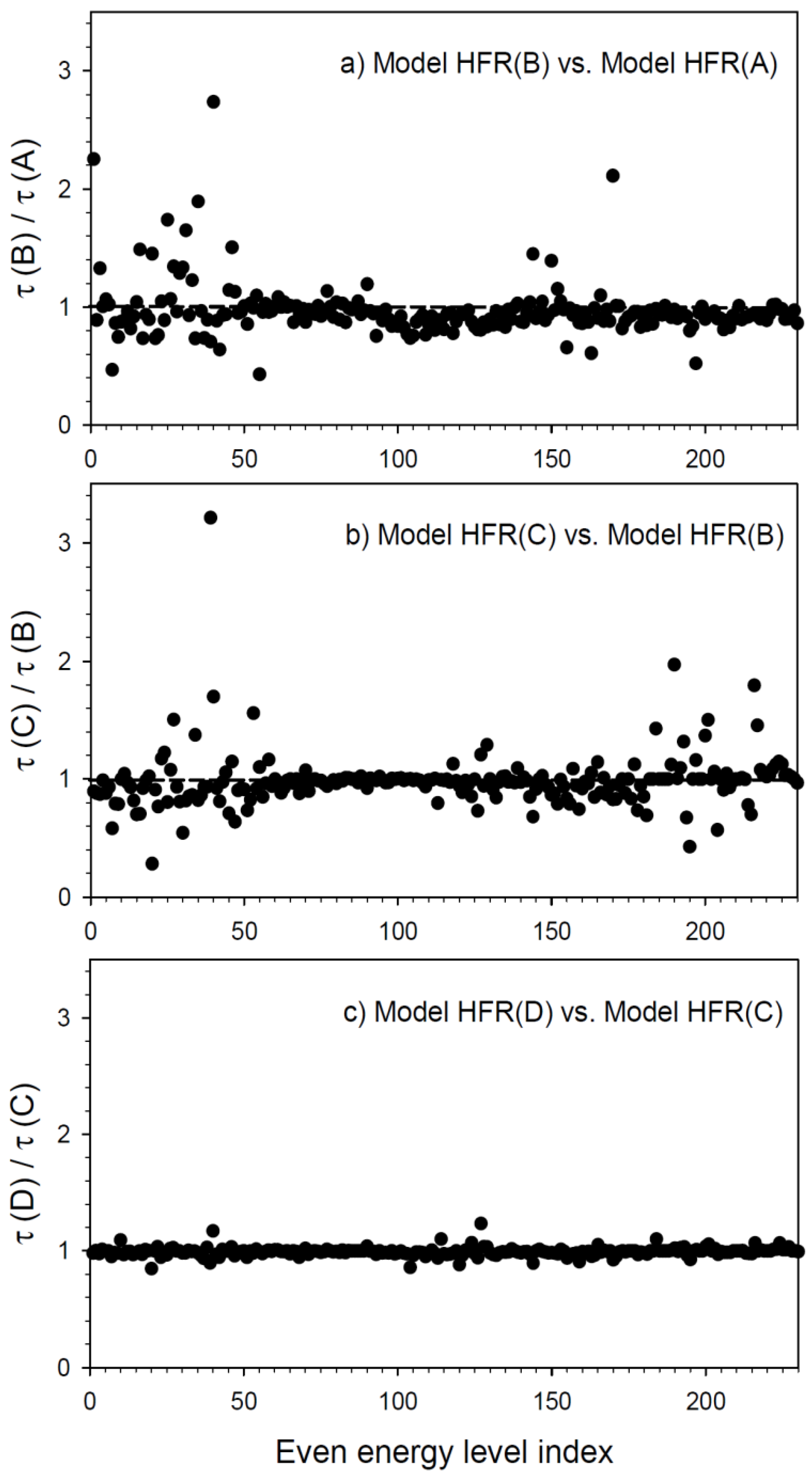
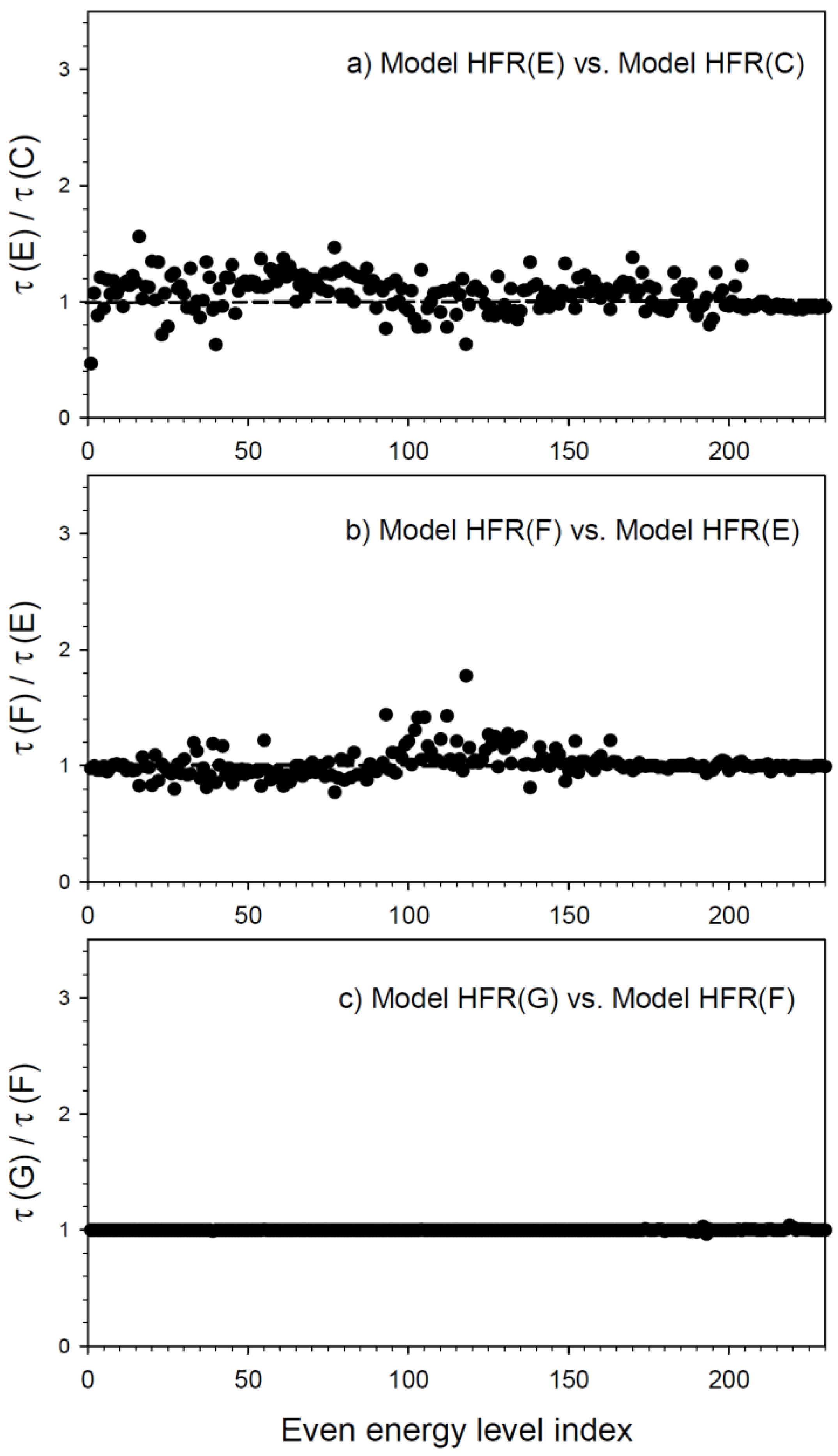
4. Radiative Parameter Calculations
| Configuration | Parameter | Fit | Unc. | Note a | Fit/HFR |
|---|---|---|---|---|---|
| Odd parity | |||||
| 4f135s25p6 | Eav | 29,053 | 0 | ||
| ζ (4f) | 4971 | 0 | 0.988 | ||
| 4f145s25p5 | Eav | 51,968 | 0 | ||
| ζ(5p) | 59,148 | 0 | 1.003 | ||
| Even parity | |||||
| 4f145s5p6 | Eav | 377,512 | f | ||
| 4f135s25p55d | Eav | 403,242 | 249 | ||
| ζ (4f) | 5022 | 48 | r11 | 0.995 | |
| ζ(5p) | 60,705 | 127 | r2 | 0.984 | |
| ζ(5d) | 4716 | 109 | r10 | 0.988 | |
| F2(4f,5p) | 52,909 | 1606 | r12 | 0.785 | |
| F2(4f,5d) | 35,345 | 2124 | r4 | 0.780 | |
| F4(4f,5d) | 17,165 | 1031 | r4 | 0.780 | |
| F2(5p,5d) | 63,984 | 2700 | r7 | 0.815 | |
| G2(4f,5p) | 28,161 | 1313 | r3 | 1.025 | |
| G4(4f,5p) | 23,435 | 1092 | r3 | 1.025 | |
| G1(4f,5d) | 13,991 | 413 | r5 | 0.876 | |
| G3(4f,5d) | 13,111 | 387 | r5 | 0.876 | |
| G5(4f,5d) | 10,482 | 309 | r5 | 0.876 | |
| G1(5p,5d) | 67,786 | 607 | r1 | 0.711 | |
| G3(5p,5d) | 42,728 | 383 | r1 | 0.711 | |
| 4f135s25p56d | Eav | 775,400 | f | ||
| 4f135s25p56s | Eav | 542,642 | 139 | ||
| ζ(4f) | 5033 | 48 | r11 | 0.995 | |
| ζ(5p) | 61,895 | 130 | r2 | 0.984 | |
| F2(4f,5p) | 53,429 | 1622 | r12 | 0.785 | |
| G2(4f,5p) | 28,352 | 1322 | r3 | 1.025 | |
| G4(4f,5p) | 23,664 | 1103 | r3 | 1.025 | |
| G3(4f,6s) | 6873 | 2032 | 1.294 | ||
| G1(5p,6s) | 9385 | 742 | r13 | 0.881 | |
| 4f135s25p57s | Eav | 813,134 | f | ||
| 4f145s25p45d | Eav | 420,745 | 400 | ||
| F2(5p,5p) | 77,035 | 2775 | r14 | 0.834 | |
| ζ(5p) | 58,775 | 123 | r2 | 0.984 | |
| ζ(5d) | 4465 | 103 | r10 | 0.988 | |
| F2(5p,5d) | 62,865 | 2653 | r7 | 0.815 | |
| G1(5p,5d) | 66,467 | 595 | r1 | 0.711 | |
| G3(5p,5d) | 41,892 | 375 | r1 | 0.711 | |
| 4f145s25p46d | Eav | 778,313 | f | ||
| 4f145s25p46s | Eav | 550,299 | 268 | ||
| F2(5p,5p) | 77,932 | 2807 | r14 | 0.838 | |
| ζ(5p) | 59,932 | 126 | r2 | 0.984 | |
| G1(5p,6s) | 9397 | 743 | r13 | 0.881 | |
| 4f145s25p47s | Eav | 813,793 | f | ||
| 4f145s5p56p | Eav | 992,590 | f | ||
| 4f145s5p55f | Eav | 1092,223 | f | ||
| 4f125s25p65d | Eav | 429,283 | 138 | ||
| F2(4f,4f) | 149,065 | 2553 | 0.843 | ||
| F4(4f,4f) | 111,500 | 6763 | 0.991 | ||
| F6(4f,4f) | 77,044 | 3283 | 0.947 | ||
| α | 22 | f | |||
| β | −1000 | f | |||
| γ | −70 | f | |||
| ζ(4f) | 5200 | 49 | r11 | 0.995 | |
| ζ(5d) | 4977 | 115 | r10 | 0.988 | |
| F2(4f,5d) | 36,300 | 1467 | r6 | 0.785 | |
| F4(4f,5d) | 17,592 | 711 | r6 | 0.785 | |
| G1(4f,5d) | 13,832 | 408 | r5 | 0.876 | |
| G3(4f,5d) | 13,147 | 388 | r5 | 0.876 | |
| G5(4f,5d) | 10,564 | 312 | r5 | 0.876 | |
| 4f125s25p66d | Eav | 819,431 | f | ||
| 4f125s25p66s | Eav | 579,803 | f | ||
| F2(4f,4f) | 147,636 | f | 0.833 | ||
| F4(4f,4f) | 110,752 | f | 0.982 | ||
| F6(4f,4f) | 78,585 | f | 0.963 | ||
| α | 22 | f | |||
| β | −1000 | f | |||
| γ | −70 | f | |||
| ζ(4f) | 5161 | f | 0.985 | ||
| G3(4f,6s) | 3974 | f | 0.758 | ||
| 4f135s25p55d – 4f145s25p45d | D2(4f,5p;4f,4f) | −5660 | 51 | r8 | 0.864 |
| D4(4f,5p;4f,4f) | −309 | 3 | r8 | 0.864 | |
| D2(5p,5p;4f,5p) | −34,864 | 312 | r8 | 0.864 | |
| D2(5p,5d;4f,5d) | −27,246 | 244 | r8 | 0.864 | |
| D4(5p,5d;4f,5d) | −17,855 | 160 | r8 | 0.864 | |
| E1(5p,5d;4f,5d) | −24,107 | 216 | r8 | 0.864 | |
| E3(5p,5d;4f,5d) | −18,067 | 162 | r8 | 0.864 | |
| 4f135s25p55d – 4f125s25p65d | D2(4f,4f;4f,5p) | −3792 | 8 | r9 | 0.827 |
| D4(4f,4f;4f,5p) | 858 | 2 | r9 | 0.827 | |
| D2(4f,5p;5p,5p) | −32,556 | 68 | r9 | 0.827 | |
| D2(4f,5d;5p,5d) | −25,604 | 54 | r9 | 0.827 | |
| D4(4f,5d;5p,5d) | −16,845 | 35 | r9 | 0.827 | |
| E1(4f,5d;5p,5d) | −22,393 | 47 | r9 | 0.827 | |
| E3(4f,5d;5p,5d) | −16,982 | 36 | r9 | 0.827 | |
| 4f145s25p45d – 4f125s25p65d | D2(4f,4f;5p,5p) | 24,592 | 52 | r9 | 0.827 |
| D4(4f,4f;5p,5p) | 20,291 | 43 | r9 | 0.827 | |
| 4f135s25p56s – 4f145s25p46s | D2(4f,5p,4f,4f) | −6391 | f | 1.000 | |
| D4(4f,5p;4f,4f) | −244 | f | 1.000 | ||
| D2(5p,5p;4f,5p) | −40,487 | f | 1.000 |
| Index | Eexp a | Ecalc b | ΔE c | J | Percentage Composition in LS-Coupling d | |
|---|---|---|---|---|---|---|
| Odd Parity | ||||||
| 1° | 0 | 0 | 0 | 7/2 | 98 4f135p6 2F | |
| 2° | 1233 | 1233 | 0 | 3/2 | 98 4f145p5 2P | |
| 3° | 17,410 | 17,410 | 0 | 5/2 | 98 4f135p6 2F | |
| 4° | 89,123 | 89,123 | 0 | 1/2 | 97 4f145p5 2P | |
| Even Parity | ||||||
| 1 | 377,119 | 377,140 | −21 | 9/2 | 28 4f135p5(3F)5d 2H + 23 4f135p5(1D)5d 2G + 8 4f135p5(3F)5d 2G | |
| 2 | 377,288 | 376,992 | 296 | 3/2 | 25 4f135p5(1D)5d 2P + 18 4f135p5(3D)5d 4F + 15 4f135p5(3D)5d 4P | |
| 3 | 377,867 | 377,714 | 153 | 5/2 | 21 4f135p5(3D)5d 4F + 12 4f145p4(1S)5d 2D + 9 4f135p5(3F)5d 2F | |
| 4 | 380,899 | 381,127 | −228 | 9/2 | 18 4f135p5(1G)5d 2G + 18 4f135p5(3G)5d 2G + 14 4f135p5(3F)5d 2G | |
| 5 | 382,019 | 382,285 | −266 | 7/2 | 22 4f135p5(1D)5d 2F + 15 4f135p5(3D)5d 2G + 13 4f135p5(3F)5d 2F | |
| 6 | 383,133 | 383,535 | −402 | 5/2 | 18 4f135p5(3D)5d 2F + 17 4f135p5(1D)5d 2D + 10 4f145p4(1S)5d 2D | |
| 7 | 384,400 | 383,622 | 778 | 9/2 | 24 4f135p5(1G)5d 2H + 20 4f135p5(3G)5d 4H + 11 4f135p5(3D)5d 4G | |
| 8 | 386,704 | 386,497 | 207 | 5/2 | 16 4f135p5(3F)5d 2D + 11 4f135p5(3G)5d 4D + 9 4f135p5(3F)5d 4P | |
| 9 | 391,541 | 392,282 | −741 | 9/2 | 14 4f135p5(1D)5d 2G + 13 4f125p6(3H)5d 2G + 5 4f135p5(3G)5d 2H | |
| 10 | 393,992 | 393,539 | 453 | 7/2 | 18 4f125p6(3H)5d 2F + 14 4f135p5(3G)5d 2F | |
| 11 | 395,276 | 395,201 | 75 | 5/2 | 19 4f135p5(3D)5d 2F + 17 4f135p5(3D)5d 4D + 16 4f135p5(3D)5d 4F | |
| 12 | 395,471 | 395,624 | −153 | 7/2 | 14 4f125p6(3F)5d 4F + 11 4f135p5(3F)5d 2G + 8 4f125p6(3F)5d 4D | |
| 13 | 395,474 | 395,124 | 350 | 1/2 | 38 4f145p4(3P)5d 4P + 17 4f135p5(3D)5d 2S + 8 4f145p4(3P)5d 2P | |
| 14 | 396,505 | 396,147 | 358 | 7/2 | 20 4f135p5(3D)5d 4F + 14 4f135p5(3F)5d 2G + 8 4f135p5(3D)5d 2F | |
| 15 | 396,894 | 396,671 | 22 | 3/2 | 17 4f135p5(3F)5d 2P + 17 4f145p4(3P)5d 4P + 16 4f145p4(3P)5d 4F | |
| 16 | 397,612 | 397,709 | −97 | 5/2 | 19 4f125p6(1G)5d 2D + 19 4f125p6(3F)5d 4D | |
| 17 | 398,707 | 398,269 | 438 | 9/2 | 15 4f135p5(1G)5d 2G + 15 4f135p5(3G)5d 4G + 13 4f135p5(1G)5d 2H | |
| 18 | 400,203 | 400,110 | 93 | 9/2 | 19 4f125p6(3F)5d 4G + 14 4f125p6(1G)5d 2H + 13 4f125p6(3F)5d 4F | |
| 19 | 401,984 | 402,399 | −415 | 5/2 | 20 4f145p4(3P)5d 4F + 17 4f135p5(3G)5d 2D + 8 4f145p4(1D)5d 2F | |
| 20 | 405,907 | 405,757 | 150 | 9/2 | 41 4f125p6(3H)5d 4G + 25 4f125p6(3H)5d 4H + 8 4f125p6(3H)5d 4F | |
| 21 | 408,086 | 407,948 | 138 | 7/2 | 42 4f125p6(3H)5d 2F + 7 4f125p6(3F)5d 2F + 7 4f125p6(1G)5d 2F | |
| 22 | 408,833 | 409,199 | −366 | 3/2 | 21 4f125p6(1G)5d 2D + 17 4f125p6(1D)5d 2D + 8 4f125p6(3F)5d 2D | |
| 23 | 409,362 | 409,047 | 315 | 5/2 | 38 4f125p6(3H)5d 4F + 25 4f125p6(3F)5d 4F + 10 4f125p6(1G)5d 2D | |
| 24 | 409,676 | 409,619 | 57 | 5/2 | 18 4f125p6(3F)5d 4P + 16 4f125p6(3F)5d 4G + 10 4f125p6(3H)5d 2F | |
| 25 | 410,258 | 409,885 | 373 | 3/2 | 17 4f125p6(3F)5d 2D + 13 4f135p5(3G)5d 4F + 12 4f135p5(1G)5d 2D | |
| 26 | 410,654 | 410,270 | 384 | 7/2 | 13 4f125p6(3F)5d 4G + 9 4f125p6(3H)5d 2G + 8 4f135p5(3D)5d 2G | |
| 27 | 411,819 | 412,499 | −680 | 5/2 | 18 4f125p6(3H)5d 2F + 10 4f135p5(3G)5d 4G + 10 4f125p6(3F)5d 4G | |
| 28 | 411,832 | 411,499 | 333 | 7/2 | 23 4f125p6(3F)5d 4D + 21 4f125p6(3F)5d 4H + 14 4f125p6(1G)5d 2G | |
| 29 | 413,450 | 413,503 | −53 | 9/2 | 28 4f125p6(3H)5d 2G + 13 4f125p6(3F)5d 4H + 12 4f125p6(3H)5d 4I | |
| 30 | 414,888 | 414,853 | 35 | 7/2 | 39 4f125p6(3F)5d 4G + 11 4f125p6(3F)5d 2F + 10 4f125p6(3F)5d 4H | |
| 31 | 415,852 | 415,874 | −22 | 5/2 | 27 4f125p6(3F)5d 4G + 16 4f125p6(1G)5d 2F + 13 4f125p6(3F)5d 4P | |
| 32 | 416,481 | 416,737 | −256 | 9/2 | 29 4f125p6(3F)5d 2G + 18 4f125p6(3H)5d 4I + 10 4f125p6(1G)5d 2G | |
| 33 | 417,394 | 417,333 | 61 | 3/2 | 42 4f125p6(3F)5d 2P + 16 4f125p6(1G)5d 2D | |
| 34 | 418,403 | 418,274 | 129 | 9/2 | 28 4f125p6(3F)5d 4H + 28 4f125p6(3H)5d 2G + 18 4f125p6(3H)5d 4G | |
| 35 | 419,585 | 419,953 | −368 | 7/2 | 35 4f125p6(3H)5d 4G + 11 4f125p6(3F)5d 4F + 10 4f125p6(3H)5d 4F | |
| 36 | 419,811 | 419,829 | −18 | 5/2 | 25 4f125p6(3H)5d 4F + 14 4f125p6(3H)5d 2F | |
| 37 | 424,781 | 424,776 | 5 | 5/2 | 26 4f125p6(3H)5d 4G + 19 4f125p6(3F)5d 4P + 15 4f125p6(1G)5d 2D | |
| 38 | 425,843 | 425,913 | −70 | 3/2 | 38 4f125p6(3H)5d 4F + 27 4f125p6(3F)5d 2P + 11 4f125p6(3F)5d 4P | |
| 39 | 428,199 | 427,900 | 299 | 3/2 | 42 4f125p6(3F)5d 4P + 11 4f125p6(3H)5d 4F + 6 4f125p6(3F)5d 2P | |
| 40 | 428,216 | 428,371 | −155 | 7/2 | 30 4f125p6(3F)5d 2G + 10 4f125p6(3H)5d 2F + 7 4f125p6(3H)5d 2G | |
| 41 | 428,777 | 428,727 | 50 | 7/2 | 26 4f125p6(3F)5d 2F + 17 4f125p6(3F)5d 4F + 11 4f125p6(3H)5d 4H | |
| 42 | 430,708 | 430,640 | 68 | 7/2 | 20 4f145p4(3P)5d 4F + 16 4f125p6(1G)5d 2F + 10 4f125p6(3H)5d 4H | |
| 43 | 432,963 | 433,564 | −601 | 5/2 | 13 4f125p6(3P)5d 4D + 10 4f145p4(3P)5d 4F + 9 4f145p4(1D)5d 2F | |
| 44 | 435,561 | 435,879 | −318 | 5/2 | 15 4f125p6(1D)5d 2F + 14 4f125p6(1G)5d 2D + 8 4f145p4(1D)5d 2F | |
| 45 | 435,658 | 435,516 | 142 | 7/2 | 14 4f125p6(3H)5d 2G + 12 4f125p6(1G)5d 2G | |
| 46 | 437,149 | 437,658 | −509 | 5/2 | 14 4f125p6(3H)5d 2F + 14 4f125p6(3H)5d 4G + 11 4f125p6(1G)5d 2D | |
| 47 | 439,561 | 439,318 | 243 | 7/2 | 15 4f125p6(3H)5d 2G + 13 4f125p6(3P)5d 2F + 12 4f125p6(1G)5d 2F | |
| 48 | 445,286 | 445,209 | 77 | 5/2 | 15 4f125p6(3P)5d 2D + 13 4f125p6(1D)5d 2D + 5 4f145p4(1D)5d 2D | |
| 49 | 447,909 | 447,860 | 49 | 5/2 | 19 4f125p6(1G)5d 2F + 14 4f125p6(3P)5d 4D + 13 4f125p6(3F)5d 2F | |
| 50 | 452,821 | 452,511 | 310 | 3/2 | 24 4f125p6(3P)5d 4P + 11 4f135p5(1G)5d 2D + 10 4f125p6(3P)5d 2P | |
| 51 | 454,067 | 454,016 | 51 | 7/2 | 66 4f125p6(1I)5d 2G + 7 4f135p5(3G)5d 4H + 5 4f125p6(3H)5d 2G | |
| 52 | 457,652 | 457,245 | 407 | 5/2 | 17 4f135p5(1G)5d 2F + 14 4f135p5(3G)5d 2F + 9 4f125p6(1D)5d 2D | |
| 53 | 457,815 | 457,776 | 39 | 9/2 | 64 4f125p6(1I)5d 2H + 7 4f135p5(1G)5d 2G + 6 4f135p5(3D)5d 2G | |
| 54 | 458,380 | 458,337 | 43 | 3/2 | 16 4f125p6(3P)5d 2P + 12 4f125p6(3P)5d 4P | |
| 55 | 459,570 | 460,304 | −734 | 5/2 | 22 4f125p6(3P)5d 2D + 6 4f125p6(3P)5d 2F | |
| 56 | 462,927 | 463,121 | −194 | 3/2 | 24 4f125p6(3P)5d 2D + 14 4f135p5(1D)5d 2D + 10 4f135p5(3F)5d 4F | |
| 57 | 466,219 | 466,223 | −4 | 5/2 | 33 4f125p6(3P)5d 2F + 10 4f125p6(1D)5d 2D + 7 4f125p6(3P)5d 4F | |
| 58 | 468,034 | 467,620 | 414 | 5/2 | 23 4f125p6(3P)5d 2F + 9 4f135p5(1D)5d 2F + 6 4f135p5(3F)5d 4G | |
| 59 | 468,523 | 468,312 | 211 | 5/2 | 52 4f125p6(3P)5d 4P + 5 4f125p6(1D)5d 2D + 5 4f135p5(3G)5d 4F | |
| 60 | 475,117 | 475,279 | −162 | 3/2 | 15 4f145p4(1D)5d 2P + 9 4f145p4(3P)5d 4F | |
| 61 | 481,035 | 480,441 | 594 | 5/2 | 26 4f145p4(3P)5d 2D + 16 4f145p4(1D)5d 2D + 9 4f135p5(1D)5d 2D | |
| 62 | 481,473 | 481,921 | −448 | 5/2 | 65 4f145p4(3P)6s 4P + 23 4f145p4(1D)6s 2D | |
| 63 | 483,243 | 483,385 | −142 | 3/2 | 18 4f135p5(1D)5d 2P + 16 4f145p4(1D)5d 2P | |
| 64 | 485,175 | 486,300 | −1125 | 5/2 | 22 4f135p5(1D)5d 2D + 11 4f135p5(1D)5d 2F + 7 4f135p5(3F)5d 4F | |
| 65 | 487,901 | 487,064 | 837 | 3/2 | 50 4f145p4(3P)6s 2P + 27 4f145p4(1D)6s 2D + 13 4f145p4(3P)6s 4P | |
| 66 | 492,337 | 493,284 | −947 | 1/2 | 32 4f145p4(1D)5d 2P + 21 4f145p4(1D)5d 2S + 16 4f145p4(3P)5d 2P | |
| 67 | 495,690 | 495,041 | 649 | 9/2 | 27 4f135p5(3D)5d 2G + 18 4f135p5(3F)5d 2G + 10 4f135p5(3G)5d 2G | |
| 68 | 498,037 | 499,096 | −1059 | 5/2 | 29 4f135p5(3G)5d 2D + 14 4f135p5(1G)5d 2D + 9 4f125p6(3P)5d 2D | |
| 69 | 498,541 | 498,826 | −285 | 3/2 | 26 4f145p4(1D)5d 2D + 13 4f125p6(1S)5d 2D + 10 4f145p4(3P)5d 2D | |
| 70 | 498,792 | 499,045 | −253 | 7/2 | 18 4f135p5(3G)5d 2F + 15 4f135p5(3F)5d 2F + 13 4f135p5(1G)5d 2F | |
| 71 | 500,313 | 500,013 | 300 | 5/2 | 56 4f135p5(1F)6s 2F + 19 4f135p5(3D)6s 2D + 11 4f135p5(3D)6s 4D | |
| 72 | 503,071 | 502,605 | 466 | 7/2 | 47 4f135p5(3F)6s 2F + 16 4f135p5(1F)6s 2F + 10 4f135p5(3F)6s 4F | |
| 73 | 504,615 | 504,586 | 29 | 9/2 | 71 4f135p5(3G)6s 2G + 24 4f135p5(3G)6s 4G | |
| 74 | 504,691 | 505,845 | −1154 | 3/2 | 32 4f125p6(1S)5d 2D + 14 4f135p5(3G)5d 2D + 7 4f135p5(3F)5d 2D | |
| 75 | 512,790 | 512,628 | 162 | 7/2 | 17 4f135p5(1D)5d 2G + 15 4f135p5(3F)5d 2G + 14 4f135p5(3G)5d 2G | |
| 76 | 514,063 | 514,203 | −140 | 5/2 | 49 4f135p5(1D)6s 2D + 26 4f135p5(3D)6s 4D + 10 4f135p5(3D)6s 2D | |
| 77 | 514,413 | 514,677 | −264 | 7/2 | 37 4f135p5(3F)6s 4F + 22 4f135p5(3F)6s 2F + 15 4f135p5(1F)6s 2F | |
| 78 | 514,628 | 515,153 | −525 | 5/2 | 50 4f135p5(3F)6s 4F + 16 4f135p5(3G)6s 4G + 14 4f135p5(1F)6s 2F | |
| 79 | 516,493 | 515,725 | 768 | 5/2 | 24 4f135p5(3G)5d 2F + 14 4f135p5(3F)5d 2F + 11 4f135p5(1D)5d 2F | |
| 80 | 521,876 | 522,299 | −423 | 5/2 | 35 4f125p6(1S)5d 2D + 26 4f135p5(3F)6s 2F + 10 4f135p5(3D)6s 4D | |
| 81 | 522,610 | 521,487 | 1123 | 5/2 | 36 4f125p6(1S)5d 2D + 25 4f135p5(3F)6s 2F + 10 4f135p5(3D)6s 4D | |
| 82 | 522,881 | 522,986 | −105 | 3/2 | 41 4f125p6(1S)5d 2D + 26 4f135p5(3G)5d 2D + 7 4f125p6(3P)5d 2D | |
| 83 | 527,376 | 527,853 | −477 | 7/2 | 46 4f135p5(1G)6s 2G + 29 4f135p5(3G)6s 4G + 23 4f135p5(3G)6s 2G | |
| 84 | 528,462 | 528,388 | 74 | 1/2 | 28 4f145p4(1D)5d 2S + 17 4f145p4(3P)5d 2P + 8 4f135p5(3D)5d 2S | |
| 85 | 528,652 | 528,582 | 70 | 3/2 | 65 4f135p5(3D)6s 2D + 30 4f135p5(3D)6s 4D | |
| 86 | 567,191 | 565,985 | 1206 | 3/2 | 28 4f145p4(3P)5d 2D + 28 4f145p4(1S)5d 2D + 10 4f145p4(3P)5d 2P | |
| 87 | 568,644 | 567,872 | 772 | 3/2 | 77 4f145p4(3P)6s 4P + 13 4f145p4(3P)6s 2P | |
| 88 | 572,004 | 572,684 | −680 | 1/2 | 66 4f145p4(3P)6s 2P + 32 4f145p4(3P)6s 4P | |
| 89 | 581,635 | 582,142 | −507 | 5/2 | 60 4f145p4(1D)6s 2D + 18 4f145p4(3P)6s 4P + 7 4f125p6(3F)6s 2F | |
| 90 | 583,560 | 583,744 | −184 | 3/2 | 60 4f145p4(1D)6s 2D + 23 4f145p4(3P)6s 2P + 8 4f125p6(3F)6s 4F | |
| 91 | 594,941 | 594,876 | 65 | 7/2 | 56 4f135p5(3D)6s 4D + 23 4f135p5(3F)6s 4F + 11 4f135p5(1F)6s 2F | |
| 92 | 597,436 | 597,803 | −367 | 5/2 | 49 4f135p5(3D)6s 2D + 14 4f135p5(3F)6s 4F + 13 4f135p5(3D)6s 4D | |
| 93 | 598,904 | 598,949 | −45 | 7/2 | 39 4f135p5(1G)6s 2G + 21 4f135p5(3F)6s 2F + 20 4f135p5(3G)6s 4G | |
| 94 | 599,423 | 599,274 | 149 | 9/2 | 44 4f135p5(1G)6s 2G + 25 4f135p5(3G)6s 4G + 19 4f135p5(3F)6s 4F | |
| 95 | 609,206 | 609,104 | 102 | 5/2 | 73 4f135p5(3G)6s 4G + 18 4f135p5(1F)6s 2F | |
| 96 | 611,283 | 611,555 | −272 | 7/2 | 50 4f135p5(3G)6s 2G + 27 4f135p5(3G)6s 4G + 16 4f135p5(1F)6s 2F | |
| 97 | 621,343 | 620,931 | 412 | 5/2 | 39 4f135p5(1D)6s 2D + 19 4f135p5(3F)6s 2F + 14 4f135p5(3D)6s 4D | |
| 98 | 622,123 | 621,607 | 516 | 3/2 | 40 4f135p5(1D)6s 2D + 28 4f135p5(3F)6s 4F + 9 4f135p5(3D)6s 4D | |
| Indexes a | Wavelength b | Lower Odd Level c | Upper Even Level c | ||||||
|---|---|---|---|---|---|---|---|---|---|
| λexp (Å) | λRitz (Å) | E (cm−1) | J | E (cm−1) | J | log gf d | gA (s-1) d | CF e | |
| 1° − 97 | 160.940 | 160.942 | 0 | 3.5 | 621,343 | 2.5 | −2.58 | 6.81E + 08 | 0.003 |
| 2° − 98 | 161.057 | 161.059 | 1233 | 1.5 | 622,123 | 1.5 | −2.41 | 1.01E + 09 | 0.045 |
| 2° − 97 | 161.260 | 161.262 | 1233 | 1.5 | 621,343 | 2.5 | −1.26 | 1.40E + 10 | 0.333 |
| 1° − 96 | 163.596 | 163.590 | 0 | 3.5 | 611,283 | 3.5 | −2.30 | 1.24E + 09 | 0.007 |
| 1° − 95 | 164.143 | 164.148 | 0 | 3.5 | 609,206 | 2.5 | −2.78 | 4.15E + 08 | 0.014 |
| 2° − 95 | 164.479 | 164.481 | 1233 | 1.5 | 609,206 | 2.5 | −3.29 | 1.27E + 08 | 0.226 |
| 3° − 98 | 165.369 | 165.368 | 17,410 | 2.5 | 622,123 | 1.5 | −0.26 | 1.34E + 11 | 0.854 |
| 3° − 97 | 165.583 | 165.581 | 17,410 | 2.5 | 621,343 | 2.5 | −0.42 | 9.25E + 10 | 0.609 |
| 1° − 94 | 166.827 | 166.827 | 0 | 3.5 | 599,423 | 4.5 | 0.15 | 3.39E + 11 | 0.872 |
| 1° − 93 | 166.971 | 166.972 | 0 | 3.5 | 598,904 | 3.5 | −0.22 | 1.44E + 11 | 0.558 |
| 1° − 92 | 167.382 | 167.382 | 0 | 3.5 | 597,436 | 2.5 | −0.04 | 2.16E + 11 | 0.721 |
| 1° − 91 | 168.084 | 168.084 | 0 | 3.5 | 594,941 | 3.5 | −0.56 | 6.57E + 10 | 0.820 |
| 3° − 96 | 168.381 | 168.386 | 17,410 | 2.5 | 611,283 | 3.5 | 0.05 | 2.62E + 11 | 0.730 |
| 3° − 95 | 168.980 | 168.977 | 17,410 | 2.5 | 609,206 | 2.5 | −0.59 | 6.03E + 10 | 0.778 |
| 2° − 90 | 171.727 | 171.725 | 1233 | 1.5 | 583,560 | 1.5 | −0.80 | 3.56E + 10 | 0.131 |
| 1° − 89 | 171.929 | 0 | 3.5 | 581,635 | 2.5 | −2.76 | 3.98E + 08 | 0.038 | |
| 3° − 93 | 171.973 | 171.971 | 17,410 | 2.5 | 598,904 | 3.5 | −1.70 | 4.48E + 09 | 0.013 |
| 2° − 89 | 172.295 | 172.294 | 1233 | 1.5 | 581,635 | 2.5 | −0.19 | 1.46E + 11 | 0.641 |
| 3° − 91 | 173.151 | 17,410 | 2.5 | 594,941 | 3.5 | −2.67 | 4.74E + 08 | 0.026 | |
| 2° − 88 | 175.199 | 175.202 | 1233 | 1.5 | 572,004 | 0.5 | −0.58 | 5.76E + 10 | 0.632 |
| 2° − 87 | 176.237 | 176.239 | 1233 | 1.5 | 568,644 | 1.5 | −0.80 | 3.38E + 10 | 0.039 |
| 3° − 90 | 176.630 | 176.632 | 17,410 | 2.5 | 583,560 | 1.5 | −1.27 | 1.15E + 10 | 0.701 |
| 2° − 86 | 176.694 | 176.692 | 1233 | 1.5 | 567,191 | 1.5 | −0.75 | 3.77E + 10 | 0.030 |
| 3° − 89 | 177.232 | 177.234 | 17,410 | 2.5 | 581,635 | 2.5 | −1.36 | 9.27E + 09 | 0.591 |
| 3° − 87 | 181.410 | 181.411 | 17,410 | 2.5 | 568,644 | 1.5 | −1.07 | 1.74E + 10 | 0.134 |
| 3° − 86 | 181.888 | 181.891 | 17,410 | 2.5 | 567,191 | 1.5 | −0.67 | 4.28E + 10 | 0.176 |
| 4° − 98 | 187.608 | 187.617 | 89,123 | 0.5 | 622,123 | 1.5 | −1.50 | 5.93E + 09 | 0.256 |
| 2° − 85 | 189.603 | 1233 | 1.5 | 528,652 | 1.5 | −2.44 | 6.70E + 08 | 0.083 | |
| 1° − 83 | 189.616 | 189.618 | 0 | 3.5 | 527,376 | 3.5 | −1.17 | 1.25E + 10 | 0.452 |
| 2° − 84 | 189.667 | 189.671 | 1233 | 1.5 | 528,462 | 0.5 | −0.59 | 4.81E + 10 | 0.030 |
| 1° − 81 | 191.348 | 191.347 | 0 | 3.5 | 522,610 | 2.5 | −0.67 | 3.89E + 10 | 0.082 |
| 1° − 80 | 191.617 | 191.616 | 0 | 3.5 | 521,876 | 2.5 | −0.46 | 6.38E + 10 | 0.102 |
| 2° − 82 | 191.700 | 1233 | 1.5 | 522,881 | 1.5 | −1.10 | 1.46E + 10 | 0.069 | |
| 2° − 81 | 191.800 | 1233 | 1.5 | 522,610 | 2.5 | −3.00 | 1.78E + 08 | 0.001 | |
| 2° − 80 | 192.070 | 192.070 | 1233 | 1.5 | 521,876 | 2.5 | −2.25 | 1.02E + 09 | 0.007 |
| 1° − 79 | 193.614 | 193.613 | 0 | 3.5 | 516,493 | 2.5 | −0.96 | 1.95E + 10 | 0.029 |
| 2° − 79 | 194.077 | 194.077 | 1233 | 1.5 | 516,493 | 2.5 | −1.37 | 7.51E + 09 | 0.095 |
| 1° − 78 | 194.315 | 194.315 | 0 | 3.5 | 514,628 | 2.5 | −2.94 | 2.05E + 08 | 0.011 |
| 1° − 77 | 194.397 | 194.396 | 0 | 3.5 | 514,413 | 3.5 | −0.59 | 4.58E + 10 | 0.047 |
| 1° − 76 | 194.527 | 194.529 | 0 | 3.5 | 514,063 | 2.5 | 0.09 | 2.19E + 11 | 0.840 |
| 2° − 76 | 194.998 | 194.996 | 1233 | 1.5 | 514,063 | 2.5 | −1.46 | 6.02E + 09 | 0.403 |
| 1° − 75 | 195.021 | 195.012 | 0 | 3.5 | 512,790 | 3.5 | −1.64 | 4.01E + 09 | 0.003 |
| 3° − 85 | 195.598 | 195.602 | 17,410 | 2.5 | 528,652 | 1.5 | 0.10 | 2.19E + 11 | 0.790 |
| 3° − 83 | 196.093 | 196.092 | 17,410 | 2.5 | 527,376 | 3.5 | 0.20 | 2.76E + 11 | 0.866 |
| 3° − 82 | 197.835 | 197.835 | 17,410 | 2.5 | 522,881 | 1.5 | 0.63 | 7.37E + 11 | 0.514 |
| 3° − 81 | 197.941 | 197.941 | 17,410 | 2.5 | 522,610 | 2.5 | −1.91 | 2.07E + 09 | 0.005 |
| 1° − 73 | 198.171 | 198.171 | 0 | 3.5 | 504,615 | 4.5 | 0.46 | 4.87E + 11 | 0.850 |
| 3° − 80 | 198.229 | 198.229 | 17,410 | 2.5 | 521,876 | 2.5 | 0.49 | 5.31E + 11 | 0.659 |
| 1° − 72 | 198.779 | 198.779 | 0 | 3.5 | 503,071 | 3.5 | 0.67 | 7.94E + 11 | 0.742 |
| 1° − 71 | 199.875 | 199.875 | 0 | 3.5 | 500,313 | 2.5 | −1.02 | 1.58E + 10 | 0.098 |
| 3° − 79 | 200.367 | 200.367 | 17,410 | 2.5 | 516,493 | 2.5 | 1.04 | 1.82E + 12 | 0.555 |
| 2° − 71 | 200.369 | 1233 | 1.5 | 500,313 | 2.5 | −2.31 | 8.23E + 08 | 0.183 | |
| 1° − 70 | 200.483 | 200.484 | 0 | 3.5 | 498,792 | 3.5 | 1.14 | 2.31E + 12 | 0.467 |
| 1° − 68 | 200.787 | 200.788 | 0 | 3.5 | 498,037 | 2.5 | 1.05 | 1.90E + 12 | 0.572 |
| 2° − 69 | 201.079 | 201.083 | 1233 | 1.5 | 498,541 | 1.5 | 0.09 | 2.05E + 11 | 0.358 |
| 3° − 78 | 201.119 | 201.119 | 17,410 | 2.5 | 514,628 | 2.5 | −0.85 | 2.33E + 10 | 0.219 |
| 3° − 77 | 201.205 | 201.206 | 17,410 | 2.5 | 514,413 | 3.5 | 0.83 | 1.13E + 12 | 0.562 |
| 2° − 68 | 201.288 | 201.287 | 1233 | 1.5 | 498,037 | 2.5 | 0.12 | 2.17E + 11 | 0.196 |
| 3° − 76 | 201.348 | 17,410 | 2.5 | 514,063 | 2.5 | −2.01 | 1.61E + 09 | 0.026 | |
| 1° − 67 | 201.739 | 201.739 | 0 | 3.5 | 495,690 | 4.5 | 1.29 | 3.22E + 12 | 0.577 |
| 3° − 75 | 201.864 | 201.865 | 17,410 | 2.5 | 512,790 | 3.5 | 0.98 | 1.56E + 12 | 0.446 |
| 4° − 90 | 202.250 | 202.250 | 89,123 | 0.5 | 583,560 | 1.5 | −0.07 | 1.39E + 11 | 0.835 |
| 2° − 66 | 203.623 | 203.623 | 1233 | 1.5 | 492,337 | 0.5 | 0.62 | 6.72E + 11 | 0.563 |
| 3° − 74 | 205.221 | 205.220 | 17,410 | 2.5 | 504,691 | 1.5 | 0.53 | 5.37E + 11 | 0.474 |
| 2° − 65 | 205.479 | 205.479 | 1233 | 1.5 | 487,901 | 1.5 | 0.32 | 3.29E + 11 | 0.754 |
| 3° − 72 | 205.905 | 17,410 | 2.5 | 503,071 | 3.5 | −3.56 | 4.31E + 07 | 0.000 | |
| 1° − 64 | 206.111 | 0 | 3.5 | 485,175 | 2.5 | −1.20 | 9.98E + 09 | 0.028 | |
| 2° − 64 | 206.634 | 206.636 | 1233 | 1.5 | 485,175 | 2.5 | 0.29 | 3.08E + 11 | 0.518 |
| 3° − 71 | 207.081 | 17,410 | 2.5 | 500,313 | 2.5 | −1.64 | 3.56E + 09 | 0.020 | |
| 4° − 88 | 207.092 | 207.090 | 89,123 | 0.5 | 572,004 | 0.5 | −0.31 | 7.59E + 10 | 0.784 |
| 2° − 63 | 207.466 | 207.465 | 1233 | 1.5 | 483,243 | 1.5 | 0.27 | 2.86E + 11 | 0.266 |
| 1° − 62 | 207.690 | 207.696 | 0 | 3.5 | 481,473 | 2.5 | −0.69 | 3.20E + 10 | 0.364 |
| 3° − 70 | 207.736 | 207.735 | 17,410 | 2.5 | 498,792 | 3.5 | −0.80 | 2.49E + 10 | 0.027 |
| 3° − 69 | 207.850 | 207.844 | 17,410 | 2.5 | 498,541 | 1.5 | −1.23 | 9.15E + 09 | 0.025 |
| 1° − 61 | 207.884 | 207.885 | 0 | 3.5 | 481,035 | 2.5 | −0.37 | 6.55E + 10 | 0.216 |
| 3° − 68 | 208.062 | 17,410 | 2.5 | 498,037 | 2.5 | −3.79 | 2.56E + 07 | 0.000 | |
| 2° − 62 | 208.227 | 208.229 | 1233 | 1.5 | 481,473 | 2.5 | −0.21 | 9.49E + 10 | 0.160 |
| 2° − 61 | 208.420 | 208.419 | 1233 | 1.5 | 481,035 | 2.5 | 0.83 | 1.04E + 12 | 0.638 |
| 4° − 87 | 208.543 | 208.541 | 89,123 | 0.5 | 568,644 | 1.5 | 0.42 | 4.04E + 11 | 0.534 |
| 4° − 86 | 209.175 | 209.175 | 89,123 | 0.5 | 567,191 | 1.5 | 0.62 | 6.31E + 11 | 0.502 |
| 2° − 60 | 211.027 | 211.022 | 1233 | 1.5 | 475,117 | 1.5 | 0.28 | 2.87E + 11 | 0.369 |
| 1° − 59 | 213.436 | 213.437 | 0 | 3.5 | 468,523 | 2.5 | −2.91 | 1.81E + 08 | 0.001 |
| 1° − 58 | 213.661 | 213.660 | 0 | 3.5 | 468,034 | 2.5 | −3.04 | 1.33E + 08 | 0.000 |
| 3° − 64 | 213.785 | 213.783 | 17,410 | 2.5 | 485,175 | 2.5 | −1.03 | 1.36E + 10 | 0.024 |
| 2° − 59 | 214.001 | 214.000 | 1233 | 1.5 | 468,523 | 2.5 | −2.50 | 4.61E + 09 | 0.013 |
| 2° − 58 | 214.229 | 214.224 | 1233 | 1.5 | 468,034 | 2.5 | −0.09 | 1.17E + 11 | 0.428 |
| 1° − 57 | 214.488 | 214.491 | 0 | 3.5 | 466,219 | 2.5 | −2.31 | 7.13E + 08 | 0.002 |
| 2° − 57 | 215.055 | 215.060 | 1233 | 1.5 | 466,219 | 2.5 | −0.21 | 8.80E + 10 | 0.439 |
| 3° − 62 | 215.496 | 215.488 | 17,410 | 2.5 | 481,473 | 2.5 | −2.22 | 8.60E + 08 | 0.023 |
| 3° − 61 | 215.692 | 215.692 | 17,410 | 2.5 | 481,035 | 2.5 | −1.75 | 2.57E + 09 | 0.012 |
| 2° − 56 | 216.596 | 216.594 | 1233 | 1.5 | 462,927 | 1.5 | −0.71 | 2.79E + 10 | 0.187 |
| 1° − 55 | 217.601 | 217.595 | 0 | 3.5 | 459,570 | 2.5 | −2.39 | 5.78E + 08 | 0.001 |
| 2° − 55 | 218.174 | 218.180 | 1233 | 1.5 | 459,570 | 2.5 | −2.25 | 7.95E + 08 | 0.004 |
| 1° − 53 | 218.429 | 218.429 | 0 | 3.5 | 457,815 | 4.5 | −0.93 | 1.66E + 10 | 0.028 |
| 3° − 60 | 218.477 | 218.480 | 17,410 | 2.5 | 475,117 | 1.5 | −2.25 | 7.91E + 08 | 0.003 |
| 1° − 52 | 218.507 | 218.507 | 0 | 3.5 | 457,652 | 2.5 | −1.24 | 8.04E + 09 | 0.011 |
| 2° − 54 | 218.747 | 218.748 | 1233 | 1.5 | 458,380 | 1.5 | −0.88 | 1.85E + 10 | 0.063 |
| 2° − 52 | 219.097 | 219.097 | 1233 | 1.5 | 457,652 | 2.5 | −2.89 | 1.76E + 08 | 0.002 |
| 1° − 51 | 220.239 | 220.232 | 0 | 3.5 | 454,067 | 3.5 | −3.13 | 1.02E + 08 | 0.000 |
| 2° − 50 | 221.443 | 221.441 | 1233 | 1.5 | 452,821 | 1.5 | −0.49 | 4.43E + 10 | 0.075 |
| 3° − 59 | 221.674 | 17,410 | 2.5 | 468,523 | 2.5 | −2.13 | 1.01E + 09 | 0.005 | |
| 3° − 58 | 221.908 | 221.915 | 17,410 | 2.5 | 468,034 | 2.5 | −0.80 | 2.14E + 10 | 0.030 |
| 3° − 57 | 222.818 | 222.812 | 17,410 | 2.5 | 466,219 | 2.5 | −1.15 | 9.46E + 09 | 0.018 |
| 1° − 49 | 223.260 | 223.260 | 0 | 3.5 | 447,909 | 2.5 | −1.33 | 6.17E + 09 | 0.028 |
| 2° − 49 | 223.876 | 1233 | 1.5 | 447,909 | 2.5 | −1.59 | 3.39E + 09 | 0.048 | |
| 3° − 56 | 224.458 | 17,410 | 2.5 | 462,927 | 1.5 | −2.63 | 3.12E + 08 | 0.002 | |
| 1° − 48 | 224.573 | 224.575 | 0 | 3.5 | 445,286 | 2.5 | −2.38 | 5.55E + 08 | 0.002 |
| 2° − 48 | 225.203 | 225.198 | 1233 | 1.5 | 445,286 | 2.5 | −1.61 | 3.22E + 09 | 0.026 |
| 3° − 55 | 226.162 | 17,410 | 2.5 | 459,570 | 2.5 | −3.04 | 1.20E + 08 | 0.000 | |
| 3° − 54 | 226.773 | 17,410 | 2.5 | 458,380 | 1.5 | −2.01 | 1.27E + 09 | 0.003 | |
| 3° − 52 | 227.148 | 17,410 | 2.5 | 457,652 | 2.5 | −2.64 | 2.96E + 08 | 0.000 | |
| 1° − 47 | 227.497 | 227.500 | 0 | 3.5 | 439,561 | 3.5 | −0.89 | 1.64E + 10 | 0.091 |
| 4° − 85 | 227.519 | 227.516 | 89,123 | 0.5 | 528,652 | 1.5 | −2.26 | 7.04E + 08 | 0.057 |
| 4° − 84 | 227.617 | 227.615 | 89,123 | 0.5 | 528,462 | 0.5 | 0.57 | 4.79E + 11 | 0.552 |
| 3° − 51 | 229.011 | 229.013 | 17,410 | 2.5 | 454,067 | 3.5 | −0.90 | 1.58E + 10 | 0.023 |
| 2° − 46 | 229.402 | 1233 | 1.5 | 437,149 | 2.5 | −1.04 | 1.16E + 10 | 0.072 | |
| 1° − 45 | 229.541 | 229.538 | 0 | 3.5 | 435,658 | 3.5 | −2.02 | 1.21E + 09 | 0.007 |
| 1° − 44 | 229.590 | 229.589 | 0 | 3.5 | 435,561 | 2.5 | −1.07 | 1.07E + 10 | 0.047 |
| 3° − 50 | 229.666 | 229.668 | 17,410 | 2.5 | 452,821 | 1.5 | −1.53 | 3.67E + 09 | 0.007 |
| 2° − 44 | 230.246 | 230.241 | 1233 | 1.5 | 435,561 | 2.5 | −1.01 | 1.23E + 10 | 0.070 |
| 4° − 82 | 230.544 | 230.543 | 89,123 | 0.5 | 522,881 | 1.5 | −0.60 | 3.17E + 10 | 0.107 |
| 1° − 43 | 230.964 | 230.967 | 0 | 3.5 | 432,963 | 2.5 | −1.44 | 4.60E + 09 | 0.019 |
| 2° − 43 | 231.629 | 231.626 | 1233 | 1.5 | 432,963 | 2.5 | −0.74 | 2.28E + 10 | 0.064 |
| 1° − 42 | 232.176 | 232.176 | 0 | 3.5 | 430,708 | 3.5 | −1.18 | 8.25E + 09 | 0.049 |
| 3° − 49 | 232.288 | 232.289 | 17,410 | 2.5 | 447,909 | 2.5 | −0.84 | 1.80E + 10 | 0.084 |
| 1° − 41 | 233.225 | 233.221 | 0 | 3.5 | 428,777 | 3.5 | −0.81 | 1.89E + 10 | 0.073 |
| 1° − 40 | 233.525 | 233.527 | 0 | 3.5 | 428,216 | 3.5 | −0.49 | 3.93E + 10 | 0.161 |
| 3° − 48 | 233.709 | 233.713 | 17,410 | 2.5 | 445,286 | 2.5 | −0.64 | 2.77E + 10 | 0.122 |
| 2° − 39 | 234.211 | 1233 | 1.5 | 428,199 | 1.5 | −2.99 | 1.25E + 08 | 0.001 | |
| 1° − 37 | 235.418 | 235.415 | 0 | 3.5 | 424,781 | 2.5 | −1.23 | 7.03E + 09 | 0.055 |
| 2° − 38 | 235.509 | 235.510 | 1233 | 1.5 | 425,843 | 1.5 | −2.07 | 1.02E + 09 | 0.126 |
| 2° − 37 | 236.101 | 1233 | 1.5 | 424,781 | 2.5 | −2.88 | 1.59E + 08 | 0.007 | |
| 3° − 47 | 236.884 | 236.882 | 17,410 | 2.5 | 439,561 | 3.5 | −1.01 | 1.16E + 10 | 0.040 |
| 1° − 36 | 238.202 | 0 | 3.5 | 419,811 | 2.5 | −3.32 | 5.62E + 07 | 0.000 | |
| 3° − 46 | 238.243 | 238.243 | 17,410 | 2.5 | 437,149 | 2.5 | −0.95 | 1.32E + 10 | 0.063 |
| 1° − 35 | 238.330 | 238.331 | 0 | 3.5 | 419,585 | 3.5 | −2.28 | 6.19E + 08 | 0.010 |
| 2° − 36 | 238.904 | 1233 | 1.5 | 419,811 | 2.5 | −3.13 | 8.56E + 07 | 0.011 | |
| 1° − 34 | 239.004 | 239.004 | 0 | 3.5 | 418,403 | 4.5 | −1.03 | 1.08E + 10 | 0.057 |
| 3° − 45 | 239.089 | 239.093 | 17,410 | 2.5 | 435,658 | 3.5 | −0.59 | 3.01E + 10 | 0.156 |
| 3° − 44 | 239.142 | 239.148 | 17,410 | 2.5 | 435,561 | 2.5 | −1.21 | 7.14E + 09 | 0.035 |
| 1° − 32 | 240.107 | 240.107 | 0 | 3.5 | 416,481 | 4.5 | −0.47 | 3.94E + 10 | 0.240 |
| 2° − 33 | 240.292 | 1233 | 1.5 | 417,394 | 1.5 | −3.24 | 6.63E + 07 | 0.004 | |
| 1° − 31 | 240.468 | 240.470 | 0 | 3.5 | 415,852 | 2.5 | −2.40 | 4.62E + 08 | 0.007 |
| 4° − 74 | 240.634 | 240.635 | 89,123 | 0.5 | 504,691 | 1.5 | −0.35 | 5.14E + 10 | 0.150 |
| 1° − 30 | 241.037 | 241.029 | 0 | 3.5 | 414,888 | 3.5 | −1.21 | 7.09E + 09 | 0.024 |
| 2° − 31 | 241.183 | 241.185 | 1233 | 1.5 | 415,852 | 2.5 | −2.36 | 4.97E + 08 | 0.065 |
| 1° − 29 | 241.867 | 241.867 | 0 | 3.5 | 413,450 | 4.5 | −0.27 | 6.16E + 10 | 0.193 |
| 3° − 42 | 241.956 | 17,410 | 2.5 | 430,708 | 3.5 | −2.16 | 7.91E + 08 | 0.007 | |
| 1° − 28 | 242.819 | 242.817 | 0 | 3.5 | 411,832 | 3.5 | −1.36 | 4.97E + 09 | 0.071 |
| 1° − 27 | 242.829 | 242.825 | 0 | 3.5 | 411,819 | 2.5 | −2.02 | 1.07E + 09 | 0.006 |
| 3° − 41 | 243.088 | 243.092 | 17,410 | 2.5 | 428,777 | 3.5 | −2.11 | 8.72E + 08 | 0.007 |
| 3° − 40 | 243.426 | 243.424 | 17,410 | 2.5 | 428,216 | 3.5 | −1.54 | 3.23E + 09 | 0.012 |
| 3° − 39 | 243.434 | 243.434 | 17,410 | 2.5 | 428,199 | 1.5 | −1.51 | 3.45E + 09 | 0.121 |
| 1° − 26 | 243.518 | 243.514 | 0 | 3.5 | 410,654 | 3.5 | −2.01 | 1.11E + 09 | 0.004 |
| 2° − 27 | 243.551 | 243.554 | 1233 | 1.5 | 411,819 | 2.5 | −1.96 | 1.23E + 09 | 0.073 |
| 1° − 24 | 244.095 | 0 | 3.5 | 409,676 | 2.5 | −3.96 | 1.24E + 07 | 0.000 | |
| 4° − 69 | 244.249 | 89,123 | 0.5 | 498,541 | 1.5 | 0.08 | 1.33E + 11 | 0.183 | |
| 1° − 23 | 244.281 | 244.283 | 0 | 3.5 | 409,362 | 2.5 | −1.30 | 5.53E + 09 | 0.088 |
| 2° − 25 | 244.484 | 1233 | 1.5 | 410,258 | 1.5 | −2.54 | 3.21E + 08 | 0.005 | |
| 2° − 24 | 244.833 | 244.832 | 1233 | 1.5 | 409,676 | 2.5 | −1.36 | 4.86E + 09 | 0.473 |
| 3° − 38 | 244.839 | 244.838 | 17,410 | 2.5 | 425,843 | 1.5 | −1.19 | 7.21E + 09 | 0.142 |
| 1° − 21 | 245.046 | 245.046 | 0 | 3.5 | 408,086 | 3.5 | −0.81 | 1.71E + 10 | 0.041 |
| 2° − 22 | 245.334 | 245.339 | 1233 | 1.5 | 408,833 | 1.5 | −2.00 | 1.11E + 09 | 0.079 |
| 3° − 37 | 245.474 | 245.476 | 17,410 | 2.5 | 424,781 | 2.5 | −1.26 | 6.09E + 09 | 0.060 |
| 1° − 20 | 246.362 | 246.362 | 0 | 3.5 | 405,907 | 4.5 | −0.73 | 2.06E + 10 | 0.359 |
| 4° − 66 | 248.007 | 248.007 | 89,123 | 0.5 | 492,337 | 0.5 | −1.01 | 1.07E + 10 | 0.016 |
| 3° − 36 | 248.508 | 248.508 | 17,410 | 2.5 | 419,811 | 2.5 | −0.71 | 2.11E + 10 | 0.080 |
| 3° − 35 | 248.649 | 248.648 | 17,410 | 2.5 | 419,585 | 3.5 | −0.61 | 2.65E + 10 | 0.130 |
| 1° − 19 | 248.765 | 248.766 | 0 | 3.5 | 401,984 | 2.5 | −0.37 | 4.61E + 10 | 0.069 |
| 2° − 19 | 249.533 | 249.532 | 1233 | 1.5 | 401,984 | 2.5 | 0.03 | 1.16E + 11 | 0.551 |
| 1° − 18 | 249.873 | 249.873 | 0 | 3.5 | 400,203 | 4.5 | −0.65 | 2.39E + 10 | 0.152 |
| 3° − 33 | 250.010 | 250.010 | 17,410 | 2.5 | 417,394 | 1.5 | −1.13 | 7.92E + 09 | 0.141 |
| 4° − 65 | 250.766 | 89,123 | 0.5 | 487,901 | 1.5 | −2.70 | 2.11E + 08 | 0.002 | |
| 1° − 17 | 250.811 | 250.811 | 0 | 3.5 | 398,707 | 4.5 | −1.06 | 9.19E + 09 | 0.031 |
| 3° − 31 | 250.978 | 250.978 | 17,410 | 2.5 | 415,852 | 2.5 | −1.01 | 1.03E + 10 | 0.057 |
| 1° − 16 | 251.500 | 251.501 | 0 | 3.5 | 397,612 | 2.5 | −1.25 | 5.87E + 09 | 0.041 |
| 3° − 30 | 251.584 | 251.586 | 17,410 | 2.5 | 414,888 | 3.5 | −0.43 | 3.94E + 10 | 0.150 |
| 1° − 14 | 252.203 | 252.204 | 0 | 3.5 | 396,505 | 3.5 | −0.34 | 4.82E + 10 | 0.116 |
| 2° − 16 | 252.285 | 252.284 | 1233 | 1.5 | 397,612 | 2.5 | −1.05 | 9.30E + 09 | 0.413 |
| 2° − 15 | 252.740 | 252.742 | 1233 | 1.5 | 396,894 | 1.5 | 0.08 | 1.27E + 11 | 0.330 |
| 1° − 12 | 252.862 | 252.863 | 0 | 3.5 | 395,471 | 3.5 | −1.54 | 3.04E + 09 | 0.001 |
| 1° − 11 | 252.989 | 252.988 | 0 | 3.5 | 395,276 | 2.5 | −1.50 | 3.31E + 09 | 0.027 |
| 3° − 28 | 253.534 | 253.536 | 17,410 | 2.5 | 411,832 | 3.5 | −0.92 | 1.23E + 10 | 0.110 |
| 3° − 27 | 253.541 | 253.544 | 17,410 | 2.5 | 411,819 | 2.5 | −0.04 | 9.56E + 10 | 0.131 |
| 2° − 13 | 253.653 | 253.652 | 1233 | 1.5 | 395,474 | 0.5 | −0.44 | 3.73E + 10 | 0.140 |
| 4° − 63 | 253.726 | 253.730 | 89,123 | 0.5 | 483,243 | 1.5 | −1.49 | 3.35E + 09 | 0.013 |
| 2° − 11 | 253.779 | 253.779 | 1233 | 1.5 | 395,276 | 2.5 | −2.40 | 4.08E + 08 | 0.024 |
| 1° − 10 | 253.812 | 253.812 | 0 | 3.5 | 393,992 | 3.5 | 0.09 | 1.26E + 11 | 0.101 |
| 3° − 26 | 254.294 | 254.295 | 17,410 | 2.5 | 410,654 | 3.5 | 0.01 | 1.04E + 11 | 0.143 |
| 3° − 25 | 254.551 | 254.551 | 17,410 | 2.5 | 410,258 | 1.5 | −0.02 | 9.92E + 10 | 0.190 |
| 3° − 24 | 254.928 | 254.929 | 17,410 | 2.5 | 409,676 | 2.5 | −0.92 | 1.23E + 10 | 0.039 |
| 3° − 23 | 255.140 | 255.133 | 17,410 | 2.5 | 409,362 | 2.5 | −2.03 | 9.57E + 08 | 0.013 |
| 1° − 9 | 255.401 | 255.401 | 0 | 3.5 | 391,541 | 4.5 | 0.32 | 2.16E + 11 | 0.165 |
| 3° − 22 | 255.479 | 255.478 | 17,410 | 2.5 | 408,833 | 1.5 | −0.99 | 1.05E + 10 | 0.076 |
| 3° − 21 | 255.967 | 255.967 | 17,410 | 2.5 | 408,086 | 3.5 | −0.40 | 4.09E + 10 | 0.115 |
| 1° − 8 | 258.592 | 258.596 | 0 | 3.5 | 386,704 | 2.5 | 0.05 | 1.10E + 11 | 0.210 |
| 4° − 60 | 259.069 | 259.071 | 89,123 | 0.5 | 475,117 | 1.5 | −0.86 | 1.39E + 10 | 0.048 |
| 2° − 8 | 259.419 | 259.423 | 1233 | 1.5 | 386,704 | 2.5 | −0.24 | 5.66E + 10 | 0.293 |
| 3° − 19 | 260.027 | 260.028 | 17,410 | 2.5 | 401,984 | 2.5 | −1.63 | 2.29E + 09 | 0.015 |
| 1° − 7 | 260.146 | 260.146 | 0 | 3.5 | 384,400 | 4.5 | −1.54 | 2.85E + 09 | 0.009 |
| 1° − 6 | 261.002 | 261.006 | 0 | 3.5 | 383,133 | 2.5 | −1.45 | 3.49E + 09 | 0.029 |
| 1° − 5 | 261.767 | 261.767 | 0 | 3.5 | 382,019 | 3.5 | −0.93 | 1.14E + 10 | 0.027 |
| 2° − 6 | 261.849 | 261.849 | 1233 | 1.5 | 383,133 | 2.5 | −2.18 | 6.41E + 08 | 0.004 |
| 1° − 4 | 262.537 | 262.537 | 0 | 3.5 | 380,899 | 4.5 | −1.28 | 5.12E + 09 | 0.005 |
| 3° − 16 | 263.018 | 17,410 | 2.5 | 397,612 | 2.5 | −2.22 | 5.79E + 08 | 0.004 | |
| 3° − 15 | 263.521 | 263.516 | 17,410 | 2.5 | 396,894 | 1.5 | −2.89 | 1.24E + 08 | 0.001 |
| 3° − 14 | 263.787 | 263.786 | 17,410 | 2.5 | 396,505 | 3.5 | −1.41 | 3.74E + 09 | 0.014 |
| 3° − 12 | 264.508 | 264.508 | 17,410 | 2.5 | 395,471 | 3.5 | −1.04 | 8.63E + 09 | 0.014 |
| 1° − 3 | 264.644 | 264.643 | 0 | 3.5 | 377,867 | 2.5 | −1.07 | 8.00E + 09 | 0.032 |
| 3° − 11 | 264.644 | 264.644 | 17,410 | 2.5 | 395,276 | 2.5 | −1.22 | 5.67E + 09 | 0.016 |
| 1° − 1 | 265.168 | 265.168 | 0 | 3.5 | 377,119 | 4.5 | −1.02 | 8.91E + 09 | 0.013 |
| 2° − 3 | 265.510 | 265.510 | 1233 | 1.5 | 377,867 | 2.5 | −1.26 | 5.18E + 09 | 0.031 |
| 2° − 2 | 265.919 | 265.919 | 1233 | 1.5 | 377,288 | 1.5 | −1.47 | 3.16E + 09 | 0.055 |
| 4° − 56 | 267.518 | 267.520 | 89,123 | 0.5 | 462,927 | 1.5 | −2.82 | 1.42E + 08 | 0.002 |
| 3° − 8 | 270.794 | 270.787 | 17,410 | 2.5 | 386,704 | 2.5 | −2.53 | 2.66E + 08 | 0.001 |
| 4° − 54 | 270.816 | 270.814 | 89,123 | 0.5 | 458,380 | 1.5 | −1.34 | 4.11E + 09 | 0.019 |
| 3° − 5 | 274.266 | 17,410 | 2.5 | 382,019 | 3.5 | −2.84 | 1.28E + 08 | 0.000 | |
| 4° − 50 | 274.953 | 89,123 | 0.5 | 452,821 | 1.5 | −1.07 | 7.47E + 09 | 0.022 | |
| 3° − 3 | 277.426 | 17,410 | 2.5 | 377,867 | 2.5 | −1.92 | 1.03E + 09 | 0.004 | |
| 4° − 39 | 294.919 | 89,123 | 0.5 | 428,199 | 1.5 | −3.08 | 6.41E + 07 | 0.003 | |
| 4° − 38 | 296.983 | 89,123 | 0.5 | 425,843 | 1.5 | −2.64 | 1.75E + 08 | 0.029 | |
| 4° − 33 | 304.626 | 89,123 | 0.5 | 417,394 | 1.5 | −2.92 | 8.72E + 07 | 0.008 | |
| 4° − 25 | 311.396 | 89,123 | 0.5 | 410,258 | 1.5 | −2.23 | 4.06E + 08 | 0.008 | |
| 4° − 22 | 312.783 | 89,123 | 0.5 | 408,833 | 1.5 | −3.21 | 4.21E + 07 | 0.004 | |
| 4° − 15 | 324.917 | 89,123 | 0.5 | 396,894 | 1.5 | −2.78 | 1.04E + 08 | 0.000 | |
| 4° − 13 | 326.423 | 89,123 | 0.5 | 395,474 | 0.5 | −2.44 | 2.28E + 08 | 0.002 | |
| 4° − 2 | 347.023 | 89,123 | 0.5 | 377,288 | 1.5 | −3.14 | 3.94E + 07 | 0.002 | |
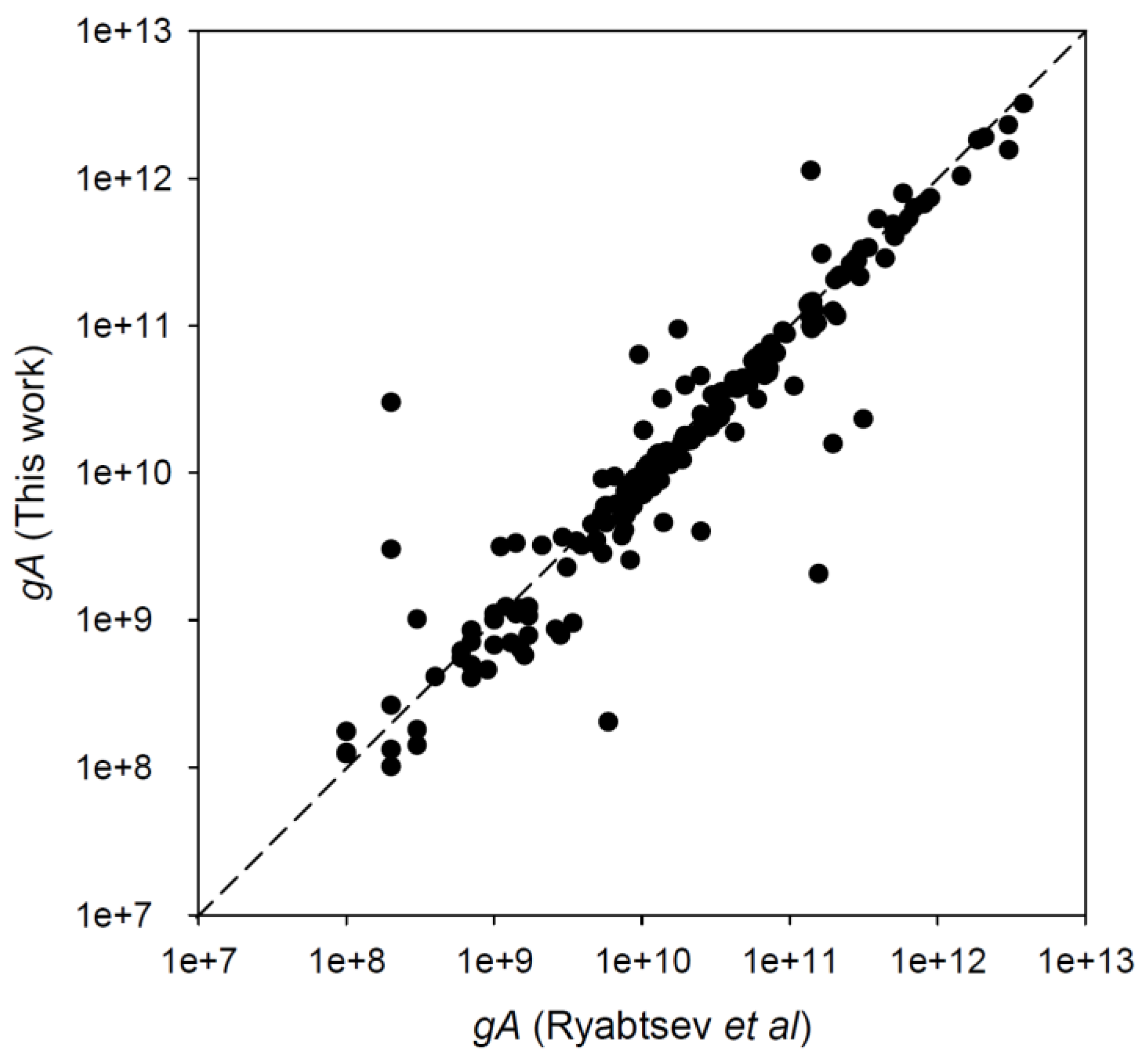
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Federici, G.; Skinner, C.H.; Brooks, J.N.; Coad, J.P.; Grisolia, C.; Haasz, A.A.; Hassanein, A.; Philipps, V.; Pitcher, C.S.; Roth, J.; et al. Plasma-material interactions in current tokamaks and their implications for next step fusion reactors. Nucl. Fusion 2001, 41, 1967–2138. [Google Scholar] [CrossRef]
- Neu, R.; Dux, R.; Kallenbach, A.; Pütterich, T.; Balden, M.; Fuchs, J.C.; Herrmann, A.; Maggi, C.F.; O’Mullane, M.; Pugno, R.; et al. Tungsten: An option for divertor and main chamber plasma facing components in future fusion devices. Nucl. Fusion 2005, 45, 209–218. [Google Scholar] [CrossRef]
- Pospieszczyk, A. Nuclear Fusion Research; Springer: Berlin, Germany, 2006. [Google Scholar]
- Skinner, C.H. Applications of EBIT to magnetic fusion diagnostics. Can. J. Phys. 2008, 86, 285–290. [Google Scholar] [CrossRef]
- Skinner, C.H. Atomic physics in the quest for fusion energy and ITER. Phys. Scr. 2009, T134, 014022. [Google Scholar] [CrossRef]
- Quinet, P.; Palmeri, P.; Biémont, E. Spectroscopic data for atomic tungsten transitions of interest in fusion plasma research. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 145005. [Google Scholar] [CrossRef]
- Nilsson, H.; Engström, L.; Lundberg, H.; Palmeri, P.; Fivet, V.; Quinet, P.; Biémont, E. Lifetime measurements and transition probability calculations in singly ionized tungsten (W II). Eur. Phys. J. D 2008, 49, 13–19. [Google Scholar] [CrossRef]
- Palmeri, P.; Quinet, P.; Fivet, V.; Biémont, E.; Nilsson, H.; Engström, L.; Lundberg, H. Lifetime measurements and calculated transition probabilities in W III. Phys. Scr. 2008, 78, 015304. [Google Scholar] [CrossRef]
- Enzonga Yoca, S.; Quinet, P.; Biémont, E. Configuration interaction and radiative decay rates in trebly ionized tungsten (W IV). J. Phys. B At. Mol. Opt. Phys. 2012, 45, 035001. [Google Scholar]
- Enzonga Yoca, S.; Quinet, P.; Palmeri, P.; Biémont, E. Comparative semi-empirical and ab initio atomic structure calculations in Yb-like tungsten W4+. J. Phys. B Mol. Opt. Phys. 2012, 45, 065001. [Google Scholar] [CrossRef]
- Enzonga Yoca, S.; Palmeri, P.; Quinet, P.; Jumet, G.; Biémont, E. Radiative properties and core-polarization effects in the W5+ ion. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 035002. [Google Scholar] [CrossRef]
- Quinet, P.; Vinogradoff, V.; Palmeri, P.; Biémont, E. Radiative decay rates for W I, W II and W III allowed and forbidden transitions of interest for spectroscopic diagnostics in fusion plasmas. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 144003. [Google Scholar] [CrossRef]
- Ryabtsev, A.N.; Kononov, E.Y.; Kildiyarova, R.R.; Tchang-Brillet, W.-Ü.L.; Wyart, J.-F. The spectrum of seven times ionized tungsten (W VIII) relevant to tokamak divertor plasmas. Phys. Scr. 2013, 87, 045303. [Google Scholar] [CrossRef]
- Kramida, A.E.; Shirai, T. Energy levels and spectral lines of tungsten, W III through W LXXIV. At. Data Nucl. Data Tables 2009, 95, 305–474. [Google Scholar] [CrossRef]
- Sugar, J.; Kaufman, V. Seventh spectrum of tungsten (W VII); resonance lines of Hf V. Phys. Rev. A 1975, 12, 994–1012. [Google Scholar] [CrossRef]
- Carlson, T.A.; Nestor, C.W., Jr.; Wasserman, N.; McDowell, J.D. Calculated ionization potentials for multiply charged ions. At. Data Nucl. Data Tables 1970, 2, 63–99. [Google Scholar] [CrossRef]
- Veres, G.; Bakos, J.S.; Kardon, B. Energy levels and the vacuum ultraviolet spectrum of W VIII. J. Quant. Spectrosc. Rad. Transfer 1996, 56, 295–301. [Google Scholar] [CrossRef]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Quinet, P.; Hansen, J.E. The influence of core excitations on energies and oscillator strengths of iron group elements. J. Phys. B At. Mol. Opt. Phys. 1995, 28, L213–L220. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deprince, J.; Quinet, P. Detailed Analysis of Configuration Interaction and Calculation of Radiative Transition Rates in Seven Times Ionized Tungsten (W VIII). Atoms 2015, 3, 299-319. https://doi.org/10.3390/atoms3030299
Deprince J, Quinet P. Detailed Analysis of Configuration Interaction and Calculation of Radiative Transition Rates in Seven Times Ionized Tungsten (W VIII). Atoms. 2015; 3(3):299-319. https://doi.org/10.3390/atoms3030299
Chicago/Turabian StyleDeprince, Jérôme, and Pascal Quinet. 2015. "Detailed Analysis of Configuration Interaction and Calculation of Radiative Transition Rates in Seven Times Ionized Tungsten (W VIII)" Atoms 3, no. 3: 299-319. https://doi.org/10.3390/atoms3030299
APA StyleDeprince, J., & Quinet, P. (2015). Detailed Analysis of Configuration Interaction and Calculation of Radiative Transition Rates in Seven Times Ionized Tungsten (W VIII). Atoms, 3(3), 299-319. https://doi.org/10.3390/atoms3030299







