Cavity Quantum Electrodynamics of Continuously Monitored Bose-Condensed Atoms
Abstract
:1. Introduction
2. Basic Model
2.1. Hamiltonian Formalism and Open System Dynamics
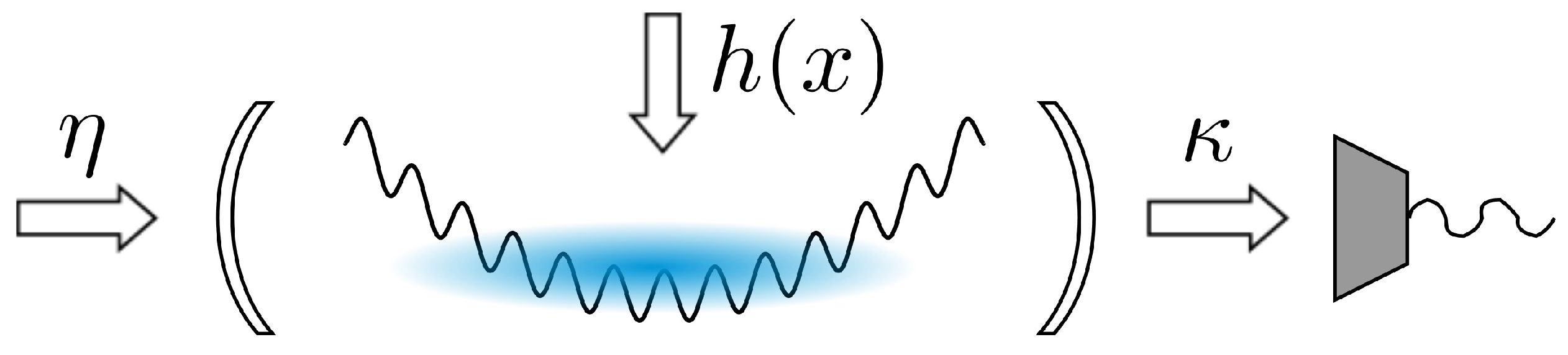
2.2. Phase-Space and Stochastic Descriptions
3. Numerical Results
3.1. Cavity Optomechanical System
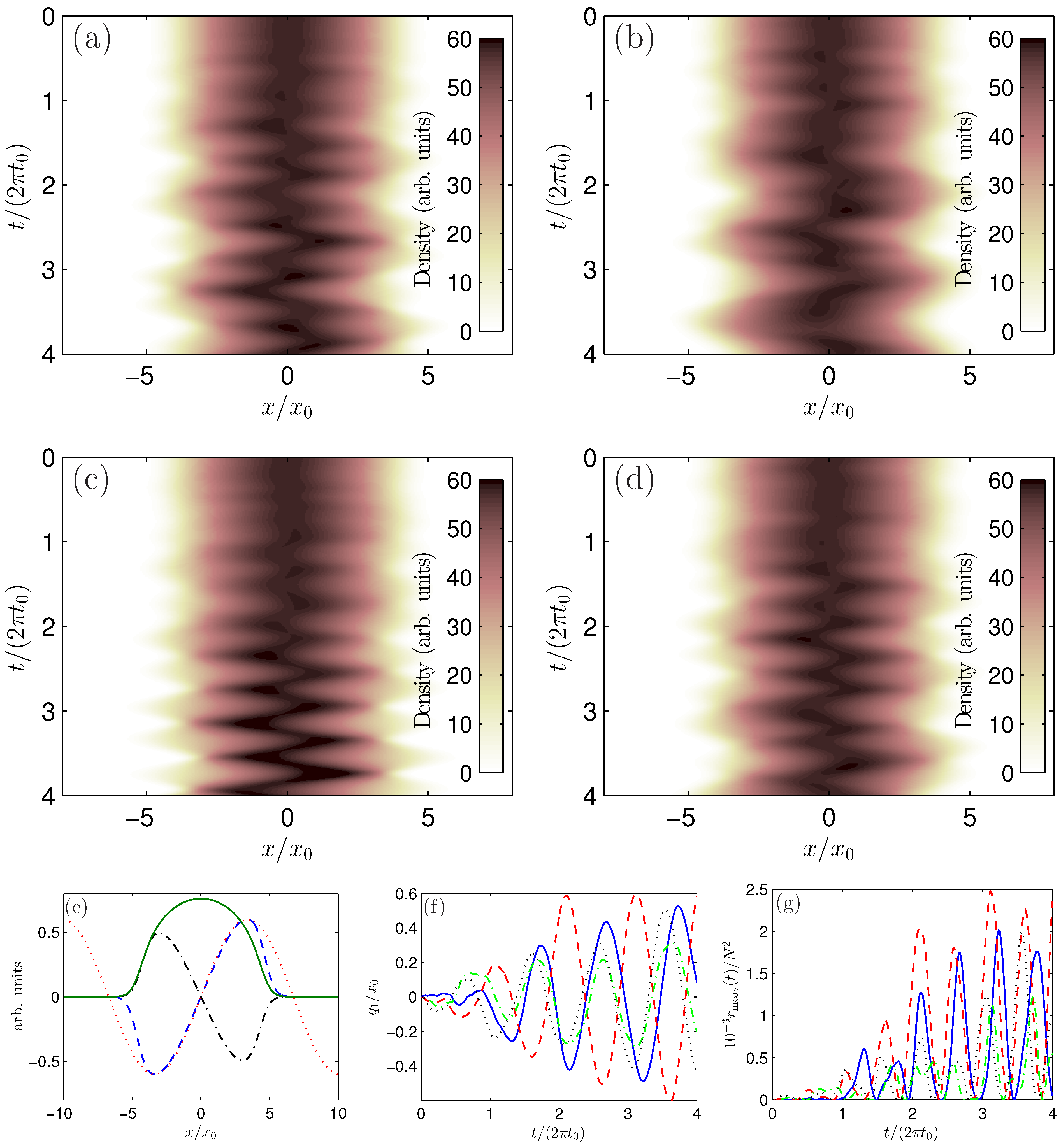
3.2. Selective Phonon Excitations and Their Measurements
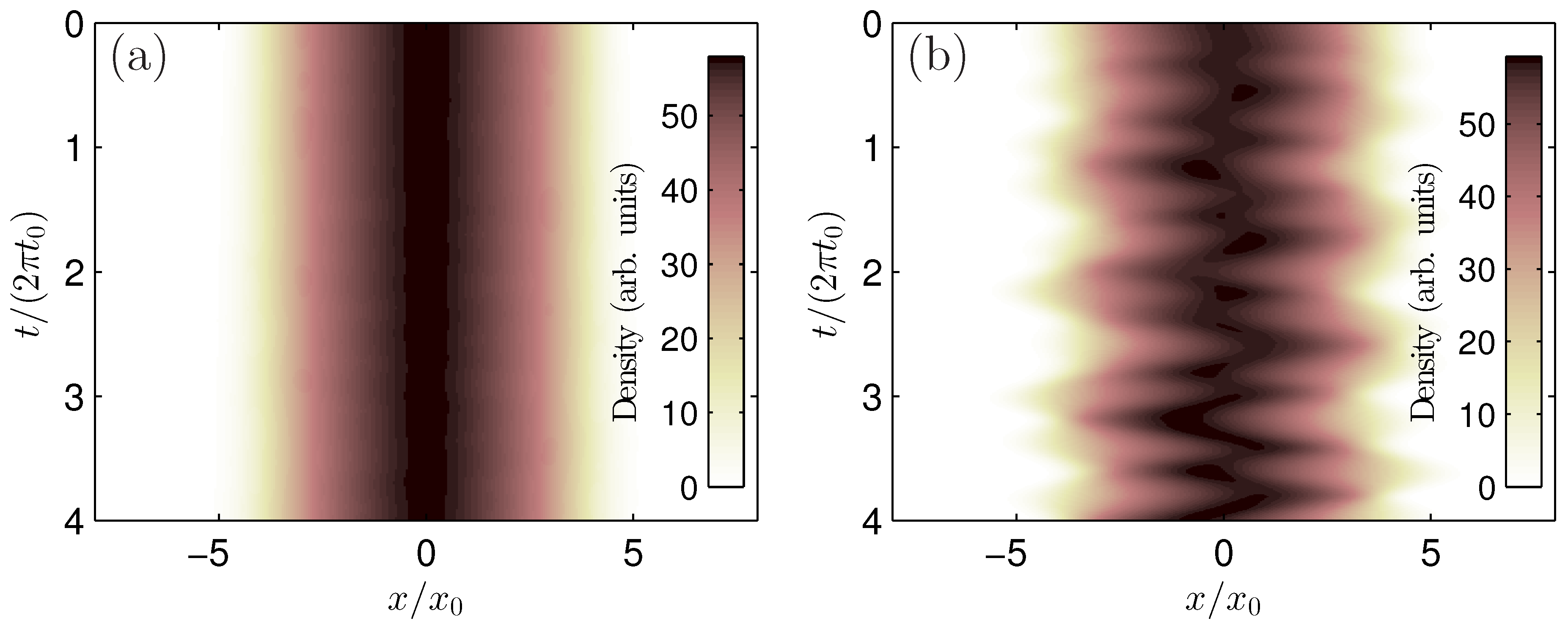


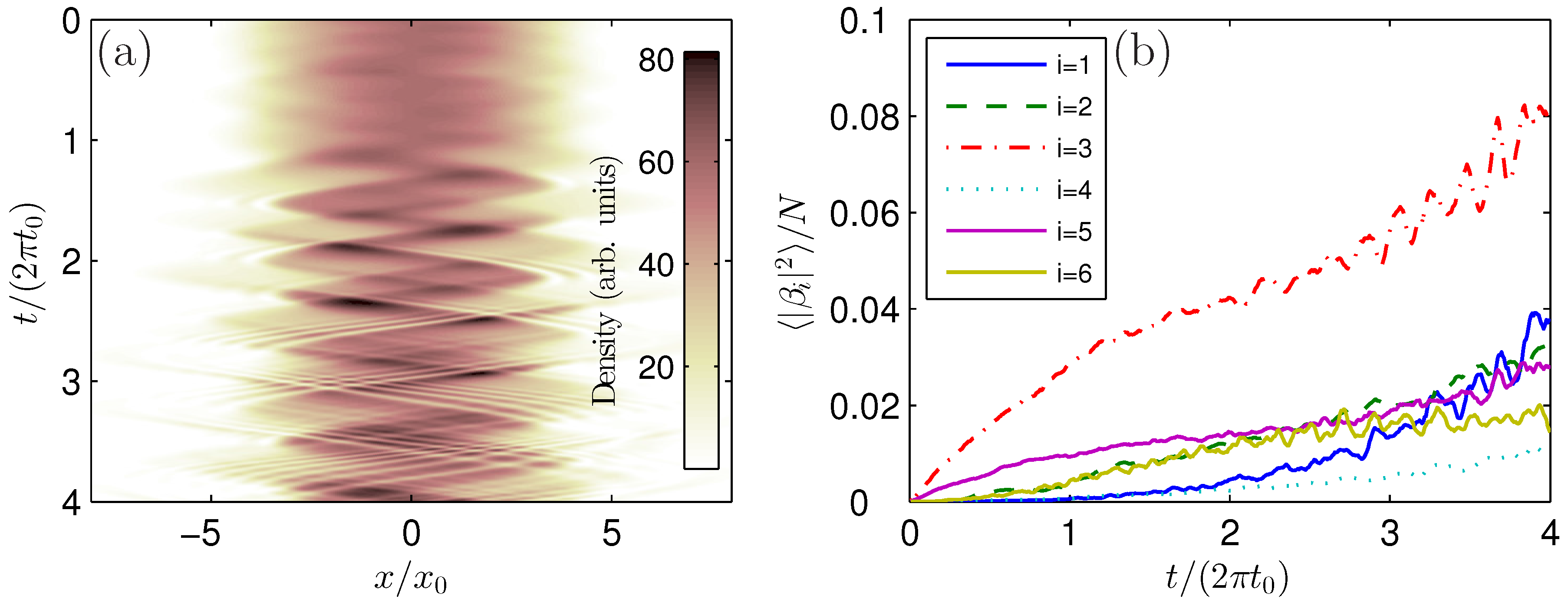
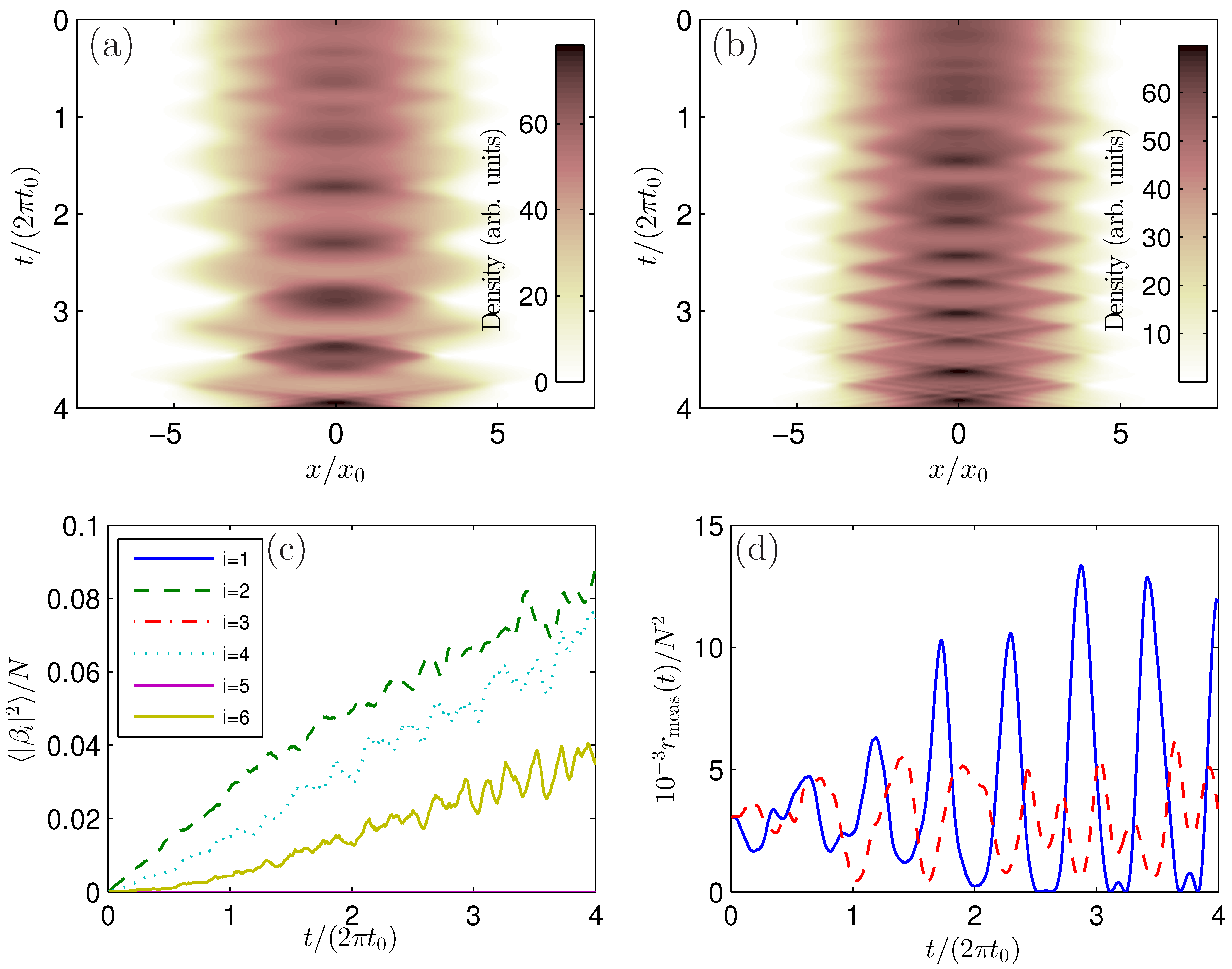
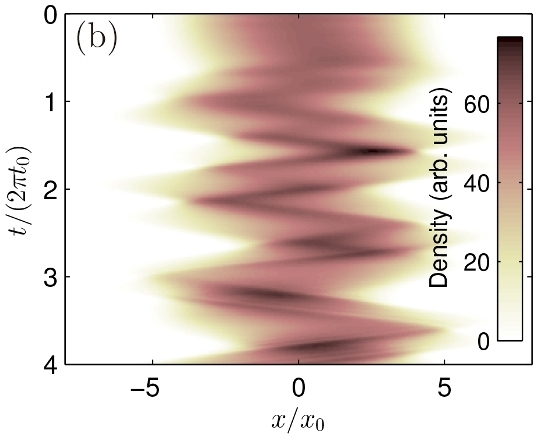
3.3. Phonon Detection
4. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
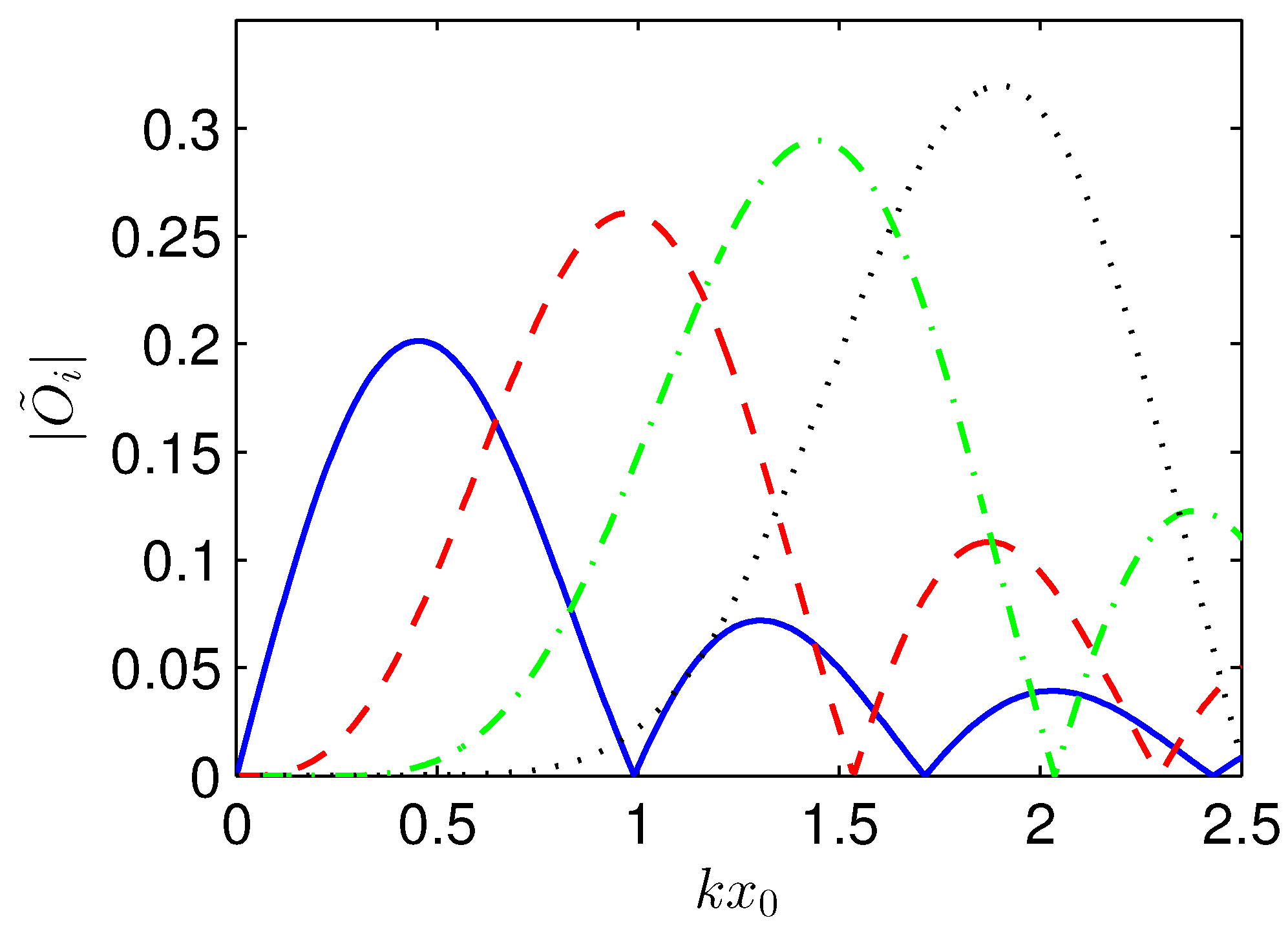
Analyzing the Collective Mode Response
References
- Carmichael, H. Statistical Methods in Quantum Optics Vol 2; Springer: Berlin, Germany, 2007. [Google Scholar]
- Brennecke, F.; Donner, T.; Ritter, S.; Bourdel, T.; Kohl, M.; Esslinger, T. Cavity QED with a Bose-Einstein condensate. Nature 2007, 450, 268–271. [Google Scholar] [CrossRef] [PubMed]
- Colombe, Y.; Steinmetz, T.; Dubois, G.; Linke, F.; Hunger, D.; Reichel, J. Strong atom-field coupling for Bose-Einstein condensates in an optical cavity on a chip. Nature 2007, 450, 272–276. [Google Scholar] [CrossRef] [PubMed]
- Murch, K.W.; Moore, K.L.; Gupta, S.; Stamper-Kurn, D.M. Observation of quantum-measurement backaction with an ultracold atomic gas. Nat. Phys. 2008, 4, 561–564. [Google Scholar] [CrossRef]
- Brahms, N.; Botter, T.; Schreppler, S.; Brooks, D.W.C.; Stamper-Kurn, D.M. Optical Detection of the Quantization of Collective Atomic Motion. Phys. Rev. Lett. 2012. [Google Scholar] [CrossRef]
- Botter, T.; Brooks, D.W.C.; Schreppler, S.; Brahms, N.; Stamper-Kurn, D.M. Optical Readout of the Quantum Collective Motion of an Array of Atomic Ensembles. Phys. Rev. Lett. 2013. [Google Scholar] [CrossRef]
- Schmidt, D.; Tomczyk, H.; Slama, S.; Zimmermann, C. Dynamical Instability of a Bose-Einstein Condensate in an Optical Ring Resonator. Phys. Rev. Lett. 2014. [Google Scholar] [CrossRef]
- Kessler, H.; Klinder, J.; Wolke, M.; Hemmerich, A. Steering Matter Wave Superradiance with an Ultranarrow-Band Optical Cavity. Phys. Rev. Lett. 2014. [Google Scholar] [CrossRef]
- Ritsch, H.; Domokos, P.; Brennecke, F.; Esslinger, T. Cold atoms in cavity-generated dynamical optical potentials. Rev. Mod. Phys. 2013, 85, 553–601. [Google Scholar] [CrossRef]
- Brennecke, F.; Ritter, S.; Donner, T.; Esslinger, T. Cavity Optomechanics with a Bose-Einstein Condensate. Science 2008, 322, 235–238. [Google Scholar] [CrossRef] [PubMed]
- Tian, L.; Carmichael, H.J. Quantum trajectory simulations of two-state behavior in an optical cavity containing one atom. Phys. Rev. A 1992, 46, R6801–R6804. [Google Scholar] [CrossRef] [PubMed]
- Dalibard, J.; Castin, Y.; Mølmer, K. Wave-function approach to dissipative processes in quantum optics. Phys. Rev. Lett. 1992, 68, 580–583. [Google Scholar] [CrossRef] [PubMed]
- Dum, R.; Zoller, P.; Ritsch, H. Monte Carlo simulation of the atomic master equation for spontaneous emission. Phys. Rev. A 1992, 45, 4879–4887. [Google Scholar] [CrossRef] [PubMed]
- Leroux, I.D.; Schleier-Smith, M.H.; Vuletić, V. Implementation of Cavity Squeezing of a Collective Atomic Spin. Phys. Rev. Lett. 2010. [Google Scholar] [CrossRef]
- Lee, M.D.; Ruostekoski, J. Classical stochastic measurement trajectories: Bosonic atomic gases in an optical cavity and quantum measurement backaction. Phys. Rev. A 2014. [Google Scholar] [CrossRef]
- Javanainen, J.; Ruostekoski, J. Emergent classicality in continuous quantum measurements. New J. Phys. 2013. [Google Scholar] [CrossRef]
- Gardiner, S.A.; Gheri, K.M.; Zoller, P. Cavity-assisted quasiparticle damping in a Bose-Einstein condensate. Phys. Rev. A 2001. [Google Scholar] [CrossRef]
- Nagy, D.; Szirmai, G.; Domokos, P. Self-organization of a Bose-Einstein condensate in an optical cavity. Eur. Phys. J. D 2008, 48, 127–137. [Google Scholar] [CrossRef]
- Szirmai, G.; Nagy, D.; Domokos, P. Excess Noise Depletion of a Bose-Einstein Condensate in an Optical Cavity. Phys. Rev. Lett. 2009. [Google Scholar] [CrossRef]
- Venkatesh, B.P.; O’Dell, D.H.J. Bloch oscillations of cold atoms in a cavity: Effects of quantum noise. Phys. Rev. A 2013. [Google Scholar] [CrossRef]
- Jaynes, E.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Walls, D.F.; Milburn, G.J. Quantum Optics, 2nd ed.; Springer: Berlin, Germany, 1994. [Google Scholar]
- Maschler, C.; Mekhov, I.B.; Ritsch, H. Ultracold atoms in optical lattices generated by quantized light fields. Eur. Phys. J. D 2008, 46, 545–560. [Google Scholar] [CrossRef]
- Carmichael, H. An Open Systems Approach to Quantum Optics; Springer-Verlag: Berlin, Germany, 1993. [Google Scholar]
- Gardiner, C.; Zoller, P. Quantum Noise; Springer: Berlin, Germany, 2004. [Google Scholar]
- Olshanii, M. Atomic Scattering in the Presence of an External Confinement and a Gas of Impenetrable Bosons. Phys. Rev. Lett. 1998, 81, 938–941. [Google Scholar] [CrossRef]
- Ruostekoski, J.; Isella, L. Dissipative Quantum Dynamics of Bosonic Atoms in a Shallow 1D Optical Lattice. Phys. Rev. Lett. 2005. [Google Scholar] [CrossRef]
- Carmichael, H. Statistical Methods in Quantum Optics Vol 1; Springer: Berlin, Germany, 1999. [Google Scholar]
- Drummond, P.D.; Hardman, A.D. Simulation of Quantum Effects in Raman-Active Waveguides. Europhys. Lett. 1993. [Google Scholar] [CrossRef]
- Steel, M.J.; Olsen, M.K.; Plimak, L.I.; Drummond, P.D.; Tan, S.M.; Collett, M.J.; Walls, D.F.; Graham, R. Dynamical quantum noise in trapped Bose-Einstein condensates. Phys. Rev. A 1998. [Google Scholar] [CrossRef]
- Sinatra, A.; Lobo, C.; Castin, Y. The truncated Wigner method for Bose-condensed gases: Limits of validity and applications. J. Phys. B 2002. [Google Scholar] [CrossRef]
- Isella, L.; Ruostekoski, J. Quantum dynamics in splitting a harmonically trapped Bose-Einstein condensate by an optical lattice: Truncated Wigner approximation. Phys. Rev. A 2006. [Google Scholar] [CrossRef]
- Blakie, P.B.; Bradley, A.S.; Davis, M.J.; Ballagh, R.J.; Gardiner, C.W. Dynamics and statistical mechanics of ultra-cold Bose gases using c-field techniques. Adv. Phys. 2008. [Google Scholar] [CrossRef]
- Martin, A.D.; Ruostekoski, J. Quantum and Thermal Effects of Dark Solitons in a One-Dimensional Bose Gas. Phys. Rev. Lett. 2010. [Google Scholar] [CrossRef]
- Polkovnikov, A. Phase space representation of quantum dynamics. Ann. Phys. 2010, 325, 1790–1852. [Google Scholar] [CrossRef]
- Opanchuk, B.; Drummond, P.D. Functional Wigner representation of quantum dynamics of Bose-Einstein condensate. J. Math. Phys. 2013. [Google Scholar] [CrossRef]
- Mathey, A.C.; Clark, C.W.; Mathey, L. Decay of a superfluid current of ultracold atoms in a toroidal trap. Phys. Rev. A 2014. [Google Scholar] [CrossRef]
- Gross, C.; Estève, J.; Oberthaler, M.K.; Martin, A.D.; Ruostekoski, J. Local and spatially extended sub-Poisson atom-number fluctuations in optical lattices. Phys. Rev. A 2011. [Google Scholar] [CrossRef]
- Plimak, L.I.; Olsen, M.K. Quantum-field-theoretical approach to phase-space techniques: Symmetric Wick theorem and multitime Wigner representation. Ann. Phys. 2014, 351, 593–619. [Google Scholar] [CrossRef]
- Martin, A.D.; Ruostekoski, J. Quantum dynamics of atomic bright solitons under splitting and recollision, and implications for interferometry. New J. Phys. 2012. [Google Scholar] [CrossRef]
- Opanchuk, B.; Egorov, M.; Hoffmann, S.; Sidorov, A.I.; Drummond, P.D. Quantum noise in three-dimensional BEC interferometry. Europhys. Lett. 2012. [Google Scholar] [CrossRef]
- Dujardin, J.; Uelles, A.A.; Schlagheck, P. Elastic and inelastic transmission in guided atom lasers: A truncated Wigner approach. Phy. Rev. A 2015. [Google Scholar] [CrossRef]
- Lewis-Swan, R.J.; Olsen, M.K.; Kheruntsyan, K.V. On the interpretation of single stochastic trajectories of the Wigner distribution. 2015; arXiv:1503.05647. [Google Scholar]
- Norrie, A.A.; Ballagh, R.J.; Gardiner, C.W.; Bradley, A.S. Three-body recombination of ultracold Bose gases using the truncated Wigner method. Phys. Rev. A 2006. [Google Scholar] [CrossRef]
- Szigeti, S.S.; Hush, M.R.; Carvalho, A.R.R.; Hope, J.J. Continuous measurement feedback control of a Bose-Einstein condensate using phase-contrast imaging. Phys. Rev. A 2009. [Google Scholar] [CrossRef]
- Hush, M.R.; Szigeti, S.S.; Carvalho, A.R.R.; Hope, J.J. Controlling spontaneous-emission noise in measurement-based feedback cooling of a Bose-Einstein condensate. New J. Phys. 2013. [Google Scholar] [CrossRef]
- Carmichael, H.J.; Nha, H. Vacuum fluctuations and the conditional homodyne detection of squeezed light. J. Opt. B Quant. Semiclass. Opt. 2004. [Google Scholar] [CrossRef]
- Ruostekoski, J.; Martin, A.D. Quantum Gases: Finite Temperature and Non-Equilibrium Dynamics, Cold Atoms Series; Proukakis, N.P., Gardiner, S.A., Eds.; Imperial College Press: London, UK, 2014. [Google Scholar]
- Cattani, F.; Gross, C.; Oberthaler, M.K.; Ruostekoski, J. Measuring and engineering entropy and spin squeezing in weakly linked Bose-Einstein condensates. New J. Phys. 2013. [Google Scholar] [CrossRef]
- Kippenberg, T.J.; Vahala, K.J. Cavity Opto-Mechanics. Opt. Express 2007, 15, 17172–17205. [Google Scholar] [CrossRef] [PubMed]
- Kippenberg, T.J.; Vahala, K.J. Cavity Optomechanics: Back-Action at the Mesoscale. Science 2008, 321, 1172–1176. [Google Scholar] [CrossRef] [PubMed]
- Meystre, P. A short walk through quantum optomechanics. Ann. Phys. 2013, 525, 215–233. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity Optomechanics. 2013; arXiv:1303.0733. [Google Scholar]
- O’Connell, A.D.; Hofheinz, M.; Ansmann, M.; Bialczak, R.C.; Lenander, M.; Lucero, E.; Neeley, M.; Sank, D.; Wang, H.; Weides, M.; et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 2010, 464, 697–703. [Google Scholar] [CrossRef] [PubMed]
- Teufel, J.D.; Donner, T.; Li, D.; Harlow, J.W.; Allman, M.S.; Cicak, K.; Sirois, A.J.; Whittaker, J.D.; Lehnert, K.W.; Simmonds, R.W. Sideband cooling of micromechanical motion to the quantum ground state. Nature 2011, 475, 359–363. [Google Scholar] [CrossRef] [PubMed]
- Chan, J.; Alegre, T.P.M.; Safavi-Naeini, A.H.; Hill, J.T.; Krause, A.; Gröblacher, S.; Aspelmeyer, M.; Painter, O. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 2011, 478, 89–92. [Google Scholar] [CrossRef] [PubMed]
- Brahms, N.; Stamper-Kurn, D.M. Spin optodynamics analog of cavity optomechanics. Phys. Rev. A 2010. [Google Scholar] [CrossRef]
- Gardiner, C. Stochastic Methods; Springer: Berlin, Germany, 2009. [Google Scholar]
- Mekhov, I.B.; Maschler, C.; Ritsch, H. Cavity-Enhanced Light Scattering in Optical Lattices to Probe Atomic Quantum Statistics. Phys. Rev. Lett. 2007. [Google Scholar] [CrossRef]
- Ruostekoski, J.; Foot, C.J.; Deb, A.B. Light Scattering for Thermometry of Fermionic Atoms in an Optical Lattice. Phys. Rev. Lett. 2009. [Google Scholar] [CrossRef]
- Douglas, J.S.; Burnett, K. Imaging of quantum Hall states in ultracold atomic gases. Phys. Rev. A 2011. [Google Scholar] [CrossRef]
- Łakomy, K.; Idziaszek, Z.; Trippenbach, M. Thermal effects in light scattering from ultracold bosons in an optical lattice. Phys. Rev. A 2009. [Google Scholar] [CrossRef]
- Rist, S.; Menotti, C.; Morigi, G. Light scattering by ultracold atoms in an optical lattice. Phys. Rev. A 2010. [Google Scholar] [CrossRef]
- Corcovilos, T.A.; Baur, S.K.; Hitchcock, J.M.; Mueller, E.J.; Hulet, R.G. Detecting antiferromagnetism of atoms in an optical lattice via optical Bragg scattering. Phys. Rev. A 2010. [Google Scholar] [CrossRef]
- Cordobes Aguilar, F.; Ho, A.F.; Ruostekoski, J. Optical Signatures of Antiferromagnetic Ordering of Fermionic Atoms in an Optical Lattice. Phys. Rev. X 2014. [Google Scholar] [CrossRef]
- Goldwin, J.; Venkatesh, B.P.; O’Dell, D.H.J. Backaction-Driven Transport of Bloch Oscillating Atoms in Ring Cavities. Phys. Rev. Lett. 2014. [Google Scholar] [CrossRef]
- Samoylova, M.; Piovella, N.; Robb, G.R.M.; Bachelard, R.; Courteille, P.W. Synchronization of Bloch oscillations by a ring cavity. Opt. Express 2015, 23, 14823–14835. [Google Scholar] [CrossRef] [PubMed]
- Horak, P.; Ritsch, H. Manipulating a Bose-Einstein condensate with a single photon. Eur. Phys. J. D Atom. Mol. Opt. Plasma Phys. 2001, 13, 279–287. [Google Scholar] [CrossRef]
- Horak, P.; Barnett, S.M.; Ritsch, H. Coherent dynamics of Bose-Einstein condensates in high-finesse optical cavities. Phys. Rev. A 2000. [Google Scholar] [CrossRef]
- Javanainen, J.; Yoo, S.M. Quantum Phase of a Bose-Einstein Condensate with an Arbitrary Number of Atoms. Phys. Rev. Lett. 1996, 76, 161–164. [Google Scholar] [CrossRef] [PubMed]
- Cirac, J.I.; Gardiner, C.W.; Naraschewski, M.; Zoller, P. Continuous observation of interference fringes from Bose condensates. Phys. Rev. A 1996, 54, R3714–R3717. [Google Scholar] [CrossRef] [PubMed]
- Castin, Y.; Dalibard, J. Relative phase of two Bose-Einstein condensates. Phys. Rev. A 1997, 55, 4330–4337. [Google Scholar] [CrossRef]
- Ruostekoski, J.; Walls, D.F. Bose-Einstein condensate in a double-well potential as an open quantum system. Phys. Rev. A 1998, 58, R50–R53. [Google Scholar] [CrossRef]
- Ruostekoski, J.; Walls, D.F. Nondestructive optical measurement of relative phase between two Bose-Einstein condensates. Phys. Rev. A 1997, 56, 2996–3006. [Google Scholar] [CrossRef]
- Javanainen, J. Nonlinearity from quantum mechanics: Dynamically unstable Bose-Einstein condensate in a double-well trap. Phys. Rev. A 2010. [Google Scholar] [CrossRef]
- Elliott, T.J.; Kozlowski, W.; Caballero-Benitez, S.F.; Mekhov, I.B. Multipartite Entangled Spatial Modes of Ultracold Atoms Generated and Controlled by Quantum Measurement. Phys. Rev. Lett. 2015. [Google Scholar] [CrossRef]
- Corney, J.F.; Milburn, G.J. Homodyne measurements on a Bose-Einstein condensate. Phys. Rev. A 1998, 58, 2399–2406. [Google Scholar] [CrossRef]
- Dalvit, D.A.R.; Dziarmaga, J.; Onofrio, R. Continuous quantum measurement of a Bose-Einstein condensate: A stochastic Gross-Pitaevskii equation. Phys. Rev. A 2002. [Google Scholar] [CrossRef]
- Lee, M.D.; Rist, S.; Ruostekoski, J. Bragg spectroscopic interferometer and quantum measurement-induced correlations in atomic Bose-Einstein condensates. New J. Phys. 2012. [Google Scholar] [CrossRef]
- Niedenzu, W.; Schütz, S.; Habibian, H.; Morigi, G.; Ritsch, H. Seeding patterns for self-organization of photons and atoms. Phys. Rev. A 2013. [Google Scholar] [CrossRef]
- Mekhov, I.B.; Ritsch, H. Quantum Nondemolition Measurements and State Preparation in Quantum Gases by Light Detection. Phys. Rev. Lett. 2009. [Google Scholar] [CrossRef]
- Wiseman, H.; Milburn, G. Quantum Measurement and Control; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, M.D.; Ruostekoski, J. Cavity Quantum Electrodynamics of Continuously Monitored Bose-Condensed Atoms. Atoms 2015, 3, 450-473. https://doi.org/10.3390/atoms3030450
Lee MD, Ruostekoski J. Cavity Quantum Electrodynamics of Continuously Monitored Bose-Condensed Atoms. Atoms. 2015; 3(3):450-473. https://doi.org/10.3390/atoms3030450
Chicago/Turabian StyleLee, Mark D., and Janne Ruostekoski. 2015. "Cavity Quantum Electrodynamics of Continuously Monitored Bose-Condensed Atoms" Atoms 3, no. 3: 450-473. https://doi.org/10.3390/atoms3030450
APA StyleLee, M. D., & Ruostekoski, J. (2015). Cavity Quantum Electrodynamics of Continuously Monitored Bose-Condensed Atoms. Atoms, 3(3), 450-473. https://doi.org/10.3390/atoms3030450