Tungsten Ions in Plasmas: Statistical Theory of Radiative-Collisional Processes
Abstract
:1. Introduction
2. Basic Equations of Statistical Theory and Fermi’s Equivalent Photons Model
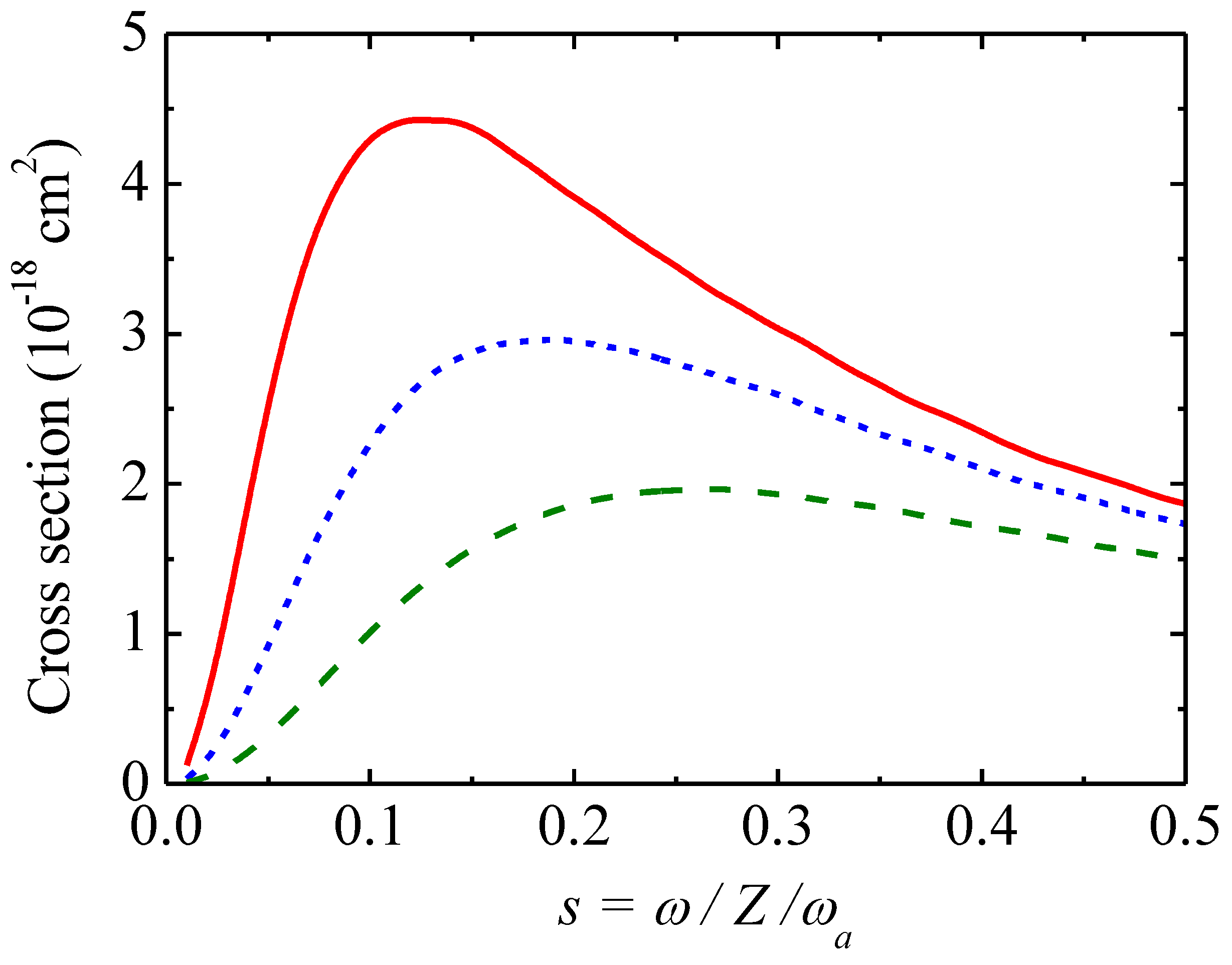
2.1. Ionization Cross-Sections and Rates
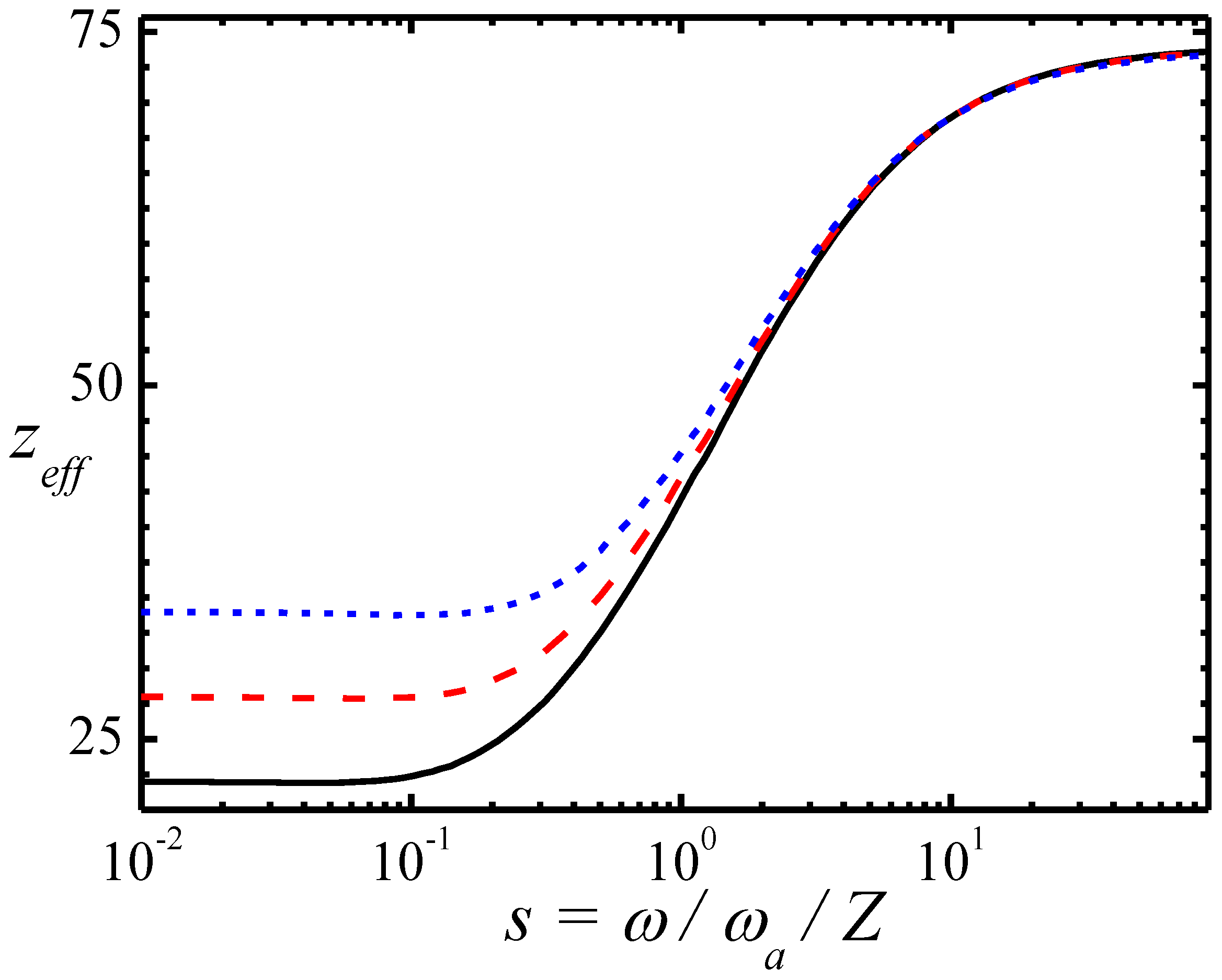
2.2. Excitation Rates
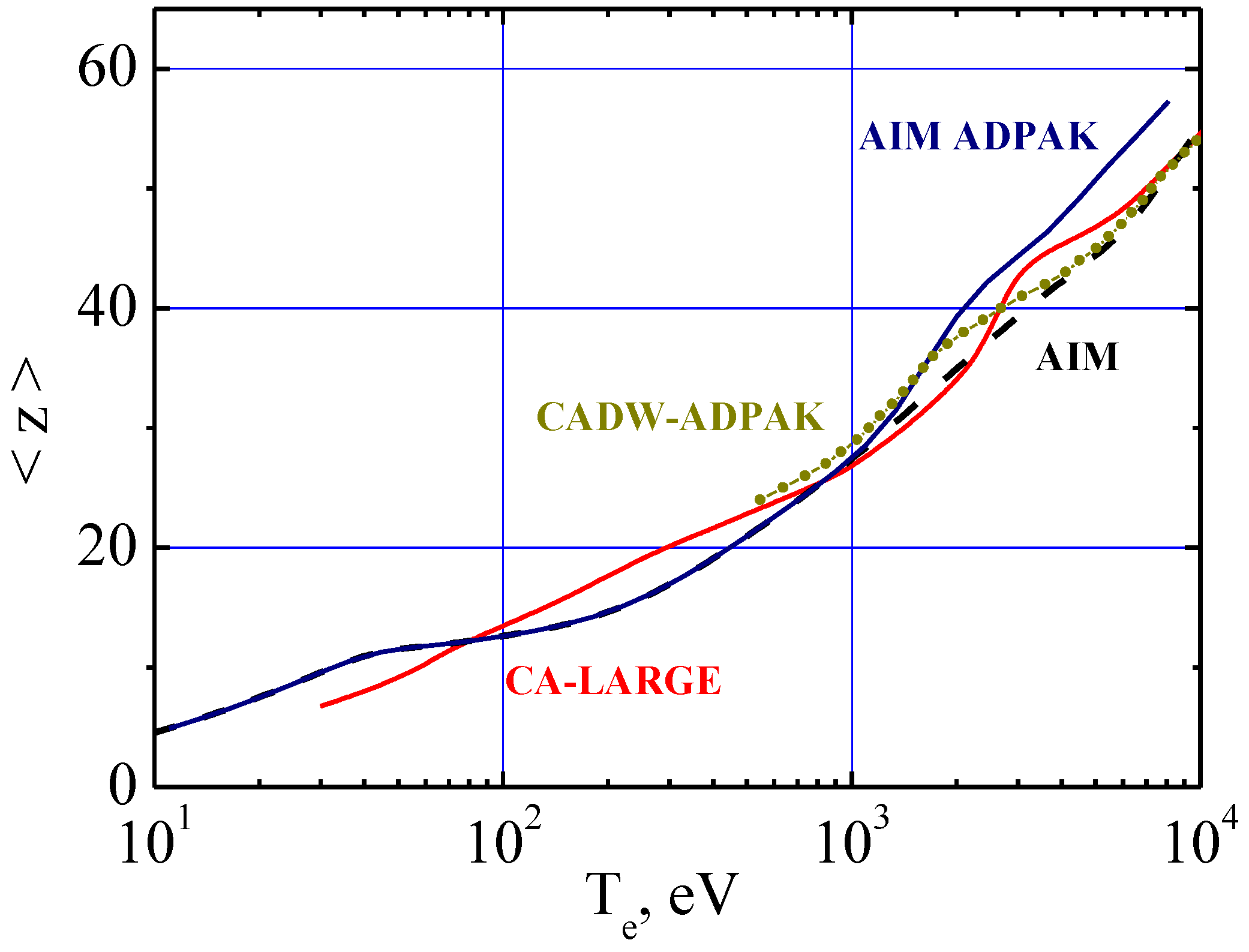
3. Ionization Balance of Impurity Tungsten Ions in Plasmas
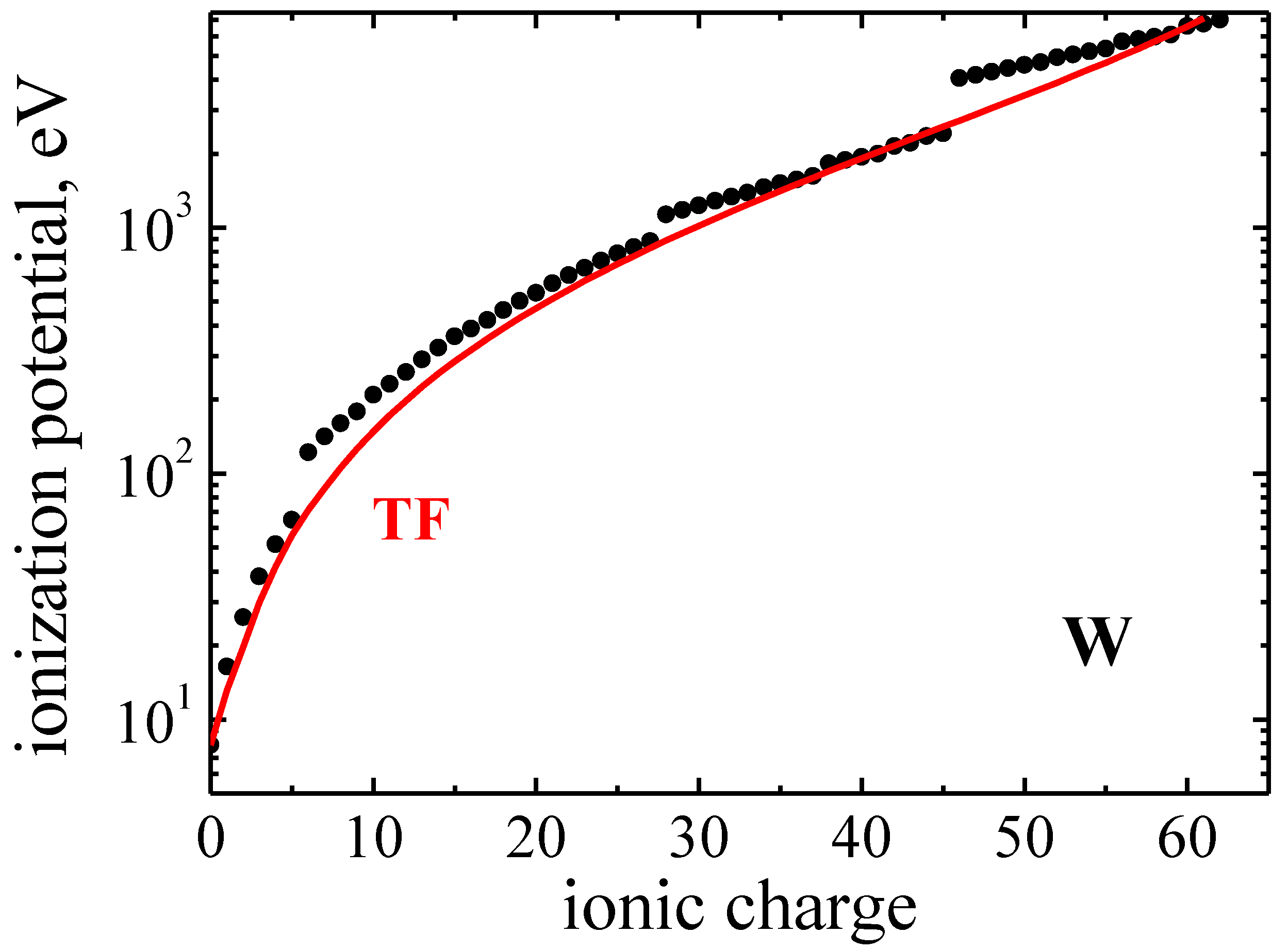
3.1. Ionization Potentials and Average Charge
3.2. Gaussian Approximation
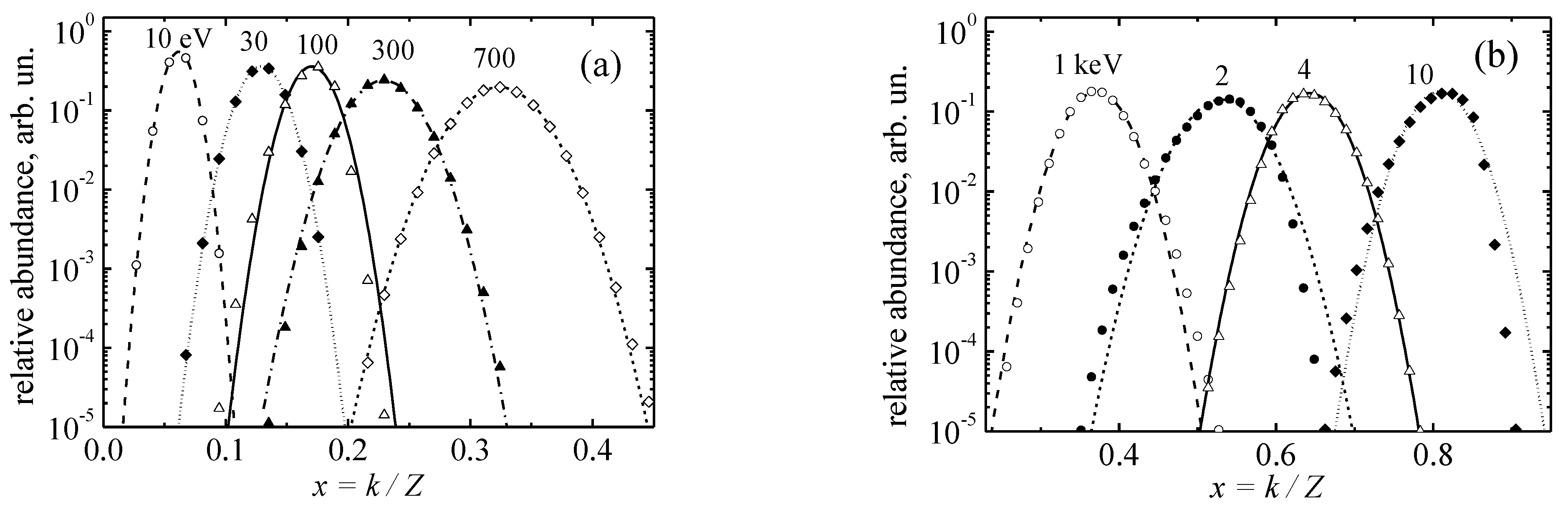
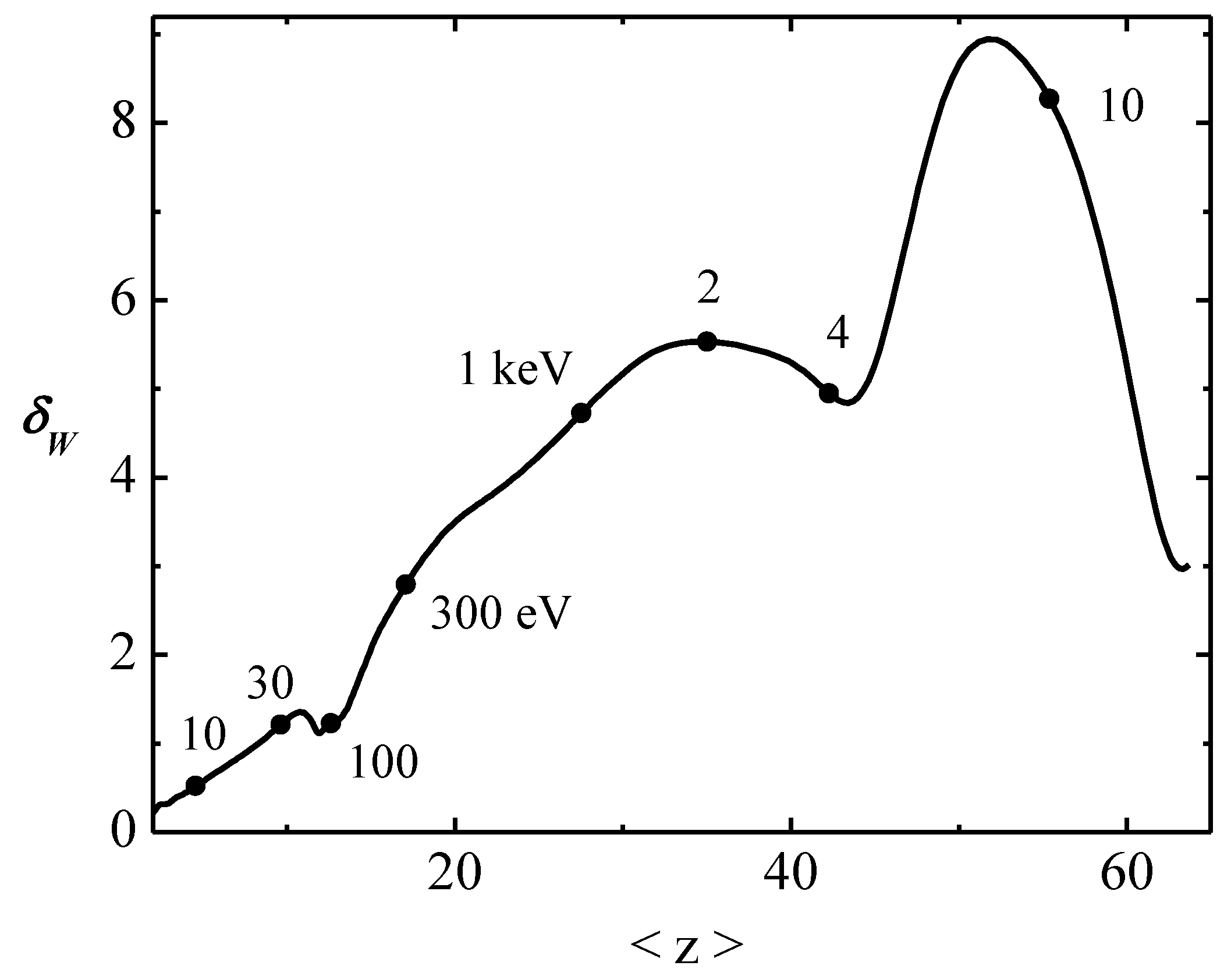
4. Plasma Radiative Losses
4.1. Coronal Radiative Losses
4.2. Transition to Boltzmann Equilibrium
5. Numerical Data
5.1. Ionization Cross-Section and Rates
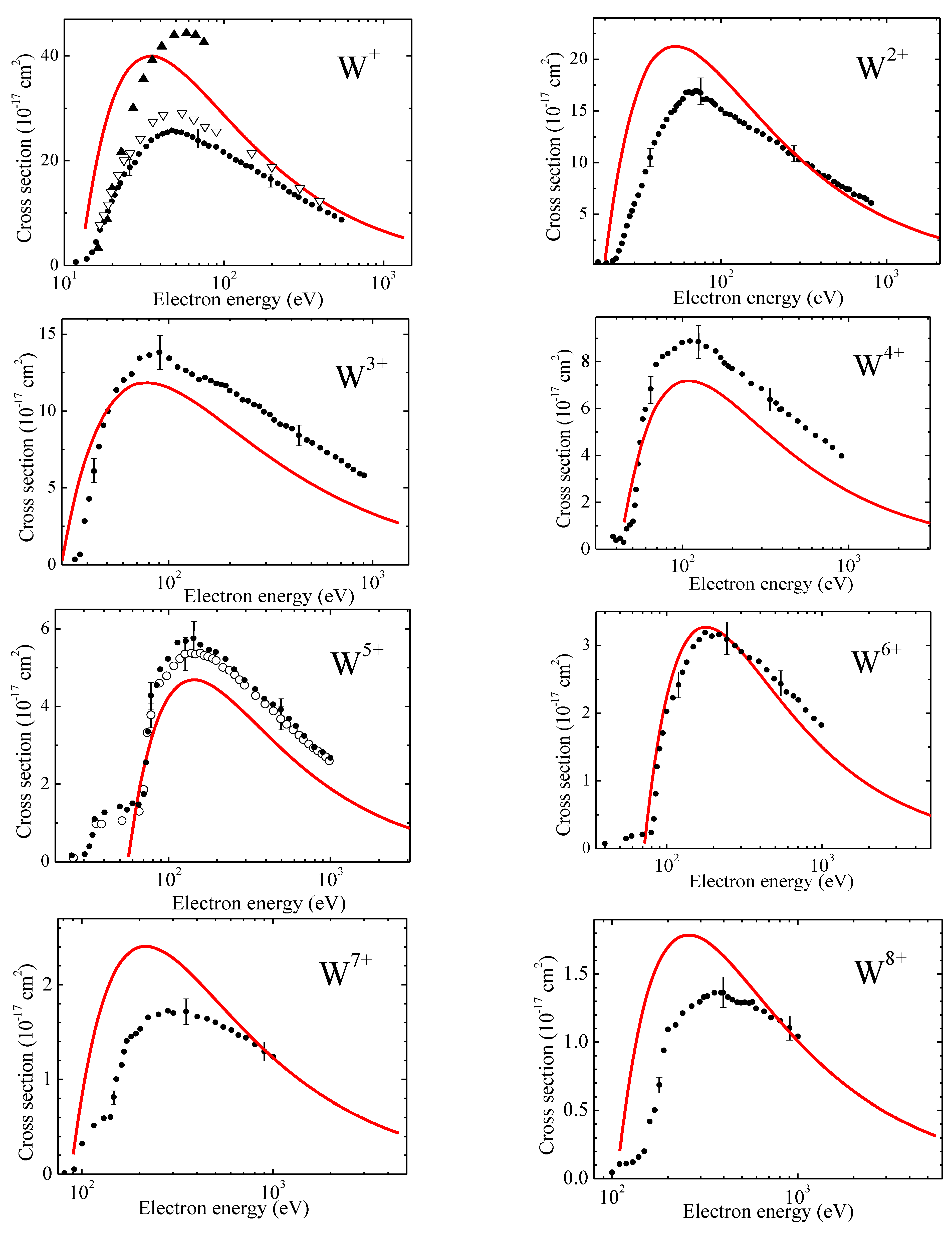
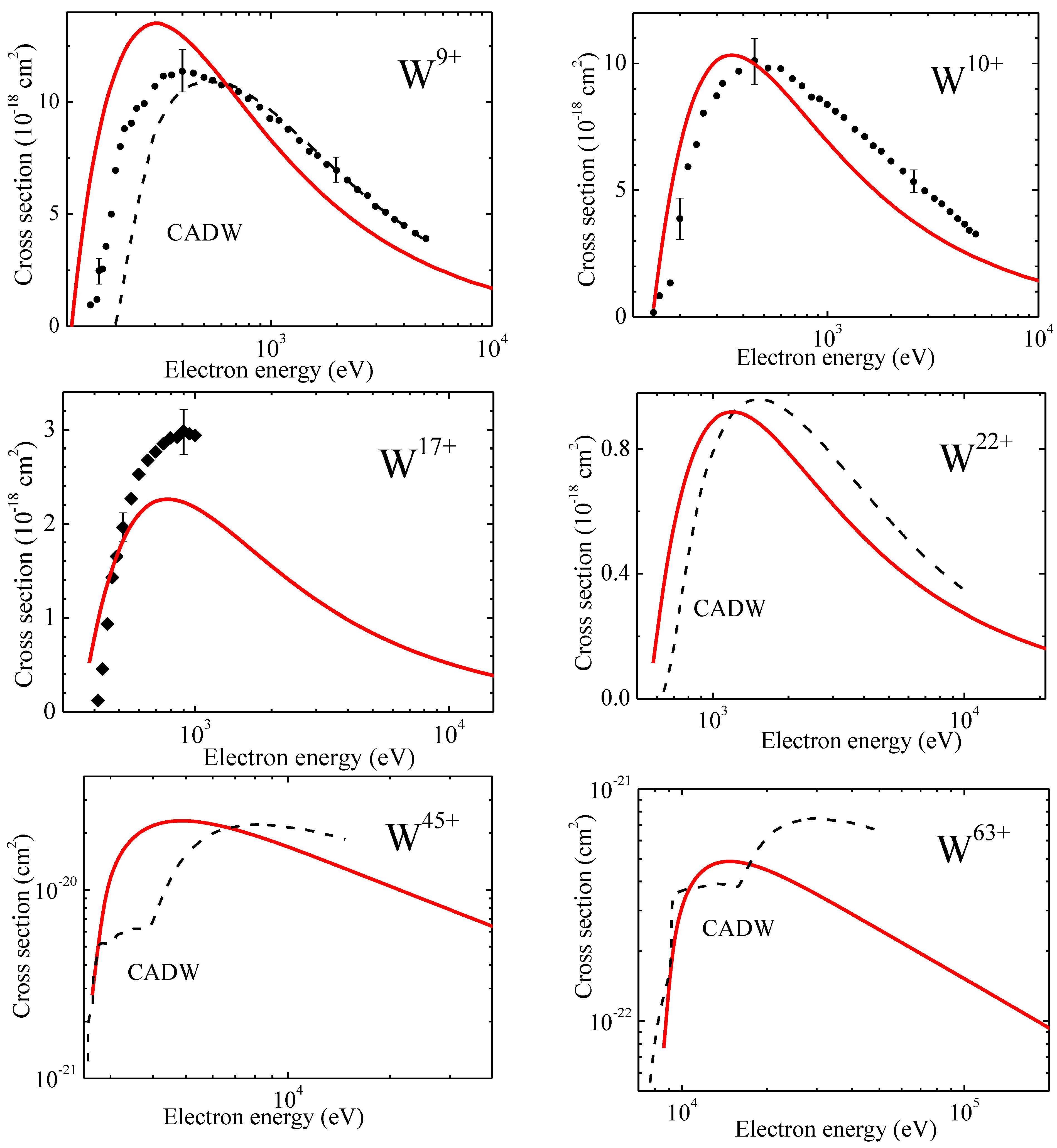
5.2. Radiative Losses
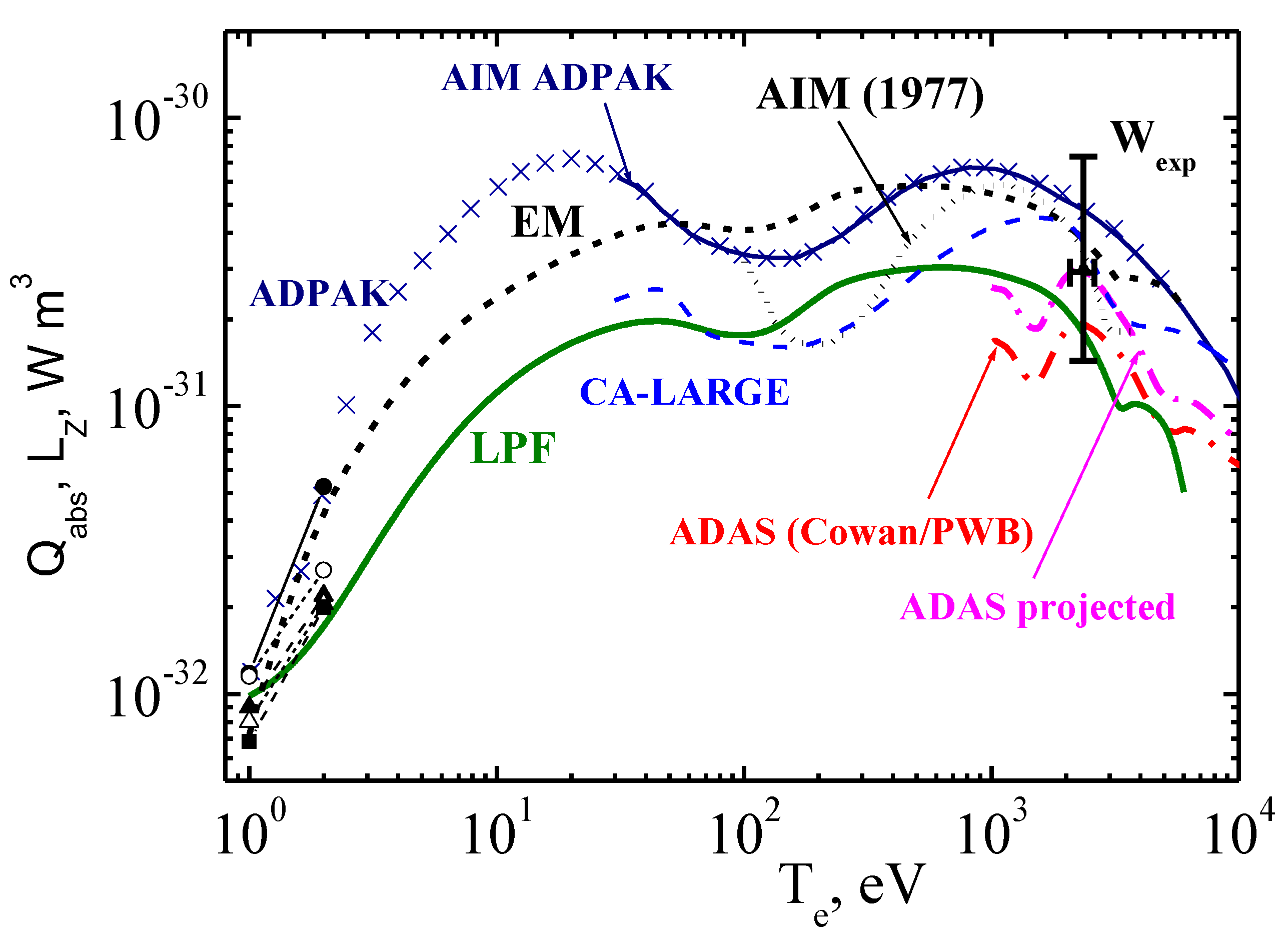
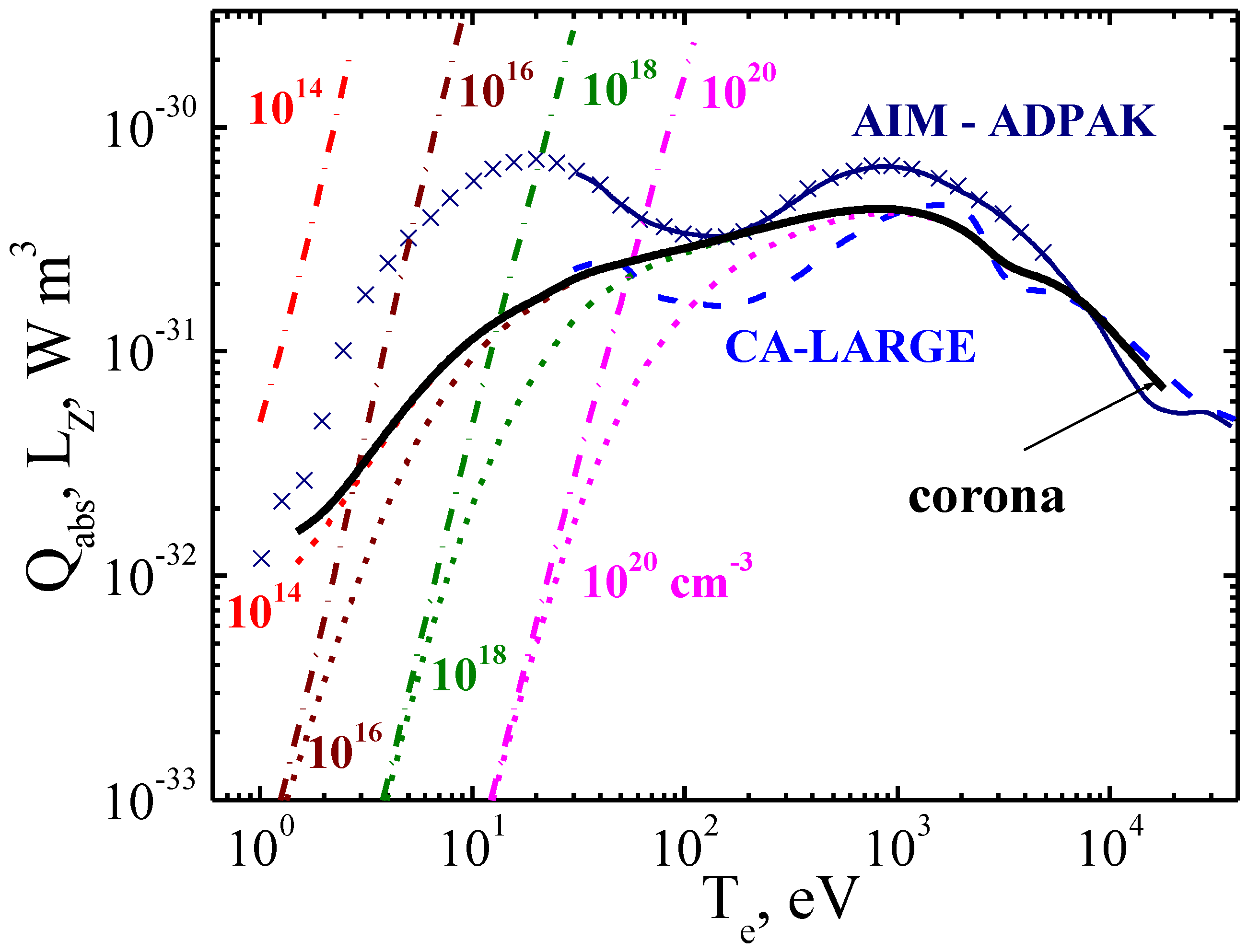
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Asmussen, K.; Fournier, K.B.; Laming, J.M.; Seely, J.F.; Dux, R.; Engelhardt, W.; Fuchs, J.C.; ASDEX Upgrade Team. Spectroscopic investigations of tungsten in the EUV region and the determination of its concentration in tokamaks. Nucl. Fusion 1998, 38, 967–986. [Google Scholar] [CrossRef]
- Neu, R.; Dux, R.; Kallenbach, A.; Pütterich, T.; Balden, M.; Fuchs, J.C.; Herrmann, A.; Maggi, C.F.; O’Mullane, M.; Pugno, R.; et al. Tungsten: An option for divertor and main chamber plasma facing components in future fusion devices. Nucl. Fusion 2005, 45, 209–218. [Google Scholar] [CrossRef]
- Pütterich, T.; Neu, R.; Dux, R.; Whiteford, A.D.; O’Mullane, M.G.; ASDEX Upgrade Team. Modelling of measured tungsten spectra from ASDEX Upgrade and predictions for ITER. Plasma Phys. Control. Fusion 2008, 50, 085016. [Google Scholar] [CrossRef]
- Pütterich, T.; Neu, R.; Dux, R.; Whiteford, A.D.; O’Mullane, M.G.; Summers, H.P.; ASDEX Upgrade Team. Calculation and experimental test of the cooling factor of tungsten. Nucl. Fusion 2010, 50, 025012. [Google Scholar] [CrossRef]
- Groth, M.; Brezinsek, S.; Belo, P.; Beurskens, M.N.A.; Brix, M.; Clever, M.; Coenen, J.W.; Corrigan, C.; Eich, T.; Flanagan, J.; et al. Impact of carbon and tungsten as divertor materials on the scrape-off layer conditions in JET. Nucl. Fusion 2013, 53, 093016. [Google Scholar] [CrossRef]
- Summers, H.P. ADAS User Manual version 2.7. 2004. Available online: http://www.adas.ac.uk/manual.php (accessed on 10 May 2015).
- Post, D.; Abdallah, J.; Clark, R.E.H.; Putvinskaya, N. Calculations of energy losses due to atomic processes in tokamaks with applications to the International Thermonuclear Experimental Reactor divertor. Phys. Plasmas 1995, 2, 2328–2336. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshits, E.M. Course of Theoretical Physics; Pergamon Press: New York, USA, 1991; Volume Ш. [Google Scholar]
- Landau, L.D.; Lifshits, E.M. Course of Theoretical Physics; Pergamon Press: New York, USA, 1981; Volume IХ. [Google Scholar]
- Gombas, P. Die Statistische Theorie der Atoms und ihre Anwendungen; Springer: Wien, Austria, 1949. (In German) [Google Scholar]
- Brandt, W.; Lundqvist, S. Atomic Oscillations in the Statistical Approximation. Phys. Rev. 1965, 139, 612–617. [Google Scholar] [CrossRef]
- Vinogradov, A.V.; Tolstikhin, O.I. Plasma approach to the theory of photoabsorption and polarizability of complex atoms. Sov. Phys. JETP 1989, 69, 683–688. [Google Scholar]
- Demura, A.V.; Kadomtsev, M.B.; Lisitsa, V.S.; Shurygin, V.A. Statistical model of radiation losses for heavy ions in plasmas. JETP Lett. 2013, 98, 786–789. [Google Scholar] [CrossRef]
- Demura, A.V.; Kadomtsev, M.B.; Lisitsa, V.S.; Shurygin, V.A. Statistical model of electron impact ionization of multielectron ions. J. Phys. B 2015, 48, 055701. [Google Scholar] [CrossRef]
- Demura, A.V.; Kadomtsev, M.B.; Lisitsa, V.S.; Shurygin, V.A. Electron impact ionization of tungsten ions in a statistical model. JETP Lett. 2015, 101, 85–88. [Google Scholar] [CrossRef]
- Kogan, V.I.; Kukushkin, A.B.; Lisitsa, V.S. Kramers electrodynamics and electron-atomic radiative-collisional processes. Phys. Rep. 1992, 213, 1–116. [Google Scholar] [CrossRef]
- Fermi, E. Über die Theorie des Stoßes zwischen Atomen und elektrisch geladenen Teilchen. Z. Phys. 1924, 29, 315–327. [Google Scholar] [CrossRef]
- Abdallah, J., Jr.; Colgan, J.; Clark, R.E.H.; Fontes, C.J.; Zhang, H.L. A collisional-radiative study of low temperature tungsten plasma. J. Phys. B 2011, 44, 075701. [Google Scholar] [CrossRef]
- Kramida, A.E.; Reader, J. Ionization energies of tungsten ions: W2+ through W71+. Atomic Data Nucl. Data Tables 2006, 92, 457–479. [Google Scholar] [CrossRef]
- Post, D.E.; Jensen, R.V.; Tarter, C.B.; Grasberger, W.H.; Lokke, W.A. Steady-state radiative cooling rates for low-density high-temperature plasmas. Atomic Data Nucl. Data Tables 1977, 20, 397–439. [Google Scholar] [CrossRef]
- Stenke, M.; Aichele, K.; Harthiramani, D.; Hofmann, G.; Steidl, M.; Volpel, R.; Salzborn, E. Electron-impact single-ionization of singly and multiply charged tungsten ions. J. Phys. B At. Mol. Opt. Phys. 1995, 28, 2711–2721. [Google Scholar] [CrossRef]
- Stenke, M.; Aichele, K.; Hathiramani, D.; Hofmann, G.; Steidl, M.; Volpel, R.; Shevelko, V.P.; Tawara, H.; Salzborn, E. Electron-impact multiple ionization of singly and multiply charged tungsten ions. J. Phys. B At. Mol. Opt. Phys. 1995, 28, 4853–4860. [Google Scholar] [CrossRef]
- Pindzola, M.S.; Griffin, D.C. Electron-impact ionization of the tungsten atom. Phys. Rev. A 1992, 46, 2486–2488. [Google Scholar] [CrossRef] [PubMed]
- Spruck, K.; Becker, A.; Borovik, A.; Gharaibeh, M.F.; Rausch, J.; Schippers, S.; Müller, A. Electron-impact ionization of multiply charged tungsten ions. J. Phys. Conf. Ser. 2014, 488, 062026. [Google Scholar] [CrossRef]
- Rausch, J.; Becker, A.; Spruck, K.; Hellhund, J.; Borovik, A.; Huber, K.; Schippers, S.; Müller, A. Electron-impact single and double ionization of W17+. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 165202. [Google Scholar] [CrossRef]
- Loch, S.D.; Ludlow, J.A.; Pindzola, M.S.; Whiteford, A.D.; Griffin, D.C. Electron-impact ionization of atomic ions in the W isonuclear sequence. Phys. Rev. A 2005, 72, 052716. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demura, A.V.; Kadomtsev, M.B.; Lisitsa, V.S.; Shurygin, V.A. Tungsten Ions in Plasmas: Statistical Theory of Radiative-Collisional Processes. Atoms 2015, 3, 162-181. https://doi.org/10.3390/atoms3020162
Demura AV, Kadomtsev MB, Lisitsa VS, Shurygin VA. Tungsten Ions in Plasmas: Statistical Theory of Radiative-Collisional Processes. Atoms. 2015; 3(2):162-181. https://doi.org/10.3390/atoms3020162
Chicago/Turabian StyleDemura, Alexander V., Mikhail B. Kadomtsev, Valery S. Lisitsa, and Vladimir A. Shurygin. 2015. "Tungsten Ions in Plasmas: Statistical Theory of Radiative-Collisional Processes" Atoms 3, no. 2: 162-181. https://doi.org/10.3390/atoms3020162
APA StyleDemura, A. V., Kadomtsev, M. B., Lisitsa, V. S., & Shurygin, V. A. (2015). Tungsten Ions in Plasmas: Statistical Theory of Radiative-Collisional Processes. Atoms, 3(2), 162-181. https://doi.org/10.3390/atoms3020162