Abstract
Collisional processes and details of atomic structure of heavy many-electron atoms and ions are not yet understood in a fully satisfying manner. Experimental studies are required for guiding new theoretical approaches. In response to fusion-related needs for collisional and spectroscopic data on tungsten atoms in all charge states, a project has been initiated in which electron-impact and photon-induced ionization as well as photorecombination of Wq+ ions are studied. Cross sections and rate coefficients were determined for charge states q ranging from q = 1 to q = 5 for photoionization, for q = 1 up to q = 19 for electron-impact ionization and for q = 18 to q = 21 for electron-ion recombination. An overview, together with a critical assessment of the methods and results is provided.
1. Introduction
Heavy impurity atoms in a plasma give rise to strong electromagnetic radiation via bremsstrahlung and characteristic line emission [1]. At the low density of a magnetically confined fusion plasma, short-wavelength radiation cannot be efficiently reabsorbed and, therefore, leaves the plasma. The resulting drain of energy shortens the overall energy containment time and thus counteracts the condition for plasma ignition. Concentrations of less than 0.01% of tungsten ions (relative to the electron density and depending on temperature) can already inhibit ignition of a deuterium-tritium plasma [2]. Nevertheless, tungsten with its low sputtering yield, its resistivity to chemical erosion, its low tritium retention and good thermal and mechanical properties appears to be an indispensable material at least for parts of the walls and for the plasma divertors of a fusion device [3]. Thus, tungsten is important for fusion research as the prime candidate for the plasma facing components of ITER [4], the International Thermonuclear Experimental Reactor, and other forefront fusion facilities.
Understanding the influence of tungsten as an impurity and its impact on the plasma requires detailed knowledge about atomic processes and atomic structures of tungsten atoms and ions in all stages of ionization [1,5]. While available plasma-related data bases for elements with low and intermediate atomic number Z have become relatively reliable during recent decades, there are still large uncertainties for heavier multi-electron ions, where even the most fundamental atomic collision processes are not yet sufficiently well understood [6]. Experimental atomic data for high-Z elements have been scarce in general and theoretical calculations are difficult because of the pronounced many-electron, relativistic and quantum-electrodynamical effects in heavy ions. Experimental data are needed for testing and guiding new theoretical developments and for improving the predictive power of theoretical calculations. This is especially true for tungsten where theoretical treatment is complicated by the presence of open d or f subshells.
Atomic processes of prime interest in fusion research are electron-impact ionization and excitation as well as electron-ion recombination. In particular, ionization and recombination determine the tungsten ion charge-state distribution in a plasma. The ion charge-state distribution at a given electron temperature directly influences the power of bremsstrahlung losses from the plasma while direct and resonant excitation together with the population of excited states in recombination processes are responsible for the emission of electromagnetic line radiation and the associated energy losses [1,7].
Although photoionization is of minor importance in magnetically confined fusion plasmas, the investigation of photoionization of tungsten ions can provide valuable information towards the role of tungsten atoms and ions in ionized matter in general. Photoionization is time-reversed (photo)recombination and the principle of detailed balance [8] relates the cross section for electron-ion recombination to that of photoionization. Moreover, photoionization with high energy resolution is a powerful spectroscopic tool for studying the atomic structure of tungsten ions and, in particular, is a detailed probe of multiply excited autoionizing states. In addition, data on atomic structure and decay processes of excited ions that can be obtained from photoabsorption experiments are needed for plasma diagnostics and modeling.
Because of the large amount of input information required for plasma modeling, only theory can provide the bulk of the input data comprising mainly the ionization equilibrium and the excitation rate coefficients along with the energy level structure and transition probabilities. Ionization equilibria are critically determined by the ionization and recombination rate coefficients which are not experimentally known for most of the tungsten ion charge states. Thus, at present, the modeling of spectroscopic plasma observations almost entirely rests on theoretical approaches such as the ones implemented in the international ADAS project (Atomic Data and Analysis Structure; see http://www.adas.ac.uk/about.php). ADAS has been developed and employed over several decades with many participating institutions world wide ( http://www.adas.ac.uk/members.php). The effort to improve data and modeling tools is strongly continuing. Applications are mainly in fusion (see e.g., [9]) but also in the lighting industry (see e.g., [10]) and in astrophysics [11]. It is essential for a project like ADAS to implement reliable knowledge about processes and structures of the atoms and ions of the chemical elements that occur in the plasma to be investigated. Over decades already, close interaction between experiment and theory has provided relatively satisfying understanding of plasma-relevant processes of light atomic ions [6]. An ongoing project for intermediate heavy ions is the systematic experimental and theoretical study of electron-impact ionization and recombination of iron L-shell and M-shell ions that is primarily motivated by the importance of iron ions in astrophysical but also in fusion-plasma environments ([12–15] and references therein).
In view of the critical importance of tungsten in magnetically confined fusion plasmas a project has been started about five years ago to study electron-impact ionization and recombination as well as photoexcitation of tungsten ions by making use of the most advanced experimental techniques suitable for the purpose and available at the time. Tungsten ions in this context also represent the more general class of multi-electron atoms which should be studied over a wide range of charge states and of electron and photon energies to overcome the existing deficiencies in the understanding of heavy many-electron atoms. In this context the physical processes of interest involving tungsten atoms and ions are
- electron-impact single ionizationand
- electron-impact multiple ionization
- recombinationand time-reversed recombination, i.e.,
- (single) photoionizationand
- multiple ionization by one photon
Within the frame of the tungsten collisions project reviewed in this communication, processes described by Equations (1)–(5) were studied for selected charge states by experiments which were partially accompanied by theory. In addition to information about the collision processes listed above, cross sections and rate coefficients for charge transfer ([18,19] and references therein), electron-impact excitation ([20,21] and references therein) together with spectroscopic information ([22] and references therein) on tungsten ions in all charge states are needed for plasma diagnostics. Spectroscopic observations and further collisional data are becoming available now and are summarized in several contributions to the present Special Issue of ATOMS on “Atomic Data for Tungsten”. Detailed information about energy levels of singly excited states in tungsten ions has been compiled by Kramida and Shirai [23–25] and can be found in the NIST Atomic Spectra Data Base [26].
2. Preparation of Ion-Target Beams
All the experiments with tungsten ions dicussed in this contribution made use of interacting-beams techniques, that is, both the ionic targets [27] and the projectiles, electrons or photons, were provided in the form of beams. Electron-impact ionization of tungsten ions was studied by using crossed electron and ion beams [16,28] while photoionization and recombination experiments were carried out in electron-ion merged-beam geometry [29].
2.1. Ion Production and Associated Population of Excited States
The production of singly charged tungsten ions can make use of dilute-plasma conditions in an ion source which is operated at low electron temperatures. When the probability for ionization and excitation is low the production of any ion A+ may ultimately proceed via a single electron-atom collision in which the singly charged ions are predominantly produced in their electronic ground state. The ions are extracted before further collisions can happen. Under such conditions, a relatively well defined beam of singly charged A+ ions in their ground level can be made available.
In contrast to singly charged ions, the efficient production of multiply or highly charged Aq+ ions (q > 1) requires a number of sequentially-ionizing collisions each providing a sufficient amount of energy to overcome the ionization thresholds for the production of the most highly charged ions desired for experiments. A textbook scenario for the production of highly charged ions is to fix atoms in space and bombard them with ionizing electromagnetic radiation or particles. An Electron-Beam-Ion-Trap (EBIT) [30] comes closest to this scheme. Ions are held in a trap potential for a time span τ and exposed to an intense electron beam of sufficiently high energy ([31–33] and references therein). The number of ionizing collisions with one ion and, hence, the final charge state of the atom is determined by the product neτ where ne is the electron number density in the beam. In an EBIT with a storage time of τ = 100 ms the product neτ may easily reach, for example, 1010 s/cm3.
Variations of this scheme are used in all other experiments in which highly charged ions are needed. One possibility is to produce a high density of electrons in a plasma and to confine ions within the space charge potential of the electrons in combination with external magnetic fields. This scheme is employed in Electron-Cyclotron-Resonance (ECR) ion sources [34] where a high density of energetic electrons is obtained by heating the source plasma with microwaves. Again, the product neτ is responsible for the ion charge states that can be reached. Since the dwell time τ of ions in the plasma cannot be directly controlled and, in particular, cannot be made sufficiently long, the average charge states
that can be reached in an ECR ion source with very heavy ions with atomic number Z are restricted to about
while for lighter ions with low Z one may reach
close to Z with efficient production of AZ+ ions. The number of ions that can be trapped in an EBIT is quite limited and hence, ion currents that can be extracted from an EBIT are small when averaged over time. In contrast, an ECR ion source can provide relatively high currents of multiply charged ions in low to moderately high charge states.
An alternative to the production of multiply charged ions in an ion source is the acceleration of low-charge-state ions to a certain velocity vi and then passing them through a sufficiently dense neutral gas or solid target. In the rest frame of the fast moving ions the electrons bound in the target atoms act like fast moving projectiles which can ionize the ion provided the relative velocity vrel = vi is sufficiently high. Again the number of ionizing collisions is determined by neτ where ne = n0Z with n0 the density of the neutral target atoms and τ the time needed by the fast ion to pass the target. These times can be very short depending on the geometrical length (or thickness) of the target. Carbon foils with thickness in the range of 0.1 µm have been used in the present recombination experiments to produce moderately charged tungsten ions with q in the vicinity of 20. Passage times of the order of 20 fs and bound target-electron densities of 6 × 1023 cm−3 result in neτ ≈ 1010 s/cm3 similar to what is used in EBIT devices.
In all scenarios described above, the electrons must have energies in the electron-ion center-of-mass frame which are sufficient to produce any of the desired ion charge states q. Hence, they also have enough energy to excite essentially any electronic level in the Aq+ ions generated in the source, except for the highest charge state qmax that can be achieved at a given electron energy
where
is the ionization potential of the ion
. As a result, all the excited states of Aq+ ions with
(and many excited states of the ions
with the maximum possible charge state) can be populated in the multi-collision scenario discussed in the previous paragraphs. As a result of this interrelationship, the population of excited states during the production of multiply charged ions cannot be avoided.
The exposure time τ of the ions to impacting electrons has an influence on the population of excited states. Most of the excited states decay with lifetimes which are between ns and fs. However, there are excited states for which the decay by emission of electromagnetic radiation is forbidden or at least strongly suppressed and, hence, ions in such states may have long lifetimes. Obviously, the presence of ions in long-lived excited metastable levels is therefore unavoidable during the production process needed to generate Aq+ ions in high ion charge states q for collision experiments. An exemption from this rule is the isoelectronic sequence of lithiumlike ions which do not support low-lying long-lived excited states.
When the desired Aq+ ions are no longer exposed to electron bombardement the excited states decay exponentially with their individual lifetimes. In a typical ion-collision experiment, the ions have to travel from the ion source (or the electron-stripper foil) to the target region where the reactions take place that are to be studied. The distance between this interaction region and the ion-production site is typically several meters in room-sized arrangements and may reach hundreds of meters at accelerators. Flight times are typically between 100 ns and 100 µms so that short-lived excited states can completely decay. Rydberg states featuring an electron with high principal quantum number n can be quenched by electromagnetic fields present in the beam transport line. The remaining long-lived metastable states, however, remain in the beam and their contribution to the measurements has to be considered.
In EBIT experiments the ion trapping time can reach several seconds. In such a scenario, i.e., in a dilute plasma where the collision rates are lower than most electromagnetic-decay rates the net population of excited states may be reduced but also cannot be avoided during the production process. By switching off the electron beam once the desired charge-state distribution of the ion inventory is reached, the excited states can be given some time to relax before the ions escape from the trap region. Since the radial confinement of the ions by the electron space-charge potential is gone with the electron beam switched off the time span that can be tolerated for relaxation of the ions is quite limited.
In experiments employing heavy-ion storage rings [15,35] the ion charge state is typically prepared by passing the ions through electron-stripper foils. Short-lived excited states can decay on their way to the storage ring which typically takes microseconds. The stored ion beam is prepared for experiments by electron cooling which needs time of the order of one second depending on the ion charge state. Under favorable conditions a beam of highly charged heavy ions can be stored for many minutes or hours [35], however, a typical lifetime is less than one minute. Thus it is possible to wait for 10 seconds or even longer before the experiment with the stored ions is started. Such long time spans are sufficient to eliminate most of the excited states present in the ensemble of stored ions [36,37].
2.2. Generating Beams of Multiply Charged Wq+ Ions
Two different methods were employed for the present collision experiments with tungsten ions to produce the desired charge states. For electron-impact ionization and photoexcitation experiments the ions were produced in an ECR ion source [38]. Tungsten hexacarbonyl, W(CO)6, was evaporated and introduced to the plasma chamber of the ion source via a finely tunable leak valve. Mainly by electron collisions the molecular complex was fragmented and then ionized. The dense, hot plasma in an ECR ion source provides a wide spectrum of ion charge states with relatively high ion densities. In the present experiments the ions were continuously extracted from the ECR plasma and accelerated by voltages of 6 to 12 kV. The emerging ion beam was focused and transported through an analyzing dipole magnet to select the ion species with the desired charge state for the experiment. Such a charge-state spectrum of the ions extracted from the ECR ion source, which was operated with W(CO)6 vapor, is shown in Figure 1. Peaks associated with tungsten have a characteristic fingerprint resulting from the natural abundance distribution of the tungsten isotopes with 180W (0.12%), 182W (14.3%), 183W (14.3%), 184W (30.6%), and 186W (28.4%).
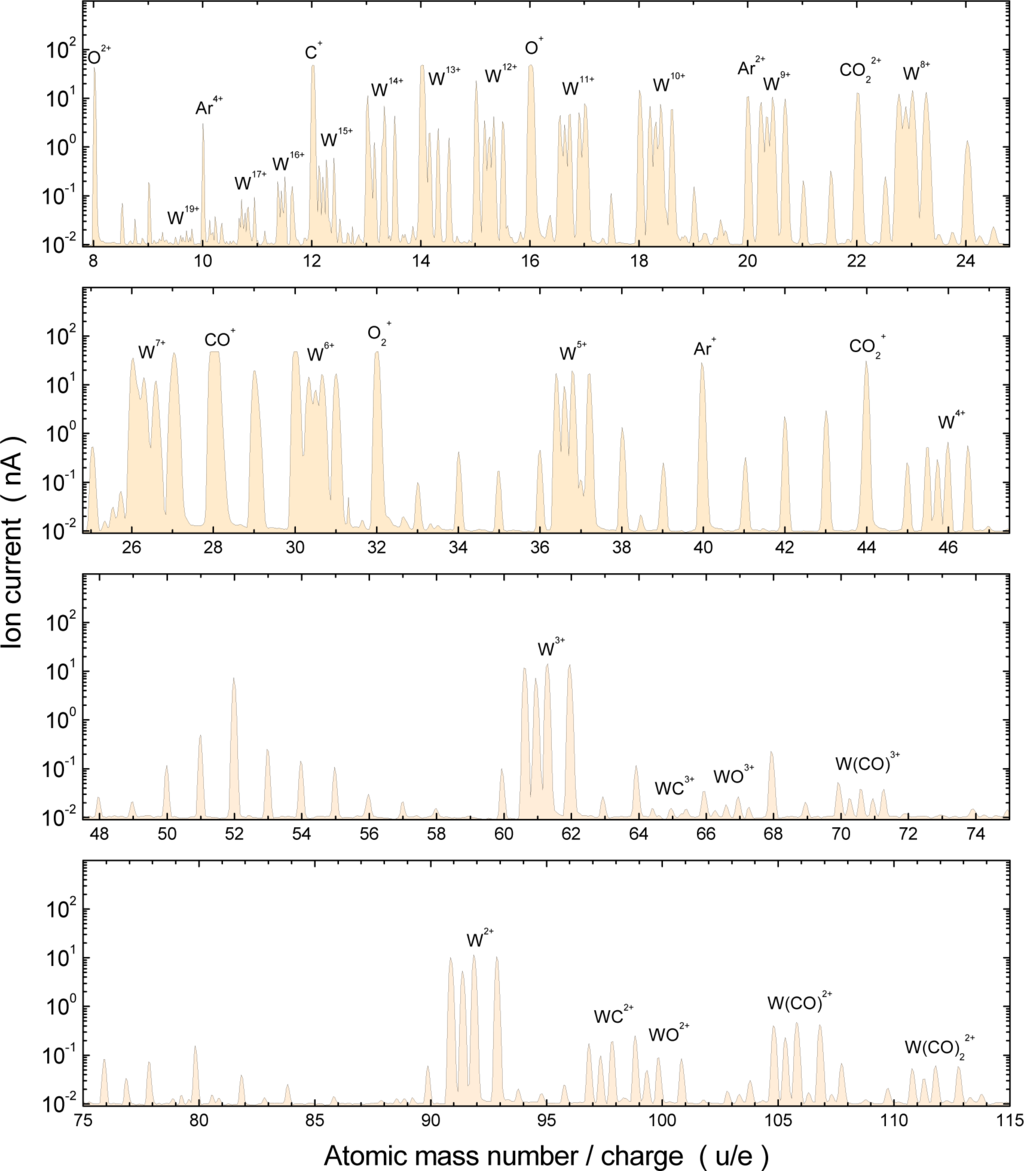
Figure 1.
Ion currents extracted from an Electron-Cyclotron-Resonance (ECR) ion source operated with W(CO)6 vapor and measured as a function of the magnetic flux density B1 of the dipole analyzing magnet. B1 was calibrated to provide the mass-over-charge ratios of the ions detected. The most prominent ion species associated with the presence of tungsten are indicated in the figure. The complete mass spectrum reaches up to
ions. For the lower charge states Wq+ the natural isotopes of tungsten are completely resolved. Peaks in the mass ranges around 52 and 80 are not identified. They are probably associated with hydrocarbon molecules residing on surfaces. The strongest peak appears to be due to CO+ ions. Here as well as for several other peaks the current amplifier was obviously saturated.
The ion source had been optimized for the production of W5+ ions prior to the measurement of the mass spectrum displayed in Figure 1. Ion currents for isotopically resolved 186W5+ were about 17 nA in that experiment. When the source was tuned for output of tungsten ions in charge states near q = 20 the highest charge state that could be observed in a mass spectrum was q = 29 with ion currents of several pA for each of the more abundant tungsten isotopes.
In the storage-ring recombination experiments the tungsten ions were produced from tungsten carbide WC. Negative WC− ions were generated in a suitable cesium-loaded ion source. The negative ions were injected into a tandem accelerator, stripped on their way through the acceleration structure and then stripped again after the acceleration. Clearly, numerous excited states were populated when running the ions through stripper foils. Most of these could be made to decay before the recombination experiments were started. Detailed information will be given in the following subsection and, where appropriate, in the context of the discussion of experimental results.
2.3. Assessment of the Presence of Metastable Excited States in Beams of Wq+ Ions Used for the Present Experiments
W+ ions for photoexcitation and electron-impact ionization experiments were produced by employing an ECR ion source [38,39] which is known for its capability to produce a relatively hot plasma. This is favorable for the production of multiply charged ions but it also implies considerable population of metastable excited states. The ground configuration of W+ is 5d46s with even parity. The energetically lowest level within this configuration has the spectroscopic notation 6D1/2. The first excited configurations 5d5 and 5d36s2 also have even parity and therefore their decay by electric dipole transitions is forbidden. Hence, the emission of electromagnetic radiation in general must be expected to be very slow. The three lowest configurations comprise 119 levels including the 5d4(5D)6s 6D1/2 ground level. Only 74 of all these possible levels are listed in the NIST Atomic Spectra Database [26].
The ionization potential of W+(5d4(5D)6s 6D1/2) is 16.37 eV [26]. Removal of the 6s electron leads to W2+(5d4 5D0), the ground level of doubly charged tungsten. The 118 excited levels within the 3 energetically lowest (even-parity) configurations of W+ have energies up to 8.77 eV above the ground level and therefore require accordingly less energy than the 16.37 eV necessary to reach the ground level of W2+ from that of W+. The situation is illustrated in Figure 2.
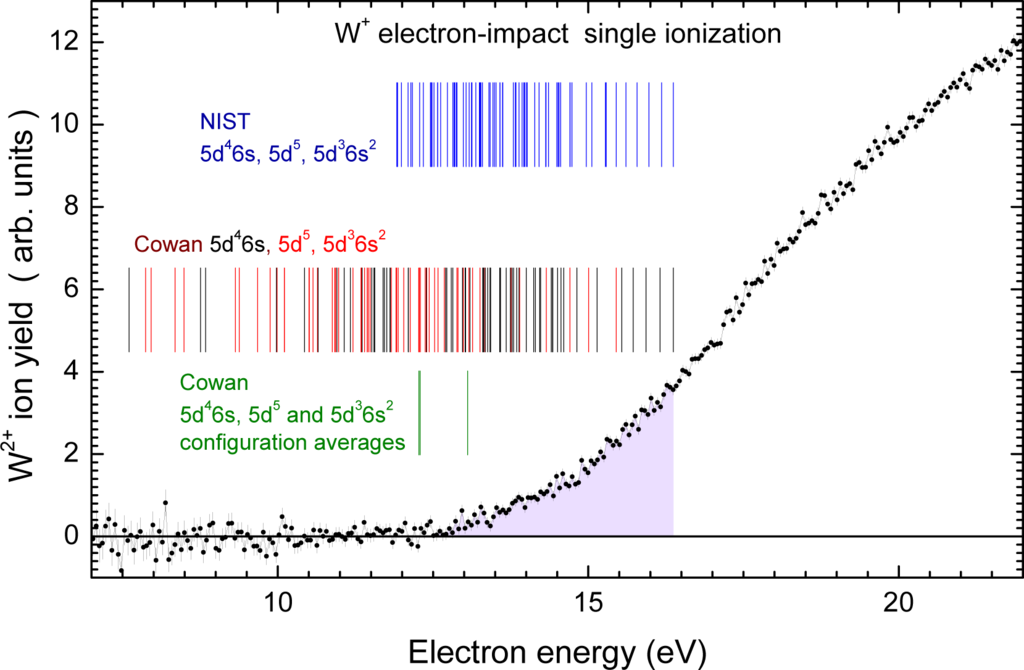
Figure 2.
W2+ ion yields (in arbitrary units) arising from electron-impact single ionization of W+ ions [40]. The yield was recorded as a function of incident-electron energy. The vertical blue bars show the threshold energies relative to the lowest of the 74 levels within the 5d46s, 5d5 and 5d36s2 configurations whose excitation energies are listed in the NIST Atomic Spectra Database [26]. The vertical black bars represent the threshold energies of the 63 levels within the 5d46s ground configuration while the red bars show the threshold energies of the 56 levels within the first excited, 5d5 and 5d36s2, configurations as calculated with the Cowan code [43]. The lowest ionization potential of W+ of 16.37 eV was taken from the NIST Atomic Spectra Database [26] for the blue, black and red bars. The green bars are related to the average energies of the 5d46s, 5d5 and 5d36s2 configurations using statistically weighted level energies. These excitation energies were calculated by employing the Cowan code [43] and then subtracted from the ground-state ionization potential of 16.37 eV to obtain the locations of the green bars. The observed yield (shaded area) below the ground-state ionization potential clearly indicates the presence of metastable states in the W+ parent ion beam.
The experimental W2+ ion yield [40] shown in Figure 2 originated from ionizing electron collisions with W+ ions. The measured onset is at about 12.5 eV well below the ionization threshold of 16.37 eV for W+ ions in their ground state. Clearly, long-lived excited states were present in the W+ parent ion beam employed for this measurement. However, the figure also shows no evidence for contributions from the more highly excited levels within the three energetically lowest configurations. The experimental onset of the W2+ ion yield is between the configuration-averaged threshold energy for the 5d46s configuration (at 13.06 eV) and the configuration-averaged threshold energies for the 5d5 and 5d36s2 configurations (12.29 eV and 12.27 eV), respectively. This means that the 63 levels within the ground configuration out of the altogether 119 possible levels associated with the first three configurations may have been present in the parent ion beam that was used for the threshold scan in Figure 2. All 63 levels may have contributed with some measurable amount to the total W2+ ion yield observed.
The above discussion clearly illustrates the problem that exists with metastable states in beams of multi-electron ions. This problem can only be avoided or at least drastically reduced in an experiment where a suitable time interval is implemented to let the long-lived excited states decay before the actual measurement is started. For this purpose, the ions have to be stored after preparation. This can be realized in an ion trap or in an ion storage ring. The latter option was used in the experiments on electron-ion recombination of Wq+ ions with q = 18, 19, 20, 21.
For the discussion of how storing the ions influences the population of excited states, W18+ is chosen as an example. The lowest level of W18+ is ([Kr]4d104f10 5I8) [26,41]. For an estimate of excited-state populations that might be present in the beam after preparation of W18+ in a stripper foil, the first excited configurations ([Kr]4d104f95s) with 396 levels and ([Kr]4d104f95p) with 1168 levels were included in the considerations together with the ground configuration ([Kr]4d104f10) (107 levels). There are 1671 levels within this set of electron configurations spanning an energy range from 0 up to 114 eV. Excitation energies and lifetimes were calculated by using the AUTOSTRUCTURE atomic structure code [41,42]. Most levels decay with lifetimes much smaller than 1 ms. Only 19 levels including the ground state of W18+ live longer than 10 ms. The ([Kr]4d104f10 3F2) level was found to have a lifetime of 3.79 × 108 s, i.e., about 12 years. Hence, there is no way to eliminate this level in an experiment by just waiting for a sufficiently long time.
In order to model the development of excited-level abundances in the W18+ parent ion beam, a system of coupled rate equations [44] describing population and decay of all levels considered in this treatment was solved numerically using the calculated transition lifetimes. Right after the production of the ions in the stripper foil, at time zero, a Maxwell-Boltzmann distribution of the levels was assumed. The resulting abundances as a function of time are shown in Figure 3. Variation of the temperature in the initial Maxwell-Boltzmann distribution had little effect on these results.
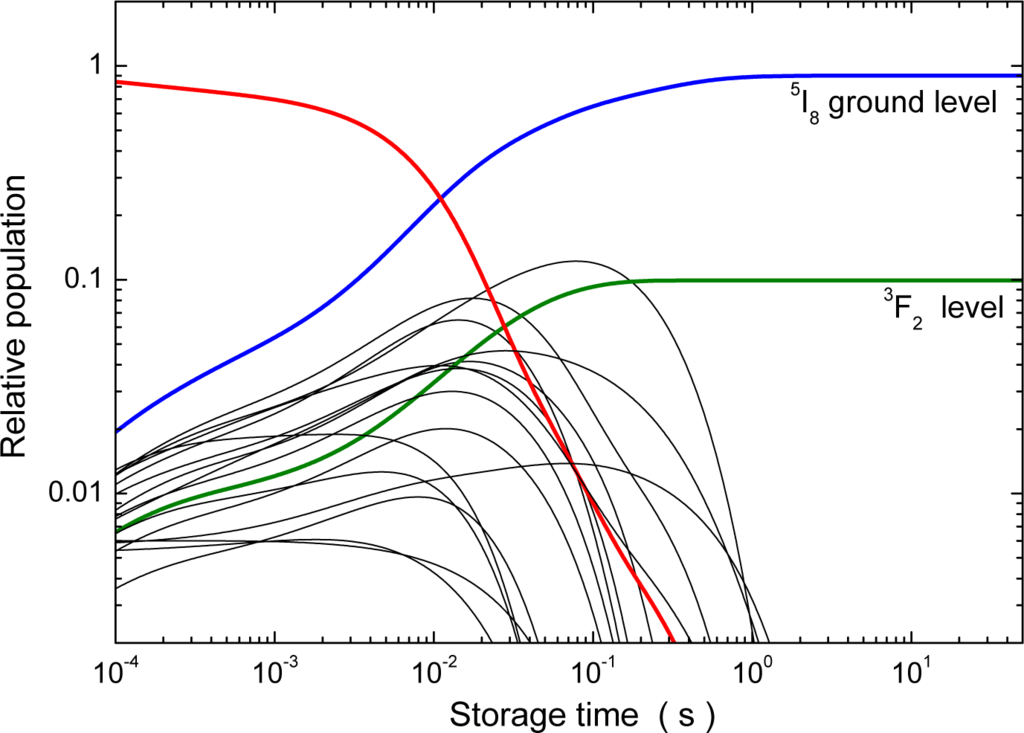
Figure 3.
Relative populations of levels within the W18+(4f10), W18+(4f95s) and W18+(4f95p) configurations with a Maxwell-Boltzmann starting condition [41]. The solid red line shows the sum of all the 1652 short-lived levels which are essentially gone before 1 s has passed. The solid blue line is the relative population of the ground level and the green line represents the population of the very long-lived ([Kr]4d104f10 3F2) level. The thin solid lines were obtained for the remaining 17 levels, all with relatively long lifetimes between 10 and 629 ms. For further details see the text.
Storing and cooling the W18+ ion beam took about 1.5 s. After that time only two levels had survived, the 5I8 ground level with an abundance of 90% and the long-lived 3F2 excited level with an abundance of 10%, both from the 4f10 ground configuration. As a result of the very long lifetime of the excited level, the beam composition 9:1 did not change during the measurement that started after the 1.5 s cooling time.
In summary one has to state that beams of tungsten ions in low to intermediate charge states with open d and f subshells can rarely be prepared in their ground state. When the ions are stored for several seconds after their production most of the long-lived states have decayed, however, the possible effects of very long-lived metastable states that still survive have to be investigated in each case individually. Storing an ensemble of highly charged ions with sufficient density for measurements at low electron energies and under clean experimental conditions requires a large accelerator facility. Beamtime at such facilities is expensive and very limited. Small-scale experiments with highly charged ions require a powerful ion source providing high electron energies which then typically also produces long-lived excited states. With an EBIT this problem can be reduced exploiting the (limited) ion storage capability even with the electron beam and its negative space-charge potential switched off. However, one cannot wait for seconds without the electron beam and its ion-confining space charge until a measurement can be started. Furthermore, the very low energies that are most interesting for tungsten ion recombination with electrons are not accessible with an EBIT.
The alternative is an experimental setup with an ion source producing useful amounts of ions in sufficiently high charge states and to transport these ions directly to the electron-ion or photon-ion interaction region. Since the flight times for the accelerated ions are only in the range of microseconds in this scenario substantial abundances of metastable levels are to be expected in beams of many-electron ions. In a multi-electron ion, such as W+, numerous excited levels at least from the ground-state configuration but probably also from excited configurations can contribute to the measured cross section. Level-to-level treatment of cross section contributions is desirable under such conditions but constitutes a very formidable task for theoretical calculations. Even if such calculations are available the fractions of ions in different excited states are not easily determined.
Fortunately, there is the possibility to treat cross sections in terms of the configuration-average approach which can provide meaningful results. At least for the higher charge states of tungsten the configuration-average distorted-wave approximation provides a useful tool for reliable calculations of cross sections for direct and excitation-autoionization contributions to net single ionization. In this context one has to keep in mind that in a real (fusion) plasma, long lived excited states are also present—probably even with a population distribution similar to that in a typical electron-ion crossed-beams experiment.
3. Overview of the Collisional Data Obtained for W Ions
Prior to the start of the present tungsten data project, the experimental situation was best for electron-impact ionization of tungsten ions in low charge states. While measurements on the neutral tungsten atom are still not available, single and multiple ionization of Wq+ ions by electron impact had been investigated already more than a decade ago by Stenke et al. [45,46]. The charge states q in these measurements varied from 1 to 10 for single ionization, from 1 to 6 for double ionization and from 1 to 4 for triple ionization. Electron energies in single-ionization measurements covered the range between the respective ionization threshold and maximum energies of 550 eV for q = 1, 1000 eV for q = 2, 3, …, 8 and 5000 eV for q = 9, 10. The data for single ionization of W+ ions by Stenke et al. [45] are in quite good agreement with preceding measurements by Montague and Harrison [47].
Photoionization of neutral tungsten atoms was previously studied in the energy range from about 27 to 60 eV by Sladeczek et al. [48]. Before this measurement, photoabsorption experiments with neutral tungsten in solid and vaporized forms had been performed by Haensel et al. [49] and by Costello et al. [50], respectively. No experimental data were available in the literature for tungsten ions prior to the present work.
Before the present project there were no recombination experiments with tungsten ions at low energies. First experimental data on radiative and dielectronic recombination of Wq+ ions with q = 60 to 67 had become available by measurements using EBITs [51,52]. The disadvantage of such measurements is in the presence of several different charge states in the trap at a time. Disentangling the observed spectra with respect to ion charge states requires substantial support by theory. To date, a measurement of absolute cross sections or rate coefficients for recombination of tungsten ions has not been accomplished (or attempted) in an EBIT experiment.
3.1. Electron-Impact Ionization
Net ionization of an ion can result from a number of different electron-ion collision mechanisms [16]:
- Direct knock-off removal of an outer-shell electron, termed direct ionization (DI)
- Excitation of an inner-shell electron so that an autoionizing intermediate state is produced; by a subsequent Auger decay an electron is released from the atom or ion; the process is termed excitation-autoionization (EA)
- Dielectronic (radiationless) capture of the incident electron with simultaneous inner-shell excitation reducing the ion charge state by one unit; the resulting highly excited state may then decay by the emission of two electrons (either sequentially or simultaneously) and, thus, an ionized ion with a charge state one unit above that of the parent ion is produced. The whole process is resonant as a result of the first step, the dielectronic capture, which is essentially a time-reversed Auger-decay process
Within the present project, electron-impact ionization of Wq+ ions has been studied for all charge states q = 1, 2, …, 19 in the energy range from below the ionization threshold to 1000 eV. The present data agree within about 15% with the measurements carried out by Montague and Harrison [47] for W+ and with the results obtained by Stenke et al. for charge states q = 1, 2, …, 10 [45,46]. In most cases the agreement is much better than 15%. An example is provided in Figure 4. The measurements by Stenke et al. [46] for electron-impact double ionization of W+ ions perfectly agree with test measurements carried out by Borovik et al. [40] which were meant to provide a consistency check for the previous versus the new data explored within the present tungsten collisions project. It is interesting to note that there is no obvious hint of the presence of metastable ions in the parent ion beam in this case.
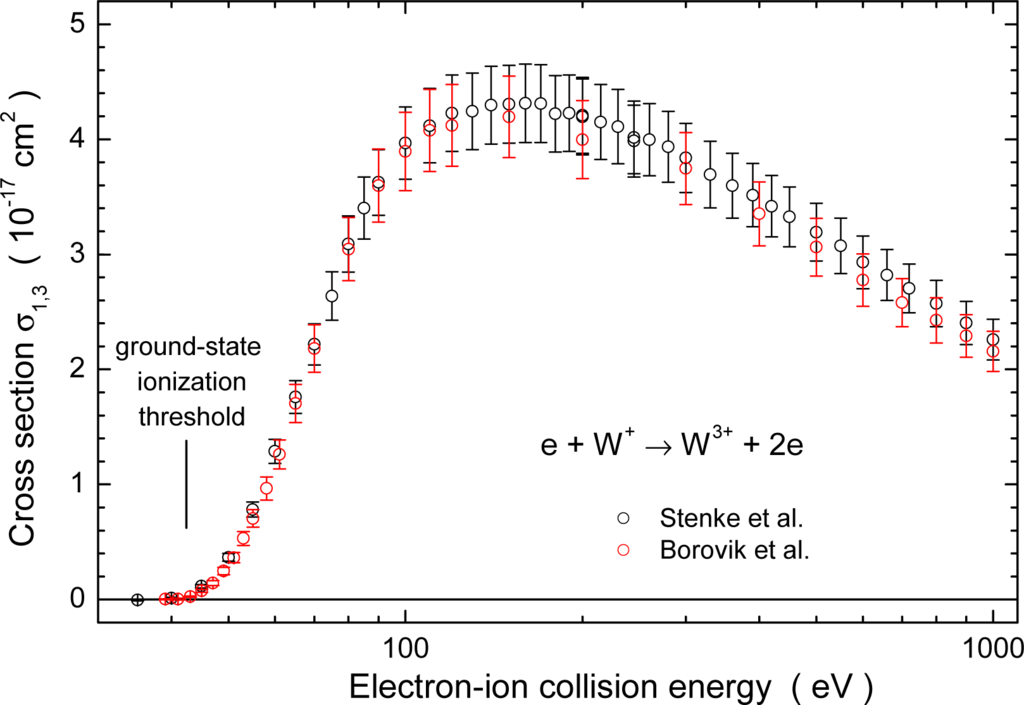
Figure 4.
Comparison of experimental cross sections for electron-impact double ionization of W+ measured previously by Stenke et al. [46] and a test measurement [40] of the same cross section carried out in the frame of the present tungsten collisions project. The vertical bar indicates the threshold for reaching the ground level of W3+ from the ground level of W+.
Theoretical calculations for single ionization of Wq+ ions were performed for all charge states q by Loch et al. [53] employing the configuration average distorted wave (CADW) approach. For very low charge states, distorted-wave theory tends to overestimate the experimental results. For W4+, W5+ and W6+, distorted-wave theory was found to be in reasonable agreement with the measurements by Stenke et al. [45]. Ionization of W9+ with good agreement between theory and experiment has been taken as a proof that the CADW calculations are reliable for higher charge states [53]. However, the cross section for single ionization of W9+ is strongly dominated by direct outer shell ionization, a process that can be quite well predicted by various methods. For configurations where indirect ionization mechanisms become important, it is desirable to test the CADW approach and its suitability to produce reliable cross section data. Therefore, the range of measurements of electron-impact ionization of tungsten ions was extended beyond the data set of Stenke et al. [45,46] going to almost twice the maximum charge state investigated previously (q = 19). In the following, the results obtained for W17+ will be presented as an example and discussed in detail.
Considering the problem with long-lived excited states in beams of multiply charged ions, fine cross-section scans in the threshold region have been carried out to find evidence for ionization onsets below the ground-state ionization threshold [54]. An example has already been discussed above for measurements with W+ ions. Figure 5 shows such a threshold scan for electron-impact single ionization of W17+ ions. According to calculations with the Cowan code [43] and according to the NIST Atomic Spectra Data Base [26] the ground level is (4f11 4I15/2). Its ionization potential is (420.7±1.4) eV which is required to reach the lowest level W18+(4f10 5I8) of the next higher charge state. With the Cowan code 41 levels are found in the ground configuration 4f11 of the parent W17+ ion. Their excitation energies were subtracted from the ground-level ionization potential (420.7 eV) to obtain the locations of the blue vertical bars in Figure 5 which represent the minimum energy required to reach the ground level W18+(4f10 5I8) from the excited levels of W17+(4f11). The onset of the measured cross section at about 400 eV indicates that probably all levels in the 4f11 ground configuration of the parent W17+ ion contributed to the measured ionization signal.
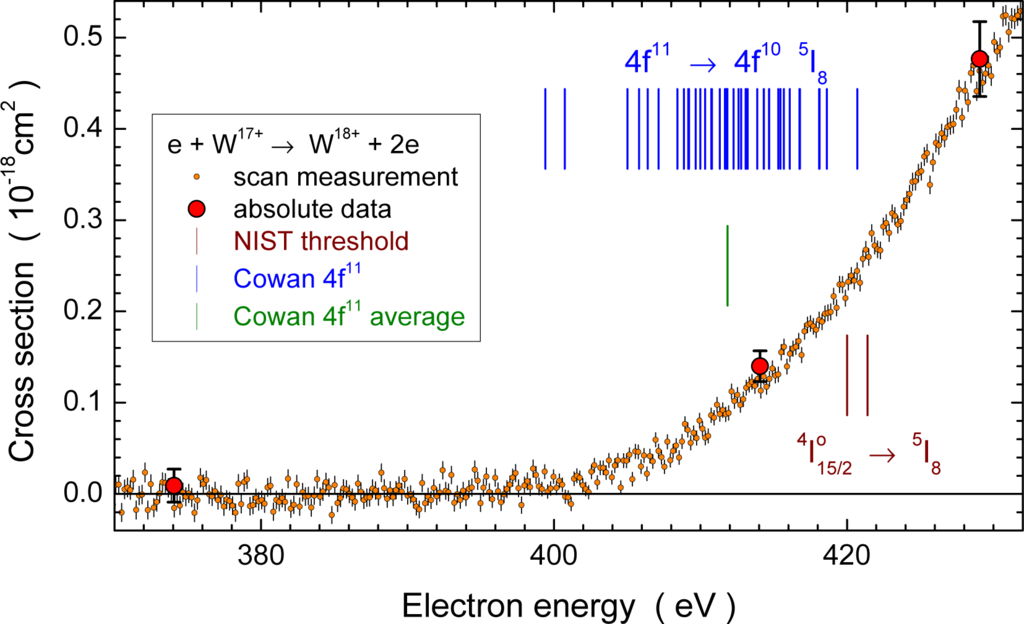
Figure 5.
Threshold-energy region of single ionization of W17+ ions. The small circles with error bars represent the fine energy scan of the cross-section function, the large red-shaded circles are the absolute cross section measurements to which the scan was normalized [55]. The ionization threshold for ground-level W17+ to ground-level W18+ transitions (4I15/2 → 5I8) is within the range spanned by the two brown vertical bars [26]. The blue vertical bars show the minimum energies required to reach the W18+(4f10 5I8) ground level from the excited levels within the ground configuration 4f11 of the parent W17+ ion. The green vertical bar represents the configuration average energy needed to produce W18+(4f10 5I8).
The positions of the various vertical bars in Figure 5 indicate a substantial spreading of threshold energies over a range of about 20 eV. When configuration-averaged cross sections are calculated the threshold energy for going from one configuration to another is just an average energy rather than the multitude of possible thresholds resulting from the accessible combinations in level-to-level calculations. Therefore, the agreement between theoretical (CADW) and experimental results in the vicinity of the ionization thresholds cannot be fully satisfying per se.
While the energy range of levels within the 4f11 ground configuration of W17+ appears to be somewhat broad in the threshold region investigated in Figure 5, the relative width of that range appears much less dramatic when seen in the broader context of the cross section for single ionization which is shown in Figure 6. As an example for the quality of theoretical calculations for the tungsten ions in the range of investigated charge states the experimental data are compared with theoretical calculations employing distorted-wave approaches to describe DI and EA. Two different approaches for DI have been applied. The larger DI cross section is obtained by using the CADW approach implemented in the GIPPER code which is available online ( http://aphysics2.lanl.gov/cgi-bin/ION/runlanl08d.pl) on the web pages of the Los Alamos National Laboratory (LANL).
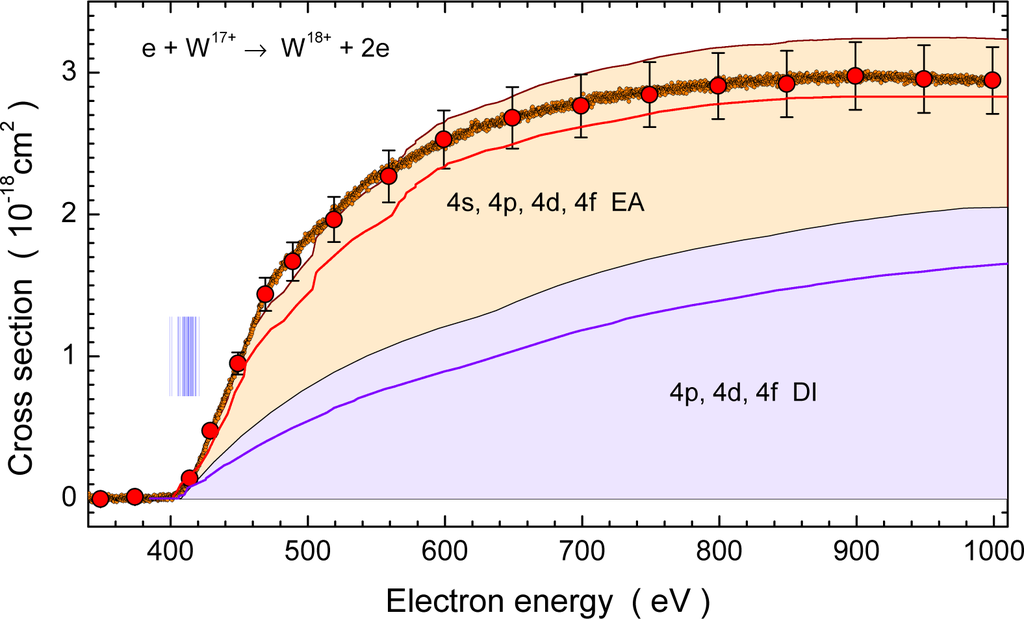
Figure 6.
Measured and calculated cross section for single ionization of W17+ ions. The red-shaded circles with error bars are the results of absolute cross section measurements and their total uncertainties given at a 2σ confidence level [55]. The closely spaced orange-shaded circles represent the energy-scan measurements carried out by Rausch et al. [55]. The scan result is normalized to the absolute data. The ionization potentials of the 41 levels within the 4f11 ground configuration of W17+ are represented by the vertical blue lines. The thin black line with violet shading is the result of configuration-average distorted wave (CADW) calculations for direct single ionization (DI) knocking off an electron from the 4p, 4d or 4f subshell. Added to this is the contribution of excitation auto-ionization (EA) processes starting from the 4s, 4p, 4d, and 4f subshells. The EA contribution was calculated by Zhang and Kwon [56] and is given by the light-orange-shaded area. Different from the total single-ionization cross section obtained by this summation (the solid brown line) Zhang and Kwon using the distorted-wave approach implemented in the FAC code obtained the solid red curve based on their result (the solid blue curve) for DI of the 4p, 4d, and 4f subshells. All theory curves are shifted by −15 eV relative to their original energy axis.
The results of the CADW calculation for the 4p, 4d, and 4f subshells of W17+(4f11) are given by the thin black line in Figure 6 with light violet shading. Added to this is the contribution of EA to the cross section which results in the solid brown line. The EA contribution is shaded in a light orange color. It was calculated by Zhang and Kwon [56] using the distorted-wave approach augmented by calculations following the Coulomb-Bethe approximation. Excitations of the 4s, 4p, 4d, and 4f subshells to all states with principal quantum numbers up to n = 36 and angular momentum quantum numbers up to 5 were included. Moreover, the branching ratios for autoionization versus radiative stabilization of multiply excited states were considered. With the many excited states included in the EA calculation by Zhang and Kwon [56] the experimental cross section is quite nicely reproduced. In Figure 6 the sum of CADW DI and EA calculations was shifted by −15 eV to match the experimentally observed onset. This shift appears justified by the substantial energy spreads within given configurations discussed in the context of Figure 5. In the paper by Zhang and Kwon [56] the DI contribution to the cross section was calculated for the ground state of W17+(4f11) and for the lowest level of the excited configuration of W17+(4f105s), separately. The solid blue curve in Figure 6 shows the result obtained by using the FAC code [57] for DI of W17+(4f11) (also shifted by −15 eV for consistency). Adding the previous EA contribution to this DI result provides the single-ionization cross section as given by Zhang and Kwon. Again with a shift by −15 eV this is shown as the red line in Figure 6 which agrees well with the experimental data.
The analysis of all the new cross section measurements for single ionization of Wq+ with q = 11, 12, …, 19 shows that very satisfying results and good agreement of experiment and theory can be found with CADW calculations of DI and EA contributions provided excitation to subshells with very high n and a sufficient range of orbital momentum quantum numbers is included. The necessity for inclusion of high-nl states in DW calculations has also been emphasized recently by Jonauskas et al. [58] for single ionization of W27+ ions.
Tungsten ions in high charge states appear to follow the expected trend that ionization of highly charged ions is practically unaffected by resonance processes. At least for the range of charge states q = 1, …, 19 where experimental data with fine energy steps and very good statistics exist there is no evidence for the presence of resonant excitation (by dielectronic capture of the incident electron) with subsequent emission of two electrons [16]. However, it is also not obvious that resonances cannot become important at yet higher charge states. W19+ still possesses 55 electrons. For xenon ions with the number of electrons going down from 53 to 37 a distinct increase of resonance contributions to single and multiple ionization has been observed [59–61]. This trend becomes stronger with increasing charge states of xenon ions [62] with the number of electrons finally reduced to 29. Thus it might become necessary to include resonance contributions in calculations of the cross sections for single ionization of the more highly charged tungsten ions.
For several charge states of tungsten ions cross sections for multiple ionization were measured. As an example Figure 7 shows the data for double ionization of W17+ obtained within the present tungsten collisions project. The threshold energy is (882.8 ± 2.8) eV [26]. Even with the uncertainty of this threshold accounted for, the experimental data clearly show an onset of ionization at a lower energy. This onset is compatible with the population of excited levels within the ground-state configuration. In principle, it is possible that double ionization proceeds in a direct process where the incident electron ejects, for example, two 4f electrons or, alternatively, it scatters off one 4f electron which, on its way out, ejects a second electron. It is also possible that a single 4s or 4p electron is released from an excited level of W17+(4f11) and some of the resulting W18+ levels can then emit an Auger electron. The n = 3 shell cannot yet be opened at the energy available in the experiments. There is no clear signature from which one might decide which processes are responsible for the observed double ionization. The cross section in the investigated energy range is still below its maximum. At 1000 eV the cross section ratio for double versus single ionization of W17+ is roughly only 1.3%.
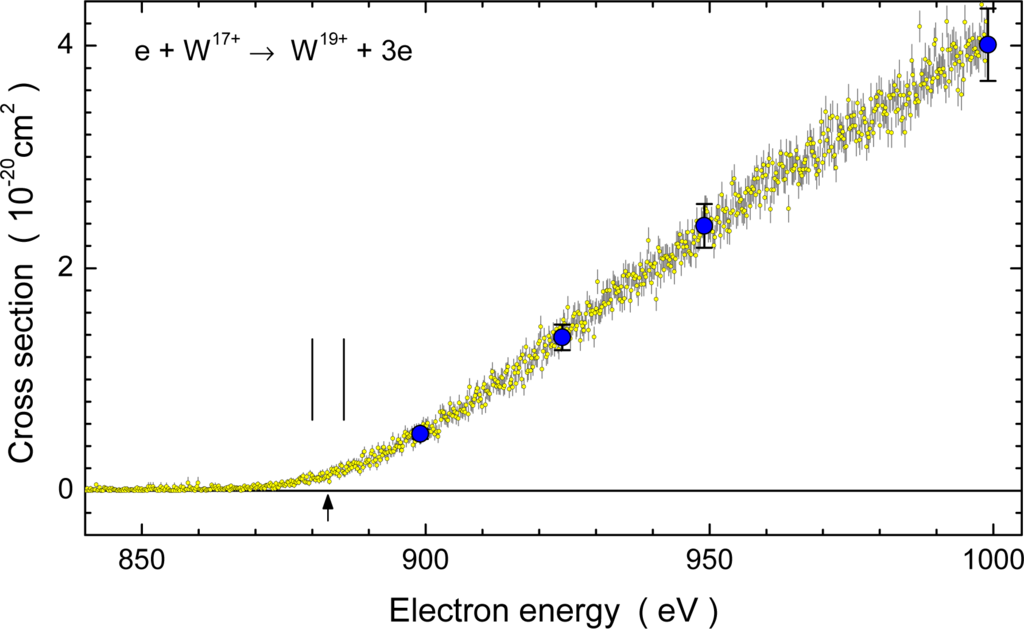
Figure 7.
Measured cross section for electron-impact double ionization of W17+ ions [55]. The blue-shaded circles represent absolute cross section measurements with their error bars. The densely spaced yellow-shaded circles are the results of an energy-scan measurement which was normalized to the absolute data points. The vertical arrow shows the ionization threshold for the ground-level W17+ to ground-level W19+ transition [26]. The vertical bars illustrate the associated uncertainty limits.
3.2. Photoionization
Photoabsorption by tungsten atoms in the gas phase has been studied experimentally by Costello et al. in the energy range from about 31 to 55 eV employing the dual-laser-plasma technique [50]. A few years after that pioneering experiment the production of W+ and W2+ photo-ions from tungsten vapor was observed by Sladeczek et al. [48]. However, no experimental data have been available in the literature for tungsten ions prior to the present project. Direct photoionization of Wq+ ions is included in the calculations by Trzhaskovskaya et al. [63] as time-reversed radiative recombination but is expected to be only a small contribution to the total photoionization cross section. Theoretical work using the many-body perturbation theory (MBPT) approach has been carried out by Boyle et al. [64] for photoionization of neutral tungsten atoms in their 4f145s25p65d46s2 5D0 ground level. Theoretical treatment of photoabsorption using a relativistic Hartree-Fock (RHF) approach was reported by Sladeczek et al. [48] for all five levels of the 5d46s2 5D ground term and for the 5d56s 7S3 excited level. Because of the lack of experimental data for ionized tungsten atoms, an attempt was made in the present tungsten project to study photoionization of Wq+ ions in charge states q ≤ 5. This work is close to being finalized.
Figure 8 shows cross sections for photoionization of neutral tungsten atoms published by Sladeczek et al. [48]. The top panel presents theoretical data obtained by the RHF approach. The bottom panel displays measured W+ and W2+ photo-ion yields which have been approximately normalized to the theoretical cross sections. Also the sum of the two yields is shown which should be close to the photoabsorption cross section. In the energy region investigated here, excitations of an electron from either the 4f or the 5p subshell prevail. A substantial increase of the cross section is observed above 36 eV. This step-like feature is reminiscent of an ionization edge. A relatively prominent narrow resonance peak is seen at a photon energy of about 34 eV. In order to match these step and peak features the theoretical curve has been shifted towards lower energies by 1.3 eV. By the RHF calculations the narrow resonance was identified to be due to photoexcitation hν + W(5p65d56s 7S3) → W(5p55d56s2 7P4) and subsequent auto-ionization.
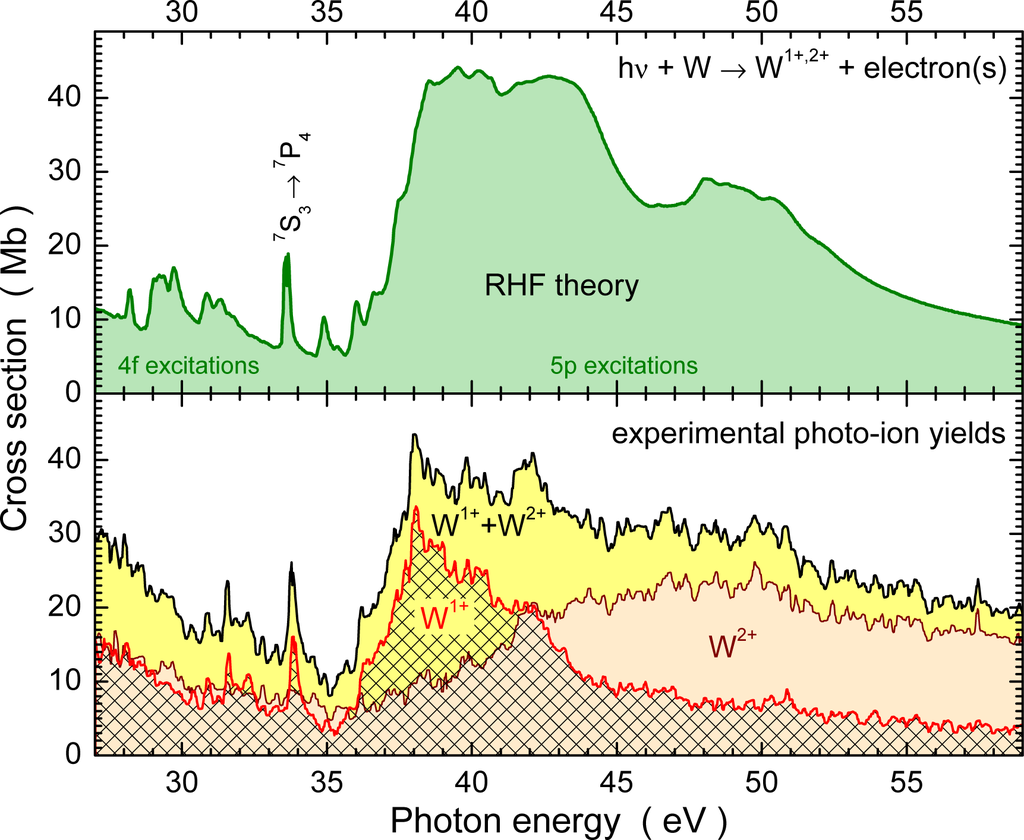
Figure 8.
Cross sections for photoionization of neutral W atoms. The upper panel shows the result of relativistic Hartree-Fock (RHF) calculations for photoabsorption by neutral tungsten atoms [48] brought into the gas phase by evaporating tungsten at 3200 K. The resulting population of long-lived excited levels has been considered. For further details see text. The lower panel shows the relative yields of W+ (solid red line) and W2+ (solid brown line) photo-ions produced from vaporized neutral tungsten [48]. The solid black line is the sum of the yields of W+ and W2+ ions. The yield measurements were normalized to the theoretical cross section provided in the upper panel. The theoretical cross section was shifted by −1.3 eV to match the prominent narrow resonance feature found in the experiment at about 34 eV. This resonance is associated with photoexcitation W(5p65d56s 7S3) → W(5p55d56s2 7P4) and subsequent auto-ionization.
For the experiment tungsten vapor from a resistively-heated wire at about 3200 K was used as a target. At this temperature with kT = 0.276 eV, where k is Boltzmann’s constant, low-lying excited levels of the tungsten atom can be populated. (The Boltzmann factor exp(−E/kT) for E =1 eV is 0.027 at 3200 K.) Under these conditions only the two lowest terms of the 5d46s2 ground configuration and the 5d56s (first) excited configuration of neutral W0 (both with even parity and therefore not supporting electric-dipole transitions to lower levels) can be present in the tungsten vapor. Assuming statistical population of the 6 possible levels (5D0,1,2,3,4) and (7S3) with appropriate weighting by the associated Boltzmann factors, the theory curve in the upper panel of Figure 8 was produced. It is in quite reasonable agreement with the experimental findings.
In the theoretical treatment of photoionization of neutral tungsten Boyle et al. applied the MBPT approach and used it to carry out calculations just for the W(5D0) ground level. It is interesting to compare the results of RHF and MBPT calculations for this case. Figure 9 shows the results of the two theoretical approaches for the photoionization of the 5D0 ground level of a neutral tungsten atom. Both calculations are on independently absolute scales both in cross sections and energies. Given the complexity of the problem with at least two open subshells after the excitation process, the calculated results are in remarkable agreement with one another. Boyle et al. [64] compared their result for photoionization of the W(5D0) ground level with the data from the DLP experiment of Costello et al. [50]. The agreement between theory and experiment was not really satisfying. Clearly, the possibility for the presence of atoms in excited levels in the initial tungsten atom ensemble has to be considered. The tungsten atoms were brought from the solid into the gas phase by one of the two lasers used in the DLP technique. Accordingly, population of metastable levels has to be expected. Unfortunately, the population of excited levels in the DLP experiment is not known leaving ambiguity in any comparison with theory.
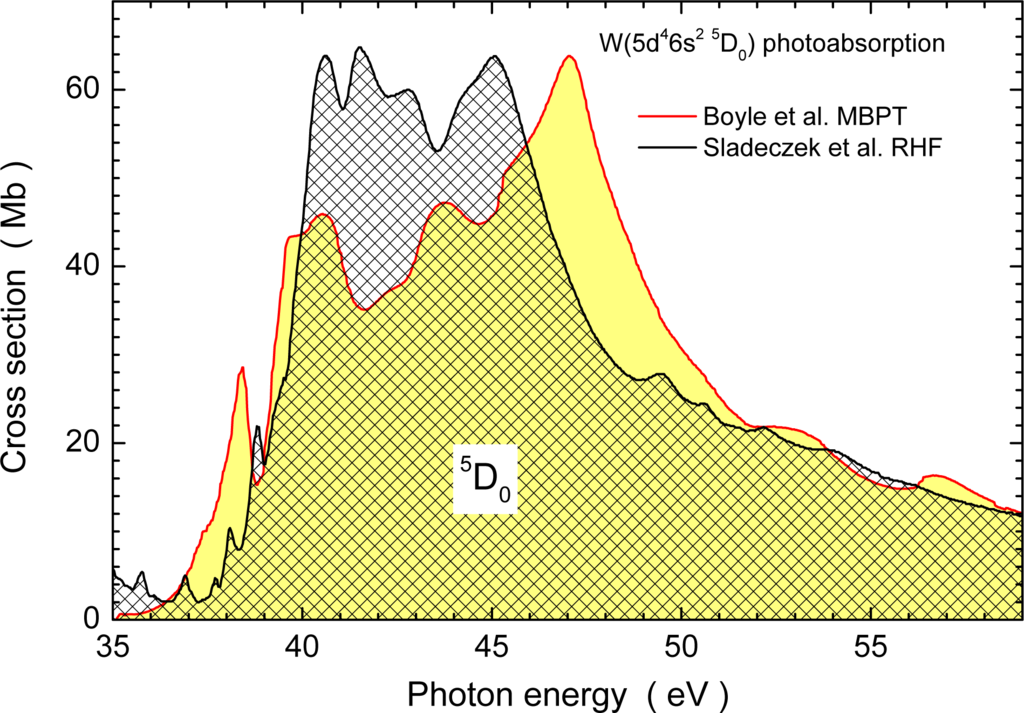
Figure 9.
Theoretical cross sections for single photoionization of neutral W atoms in their 5d46s 5D0 ground-level. The solid red line with yellow shading is the result of many-body perturbation theory (MBPT) calculations by Boyle et al. [64] and the solid black line with cross-hatching is the relativistic Hartree-Fock (RHF) calculation by Sladeczek et al. [48]. No normalization procedures or energy shifts were applied to the two data sets.
For a demonstration of the possible modeling of the experimental results by the available theoretical approaches, Figure 10 shows the experimental result of Costello et al. [50] together with the cross section for photoionization of the W(5d46s2 5D3) level calculated by Sladeczek et al. [48]. The DLP measurements were not absolute. Therefore, the experimental signal was approximately normalized to the theoretical curve. Justification for the choice of the calculation for the W(5d46s2 5D3) level is nothing else but the relatively good agreement between the experimental and theoretical cross-section dependence on the photon energy. The overall course of the experimental cross-section function with two broad peaks approximately separated by an energy that corresponds to the 5p3/2 – 5p1/2 fine structure splitting, is reproduced amazingly well by the theoretical calculation for a selected initial level of the tungsten atoms. Very recently, Ballance and McLaughlin have carried out large-scale R-matrix calculations for several levels of the neutral tungsten atom [65]. Their statistically weighted sum of cross-section contributions arising from different initial levels of primary tungsten atoms is in moderate agreement with the experimental results used for the comparisons (e.g., the data obtained by Costello et al. [50]).
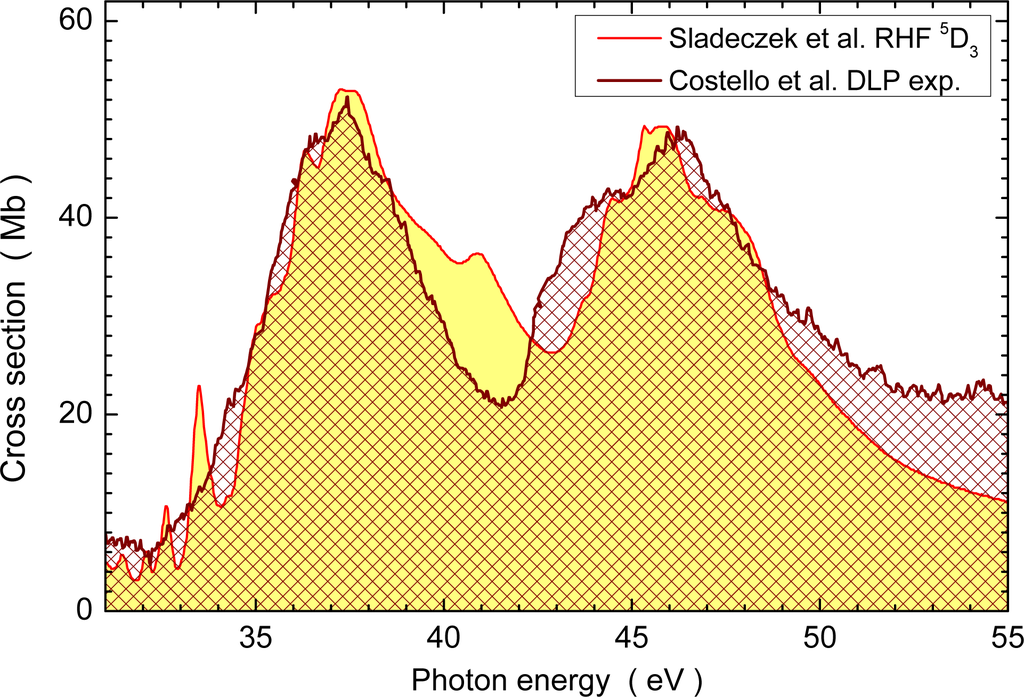
Figure 10.
Cross sections for photoabsorption by neutral W atoms. The solid brown line with cross-hatching is the experimental result obtained by Costello et al. using the dual laser plasma (DLP) technique. Without knowing the distribution of excited states of the parent neutral tungsten atoms a comparison is made with the RHF calculation carried out by Sladeczek et al. [48] for W atoms in the 4f145s25p65d46s2 5D3 level. The experimental data are normalized to the calculated cross section.
Within the tungsten collisions project mentioned above, measurements on photoionization of Wq+ ions in charge states q =1,2,3,4 and 5 are carried out at the photon-ion merged-beam facility of the Advanced Light Source in Berkeley. The measurements are accompanied by large-scale close-coupling calculations within the Dirac-Coulomb R-matrix (DARC) approximation (R-matrix theory using the Dirac Hamiltonian was formulated and applied to electron-atom scattering by Chang [66]. His code was substantially rewritten by Norrington and Grant [67] for calculating electron scattering from highly charged iron ions. Since then further developments have led to a parallelized version of the DARC code package [68] which can be applied to electronic and photonic collisions with atoms and ions. A recent set of further references has been provided by Müller et al. [69].). This work is still in progress, however, final results are expected to be published within the current year. While the photoionization spectra of W0, W1+, W2+, and W3+ are characterized by very broad peak structures, a transition to narrow resonance features starts with W4+ and leads to a very complex photoionization resonance structure in W5+. This behaviour is similar to the findings of experiments on the Ce isonuclear sequence by Habibi et al. [70].
Figure 11 shows a comparison of the theoretical and experimental cross section functions for photoionization of W4+ ions [71]. The calculated and measured data were normalized to the peak cross section and, hence, are given in percent of the maximum. Different from the data shown in the previous figures for neutral tungsten, the cross section for W4+ shows detailed resonance structures. The experimental data obviously contain some contribution from parent ions in the 5d6s excited configuration. This can be inferred from the comparison of the measured onset of the photoionization signal and the threshold energies indicated by the vertical bars. The resonance features at energies 44 to 47 eV, i.e., below the ground-state ionization threshold, are most likely associated with photoexcitation-autoionization processes which start from metastable levels in the 5d2 and 5d6s parent ion configurations and probably produce autoionizing intermediate levels with 4f vacancies. Subsequently, these levels decay to W5+ final states. The theoretical results in this comparison do not show the 44-to-47 eV feature. They were obtained by DARC calculations including 52 close-coupling states to represent photoionization of the 5s25p65d2 3FJ levels of the ground term and a statistically weighted distribution of ions in states with J = 2, 3, 4 was assumed. Calculations including 385 instead of 52 states are presently underway.
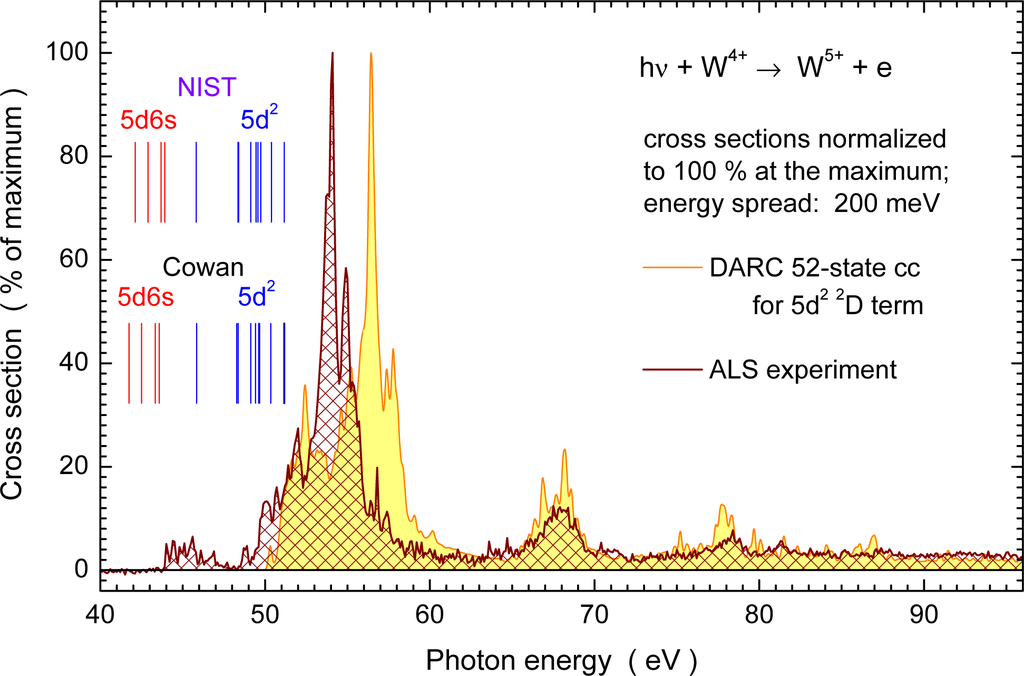
Figure 11.
Cross section for single photoionization of W4+ ions. Theoretical and experimental results are preliminary. They are shown with their maxima normalized to 100%. The solid brown line is the experimental result obtained by Müller et al. [71] at the Advanced Light Source (ALS) at a resolution of 200 meV and the solid orange line with yellow shading represents the associated calculation [71] using the Dirac-Atomic R-matrix codes (DARC) with a 52-state basis set to describe photoionization of the 5d2 2D term. The theoretical data were convoluted with a 200 meV FWHM (full-width-at-half-maximum) Gaussian to simulate the experimental energy spread. Ionization energies of W4+ levels within the 5d2 ground-state configuration and the 5d6s excited configuration are indicated by blue and red vertical bars, respectively. The threshold energies are from the NIST Atomic Spectra Database [26] and from a calculation using the Cowan code [43]. The experimental energy axis has an absolute uncertainty of no more than 0.1 eV.
3.3. Electron-Ion Recombination
Due to the importance of tungsten ions in fusion plasmas and because of the essential role that recombination plays in the charge-state balance of Wq+ ions in a plasma, extensive production of theoretical data on recombination has been initiated. Radiative recombination of tungsten ions was extensively explored using advanced theoretical techniques [63]. Dielectronic recombination data are being produced in large-scale calculations using existing atomic physics program packages. With emphasis on theory, the published work on dielectronic recombination of tungsten ions has been compiled recently by Li et al. [72].
Theoretical studies on dielectronic recombination covering ions with low numbers of electrons can employ well tested theoretical approaches [73–75]. Calculations become drastically more difficult when there are still 50 or more electrons present in a highly charged ion with several open d and f subshells [76,77]. For such complex many-electron systems, experimental guidance of theoretical developments is desirable. Theoretical cross sections well tested by experiments are essential for meaningful implementation of recombination rates in plasma modeling systems, such as ADAS.
Within the tungsten collisions project storage-ring recombination rate coefficients and plasma rate coefficients were obtained for W18+, W19+, W20+ and W21+. Experimental and theoretical results for electron-ion recombination of W18+ and W20+ have been published by Spruck et al. [41] and Schippers et al. [78], respectively. Analysis of the data for W19+ and W21+ is in progress.
Each collision experiment has its characteristic energy spread and, resulting from that, provides primarily an experiment-specific rate coefficient rather than a cross section. The real cross section would be accessible only at infinitely small collision-energy spread. For a smooth cross section function this is not an important issue. However, when resonances are to be measured, the height and width of the apparent resonance cross section depends on the collision-energy–distribution function. For the measurement of cross sections of a given collision process reaction rates for that process have to be observed. In the present context collisions of electrons with ions are considered. The rate R of reactions resulting from a defined process that occurs in a volume τ is given by convolution of the experimental phase space overlap between the beams of colliding electrons and ions [16]
The electrons with a spatial number density
and the ions with a spatial number density
interact in a volume τ via the cross section σ(vrel), where
is the vector of relative velocity between the collision partners and
its absolute value. The distribution function
of the relative velocities between the colliding particles can usually be assumed to be independent of the location
.
The two integrations in Equation (6) can then be carried out separately. By defining the rate coefficient
the rate R is given by
The spatial overlap between electrons and ions and the effective collision-energy distribution depend on the particular experimental arrangement. By observing R in an experiment, one can only obtain the rate coefficient α. If the energy spread ΔE is small compared to the collision energy E it makes sense to define an apparent cross section as σapp = α/vrel. The difference between σ and σapp is that the latter is obtained from σ by convolution with the experimental energy distribution function.
In storage-ring recombination experiments the collision-energy distribution is non-isotropic. The associated velocity distribution function that directly enters Equation (7) can be represented by
with
the relative average velocity between electrons and ions in the colliding beams. Around this average value the relative electron-ion velocities
are distributed according to Equation (9). The variable velocities v║ and v⊥ denote the components of
in the perpendicular and parallel directions with respect to the electron beam axis, respectively. With T║ = T⊥ and vav = 0, Equation (9) represents an isotropic Maxwellian electron velocity distribution. In a beam of accelerated electrons, however, T║ ≪ T⊥. Therefore, Equation (9) with T║ < T⊥ is termed a “flattened” Maxwellian distribution. The width of this distribution determines the experimental electron energy spread
According to Equation (10) the experimental energy spread increases towards higher relative energies E.
The so-called “storage-ring recombination rate coefficients” αSR result from Equation (7) with the specific velocity (and, hence, also energy-dependent) distribution function given by Equation (9). The associated energy distribution is narrow for relative energies E > 0.1 eV. Dividing αSR by the velocity vav results in a relatively good approximation to σapp as long as ΔE ≪ E. At lower energies the calculation of σapp is meaningless and, therefore, the presentation of storage-ring recombination rate coefficients αSR is usually preferred over the display of apparent cross sections σapp. As an example, storage-ring recombination rate coefficients in the low-energy regime are provided for W18+ [41] in Figure 12. The figure covers a range of electron-ion collision energies from 2 × 10−4 to 20 eV. The experimental data at these energies are described quite well by “partitioned and damped” (PD) calculations [41,79]. The intermediate-coupling (IC) theory commonly used with good success in calculations of dielectronic recombination is much below the experimental data. Detailed analysis shows that one can neglect the recombination contribution of the metastable W18+(4f10 3F2) level discussed in the context of Figure 3. Within their total error bars the experimental results represent the recombination of ground-level W18+(4f10 5I8).
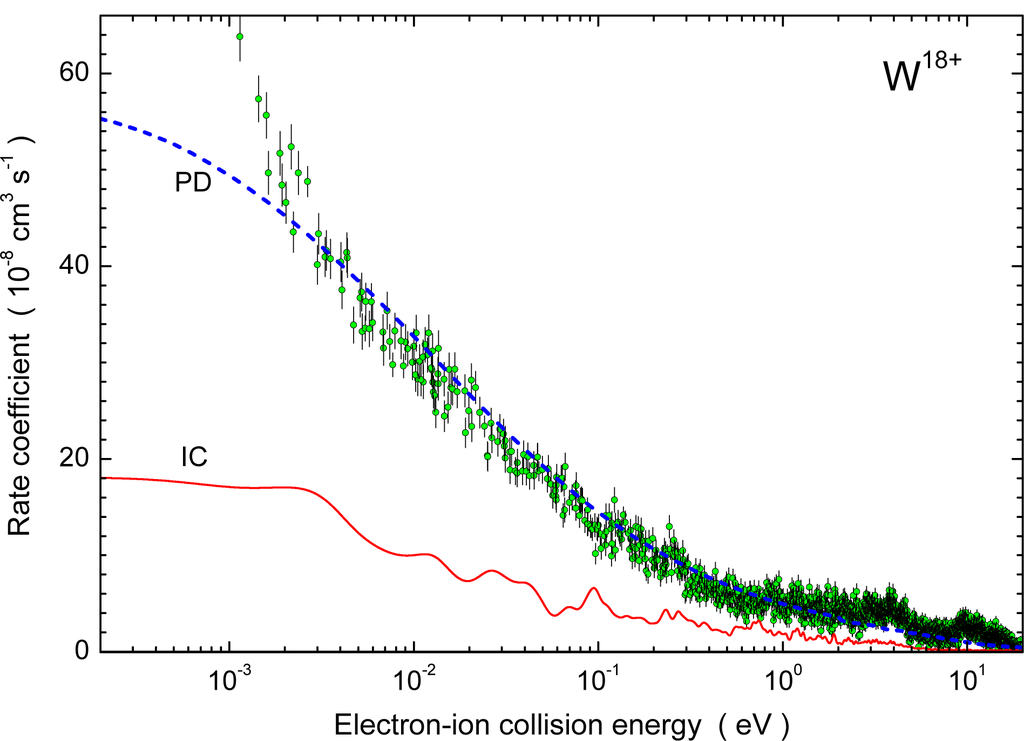
Figure 12.
Measured and calculated storage-ring rate coefficient for recombination of W18+ with an electron: low-energy range [41]. The experimental results are displayed as green circles with statistical error bars. The solid red curve is a conventional intermediate-coupling (IC) calculation for dielectronic recombination [41]. The blue dashed curve is the result of the fully partitioned calculation including autoionizing (and radiative) damping (PD) [41].
At energies below 2 meV the experimental data points start to deviate also from the PD result. The reason for the excursion of the storage-ring rate coefficient at very low energies is specific to electron-ion merged-beam experiments and depends on the electron density, the electron-beam temperatures and the magnetic and electric fields present in and around the electron-ion interaction region. The effect is known as low-energy recombination enhancement in merged-beam measurements and has been investigated and discussed in detail previously [80–88]. In the present case the maximum storage-ring rate coefficient reached 227 × 10−8 cm3s−1 at 70 µeV. The enhancement effect is not expected to contribute to the rate coefficients required in (fusion) plasma modeling.
It is interesting to note that radiative recombination (RR) of W18+ has a maximum storage-ring recombination rate coefficient αSR = 0.14 × 10−8 cm3s−1 at 70 µeV, i.e., it contributes only 0.06% to the measured recombination rate at very low relative energies. This comparison illustrates the enormous size of the observed recombination rate of W18+ below 20 eV with a steep increase towards the meV region. Therefore, two figures are used to illustrate the results for recombination in the investigated energy range. Figure 13 shows αSR for W18+ in the high-energy range up to 265 eV. Symbols and lines have already been discussed in the context of Figure 12.
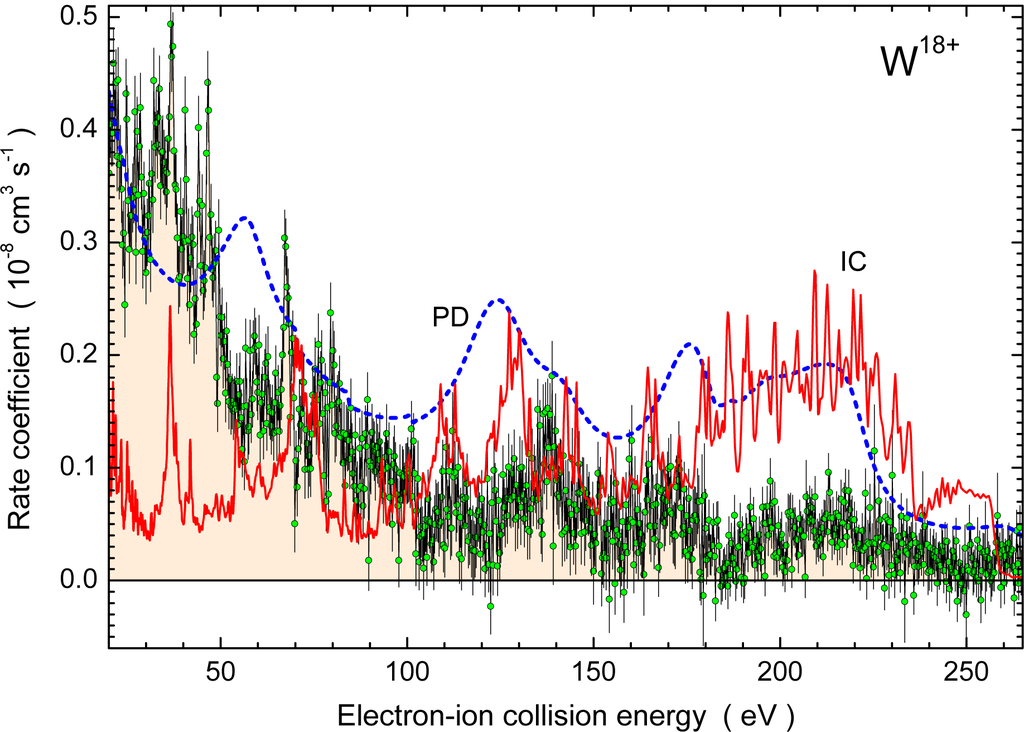
Figure 13.
Measured and calculated storage-ring rate coefficient for recombination of W18+ with an electron: high-energy range [41]. The experimental results are displayed as green circles with statistical error bars. The solid red curve is a conventional intermediate-coupling (IC) calculation for dielectronic recombination [41]. The blue dashed curve is the result of the fully partitioned calculation including autoionizing (and radiative) damping (PD) [41].
As mentioned above, the storage-ring recombination rate coefficients αSR are specific to electron-ion merged-beam experiments characterized by individual parameters such as the transverse and longitudinal temperatures in the electron beam. For plasma modeling one needs rate coefficients based on a suitable energy distribution function describing the situation in a generic plasma. A common choice for that is an isotropic Maxwell-Boltzmann distribution of electron-ion collision energies. The derivation of such plasma rate coefficients α(T) from storage-ring rate coefficients is straightforward [89]. They are determined from the apparent cross sections σapp = αSR/vrel (see above) measured at storage rings in a merged-beam geometry
Different from the situation in merged beams experiments, the plasma temperature T is assumed to be isotropic in this case. The parameter m is the reduced mass of the electron-ion collision system and as such is very close to me, the electron rest mass. In the storage ring measurements the ensembles of colliding particles, the electrons and ions, have a well defined average relative velocity vrel. As a consequence, high resolution is obtained in the whole range of accessible energies and hence, cross sections can be measured in great detail. In contrast to that, convolution of the measured data following Equation (11) leads to broad smooth dependences of plasma rate coefficients αP(T) on temperature, where most of the details in the cross sections are washed out. Nevertheless, the details of the cross sections at low energies have a strong influence on the size of plasma rate coefficients even at comparatively high temperatures.
Figure 14 shows plasma rate coefficients for recombination of W18+ derived from the experimental data displayed in Figures 12 and 13. Data previously entered into the ADAS data base significantly differ from the new theoretical and experimental data at temperatures below kT = 20 eV with deviations of more than two orders of magnitude. Even in the temperature range where W18+ is formed in a plasma the ADAS data are smaller than the experimental rate coefficients by factors 5 to 10. The new theory results labeled IC and PD are much closer to the experiment and provide good data for the temperature region of highest interest in plasma physics and particularly in fusion research.
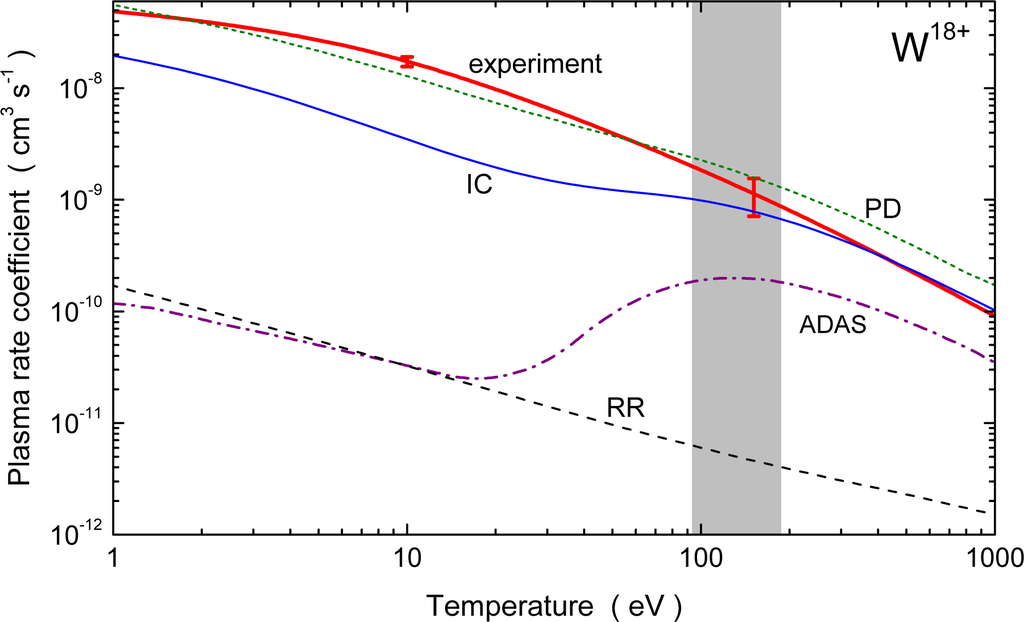
Figure 14.
Plasma rate coefficients for recombination of W18+ with an electron [41]. The shaded area indicates the temperature range where W18+ is expected to be produced with significant abundances in plasma under equilibrium conditions [9]. Experimentally derived rate coefficients are represented by the solid red line. The combined statistical and systematic uncertainty is indicated by error bars. The solid blue (labeled IC: intermediate-coupling theory) and the short dashed green line (labeled PD: partitioned and damped statistical theory) are the theoretical rate coefficients for electron-ion recombination of W18+ in a plasma. The dash-dot line is the plasma recombination rate coefficient from the ADAS database. The dashed curve is the calculated radiative-recombination (RR) plasma rate coefficient. For details see text.
A second example for recombination of a multi-electron tungsten ion, W20+, is shown in Figure 15. Actually, it was the first recombination measurement within the tungsten collisions project discussed in this overview. The ion charge state had been chosen because W20+ is isoelectronic with Au25+, for which previous experiments [90] had shown excessive recombination rate coefficients. Indeed, recombination of W20+ ions reached up to about 2 × 10−6 cm3s−1 at 1 meV relative energy. The inset of Figure 15 emphasizes the low-energy region of the recombination measurement but leaves out the enhancement at the lowest energies below 1 meV which is not relevant for plasma modeling. The result of the statistical theory developed by Dzuba et al. [91] is in fairly good agreement with the experiment. Also the fully partitioned theoretical calculation by Badnell et al. [79] reproduces the measured storage-ring recombination rate coefficient quite well at energies below 1 eV. This treatment overestimates the experimental findings with discrepancies increasing with the electron-ion collision energy. The intermediate coupling calculation, in turn, strongly underestimates the experimental data at energies up to about 40 eV but then approaches the magnitude of the experimental rate coefficients. The details of the resonance structures observed in the experiment are not reproduced, however. The calculation by Dzuba et al. [92] is in slightly better agreement than the intermediate-coupling result.
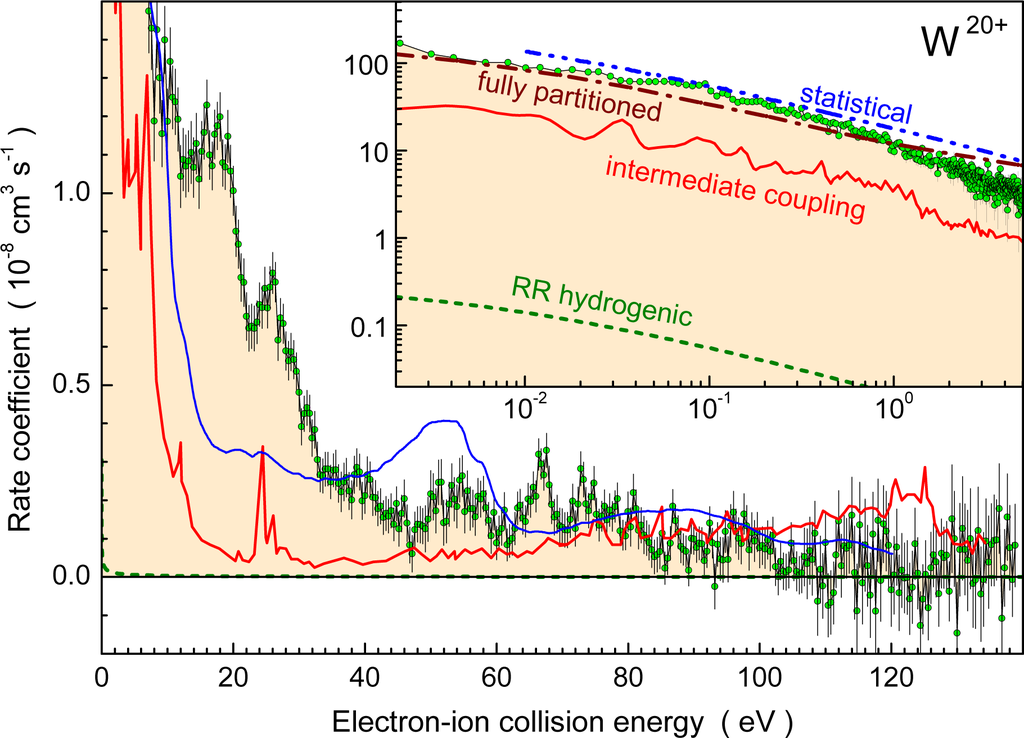
Figure 15.
Measured and calculated storage-ring rate coefficient for recombination of W20+ with an electron [93]. The inset shows the theoretical and experimental low-energy results on a double-logarithmic scale. The green circles with statistical error bars represent the experimental data. The brown dot-dashed line is obtained from the fully partitioned calculation by Badnell et al. [79]. The solid red curve is a conventional intermediate-coupling calculation for dielectronic recombination [79]. The long-dashed green line shows the results of a calculation of radiative recombination (RR) carried out on the basis of an approach for hydrogenlike levels [94]. The blue dash-dot-dot line is the statistical theory for chaotic resonances in the low-energy range by Dzuba et al. [91]. The solid blue line is the result obtained by that same group for the high-energy region [92].
The phenomenon of excessive recombination rates observed for multi-electron ions was discovered [95] in recombination studies employing a single-pass merged-beam setup at the UNILAC accelerator of the GSI Heavy-Ion Research center in Darmstadt, Germany. For U28+ [96,97] and Au25+ [90] ions, merged-beam recombination rate coefficients as high as about 1.7 × 10−7 cm3s−1 and even up to 1.2 × 10−6 cm3s−1, respectively, were measured at relative energies below 0.1 meV, respectively. The observed maximum rates depended on the electron density and the magnetic field present in the electron-ion interaction region. Their size is influenced by the merged-beam recombination-enhancement effect briefly addressed already above. This effect showed some characteristic dependencies on experimental parameters such as electron-beam temperatures and -as just mentioned-magnetic field and electron density [82–85]. This additional enhancement is understood to amplify the existing recombination rate coefficient at relative energies below about 0.1 meV ([88] and references therein) of all ions including completely stripped nuclei. Factor-of-three enhancements have been typical for this effect at the Heidelberg storage ring TSR [82,83]. However, even when the enhancement of merged-beam recombination at very low relative energies by factors around 3 is considered and subtracted from the observed total recombination rate, the remaining recombination rate coefficients of the multi-electron ions mentioned above are enormously high and are of a magnitude that is orders of magnitude above expected radiative recombination rate coefficients for ions in such high charge states.
Short lifetimes observed at CERN when a beam of Pb53+ was subject to electron cooling [98] stimulated further recombination measurements with the goal to explain the short cooling lifetime with high electron-ion recombination rates. Multi-electron ions Au49+, Au50+, and Au51+ were studied at the TSR storage ring in Heidelberg [99] and Pb53+ together with Pb54+ [100] at the CRYRING in Stockholm. More recently, the recombination of Au20+ was shown to exhibit a similar effect [101]. Merged-beam recombination rates below 0.1 meV were about 8.7 × 10−6 cm3s−1 for Pb53+ and about 1.9 × 10−6 cm3s−1 for iso-electronic Au50+. The neighbor charge states of Au50+ were found to have lower but still very high recombination rates [99]. The Au20+ measurement revealed a recombination rate of 4 × 10−7 cm3s−1.
Already in the first description of the phenomenon of excessive recombination rates it was speculated [95] that the density of dielectronic recombination resonances present in collisions of electrons with many-electron ions could be so high, that several such resonances might fall within the 0.1 meV interval around zero relative energy. The associated high density of resonances could therefore be the reason for the high recombination rates.
The high density of accessible intermediate resonant states possibly contributing to the recombination of W20+ is illustrated by Figure 16. The recombination spectrum of W20+ is predominantly associated with core excitations of the ([Kr]4d104f8 7F6 ground level. There are 292 excited levels within the ground configuration. They have excitation energies Eexc of up to about 52 eV. Resonance energies E(n) of associated dielectronic-capture states [16] with configurations (4f8nl) can be estimated with the assumption of hydrogenic electron binding energies
with Ry = 13.606 eV and q = 20. This estimate is good for large principal quantum numbers n. Using Eexc = 52 eV one finds that n = 11 is the smallest quantum number yielding a positive resonance energy. For smaller Eexc the minimum principal quantum number n that provides non-negative resonance energies E(n) is greater than 11. For principal quantum numbers n ≥ 11 Equation (12) should give quite accurate resonance energies.
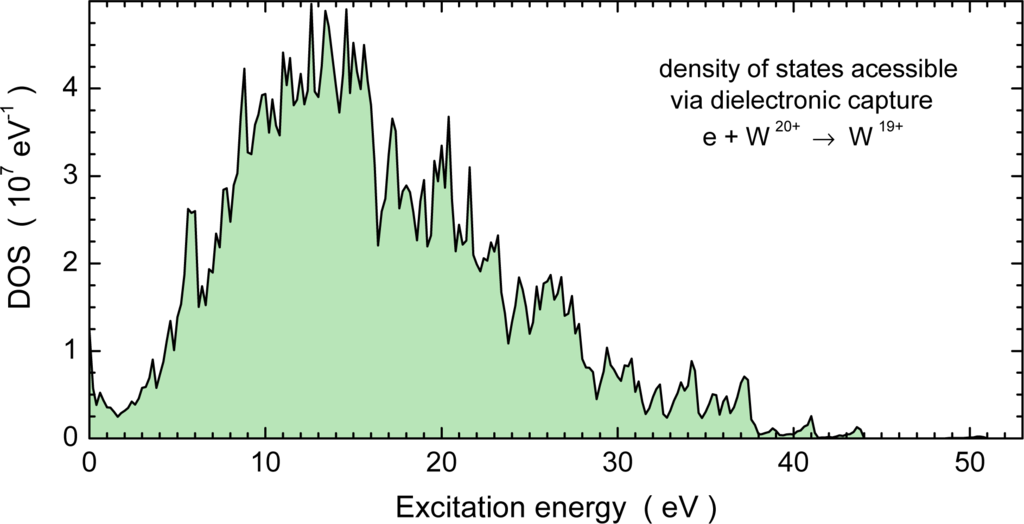
Figure 16.
Density of states (DOS) of W19+ ions that can be populated by dielectronic recombination of W20+ comprising all doubly excited 4f8nl states above the W20+(4f8 7F6) ground level with n ≤ 72 [93].
Recombined ions with an electron in a high-n shell have long lifetimes. These ions can survive the flight path from the electron-ion interaction region to the next downstream storage-ring bending magnet. In the motional electric
field seen by the ions in the magnet (with flux density
), high-n Rydberg states are field ionized. In the W20+ experiment the cutoff principal quantum number was nmax = 72. The smallest excitation energy of the W20+ ground configuration which yields non-negative E(n) for n = 72 is 1.05 eV. With these boundary conditions the density of states (DOS) within the
manifold with n ≤ 72 which could contribute to the recombination spectrum in the energy range 1.05 to 52 eV was calculated employing statistical weights 2n2(2j + 1)of the associated recombination resonances. As can be seen from Figure 16 the resulting DOS is enormous and amounts to more than 107 states per eV for energies near 5.28 eV. Clearly, such a situation calls for new theoretical approaches. “Classical” treatment of dielectronic recombination is insufficient to deal with the huge density of resonant channels featured by many-electron systems with open high–angular-momentum subshells. This was recognized in a theoretical study by Gribakin et al. [102] addressing the excessive electron-ion recombination of multi-electron ions as a consequence of high level densities of chaotic multiply-excited electron states. A statistical approach was therefore applied to the analysis of this complex system.
In a series of follow-up publications the idea of quantum-chaos in the recombination of complex ions and the use of statistical theory to obtain quantitative results was extended and refined. Treatment of Au25+ recombination by Flambaum et al. [103] provided remarkable agreement with the experimental findings. The theory was developed further by Gribakin and Sahoo [104] considering strong configuration mixing between doubly excited states and multiply excited states which account for the large electron recombination rates. The recombination measurements with tungsten ions stimulated further work [91,92] and the results for electron recombination with W20+ are close to the experimental data. Parallel to this work by Dzuba et al. Ballance et al. [105] and Badnell et al. [79] developed theoretical methods to describe recombination of complex ions such as Au20+ and W20+, respectively. By assuming complete (chaotic) mixing of near-threshold autoionizing states their results came into agreement with experiment at energies below about 2 eV.
As in the case of W18+ the huge storage-ring recombination rate coefficients found for W20+ at energies below about 2 eV influence the (Maxwell-Boltzmann averaged) plasma recombination rate coefficients even at kT = 200 eV. Comparisons of theory and experiment are provided in Figure 17. The data previously used in the ADAS data base differ from the experimentally derived plasma rate coefficient by almost three orders of magnitude. Even in the temperature range where W20+ is formed in a plasma the ADAS data are smaller than the experimental rate coefficients by factors of 5 to 10. The new theory results by Badnell et al. [79] and by Dzuba et al. [91,92] are much closer to the experiment.
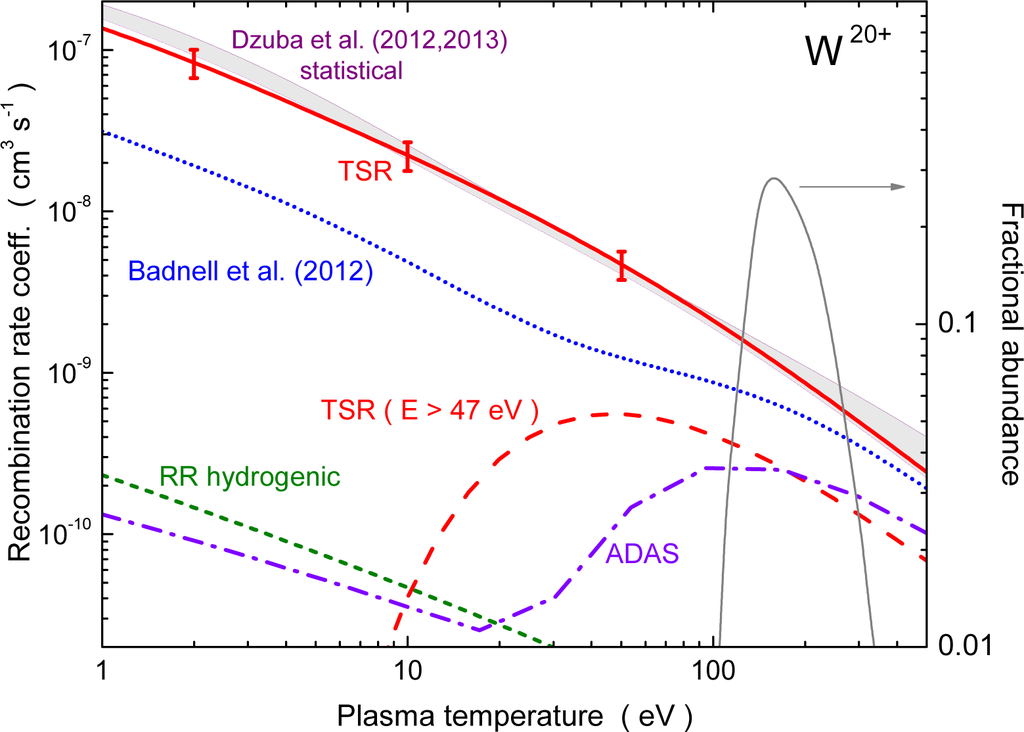
Figure 17.
Derived experimental and theoretical plasma rate coefficient for recombination of W20+ with an electron. Left scale: Experimentally derived rate coefficient for recombination of W20+ ions in a plasma (solid red line) including radiative recombination (RR) and dielectronic recombination with resonance energies below 140 eV [93]. Error bars denote the 20% experimental systematic uncertainty. The long-dashed red curve results from the experimental data displayed in Figure 15 with the collision energies restricted to the range 47 to 140 eV. The dash-dot violet curve is the recombination rate coefficient from the ADAS database. The short-dashed green curve is the result of a hydrogenic approach [106] to the radiative-recombination (RR) rate coefficient. The dotted magenta line is from the intermediate coupling calculation by Badnell et al. [79]. The shaded area between thin violet lines represents the results of the statistical theory of Dzuba et al. [91,92]. The width indicated by the shaded area results from the relative arbitrariness of the interpolations between their low-energy [91] and high-energy [92] results. Right scale: The thin full black line represents the calculated fractional abundance of W20+ in a fusion plasma [9] as a function of temperature.
4. Conclusions
Recombination of tungsten ions was probably the most important topic addressed within the present tungsten collisions project. It has most likely the highest impact on fusion-plasma modeling. The main reason is that theoretical methods previously employed to obtain plasma rate coefficients for recombination of complex many-electron ions were not adequate and were never tested against direct experiments with tungsten ions (because there were none). Recombination rate coefficients and cross sections have been measured now for W18+, W19+, W20+, and W21+ in the energy range from 0 to several 100 eV. The experiments show that the total recombination cross sections, especially at low energies, are orders of magnitude above radiative recombination. New theoretical attempts to describe the experimental data use approaches characterized as “damped and partitioned” (Badnell et al.) and “statistical” (Flambaum et al.). The plasma rate coefficients obtained by theory and experiment as a function of temperature are now beginning to converge.
Experimentally determined electron-impact ionization cross sections are now available for all ions from W1+ to W19+ at electron energies from below the ionization thresholds up to 1000 eV and up to higher energies for tungsten ions in lower charge states. A problem in all measurements with multiply charged ions and particularly also in the ionization measurements on tungsten ions is the possible presence of ions in long-lived excited states in the parent ion beam. Even when ions are stored for several seconds prior to the start of a measurement, metastable ions may still be present. The population of such excited states can be detected by suitable experimental techniques. Fine energy scans with very good statistics at small energy steps reveal ionization thresholds of different beam components [107]. Theoretical modeling of the resulting apparent cross sections which are typically measured with uncertainties of less than 10% provides information about the fractions of beam components and hence reliable cross sections for the ground state of the investigated ion, which is usually the dominant beam component. It is pointed out that a plasma of course also contains long lived excited states whose ionization cross sections are needed.
Experience shows that DI and EA of tungsten ions in charge states q ≤ 19 can be fairly well described by distorted-wave calculations. It is necessary, however, that these calculations include all relevant excitations from different inner shells to all excited states that significantly contribute to EA processes. It is also necessary to consider the branching ratios for different decay paths of the intermediate highly excited states. For Auger decay of autoionizing states the branching ratio was usually assumed to be 100% in the past. Recent calculations include the determination of real branching ratios. Comparison of the measurements on electron-impact ionization of tungsten ions (in charge states up to q = 19) with distorted-wave calculations including a sufficient number of excitations shows remarkably good agreement.
Expectations for the theoretical description of ionization cross sections for ions imply that the distorted-wave calculations become increasingly better with increasing charge state of the parent ion while resonances [17,107,108] are of decreasing significance. In the experiments studying electron-impact ionization of tungsten ions, no significant contributions of resonant processes could be found in the range of charge states q from 1 to 19 at energies up to 1 keV. This fact together with the observations that distorted wave calculations for DI and EA are in quite good agreement with the experimental data might lead one to the conclusion that electron-impact ionization cross sections for tungsten ions may be calculated with good accuracy up to the highest charge states without considering resonance contributions. However, measurements for xenon ions in charge states beyond q = 18 (up to 25) provide evidence for strong contributions of resonant processes to net single ionization [62]. Considering the predictions by theory groups, this finding is quite unexpected for such high charge states. Radiative decay of intermediate highly excited states is strongly increasing with increasing ion charge states and should eventually take over relative to Auger decays. But it is not obvious for which charge states and which intermediate resonances this will happen. The experiments with xenon ions suggest, that resonances might also appear in tungsten ions for charge states beyond the presently available experimental data. Charge states of tungsten ions, isoelectronic with Xe19+ to Xe25+, are W39+ to W45+. Calculations of cross sections in this range of charge states using the R-matrix approach should be feasible and might help to clarify if resonances are important for these ions.
Photoionization of tungsten atoms and ions has been studied experimentally and theoretically for W0, W1+, W2+, W3+, W4+, and W5+. Single ionization and in some cases also multiple ionization was studied. Absolute cross sections with high energy resolution were determined over wide energy ranges. The idea for the measurements with tungsten ions was to exploit, firstly, the time-reversal relation between recombination and photoionization [109–120], and secondly, to contribute to the exploration of the electronic structure of tungsten ions. It is known that the plasma density in a fusion device is low so that absorption of high-energy photons is unlikely. Thus, cross sections for photoionization are not of prime importance for fusion. It is satisfying to see, however, that state-of-the-art theory including R-matrix approaches can reproduce the main features of the experimental results. This is important since R-matrix calculations can also be used to obtain electron-impact ionization, excitation and recombination cross sections. Thus, photoionization is a good testing area for R-matrix approaches to fusion-relevant processes.
Acknowledgments
I am indebted to numerous colleagues who have contributed to the tungsten collisions project reviewed in the present paper. In alphabetical order they are Nigel R. Badnell, Connor P. Ballance, Arno Becker, Dietrich Bernhardt, Alexander Borovik Jr., David Esteves-Macaluso, Mohammad F. Gharaibeh, Manfred Grieser, Michael Hahn, Jonas Hellhund, Kristof Holste, Kurt Huber, A. L. David Kilcoyne, Claude Krantz, Michael Lestinsky, Brendan M. McLaughlin, Oldrich Novotný, Ronald A. Phaneuf, Joachim Rausch, Roland Repnow, Daniel W. Savin, Stefan Schippers, Kaija Spruck, and Andreas Wolf. I thank Ron Phaneuf for his valuable suggestions concerning this manuscript. Support by Deutsche Forschungsgemeinschaft through grant number Mu – 1068/20 is gratefully acknowledged.
Conflicts of Interest
The author declares no conflict of interest.
Appendix: Plasma Rate Coefficients
As mentioned in the main text of this review on what has been called tungsten collisions project, the storage-ring dielectronic recombination measurements have produced the most important results on fusion-related tungsten collision processes. The plasma rate coefficients derived from these experiments are substantially different from previous expectations and from previously recommended recombination data which have actually also been employed for fusion-plasma modeling and inevitably produced erroneous results. The new experimental findings have challenged our understanding of complex electron-ion recombination processes and triggered new theoretical models trying to reproduce measured cross sections and rates. Therefore, the experimentally derived new plasma rate coefficients for recombination of W18+ and W20+ initially in their ground levels are provided in tabular form in this appendix to emphasize their importance.

Table A1.
Experimentally derived plasma rate coefficients
for recombination of W18+ with electrons [41]. The uncertainties of these rate coefficients change with temperature and are approximately ±10% at kT = 10 eV and ±37% at kT = 150 eV.
| Plasma temperature [eV] | |
|---|---|
| 1 | 4.88 × 10−8 |
| 1.5 | 4.36 × 10−8 |
| 2 | 3.98 × 10−8 |
| 3 | 3.42 × 10−8 |
| 5 | 2.70 × 10−8 |
| 7 | 2.22 × 10−8 |
| 10 | 1.74 × 10−8 |
| 15 | 1.26 × 10−8 |
| 20 | 9.78 × 10−9 |
| 30 | 6.66 × 10−9 |
| 50 | 3.96 × 10−9 |
| 70 | 2.76 × 10−9 |
| 100 | 1.85 × 10−9 |
| 150 | 1.15 × 10−9 |
| 200 | 8.04 × 10−10 |
| 300 | 4.78 × 10−10 |
| 500 | 2.40 × 10−10 |
| 700 | 1.51 × 10−10 |
| 1000 | 9.07 × 10−11 |

Table A2.
Experimentally derived plasma rate coefficients
for recombination of W20+ with electrons [93]. The uncertainties of these rate coefficients are approximately ±20%.
| Plasma temperature [eV] | |
|---|---|
| 1 | 1.37 × 10−7 |
| 1.5 | 1.03 × 10−7 |
| 2 | 8.34 × 10−8 |
| 3 | 6.09 × 10−8 |
| 5 | 4.01 × 10−8 |
| 7 | 3.02 × 10−8 |
| 10 | 2.23 × 10−8 |
| 15 | 1.55 × 10−8 |
| 20 | 1.19 × 10−8 |
| 30 | 8.02 × 10−9 |
| 50 | 4.70 × 10−9 |
| 70 | 3.23 × 10−9 |
| 100 | 2.11 × 10−9 |
| 150 | 1.26 × 10−9 |
| 200 | 8.65 × 10−10 |
| 300 | 4.98 × 10−10 |
| 500 | 2.42 × 10−10 |
| 700 | 1.49 × 10−10 |
| 1000 | 8.88 × 10−11 |
References
- Drawin, H.W. Atomic Physics and Thermonuclear Fusion Research. Phys. Scr. 1981, 24, 622–655. [Google Scholar]
- Neu, R.; Dux, R.; Geier, A.; Gruber, O.; Kallenbach, A.; Krieger, K.; Maier, H.; Pugno, R.; Rohde, V.; Schweizer, S.; ASDEX Upgrade Team. Tungsten as plasma-facing material in ASDEX Upgrade. Fusion Eng. Des. 2003, 65, 367–374. [Google Scholar]
- Neu, R.; Arnoux, G.; Beurskens, M.; Bobkov, V.; Brezinsek, S.; Bucalossi, J.; Calabro, G.; Challis, C.; Coenen, J.W.; de la Luna, E.; et al. First operation with the JET International Thermonuclear Experimental Reactor-like wall. Phys. Plasmas 2013, 20, 056111. [Google Scholar]
- Aymar, R.; Barabaschi, P.; Shimomura, Y. The ITER design. Plasma Phys. Control. Fusion 2002, 44, 519–565. [Google Scholar]
- O’Mullane, M.G.; Summers, H.P.; Whiteford, A.D.; Meigs, A.G.; Lawson, K.D.; Zastrow, K.D.; Barnsley, R.; Coffey, I.H. JET-EFDA Contributors. Atomic modeling and instrumentation for measurement and analysis of emission in preparation for the ITER-like wall in JET. Rev. Sci. Instrum. 2006, 77, 10F520. [Google Scholar]
- Summers, H.P.; Dickson, W.J.; O’Mullane, M.G.; Badnell, N.R.; Whiteford, A.D.; Brooks, D.H.; Lang, J.; Loch, S.D.; Griffin, D.C. Ionization State, Excited Populations Emission of Impurities in Dynamic Finite Density Plasmas: I. The Generalized Collisional-Radiative Model for Light Elements. Plasma Phys. Control. Fusion 2006, 48, 263–293. [Google Scholar]
- Post, D.; Abdallah, J.; Clark, R.E.H.; Putvinskaya, N. Calculations of energy losses due to atomic processes in tokamaks with applications to the International Thermonuclear Experimental Reactor divertor. Phys. Plasmas 1995, 2, 2328–2336. [Google Scholar]
- Flannery, M.R. Electron-ion and ion-ion recombination. In SpringerHandbook of Atomic, Molecular & Optical Physics; Drake, G.W., Ed.; Springer: New York, NY, USA, 2006; pp. 800–827. [Google Scholar]
- Pütterich, T.; Neu, R.; Dux, R.; Whiteford, A.D.; O’Mullane, M.G. the ASDEX Upgrade Team. Modelling of measured tungsten spectra from ASDEX Upgrade and predictions for ITER. Plasma Phys. Control. Fusion 2008, 50, 085016. [Google Scholar]
- Krücken, T.; Bergmann, K.; Juschkin, L.; Lebert, R. Fundamentals and limits for the EUV emission of pinch plasma sources for EUV lithography. J. Phys. D 2004, 37, 3213–3224. [Google Scholar]
- Summers, H.P.; Badnell, N.R.; O’Mullane, M.G.; Whiteford, A.D.; Bingham, R.; Kellett, B.J.; Lang, J.; Behringer, K.H.; Fantz, U.; Zastrow, K.D.; et al. Atomic data for modelling fusion and astrophysical plasmas. Plasma Phys. Control. Fusion 2002, 44, B323–B338. [Google Scholar]
- Schippers, S. Storage-ring ionization and recombination experiments with multiply charged ions relevant to astrophysical and fusion plasmas. J. Phys. Conf. Ser. 2012, 388, 012010. [Google Scholar]
- Bernhardt, D.; Becker, A.; Grieser, M.; Hahn, M.; Krantz, C.; Lestinsky, M.; Novotný, O.; Repnow, R.; Savin, D.W.; Spruck, K.; et al. Absolute rate coefficients for photorecombination and electron-impact ionization of magnesiumlike iron ions from measurements at a heavy-ion storage ring. Phys. Rev. A 2014, 90, 012702. [Google Scholar]
- Hahn, M.; Badnell, N.R.; Grieser, M.; Krantz, C.; Lestinsky, M.; Müller, A.; Novotný, O.; Repnow, R.; Schippers, S.; Wolf, A.; Savin, D.W. Electron-Ion Recombination of Fe12+ Forming Fe11+: Laboratory Measurements and Theoretical Calculations. Astrophys. J. 2014, 788, 46. [Google Scholar]
- Schippers, S. Electron-ion merged-beam experiments at heavy-ion storage rings. Nucl. Instrum. Meth. in Phys. Res. 2015, 350, 61–65. [Google Scholar]
- Müller, A. Electron-Ion Collisions: Fundamental Processes in the Focus of Applied Research. Adv. At. Mol. Opt. Phys. 2008, 55, 293–417. [Google Scholar]
- Müller, A. Resonance phenomena in electron-ion and photon-ion collisions. J. Phys. Conf. Ser. 2009, 194, 012002. [Google Scholar]
- Imai, A.M.; Iriki, Y.; Ohta, Y.; Majima, T.; Tsuchida, H.; Shibata, H.; Itoh, A. Single-electron-capture cross-section scaling for low-q heavy ions at low energy. J. Phys. Conf. Ser 2014, 488, 082010. [Google Scholar]
- Tolstikhina, I.Y.; Song, M.Y.; Imai, M.; Iriki, Y.; Itoh, A.; Kato, D.; Tawara, H.; Yoon, J.S.; Shevelko, V.P. Charge-changing collisions of tungsten and its ions with neutral atoms. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 145201. [Google Scholar]
- Dipti; Das, T.; Sharma, L.; Srivastava, R. L-shell electron excitations of Mg-through O-like tungsten ions. Phys. Scr. 2014, 89, 085403. [Google Scholar]
- Ballance, C.P.; Loch, S.D.; Pindzola, M.S.; Griffin, D.C. Electron-impact excitation and ionization of W3+ for the determination of tungsten influx in a fusion plasma. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 055202. [Google Scholar]
- Safronova, U.I.; Safronova, A.S.; Beiersdorfer, P. Relativistic many-body calculations of excitation energies, oscillator strengths, transition rates, and lifetimes in samariumlike ions. Phys. Rev. A 2013, 87, 032508. [Google Scholar]
- Kramida, A.E.; Shirai, T. Compilation of Wavelengths, Energy Levels, and Transition Probabilities for W I and W II. J. Phys. Chem. Ref. Data 2006, 35, 423. [Google Scholar]
- Kramida, A.E.; Shirai, T. Energy levels and spectral lines of tungsten, W III through W LXXIV. At. Data Nucl. Data Tables 2009, 95, 305–474. [Google Scholar]
- Kramida, A.E.; Shirai, T. Erratum to “Energy levels and spectral lines of tungsten, W III through W LXXIV” [Atomic Data and Nuclear Data Tables 95 (2009) 305–474]. At. Data Nucl. Data Tables 2009, 95, 1051. [Google Scholar]
- Kramida, A.E.; Ralchenko, Y.; Reader, J. NIST ASD Team, NIST Atomic Spectra Database (version 5.2); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2014. [Google Scholar]
- Müller, A. Targets Consisting of Charged Particles. Nucl. Instrum. Methods A 1989, 282, 80–86. [Google Scholar]
- Müller, A.; Huber, K.; Tinschert, K.; Becker, R.; Salzborn, E. An improved crossed-beams technique for the measurement of absolute cross sections for electron impact ionisations of ions and its application to Ar+ ions. J. Phys. B At. Mol. Opt. Phys 1985, 18, 2993–3009. [Google Scholar]
- Phaneuf, R.A.; Havener, C.C.; Dunn, G.H.; Müller, A. Merged-beams experiments in atomic and molecular physics. Rep. Prog. Phys. 1999, 62, 1143–1180. [Google Scholar]
- Currell, F.J. Electron Beam Ion Traps their Use in the Study of Highly Charged Ions. In The Physics of Multiply and Highly Charged Ions, Volume 1; Currell, F., Ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003; pp. 39–75. [Google Scholar]
- Bernitt, S.; Brown, G.V.; Rudolph, J.K.; Steinbrügge, R.; Graf, A.; Leutenegger, M.; Epp, S.W.; Eberle, S.; Kubicek, K.; Mäckel, V.; et al. An unexpectedly low oscillator strength as the origin of the Fe XVII emission problem. Nature 2012, 492, 225. [Google Scholar]
- Rudolph, J.K.; Bernitt, S.; Epp, S.W.; Steinbrügge, R.; Beilmann, C.; Brown, G.V.; Eberle, S.; Graf, A.; Harman, Z.; Hell, N.; et al. X-ray resonant photoexcitation: Linewidths and energies of Kα transitions in highly charged Fe ions. Phys. Rev. Lett. 2013, 111, 103002. [Google Scholar]
- Steinbrügge, R.; Bernitt, S.; Epp, S.W.; Rudolph, J.K.; Beilmann, C.; Bekker, H.; Eberle, S.; Müller, A.; Versolato, O.O.; Wille, H.C.; et al. Absolute measurement of radiative and Auger rates of K-vacancy states in highly charged Fe ions. Phys. Rev. A 2015, 91, 032502. [Google Scholar]
- Trassl, R. ECR Ion Sources. In The Physics of Multiply and Highly Charged Ions; Volume 1, Currell, F., Ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003; pp. 3–37. [Google Scholar]
- Müller, A.; Wolf, A. Heavy ion storage rings. In Accelerator-Based Atomic Physics Techniques and Applications; Austin, J.C., Shafroth, S.M., Eds.; AIP Press: Woodbury, NJ, USA, 1997; p. 147. [Google Scholar]
- Linkemann, J.; Müller, A.; Kenntner, J.; Habs, D.; Schwalm, D.; Wolf, A.; Badnell, N.R.; Pindzola, M.S. Electron-impact ionization of Fe15+ ions: An ion storage ring cross section measurement. Phys. Rev. Lett. 1995, 74, 4173–4176. [Google Scholar]
- Hahn, M.; Bernhardt, D.; Grieser, M.; Krantz, C.; Lestinsky, M.; Müller, A.; Novotný, O.; Repnow, R.; Schippers, S.; Wolf, A.; Savin, D.W. Storage Ring Cross Section Measurements for Electron Impact Ionization of Fe11+ Forming Fe12+ and Fe13+. Astrophys. J. 2011, 729, 76. [Google Scholar]
- Brötz, F.; Trassl, R.; McCullough, R.W.; Arnold, W.; Salzborn, E. Design of Compact All-Permanent Magnet Electron Cyclotron Resonance (ECR) Ion Sources for Atomic Physics Experiments. Phys. Scr. 2001, 2001, 278–280. [Google Scholar]
- Trassl, R.; Thompson, W.R.; Broetz, F.; Pawlowsky, M.; McCullough, R.W.; Salzborn, E. Development of a 10 GHz “Multi-Mode” ECR Ion Source for the Production of Multiply Charged Ions from Metallic Elements. Phys. Scr. 1999, 1999, 504–506. [Google Scholar]
- Borovik, A., Jr.; Rausch, J.; Becker, A.; Spruck, K.; Schury, D.; Ebinger, B.; Gharaibeh, M.; Schippers, S.; Müller, A. Test experiments in preparation of studies on electron-impact ionization of tungsten ions, unpublished.
- Spruck, K.; Badnell, N.R.; Krantz, C.; Novotný, O.; Becker, A.; Bernhardt, D.; Grieser, M.; Hahn, M.; Repnow, R.; Savin, D.W.; et al. Recombination of W18+ ions with electrons: Absolute rate coefficients from a storage-ring experiment and from theoretical calculations. Phys. Rev. A 2014, 90, 032715. [Google Scholar]
- Badnell, N. A Breit-Pauli distorted wave implementation for AUTOSTRUCTURE. Comput. Phys. Commun. 2011, 182, 1528–1536. [Google Scholar]
- Cowan, R.D. The Theory of Atomic Structure and Spectra; University of California Press: Berkeley, CA, USA, 1981. [Google Scholar]
- Lestinsky, M.; Badnell, N.R.; Bernhardt, D.; Bing, D.; Grieser, M.; Hahn, M.; Hoffmann, J.; Jordon-Thaden, B.; Krantz, C.; Novotný, O.; et al. Electron-Ion Recombination of Mg6+ Forming Mg5+ and of Mg7+ Forming Mg6+: Laboratory Measurements and Theoretical Calculations. Astrophys. J. 2012, 758, 40. [Google Scholar]
- Stenke, M.; Aichele, K.; Harthiramani, D.; Hofmann, G.; Steidl, M.; Völpel, R.; Salzborn, E. Electron-impact single-ionization of singly and multiply charged tungsten ions. J. Phys. B At. Mol. Opt. Phys. 1995, 28, 2711–2721. [Google Scholar]
- Stenke, M.; Aichele, K.; Harthiramani, D.; Hofmann, G.; Steidl, M.; Völpel, R.; Shevelko, V.P.; Tawara, H.; Salzborn, E. Electron-impact multiple ionization of singly and multiply charged tungsten ions. J. Phys. B At. Mol. Opt. Phys. 1995, 28, 4853–4859. [Google Scholar]
- Montague, R.G.; Harrison, M.F.A. A measurement of the cross section for electron impact ionisation of singly charged tungsten ions. J. Phys. B At. Mol. Opt. Phys. 1984, 17, 2707–2711. [Google Scholar]
- Sladeczek, P.; Feist, H.; Feldt, M.; Martins, M.; Zimmermann, P. Photoionization Experiments with an Atomic Beam of Tungsten in the Region of the 5p and 4f Excitation. Phys. Rev. Lett. 1995, 75, 1483. [Google Scholar]
- Haensel, R.; Radler, K.; Sonntag, B.; Kunz, C. Optical absorption measurements of tantalum, tungsten, rhenium and platinum in the extreme ultraviolet. Solid State Commun. 1969, 7, 1495. [Google Scholar]
- Costello, J.T.; Kennedy, E.T.; Sonntag, B.F.; Cromer, C.L. XUV photoabsorption of laser-generated W and Pt vapours. J. Phys. B At. Mol. Opt. Phys. 1991, 24, 5063. [Google Scholar]
- Watanabe, H.; Nakamura, N.; Kato, D.; Nakano, T.; Ohtani, S. X-Ray Spectra from Neon-like Tungsten Ions in the Interaction with Electrons. J. Plasma, Fusion Res. 2007, 2, 27. [Google Scholar]
- Biedermann, C.; Radtke, R.; Seidel, R.; Behar, E. Dielectronic and radiative recombination of Si- to N-like tungsten ions. J. Phys. Conf. Ser. 2009, 163, 012034. [Google Scholar]
- Loch, S.D.; Ludlow, J.A.; Pindzola, M.S.; Whiteford, A.D.; Griffin, D.C. Electron-impact ionization of atomic ions in the W isonuclear sequence. Phys. Rev. A 2005, 72, 052716. [Google Scholar]
- Spruck, K.; Becker, A.; Borovik, A., Jr.; Gharaibeh, M.F.; Rausch, J.; Schippers, S.; Müller, A. Electron-impact ionization of multiply charged tungsten ions. J. Phys. Conf. Ser. 2014, 488, 062026. [Google Scholar]
- Rausch, J.; Becker, A.; Spruck, K.; Hellhund, J.; Borovik, A., Jr.; Huber, K.; Schippers, S.; Müller, A. Electron-impact single and double ionization of W17+. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 165202. [Google Scholar]
- Zhang, D.H.; Kwon, D.H. Theoretical electron-impact ionization of W17+ forming W18+. J. Phys. B: At. Mol. Opt. Phys. 2014, 47, 075202. [Google Scholar]
- Gu, M.F. The flexible atomic code. Can. J. Phys. 2008, 86, 675–689. [Google Scholar]
- Jonauskas, V.; Kynienė, A.; Merkelis, G.; Gaigalas, G.; Kisielius, R.; Kučas, S.; Masys,, Š.; Radžiūtė, L.; Rynkun,, P. Contribution of high-nl shells to electron-impact ionization processes. Phys. Rev. A 2015, 91, 012715. [Google Scholar]
- Borovik, A., Jr.; Brandau, C.; Jacobi,, J.; Schippers,, S.; Müller,, A. Electron-impact single ionization of Xe10+ ions. J. Phys. B At. Mol. Opt. Phys 2011, 44, 205205. [Google Scholar]
- Pindzola, M.S.; Loch, S.D.; Borovik, A., Jr.; Gharaibeh, M.F.; Rudolph, J.K.; Schippers, S.; Müller, A. Electron-impact ionization of moderately charged xenon ions. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 215202. [Google Scholar]
- Borovik, A., Jr.; Gharaibeh, M.F.; Schippers, S.; Müller, A. Plasma rate coefficients for electron-impact ionization of Xeq+ ions (q = 8,…,17). J. Phys. B At. Mol. Opt. Phys. 2015, 48, 035203. [Google Scholar]
- Borovik, A., Jr.; Rausch, J.; Rudolph, J.; Gharaibeh, M.; Schippers, S.; Müller, A. Electron impact ionization of xenon ions. J. Phys. Conf. Ser. 2009, 194, 062014. [Google Scholar]
- Trzhaskovskaya, M.; Nikulin, V.; Clark, R.E.H. Radiative recombination rate coefficients for highly-charged tungsten ions. At. Data Nucl. Data Tables 2010, 96, 1–25. [Google Scholar]
- Boyle, J.; Altun, Z.; Kelly, H.P. Photoionization cross-section calculation of atomic tungsten. Phys. Rev. A 1993, 47, 4811. [Google Scholar]
- Ballance, P.C.; McLaughlin, B.M. Photoionization of the valence shells of the neutral tungsten atom. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 085201. [Google Scholar]
- Chang, J.J. The R-matrix theory of electron-atom scattering using the Dirac Hamiltonian. J. Phys. B At. Mol. Phys. 1975, 8, 2327. [Google Scholar]
- Norrington, P.H.; Grant, I.P. Low-energy electron scattering by Fe XXIII and Fe VII using the Dirac R-matrix method. J. Phys. B At. Mol. Phys. 1987, 20, 4869–4881. [Google Scholar]
- Ballance, C.P.; Griffin, D.C. Relativistic radiatively damped R-matrix calculation of the electron-impact excitation of W46+. J. Phys. B At. Mol. Opt. Phys. 2006, 39, 3617. [Google Scholar]
- Müller, A.; Schippers, S.; Esteves-Macaluso, D.; Habibi, M.; Aguilar, A.; Kilcoyne, A.L.D.; Phaneuf, R.A.; Ballance, C.P.; McLaughlin, B.M. Valence-shell photoionization of Ag-like Xe7+ ions: Experiment and theory. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 215202. [Google Scholar]
- Habibi, M.; Esteves, D.A.; Phaneuf, R.A.; Kilcoyne, A.L.D.; Aguilar, A.; Cisneros, C. Photoionization cross sections for ions of the cerium isonuclear sequence. Phys. Rev. A 2009, 80, 033407. [Google Scholar]
- Müller, A.; Schippers, S.; Hellhund, J.; Kilcoyne, A.L.D.; Phaneuf, R.A.; Ballance, C.P.; McLaughlin, B.M. Single and multiple photoionization of Wq+ tungsten ions in charge states q=1,2,..,5: Experiment and theory. J. Phys. Conf. Ser 2014, 488, 022032. [Google Scholar]
- Li, M.; Fu, Y.; Su, M.; Dong, C.; Koike, F. Dielectronic Recombination of Br-Like Tungsten Ions. Plasma Sci. Technol 2014, 16, 182–187. [Google Scholar]
- Safronova, U.; Safronova, A.; Beiersdorfer, P. Excitation energies, radiative and autoionization rates, dielectronic satellite lines, and dielectronic recombination rates for excited states of Na-like W from Ne-like W. At. Data Nucl. Data Tables 2009, 95, 751–785. [Google Scholar]
- Behar, E.; Mandelbaum, P.; Schwob, J.L. Dielectronic recombination of Ne-like tungsten. Phys. Rev. A 1999, 59, 2787–2793. [Google Scholar]
- Badnell, N.R. Dielectronic recombination of Fe 13+: Benchmarking the M-shell. J. Phys. B At. Mol. Opt. Phys. 2006, 39, 4825–4852. [Google Scholar]
- Safronova, U.I.; Safronova, A.S. Dielectronic recombination of Er-like tungsten. Phys. Rev. A 2012, 85, 032507. [Google Scholar]
- Safronova, U.I.; Safronova, A.S.; Beiersdorfer, P. Excitation energies, radiative and autoionization rates, dielectronic satellite lines, and dielectronic recombination rates for excited states of Yb-like W. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 085001. [Google Scholar]
- Schippers, S. Analytical Expression for the Convolution of a Fano Line Profile with a Gaussian. Int. Rev. At. Mol. Phys. 2011, 2, 151–156. [Google Scholar]
- Badnell, N.R.; Ballance, C.P.; Griffin, D.C.; O’Mullane, M. Dielectronic recombination of W20+(4d104f8): Addressing the half-open f shell. Phys. Rev. A 2012, 85, 052716. [Google Scholar]
- Müller, A.; Wolf, A. Production of Antihydrogen by Recombination of with e+: What Can We Learn from Electron-Ion Collision Studies? Hyperfine Interact 1997, 109, 233–267. [Google Scholar]
- Gao, H.; DeWitt, D.R.; Schuch, R.; Zong, W.; Asp, S.; Pajek, M. Observation of Enhanced Electron-Ion Recombination Rates at Very Low Energies. Phys. Rev. Lett. 1995, 75, 4381–4384. [Google Scholar]
- Gwinner, G.; Hoffknecht, A.; Bartsch, T.; Beutelspacher, M.; Eklöw, N.; Glans, P.; Grieser, M.; Krohn, S.; Lindroth, E.; Müller, A.; et al. Influence of Magnetic Fields on Electron-Ion Recombination at Very Low Energies. Phys. Rev. Lett. 2000, 84, 4822–4825. [Google Scholar]
- Hoffknecht, A.; Brandau, C.; Bartsch, T.; Böhme, C.; Knopp, H.; Schippers, S.; Müller, A.; Kozhuharov, C.; Beckert, K.; Bosch, F.; et al. Recombination of Bare Bi83+ Ions with Electrons. Phys. Rev. A 2001, 63, 012702. [Google Scholar]
- Hoffknecht, A.; Schippers, S.; Müller, A.; Gwinner, G.; Schwalm, D.; Wolf, A. Recombination of Bare Cl17+ Ions in an Electron Cooler. Phys. Scr. 2001, T92, 402–405. [Google Scholar]
- Shi, W.; Böhm, S.; Böhme, C.; Brandau, C.; Hoffknecht, A.; Kieslich, S.; Schippers, S.; Müller, A.; Kozhuharov, C.; Bosch, F.; et al. Recombination of U92+ Ions with Electrons. Eur. Phys. J. D 2001, 15, 145–154. [Google Scholar]
- Heerlein, C.; Zwicknagel, G.; Toepffer, C. Radiative Recombination Enhancement of Bare Ions in Storage Rings with Electron Cooling. Phys. Rev. Lett. 2002, 89, 083202. [Google Scholar]
- Hörndl, M.; Yoshida, S.; Wolf, A.; Gwinner, G.; Burgdörfer, J. Enhancement of Low Energy Electron-Ion Recombination in a Magnetic Field: Influence of Transient Field Effects. Phys. Rev. Lett. 2005, 95, 243201. [Google Scholar]
- Hörndl, M.; Yoshida, S.; Burgdörfer, J.; Gwinner, G.; Wolf, A. Enhanced electron-ion recombination in ion storage rings: Influence of transient field effects. Hyperfine Interact 2006, 173, 67–72. [Google Scholar]
- Müller, A. Plasma Rate Coefficients for Highly Charged Ion-Electron Collisions: New Experimental Access Via Ion Storage Rings. Int. J. Mass Spectrom 1999, 192, 9–22. [Google Scholar]
- Hoffknecht, A.; Uwira, O.; Frank, A.; Schennach, S.; Spies, W.; Wagner, M.; Schippers, S.; Müller, A.; Becker, R.; Kleinod, M.; et al. Recombination of Au25+ with Free Electrons at Very Low Energies. J. Phys. B At. Mol. Opt. Phys. 1998, 31, 2415–2428. [Google Scholar]
- Dzuba, V.A.; Flambaum, V.V.; Gribakin, G.F.; Harabati, C. Chaos-induced enhancement of resonant multielectron recombination in highly charged ions: Statistical theory. Phys. Rev. A 2012, 86, 022714. [Google Scholar]
- Dzuba, V.A.; Flambaum, V.V.; Gribakin, G.F.; Harabati, C.; Kozlov, M.G. Electron recombination, photoionization, and scattering via many-electron compound resonances. Phys. Rev. A 2013, 88, 062713. [Google Scholar]
- Schippers, S.; Bernhardt, D.; Müller, A.; Krantz, C.; Grieser, M.; Repnow, R.; Wolf, A.; Lestinsky, M.; Hahn, M.; Novotný, O.; Savin, D.W. Dielectronic recombination of xenonlike tungsten ions. Phys. Rev. A 2011, 83, 012711. [Google Scholar]
- Stobbe, M. Zur Quantenmechanik Photoelektrischer Prozesse. Ann. Phys. 1930, 7, 661–715. [Google Scholar]
- Müller, A.; Schennach, S.; Wagner, M.; Haselbauer, J.; Uwira, O.; Spies, W.; Jennewein, E.; Becker, R.; Kleinod, M.; Pröbstel, U.; et al. Recombination of free electrons with ions. Phys. Scr. 1991, T37, 62–65. [Google Scholar]
- Uwira, O.; Müller, A.; Spies, W.; Frank, A.; Linkemann, J.; Empacher, L.; Mokler, P.H.; Becker, R.; Kleinod, M.; Ricz, S. Recombination of U28+ Ions in a Dense, Cold Electron Target. Nucl. Instrum. Methods B 1995, 98, 162–164. [Google Scholar]
- Mitnik, D.M.; Pindzola, M.S.; Robicheaux, F.; Badnell, N.R.; Uwira, O.; Müller, A.; Frank, A.; Linkemann, J.; Spies, W.; Angert, N.; et al. Dielectronic Recombination of U28+ Atomic Ions. Phys. Rev. A 1998, 57, 4365–4372. [Google Scholar]
- Baird, S.; Bosser, J.; Carli, C.; Chanel, M.; Lefèvre, P.; Ley, R.; Maccaferri, R.; Maury, S.; Meshkov, I.; Möhl, D.; et al. Measurements of the Lifetime of Pb52+, Pb53+ and Pb54+ Beams at 4.2 MeV Per Nucleon Subject to Electron Cooling. Phys. Lett. B 1995, 361, 184. [Google Scholar]
- Uwira, O.; Müller, A.; Linkemann, J.; Bartsch, T.; Brandau, C.; Schmitt, M.; Wolf, A.; Schwalm, D.; Schuch, R.; Zong, W.; et al. Recombination Measurements at Low Energies with Au49+,50+,51+ at the TSR. Hyperfine Interact 1997, 108, 149–154. [Google Scholar]
- Lindroth, E.; Danared, H.; Glans, P.; Pesic, Z.; Tokman, M.; Vikor, G.; Schuch, R. QED Effects in Cu-Like Pb Recombination Resonances Near Threshold. Phys. Rev. Lett. 2001, 86, 5027–5030. [Google Scholar]
- Schippers, S.; Bernhardt, D.; Grieser, M.; Hahn, M.; Krantz, C.; Lestinsky, M.; Novotný, O.; Repnow, R.; Savin, D.W.; Wolf, A.; Müller, A. Recombination of Au20+ at low electron-ion collision energies. Phys. Scr. 2011, 2011, 014039. [Google Scholar]
- Gribakin, G.F.; Gribakina, A.A.; Flambaum, V.V. Quantum Chaos in Multicharged Ions and Statistical Approach to the Calculation of Electron-Ion Resonant Radiative Recombination. Aust. J. Phys. 1999, 52, 443–457. [Google Scholar]
- Flambaum, V.V.; Gribakina, A.A.; Gribakin, G.F.; Harabati, C. Electron Recombination with Multicharged Ions Via Chaotic Many-Electron States. Phys. Rev. A 2002, 66, 012713. [Google Scholar]
- Gribakin, G.F.; Sahoo, S. Mixing of dielectronic and multiply excited states in electron-ion recombination: A study of Au24+. J. Phys. B At. Mol. Opt. Phys. 2003, 36, 3349–3370. [Google Scholar]
- Ballance, C.P.; Griffin, D.C.; Loch, S.D.; Badnell, N.R. Dielectronic recombination of Au20+: A theoretical description of the resonances at low electron energies. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 045001. [Google Scholar]
- Schippers, S.; Müller, A.; Gwinner, G.; Linkemann, J.; Saghiri, A.A.; Wolf, A. Storage Ring Measurement of the C IV Recombination Rate Coefficient. Astrophys. J 2001, 555, 1027–1037. [Google Scholar]
- Müller, A.; Borovik, A., Jr; Huber, K.; Schippers, S.; Fursa, D.V.; Bray, I. Double-K-vacancy states in electron-impact single ionization of metastable two-electron N5+(1s2s 3S1) ions. Phys. Rev. A 2014, 90, 010701(R). [Google Scholar]
- Müller, A.; Teng, H.; Hofmann, G.; Phaneuf, R.A.; Salzborn, E. Autoionizing Resonances in Electron-Impact Ionization of O5+ Ions. Phys. Rev. A 2000, 62, 062720. [Google Scholar]
- Müller, A.; Phaneuf, R.A.; Aguilar, A.; Gharaibeh, M.F.; Schlachter, A.S.; Alvarez, I.; Cisneros, C.; Hinojosa, G.; McLaughlin, B.M. Photoionization of C2+ Ions: Time-Reversed Recombination of C3+ with Electrons. J. Phys. B At. Mol. Opt. Phys. 2002, 35, L137–L143. [Google Scholar]
- Schippers, S.; Kieslich, S.; Müller, A.; Gwinner, G.; Schnell, M.; Wolf, A.; Bannister, M.; Covington, A.; Zhao, L.B. Interference Effects in the Photorecombination of Argonlike Sc3+ Ions: Storage Ring Experiment and Theory. Phys. Rev. A 2002, 65, 042723. [Google Scholar]
- Schippers, S.; Müller, A.; Ricz, S.; Bannister, M.E.; Dunn, G.H.; Bozek, J.D.; Schlachter, A.S.; Hinojosa, G.; Cisneros, C.; Aguilar, A.; et al. Experimental Link of Photoionization of Sc2+ to Photorecombination of Sc3+: An Application of Detailed Balance in a Unique Atomic System. Phys. Rev. Lett. 2002, 89, 193002. [Google Scholar]
- Müller, A.; Phaneuf, R.A.; Aguilar, A.; Gharaibeh, M.F.; Schlachter, A.S.; Alvarez, I.; Cisneros, C.; Hinojosa, G.; McLaughlin, B.M. Photoionization of C2+ ions. Nucl. Instrum. Methods B 2003, 205, 301–305. [Google Scholar]
- Müller, A.; Schippers, S.; Aguilar, A.; Alvarez, I.; Bannister, M.E.; Bozek, J.; Cisneros, C.; Covington, A.; Dunn, G.H.; Gharaibeh, M.F.; et al. Time-reversal studies in photorecombination and photoionization experiments with ion beams. In Application of Accelerators in Research and Industry; Duggan, J.L., Morgan, I.L., Eds.; American Institute of Physics; Melville, NY, USA, 2003; Volume 680, pp. 191–194. [Google Scholar]
- Schippers, S.; Müller, A.; Ricz, S.; Bannister, M.E.; Dunn, G.H.; Schlachter, A.S.; Hinojosa, G.; Cisneros, C.; Aguilar, A.; Covington, A.M.; et al. Photoionization of Sc2+ Ions by Synchrotron Radiation: Measurements and Absolute Cross Sections in the Photon Energy Range 23–68 eV. Phys. Rev. A 2003, 67, 032702. [Google Scholar]
- Schippers, S.; Müller, A.; Ricz, S.; Bannister, M.E.; Dunn, G.H.; Bozek, J.; Schlachter, A.S.; Hinojosa, G.; Cisneros, C.; Aguilar, A.; et al. Photoionization of Sc2+: Experimental Link with Photorecombination of Sc3+ by Application of Detailed Balance. Nucl. Instrum. Methods B 2003, 205, 297–300. [Google Scholar]
- Schippers, S.; Bartsch, T.; Brandau, C.; Gwinner, G.; Linkemann, J.; Müller, A.; Saghiri, A.A.; Wolf, A. Photorecombination of Ti4+ Ions: Search for Interference Effects, Recombination at Low Energies and Rate Coefficient in Plasmas. J. Phys. B At. Mol. Opt. Phys. 1998, 31, 4873–4886. [Google Scholar]
- Schippers, S.; Müller, A.; Phaneuf, R.A.; van Zoest, T.; Álvarez, I.; Cisneros, C.; Emmons, E.D.; Gharaibeh, M.F.; Hinojosa, G.; Schlachter, A.S.; Scully, S.W.J. Threshold truncation of a ‘giant’ dipole resonance in photoionization of Ti3+. J. Phys. B At. Mol. Opt. Phys. 2004, 37, L209–L216. [Google Scholar]
- Müller, A.; Schippers, S.; Phaneuf, R.A.; Scully, S.W.J.; Aguilar, A.; Covington, A.M.; Álvarez, I.; Cisneros, C.; Emmons, E.D.; Gharaibeh, M.F.; et al. K-shell photoionization of ground-state Li-like carbon ions [C3+]: Experiment, theory and comparison with time-reversed photorecombination. J. Phys. B At. Mol. Opt. Phys. 2009, 42, 235602. [Google Scholar]
- Müller, A.; Schippers, S.; Phaneuf, R.A.; Scully, S.W.J.; Aguilar, A.; Cisneros, C.; Gharaibeh, M.F.; Schlachter, A.S.; McLaughlin, B.M. K-shell photoionization of ground-state Li-like boron ions [B2+]: Experiment and Theory. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 135602. [Google Scholar]
- Müller, A.; Schippers, S.; Phaneuf, R.A.; Scully, S.W.J.; Aguilar, A.; Cisneros, C.; Gharaibeh, M.F.; Schlachter, A.S.; McLaughlin, B.M. K -shell photoionization of Be-like boron (B+) ions: Experiment and theory. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 135201. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).