Abstract
The statistical model for calculations of the collisional-radiative processes in plasmas with tungsten impurity was developed. The electron structure of tungsten multielectron ions is considered in terms of both the Thomas-Fermi model and the Brandt-Lundquist model of collective oscillations of atomic electron density. The excitation or ionization of atomic electrons by plasma electron impacts are represented as photo-processes under the action of flux of equivalent photons introduced by E. Fermi. The total electron impact single ionization cross-sections of ions Wk+ with respective rates have been calculated and compared with the available experimental and modeling data (e.g., CADW). Plasma radiative losses on tungsten impurity were also calculated in a wide range of electron temperatures 1 eV–20 keV. The numerical code TFATOM was developed for calculations of radiative-collisional processes involving tungsten ions. The needed computational resources for TFATOM code are orders of magnitudes less than for the other conventional numerical codes. The transition from corona to Boltzmann limit was investigated in detail. The results of statistical approach have been tested by comparison with the vast experimental and conventional code data for a set of ions Wk+. It is shown that the universal statistical model accuracy for the ionization cross-sections and radiation losses is within the data scattering of significantly more complex quantum numerical codes, using different approximations for the calculation of atomic structure and the electronic cross-sections.
1. Introduction
Description of the radiative-collisional processes in plasmas with tungsten impurity ions became relevant in connection with the application of tungsten as the construction material of divertor plates in the future tokamak reactor ITER [1,2,3,4,5]. The problem has to be solved over a wide range of plasma electron temperature from a few eV in the edge and up to 20 keV in the center of plasma. Moreover, in all temperature ranges of interest, the multielectron tungsten ions have a very complex energy structure that results in time-consuming quantum mechanical calculations both of atomic structure and elementary processes, responsible for populations, ionization and radiative properties of tungsten ions in plasmas.
As far as additional approximations applicable only in limited temperature ranges are used for atomic processes calculations, the noticeable discrepancies arise between the results of complex specific codes [6,7]. The analysis of this problem has shown a possibility of its solution within the general statistical methods [8,9] for modeling of the atomic processes with multielectron ions [10,11,12]. Indeed, according to the recently developed statistical model for radiative and collisional processes with multielectron ions [13,14,15], this way of consideration would be advantageous for the determination of atomic process scaling laws in a wide temperature range.
The physical essence of the model is a representation of the electron structure of tungsten charge states similar to a plasma system, whereby excitations are equivalent to the excitations of local classical plasma oscillations in the atomic electron structure. The majority of atomic electrons occupy the atomic states with the large values of principle and orbital momentum quantum numbers where the electron motion is quasi classical [8,9,10]. The motion of plasma electrons, exciting electron shells of impurity ions, is also considered in the frames of classical approximation. The latter is based on the applicability of classical approximation to the Thomas-Fermi (TF) statistical potential. This was demonstrated in calculations of bremsstrahlung spectra [16] on multielectrons systems, which are in excellent agreement with quantum calculations of corresponding effects. The application of the Fermi method of equivalent photons [17] allows the consideration of the excitation processes in atoms as photoabsorption of the equivalent photon flux. The most detail modeling [18] estimates the accuracy of approximations under consideration.
The statistical method describes the radiative properties of radiating tungsten ions in terms of simple functionals of electron density distribution inside the atom. The corresponding numerical realization of statistical models will be much less time-consuming and at the same time enough accurate as compared with more detail numerical codes.
It is worth noting that the applications of conventional numerical codes over a wide range of plasma parameters result in strong discrepancies (up to 2–3 times depending on the specific situation). This is due to the very complicated atomic structure of multielectron tungsten ions making problematic the selection of universal model for calculations of atomic data. For instance, in the low temperature range, the most adequate approximations are based on the strong coupling method (see, e.g., [18]). However, in this case, the results are strongly dependent on the number of atomic states which increase rapidly with an increase of the number of bound electrons. As the temperature grows, the Coulomb−Born approximation, together with its modification [18] using distorted waves, starts to be more effective for calculations of collisional-radiative processes. At last the pure Coulomb−Born or Born approaches are successfully used in plasmas with the high temperatures.
The most popular approach in atomic structure calculations is the Hartree−Fock method. However, its accuracy depends on the number of atomic states taken into account, and on the complicated electron coupling in complex tungsten ions. As these models need very laborious calculations, their joint application with the plasma codes (for instance, the transport ones) is all the more time consuming.
The alternative possibilities of presented statistical theory in solving these problems are illustrated below by the specific calculations of atomic processes with tungsten ions in plasmas. It will be shown that the statistical theory data hit the scatter of discrepancies between more detailed conventional calculations.
2. Basic Equations of Statistical Theory and Fermi’s Equivalent Photons Model
2.1. Ionization Cross-Sections and Rates
The interactions of plasma electrons with tungsten ions are considered using the method of equivalent photons (EQP) given by E. Fermi [17]. In this method, the action of the electric field of plasma electrons on the tungsten impurity ions is described as the photoabsorption of equivalent photons flux. Its intensity is determined by Fourier transform of the electric field of the plasma electron, moving along the classical trajectory in the TF ion potential. Thus the moving plasma electrons produce the electromagnetic field, which is absorbed by atomic electrons at the frequencies, related to the atomic plasma oscillations, while the EQP approach makes it possible to express the electron impact ionization in terms of photoionization cross-section. Moreover, the cross-section of any elementary process due to the multielectron ion interactions with plasma-charged particles may be represented in the dipole approximation in terms of cross-sections of photo-processes with EQP.
In accordance with the statistical model [13], the electron impact ionization cross-section is given in terms of the photoionization cross-section at the frequency ω, which satisfies the resonance condition [11]
which determines the effective absorption radius being the solution of the equation above.
The conventional dimensionless reduced frequency satisfies the local resonance condition (1) via the implicit dependence of the reduced distance from the nuclear where is the TF radius, is the Bohr radius and then
where is the standard screening function in the TF model.
The plasma electron trajectory in the TF ion potential could be described in the Coulomb approximation by the effective charge , determined by the resonance condition (1)
where is the TF ion radius for given q = zi/Z.
The value of zeff is changed smoothly from zi at small frequencies up to Z at large frequencies. Such deviation for the tungsten ions with zi = 22,28,34 is given in Figure 1 versus s.
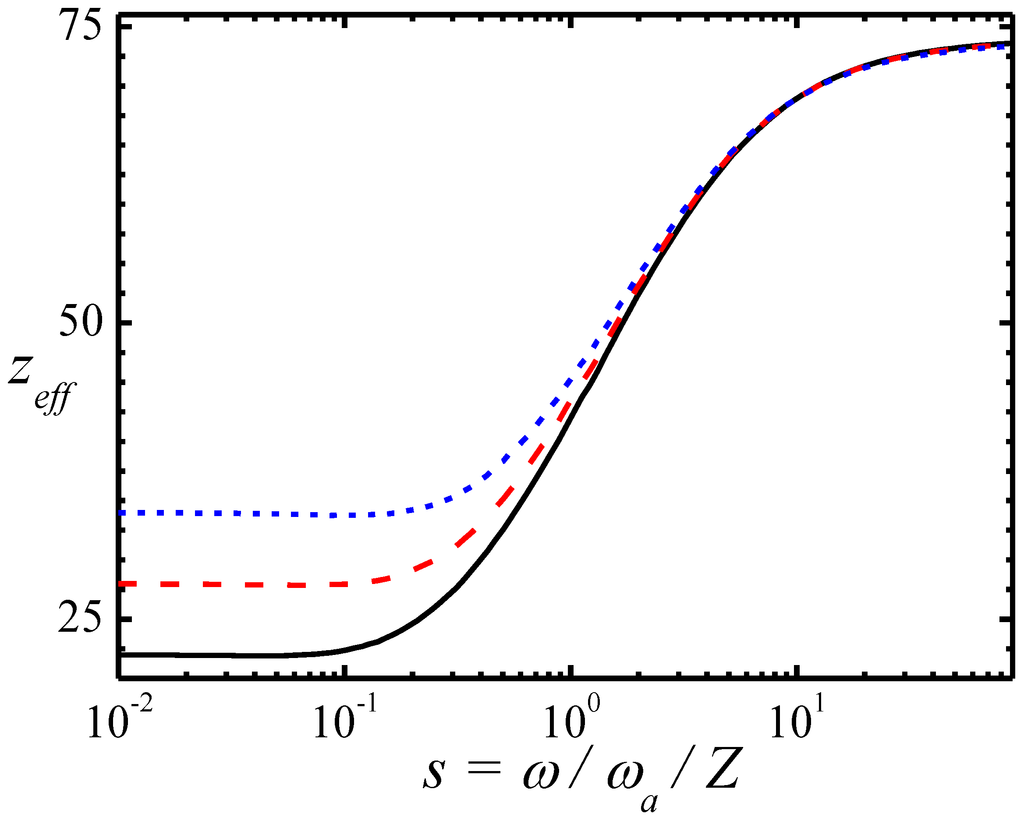
Figure 1.
Effective charge in Thomas-Fermi model, calculated from Equation (3) versus reduced frequency for ions W22+ (solid curve), W28+ (dashed curve), W34+ (short dashed curve).
Figure 1.
Effective charge in Thomas-Fermi model, calculated from Equation (3) versus reduced frequency for ions W22+ (solid curve), W28+ (dashed curve), W34+ (short dashed curve).
The EQP number with the reduced frequency s per unit frequency interval ds for the given reduced energy of electrons could be written in the form (compare with [14])
where с is the speed of light, е is the electron charge, is the Gaunt-factor, that describes the curvature of electron trajectory in the given potential of an ion with the charge zi and the charge of nuclei Z in the Coulomb approximation [13,14,15,16].
Now we multiply the photoionization cross-section by the number of EQP (4) and then integrate overall EQP frequencies s from the reduced ionization potential up to , that results in the following expression for the total electron impact single ionization cross-section (compare with [14,15]
where IR is calculated using the TF form for Ii to make the theory self-consistent, while the fitting expression for the Gaunt factor is provided by the Coulomb approximation (see [13,14,15,16]). We use Equation (5) for calculations of ionization cross-sections for a large set of tungsten ions, presented below.
2.2. Excitation Rates
The representation of atomic structure as a set of oscillators, being excited by collisions with external plasma electrons, is in the background of the present approach. The interaction of plasma electrons with atoms is considered in the Fermi approximation of EQP, where the electric field of equivalent photon flux is determined by the Fourier expansion of the electric field of electron, moving along the classical trajectory in the field of atom being excited. In this formulation the excitation of bound electrons in multielectron ion is expressed in terms of the photoabsorption cross-section, for which in its turn the aforementioned statistical models of multielectron atoms could be used [8,9,10,11,12,13,14,15].
In the LPF model [8], the photoabsorption cross-section is expressed in the form
where m is the electron mass.
If the atomic electron density distribution given by the Thomas-Fermi model is additionally used, Equation (6) is transformed to
The behavior of the universal photoexcitation cross-section (7) versus s for three values of stripping q is shown in Figure 2.
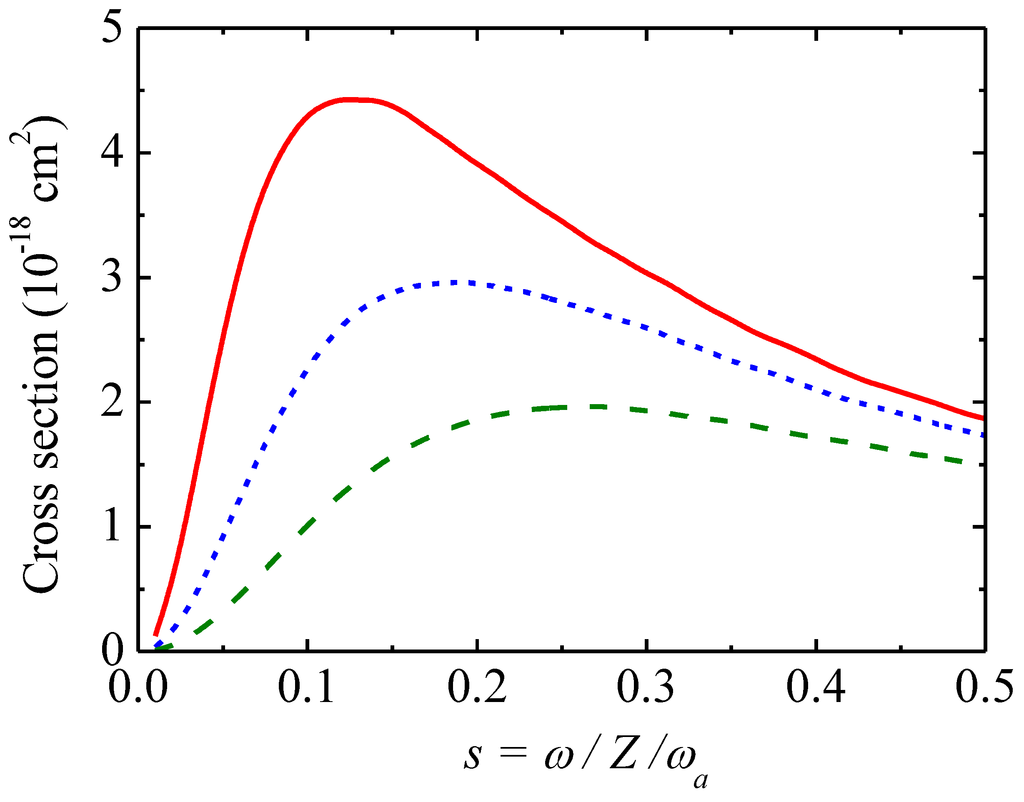
Figure 2.
Photoabsorption cross-section σ(s) in LPF model and statistical Thomas-Fermi model versus the reduced frequency s = ω/Z/ωa for three values of q: solid (red) curve—q = 0.3; short dashed (blue) curve—q = 0.4; long dashed (green) curve—q = 0.5.
Figure 2.
Photoabsorption cross-section σ(s) in LPF model and statistical Thomas-Fermi model versus the reduced frequency s = ω/Z/ωa for three values of q: solid (red) curve—q = 0.3; short dashed (blue) curve—q = 0.4; long dashed (green) curve—q = 0.5.
According to the universal statistical theory proposed in this work, the excitation rates now could be obtained by multiplying the photoabsorption cross-section Equation (7) by Equation (4) and the value of electron flux ne ve (where ne is the plasma electron density and ve is the electron thermal velocity), and then integrating over the Maxwell distribution over energy of plasma electrons.
3. Ionization Balance of Impurity Tungsten Ions in Plasmas
3.1. Ionization Potentials and Average Charge
For the self-consistency within the statistical theory in calculations of the electron impact ionization cross-sections, the ionization and excitation rates we use are the reduced ionization potentials IR, determined by the following expression (compare with [10])
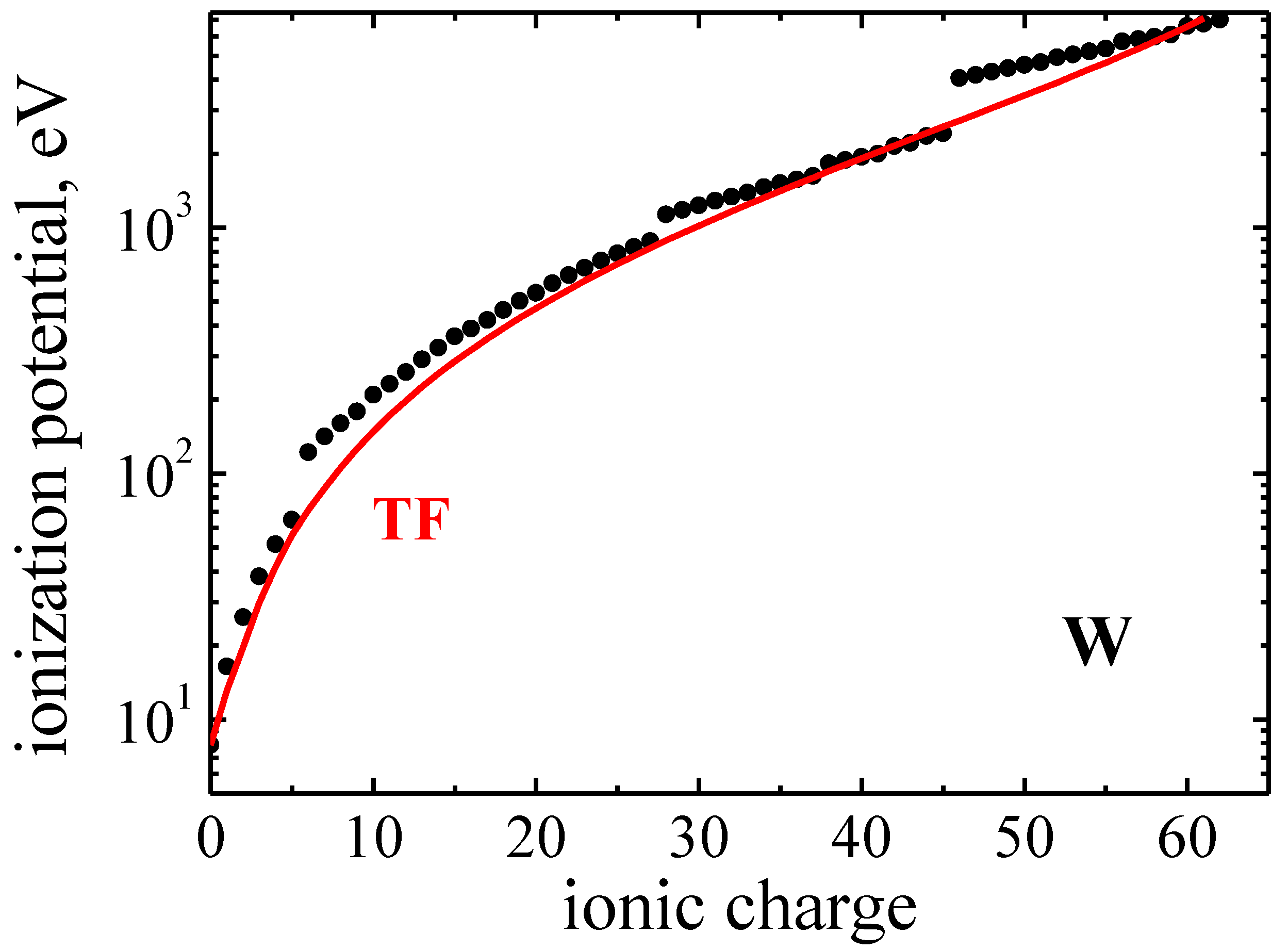
In Figure 3, the comparison of tabulated ionization potentials [19] for of tungsten ions with the Thomas-Fermi model values calculated from Equation (8) is presented. As can be seen by the figure, the statistical model quite reasonably approximates the available data [19].
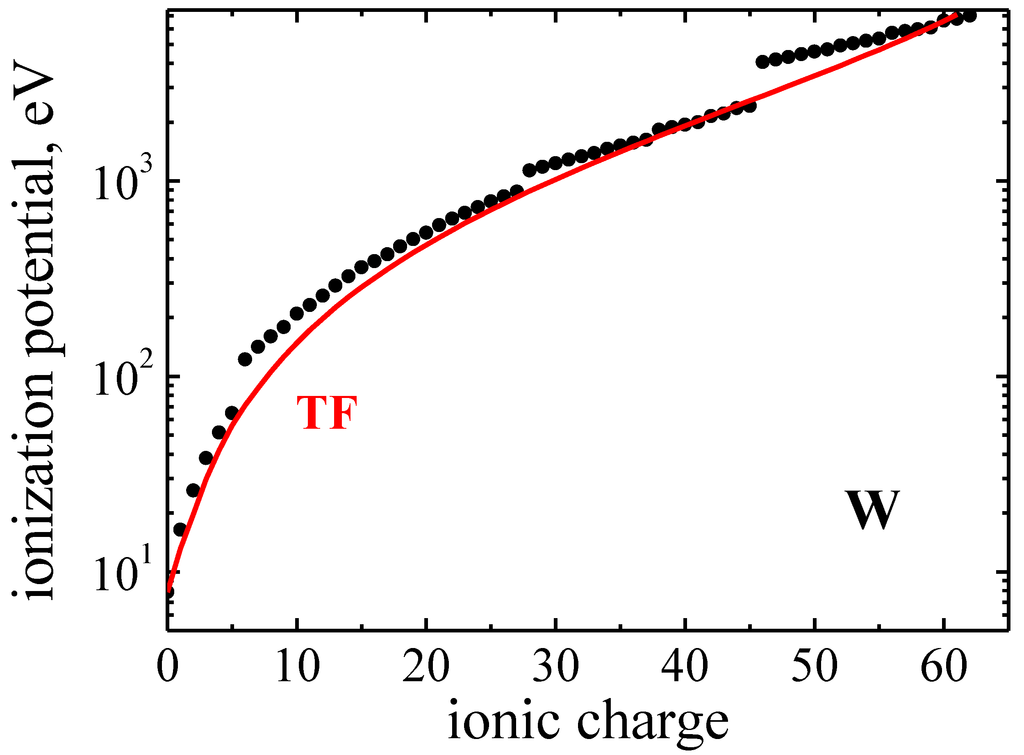
Figure 3.
Ionization potentials of W ions: solid lines—approximation in Thomas-Fermi model (TF); points—tabulated ionization potentials of W [19].
Figure 3.
Ionization potentials of W ions: solid lines—approximation in Thomas-Fermi model (TF); points—tabulated ionization potentials of W [19].
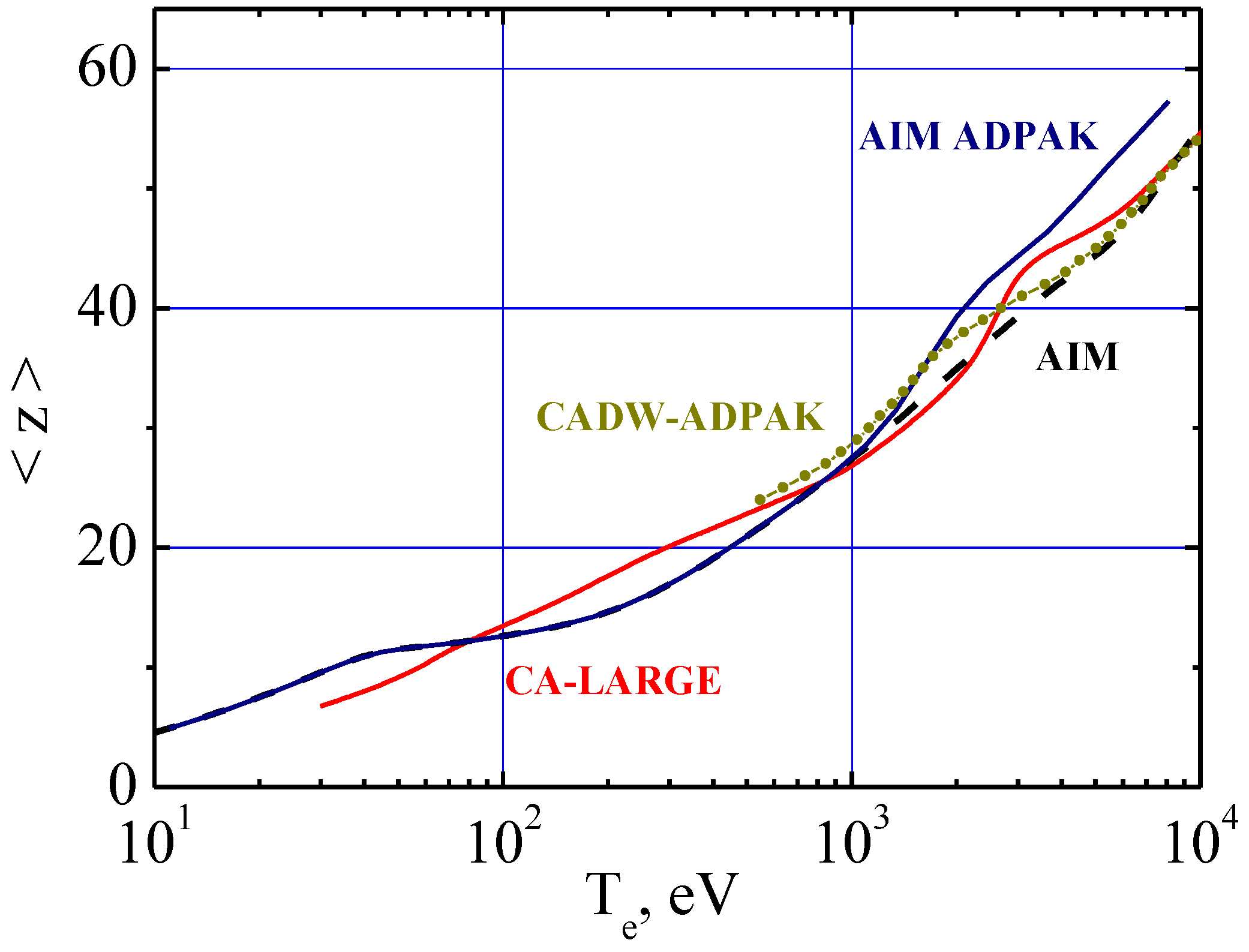
The calculations of total radiation losses need information on the charge state distribution (CSD) of radiating tungsten ions with the detailed knowledge of their ionization and recombination rates entering the ionization balance equations. In the present consideration we used the available in literature data on the average charge <z(Te)> instead of the detailed procedure of averaging over the CSD function. The performed analysis has shown that the accuracy of this approach is the same as of the statistical model itself. In Figure 4, we present the <z(Te> dependencies according to the current complex codes. The range of Te typical for large tokamaks corresponds to ions W20+—W56+.
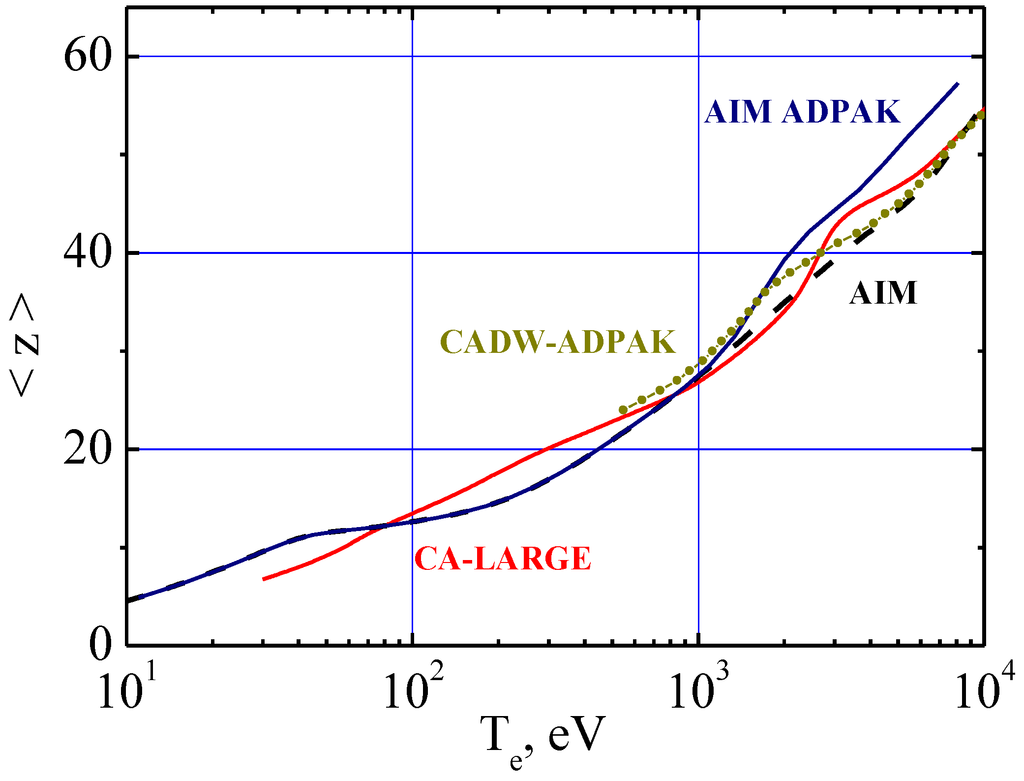
Figure 4.
Average charge of tungsten ions versus electron temperature in coronal equilibrium according to data from [1,7] (AIM ADPAK), [3] (CADW-ADPAK), [4] (CA-LARGE) and [20] (AIM).
Figure 4.
Average charge of tungsten ions versus electron temperature in coronal equilibrium according to data from [1,7] (AIM ADPAK), [3] (CADW-ADPAK), [4] (CA-LARGE) and [20] (AIM).
3.2. Gaussian Approximation
In Figure 4, the appreciable discrepancies in the <z(Te> dependencies due to the difference in ionization and recombination rates, which are provided by the different approaches for the complex atomic electron structure of tungsten ions, become evident. We would like to demonstrate below some general properties of CSD for heavy ions based on peculiarities of their ionization balance equations.
The standard set of balance equations for ionization and recombination processes for the impurity CSD function fk has the form
where Rk and Sk are recombination and ionization rates respectively for the k-th charge states of the impurity, k = 0,1,2,...,Z.
In the case of heavy ions, the relative charge state change is rather small as compared with the nuclear charge Z, and so it is possible to consider the parameter k as continuous.
Let us introduce the relative charge xk = k / Z changing from 0 to 1, then it is possible to transform Equation (9) to the equivalent differential equation. Assuming that k >> Δk = 1, we expand both
and
where the derivations can be determined using the interpolation Lagrange formula. Substituting Equations (10)–(11) into Equation (9) gives the expression
where . The coefficients in Equation (12) take the form
Equation (12) belongs to the Fokker−Plank−Kolmogorov type in the charge state space where all series of coefficients are expressed in terms of the variable combinations Sk and Rk. As it follows from Equation (13), the series and the coefficients Сnk are decreasing rapidly. It thus makes it possible to limit the consideration by the first two terms in the case of large z values
Equation (14) is of the diffusion type, where the diffusion coefficient is inverse proportional to Z2. This means that the CSD of heavy ions could be very sharp with the increase of Z, and the coefficients (13) change slowly on the width of the CHS distribution.
In this case, Equations (12)–(14) could be transformed to the parabolic type equation with the approximately constant coefficients. It is well known that the solution of such equation is close to Gaussian distribution, which can be written in our case in the form
where xa = <z> / Z is the relative average charge of CHS distribution and δ is its dispersion.
The main feature of the tungsten impurity CSD is demonstrated in Figure 5 by the comparison between Gaussian distributions and ones obtained with ionization-recombination rates used in AIM-ADPAK code [1] for a wide range of temperatures. Some deflection of these CSDs from the Gaussian form can be seen near Te = 100 eV and 2 keV, where the ramps of ionization rates between neighboring atomic shells affect the correct solutions of Equation (9).
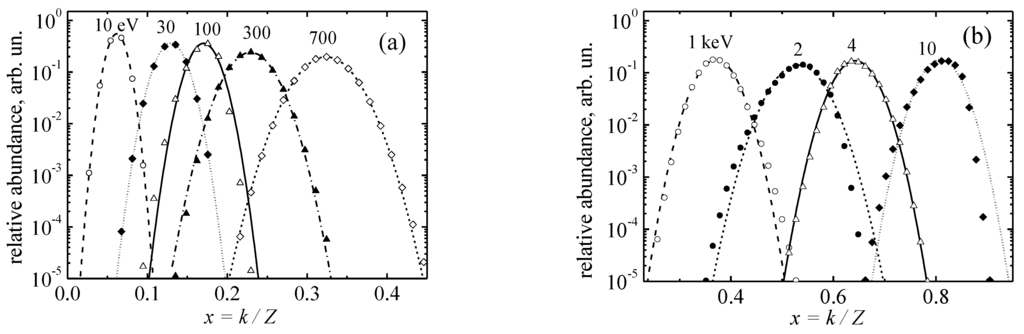
Figure 5.
Comparison of the tungsten impurity equilibrium CSDs, obtained as the steady-state solutions of Equation (9), with the Gaussian distributions, calculated by Equation (15): (a)—for Te < 1 keV; (b)—for Te > 1 keV (the curves are labeled by corresponding Te values).
Figure 5.
Comparison of the tungsten impurity equilibrium CSDs, obtained as the steady-state solutions of Equation (9), with the Gaussian distributions, calculated by Equation (15): (a)—for Te < 1 keV; (b)—for Te > 1 keV (the curves are labeled by corresponding Te values).
The dispersion δ of the impurity CSD has the form
In the case of tungsten plasma impurity the calculated function δ(<z>) is shown in Figure 6. It is seen that by using Equation (15) for Gaussian distributions with δ(<z>), one can rather accurately approximate the solutions of Equation (9) for tungsten impurity in a wide range of plasma electron temperatures.
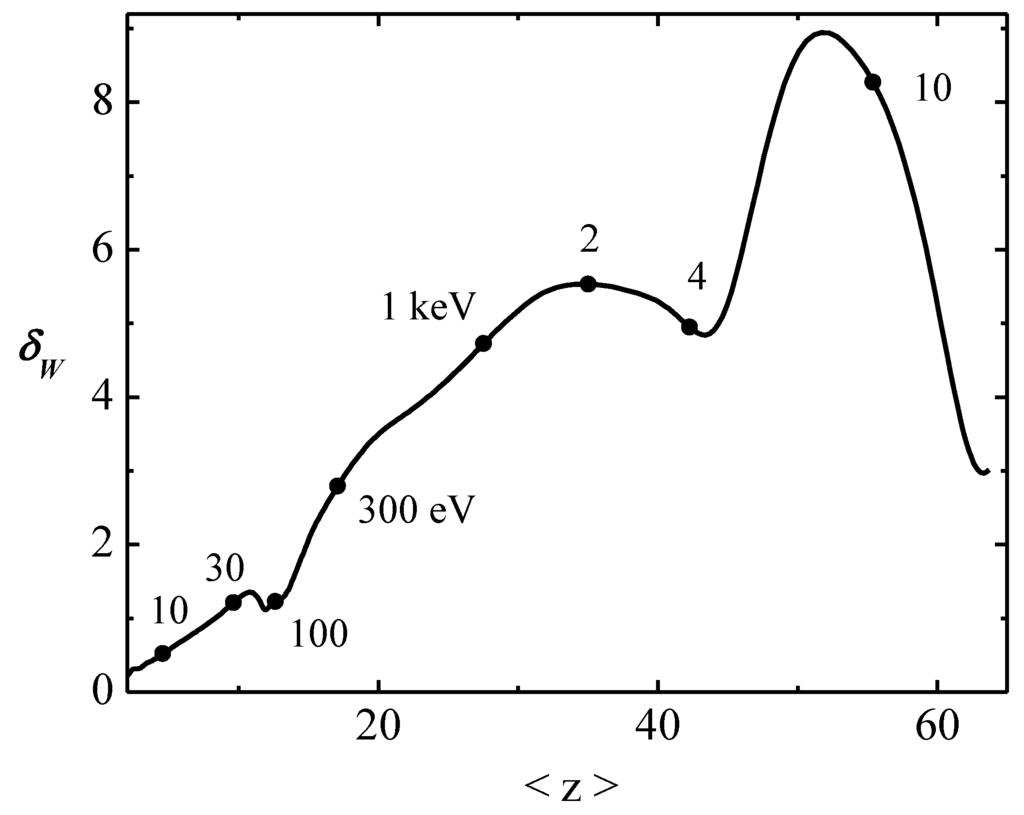
Figure 6.
Dispersion of tungsten impurity in coronal equilibrium versus average charge of CSD: calculated from the data of AIM-ADPAK code [1] for ionization and recombination rates (the corresponding Te values are noted by points along the curve).
Figure 6.
Dispersion of tungsten impurity in coronal equilibrium versus average charge of CSD: calculated from the data of AIM-ADPAK code [1] for ionization and recombination rates (the corresponding Te values are noted by points along the curve).
4. Plasma Radiative Losses
4.1. Coronal Radiative Losses
It can be shown that the conditions of coronal model, in which the radiation losses are determined totally by collisional excitation rates of ions, are mainly fulfilled in the applications for thermonuclear fusion with magnetic confinement. Therefore, within the aforementioned approximations, the radiation losses of energy per an electron and per a given ion of multielectron impurity take the universal form, expressed in terms of photoexcitation rates of atoms in the field of EQP.
Taking into account only the bound states, the integration over frequencies is performed up to the ionization potential of a given ion. The integration over energies of incident electron goes from the equivalent photon frequency, which corresponds to the excitation thresholds of atomic transitions in the statistical model.
So, the radiative energy losses in corona approximations can be expressed in terms of the absorption power in electron-ions collisions. As it was already noted the electron excitation rates can be expressed in terms of photoexcitation cross-sections from Section 2.2, multiplied by the intensity of the EQP flux that could be obtained, using results of Section 2.1. This allows the writing of the radiative losses power per one electron and one ion in the form
where and u = ER / TR, σph (s) is the ion photoexcitation or photoionization cross-section; is the introduced above Gaunt factor; is the intensity of equivalent photon flux with the reduced frequency s per unit frequency interval ds, averaged over energy ER of the electron projectile, scattered by the target.
Thus, in the frame of the statistical Thomas-Fermi model, the radiation losses in coronal equilibrium could be represented in the form (compare with [13])
and for g(s,u) = 1
In the case of the electromagnetic method (EM) [13], the numerical values of the corresponding photoabsorption cross-sections from [12] were substituted into Equation (17).
4.2. Transition to Boltzmann Equilibrium
The consideration above deals with the corona approximation related to low densities and high temperature plasmas. When temperature falls down or density increases, one has to use a more complex radiative-collisional model for calculations of radiative losses. The appropriate model could be constructed in the frames of statistical theory [8,9,10,11,12,13,14,15].
In order to obtain the Boltzmann limit, we need to derive expressions for the excitation and deexcitation rates, connected by the detailed balance relation that contains the Boltzmann exponent with the plasma frequency in its power in terms of the atomic “plasma model,” using the Fermi EQP method and operating with the cross-sections of emission and absorption.
It is presumed here that plasma electrons have isotropic Maxwell distribution over velocities and the EQP flux is unpolarized. As it was already implemented above, the photoabsorption cross-section in the local plasma frequency model (LPF) could be represented in the form [11]
Based on this, we can express the Einstein coefficient for spontaneous emission in the form
The total emission probability then is
Hence, the total Einstein coefficient for induced radiation has the form
Let Nvp(ω) be the EQP number, Bij Nvp(ω) and Bji Nvp(ω) the deexcitation and excitation rates correspondingly under the action of EQP flux. Then from the equality of the direct and reverse processes we have
Taking into account the Boltzmann distribution of level population
we obtain
On the other hand, the excitation rate under the influence of the EQP flux could be represented as the photoexcitation rate in terms of the photoabsorption cross-section. Let us write down the probability of EQP-induced absorption. The probability of induced radiation is determined by the product of the Einstein coefficient for the induced radiation and the radiation energy density (erg/cm3) with the polarization σ, connected with the integral over solid angles Ω of the radiation spectral intensity with the polarization σ in the direction, determined by the wave vector and divided by the speed of ligh c
The intensity of EQP flux produced in the elastic scattering of electrons by the Coulomb center and averaged over the electron energy could be expressed as
It is presumed here, that electrons have the isotropic Maxwell distribution over velocities and the EQP flux is unpolarized. As was already implemented the photoabsorption cross-section, the plasma model has the form
This integral represents the sum over the oscillator strengths of all transitions, while the separate transition could be represented through the oscillator strength differentia
Considering each pair of levels in the two states’ approximation, and equating the excitation rate due to the EQP photoabsorption to the deexcitation rate due to the spontaneous and induced radiation decay initiated by the EQP flux, we can write the balance equation in the two-level approximation within the “plasma” statistical model. Then the population of excited state via population of the lower one is by the relation
The radiation losses due to the transition i→j could be presented in the following way
In order to obtain the total radiation losses Q for the particular charge state of ion, one has to add contributions from all possible transitions. Summation over the contributions from the different transitions i→j involves the populations of different levels and then the integration over where is the density of ions with the stripping q. Performing these operations, we arrive to the general form of the specific integral radiation losses in the effective two-state approximation in the plasma model and the Coulomb approximation of effective charge
One can check that Equation (33) reproduces the coronal radiative losses (18) in the case of low values of electron density. In the opposite limit radiative losses (33) reproduce the Boltzmann result. In the last case, it is usually necessary to take into account the optical thickness of the medium.
5. Numerical Data
5.1. Ionization Cross-Section and Rates
We developed the numerical code TFATOM to perform calculations on the basis of general equations presented above. The calculation time for orders of magnitude is less than other numerical codes because the code TFATOM deals with is comprised of calculations of single or double integrals from the known Thomas-Fermi functions only. The results of comparison of the TFATOM code data for the electron impact ionization cross-sections with available series of experimental data [21,22,23,24,25,26] and the code CADW data [23,26] for ions Wk+ with k = 1,2,...10,17,22,45,63 are shown in Figure 7 (compare with [15]).
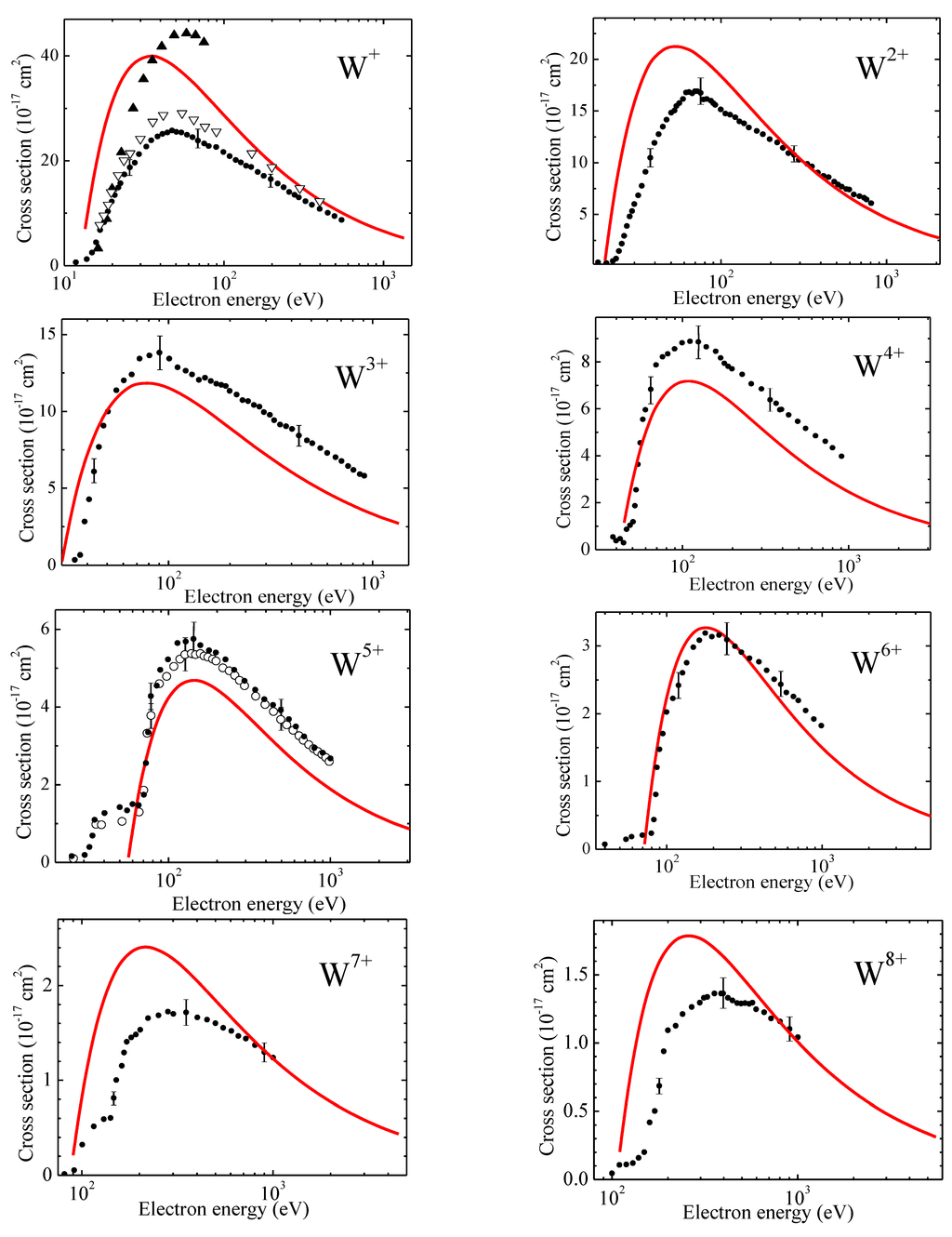
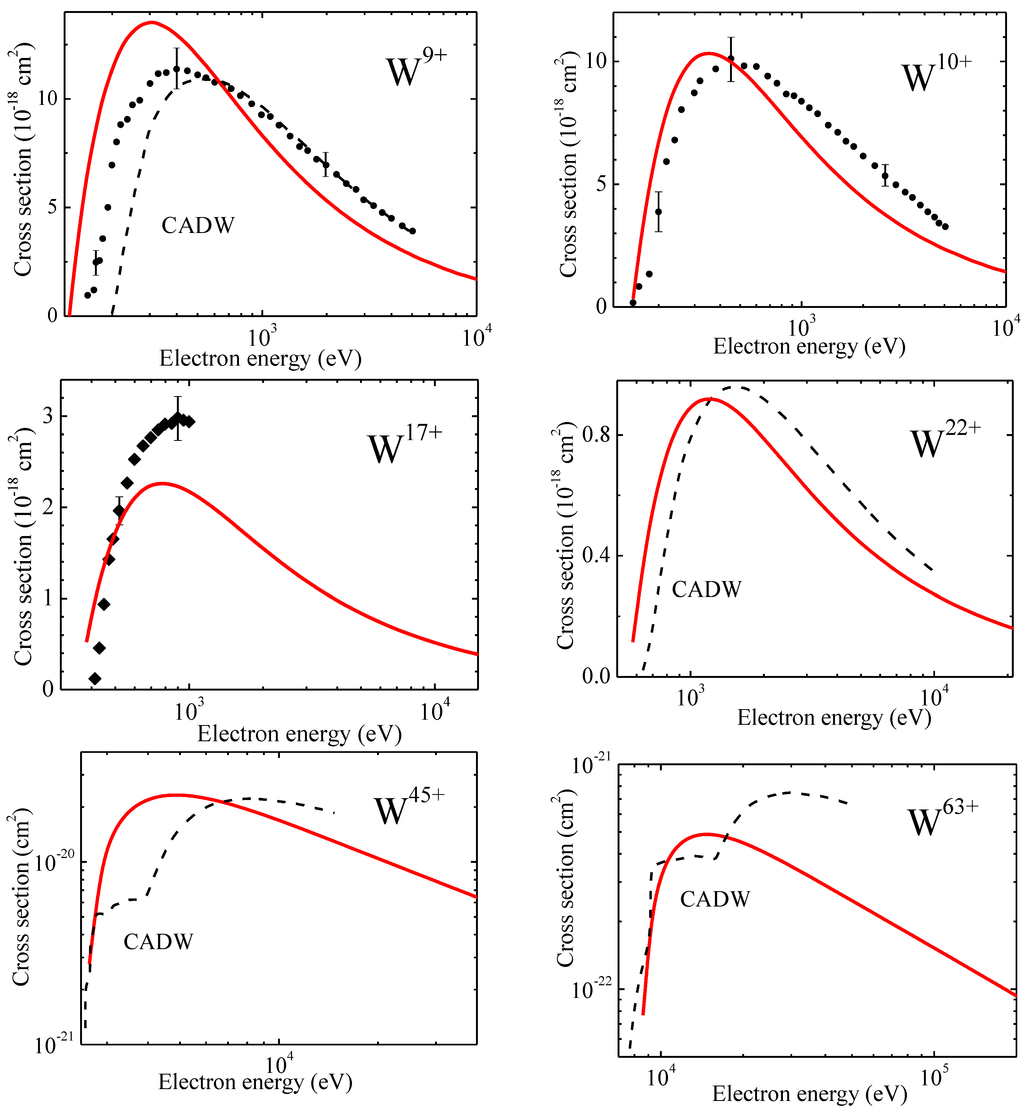
Figure 7.
Comparison of theoretical electron impact ionization cross-sections with experimental data for ions Wk+ with k = 1,2,...10,17,22,45,63: solid curves—present statistical model; black points—[21]; open triangles—[22]; full triangles—CADW data [23]; open circles [24]; full squares—[25]; dashed curves signed CADW—[26].
Figure 7.
Comparison of theoretical electron impact ionization cross-sections with experimental data for ions Wk+ with k = 1,2,...10,17,22,45,63: solid curves—present statistical model; black points—[21]; open triangles—[22]; full triangles—CADW data [23]; open circles [24]; full squares—[25]; dashed curves signed CADW—[26].
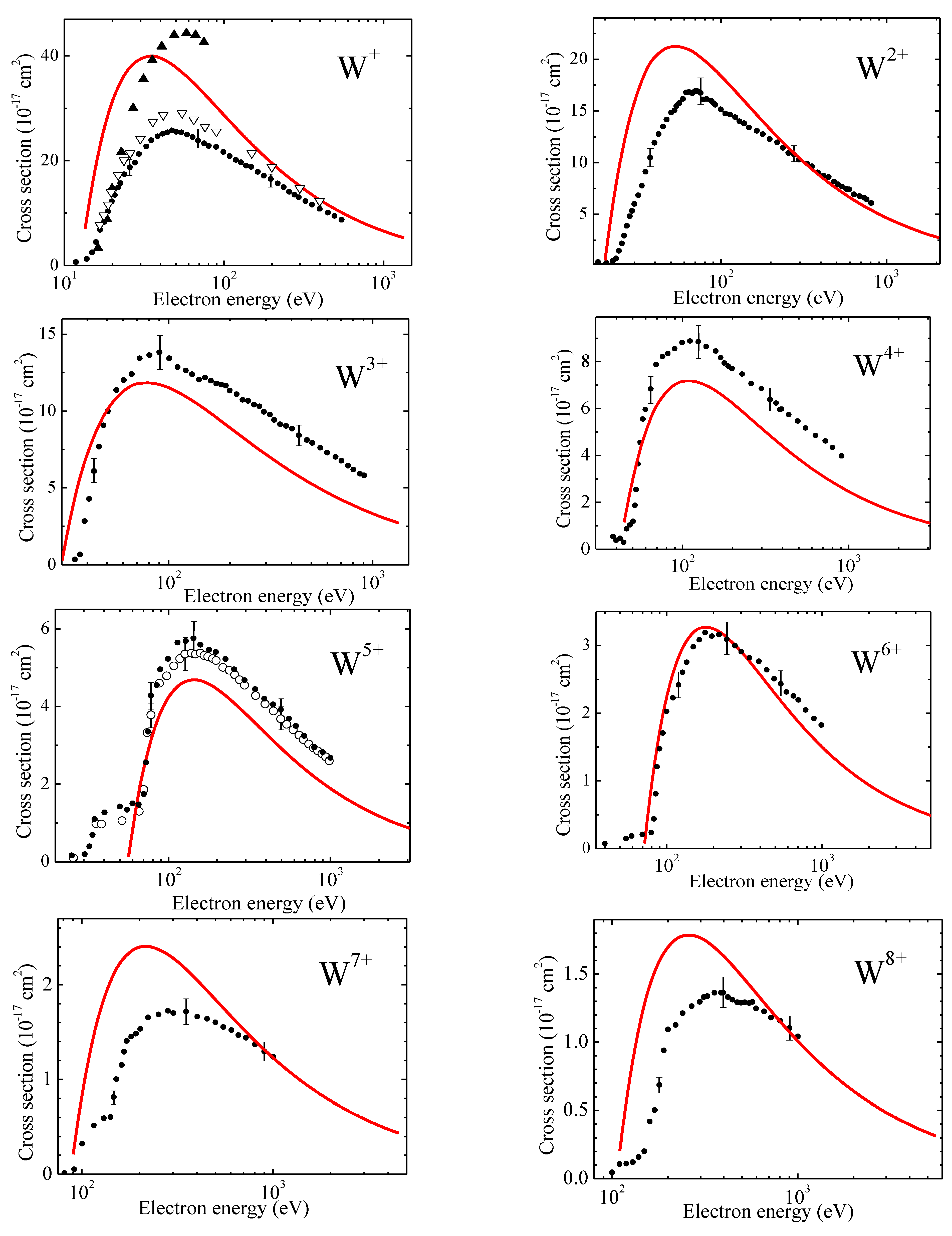
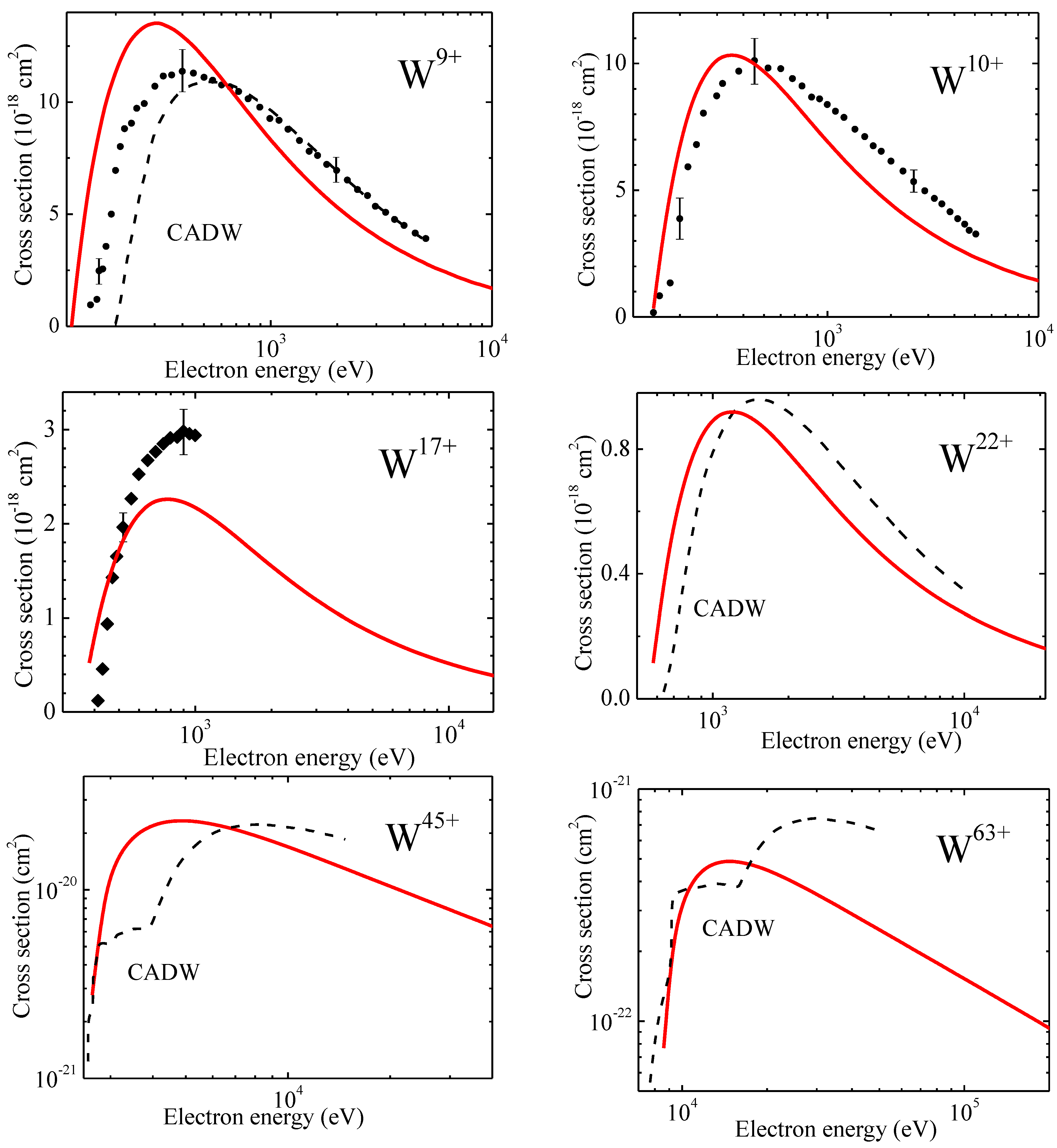
It is seen from the figure that there is quite reasonable agreement both with the experimental and theoretical data except highly ionized ions, where the number of bound electrons is not enough for application of the statistical methods.
The TFATOM code data for the electron impact ionization rates are presented in Figure 8 for ions Wk+ with k = 28,33,38,41,44,46,51,56 in comparison with the data of code ADPAK [1] and CADW modeling data [3] (compare with [15]). Here, one can see also see quite satisfactory agreements between the statistical model and the quantum mechanical calculations.
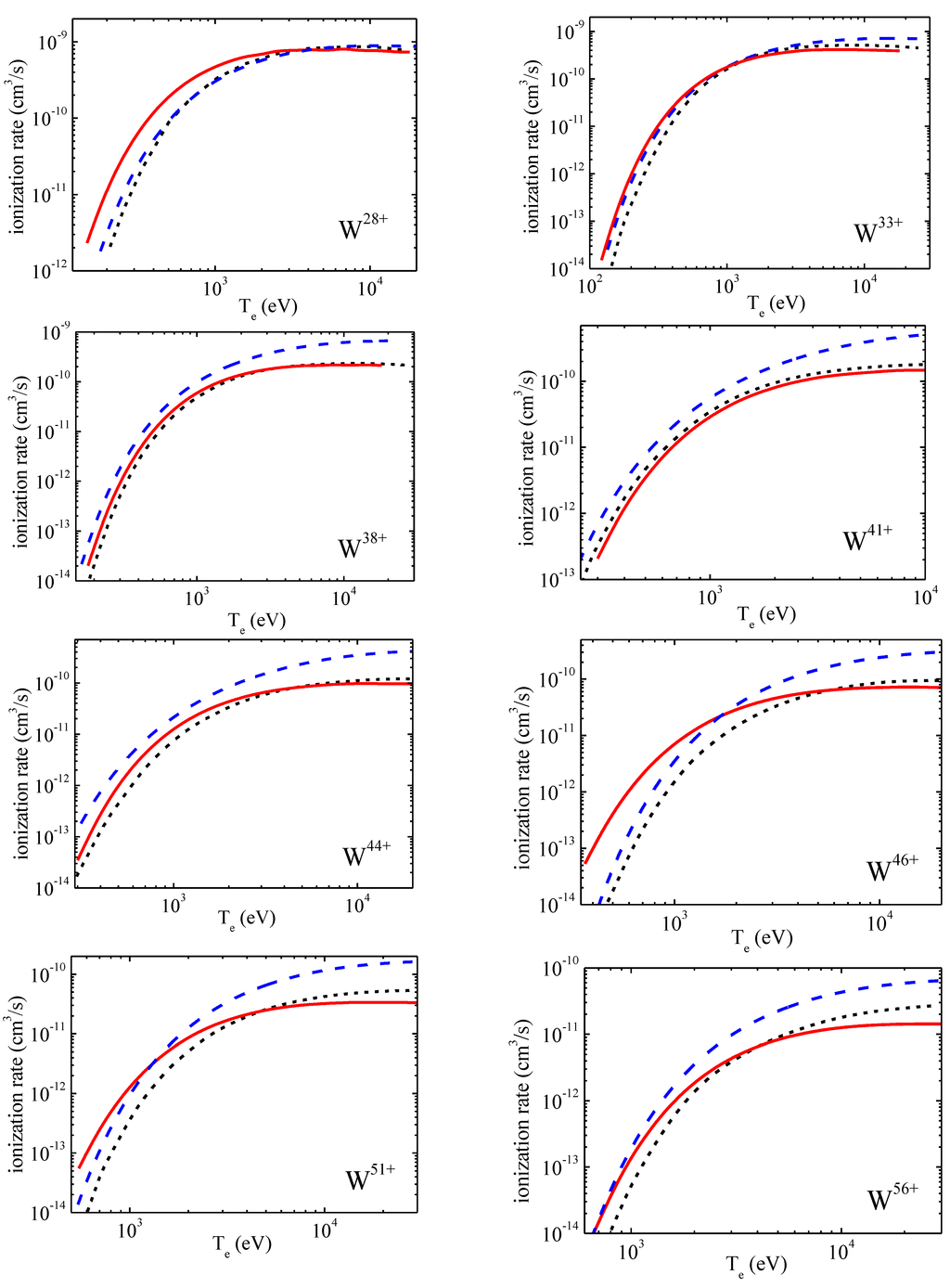
Figure 8.
Comparison of electron impact ionization rates of ions Wk+ with k = 28, 33, 38, 41, 44, 46, 51, 56: solid curves—present statistical model; dashed curves—code ADPAK data [1], short dashed curve—CADW modeling data [3].
Figure 8.
Comparison of electron impact ionization rates of ions Wk+ with k = 28, 33, 38, 41, 44, 46, 51, 56: solid curves—present statistical model; dashed curves—code ADPAK data [1], short dashed curve—CADW modeling data [3].
5.2. Radiative Losses
The calculations of radiative losses within the statistical LPF and EM models in corona approximation are presented in Figure 9 (see also [13]). Here, only the contribution into the radiation losses due to the collisional excitation of atoms by plasma electrons, described in the EQP Fermi approximation is presented.
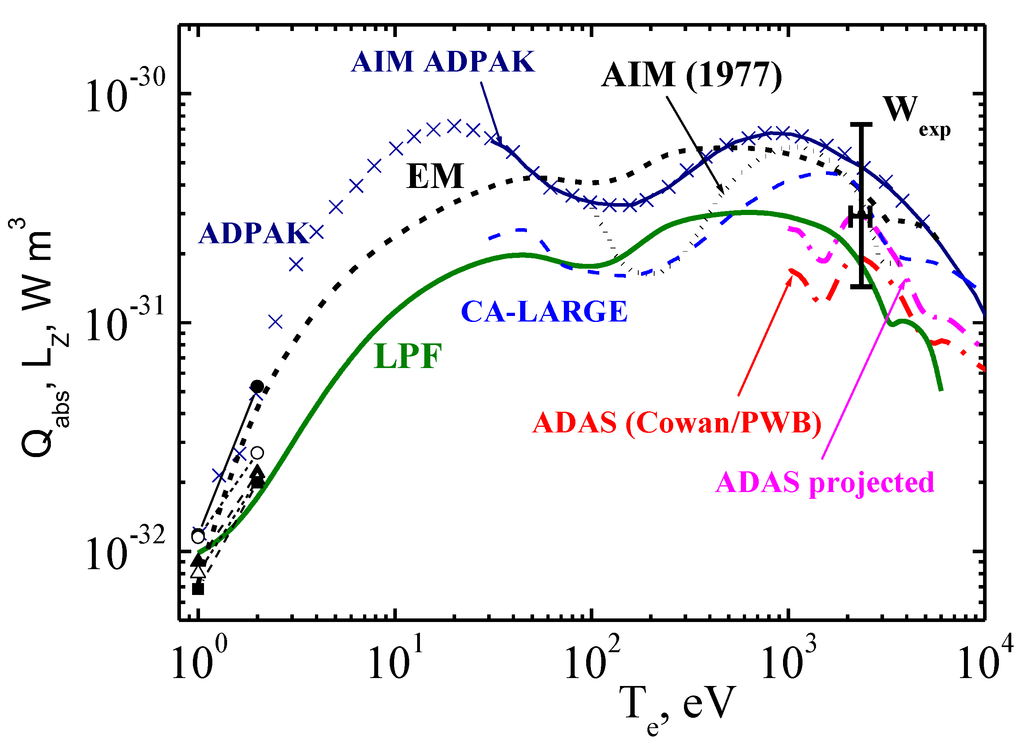
Figure 9.
Comparison of radiation losses on tungsten impurity within universal statistical approach (EM—electromagnetic method, LPF—method of local plasma frequency) with results of known codes versus plasma temperature: ADPAK—[6]; AIM ADPAK [7]; AIM—averaged ion model [20]; ADAS projected—[2,7]; ADAS COWAN/PWB—[2,7]; CA-LARGE—[4]; dark circles—ADPAK, light circles—CFG-AVE, dark triangles—FS-NOCI, light triangles—FS-CI, dark squares—FS-FOM data of radiative-collisional models from [18]; Wexp—experimental estimate of radiation losses value [4].
Figure 9.
Comparison of radiation losses on tungsten impurity within universal statistical approach (EM—electromagnetic method, LPF—method of local plasma frequency) with results of known codes versus plasma temperature: ADPAK—[6]; AIM ADPAK [7]; AIM—averaged ion model [20]; ADAS projected—[2,7]; ADAS COWAN/PWB—[2,7]; CA-LARGE—[4]; dark circles—ADPAK, light circles—CFG-AVE, dark triangles—FS-NOCI, light triangles—FS-CI, dark squares—FS-FOM data of radiative-collisional models from [18]; Wexp—experimental estimate of radiation losses value [4].
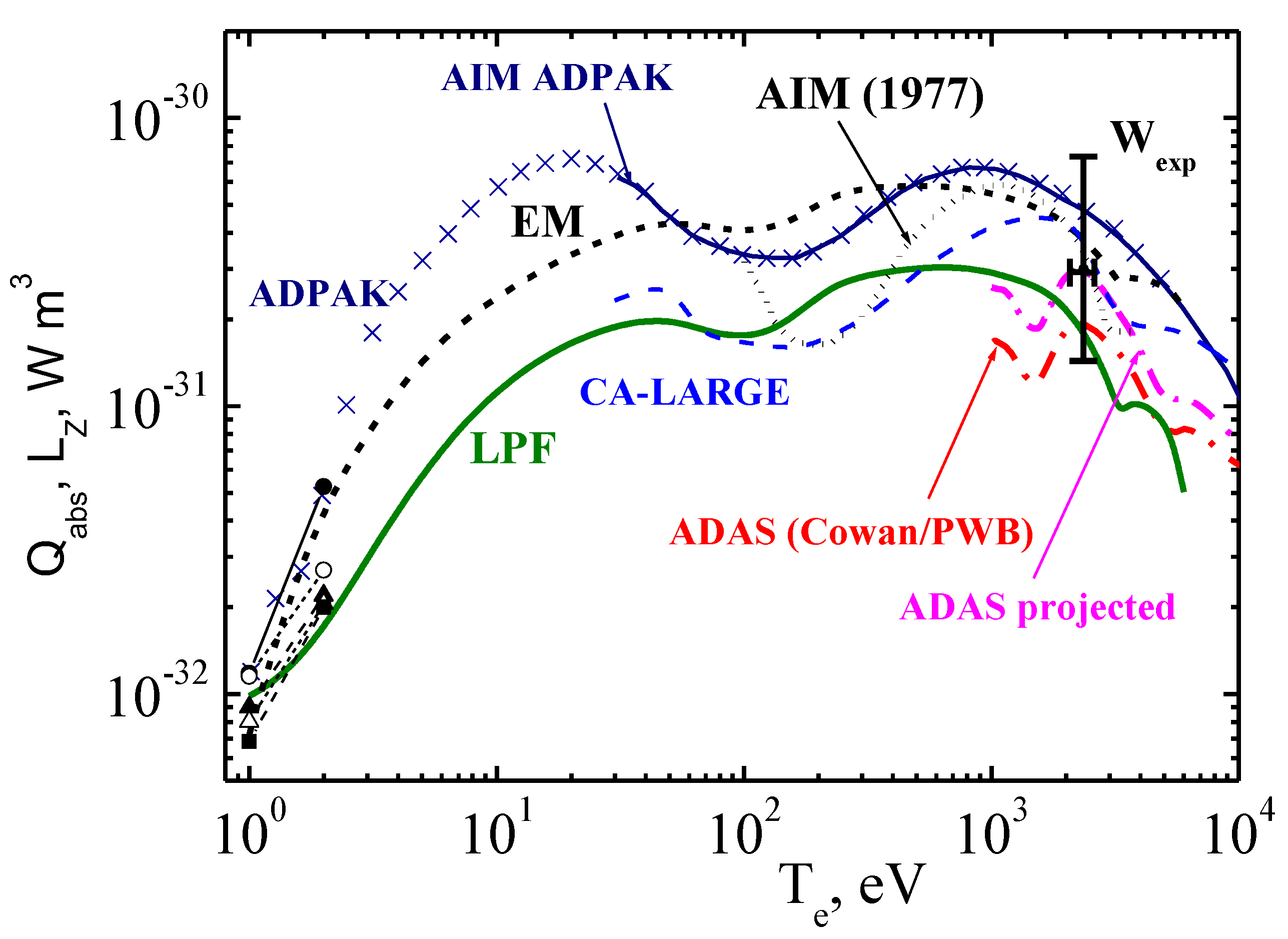
The calculations of radiation losses by the known numerical codes [2,4,6,7,18,20] are presented in Figure 9 as well. It is seen that the discrepancy between the results of these numerical calculations are of the same order as for the statistical models. The largest difference of the statistical models with the numerical calculations is observed in the region of small temperatures, where the excitation of the outer ion shells becomes essential, and the statistical model application starts to be problematic. At the same time, the interesting circumstance is the sufficiently good conformity of the results of detailed numerical calculations [18] and those due to the statistical model at lowest temperatures 1–2 eV.
Thus it is shown that the results of the universal statistical approach for the radiation losses are within the data scattering of known numerical codes [2,4,6,7,18,20], which use different approximations for the calculation of atomic structure and the electronic excitation cross-sections of complex ions.
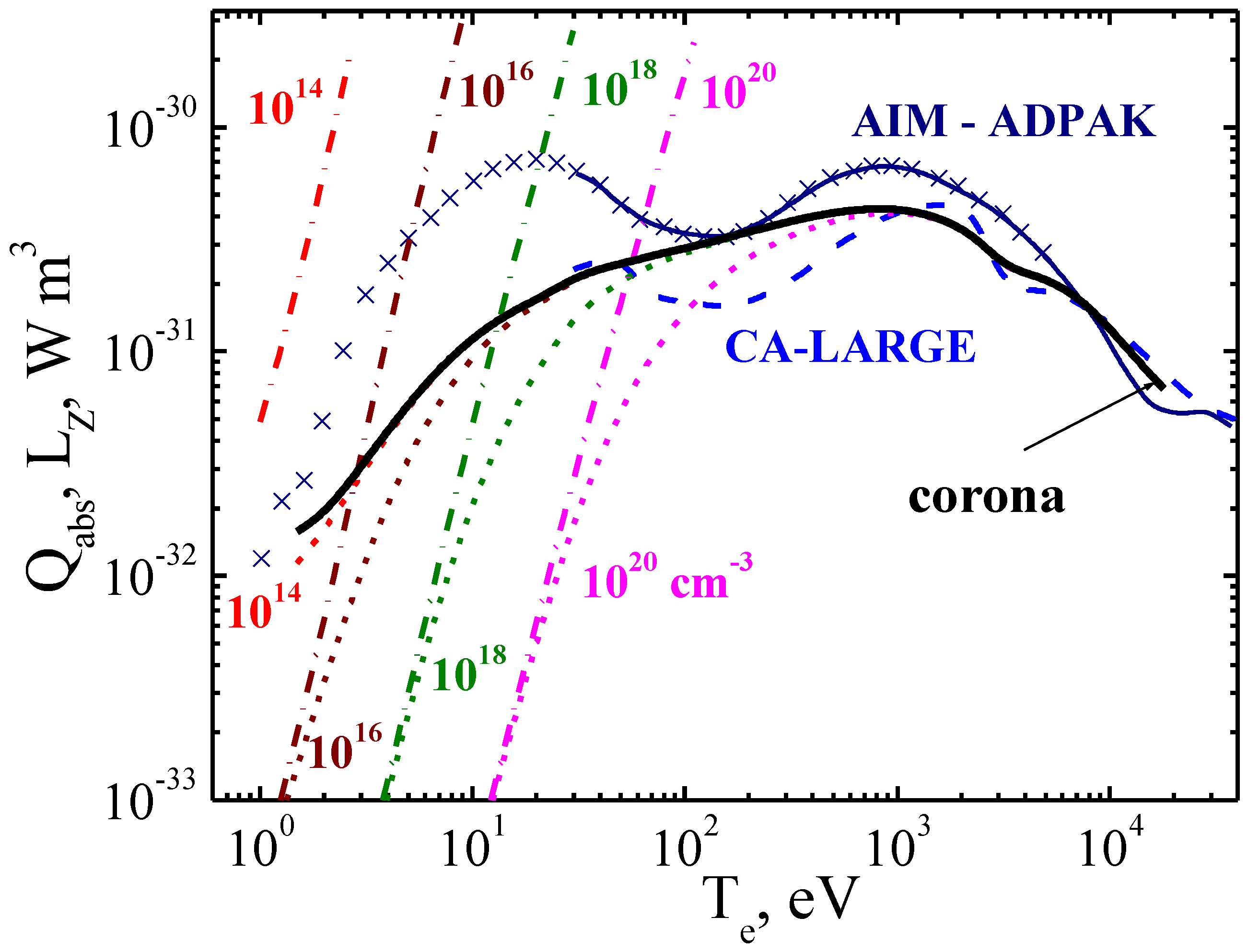
The calculated radiative losses in corona and Boltzmann approximations are shown in Figure 10. The calculations were made by the TFATOM code based on general expression for radiative losses (33). The Boltzmann limit is presented by the straight lines for the different electron densities. One can see that for tokamak plasma the conditions of Boltzmann limit are practically unrealizable, except maybe for the temperature range less than 1 eV.
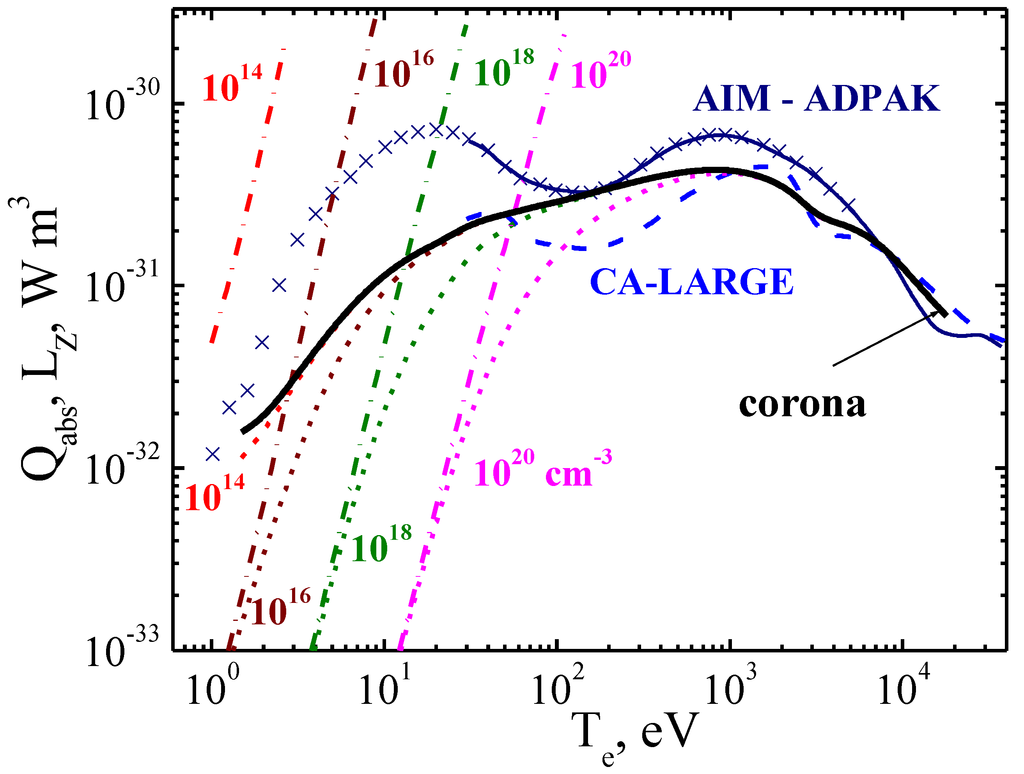
Figure 10.
Comparison of radiation losses on tungsten impurity within universal statistical approach Equation (33) (dashed lines, marked by values of electron density), accounting to transition between corona (solid line) and Boltzmann (straight dash-dotted lines) limits.
Figure 10.
Comparison of radiation losses on tungsten impurity within universal statistical approach Equation (33) (dashed lines, marked by values of electron density), accounting to transition between corona (solid line) and Boltzmann (straight dash-dotted lines) limits.
6. Conclusions
The consideration above demonstrates the efficiency of a statistical model for calculations of the atomic collisional-radiative processes with tungsten multielectron ions in plasmas. The results of the statistical approach have been tested by comparison with the experimental and code data for tungsten ions. The agreement between the statistical model and the available theoretical and experimental data is quite satisfactory in general. Some discrepancies are typical for charge states with the relatively small number of atomic electrons. The reasonable correspondence of the statistical model with the experimental data on the total electron impact single ionization cross-sections for multielectron ions seems to be due to the rather satisfactory implicit description of significant contribution of the excitation-autoionization cascades to the ionization processes. Indeed, these channels seem to be partly taken into account because of the collective nature of excitation and ionization processes in the statistical model. The larger discrepancies are observed for strongly ionized multiply charged ions, where the number of bound electrons is not enough for application of statistical description.
The numerical TFATOM code was developed for calculation of atomic radiative-collisional processes with multielectron tungsten ions in plasmas. The code is based on the general principles of atomic statistical theory, making it possible to calculate universally both the atomic structure characteristics and the probabilities of radiative-collisional processes in plasmas.
The results of the comparison with the other codes show that the developed TFATOM code is of the same accuracy as the codes based on more detailed description of atomic processes. The time-consuming efforts of the TFATOM code for orders of magnitude are less than for the other numerical codes. This makes it possible to apply the numerical TFATOM code as the suitable routine in constructing complex plasma modeling codes.
Acknowledgments
This work was partially supported by the Russian Foundation for Basic Research (project no. 13-02-00812) and by the Council of the President of the Russian Federation for Support of Young Scientists and Leading Scientific Schools (project no. NSh-3328.2014.2).
Author Contributions
Valery S. Lisitsa proposed the principal ideas of implementation of the collective atomic excitations notion for consideration of elementary processes with complex multicharged ions using the TF model together with the Local Plasma Frequency model, the transition between corona and Boltzmann equilibrium, suggested Coulomb approximation for determination of the effective charge using the LPFA resonance relation, took part in writing and editing the paper.
Alexander V. Demura elaborated the general notions and formalism of the statistical approach and consideration of elementary processes with complex multicharged ions using the TF model together with the Local Plasma Frequency model, performed derivation of equations for the radiation losses in general form, that allows to obtain limiting cases of the corona and Boltzmann equilibrium and the transition between them in the two state approximation, the equation for ionization cross-sections and rates, found and analyzed the corresponding literature, contributed essentially in writing and editing the paper.
Vladimir A. Shurygin found, analyzed, extracted and processed the data for description of TF model, ionization equilibrium, radiation losses and electron impact ionization cross-sections with ionization rates, performed programming, calculations, graphical representation of comparison of various results, created fitting of the statistical electromagnetic model data, contributed essentially in writing and editing the paper.
Mikhail B. Kadomtsev took part in elaborating general notions of the statistical approach, performed studies of limiting cases, using various approximations, and checked the results by numerical estimates from the first principles.
All authors contributed equally to the rest of the work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Asmussen, K.; Fournier, K.B.; Laming, J.M.; Seely, J.F.; Dux, R.; Engelhardt, W.; Fuchs, J.C.; ASDEX Upgrade Team. Spectroscopic investigations of tungsten in the EUV region and the determination of its concentration in tokamaks. Nucl. Fusion 1998, 38, 967–986. [Google Scholar] [CrossRef]
- Neu, R.; Dux, R.; Kallenbach, A.; Pütterich, T.; Balden, M.; Fuchs, J.C.; Herrmann, A.; Maggi, C.F.; O’Mullane, M.; Pugno, R.; et al. Tungsten: An option for divertor and main chamber plasma facing components in future fusion devices. Nucl. Fusion 2005, 45, 209–218. [Google Scholar] [CrossRef]
- Pütterich, T.; Neu, R.; Dux, R.; Whiteford, A.D.; O’Mullane, M.G.; ASDEX Upgrade Team. Modelling of measured tungsten spectra from ASDEX Upgrade and predictions for ITER. Plasma Phys. Control. Fusion 2008, 50, 085016. [Google Scholar] [CrossRef]
- Pütterich, T.; Neu, R.; Dux, R.; Whiteford, A.D.; O’Mullane, M.G.; Summers, H.P.; ASDEX Upgrade Team. Calculation and experimental test of the cooling factor of tungsten. Nucl. Fusion 2010, 50, 025012. [Google Scholar] [CrossRef]
- Groth, M.; Brezinsek, S.; Belo, P.; Beurskens, M.N.A.; Brix, M.; Clever, M.; Coenen, J.W.; Corrigan, C.; Eich, T.; Flanagan, J.; et al. Impact of carbon and tungsten as divertor materials on the scrape-off layer conditions in JET. Nucl. Fusion 2013, 53, 093016. [Google Scholar] [CrossRef]
- Summers, H.P. ADAS User Manual version 2.7. 2004. Available online: http://www.adas.ac.uk/manual.php (accessed on 10 May 2015).
- Post, D.; Abdallah, J.; Clark, R.E.H.; Putvinskaya, N. Calculations of energy losses due to atomic processes in tokamaks with applications to the International Thermonuclear Experimental Reactor divertor. Phys. Plasmas 1995, 2, 2328–2336. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshits, E.M. Course of Theoretical Physics; Pergamon Press: New York, USA, 1991; Volume Ш. [Google Scholar]
- Landau, L.D.; Lifshits, E.M. Course of Theoretical Physics; Pergamon Press: New York, USA, 1981; Volume IХ. [Google Scholar]
- Gombas, P. Die Statistische Theorie der Atoms und ihre Anwendungen; Springer: Wien, Austria, 1949. (In German) [Google Scholar]
- Brandt, W.; Lundqvist, S. Atomic Oscillations in the Statistical Approximation. Phys. Rev. 1965, 139, 612–617. [Google Scholar] [CrossRef]
- Vinogradov, A.V.; Tolstikhin, O.I. Plasma approach to the theory of photoabsorption and polarizability of complex atoms. Sov. Phys. JETP 1989, 69, 683–688. [Google Scholar]
- Demura, A.V.; Kadomtsev, M.B.; Lisitsa, V.S.; Shurygin, V.A. Statistical model of radiation losses for heavy ions in plasmas. JETP Lett. 2013, 98, 786–789. [Google Scholar] [CrossRef]
- Demura, A.V.; Kadomtsev, M.B.; Lisitsa, V.S.; Shurygin, V.A. Statistical model of electron impact ionization of multielectron ions. J. Phys. B 2015, 48, 055701. [Google Scholar] [CrossRef]
- Demura, A.V.; Kadomtsev, M.B.; Lisitsa, V.S.; Shurygin, V.A. Electron impact ionization of tungsten ions in a statistical model. JETP Lett. 2015, 101, 85–88. [Google Scholar] [CrossRef]
- Kogan, V.I.; Kukushkin, A.B.; Lisitsa, V.S. Kramers electrodynamics and electron-atomic radiative-collisional processes. Phys. Rep. 1992, 213, 1–116. [Google Scholar] [CrossRef]
- Fermi, E. Über die Theorie des Stoßes zwischen Atomen und elektrisch geladenen Teilchen. Z. Phys. 1924, 29, 315–327. [Google Scholar] [CrossRef]
- Abdallah, J., Jr.; Colgan, J.; Clark, R.E.H.; Fontes, C.J.; Zhang, H.L. A collisional-radiative study of low temperature tungsten plasma. J. Phys. B 2011, 44, 075701. [Google Scholar] [CrossRef]
- Kramida, A.E.; Reader, J. Ionization energies of tungsten ions: W2+ through W71+. Atomic Data Nucl. Data Tables 2006, 92, 457–479. [Google Scholar] [CrossRef]
- Post, D.E.; Jensen, R.V.; Tarter, C.B.; Grasberger, W.H.; Lokke, W.A. Steady-state radiative cooling rates for low-density high-temperature plasmas. Atomic Data Nucl. Data Tables 1977, 20, 397–439. [Google Scholar] [CrossRef]
- Stenke, M.; Aichele, K.; Harthiramani, D.; Hofmann, G.; Steidl, M.; Volpel, R.; Salzborn, E. Electron-impact single-ionization of singly and multiply charged tungsten ions. J. Phys. B At. Mol. Opt. Phys. 1995, 28, 2711–2721. [Google Scholar] [CrossRef]
- Stenke, M.; Aichele, K.; Hathiramani, D.; Hofmann, G.; Steidl, M.; Volpel, R.; Shevelko, V.P.; Tawara, H.; Salzborn, E. Electron-impact multiple ionization of singly and multiply charged tungsten ions. J. Phys. B At. Mol. Opt. Phys. 1995, 28, 4853–4860. [Google Scholar] [CrossRef]
- Pindzola, M.S.; Griffin, D.C. Electron-impact ionization of the tungsten atom. Phys. Rev. A 1992, 46, 2486–2488. [Google Scholar] [CrossRef] [PubMed]
- Spruck, K.; Becker, A.; Borovik, A.; Gharaibeh, M.F.; Rausch, J.; Schippers, S.; Müller, A. Electron-impact ionization of multiply charged tungsten ions. J. Phys. Conf. Ser. 2014, 488, 062026. [Google Scholar] [CrossRef]
- Rausch, J.; Becker, A.; Spruck, K.; Hellhund, J.; Borovik, A.; Huber, K.; Schippers, S.; Müller, A. Electron-impact single and double ionization of W17+. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 165202. [Google Scholar] [CrossRef]
- Loch, S.D.; Ludlow, J.A.; Pindzola, M.S.; Whiteford, A.D.; Griffin, D.C. Electron-impact ionization of atomic ions in the W isonuclear sequence. Phys. Rev. A 2005, 72, 052716. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
