Line-Shape Code Comparison through Modeling and Fitting of Experimental Spectra of the C ii 723-nm Line Emitted by the Ablation Cloud of a Carbon Pellet
Abstract
:1. Introduction
2. Description of the Atomic System and the Line-Shape Modeling Codes
2.1. Description of the Line-Shape Modeling Codes

| Terms | Energies Ei–Ek (cm−1) | σik (cm−1) | Sij(a.u) | fki(a.u.) | Line-Shape Code(s) |
|---|---|---|---|---|---|
| 3s 2S-3p 2P° | 116,537.65–131 731.80 | 15,194.15 | 0.715(18) | INTDPH SIMU | |
| 3p 2P°-3d 2D | 131,731.80–145 550.13 | 13,818.33 | 0.547(18) | INTDPH SIMU | |
| 3p 2P°1/2-3d 2D3/2 | 131,724.37–145,549.27 | 13,824.92 | 26.00(18) // 11.66(19) 13.84(20) | - - - | PPP-B WEAKZEE PPP-B * SCRAM |
| 3p 2P°3/2-3d 2D5/2 | 131,735.52–145 550.70 | 13,815.18 | 46.90(18) // 21.00(19) 33.31(20) | - - - | PPP-B WEAKZEE PPP-B * SCRAM |
| 3p 2P°3/2-3d 2D3/2 | 131,735.52–145 549.27 | 13,813.75 | 5.21(18) // 2.33(19) 5.56(20) | - - - | PPP-B WEAKZEE PPP-B * SCRAM |
2.2. Brief Description of the Atomic System Representing the Emitter
3. Cross-Comparison of the Line Profiles Computed with the Different Codes
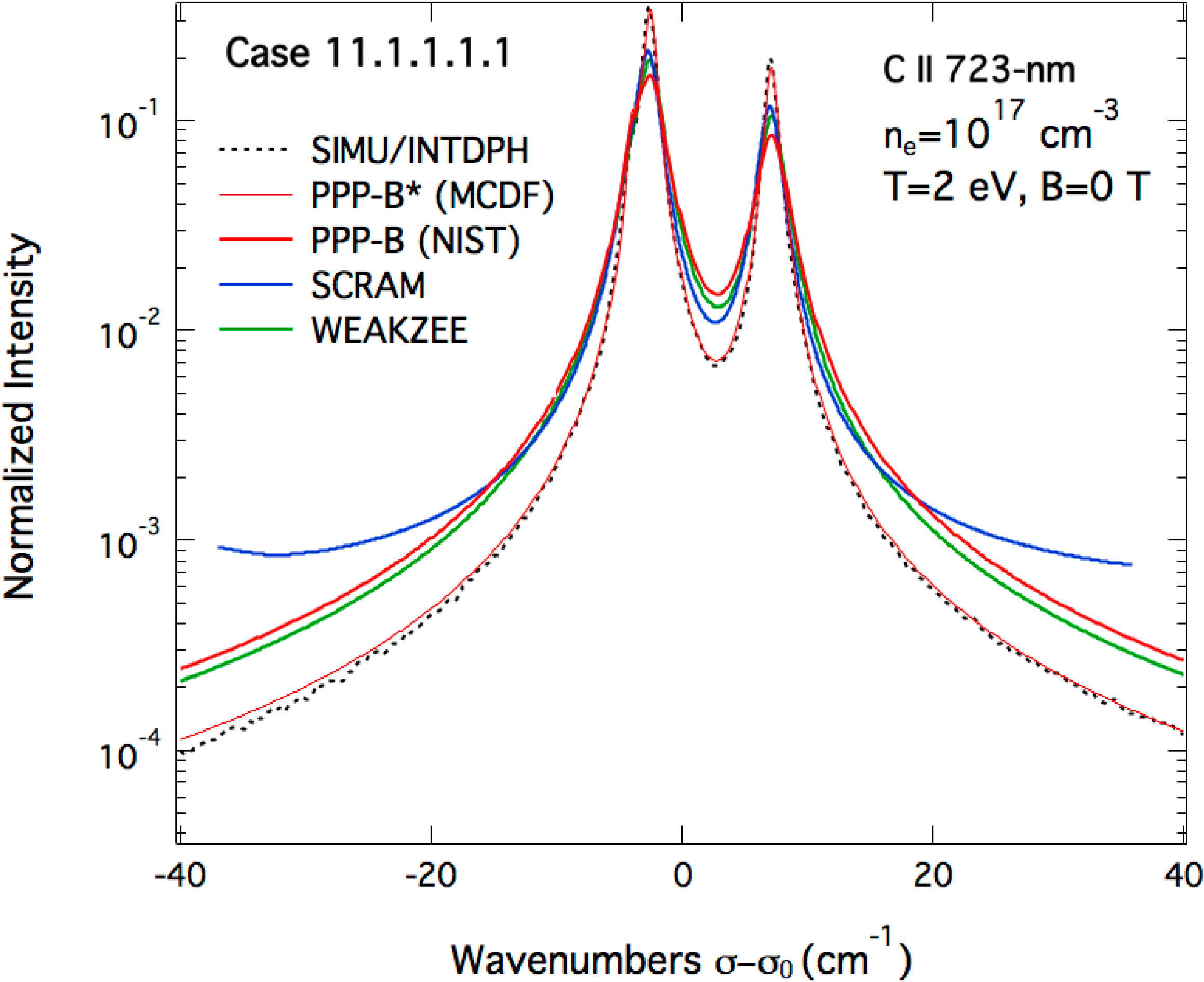
3.1. Magnetic Field-Free Case

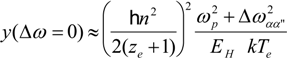

| Code | PPP-B | PPP-B * | SIMU/INTDPH | SCRAM | WEAKZEE |
|---|---|---|---|---|---|
| ∆σ/∆σ0 | 1.2 | 0.6 | 0.5 | 0.9 | 1.0 |
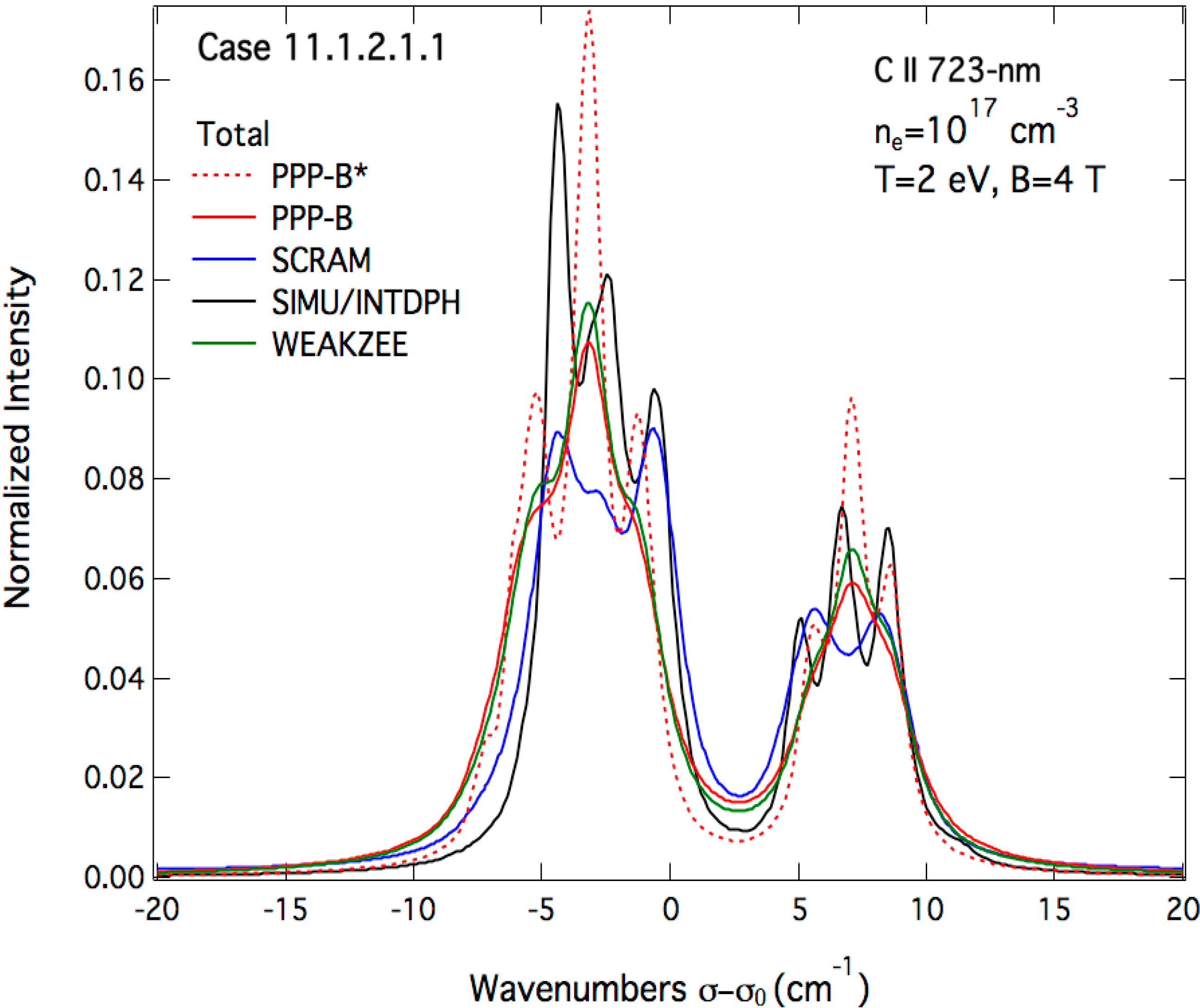
3.2. Magnetic Field Case

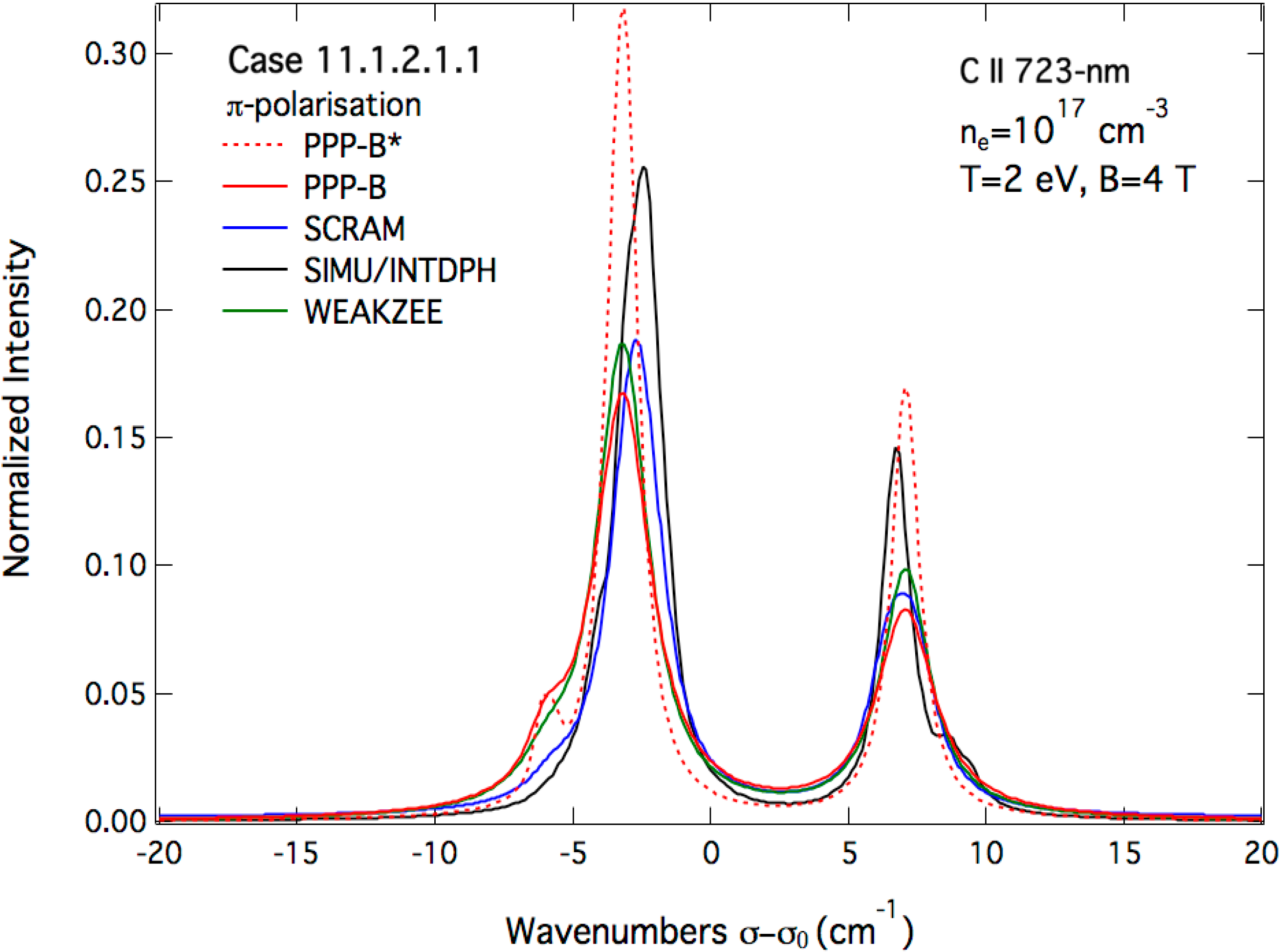
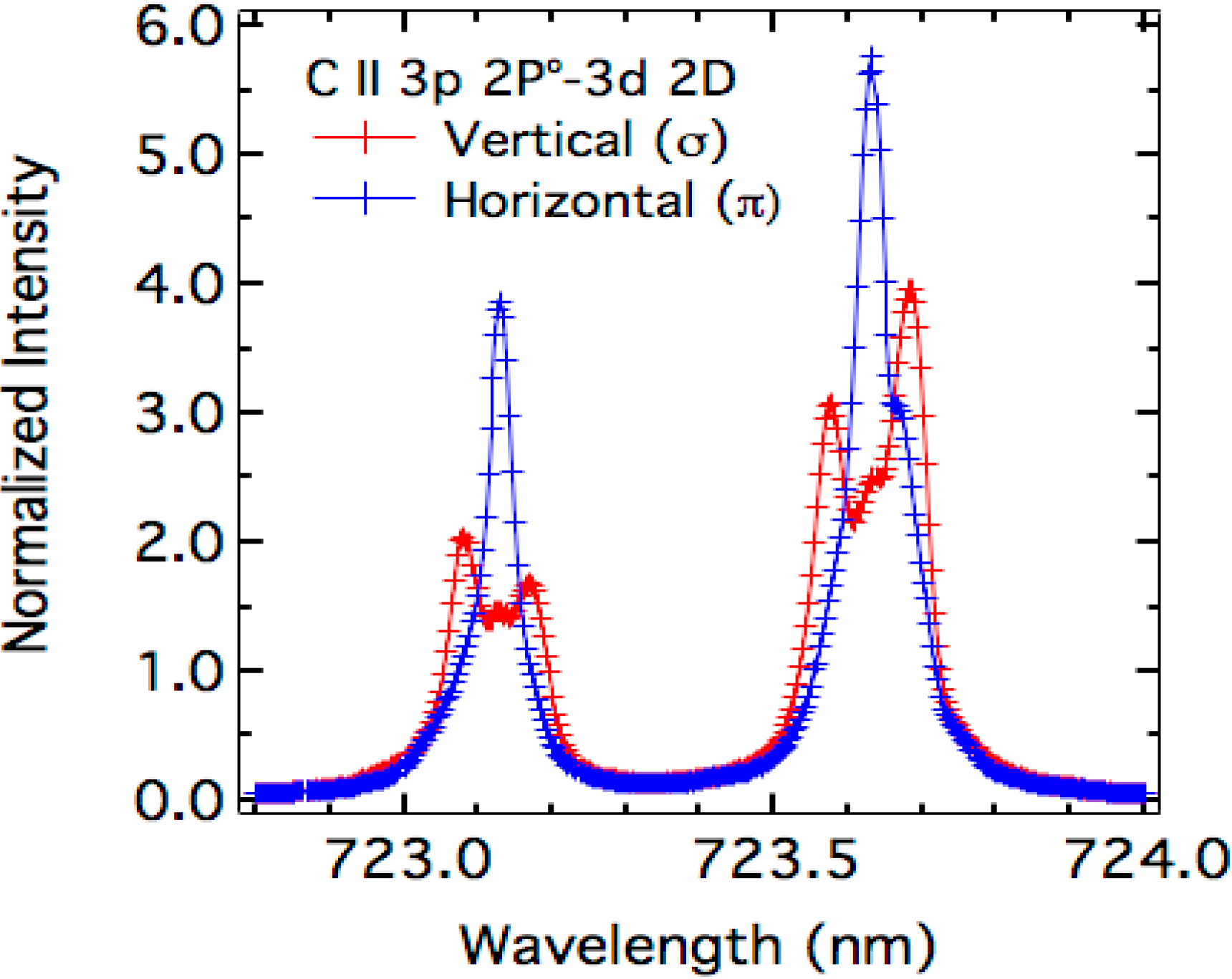
4. Comparison to the Experimental Spectra
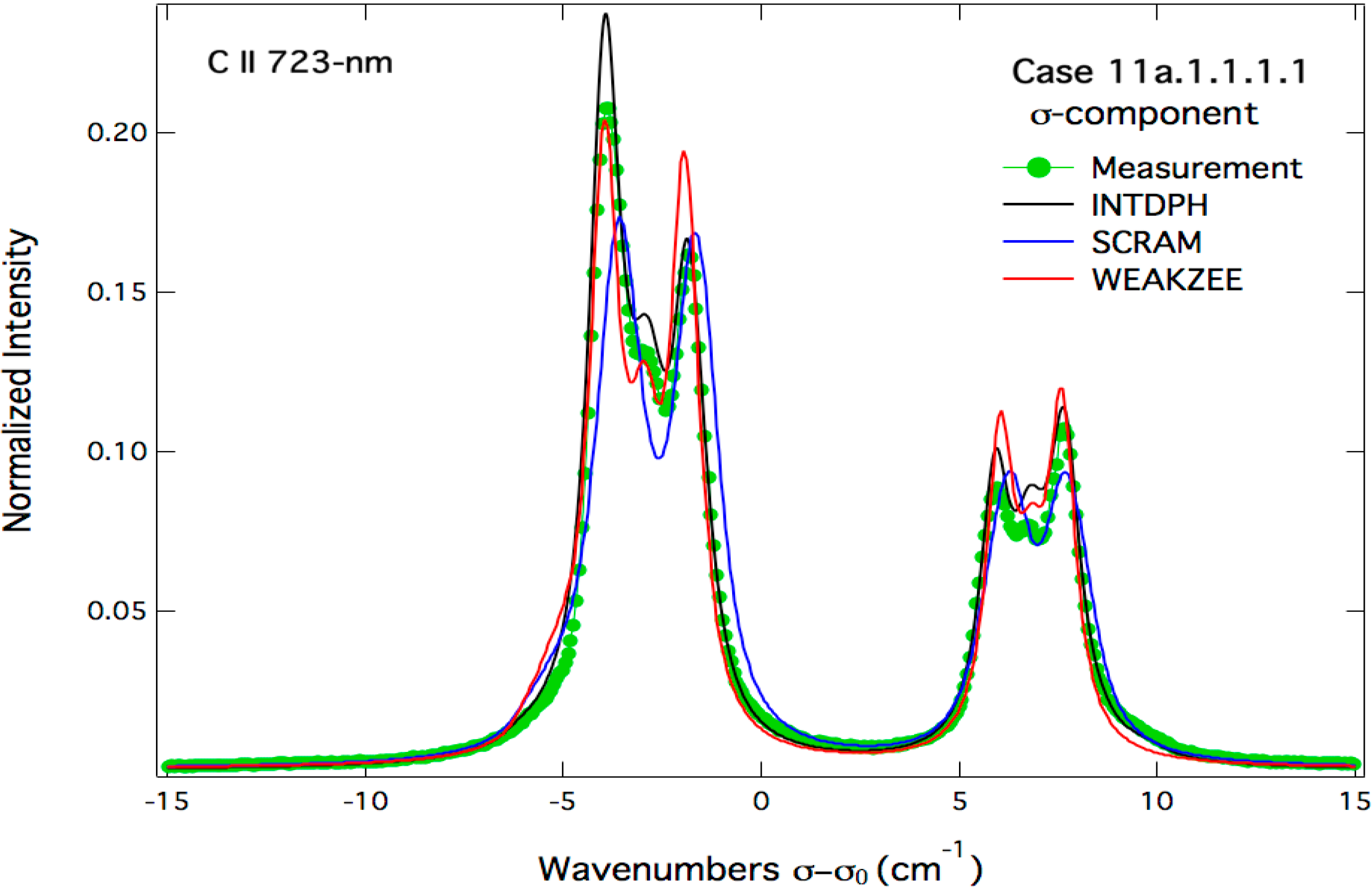
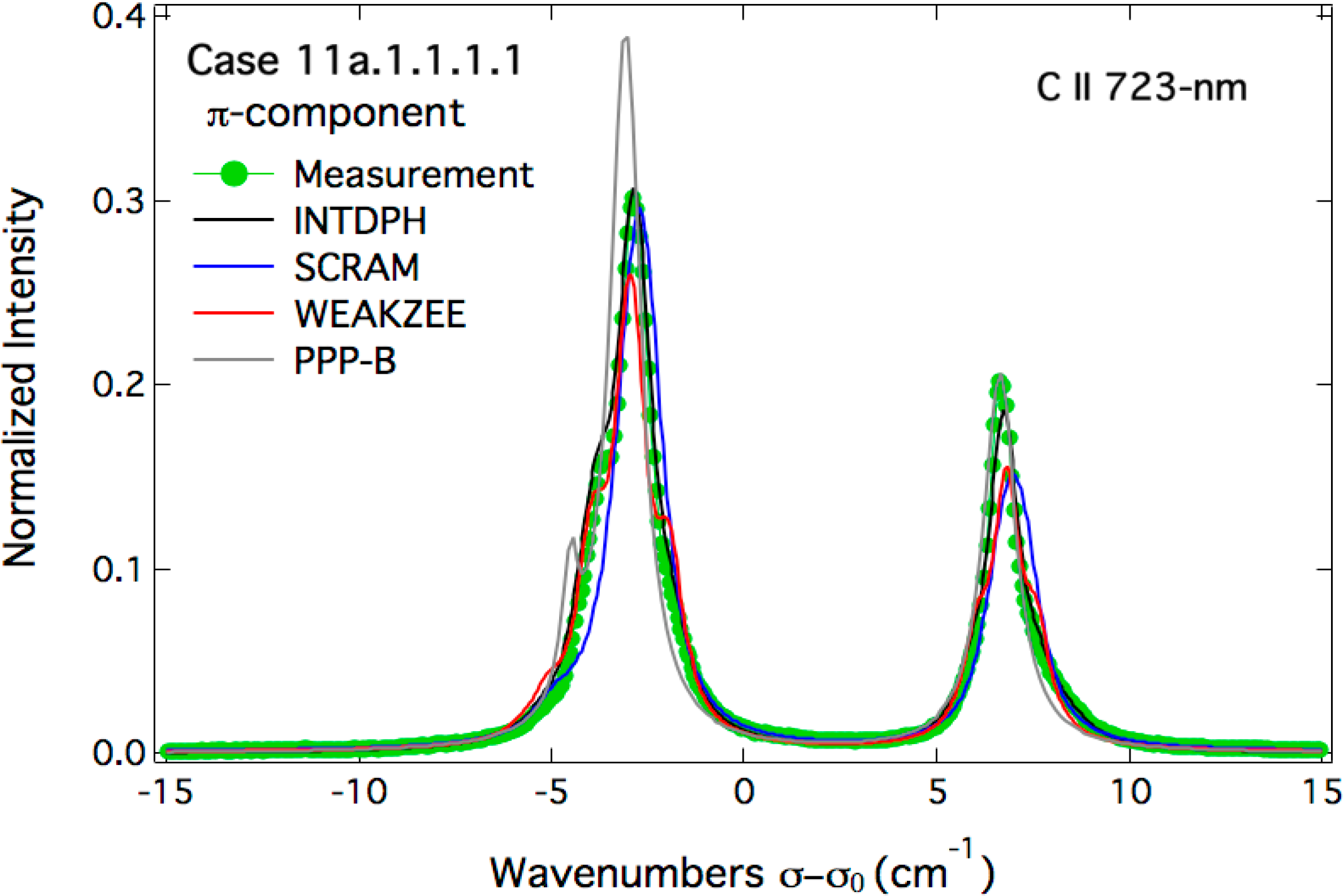
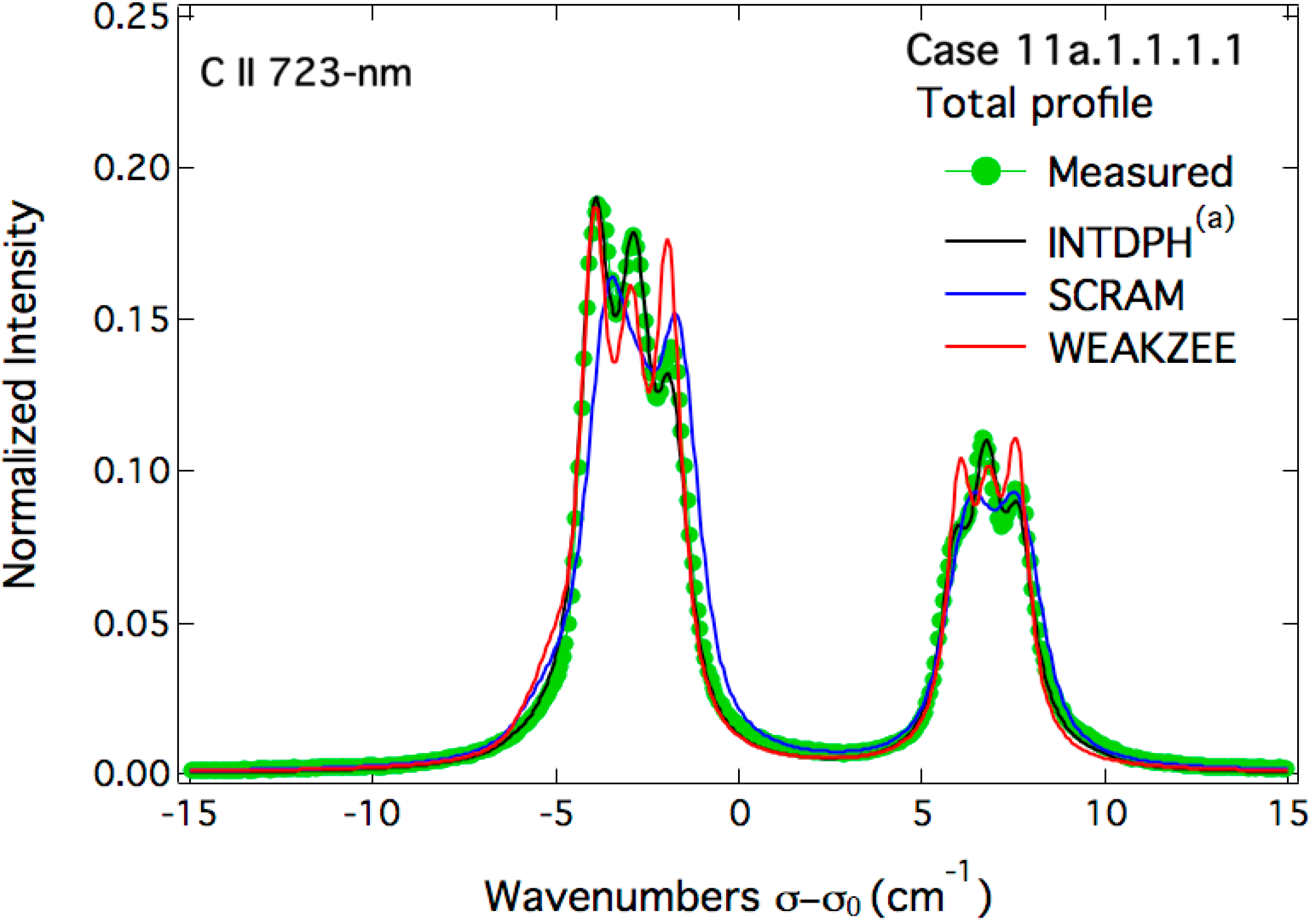
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Stambulchik, E. Review of the 1st Spectral line shapes in plasmas: Code comparison. High Energy Density Phys. 2013, 9, 528–534. [Google Scholar] [CrossRef]
- Goto, M.; Morita, S.; Koubiti, M. Spectroscopic study of a carbon pellet ablation cloud. J. Phys. B-At. Mol. Opt. Phys. 2010, 43, 144023. [Google Scholar] [CrossRef]
- Cvejić, M.; Gavrilović, M.R.; Jovićević, S.; Konjević, N. Stark broadening of Mg i and Mg ii spectral lines and Debye shielding effect in laser induced plasma. Spectrochim. Acta Part B: Atomic Spectrosc. 2013, 85, 20–33. [Google Scholar] [CrossRef]
- Condon, E.U.; Shortley, G.H. One-Electron Spectra. In The Theory of Atomic Spectra; Cambridge University Press: London, UK, 1964; pp. 149–157. [Google Scholar]
- Weissbluth, M. Static Fields in Atoms and Molecules; Student edition, Academic Press: New York, NY, USA, 1978; pp. 346–355. [Google Scholar]
- Ferri, S.; Calisti, A.; Mossé, C.; Mouret, L.; Talin, B.; Gigosos, M.A.; Gonzalès, M.A.; Lisitsa, V. Frequency-fluctuation model applied to Stark–Zeeman spectral line shapes in plasmas. Phys. Rev. E 2011, 84, 026407. [Google Scholar] [CrossRef]
- Talin, B.; Calisti, A.; Godbert, L.; Stamm, R.; Lee, R.W.; Klein, L. Frequency-fluctuation model for line-shape calculations in plasma spectroscopy. Phys. Rev. A 1995, 51, 1918. [Google Scholar] [CrossRef]
- Calisti, A.; Mossé, C.; Ferri, S.; Talin, B.; Rosmej, F.; Bureyeva, L.A.; Lisitsa, V.A. Dynamic Stark broadening as the Dicke narrowing effect. Phys. Rev. E 2010, 81, 016406. [Google Scholar]
- Sahal-Brechot, S.; Dimitrijević, M.S.; Moreau, N. Observatory of Paris, LERMA and Astronomical Observatory of Belgrade Stark-B Database. Available online: http://stark-b.obspm.fr (accessed on 16 April 2014).
- Mahmoudi, W.F.; ben Nessib, N.; Sahal-Bréchot, S. Semi-classical calculations of Stark broadeningimpact theory of singly-ionized carbon, nitrogen and oxygen spectral lines. Phys. Scr. 2004, 70, 142. [Google Scholar] [CrossRef]
- Sahal-Bréchot, S.; Dimitrijević, M.S.; ben Nessib, N. Comparisons and comments on electron and ion impact profiles of spectral lines. Balt. Astron. 2011, 20, 523–530. [Google Scholar]
- Hansen, S.B. Configuration interaction in statistically complete hybrid-structure atomic models. Can. J. Phys. 2011, 89, 633–638. [Google Scholar] [CrossRef]
- Hansen, S.B.; Bauche, J.; Bauche-Arnoult, C.; Gu, M.F. Hybrid atomic models for spectroscopic plasma diagnostics. High Energy Density Phys. 2007, 3, 109–114. [Google Scholar] [CrossRef]
- Stambulchik, E.; Maron, Y. A study of ion-dynamics and correlation effects for spectral line broadening in plasma: K-shell lines. J. Quant. Spectr. Rad. Transf. 2006, 99, 730–749. [Google Scholar] [CrossRef]
- Stambulchik, E.; Alexiou, S.; Griem, H.R.; Kepple, P.C. Stark broadening of high principal quantum number hydrogen Balmer lines in low-density laboratory plasmas. Phys. Rev. E 2007, 75, 016401. [Google Scholar]
- Stambulchik, E.; Maron, Y. Effect of high-n and continuum eigenstates on the Stark effect of resonance lines of atoms and ions. Phys. Rev. A 1997, 56, 2713–2719. [Google Scholar] [CrossRef]
- Tessarin, S.; Mikitchuk, D.; Doron, R.; Stambulchik, E.; Kroupp, E.; Maron, Y.; Hammer, D.A.; Jacobs, V.L.; Seely, J.F.; Oliver, B.V.; et al. Beyond Zeeman spectroscopy: Magnetic-field diagnostics with Stark-dominated line shapes. Phys. Plasmas 2011, 18, 093301. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team (2013). NIST Atomic Spectra Database (ver. 5.1). Available online: http://physics.nist.gov/asd (accessed on 9 May 2014).
- Grant, I.P.; McKenzie, B.J.; Norrington, P.H.; Mayers, D.F.; Pyper, N.C. An atomic multiconfigurational Dirac-Fock package. Comput. Phys. Commun. 1980, 21, 207–231. [Google Scholar] [CrossRef]
- Gu, M.F. The Flexible Atomic Code. Can. J. Phys. 2008, 86, 675–689. [Google Scholar]
- Calisti, A.; Ferri, S.; Stamm, R.; Talin, B.; Lee, R.W.; Klein, L. Discussion of the validity of binary collision models for electron broadening in plasmas. J. Quant. Spectrosc. Radiat. Transf. 2000, 65, 109–116. [Google Scholar] [CrossRef]
- Alexiou, S. Collision operator for isolated ion lines in the standard Stark-broadening theory with applications to the Z scaling of the Li isoelectronic series 3P-3S transition. Phys. Rev. A 1994, 49, 106–119. [Google Scholar] [CrossRef]
- Griem, H.R.; Blaha, M.; Kepple, P.C. Stark-profile calculations for Lyman-series lines of one-electron ions in dense plasmas. Phys. Rev. A 1979, 19, 2421–2432. [Google Scholar] [CrossRef]
- Calisti, A.; Khelfaoui, F.; Stamm, R.; Talin, B.; Lee, R.W. Model for the line shapes of complex ions in hot and dense plasmas. Phys. Rev. A 1990, 42, 5433–5440. [Google Scholar] [CrossRef]
- Alexiou, S.; Dimitrijević, M.S.; Sahal-Brechot, S.; Stambulchik, E.; Duan, B.; Gonzalez-Herrero, D.; Gigosos, M.A. The Second Workshop on Lineshape Code Comparison: Isolated Lines. Atoms 2014, 2, 157–177. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Koubiti, M.; Goto, M.; Ferri, S.; Hansen, S.B.; Stambulchik, E. Line-Shape Code Comparison through Modeling and Fitting of Experimental Spectra of the C ii 723-nm Line Emitted by the Ablation Cloud of a Carbon Pellet. Atoms 2014, 2, 319-333. https://doi.org/10.3390/atoms2030319
Koubiti M, Goto M, Ferri S, Hansen SB, Stambulchik E. Line-Shape Code Comparison through Modeling and Fitting of Experimental Spectra of the C ii 723-nm Line Emitted by the Ablation Cloud of a Carbon Pellet. Atoms. 2014; 2(3):319-333. https://doi.org/10.3390/atoms2030319
Chicago/Turabian StyleKoubiti, Mohammed, Motoshi Goto, Sandrine Ferri, Stephanie B. Hansen, and Evgeny Stambulchik. 2014. "Line-Shape Code Comparison through Modeling and Fitting of Experimental Spectra of the C ii 723-nm Line Emitted by the Ablation Cloud of a Carbon Pellet" Atoms 2, no. 3: 319-333. https://doi.org/10.3390/atoms2030319
APA StyleKoubiti, M., Goto, M., Ferri, S., Hansen, S. B., & Stambulchik, E. (2014). Line-Shape Code Comparison through Modeling and Fitting of Experimental Spectra of the C ii 723-nm Line Emitted by the Ablation Cloud of a Carbon Pellet. Atoms, 2(3), 319-333. https://doi.org/10.3390/atoms2030319