Abstract
Modeling the Stark broadening of spectral lines in plasmas is a complex problem. The problem has a long history, since it plays a crucial role in the interpretation of the observed spectral lines in laboratories and astrophysical plasmas. One difficulty is the characterization of the emitter’s environment. Although several models have been proposed over the years, there have been no systematic studies of the results, until now. Here, calculations from stochastic models and numerical simulations are compared for the Lyman-α and -β lines in neutral hydrogen. Also discussed are results from the Helium-α and -β lines of Ar XVII.
1. Introduction
Line shape analysis is one of the most important tools for plasma diagnostics, as it provides information on the underlying physical processes involved in the line formation. With the increasing number of applications in different areas of plasma physics, the modeling of line broadening from neutral or charged emitters has been in perpetual development and remains a keystone in plasma spectroscopy [1].
In the formation of a line shape, Stark broadening is the most computationally challenging contribution, since the main difficulty is to properly characterize the emitter environment. It involves a complex combination of atomic physics, statistical mechanics and detailed plasma physics [2]. In particular, it is well known that the quasi-static ion approximation can lead to discrepancies with experimental data near the line center. This happens whenever the electric microfields produced at the emitter by the surrounding ions fluctuate during the inverse half-width at half-maximum (HWHM) time scale. The first attempts to account for ion dynamics in theoretical models were done in the 1970s, followed by experimental proof (see the historic introduction in [3] and the references therein). Since then, several models based on stochastic or collisional approaches have been developed, together with numerical simulations ([4] and the references therein). Necessarily, their limit of applicability, accuracy and, thus, results differ from one another, and up to now, no systematic comparison have existed [5].
The purpose here is to present cross-comparisons of different models that account for the ion dynamics effect. The line shape formalism is briefly recalled in Section 2, which serves to introduce notation. The specifics of the various models and numerical simulations are also presented in this section. We review the simulations Euler–Rodrigues (ER)-simulation [6], HSTRK [7], HSTRK_frequency separation technique (FST) [8], SimU [9,10], Xenomorph [11] and the models QuantST.MMM (MMM—model microfield method) [12], quasicontiguous (QC)-frequency fluctuation model (FFM) [13], multi-electron line-shape (MELS) [14], multi-electron radiator line-shape (MERL) [15,16], PPP [17], ST-PST [18] and UTPP [19] that have been used for the present purpose. The ion dynamics effect on the hydrogen Lyman-α and -β lines is discussed in Section 3.1, demonstrating the difficulty of such modeling even for these well-known lines. In Section 3.2, results on helium-α and -β lines of Ar XVII produced by the two stochastic models (Boerker–Iglesias–Dufty (BID) [20] and FFM [4,21]) are discussed with the help of the numerical simulation (SimU). The reliability of such calculations is of interest in the diagnostics of inertial confinement fusion core plasma conditions. Conclusions are given in Section 4.
2. Theory, Models and Simulations
We recall that the line shape is given by:
where is the autocorrelation function of the radiator dipole operator , which can be expressed in Liouville space as:
where the double bra and ket vectors are defined as usual in Liouville space. Here, is the density operator for the emitter only at the thermodynamical equilibrium and is the bath averaged evolution operator of the emitter. l belongs to a measurable functional space, , which provides a statistical method for the calculation of average quantities. The main problem is to determine . One has thus:
- to find the time evolution of for a given microfield configuration, which means solving the following equation:where represents the Liouvillian of the unperturbed radiator and represents the Stark effect that connects the dipole operator to the microfield created by surrounding charged particles (including ions and electrons),
- and to average it over a statistical ensemble of the microfields .
In its general form, the problem cannot be treated analytically. Nevertheless, can be obtained by numerical simulation integrating Equation (3) on simulated sampling of microfield histories. Usually, such a calculation is split into two independent steps [3]. First, the plasma particle trajectories are obtained by a numerical solution of Newton’s equations of motion or an alternative method. Knowing the trajectory of each particle, the electric fields at the emitter are evaluated and stored to be used in the second step. Then, the line shape simulation follows: a step-by-step integration of Equation (3) is performed using these field histories. The evolution operator of the emitter is calculated, and the whole procedure is repeated several times in order to average over a representative sample set of independent perturbing field histories . As a result, is given by:
and the line shape is obtained by a Fourier transform of . Although all line shape simulations are based on the same scheme, we will see in the next section that they can differ slightly depending on the details of the models.
Alternatively, efficient analytical models based on fundamental assumptions and approximations have been developed [1]. In the standard theory (ST), the line shape calculation is based on the separation between the ions and the electrons due to the radically different dynamical properties of the microfields they create. Indeed, the typical fluctuation rate of the electric field created by perturber species p with a velocity relative to the center of mass and a density is defined by:
where is a typical interparticle distance. Assuming equal temperature for ions and electrons and plasma neutrality, one has [3]:
Thus, the perturbation due to the electrons (with reduced mass ) is nearly two orders of magnitude faster than that of ions (with reduced mass and charge ). This allows for treating the electrons and the ions in a different way. The fast electrons are assumed to perturb the emitter by means of collisions, treated in the impact approximation, and the slow ions are assumed to be quasi-static. This results in a quantum-emitter system perturbation operator , containing a non-Hermitian homogeneous electron-impact broadening contribution and the ion microfield interaction , which has to be numerically averaged with a static-field probability distribution , or because of isotropy, with . The later can be calculated numerically in the ideal gas limit for perturbing ions [22] or using more sophisticated models that account for ion correlations [23]. Using the set of above assumptions, the quasi-static line shape is written as:
in which the resolvent operator is given by:
Although the electrons are often well described within the impact approximation, a quasi-static treatment of the ions can lead to large errors for plasma conditions, such as the ion microfields fluctuate during the inverse HWHM time scale. In the next section, we briefly review the simulations and the models that have been developed to account for the ion dynamics effect and that have been used for the present cross-comparisons.
2.1. The Numerical Simulations
The results from four numerical simulation codes based on different models have been submitted. They differ either in the way they model the motions of the plasma particles or in the procedure for the integration of the Schrödinger equation.
In the ER-simulation, the simulated plasma is an electrically neutral ensemble of statistically independent charged particles made of ions and electrons moving along straight line trajectories within a spherical volume. An emitter is assumed to be placed at the center of such a box. The temporal evolution of the whole system is measured along a discrete time axis from zero to a definite number of times of a fixed increment. Every temporal state is given by the set of values of the positions and velocities of the particles in the system. At every time step, the electric field produced by ions and electrons is calculated using Coulomb’s law or a Debye-screened field. This electric field is an input to the Schrödinger equation that computes the emitter time evolution operator. For hydrogen and when the no-quenching approximation is considered, the atom state is described with the Euler–Rodrigues parameters [24].
The HSTRK and HSTRK_FST codes also use the Gigosos–Cardeñoso approach [25]. Both codes rely on the Hegerfeld–Kesting–Seidel method of collision-time statistics [26] and compute . Depending on the appropriate option, HSTRK can do an electron only, ion only or joint simulation, but one can also do combinations, e.g., electron simulation and quasi-static ions or impact electrons and ion simulation. For the Fourier transform, if a long-time exponential behavior is detected for times , then the contribution to the Fourier transform of the () region is computed analytically using the detected exponential decay and added to . τ is determined via start-up runs, e.g., a run with a small number of configurations is done to obtain a rough idea of the HWHM and τ is adjusted to cover at least a number of inverse HWHMs. The integral is done by Filon’s rule [27].
HSTRK_FST implements the frequency separation technique, which first identifies the “impact” phase space of ion perturbers (e.g., impact parameters and velocities), which produce a width much less (in these runs, “much less” was 10-times less) than the field fluctuation frequency. This meant:
where the HWHM is computed by including all ion perturbers with impact parameter ρ and velocity . Hence, the calculation is essentially the same, except that only slow ions are included in the simulation. The obtained from the simulation of these slow ions is then multiplied by , and the Fourier transform is taken as in HSTRK. The use of a pure exponential form for the rapidly fluctuating (impact) part is a consequence of using the complete collision assumption for solving the impact part [28,29] and results in a that is not correct for very short times. This is manifested in the (far) wing behavior of the HSTRK_FST profiles and can be remedied by using the incomplete collision formulas of the above-cited analytical solutions.
SimU is a combination of two codes: a molecular dynamics (MD) simulation of variable complexity and a solver for the evolution of an atomic system with the MD field history used as a (time-dependent) perturbation. A technical difference from other numerical simulation methods is the way the spectrum is calculated. Instead of employing the dipole autocorrelation function via Equation (1), SimU calculates the Fourier transform of the dipole matrix:
and then uses it directly instead of :
where is the light polarization direction and each initial state i is assigned a population factor . Similarly to other methods, this procedure is repeated many times and averaged (cf. Equation (4)).
The recently developed code, Xenomorph, is based on the models of Gigosos and González [30], where a straight line assumption is made. A general Schrödinger solver described in [31] is used to obtain the eigenvalues and eigenvectors at every time step of the simulation. The emitter time evolution operator is then evaluated:
and is used to obtain the dipole matrix. The Fourier transform of the latter is computed to obtain the line shape function, as is done in SimU (cf. Equations (10) and (11)).
2.2. The Models
The main difficulty in introducing the ion dynamics in the Stark line shape calculations is to develop a model that provides a sufficiently accurate solution of the evolution Equation (2) assuming an idealized stochastic process that conserves the statistical properties of the “real” interaction between the microfields and the radiating atom.
A successful model developed for neutral emitters—the model microfield method (MMM), due to Brissaud and Frisch [32,33]—involves stochastic fields that are constant in a given time interval and suddenly jump from one value to the next one at random times. The amplitudes of the field sequences are determined in order to be consistent with the static properties of the microfield, i.e., the static-field probability distribution . The jumping frequency has to be chosen properly in order to reproduce the dynamics properties of the microfields represented by their autocorrelation function . In QuantSt.MMM, MMM (for ions) is combined with a quantum-statistical approach to calculate pressure broadening due to plasma electrons. The perturbation by electrons is considered to second order in the potential [34,35].
MELS and MERL are based upon the BID model. The latter derives from the MMM, but its formulation is based on statistical mechanics [36] and provides a unified description of radiative and transport properties for charged emitters [20]. The stochastic line shape is written as:
in which the resolvent is given by:
The jumping frequency is chosen as:
where the two parameters and τ are defined in this model by the low- and high-frequency limits of the momentum autocorrelation function. Here, τ is assumed to be null.
Another approach is the frequency fluctuation model (FFM), on which the PPP code and, recently, the QC-FFM code rely. The latter is a hybrid model using the quasi-contiguous approximation [37] for H-like transitions and the FFM for modeling the microfield dynamics effect. The FFM relies on a different idealization of the stochastic process than MMM and BID. Here, the quantum system perturbed by a time-dependent microfield behaves like a set of field-dressed two-level transitions (SDT) subject to a collision-type mixing process. More precisely, the fluctuation mechanism of these SDT obeys a stationary Markov process defined by the instantaneous probability of states ( being the intensity of the SDT, j) and the transition rates between these states , where and .
The typical fluctuation rate of the electric field, given by Equation (5), is used. Working in the Liouville space of the dressed two-level radiators, the line shape is written as [38]:
with the resolvent:
where is the Liouville operator involving the transition energies of the SDT () and are the matrix elements of the dipole moment for the SDT. Due to the particular form of the matrix of transition rates , the dynamic line shape is written as [4]:
Despite the fact that the two stochastic models lead to different functional forms, it follows that both BID and FFM recover the static limit for in Equation (14) and for in Equation (18). In the opposite limit, both models recover the fast fluctuation limit () that should approximate the “no ions” profile. However, BID recovers the impact limit in the line center whenever ν is large, while the FFM does not (see [39] for a more detailed discussion). We note that QC-FFM uses the FFM approximation for ions and electrons alike. For the latter, correctly approaching the impact approximation in the fast fluctuation limit becomes especially important. To this end, a modification to the effective fluctuation rate was introduced:
where is an empirically obtained constant (for details, see [13]).
Two other models based on the collisional approach have been used, too. The ST-PST model is based on the standard theory with a number of options. Specifically, apart from the pure ST results, ST-PST can (and by default does) also compute the results of ST with penetrating collisions correctly accounted for analytically [18]. In addition, an FST-FFM calculation is also done [8]: first, an Ω is determined, exactly as described above for HSTRK_FST. Next, the FFM is applied to the field that excludes the fast, impact part. Last, the two profiles are convolved. As a result, the impact limit is correctly built in and recovered, hence extending the FFM validity without sacrificing its speed. Note, however, that with the current FST implementation, which uses the completed collision assumption for the impact phase space, the far wings are not accurate, as already discussed.
The UTPP code is devoted to the calculation of hydrogen line shapes in regimes where the impact approximation for ions is reasonably accurate. Such a regime is attained for lines with a low principal quantum number in magnetic fusion experiments in the absence of Doppler broadening (Doppler-free line shape models were required for radiation transport simulations, e.g., [40]). In UTPP, a line shape is calculated using the following formula:
where and is a collision operator calculated in a framework similar to that used in the Voslamber unified theory (Bogoliubov-Born-Green-Kirkwood-Yvon (BBGKY) hierarchy), but here adapted to ions [19]. The main advance with respect to the unified theory is that the collision operator accounts for the finite lifetime of the atom during each collision; this lifetime yields an effective range for the action of the microfield of the order of , where is a typical matrix element of the collision operator (see the discussion in [41]). This model (and its adaptation to electrons) does not lead to a divergent collision operator if the Debye length is assumed infinite, which is in contrast to standard hydrogen models (see [42]); this makes it suitable for the presented cases, provided the perturbing species under consideration is strongly dynamic.
3. Comparisons and Discussion
To test the accuracy of the different numerical codes based either on stochastic and collisional models or numerical simulations, calculations for standardized case problems were carried out and analyzed [5]. A preselected set of transitions on a grid of electron densities () and temperatures () have been proposed, and for each case, the atomic and plasma models have been specified. In this way, various contributions that can affect the Stark broadened line shape, such as the influence of particle correlations on electric microfields, the effects of external fields, the high-n merging with continuum or the satellite broadening, have been investigated. For the present purpose, we will only focus on cases where the ion dynamics effect was studied.
3.1. Hydrogen Lyman-α and Lyman-β Lines
The following examples consider the hydrogen Lyman-α and Lyman-β lines in an ideal plasma consisting of protons for electron densities cm and temperatures eV. These cases are not necessarily practical, but permit basic comparisons to assess the influence of ion dynamics on the line profiles. Here, only pure ionic linear Stark effect is considered ( interactions are ignored) and the fine structure is not taken into account. The concept of ideal plasma means that unscreened particles moving along straight path trajectories are considered in the numerical simulations, and the Holtsmark static-field distribution function [22] is used in the models.
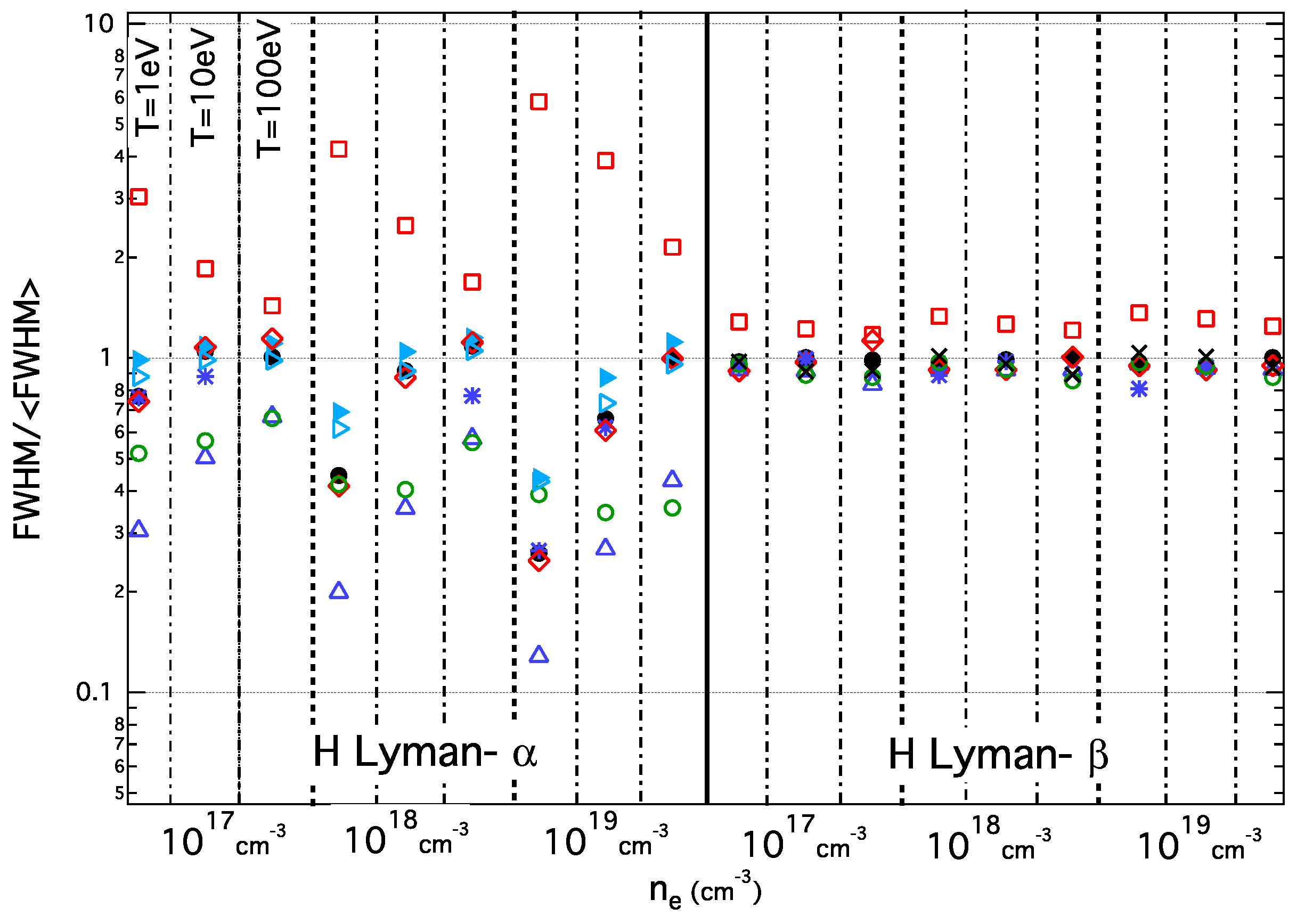
An overall comparison of the results is presented in Figure 1. For each subcase (determined by a combination of ) and for each code, ratios between the full-width at half-maximum (FWHM) and an average of FWHM of all submitted results have been evaluated [5]:
The graph is divided in two regions: the left side corresponds to results for the Lyman-α line and the right side to the Lyman-β line. Each region is divided into three sub-regions that correspond to the three densities chosen. Finally, in each sub-region, each set of results corresponds to the temperatures, eV, respectively. For the Lyman-α case, the results present a large dispersion, deviating from the average by more than a factor of five in each direction. In contrast, the scatter for the Lyman-β shows a rather good agreement between the codes. In fact, these two lines present a completely different behavior concerning the ion dynamics effect.
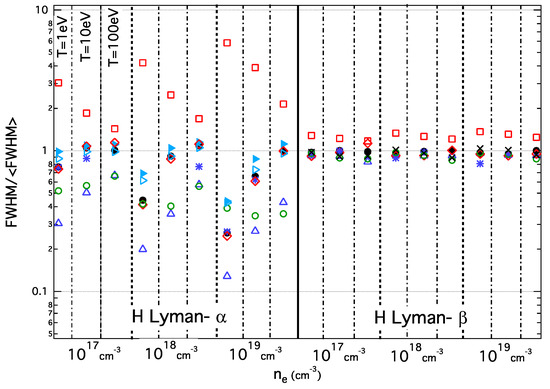
Figure 1.
Overall comparison of the workshop results of the ion dynamics effect on Lyman-α and -β hydrogen lines. For each subcase, i.e., different pairs of , the scatter of ratios between the different results and an average value is plotted. The different symbols correspond to: (black dot) SimU; (red square) UTPP; (blue triangle) PPP; (blue asterisk) Xenomorph; (cyan open triangle) HSTRK; (cyan triangle) HSTRK_FST; (red diamond) ER-simulation; (green circle) QuantST.MMM; (black cross) QC-FFM.
Figure 1.
Overall comparison of the workshop results of the ion dynamics effect on Lyman-α and -β hydrogen lines. For each subcase, i.e., different pairs of , the scatter of ratios between the different results and an average value is plotted. The different symbols correspond to: (black dot) SimU; (red square) UTPP; (blue triangle) PPP; (blue asterisk) Xenomorph; (cyan open triangle) HSTRK; (cyan triangle) HSTRK_FST; (red diamond) ER-simulation; (green circle) QuantST.MMM; (black cross) QC-FFM.
3.1.1. The Lyman-α Line
The static Stark effect of the Lyman-α line (as all the lines, where n and are the principal quantum number of the upper and lower states, respectively) features a strong unshifted component that is highly sensitive to the ion dynamics effect. Thus, even though the Lyman-α line is the simplest case from the atomic structure point of view, it presents a non-trivial Stark-broadening behavior.
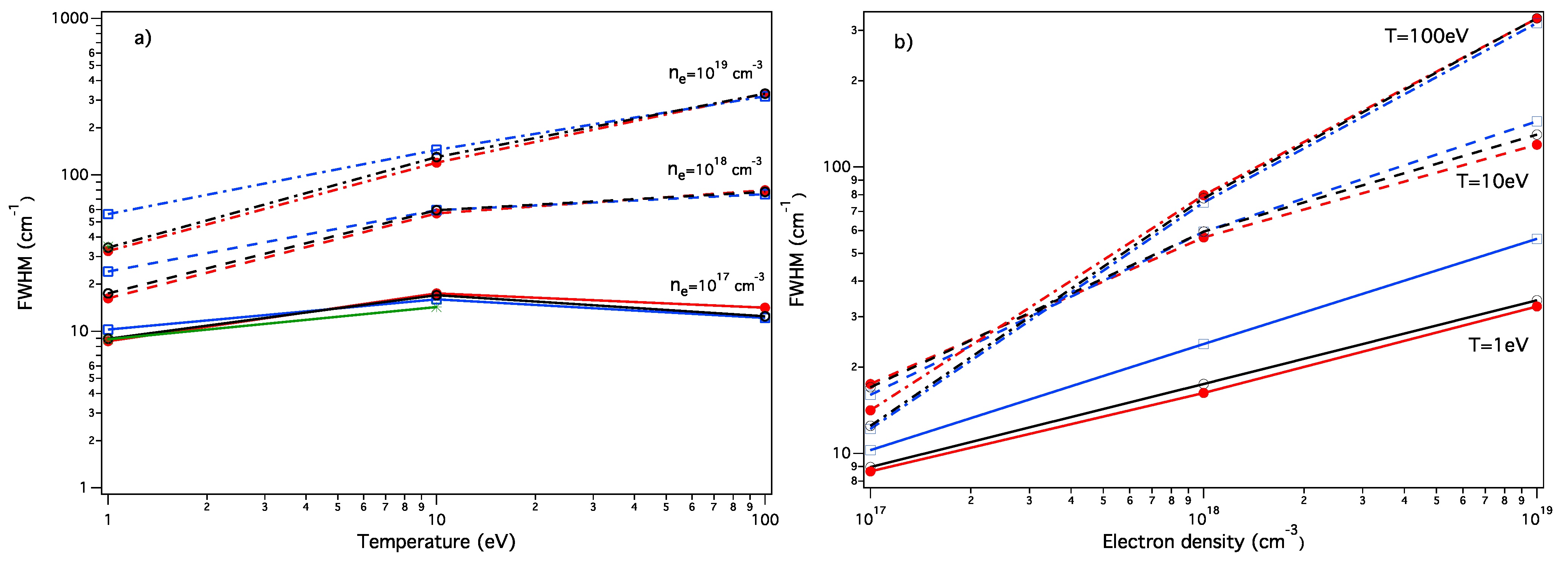
In Figure 2, only results from the numerical simulations are plotted for the sake of clarity. One sees that in the range of 1 to 100 eV, the simulations either predict that the width increases when the plasma temperature increases (for the fixed density cm, they present a temperature dependency as ∼) or predict that the width is mostly insensitive to the temperature’s rise (for the fixed density cm). Concerning the dependence on the plasma density, the width, which is mainly due to the width of the central component for eV, increases as . For eV, the results show a dependence, corresponding to the quasi-static behavior of the lateral components [2]. We mention, however, that the cutoff of the Coulomb interaction at a finite box size may not accurately reproduce an ideal plasma [42].
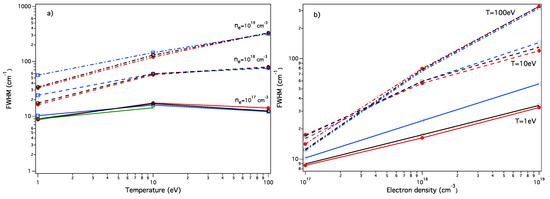
Figure 2.
Lyman-α ion FWHMs as a function of (a) of T at fixed densities and (b) of at fixed temperatures. The ideal, one-component plasma consisting of protons is assumed. Only results from numerical simulations are presented: (red circle) ER-simulation; (blue square) HSTRK; (black dot) SimU; (green asterisk) Xenomorph.
Figure 2.
Lyman-α ion FWHMs as a function of (a) of T at fixed densities and (b) of at fixed temperatures. The ideal, one-component plasma consisting of protons is assumed. Only results from numerical simulations are presented: (red circle) ER-simulation; (blue square) HSTRK; (black dot) SimU; (green asterisk) Xenomorph.
In general, the highest temperature results in the best agreement among simulation codes, for all densities. For lower temperature differences are more discernible, with the most discernible being the appearance of shoulders in ER-simulation and SimU for the highest density and lowest temperature and the lack of such shoulders in HSTRK. This is a general trend at the lowest temperature of 1 eV for all densities, with HSTRK producing significantly larger widths than both ER-simulation and SimU.
The dispersion of the results of the various models demonstrates the difficulties in accurately treating the ion dynamics effect (see Figure 3). In every studied case, the PPP displays a weaker ion dynamics effect on this line, probably due to an incomplete description of this effect on the central component. The FFM mixes the unshifted components with the Stark-shifted components with a unique fluctuation rate. Yet, the unshifted components are not sensitive to the microfield intensity, but only to its rotation, whereas the Stark-shifted components are sensitive to the microfield vibration [43]. A more detailed discussion on the influence of the microfield directionality in the line shape is presented in a separate study [44].
Concerning the description of the ion dynamics effect in terms of microfields mixing, the QuantST.MMM results compare less favorably to the simulations, especially in the far wings.
As already discussed, the far wings of HSTRK_FST are not reliable in this version, due to the complete collision assumption used in the computation of the impact part. This is an artifact of this assumption rather than an inherent limitation of the method.
The UTPP code yields a line width systematically larger than the results obtained from other codes or models and, in particular, the results from numerical simulations. If the latter give reference profiles, this result is expected in general, because the plasma conditions are such that static effects with simultaneous strong collisions are important. However, the application of the UTPP to the electron broadening (not presented here) also indicates a significant discrepancy, with an overestimate of the numerical simulation results by a factor of two. It has been suggested that this discrepancy stems from the fact that the simulations that use a box actually miss a significant contribution to the line broadening, due to the far perturbers, namely, those inside the sphere, but outside the simulation box. It is quite difficult to test this argument by enlarging the simulation box up to , because this would imply a very large number of particles (up to several billions). An adaptation of UTPP able to account for a plasma of finite size has been performed and has led to a line shape in good agreement with the simulations [42]. This could suggest that an artificial setting of an infinite Debye length in the numerical simulations able to work with an infinite Debye length requires a careful interpretation of the results.
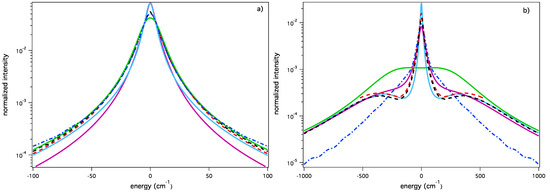
Figure 3.
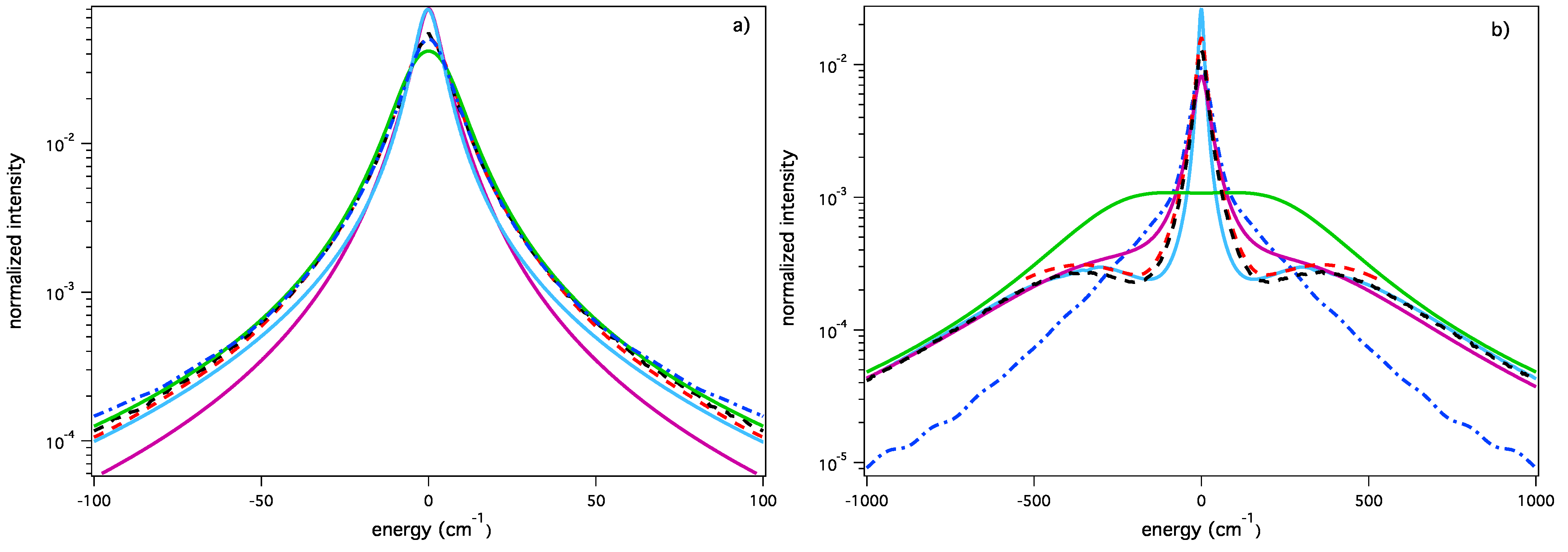
Lyman-α line shape in ideal ionic one component plasma (OCP) calculated for (a) the more dynamical regime ( cm and eV) and (b) the more static regime ( cm and eV): SimU (black dash); ER-simulation (red dash); HSTRK_FST (blue dot-dash); PPP (solid cyan); QuantST.MMM (solid purple); UTPP (solid green).
Figure 3.
Lyman-α line shape in ideal ionic one component plasma (OCP) calculated for (a) the more dynamical regime ( cm and eV) and (b) the more static regime ( cm and eV): SimU (black dash); ER-simulation (red dash); HSTRK_FST (blue dot-dash); PPP (solid cyan); QuantST.MMM (solid purple); UTPP (solid green).
3.1.2. The Lyman-β Line
The static profile of the Lyman-β line (as all of the lines) normally shows a dip at the line center. One sees in Figure 4 that, due to the ion dynamics effect, the simulations fill this dip, and the width increases with increasing temperature. This trend is seen for plasma conditions that correspond to typical microfield fluctuation rate values (see Equation (5)) smaller than the splitting of the two Stark components measured in the static case. Here, for cm, the Stark splitting of the static line shape is equal to eV, and the typical fluctuation rate is equal to eV and eV for eV and eV, respectively. For eV, eV, i.e., three-times greater that the Stark splitting in the static case. The two components merge, leading to a line shape that is narrower than the one calculated for eV, as is seen in Figure 4a. Note that for an infinite fluctuation rate, the line shape becomes the Dirac δ-function.
The agreement between the Lyman-β FWHM results of different codes is much better than that for Lyman-α, as is shown in Figure 1. Nevertheless, the concept of FWHM is not really adequate for such a line with a dip in the center. A better way to discuss the ion dynamics effect on a Lyman-β line would be the measure of the relative dip given by:
where and are the maximum intensity and the intensity at the center of the line, respectively. Table 1 shows the relative dip from the different codes for cm, while the line shapes are shown in Figure 5.
Obviously, the QC approximation, and, hence, the QC-FFM method, is inherently unable to reproduce the central structure (a peak or a dip) of a low-n spectral line. However, the wings of such lines, as well as entire profiles of higher-n transitions, show a very good agreement with numerical simulations [13].
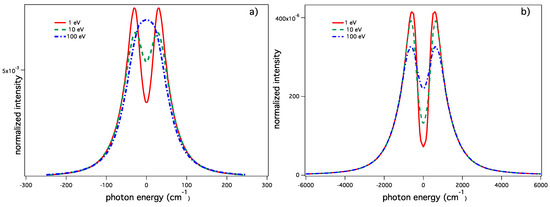
Figure 4.
The ion dynamics effect on the Lyman-β line for different values of T obtained by SimU: (solid red eV; (green dash) eV and (blue dot-dash) eV at a fixed (a) cm and (b) cm. The ideal one-component plasma consisting of protons is assumed.
Figure 4.
The ion dynamics effect on the Lyman-β line for different values of T obtained by SimU: (solid red eV; (green dash) eV and (blue dot-dash) eV at a fixed (a) cm and (b) cm. The ideal one-component plasma consisting of protons is assumed.
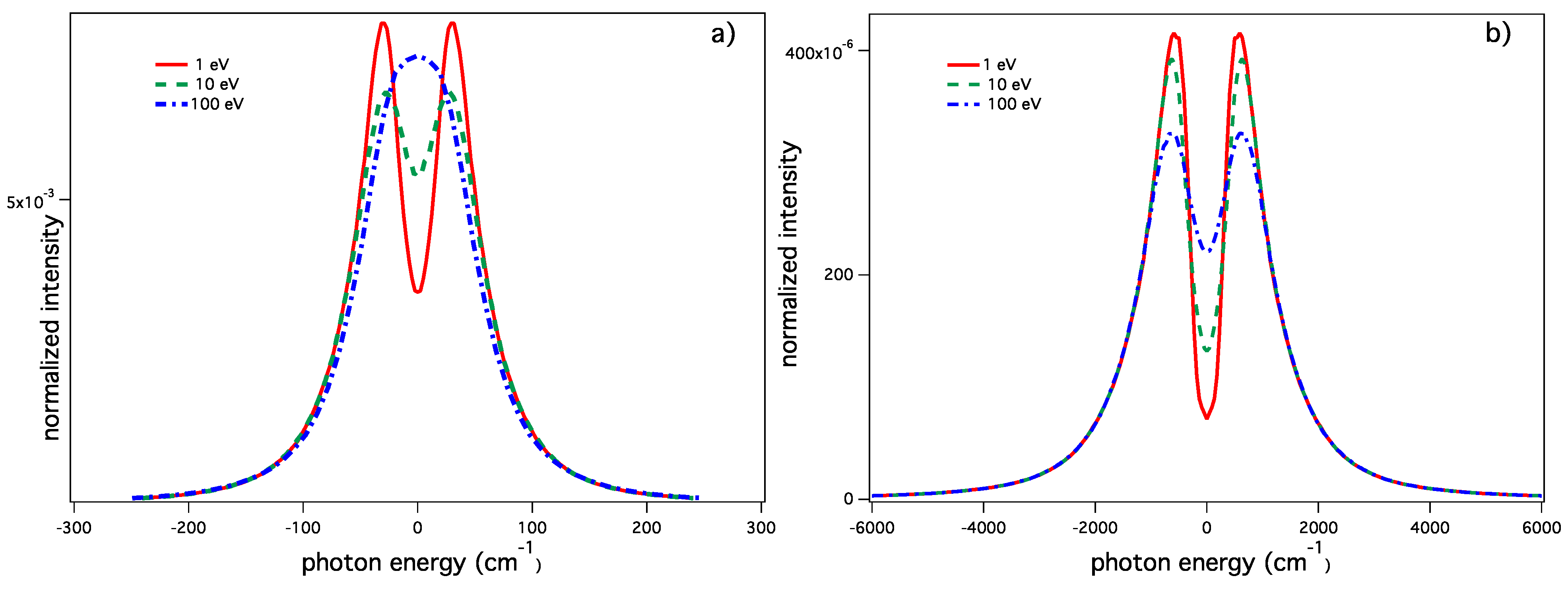
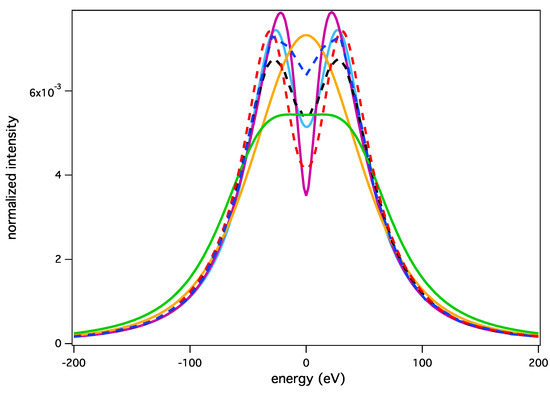
Figure 5.
Lyman-β line for cm and eV: SimU (black dash); ER-simulation (red dash); Xenomorph (blue dot-dash); PPP (solid cyan); QC-FFM (solid orange); QuantST. MMM (solid purple); UTPP (solid green).
Figure 5.
Lyman-β line for cm and eV: SimU (black dash); ER-simulation (red dash); Xenomorph (blue dot-dash); PPP (solid cyan); QC-FFM (solid orange); QuantST. MMM (solid purple); UTPP (solid green).
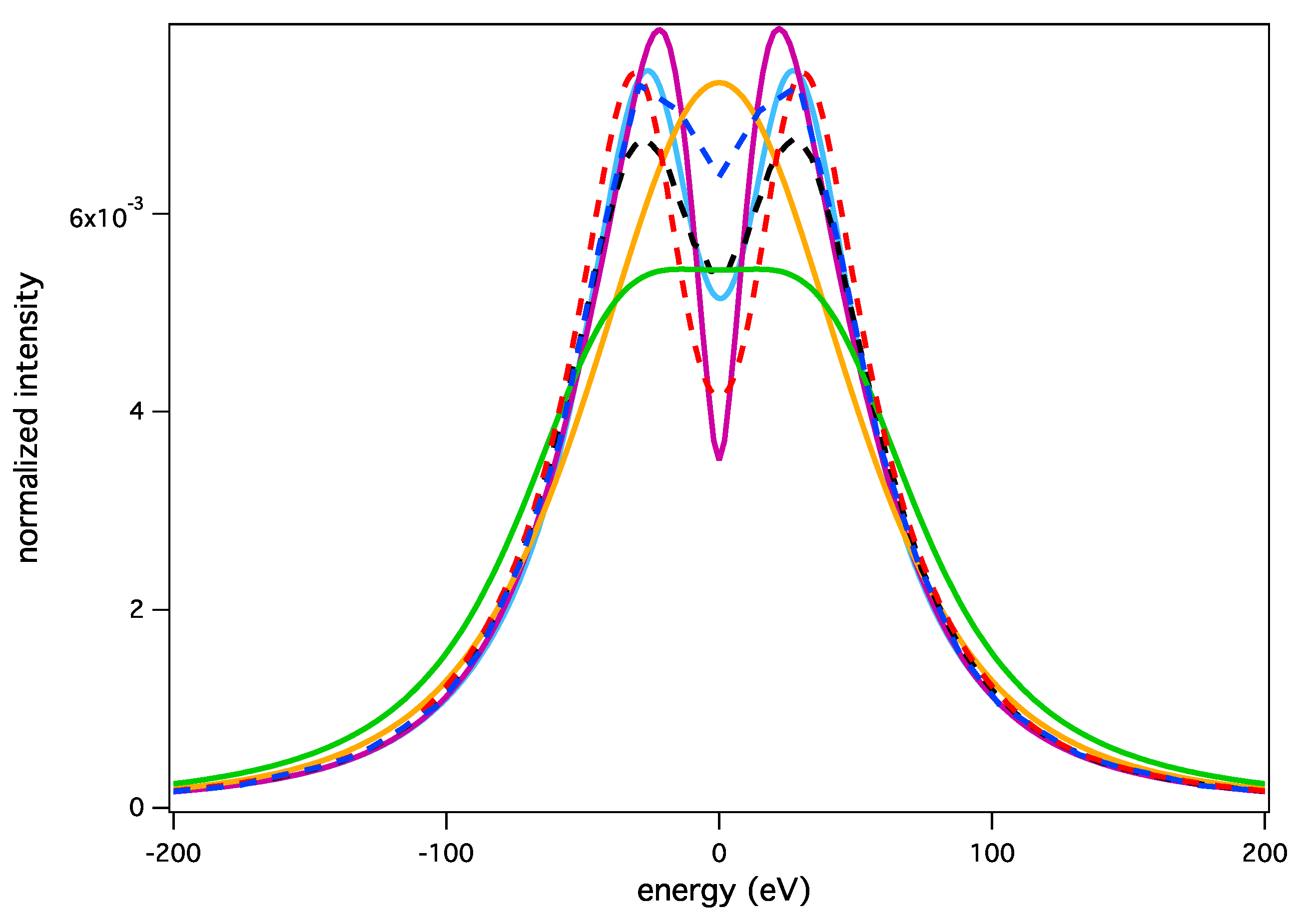

Table 1.
The relative dip (%) measured on the Lyman-β line from the different codes for cm.
| T (eV) = | 1 | 10 | 100 |
| ER-simulation | 75 | 44 | 10 |
| SimU | 56 | 19 | 0 |
| Xenomorph | 56 | 14 | / |
| PPP | 70 | 31 | 0 |
| QuantSt.MMM | 71 | 55 | 32 |
| UTPP | 0.6 | 0.6 | 0 |
3.2. Argon He-α and He-β Lines
The argon H- and He-like lines are observed in inertial confinement fusion implosion core plasmas when a tracer amount of argon is added to the deuterium gas fill to diagnose the plasma conditions [45]. Such a diagnostic relies on the temperature sensitivity of the satellite line;s relative intensity to the resonance one and the density dependence in the Stark broadening of both satellite and resonance line profiles [46]. Moreover, they are sensitive to the ion dynamics effects and present a challenge for theoretical models [47]. We only focus here on the He-α and He-β lines. A specific study of the effect of satellite line shapes on the He-β line can be found elsewhere [48].
Two electron densities, cm and cm, and a plasma temperature of keV were selected for this comparison. Plasma ions are deuterons with Argon XVII. The MELS and MERL (BID) and the PPP (FFM) models submitted results, and the numerical simulation, SimU, was recently extended to describe such lines. Here, the simulation accounts for all interactions; no artificial cutoff arises as for the ideal case conditions. We consider it as a reference.
Figure 6 displays the He-α profiles calculated with the PPP code within the quasi-static approximation. For clarity, results from MELS are not plotted here, but the agreement between the two codes is very good. The small differences observed between both codes are explained by the difference in the electron broadening treatment (the impact approximation is used in PPP, while a frequency dependent collision operator is used in MELS). The quasi-static profile is the superimposition of a strong intensity component, which corresponds to the resonance transition, and a weak intensity component, which corresponds to the intercombination transition. The pure electron broadened profiles are plotted for each component for a better understanding of the ionic Stark effect on the line shapes. Both components display a pronounced quadratic Stark effect in their “blue” wing, and forbidden lines appear on top of their “red” wing.
Concerning the ion dynamics effect, BID and FFM show a different behavior. BID profiles present a more pronounced deviation relative to the static calculation than the FFM. Figure 7 and Figure 8 illustrate this for the two densities. These discrepancies cannot be explained by the use of a different fluctuation rate in both models. A specific study using the same fluctuation rate for both models shows that the BID and FFM are in good agreement for varying values of this parameter for the resonance line, but not for the intercombination line [39]. Figure 9 shows this difference using both models with the same fluctuation rate. The difference seen on the forbidden component of the intercombination line might be due to a numerical inaccuracy, because of the very weak value of its intensity.
Moreover, numerical simulation results from the SimU code do not discriminate between the stochastic models. For example, in Figure 9, both models agree with the simulation on the allowed transitions, but not on the forbidden transitions. This might be due to a different dynamics between strong microfields, which are emphasized by the quadratic Stark effect of the allowed transitions, and weak microfields, which are the cause of the linear Stark effect of the forbidden transitions.
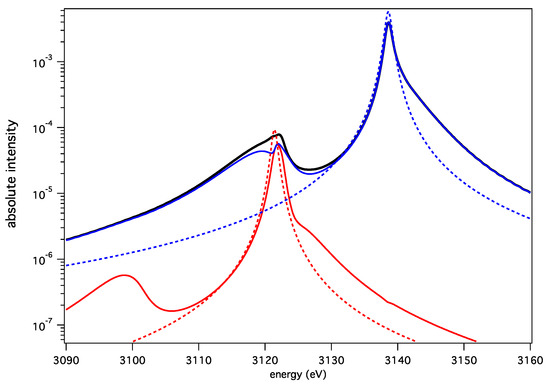
Figure 6.
The He-α line calculated within the quasi-static approximation for keV and cm. (Black line) the entire profile; (blue line) resonant line profile; (red line) intercombination line profile. The pure electron-broadened profiles are plotted in dashed lines for each component.
Figure 6.
The He-α line calculated within the quasi-static approximation for keV and cm. (Black line) the entire profile; (blue line) resonant line profile; (red line) intercombination line profile. The pure electron-broadened profiles are plotted in dashed lines for each component.
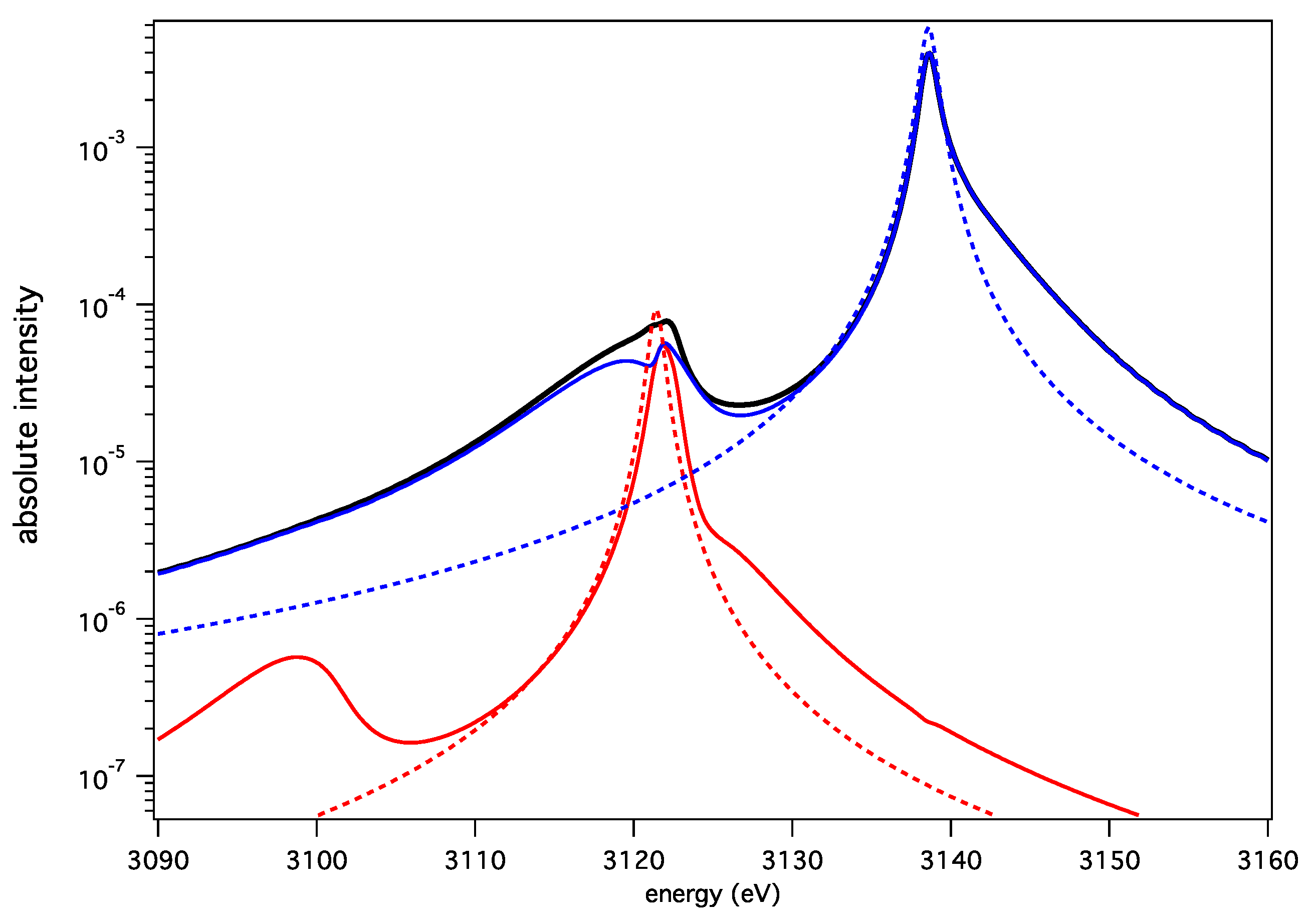
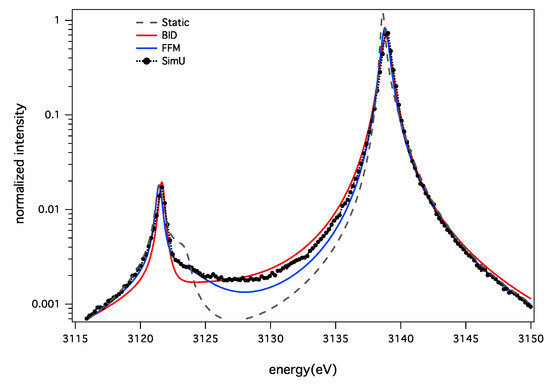
Figure 7.
The He-α line for keV and cm: static ions MELS (grey dash); ion dynamics BID (solid red); FFM (solid blue) and SimU (black dot).
Figure 7.
The He-α line for keV and cm: static ions MELS (grey dash); ion dynamics BID (solid red); FFM (solid blue) and SimU (black dot).
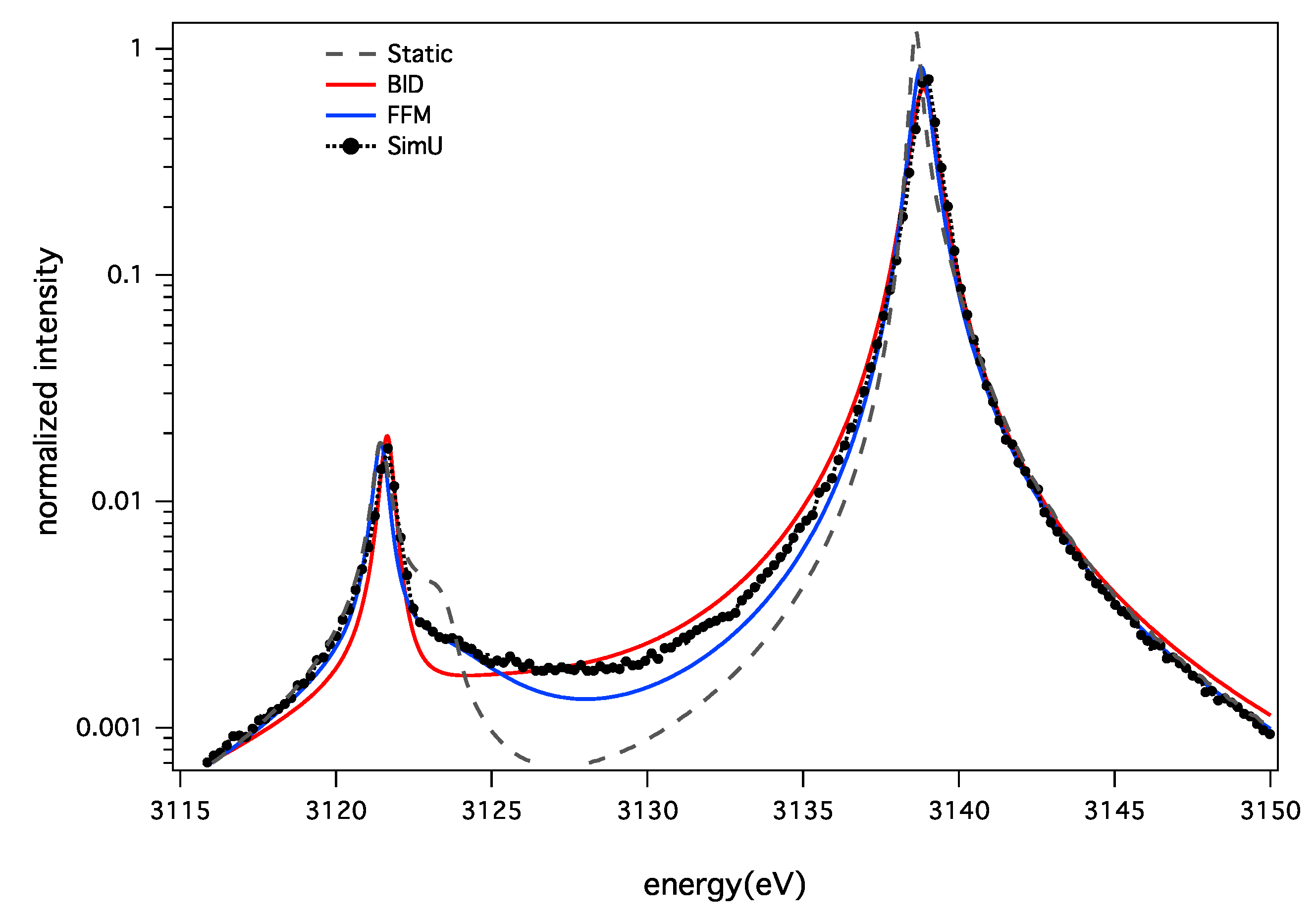
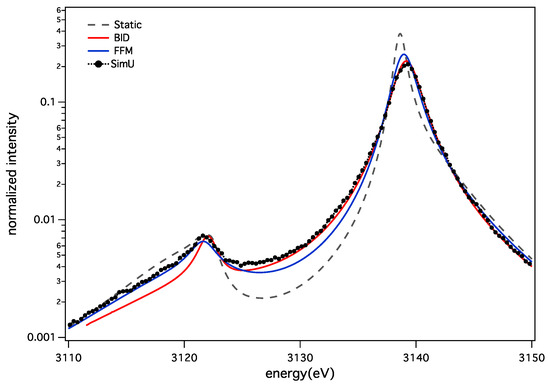
Figure 8.
The He-α line for keV and cm: static ions (grey dash); ion dynamics BID (solid red); FFM (solid blue); and SimU (black dot).
Figure 8.
The He-α line for keV and cm: static ions (grey dash); ion dynamics BID (solid red); FFM (solid blue); and SimU (black dot).
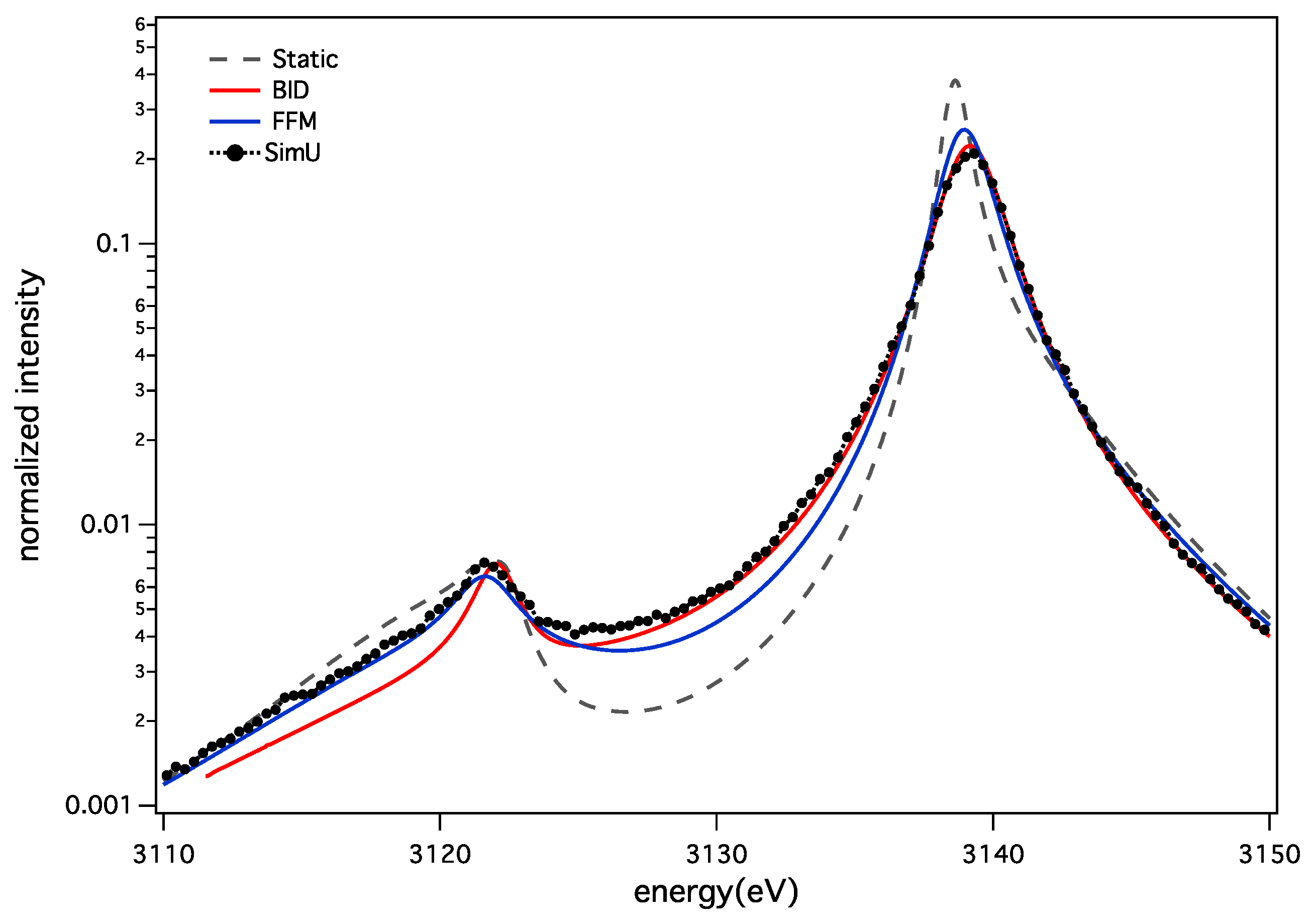
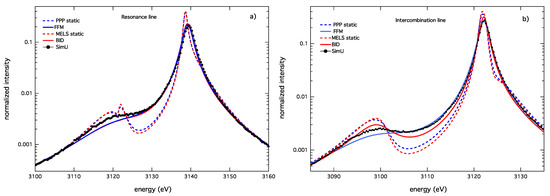
Figure 9.
The He-α line for keV and cm: (a) resonance line and (b) intercombination line. Static ions MELS (red dash) and PPP (blue dash); ion dynamics BID (solid red); FFM (solid blue); and SimU (black dot).
Figure 9.
The He-α line for keV and cm: (a) resonance line and (b) intercombination line. Static ions MELS (red dash) and PPP (blue dash); ion dynamics BID (solid red); FFM (solid blue); and SimU (black dot).
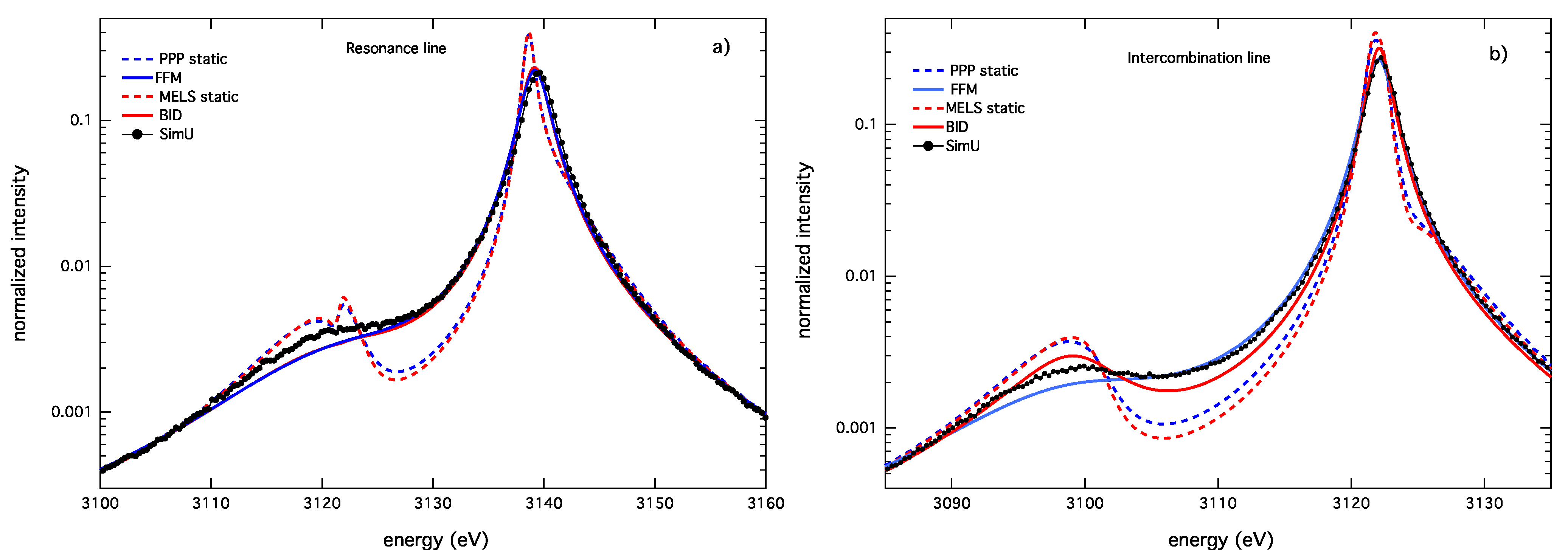
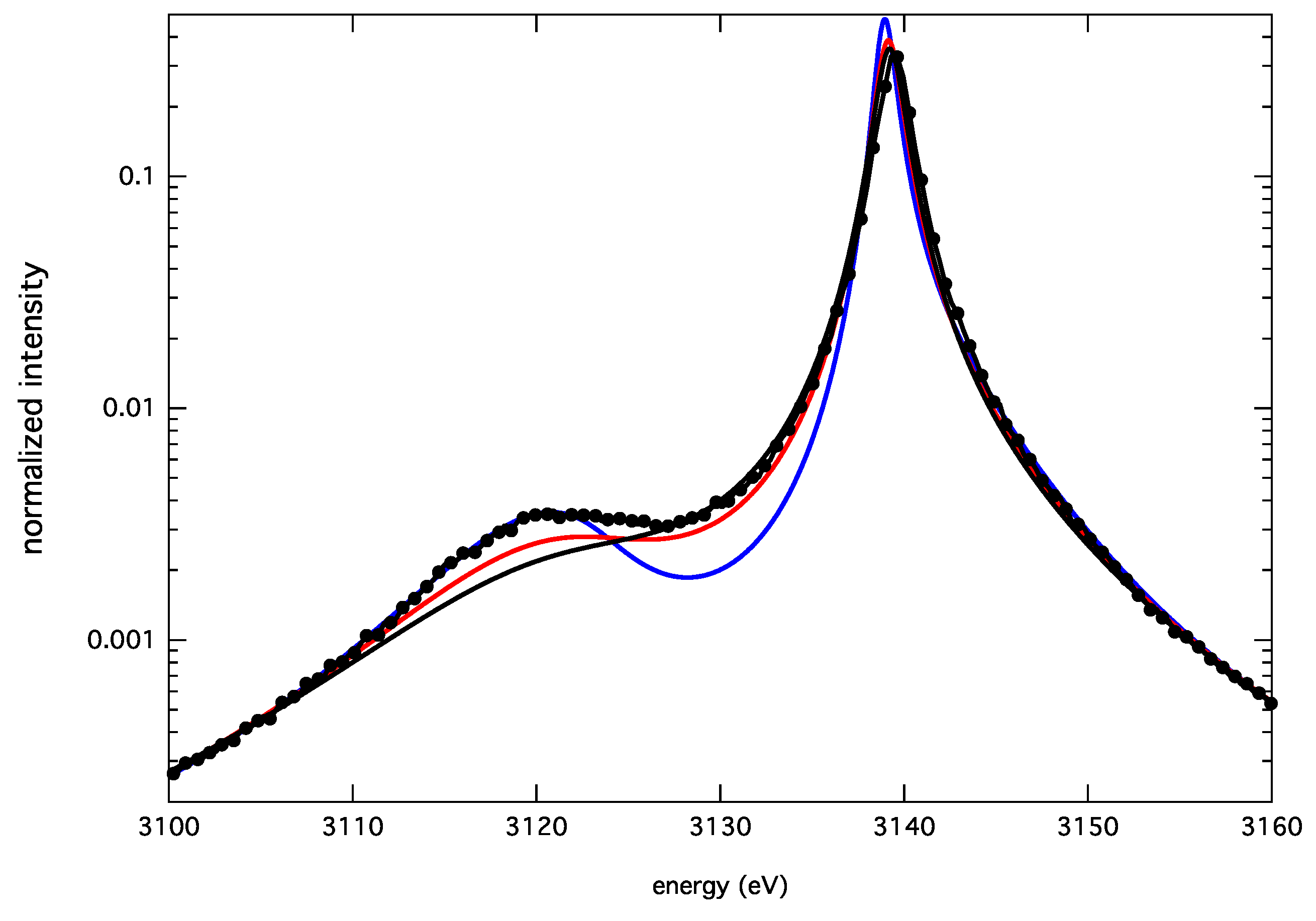
In order to explain these differences, a specific study on the pure ion-broadened profiles was carried out. As both resonance and intercombination lines present similar atomic systems, we will only focus the discussion of the resonance line. Figure 10 shows FFM profiles for different fluctuation rates and the SimU profile. It seems that different values of ν are needed to reproduce different portions of the simulated profile. A lower fluctuation rate has to be used to fit the forbidden component, whereas a higher ν is needed to reproduce the allowed component. This can be interpreted as weak and strong microfields not producing the same dynamics effect on the line shape.
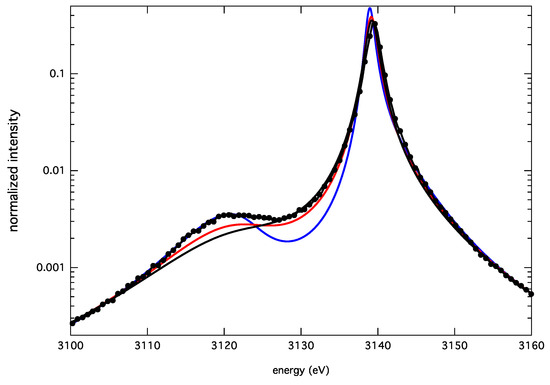
Figure 10.
The He-α line, the strong component for keV and cm: SimU (black circles); FFM with eV (solid blue); eV (solid red); and eV (solid black).
Figure 10.
The He-α line, the strong component for keV and cm: SimU (black circles); FFM with eV (solid blue); eV (solid red); and eV (solid black).
Finally, the He-β line is presented in Figure 11. At the chosen plasma conditions, as the Stark splitting of the He-β quasi-static line shape is greater than the fluctuation rate and the electron width is larger, the ion dynamics effect is less pronounced than on the He-α. Figure 11 shows SimU, BID and FFM in rather good agreement relative to the discrepancies of their quasi-static profiles. The measure of the dynamics-to-static relative depth is defined by:
There is a fairly good agreement between the BID and the FFM (see Table 2).
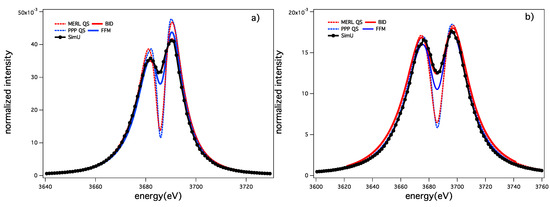
Figure 11.
The He-β line for keV and (a) cm; (b) cm. Static ions: MERL (red dot), PPP (blue dot); SimU (black dot); BID (solid red); FFM (solid blue).
Figure 11.
The He-β line for keV and (a) cm; (b) cm. Static ions: MERL (red dot), PPP (blue dot); SimU (black dot); BID (solid red); FFM (solid blue).

Table 2.
Dynamics-to-static relative dip (%) measured on the argon He-β line for keV.
| Models | BID | FFM |
|---|---|---|
| cm | 58 | 57 |
| cm | 50 | 51 |
| cm | 47 | 48 |
4. Conclusions
Line shape calculations from different numerical codes that account for the ion dynamics effect were presented. To test the accuracy of the different codes, standardized case problems have been chosen and a systematic cross-comparison has been done. Results from four numerical simulations based on different algorithms and seven models relying on either stochastic or collisional processes, have been then submitted.
Surprisingly, the results obtained on the hydrogen Lyman-α line in an ideal OCP plasma consisting of protons presents a large dispersion. While the numerical simulations show a relatively good agreement between each other, the FFM and MMM models systematically display a weaker width than the averaged results. This can be explained by an incomplete description of the ion dynamics effect on the central component of this line. The detailed study on the influence of the microfields directionality in the line shape presented in this volume, [44] or other methods discussed here can help improve the modeling of lines with unshifted components. The overestimate of the UTPP code based on a collisional approach is explained by an incomplete description of ion static effects. The results obtained on the H Lyman-β line present a better agreement between all codes.
Concerning the ion dynamics effect on the argon He-α and -β lines, BID and FFM show a different behavior that has been attributed, up to now, to numerical inaccuracies, due to the very weak value of the line intensities. The recently developed numerical simulation code, SimU, could not help discriminate between the two models, but highlighted another problem: it seems that different values of fluctuation rates have to be used to reproduce different portions of the simulated profile. As both the linear and quadratic Stark effect, which are linked to the weak and strong values of microfields, respectively, are involved in producing the shape of this line, one can wonder if a frequency- (or field-) dependent fluctuation rate is needed to give a better description of ion dynamics on this line.
Acknowledgments
The authors would like to acknowledge the International Atomic Energy Agency B.J. Braams and H.-K. Chung for the organizational and financial support of this workshop.
Author Contributions
The present work is based on codes developed by all authors, who also participated in all aspects of this work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Griem, H.R. Principles of Plasma Spectroscopy; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Griem, H.R. Spectral Line Broadening by Plasmas; Academic Press: New York, NY, USA, 1974; ISBN 0-12-302850-7. [Google Scholar]
- Stambulchik, E.; Maron, Y. Plasma line broadening and computer simulations: A mini-review. High Energy Density Phys. 2010, 6, 9–14. [Google Scholar] [CrossRef]
- Calisti, A.; Mossé, C.; Ferri, S.; Talin, B.; Rosmej, F.; Bureyeva, L.A.; Lisitsa, V.S. Dynamic Stark broadening as the Dicke narrowing effect. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010, 81, 016406. [Google Scholar] [CrossRef]
- Stambulchik, E. Review of the 1st Spectral Line Shapes in Plasmas code comparison workshop. High Energy Density Phys. 2013, 9, 528–534. [Google Scholar] [CrossRef]
- Gigosos, M.A.; Gonzalez, M.A. Comment on “A study of ion-dynamics and correlation effects for spectral line broadening in plasmas: K-shell lines”. J. Quant. Spectrosc. Radiat. Transf. 2007, 105, 533–535. [Google Scholar] [CrossRef]
- Alexiou, S. Stark broadening of hydrogen lines in dense plasmas: Analysis of recent experiments. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005, 71, 066403. [Google Scholar] [CrossRef]
- Alexiou, S. Implementation of the Frequency Separation Technique in general lineshape codes. High Energy Density Phys. 2013, 9, 375–384. [Google Scholar] [CrossRef]
- Stambulchik, E.; Maron, Y. A study of ion-dynamics and correlation effects for spectral line broadening in plasma: K-shell lines. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 730–749. [Google Scholar] [CrossRef]
- Stambulchik, E.; Alexiou, S.; Griem, H.R.; Kepple, P.C. Stark broadening of high principal quantum number hydrogen Balmer lines in low-density laboratory plasmas. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007, 75, 016401. [Google Scholar] [CrossRef]
- Gomez, T.A.; Mancini, R.C.; Montgomery, M.H.; Winget, D.E. White dwarf line shape theory including ion dynamics and asymmetries. 2014. in preparation. [Google Scholar]
- Lorenzen, S. Comparative Study on Ion-Dynamics for Broadening of Lyman Lines in Dense hydrogen Plasmas. Contrib. Plasma Phys. 2013, 53, 368–374. [Google Scholar] [CrossRef]
- Stambulchik, E.; Maron, Y. Quasicontiguous frequency-fluctuation model for calculation of hydrogen and hydrogen-like Stark-broadened line shapes in plasmas. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2013, 87, 053108. [Google Scholar] [CrossRef]
- Iglesias, C.A.; Vijay, S. Robust algorithm for computing quasi-static Stark broadening of spectral lines. High Energy Density Phys. 2010, 6, 399–405. [Google Scholar] [CrossRef]
- Woltz, L.A.; Hooper, C.F., Jr. Calculation of spectral line profiles of multielectron emitters in plasmas. Phys. Rev. A 1988, 38, 4766–4771. [Google Scholar] [CrossRef] [PubMed]
- Mancini, R.C.; Kilcrease, D.P.; Woltz, L.A.; Hooper, C.F. Calculational Aspects of the Stark Line Broadening of Multielectron Ions in Plasmas. Comput. Phys. Commun. 1991, 63, 314–322. [Google Scholar] [CrossRef]
- Calisti, A.; Khelfaoui, F.; Stamm, R.; Talin, B.; Lee, R.W. Model for the line shapes of complex ions in hot and dense plasmas. Phys. Rev. A 1990, 42, 5433–5440. [Google Scholar] [CrossRef] [PubMed]
- Alexiou, S.; Poquérusse, A. Standard line broadening impact theory for hydrogen including penetrating collisions. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005, 72, 046404. [Google Scholar] [CrossRef]
- Rosato, J.; Capes, H.; Stamm, R. Influence of correlated collisions on Stark-broadened lines in plasmas. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2012, 86, 046407. [Google Scholar] [CrossRef]
- Boercker, D.B.; Iglesias, C.A.; Dufty, J.W. Radiative and transport properties of ions in strongly coupled plasmas. Phys. Rev. A 1987, 36, 2254–2264. [Google Scholar] [CrossRef] [PubMed]
- Talin, B.; Calisti, A.; Godbert, L.; Stamm, R.; Lee, R.W.; Klein, L. Frequency-fluctuation model for line shape calculations in plasma spectroscopy. Phys. Rev. A 1995, 51, 1918–1928. [Google Scholar] [CrossRef] [PubMed]
- Holtsmark, J. Über die Verbreiterung von Spektrallinien. Ann. Phys. 1919, 58, 577–630. [Google Scholar] [CrossRef]
- Iglesias, C.A.; Boercker, D.B.; Iglesias, C.A. Electric field distributions in strongly coupled plasmas. Phys. Rev. A 1985, 31, 1681–1686. [Google Scholar]
- Gigosos, M.A.; Gonzalez, M.A.; Cardeñoso, V. Computer simulated Balmer-alpha, -beta and -gamma Stark line profiles for non-equilibrium plasmas diagnostics. Spectrochim. Acta Part B 2003, 58, 1489–1504. [Google Scholar] [CrossRef]
- Gigosos, M.A.; Cardeñoso, V. New plasma diagnostics table of hydrogen Stark broadening including ion dynamics. J. Phys. B-At. Mol. Opt. Phys. 1996, 29, 4795–4838. [Google Scholar] [CrossRef]
- Hegerfeldt, G.; Kesting, V. Collision-time simulation technique for pressure-broadened spectral lines with applications to Ly-α. Phys. Rev. A 1988, 37, 1488–1496. [Google Scholar] [CrossRef] [PubMed]
- Filon, L.N.G. On a quadrature formula for trigonometric integrals. Proc. R. Soc. Edinb. 1928, 49, 38–47. [Google Scholar]
- Pfennig, H. On the Time-Evolution Operator in the Semiclassical Theory of Stark-Broadening of hydrogen Lines. J. Quant. Spectrosc. Radiat. Transf. 1972, 12, 821–837. [Google Scholar] [CrossRef]
- Lisitsa, V.S.; Sholin, G.V. Exact Solution of the Problem of the Broadening of the hydrogen Spectral Lines in the One-Electron Theory. Sov. J. Exp. Theor. Phys. 1972, 34, 484–489. [Google Scholar]
- Gigosos, M.A.; González, M.A. Calculations of the polarization spectrum by two-photon absorption in the hydrogen Lyman-α line. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 1998, 58, 4950–4959. [Google Scholar] [CrossRef]
- Djurović, S.; Ćiris̎an, M.; Demura, A.V.; Demchenko, G.V.; Nikolić, D.; Gigosos, M.A.; Gonzalez, M.Á. Measurements of Hβ Stark central asymmetry and its analysis through standard theory and computer simulations. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009, 79, 046402. [Google Scholar] [CrossRef] [PubMed]
- Frisch, U.; Brissaud, A. Theory of Stark broadening—I soluble scalar model as a test. J. Quant. Spectrosc. Radiat. Transf. 1971, 11, 1753–1766. [Google Scholar] [CrossRef]
- Frisch, U.; Brissaud, A. Theory of Stark broadening—II exact line profile with model microfield. J. Quant. Spectrosc. Radiat. Transf. 1971, 11, 1767–1783. [Google Scholar]
- Günter, S.; Hitzschke, L.; Röpke, G. Hydrogen spectral lines with the inclusion of dense-plasma effects. Phys. Rev. A 1991, 44, 6834–6844. [Google Scholar] [CrossRef] [PubMed]
- Lorenzen, S.; Omar, B.; Zammit, M.C.; Fursa, D.V.; Bray, I. Plasma pressure broadening for few-electron emitters including strong electron collisions within a quantum-statistical theory. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2014, 89, 023106. [Google Scholar] [CrossRef]
- Dufty, J.W. Spectral Lines Shapes; Wende, B., Ed.; De Gruyter: New York, NY, USA, 1981. [Google Scholar]
- Stambulchik, E.; Maron, Y. Stark effect of high-n hydrogen-like transitions: Quasi-contiguous approximation. J. Phys. B-At. Mol. Opt. Phys. 2008, 41, 095703. [Google Scholar] [CrossRef]
- Mossé, C.; Calisti, A.; Stamm, R.; Talin, B.; Lee, R.W.; Klein, L. Redistribution of resonance radiation in hot and dense plasmas Phys. Rev. A 1999, 60, 1005–1014. [Google Scholar] [CrossRef]
- Iglesias, C. Efficient algorithms for stochastic Stark-profile calculations. High Energy Density Phys. 2013, 9, 209–221. [Google Scholar] [CrossRef]
- Rosato, J.; Reiter, D.; Kotov, V.; Marandet, Y.; Capes, H.; Godbert-Mouret, L.; Koubiti, M.; Stamm, R. Progress on radiative transfer modelling in optically thick divertor plasmas. Contrib. Plasma Phys. 2010, 50, 398–403. [Google Scholar] [CrossRef]
- Rosato, J.; Capes, H.; Stamm, R. Divergence of the Stark collision operator at large impact parameters in plasma spectroscopy models. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2013, 88, 035101:1–035101:3. [Google Scholar] [CrossRef]
- Rosato, J.; Capes, H.; Stamm, R. Ideal Coulomb plasma approximation in line shape models: Problematic issues. Atoms 2014, 2(2), 277–298. [Google Scholar] [CrossRef]
- Lisitsa, V. Private communication.
- Calisti, A.; Demura, A.V.; Gigosos, M.A.; González-Herrero, D.; Iglesias, C.A.; Lisitsa, V.S.; Stambulchik, E. Influence of Microfield Directionality on Line Shapes. Atoms 2014, 2, 259–276. [Google Scholar] [CrossRef]
- Chung, H.-K.; Lee, R.W. Application of NLTE population kinetics. High Energy Density Phys. 2009, 5, 1–14. [Google Scholar] [CrossRef]
- Woolsey, N.C.; Hammel, B.A.; Keane, C.J.; Asfaw, A.; Back, C.A.; Moreno, J.C.; Nash, J.K.; Calisti, A.; Mossé, C.; Stamm, R.; et al. Evolution of electron temperature and electron density in indirectly driven spherical implosions. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 1996, 56, 2314. [Google Scholar] [CrossRef]
- Haynes, D.A.; Garber, D.T.; Hooper, C.F.; Mancini, R.C.; Lee, Y.T.; Bradley, D.K.; Delettrez, J.; Epstein, R.; Jaanimagi, P.A. Effects of ion dynamics and opacity on Stark-broadened argon line profiles. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 1996, 53, 1042–1050. [Google Scholar] [CrossRef]
- Mancini, R.C.; Iglesias, C.A.; Ferri, A.; Calisti, S.; Florido, R. The effects of improved satellite line shapes on the argon Heβ spectral feature. High Energy Density Phys. 2013, 9, 731–736. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
