Abstract
The study deals with two conceptual problems in the theory of Stark broadening by plasmas. One problem is the assumption of the density matrix diagonality in the calculation of spectral line profiles. This assumption is closely related to the definition of zero wave functions basis within which the density matrix is assumed to be diagonal, and obviously violated under the basis change. A consistent use of density matrix in the theoretical scheme inevitably leads to interdependence of atomic kinetics, describing the population of atomic states with the Stark profiles of spectral lines, i.e., to spectral-kinetic coupling. The other problem is connected with the study of the influence of microfield fluctuations on Stark profiles. Here the main results of the perturbative approach to ion dynamics, called the theory of thermal corrections (TTC), are presented, within which the main contribution to effects of ion dynamics is due to microfield fluctuations caused by rotations. In the present study the qualitative behavior of the Stark profiles in the line center within predictions of TTC is confirmed, using non-perturbative computer simulations.
In Memory of Professor of Moscow Physical and Engineering Institute—Vladimir Il’ich Kogan (11 July 1923–7 December 2013)—passionate outstanding scientist, pioneer of plasma physics and nuclear fusion research at Kurchatov Institute of Atomic Energy, eminent enthusiastic lecturer, great kind teacher and famous witty connoisseur of courtly linguistics and many more…

1. Introduction
The study of Stark broadening in experiments, theory and simulations has up to now achieved significant progress [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78]. This allowed the beginning of profound detailed comparisons of various computer codes developed for calculation of spectral lines profiles in plasmas, which was the main purpose of the first two SLSP workshops [74]. However, the understanding and comparison of realizations of most successful contemporary codes on a wide set of physical cases (see [74,75,76,77] and other articles of this issue) give good reason to once more discuss, check, and revise the physical notions and ideas which form the foundation of the contemporary theory of spectral line broadening by plasmas. The present article pursues these aims.
In fact, this article deals only with two questions from the list of conceptual problems in the theory of Stark broadening by plasmas [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77]. The first one is the construction of the spectral line broadening theory without assumption of the density matrix diagonality. Very often this assumption cannot be validated when there is an interaction mixing of states whose energy splitting is less than or comparable with the magnitude of interaction [42,43,44,45,50,53]. A consistent introduction of density matrix inevitably leads to interdependence of atomic kinetics, describing the population of atomic states with the Stark profiles of spectral lines that evidently could be defined as spectral-kinetic coupling [42,43,44,45,50,53]. Usually, this is also interrelated with the appearance of interference effects [42,43,44,45,50,53]. The other problem is related to the attempts to separate the influence of microfield fluctuations on Stark profiles into two components, perpendicular and parallel to the microfield direction [5,6], in order to separate the contribution from microfield rotation effects [12,23,24,25,30,33], predicted to be dominating in the central part of the line [23,24,25]. The necessity of this discussion arose when it was recently shown that existing approaches to accounting for ion dynamics give results that differ from one another [74,75,76]. This inspired attempts to describe ion dynamics effects in terms of physical mechanisms, instead of practically tacit conventional numerical comparison of complicated simulations that began with the first works done using the Model Microfield Method (MMM) in the 1970s [14,15,28,29]. The basics of the theory of thermal corrections for Stark profiles along with the results of [7,8,9,12,23,24,25] are given in Section 3. Later, the predictions, given in [12,23,24,25] about significance of microfield rotation effects in ion dynamics, were confirmed within other approaches [30,33], but until now it has not been explicitly shown in the results of computer simulations (see also [75]). In the present work, simultaneously with [75], the approximate way to separate microfield rotation effects in the profile of Ly-alpha within MD simulations is realized and described in Section 4. However, this separation could not in fact be achieved rigorously, due to the existence of correlations between statistical characteristics and dynamics of atomic systems that we call statistical-dynamical coupling. The specially designed numerical experiments allowed for confirming the qualitative predictions of behavior of the ion dynamical Stark profiles for Ly-alpha, given earlier in [23,24,25]. This includes: (1) predominance of microfield rotation in the formation of the central part of the Stark profile in plasmas for lines with the central components; (2) a specific spectral behavior of the Stark profiles near the line center as a function of the plasma temperature and reduced mass of the perturber-radiator pair; (3) a universal spectral behavior of the difference Stark profiles for two different reduced mass of the perturber-radiator pair.
For the purpose of discussion a short review of theoretical approaches and methods developed for and applied to the study of the Stark broadening by plasmas is entwined into the argumentation of each section.
2. Spectral-Kinetic Coupling
Let us consider broadening of the hydrogen atom in the well-known setting of the so-called standard theory (ST), related to formulation given in [17,18,21,51]. Then the total Stark profile of spectral line I(Δω) is represented as the convolution of the Stark subprofiles, corresponding to the transitions between upper and lower substates being broadened by electrons in the fixed value of ion microfield, and integrated over ion microfield values with the microfield probability distribution function as a weight:
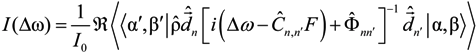 In Equation (1) Δω = ω − ω0 is the detuning of cyclic frequency from the line center, the outer angle brackets correspond as usual to an averaging over the microfield values F (F is the absolute value of microfield),
In Equation (1) Δω = ω − ω0 is the detuning of cyclic frequency from the line center, the outer angle brackets correspond as usual to an averaging over the microfield values F (F is the absolute value of microfield),  is the operator of density matrix,
is the operator of density matrix,  is the operator of dipole moment,
is the operator of dipole moment,  is the operator of resolvent,
is the operator of resolvent, 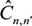 is the operator of the linear Stark shift between sublevels of the upper n and lower level n’ in the line space (the direct product of subspaces of the upper and lower energy levels with the principal quantum numbers n and n’),
is the operator of the linear Stark shift between sublevels of the upper n and lower level n’ in the line space (the direct product of subspaces of the upper and lower energy levels with the principal quantum numbers n and n’), 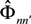 is the electron broadening operator, indexes αβ and α’β’ designate quantum states of the upper and lower levels in the bra and ket vectors of the line space, respectively.
is the electron broadening operator, indexes αβ and α’β’ designate quantum states of the upper and lower levels in the bra and ket vectors of the line space, respectively.
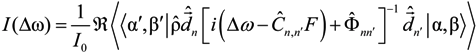
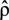 is the operator of density matrix,
is the operator of density matrix, 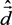 is the operator of dipole moment,
is the operator of dipole moment, 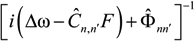 is the operator of resolvent,
is the operator of resolvent, 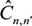 is the operator of the linear Stark shift between sublevels of the upper n and lower level n’ in the line space (the direct product of subspaces of the upper and lower energy levels with the principal quantum numbers n and n’),
is the operator of the linear Stark shift between sublevels of the upper n and lower level n’ in the line space (the direct product of subspaces of the upper and lower energy levels with the principal quantum numbers n and n’), 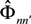 is the electron broadening operator, indexes αβ and α’β’ designate quantum states of the upper and lower levels in the bra and ket vectors of the line space, respectively.
is the electron broadening operator, indexes αβ and α’β’ designate quantum states of the upper and lower levels in the bra and ket vectors of the line space, respectively.Conventionally assuming that density matrix is diagonal in Equation (1), it could be factored out since in the region of small values of microfield all sublevels are degenerate and thus equally populated [17,18,21]. For now, the fine structure splitting is neglected. In this region, the spherical quantum functions (labeled by the quantum numbers n, l, m) form a natural zero basis of the problem due to the spherical symmetry [17,18,21]. Suppose now that the value of the ion microfield is increased, thus the sublevels are split due to the linear Stark effect in the ion electric microfield, and the degeneracy is partially removed. Now the parabolic quantum functions (labeled by the parabolic quantum numbers n1, n2, m) form the natural zero basis of the problem due to the cylindrical symmetry [17,18]. For sufficiently large values of the microfield, the impacts of electrons could not equate populations of sublevels [17,18], and thus the assumption of population equipartition [17,18,21], made as an initial condition, becomes violated. Evidently, since the density matrix could not have the diagonal equipartition form in the two different bases, the initial assumption of the theory [17,18,21] becomes invalid (see [42,43,44,45]). This simple example thus shows that a more consistent approach should simultaneously consider atomic kinetics and formation of spectral line profiles, that just signifies the spectral-kinetic coupling [42,43,44,45,50,53]. Those drawbacks in constructing Stark profiles under assumption of diagonal form of density matrix are weakened partially, if one introduces the dependence of electron impact broadening operator on the Stark levels splitting in the ion microfield [17,18]. Then the non-diagonal matrix elements will be the next order corrections in comparison with the impact widths for large values of the ion microfield, and terms responsible for the line mixing will drop down more rapidly in the line wings [17,18]. On the other hand, for small values of the ion microfield, for which the Stark splitting is of the order of the non-diagonal matrix elements of the electron-impact-broadening operator, the Stark components collapse to the center, thus becoming effectively degenerate [16,17,18], as it should be due to the straightforward physical reasoning (it is worth reminding that it was academician V.M. Galitsky who pointed out this effect to the authors of [16]). This collapse phenomenon is characterized by the appearance of the dependence of the decay constants and intensities of the “redefined” inside the collapse region “Stark components” on the microfield, while the energy splitting of these “Stark components” disappears. These “redefined” Stark components appear in the process of solution of the secular equation for the resolvent operator in the line space [13,14,15]. At F = 0, the intensity of one of the “redefined” components becomes equal to zero, while the other one gives contribution to the center of the profile identical to the contribution of the two symmetrical lateral Stark components without their redefinition during the solution of secular equation for the diagonalization of resolvent [14,15,16]. Therefore the collapse phenomenon of Stark components signifies the necessity to change the wave functions basis from the parabolic to spherical wave functions, or vice versa, depending on whether ion microfield value decreases or increases. Simultaneously, of course, this means the region of singularity for the ST assumption of the density matrix diagonality [21,51]. From this consideration it is obvious that the collapse phenomenon has the kinetic character and in fact is one of the examples of spectral-kinetic coupling. Thus the existence of the collapse phenomenon of Stark components at the same time means the necessity of more complete consideration of the Stark broadening within the formalism of kinetic equations for the density matrix [42,43,44,45,50,55], or in other terms, the necessity of application of the kinetic theory of Stark broadening.
The spectral-kinetic coupling discussed above is a common thing in laser physics [42]. Indeed, the lasing condition is directly connected with the difference of populations that, in turn, is proportional to the non-diagonal matrix elements of the density matrix (called coherences), describing the mixing of the upper and lower levels due to the interaction with the radiation field [42]. In the density matrix formalism it is necessary to solve the kinetic equation that leads to the system of much larger rank in comparison with conventional amplitude approach that significantly complicates finding the solution [42,43,44,45,50,55]. Moreover, the construction of terms, describing sinks and sources, is not straightforward as during their derivation it is necessary to average over a subset of variables taking account of specific physical conditions [37,42,43,44,45]. So, as a rule, these terms could be derivedin a more or less general form only in the impact limit, and their concrete expressions are rather arbitrary [37,42,43,44,45,50,55]. Moreover, even the formula (1) should be changed to a more general and complex expression for the power that is absorbed or emitted by the medium [42,43,44,45,50,55].
3. Ion Dynamics in Statistical and Spectral Characteristics of Stark Profiles
Within the assumptions of ST the plasma ions are considered as static [17,18,21], and hence the resultant Stark profiles are called static or quasistatic. We now consider the ion dynamics effects, i.e., the deviations from the static Stark profiles due to the thermal motion (see, for example, [7,8,9,12,17,18,20,21,23,24,25,26,27,28,29,30,31,32,33,34,35,36,74,75,76]). If these deviations are small enough (called in earlier works “thermal corrections” [7,8,9,12,21,23,24,25]), then it is possible to express them through the second moments of ion microfield time derivatives of the joint distribution functions W( 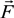 ,
, 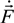 ,
, 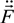 ) of the ion electric microfield strength vector
) of the ion electric microfield strength vector 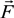 and its first
and its first 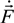 and second
and second 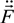 time derivatives [5,6,7,8,9,12,21,23,24,25,48,67]. The basic idea of Markov construction of these joint distributions is that
time derivatives [5,6,7,8,9,12,21,23,24,25,48,67]. The basic idea of Markov construction of these joint distributions is that 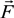 ,
, 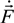 and
and 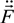 are stochastic independent variables, formed by summation of electric fields or its derivatives over all individual ions of the medium [1,5,6]. So, these probability distribution functions are the many body objects [5,6,7,8,9,12,21,23,24,25,48,67]. However, those joint distributions possess nonzero constraint moments over, for example, microfield time derivatives, the value and direction of electric ion microfield strength vector being fixed [5,6,7,8,9,12,21,23,24,25,48,67]. So, each value of the ion microfield corresponds, for example, in fact to a nonzero “mean” value of the square of its derivative. In other words, it means that by fixing one of the initially independent stochastic variables, the mean values of the other ones become nonzero and functionally dependent on the value of the fixed variable [5,6]. So, the direct correlations between fixed stochastic variables with the moments over the other ones under this condition are evident. Another kind of correlations appears if one considers large values of ion microfields, which are produced by the nearest particle (so called “nearest neighbor approximation”) [5,6,7,8,9,12,21,23,24,25,48,67]. In this case there is a direct proportionality between the value of the ion electric field and its time derivative, where the stochasticity is involved due to another stochastic variable—particle velocity. Indeed, the mean square value of particle velocities is a necessary factor in the second moments over the microfield time derivatives [5,6,7,8,9,12,21,23,24,25,48,67].
are stochastic independent variables, formed by summation of electric fields or its derivatives over all individual ions of the medium [1,5,6]. So, these probability distribution functions are the many body objects [5,6,7,8,9,12,21,23,24,25,48,67]. However, those joint distributions possess nonzero constraint moments over, for example, microfield time derivatives, the value and direction of electric ion microfield strength vector being fixed [5,6,7,8,9,12,21,23,24,25,48,67]. So, each value of the ion microfield corresponds, for example, in fact to a nonzero “mean” value of the square of its derivative. In other words, it means that by fixing one of the initially independent stochastic variables, the mean values of the other ones become nonzero and functionally dependent on the value of the fixed variable [5,6]. So, the direct correlations between fixed stochastic variables with the moments over the other ones under this condition are evident. Another kind of correlations appears if one considers large values of ion microfields, which are produced by the nearest particle (so called “nearest neighbor approximation”) [5,6,7,8,9,12,21,23,24,25,48,67]. In this case there is a direct proportionality between the value of the ion electric field and its time derivative, where the stochasticity is involved due to another stochastic variable—particle velocity. Indeed, the mean square value of particle velocities is a necessary factor in the second moments over the microfield time derivatives [5,6,7,8,9,12,21,23,24,25,48,67].
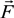 ,
, 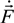 ,
, 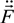 ) of the ion electric microfield strength vector
) of the ion electric microfield strength vector 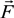 and its first
and its first 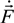 and second
and second 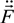 time derivatives [5,6,7,8,9,12,21,23,24,25,48,67]. The basic idea of Markov construction of these joint distributions is that
time derivatives [5,6,7,8,9,12,21,23,24,25,48,67]. The basic idea of Markov construction of these joint distributions is that 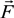 ,
, 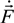 and
and 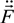 are stochastic independent variables, formed by summation of electric fields or its derivatives over all individual ions of the medium [1,5,6]. So, these probability distribution functions are the many body objects [5,6,7,8,9,12,21,23,24,25,48,67]. However, those joint distributions possess nonzero constraint moments over, for example, microfield time derivatives, the value and direction of electric ion microfield strength vector being fixed [5,6,7,8,9,12,21,23,24,25,48,67]. So, each value of the ion microfield corresponds, for example, in fact to a nonzero “mean” value of the square of its derivative. In other words, it means that by fixing one of the initially independent stochastic variables, the mean values of the other ones become nonzero and functionally dependent on the value of the fixed variable [5,6]. So, the direct correlations between fixed stochastic variables with the moments over the other ones under this condition are evident. Another kind of correlations appears if one considers large values of ion microfields, which are produced by the nearest particle (so called “nearest neighbor approximation”) [5,6,7,8,9,12,21,23,24,25,48,67]. In this case there is a direct proportionality between the value of the ion electric field and its time derivative, where the stochasticity is involved due to another stochastic variable—particle velocity. Indeed, the mean square value of particle velocities is a necessary factor in the second moments over the microfield time derivatives [5,6,7,8,9,12,21,23,24,25,48,67].
are stochastic independent variables, formed by summation of electric fields or its derivatives over all individual ions of the medium [1,5,6]. So, these probability distribution functions are the many body objects [5,6,7,8,9,12,21,23,24,25,48,67]. However, those joint distributions possess nonzero constraint moments over, for example, microfield time derivatives, the value and direction of electric ion microfield strength vector being fixed [5,6,7,8,9,12,21,23,24,25,48,67]. So, each value of the ion microfield corresponds, for example, in fact to a nonzero “mean” value of the square of its derivative. In other words, it means that by fixing one of the initially independent stochastic variables, the mean values of the other ones become nonzero and functionally dependent on the value of the fixed variable [5,6]. So, the direct correlations between fixed stochastic variables with the moments over the other ones under this condition are evident. Another kind of correlations appears if one considers large values of ion microfields, which are produced by the nearest particle (so called “nearest neighbor approximation”) [5,6,7,8,9,12,21,23,24,25,48,67]. In this case there is a direct proportionality between the value of the ion electric field and its time derivative, where the stochasticity is involved due to another stochastic variable—particle velocity. Indeed, the mean square value of particle velocities is a necessary factor in the second moments over the microfield time derivatives [5,6,7,8,9,12,21,23,24,25,48,67].Consider now the components of the microfield time derivative that are perpendicular and parallel to the direction of the ion microfield strength vector [5,6,7,8,9,12,21,23,24,25,48,67]. By calculating the second moments of the perpendicular and parallel components of time derivative, it is possible to establish relations between them in the limits of small and large reduced microfields values β = F/F0 (F0 is the Holtsmark normal field value [1,5,6,7,8,9,12,21,23,24,25,48,67] and F is the current microfield value), assuming for simplicity (but without loss of generality) that ions produce the Coulomb electric field. In the case of β ≪ 1, the ion microfield is formed by many distant ions and due to isotropy the following relation takes place [5,6,24,25]:
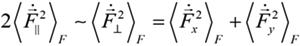
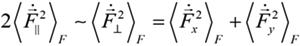
On the other hand, in the case of β ≫ 1, the ion microfield is formed by the nearest neighbor and the corresponding relation shows preferential direction of the microfield fluctuations along the microfield vector [5,6,24,25]:
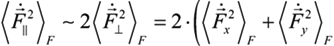
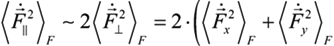
The general expression for 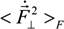 in the case of a Coulomb electric field of point charges is
in the case of a Coulomb electric field of point charges is
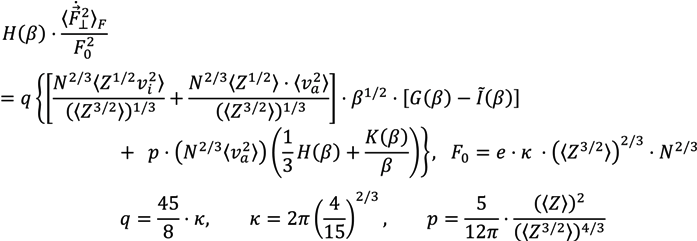
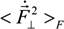 in the case of a Coulomb electric field of point charges is
in the case of a Coulomb electric field of point charges is
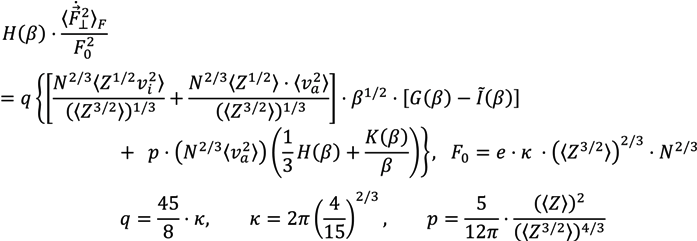
Here e is the elementary charge and 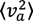 designates the mean of the radiator velocity square. The complex ionization composition is accounted for in Equation (4) (note the generalization of the F0 definition). The definitions of the mean values for composition of various ion species “s” with the charges Zs and thermal velocity vi,s are given by the following relations:
designates the mean of the radiator velocity square. The complex ionization composition is accounted for in Equation (4) (note the generalization of the F0 definition). The definitions of the mean values for composition of various ion species “s” with the charges Zs and thermal velocity vi,s are given by the following relations:
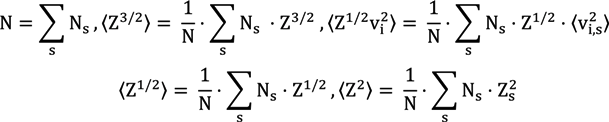
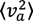 designates the mean of the radiator velocity square. The complex ionization composition is accounted for in Equation (4) (note the generalization of the F0 definition). The definitions of the mean values for composition of various ion species “s” with the charges Zs and thermal velocity vi,s are given by the following relations:
designates the mean of the radiator velocity square. The complex ionization composition is accounted for in Equation (4) (note the generalization of the F0 definition). The definitions of the mean values for composition of various ion species “s” with the charges Zs and thermal velocity vi,s are given by the following relations:
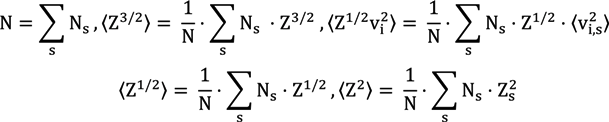
Similarly to Equation (4), an expression for the parallel component 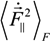 is
is
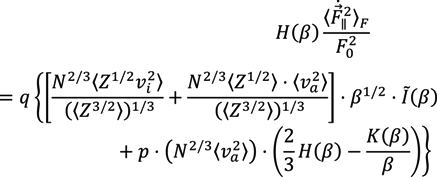 In Equations (4) and (6), H(β) is the Holtsmark function (1). The other functions are related to it through integral or differential equations (see [5,6])
In Equations (4) and (6), H(β) is the Holtsmark function (1). The other functions are related to it through integral or differential equations (see [5,6])
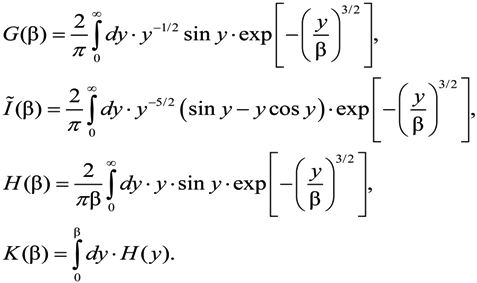
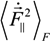 is
is
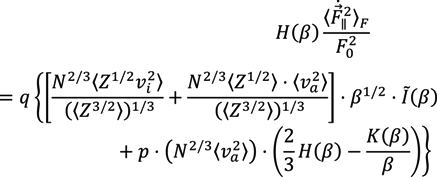
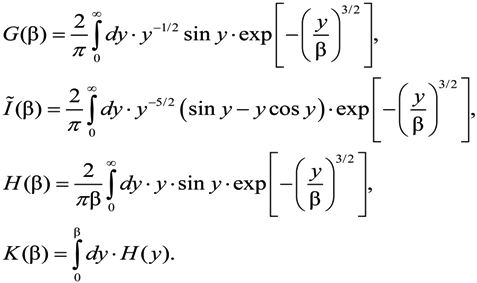
The properties of asymptotics for these functions are given by the relations [3]
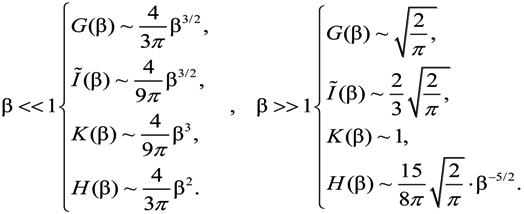 The results of [5,6] for joint distribution functions and their moments for the Coulomb potential were generalized within the Baranger–Mozer scheme, accounting for the electron Debye screening and the ion-ion correlations [38,48,67]. The quantities
The results of [5,6] for joint distribution functions and their moments for the Coulomb potential were generalized within the Baranger–Mozer scheme, accounting for the electron Debye screening and the ion-ion correlations [38,48,67]. The quantities 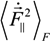 and
and 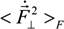 characterize the statistical properties of plasma microfield and play a key role within the idea of thermal corrections to Stark profiles [7,8,9,12,24,25]. The terms proportional to the mean of radiator velocity square in Equations (4) and (6), in square brackets, describe the fluctuations of microfield, induced by the relative thermal motion of the radiator atoms. The other terms, proportional to the mean of radiator velocity square in Equations (4) and (6) besides the factor p are due to the effects of ion-dynamics friction on the radiator motion. As one can see, the latter terms could not be made proportional to the reduced mass of the ion-radiator pair. However, the cases when the influence of the effects of ion-dynamics friction on Stark profiles is significant have not been revealed up to now, since the corresponding deviations of profiles turn out to be small. And indeed, the full scale Molecular Dynamics (MD) simulations confirmed that the effects of ion dynamics could be well described by a so-called “reduced mass” model (RM), where the motion of radiator is neglected for moderately coupled plasma with the ion couplingparameter Γi ≤ 1 [34,61,75]. This greatly facilitates the study of ion dynamics in simulations, since the consistent consideration of radiator motion effects in MD is quite time-consuming. The expressions for the fluctuation rates, Equation (4) and Equation (6), also show that for plasmas with complex ion composition there could be some deviations from the RM model, caused by peculiar distributions of ion charges. As the main precision experiments have, up to now, been conducted for simple charge distributions, the expressions in Equation (5) and Equation (6) could be greatly simplified and the terms, corresponding to the ion friction, could be omitted. Hence the charge distribution is neglected below.
characterize the statistical properties of plasma microfield and play a key role within the idea of thermal corrections to Stark profiles [7,8,9,12,24,25]. The terms proportional to the mean of radiator velocity square in Equations (4) and (6), in square brackets, describe the fluctuations of microfield, induced by the relative thermal motion of the radiator atoms. The other terms, proportional to the mean of radiator velocity square in Equations (4) and (6) besides the factor p are due to the effects of ion-dynamics friction on the radiator motion. As one can see, the latter terms could not be made proportional to the reduced mass of the ion-radiator pair. However, the cases when the influence of the effects of ion-dynamics friction on Stark profiles is significant have not been revealed up to now, since the corresponding deviations of profiles turn out to be small. And indeed, the full scale Molecular Dynamics (MD) simulations confirmed that the effects of ion dynamics could be well described by a so-called “reduced mass” model (RM), where the motion of radiator is neglected for moderately coupled plasma with the ion couplingparameter Γi ≤ 1 [34,61,75]. This greatly facilitates the study of ion dynamics in simulations, since the consistent consideration of radiator motion effects in MD is quite time-consuming. The expressions for the fluctuation rates, Equation (4) and Equation (6), also show that for plasmas with complex ion composition there could be some deviations from the RM model, caused by peculiar distributions of ion charges. As the main precision experiments have, up to now, been conducted for simple charge distributions, the expressions in Equation (5) and Equation (6) could be greatly simplified and the terms, corresponding to the ion friction, could be omitted. Hence the charge distribution is neglected below.
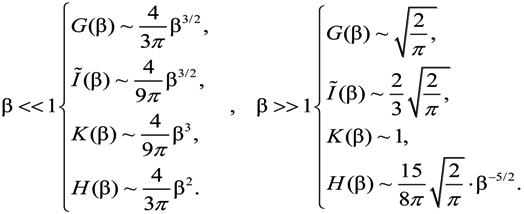
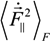 and
and 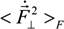 characterize the statistical properties of plasma microfield and play a key role within the idea of thermal corrections to Stark profiles [7,8,9,12,24,25]. The terms proportional to the mean of radiator velocity square in Equations (4) and (6), in square brackets, describe the fluctuations of microfield, induced by the relative thermal motion of the radiator atoms. The other terms, proportional to the mean of radiator velocity square in Equations (4) and (6) besides the factor p are due to the effects of ion-dynamics friction on the radiator motion. As one can see, the latter terms could not be made proportional to the reduced mass of the ion-radiator pair. However, the cases when the influence of the effects of ion-dynamics friction on Stark profiles is significant have not been revealed up to now, since the corresponding deviations of profiles turn out to be small. And indeed, the full scale Molecular Dynamics (MD) simulations confirmed that the effects of ion dynamics could be well described by a so-called “reduced mass” model (RM), where the motion of radiator is neglected for moderately coupled plasma with the ion couplingparameter Γi ≤ 1 [34,61,75]. This greatly facilitates the study of ion dynamics in simulations, since the consistent consideration of radiator motion effects in MD is quite time-consuming. The expressions for the fluctuation rates, Equation (4) and Equation (6), also show that for plasmas with complex ion composition there could be some deviations from the RM model, caused by peculiar distributions of ion charges. As the main precision experiments have, up to now, been conducted for simple charge distributions, the expressions in Equation (5) and Equation (6) could be greatly simplified and the terms, corresponding to the ion friction, could be omitted. Hence the charge distribution is neglected below.
characterize the statistical properties of plasma microfield and play a key role within the idea of thermal corrections to Stark profiles [7,8,9,12,24,25]. The terms proportional to the mean of radiator velocity square in Equations (4) and (6), in square brackets, describe the fluctuations of microfield, induced by the relative thermal motion of the radiator atoms. The other terms, proportional to the mean of radiator velocity square in Equations (4) and (6) besides the factor p are due to the effects of ion-dynamics friction on the radiator motion. As one can see, the latter terms could not be made proportional to the reduced mass of the ion-radiator pair. However, the cases when the influence of the effects of ion-dynamics friction on Stark profiles is significant have not been revealed up to now, since the corresponding deviations of profiles turn out to be small. And indeed, the full scale Molecular Dynamics (MD) simulations confirmed that the effects of ion dynamics could be well described by a so-called “reduced mass” model (RM), where the motion of radiator is neglected for moderately coupled plasma with the ion couplingparameter Γi ≤ 1 [34,61,75]. This greatly facilitates the study of ion dynamics in simulations, since the consistent consideration of radiator motion effects in MD is quite time-consuming. The expressions for the fluctuation rates, Equation (4) and Equation (6), also show that for plasmas with complex ion composition there could be some deviations from the RM model, caused by peculiar distributions of ion charges. As the main precision experiments have, up to now, been conducted for simple charge distributions, the expressions in Equation (5) and Equation (6) could be greatly simplified and the terms, corresponding to the ion friction, could be omitted. Hence the charge distribution is neglected below.By analyzing the difference between profiles formed for two different reduced masses of the plasma ions, it is seen that within the idea of thermal corrections they are proportional to the second moments of parallel 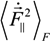 and perpendicular
and perpendicular 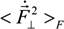 components of the ion microfield fluctuations. The general analysis, performed in different approximations [7,8,9,12,24,25], has shown that the ion dynamical perturbations of Stark profiles are controlled by three main mechanisms. The first mechanism is due to the amplitude modulation, induced by the rotation of the atomic dipole along with the rotating ion microfield [12]. Due to the amplitude modulation, the projections of the atomic dipole on the coordinate axis, being at rest, are changing (or “modulated”), while the atomic dipole rotates together with the rotation of the electric microfield strength vector. The second mechanism exists due to the atomic dipole inertia with respect to the microfield rotation, and results in nonadiabatic transitions between states defined in the frame with the quantization axis along the rotating field direction [12]. The third mechanism (historically considered the first) is the phase modulation related to changes in the microfield magnitude [7,8,9,12,24,25]. Only this mechanism was taken into account in the earlier works (in the 1950s) [7,8,9], where the Stark broadening by ions was analyzed in the adiabatic approximation, i.e., only within the framework of phase modulation or frequency Stark shift [21]. As it was demonstrated in the works [24,25] within the approach of thermal corrections, the amplitude modulation gives the largest contribution to the Stark contour deformation due to ion dynamics in the vicinity of the line center. The general ideas of amplitude modulation, non-adiabatic effects and usage of the electron broadening for extending the theory of thermal corrections to the line center were proposed by Gennadii V. Sholin.
components of the ion microfield fluctuations. The general analysis, performed in different approximations [7,8,9,12,24,25], has shown that the ion dynamical perturbations of Stark profiles are controlled by three main mechanisms. The first mechanism is due to the amplitude modulation, induced by the rotation of the atomic dipole along with the rotating ion microfield [12]. Due to the amplitude modulation, the projections of the atomic dipole on the coordinate axis, being at rest, are changing (or “modulated”), while the atomic dipole rotates together with the rotation of the electric microfield strength vector. The second mechanism exists due to the atomic dipole inertia with respect to the microfield rotation, and results in nonadiabatic transitions between states defined in the frame with the quantization axis along the rotating field direction [12]. The third mechanism (historically considered the first) is the phase modulation related to changes in the microfield magnitude [7,8,9,12,24,25]. Only this mechanism was taken into account in the earlier works (in the 1950s) [7,8,9], where the Stark broadening by ions was analyzed in the adiabatic approximation, i.e., only within the framework of phase modulation or frequency Stark shift [21]. As it was demonstrated in the works [24,25] within the approach of thermal corrections, the amplitude modulation gives the largest contribution to the Stark contour deformation due to ion dynamics in the vicinity of the line center. The general ideas of amplitude modulation, non-adiabatic effects and usage of the electron broadening for extending the theory of thermal corrections to the line center were proposed by Gennadii V. Sholin.
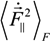 and perpendicular
and perpendicular 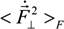 components of the ion microfield fluctuations. The general analysis, performed in different approximations [7,8,9,12,24,25], has shown that the ion dynamical perturbations of Stark profiles are controlled by three main mechanisms. The first mechanism is due to the amplitude modulation, induced by the rotation of the atomic dipole along with the rotating ion microfield [12]. Due to the amplitude modulation, the projections of the atomic dipole on the coordinate axis, being at rest, are changing (or “modulated”), while the atomic dipole rotates together with the rotation of the electric microfield strength vector. The second mechanism exists due to the atomic dipole inertia with respect to the microfield rotation, and results in nonadiabatic transitions between states defined in the frame with the quantization axis along the rotating field direction [12]. The third mechanism (historically considered the first) is the phase modulation related to changes in the microfield magnitude [7,8,9,12,24,25]. Only this mechanism was taken into account in the earlier works (in the 1950s) [7,8,9], where the Stark broadening by ions was analyzed in the adiabatic approximation, i.e., only within the framework of phase modulation or frequency Stark shift [21]. As it was demonstrated in the works [24,25] within the approach of thermal corrections, the amplitude modulation gives the largest contribution to the Stark contour deformation due to ion dynamics in the vicinity of the line center. The general ideas of amplitude modulation, non-adiabatic effects and usage of the electron broadening for extending the theory of thermal corrections to the line center were proposed by Gennadii V. Sholin.
components of the ion microfield fluctuations. The general analysis, performed in different approximations [7,8,9,12,24,25], has shown that the ion dynamical perturbations of Stark profiles are controlled by three main mechanisms. The first mechanism is due to the amplitude modulation, induced by the rotation of the atomic dipole along with the rotating ion microfield [12]. Due to the amplitude modulation, the projections of the atomic dipole on the coordinate axis, being at rest, are changing (or “modulated”), while the atomic dipole rotates together with the rotation of the electric microfield strength vector. The second mechanism exists due to the atomic dipole inertia with respect to the microfield rotation, and results in nonadiabatic transitions between states defined in the frame with the quantization axis along the rotating field direction [12]. The third mechanism (historically considered the first) is the phase modulation related to changes in the microfield magnitude [7,8,9,12,24,25]. Only this mechanism was taken into account in the earlier works (in the 1950s) [7,8,9], where the Stark broadening by ions was analyzed in the adiabatic approximation, i.e., only within the framework of phase modulation or frequency Stark shift [21]. As it was demonstrated in the works [24,25] within the approach of thermal corrections, the amplitude modulation gives the largest contribution to the Stark contour deformation due to ion dynamics in the vicinity of the line center. The general ideas of amplitude modulation, non-adiabatic effects and usage of the electron broadening for extending the theory of thermal corrections to the line center were proposed by Gennadii V. Sholin.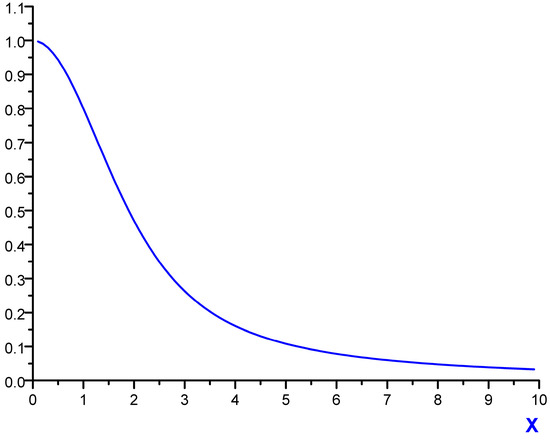
Figure 1.
Function M⊥(x).
Recall that the thermal corrections are defined as a difference between the total profile, calculated accounting for perturbations due to ion dynamics, and the Stark profile within the ST approach [24,25]. In the case of equal temperatures of plasma ions and radiators, as well as electrons, this gives for Ly-alpha (compare with [24,25]) in the approximation of isolated individual Stark components (i.e., neglecting non-diagonal elements of the electron impact broadening operator)
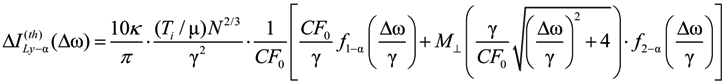 The f1−α(x) function describes the central component contribution to the Stark profile due to amplitude modulation, while the f2−α(x) function describes the contribution of lateral components to the Stark profile, related to the combined action of the amplitude modulation and non-adiabatic effects. Below, the explicit expressions for f1−α(x), f2−α(x) are given (Γ(z) is the gamma function):
The f1−α(x) function describes the central component contribution to the Stark profile due to amplitude modulation, while the f2−α(x) function describes the contribution of lateral components to the Stark profile, related to the combined action of the amplitude modulation and non-adiabatic effects. Below, the explicit expressions for f1−α(x), f2−α(x) are given (Γ(z) is the gamma function):
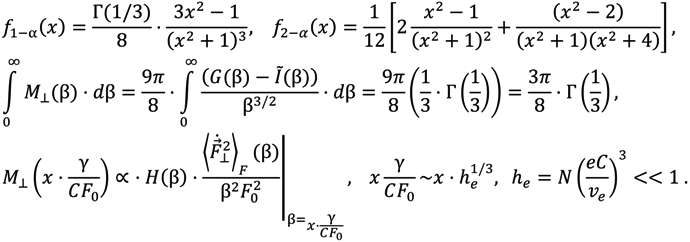 In (9) and (10) the
In (9) and (10) the 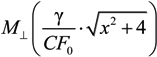 dimensionless function is introduced (see Figure 1), proportional to the second moment of the microfield time derivative component, perpendicular to the microfield direction according to Equation (4) and defining in fact the mean square of microfield rotation frequency. It is defined in such a way, that M⊥(0) = 1, while the corresponding constant in the limit of β ≪ 1 was included in the definition of the f2−α(x) function. The behavior of f1−α(x) and f2−α(x) is presented in the Figure 2 and Figure 3, respectively. The parameter γ in Equations (9) and (10) is the impact electron width of the central component in the parabolic basis. As it follows from the results of [24,25], the corrections due to the ion dynamics effects are negative in the center of a line with the central components, corresponding to decreasing of the intensity in the line center due to the ion dynamics effects and its increasing in the shoulders (the transient region between approximately the half width and the nearest line wings). As the thermal corrections have perturbative character, functions f1−α(x) and f2−α(x) have zero integrals. So, due to ion dynamics effects, the intensity is redistributed from the line center, increasing the total width of the lines with central Stark components [24,25]. These general features are confirmed below in the next Section 4 using MD simulations (see also [75]), that are believed to be not limited by applicability conditions of the perturbation approach [24,25]. It should be noted that within the approach of [24,25], an exact analytical expression due to the ion-dynamics corrections for Ly-alpha, accounting for the collapse of the lateral Stark components [13,14,15], was also derived [24]. It has a rather complex structure and is not presented here, but the comparison of its functional behavior with the approximation of isolated individual Stark components f2−α(x) is shown in Figure 3.
dimensionless function is introduced (see Figure 1), proportional to the second moment of the microfield time derivative component, perpendicular to the microfield direction according to Equation (4) and defining in fact the mean square of microfield rotation frequency. It is defined in such a way, that M⊥(0) = 1, while the corresponding constant in the limit of β ≪ 1 was included in the definition of the f2−α(x) function. The behavior of f1−α(x) and f2−α(x) is presented in the Figure 2 and Figure 3, respectively. The parameter γ in Equations (9) and (10) is the impact electron width of the central component in the parabolic basis. As it follows from the results of [24,25], the corrections due to the ion dynamics effects are negative in the center of a line with the central components, corresponding to decreasing of the intensity in the line center due to the ion dynamics effects and its increasing in the shoulders (the transient region between approximately the half width and the nearest line wings). As the thermal corrections have perturbative character, functions f1−α(x) and f2−α(x) have zero integrals. So, due to ion dynamics effects, the intensity is redistributed from the line center, increasing the total width of the lines with central Stark components [24,25]. These general features are confirmed below in the next Section 4 using MD simulations (see also [75]), that are believed to be not limited by applicability conditions of the perturbation approach [24,25]. It should be noted that within the approach of [24,25], an exact analytical expression due to the ion-dynamics corrections for Ly-alpha, accounting for the collapse of the lateral Stark components [13,14,15], was also derived [24]. It has a rather complex structure and is not presented here, but the comparison of its functional behavior with the approximation of isolated individual Stark components f2−α(x) is shown in Figure 3.
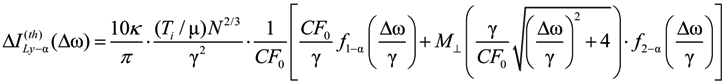
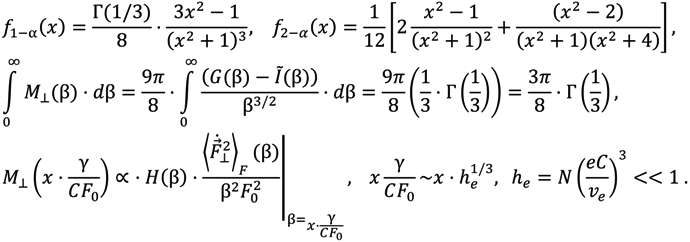
 dimensionless function is introduced (see Figure 1), proportional to the second moment of the microfield time derivative component, perpendicular to the microfield direction according to Equation (4) and defining in fact the mean square of microfield rotation frequency. It is defined in such a way, that M⊥(0) = 1, while the corresponding constant in the limit of β ≪ 1 was included in the definition of the f2−α(x) function. The behavior of f1−α(x) and f2−α(x) is presented in the Figure 2 and Figure 3, respectively. The parameter γ in Equations (9) and (10) is the impact electron width of the central component in the parabolic basis. As it follows from the results of [24,25], the corrections due to the ion dynamics effects are negative in the center of a line with the central components, corresponding to decreasing of the intensity in the line center due to the ion dynamics effects and its increasing in the shoulders (the transient region between approximately the half width and the nearest line wings). As the thermal corrections have perturbative character, functions f1−α(x) and f2−α(x) have zero integrals. So, due to ion dynamics effects, the intensity is redistributed from the line center, increasing the total width of the lines with central Stark components [24,25]. These general features are confirmed below in the next Section 4 using MD simulations (see also [75]), that are believed to be not limited by applicability conditions of the perturbation approach [24,25]. It should be noted that within the approach of [24,25], an exact analytical expression due to the ion-dynamics corrections for Ly-alpha, accounting for the collapse of the lateral Stark components [13,14,15], was also derived [24]. It has a rather complex structure and is not presented here, but the comparison of its functional behavior with the approximation of isolated individual Stark components f2−α(x) is shown in Figure 3.
dimensionless function is introduced (see Figure 1), proportional to the second moment of the microfield time derivative component, perpendicular to the microfield direction according to Equation (4) and defining in fact the mean square of microfield rotation frequency. It is defined in such a way, that M⊥(0) = 1, while the corresponding constant in the limit of β ≪ 1 was included in the definition of the f2−α(x) function. The behavior of f1−α(x) and f2−α(x) is presented in the Figure 2 and Figure 3, respectively. The parameter γ in Equations (9) and (10) is the impact electron width of the central component in the parabolic basis. As it follows from the results of [24,25], the corrections due to the ion dynamics effects are negative in the center of a line with the central components, corresponding to decreasing of the intensity in the line center due to the ion dynamics effects and its increasing in the shoulders (the transient region between approximately the half width and the nearest line wings). As the thermal corrections have perturbative character, functions f1−α(x) and f2−α(x) have zero integrals. So, due to ion dynamics effects, the intensity is redistributed from the line center, increasing the total width of the lines with central Stark components [24,25]. These general features are confirmed below in the next Section 4 using MD simulations (see also [75]), that are believed to be not limited by applicability conditions of the perturbation approach [24,25]. It should be noted that within the approach of [24,25], an exact analytical expression due to the ion-dynamics corrections for Ly-alpha, accounting for the collapse of the lateral Stark components [13,14,15], was also derived [24]. It has a rather complex structure and is not presented here, but the comparison of its functional behavior with the approximation of isolated individual Stark components f2−α(x) is shown in Figure 3.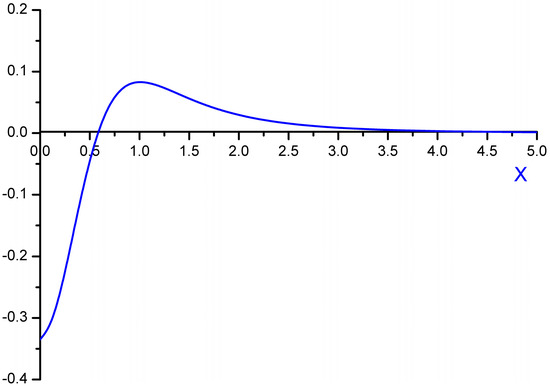
Figure 2.
Function f1−α(x).
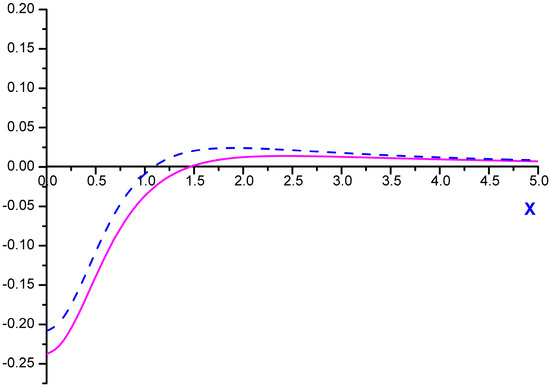
Figure 3.
Function f2−α(x)—dashed line. The solid line is the behavior of f2−α(x;ε = 1), obtained in numerical calculations accounting for the collapse effect [24].
It is interesting to note several properties of the above-mentioned complex function f2−α(x;ε), which takes into account the collapse effect of lateral Stark components (where ε is the ratio of the non-diagonal matrix element of the electron impact broadening operator to the electron impact width of the central component of Ly-alpha). Neglecting dependence of the non-diagonal matrix element of the electron impact broadening operator on the value of the ion microfield F according to [17,18], which mainly is important for large F for transition from the overlapping to isolated broadening regime of the Stark components (since ε(β) → 0 for β → ∞), corresponds to ε = 1. The ratio of the lateral component electron impact width to the central component electron impact width is equal to 2 for Ly-alpha in parabolic basis [17,18]. This is reflected in the argument of  , whose value is taken in the pole of resolvent
, whose value is taken in the pole of resolvent 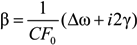 , corresponding to the one lateral component. So, remembering that the central component is more intense than the lateral ones, its strong influence on the Ly-alpha Stark shape becomes obvious. Comparing f2−α(x;ε = 0) with f2−α(x;ε = 1) at x = 0, their ratio comes out to be about 1.26 [24]. At first glance, putting ε = 0 in f2−α(x;ε) allows obtaining the limit of isolated Stark components, but it turns out that f2−α(x;ε = 0) ≠ f2−α(x). This means that there is no commutativity in the sequence of performed mathematical operations, since the f2−α(x;ε) function is obtained in the solution of secular problem and inverting the resolvent. It is seen in Figure 3, that the difference between the approximation of isolated components (f2−α(x)) and the exact solution accounting for the collapse effect (f2−α(x;ε = 1)) at x = 0 is noticeably smaller than that between f2−α(0;ε = 1) and f2−α(0;ε = 0), as their ratio f2−α(0;ε = 1)/f2−α(0) is only about ~1.14. Thus this comparison demonstrates an acceptable accuracy of the approximation of isolated individual Stark components [18,19] for calculations of the thermal corrections to the Ly-alpha Stark profile.
, corresponding to the one lateral component. So, remembering that the central component is more intense than the lateral ones, its strong influence on the Ly-alpha Stark shape becomes obvious. Comparing f2−α(x;ε = 0) with f2−α(x;ε = 1) at x = 0, their ratio comes out to be about 1.26 [24]. At first glance, putting ε = 0 in f2−α(x;ε) allows obtaining the limit of isolated Stark components, but it turns out that f2−α(x;ε = 0) ≠ f2−α(x). This means that there is no commutativity in the sequence of performed mathematical operations, since the f2−α(x;ε) function is obtained in the solution of secular problem and inverting the resolvent. It is seen in Figure 3, that the difference between the approximation of isolated components (f2−α(x)) and the exact solution accounting for the collapse effect (f2−α(x;ε = 1)) at x = 0 is noticeably smaller than that between f2−α(0;ε = 1) and f2−α(0;ε = 0), as their ratio f2−α(0;ε = 1)/f2−α(0) is only about ~1.14. Thus this comparison demonstrates an acceptable accuracy of the approximation of isolated individual Stark components [18,19] for calculations of the thermal corrections to the Ly-alpha Stark profile.
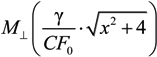 , whose value is taken in the pole of resolvent
, whose value is taken in the pole of resolvent 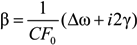 , corresponding to the one lateral component. So, remembering that the central component is more intense than the lateral ones, its strong influence on the Ly-alpha Stark shape becomes obvious. Comparing f2−α(x;ε = 0) with f2−α(x;ε = 1) at x = 0, their ratio comes out to be about 1.26 [24]. At first glance, putting ε = 0 in f2−α(x;ε) allows obtaining the limit of isolated Stark components, but it turns out that f2−α(x;ε = 0) ≠ f2−α(x). This means that there is no commutativity in the sequence of performed mathematical operations, since the f2−α(x;ε) function is obtained in the solution of secular problem and inverting the resolvent. It is seen in Figure 3, that the difference between the approximation of isolated components (f2−α(x)) and the exact solution accounting for the collapse effect (f2−α(x;ε = 1)) at x = 0 is noticeably smaller than that between f2−α(0;ε = 1) and f2−α(0;ε = 0), as their ratio f2−α(0;ε = 1)/f2−α(0) is only about ~1.14. Thus this comparison demonstrates an acceptable accuracy of the approximation of isolated individual Stark components [18,19] for calculations of the thermal corrections to the Ly-alpha Stark profile.
, corresponding to the one lateral component. So, remembering that the central component is more intense than the lateral ones, its strong influence on the Ly-alpha Stark shape becomes obvious. Comparing f2−α(x;ε = 0) with f2−α(x;ε = 1) at x = 0, their ratio comes out to be about 1.26 [24]. At first glance, putting ε = 0 in f2−α(x;ε) allows obtaining the limit of isolated Stark components, but it turns out that f2−α(x;ε = 0) ≠ f2−α(x). This means that there is no commutativity in the sequence of performed mathematical operations, since the f2−α(x;ε) function is obtained in the solution of secular problem and inverting the resolvent. It is seen in Figure 3, that the difference between the approximation of isolated components (f2−α(x)) and the exact solution accounting for the collapse effect (f2−α(x;ε = 1)) at x = 0 is noticeably smaller than that between f2−α(0;ε = 1) and f2−α(0;ε = 0), as their ratio f2−α(0;ε = 1)/f2−α(0) is only about ~1.14. Thus this comparison demonstrates an acceptable accuracy of the approximation of isolated individual Stark components [18,19] for calculations of the thermal corrections to the Ly-alpha Stark profile.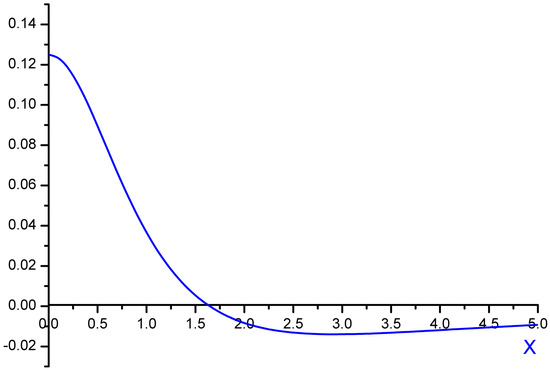
Figure 4.
The function f2−β(x).
Similar to Equations (9) and (10), result for Ly-beta is [24,25].
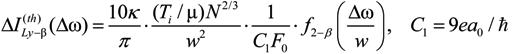 where f2−β(x) describes the lateral components contribution to the Stark profile, comprising to the action of only non-adiabatic effects in the case of lines without the central component [24,25],
where f2−β(x) describes the lateral components contribution to the Stark profile, comprising to the action of only non-adiabatic effects in the case of lines without the central component [24,25],
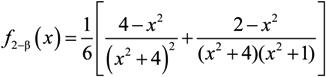 and “w” is the electron impact width of the Stark sublevel (002), designated by parabolic quantum numbers. The graph of f2−β(x) is presented in the Figure 4. The case of Lyman-beta illustrates that the ion dynamics effect increases the intensity in the center of the line without the central components and slightly decreases its width due to the lowering intensity in the nearest wings that is clearly seen in Figure 4.
and “w” is the electron impact width of the Stark sublevel (002), designated by parabolic quantum numbers. The graph of f2−β(x) is presented in the Figure 4. The case of Lyman-beta illustrates that the ion dynamics effect increases the intensity in the center of the line without the central components and slightly decreases its width due to the lowering intensity in the nearest wings that is clearly seen in Figure 4.
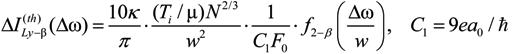
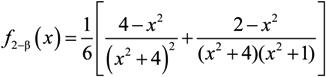
Expressions (9) and (12) are derived assuming the concrete numerical values of the Stark shifts and dipole matrix elements, calculated in the parabolic basis for corresponding Stark sublevels and components of considered transitions [17,18]. The above results are obtained analytically by the perturbation theory for non-Hermitian operators and with the analytical continuation of the microfield distribution function and the second moments of its time derivatives that were shown to possess analytical properties in the upper complex plane (see [24,25]). As it follows from the validity conditions of this approach, the main contribution to integrals, describing the amplitude modulation of lines with central components, give regions of detunings near the line center, where the argument of the universal functions, describing the second moments of derivatives, is small. Moreover, the principal term of the expansion, corresponding to the amplitude modulation of the central component, does not depend on the microfield, that allows for integrating over the microfield distribution analytically [24,25]. On the other hand, the principal terms of the expansion for the lateral components related to the amplitude modulation and non-adiabatic effects, are obtained analytically via integration in the upper half of the complex plane [24,25]. As it follows from the asymptotic properties of these functions in the region of small values of argument, the effective frequency of rotations is practically constant. Due to this, in [24,25] the value of the dimensionless function M⊥(z) in Equations (9) and (11) was substituted for small values of argument near zero, corresponding to the line center. Moreover, as M⊥(z) varies very slowly on the characteristic frequency scale in the line center, in [24,25] its variation in the numerical results of Equations (9) and (11) was neglected. It allowed to neglect the difference of values of 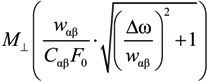 standing beside the terms, obtained due to residue in the various poles, and equate them in fact to the common constant due to the smallness of argument. Then summation of terms due to perturbation expansion leads to more simple formulas, which are expressed as the functions f, and finalized by introduction of some general scales for the Stark constants C and impact widths w. Moreover, the significant simplification of the result also is due to the constant output of the M⊥(z) function in the region near the line center, where its argument is small. Then all the derivatives of M⊥(z) turn out to be zero (or could be considered as higher order terms of expansion), thus one is left only with the derivatives of the dispersion functions in perturbation series (see [24,25]). However, from the principal point of view, it is important that functional behavior of M⊥(z) is proportional to the fluctuation of microfield component perpendicular to the microfield direction in Equations (4) and (10). It could be kept in the final result which would then look more cumbersome in this case than expressions (11) and (12). Indeed, the result would contain the sum of contributions of each Stark component, determined by its values of the electron impact widths and Stark constants, being multiplied by M⊥(z) from the different arguments, as explained just above (see explicit formulas for perturbation expansion, presented in [24,25]).
standing beside the terms, obtained due to residue in the various poles, and equate them in fact to the common constant due to the smallness of argument. Then summation of terms due to perturbation expansion leads to more simple formulas, which are expressed as the functions f, and finalized by introduction of some general scales for the Stark constants C and impact widths w. Moreover, the significant simplification of the result also is due to the constant output of the M⊥(z) function in the region near the line center, where its argument is small. Then all the derivatives of M⊥(z) turn out to be zero (or could be considered as higher order terms of expansion), thus one is left only with the derivatives of the dispersion functions in perturbation series (see [24,25]). However, from the principal point of view, it is important that functional behavior of M⊥(z) is proportional to the fluctuation of microfield component perpendicular to the microfield direction in Equations (4) and (10). It could be kept in the final result which would then look more cumbersome in this case than expressions (11) and (12). Indeed, the result would contain the sum of contributions of each Stark component, determined by its values of the electron impact widths and Stark constants, being multiplied by M⊥(z) from the different arguments, as explained just above (see explicit formulas for perturbation expansion, presented in [24,25]).
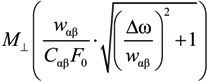 standing beside the terms, obtained due to residue in the various poles, and equate them in fact to the common constant due to the smallness of argument. Then summation of terms due to perturbation expansion leads to more simple formulas, which are expressed as the functions f, and finalized by introduction of some general scales for the Stark constants C and impact widths w. Moreover, the significant simplification of the result also is due to the constant output of the M⊥(z) function in the region near the line center, where its argument is small. Then all the derivatives of M⊥(z) turn out to be zero (or could be considered as higher order terms of expansion), thus one is left only with the derivatives of the dispersion functions in perturbation series (see [24,25]). However, from the principal point of view, it is important that functional behavior of M⊥(z) is proportional to the fluctuation of microfield component perpendicular to the microfield direction in Equations (4) and (10). It could be kept in the final result which would then look more cumbersome in this case than expressions (11) and (12). Indeed, the result would contain the sum of contributions of each Stark component, determined by its values of the electron impact widths and Stark constants, being multiplied by M⊥(z) from the different arguments, as explained just above (see explicit formulas for perturbation expansion, presented in [24,25]).
standing beside the terms, obtained due to residue in the various poles, and equate them in fact to the common constant due to the smallness of argument. Then summation of terms due to perturbation expansion leads to more simple formulas, which are expressed as the functions f, and finalized by introduction of some general scales for the Stark constants C and impact widths w. Moreover, the significant simplification of the result also is due to the constant output of the M⊥(z) function in the region near the line center, where its argument is small. Then all the derivatives of M⊥(z) turn out to be zero (or could be considered as higher order terms of expansion), thus one is left only with the derivatives of the dispersion functions in perturbation series (see [24,25]). However, from the principal point of view, it is important that functional behavior of M⊥(z) is proportional to the fluctuation of microfield component perpendicular to the microfield direction in Equations (4) and (10). It could be kept in the final result which would then look more cumbersome in this case than expressions (11) and (12). Indeed, the result would contain the sum of contributions of each Stark component, determined by its values of the electron impact widths and Stark constants, being multiplied by M⊥(z) from the different arguments, as explained just above (see explicit formulas for perturbation expansion, presented in [24,25]).In the case of a line without the central component, the ion dynamics corrections are positive in the line center (see Figure 4). Thus, the intensity in the center increases, while it is decreases in the nearest wings (see Figure 4). The results of [24,25] qualitatively confirm the experimental patterns, observed in [20,22,27,31]. Also in [24,25] the difference profiles, corresponding to two different values of the reduced mass, were considered and compared with the results of experiments [20,22] for the Balmer-beta line. It was shown that relative behavior of the thermal corrections versus wavelength detuning from the line center Δλ describes sufficiently accurately [24,25] the experimental results [20,22]. In [24,25] the difference profiles δR(Δλ), corresponding to the two different values of the reduced mass, were also considered. Within the notion of thermal corrections this difference is
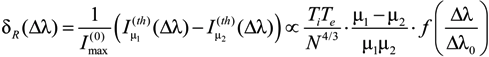 In Equation (13) f(x) is the relative behavior of the difference profile in the line center. In [24,25] it was shown, that the dependences versus frequency detunings from the line center, spanned by the profile difference (10), coincide well with the corresponding experimental data for the Balmer-beta line, given in [20,22].
In Equation (13) f(x) is the relative behavior of the difference profile in the line center. In [24,25] it was shown, that the dependences versus frequency detunings from the line center, spanned by the profile difference (10), coincide well with the corresponding experimental data for the Balmer-beta line, given in [20,22].
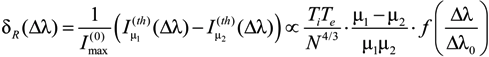
So, according to the results and ideas of [24,25] and the discussion above, the difference profiles are proportional to the statistical characteristics of microfield and, more precisely, to the characteristics of the microfield fluctuations, related to the microfield rotations (compare with [24,25]). That is why this property could in principal be used to study microfield statistics in experiments and simulations.
In short time the ideas of [12,24,25] were accepted and the notion of dominating effect of microfield rotation into ion dynamics became widely spread [30,33].
Nowadays, the computer simulation technique has become a powerful tool for studying the physics of various non-stationary processes, and particularly plasma microfield ion dynamics effects. However, computer simulations are rather time-consuming and at present impractical for large-scale calculations. Thus, simultaneously with the computer simulations the development of model approaches, that accounted for the ion dynamical effects in an approximate manner, were carried on independently [32,33,34,35,36,37,39,41,46,49,53,54,56,59,60,61,62,63,64,68,69,70,71,72,73,74,75,76]. The first such model (actually, predating computer simulations) was MMM [14,15,28,29,52], later followed by various applications of the BID [37,71] and Frequency Fluctuation Model (FFM) [46,56,66] methods. Notably, neither of these models explicitly accounts for the effects of microfield rotation [24,25,30,33,53].
It is necessary now to consider the formal conditions of validity of thermal corrections approach [7,8,9,12,24,25]. The results of reference [12] are applicable only for the lateral Stark components and quasistatic ions, when
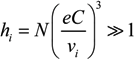 and in the spectral region of detunings from the line center Δω, corresponding to the line wings
and in the spectral region of detunings from the line center Δω, corresponding to the line wings
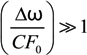 On the other hand, the spectral region of applicability of the theoretical approach in [24,25] is expanded till the line center only due to the additional inclusion into consideration, besides the quasistatic ions -Equation (14), of the electron impact effect, that allowed to analyze the central Stark components, too. However, the applicability criteria of [24,25] are rather complicated and depend on the spectral region under consideration. For example, in the line center for the central Stark components the criterion of validity of [24] has the form
On the other hand, the spectral region of applicability of the theoretical approach in [24,25] is expanded till the line center only due to the additional inclusion into consideration, besides the quasistatic ions -Equation (14), of the electron impact effect, that allowed to analyze the central Stark components, too. However, the applicability criteria of [24,25] are rather complicated and depend on the spectral region under consideration. For example, in the line center for the central Stark components the criterion of validity of [24] has the form
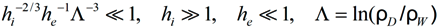 where ρD and ρW designate the Debye and Weisskopf radii, respectively (see [21,45,58]). It is seen that condition (16) (and other criteria from [24,25]) is difficult to fulfill, which somewhat limits the practical applicability of the theory. For the line wings, the results of [24,25] reproduce the results of the earlier work [12] under the criterion for the separate Stark components
where ρD and ρW designate the Debye and Weisskopf radii, respectively (see [21,45,58]). It is seen that condition (16) (and other criteria from [24,25]) is difficult to fulfill, which somewhat limits the practical applicability of the theory. For the line wings, the results of [24,25] reproduce the results of the earlier work [12] under the criterion for the separate Stark components
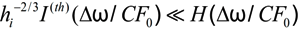 where I(th)(Δω/CF0) is the thermal correction profile that represents, within the assumptions of [18,19], a sum of contributions from the amplitude modulation, non-adiabatic effects, and phase modulation, and H (Δω/CF0) is a microfield distribution function.
where I(th)(Δω/CF0) is the thermal correction profile that represents, within the assumptions of [18,19], a sum of contributions from the amplitude modulation, non-adiabatic effects, and phase modulation, and H (Δω/CF0) is a microfield distribution function.
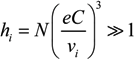
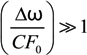
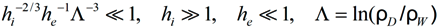
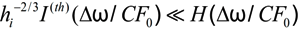
The results of [12,24,25] proved the numerical predominance of amplitude modulation and non-adiabatic effects contributions over the phase modulation one in the line wings, where the perturbation approach of [12,24,25] is applicable practically for any plasma parameter. The magnitudes of amplitude modulation and non-adiabatic effects contributions are of the same order in this region of Stark profiles [12]. Moreover, the amplitude modulation and non-adiabatic effects contributions have the same sign, which is opposite to the sign of the phase modulation correction [12]. So, the cancellation of non-adiabatic and atom reorientation effects (amplitude modulation) does not take place, as was proposed earlier by Spitzer in his very instructive papers [2,3,4], and they play the dominant role in the line wings.
4. Ion Dynamics Modeling and Statistical-Dynamical Coupling
The work during the preparation of SLSP workshops and along with their conduction revealed unexpected spread of results of various computational models, done for ion perturbers only (see for example [74,75,76]).
In this respect, the study of directionality correlations, presented at SLSP-1 [65], inspired the authors to test whether the rotation effects really are responsible for a dominating contribution according to the predictions of [24,25].
To this end the Ly-α profile was calculated using a computer simulation (CS) method [57]. A one-component plasma (OCP) was assumed, consisting only of one type of ions. Furthermore, to avoid effects of plasma non-ideality such as the Debye screening, the ions were assumed moving along straight path trajectories. Time histories of the electric field 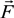 (t), formed by the ions, were stored, to be used as an input when numerically solving the time-dependent Schrödinger equation of the hydrogen atom.
(t), formed by the ions, were stored, to be used as an input when numerically solving the time-dependent Schrödinger equation of the hydrogen atom.
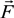 (t), formed by the ions, were stored, to be used as an input when numerically solving the time-dependent Schrödinger equation of the hydrogen atom.
(t), formed by the ions, were stored, to be used as an input when numerically solving the time-dependent Schrödinger equation of the hydrogen atom.It is instructive to separately analyze how changing the direction, and the magnitude of the microfield influence the line shape. Let us define “rotational” and “vibrational” microfields as
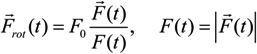 and
and
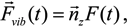 respectively (compare with [75]), where F0 is again the Holtsmark normal field for singly charged ions [1].
respectively (compare with [75]), where F0 is again the Holtsmark normal field for singly charged ions [1].
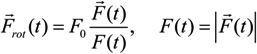
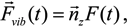
The effect of varying reduced mass was modeled by enabling time dilation of the field histories. Evidently, the field that is changing slower by a factor of s, corresponds to that, formed by particles moving s times more slowly, i.e., with an s2-times larger reduced mass. We note that by reusing the field histories generated only once, any possible inaccuracy due to a finite statistical quality of the simulations, such as a deviation from the Holtsmark distribution of the field magnitudes [1], should be present in all calculations and thus, cancel out when the difference profiles are evaluated. The parameters of the base run (s = 1) were selected to correspond to protons (i.e., μ0 = 0.5) with the particle density N = 1017 cm3 and temperature T = 1 eV, while the additional runs with s = 2, 4, and 8 corresponded to μ = 2, 8, and 32, respectively.
The resulting Ly-α profiles are presented in Figure 5. It is seen that the rotational microfield component has a significantly more pronounced effect on the total line shapes, while changing only the magnitude of the field while keeping its direction constant (the “vibrational” component) has only a minor effect on the shape of the lateral components. Evidently, with no change in the field direction, the central component remains the δ-function (not shown on Figure 5b). We note that the width of the central component due to the rotational microfield component increases when μ decreases. This is in a qualitative agreement with Equation (9).
The Ly-α profiles calculated with the full microfields (Figure 6a) show a resembling behavior: the line HWHM, mostly determined by the central component, scales approximately inversely with s within the range of parameters assumed, while the shape of the lateral components remains mostly unchanged. We note that varying s may alternatively be interpreted as scaling the temperature according to T = T0/s2. The observed dependence is, thus, qualitatively similar to the Ly-α T-dependence inferred in an ion-dynamics study [76]. We note that the shape of the central component is practically Lorentzian.
We now turn to analyzing the difference profiles defined in the spirit of Equation (13). However, the theory of thermal corrections [24,25] was derived perturbatively with the zero-order broadening due to the electron impact effect, while in the present CS calculations no electron broadening was included.
Therefore, it is the ion-dynamical broadening itself that fulfills this role, and one should expect to find a self-similar solution. We checked it by calculating difference between the line shapes calculated with the time-dilation factors s and s′ = s + δs, keeping the δs/s ratio constant, and normalizing the frequency axis of the resulting difference profiles to the line width. In other words, the ion-induced HWHM wi plays the role of the electron impact one in Equation (9).
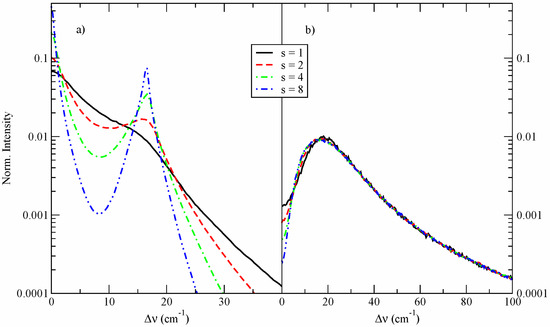
Figure 5.
CS Ly-α profiles, broadened by an OCP, assuming N = 1017 cm−3 and T = 1 eV. The ion radiator reduced mass μ = s2μ0, where μ0 = 0.5. (a) Line shapes influenced by the rotational field component (18); (b) Line shapes influenced by the vibrational field component (19).
Although it is desirable to keep δs/s as “infinitesimal” as possible, in practice too small a ratio results in rather noisy profiles due to a finite accuracy of the simulations; for this reason, δs/s = 1/4, corresponding to δμ/μ = 9/16, was used. The results are shown in Figure 6b. Indeed, the normalized difference profiles remain practically the same over the 64-fold variation of μ tested. Furthermore, the profiles in the central region are qualitatively similar to the prediction of the theory of thermal corrections [24,25] (cf. Figure 2). It appears, however, that the functional form is rather close to
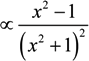 also shown in Figure 6b. It is easy to see that such a functional form corresponds to a difference between two Lorentzians, confirming the shape of the Ly-α central component inferred from our CS calculations.
also shown in Figure 6b. It is easy to see that such a functional form corresponds to a difference between two Lorentzians, confirming the shape of the Ly-α central component inferred from our CS calculations.
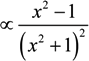
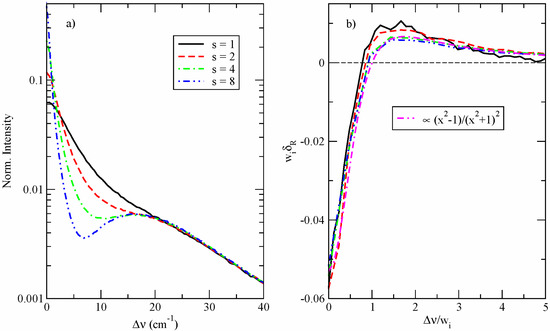
Figure 6.
(a) CS full Ly-α profiles, broadened by an OCP, assuming N = 1017 cm−3 and T = 1 eV. The ion radiator reduced mass μ = s2μ0, where μ0 = 0.5; (b) Profiles differences between line shapes, calculated with s and sʹ = s + δs = 5/4s (i.e., δμ/μ = 9/16). The profile differences are scaled to the lineshape HWHM wi.
5. Discussion
Let us discuss the separation of rotational and vibrational (phase modulation) effects of ion dynamics (used also in [75]). It is assumed that the mean magnitude of the field is equal to the normal Holtsmark field value. On the other hand, the solution for a fixed angular velocity and a fixed magnitude of the electric field for hydrogen is known exactly [10,13]. Furthermore, the solution of the Schrödinger equation for this problem and hence the profile strongly depends on the microfield value, which is set equal to F0. These profiles are characterized by well distinguished properties that are consequences of atom dynamics in the rotating microfield [10,13,75]. When the profile patterns are averaged over all microfield directional histories, the fixed value of the microfield leads to a statistical-dynamical coupling through specifics of solutions of the Schrödinger equation, i.e., coupling between the microfield statistics and specific dynamics of the atomic system [10,13]. This is illustrated by the instructive detailed patterns presented in [75] for the rotational contribution of ion dynamics effects. Let us now consider the proposed separation of phase modulation or vibrational effects. Here only the microfield orientation is assumed to be constant, while its magnitude as a function of time is preserved. The solution of the Schrödinger equation in this case reflects the specifics of a fixed orientation, and after averaging over microfield histories this imposes very characteristic features of the Stark profiles [7,8,75]. These profiles are also subject to statistical-dynamical coupling caused only by the fixed microfield orientation.
The present CS results show that the convolution of the separated rotational and vibrational profiles does not equal to the one, obtained by using the full microfield histories. This is due to constrains, involved in the separation of the rotational and vibrational effects, and is clearly a consequence of the statistical-dynamical coupling. In fact, it has the same origin as the coupling between the fixed microfield values and the means of their derivatives [5,6], discussed in the beginning of Section 3.
The analysis performed in the previous section has confirmed the formation of the central part of the hydrogen line with the central component, predominantly broadened under the action of the amplitude modulation. While in the quasistatic region of the Stark broadening the natural scaling is defined by CF0 ~ n2 Ni2/3, and in the impact regime it is proportional to ~n4 (Ti//µ)−1/2 Ni, from the dimension consideration it follows that in the regime of Stark broadening controlled by the ion dynamics the characteristic scale wi could be just proportional to (Ti//µ)1/2 Ni1/3 as there could be no dependence on the dipole atomic moment or microfield. On the right hand side in Figure 6b the difference profiles for the same set of artificial values of reduced mass are plotted. Their qualitative behavior is similar to the ones discussed in the Section 2 functions f1−α(x), f2−α(x). From the performed analysis in the previous section it could be deduced that the characteristic scale of HWHM is proportional to (2Ti/µ)1/2, and at the same time the analysis, given in [67], has shown that in this range of parameters (Ne ~ 1017 cm−3, T~ 1 eV) HWHM is proportional to Ni1/3. Combining these two dependences lead to the conclusion that, for the chosen plasma parameters, the HWHM needs to be proportional to the typical ion microfield frequency: wi ~ (2Ti/µ)1/2Ni1/3.
These properties discovered in the process of CS could be in fact treated in a quite simple manner. Indeed, the main contribution to the broadening is due to the central component. The existence of the field and its orientation define those Stark sublevels that give rise to the central Stark component, but the microfield does not affect those states, and they do not depend on the microfield value since they do not possess a dipole moment. The microfield rotations change the quantization of quantum states, which can be considered as their decay or determination of their life time. Earlier, the formal model of this type with the decay rate, depending on the microfield value and based on equations like Equation (4), was suggested in [17], but was not thoroughly studied. From this idea it follows that any interaction should lead to a finite life time of the system. This hypothesis is supported by the observation of a nearly Lorentzian profile of the central component in the simulations with wi ∝ viNi1/3.
6. Conclusions
The existence of spectral-kinetic coupling in the formation of Stark profiles is stated. It arises since the spectral profiles and balance equations could not, in general, be considered separately. A consistent approach should include balance equations as well as spectral line profiles in one system of equations for density matrix.
MD simulations qualitatively confirm the results, obtained within the notion of thermal corrections, namely that the formation of the Stark profile center is mainly due to the microfield rotation, while the wings are affected by the phase modulation. Here, it is worth mentioning that in the line wings, where the theory of thermal corrections is practically always valid, the ion dynamics contributions of the amplitude modulation and the non-adiabatic effects have the same sign and significantly exceed numerically the contribution of the phase modulation, which has the opposite sign.
The existence of the statistical-dynamical coupling between the plasma microfield statistics and the dynamics of atomic system of radiators, applied to the averaging of the dynamic solution over samples of histories of microfield evolution in plasma (which is a special case of time dependence in quantum mechanics induced by the environment [78]), may be the cause that prevents the convolution of separate contributions to the Stark profile from the rotational and vibrational effects to be equal to the Stark profile, obtained under the full microfield evolution.
The difference profiles, obtained by a subtraction of experimental or simulated profiles, corresponding to two different reduced masses of perturber-radiator pair, could be used as a tool for studying the statistical properties of microfields.
It is pointed out that results of MD simulations of ion dynamics could be treated by a hypothetical model of the quantum states decay caused by the changes of quantization axes due to the microfield rotations. This may allow for explaining the success of a variety of models that consider neither the microfield rotation, nor the detailed evolution of the microfields.
We hope that this work will inspire further studies of the ion dynamics effects on Stark profiles.
Acknowledgments
We wish to thank A. Calisti, S. Ferri, M.A. Gigosos, M.A. Gonzalez, C.A. Iglesias and V.S. Lisitsa for many fruitful discussions on the subject.
The work of A.V.D. was partially supported by the Russian Foundation for Basic Research (project No. 13-02-00812) and by the Council of the President of the Russian Federation for Support of Young Scientists and Leading Scientific Schools (project No. NSh-3328.2014.2). The work of E.S. was partially supported by Israel Science Foundation and the Cornell University Excellence Center.
A.V.D. greatly appreciates the invitations and support of the Organizing Committee of the SLSP-1&2 workshops and the International Atomic Energy Agency that made possible his participation in these meetings.
Author Contributions
Conflicts of Interest
The authors declare no conflict of interest.
References
- Holtsmark, J. Über die Verbreiterung von Spektrallinien. Ann. Phys. (Leipz.) 1919, 58, 577–630. [Google Scholar] [CrossRef]
- Spitzer, L. Stark-Effect broadening of hydrogen lines. I Single encounters. Phys. Rev. 1939, 55, 699–708. [Google Scholar]
- Spitzer, L. II. Observable profiles. Phys. Rev. 1939, 56, 39–47. [Google Scholar] [CrossRef]
- Spitzer, L. Impact broadening of spectral lines. Phys. Rev. 1940, 58, 348–357. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; von Neumann, J. The statistics of gravitational field arising from random distributions of stars. I. The speed of fluctuations. Astrophys. J. 1942, 95, 489–531. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; von Neumann, J. II. The speed of fluctuations; dynamical friction; spatial correlations. Astrophys. J. 1943, 97, 1–27. [Google Scholar] [CrossRef]
- Kogan, V.I. Broadening of Spectral Lines in Hot Plasma. In Plasma Physics and the Problem of Controlled Thermonuclear Reactions; Leontovich, M.A., Ed.; Academy of Science USSR Press: Moscow, Russia, 1958; Volume IV, pp. 259–304. [Google Scholar]
- Kogan, V.I. Broadening of Spectral Lines in Hot Plasma. In Plasma Physics and the Problem of Controlled Thermonuclear Reactions; Leontovich, M.A., Ed.; Pergamon Press: London, UK, 1960; Volume IV, p. 305. [Google Scholar]
- Wimmel, H.K. Statistical ion broadening in plasmas. J. Quant. Spectrosc. Radiat. Transf. 1960, 1, 1–29. [Google Scholar]
- Wimmel, H.K. Erratum. J. Quant. Spectrosc. Radiat. Transf. 1964, 4, 497–499. [Google Scholar] [CrossRef]
- Ishimura, T. Stark effect of the Lyman alpha line by a rotating electric field. J. Phys. Soc. Jpn. 1967, 23, 422–429. [Google Scholar] [CrossRef]
- Kogan, V.I.; Selidovkin, A.D. On fluctuating microfield in system of charged particles. Beitr. Aus. Plasmaphys. 1969, 9, 199–216. [Google Scholar] [CrossRef]
- Sholin, G.V.; Lisitsa, V.S.; Kogan, V.I. Amplitude modulation and non-adiabaticity in the Stark broadening of hydrogen lines in a plasma. Sov. Phys. JETP 1971, 32, 758–765. [Google Scholar]
- Lisitsa, V.S. Hydrogen Atom in Rotating Electric Field. Opt. Spectrosc. USSR 1971, 31, 468. [Google Scholar]
- Frisch, U.; Brissaud, A. Theory of Stark broadening—I. Soluble scalar model as a test. J. Quant. Spectrosc. Radiat. Transf. 1971, 11, 1753–1766. [Google Scholar] [CrossRef]
- Brissaud, A.; Frisch, U. —Exact line profile with model microfield. J. Quant. Spectrosc. Radiat. Transf. 1971, 11, 1767–1783. [Google Scholar] [CrossRef]
- Strekalov, M.L.; Burshtein, A.I. Collapse of shock-broadened multiplets. JETP 1972, 34, 53–58. [Google Scholar]
- Sholin, G.V.; Demura, A.V.; Lisitsa, V.S. Theory of Stark broadening of hydrogen lines in plasma. Sov. Phys. J. Exp. Theor. Phys. 1973, 37, 1057–1065. [Google Scholar]
- Sholin, G.V.; Demura, A.V.; Lisitsa, V.S. Electron. Impact Broadening of Stark Sublevels of Hydrogen Atom in Plasmas; Preprint IAE-2332, Kurchatov Institute of Atomic Energy: Moscow, Russia, 1972; pp. 1–21. [Google Scholar]
- Vidal, C.R.; Cooper, J.; Smith, E.W. Hydrogen Stark-broadening tables. Astrophys. J. Suppl. Ser. 1973, 25, 37–136. [Google Scholar] [CrossRef]
- Kelleher, D.E.; Wiese, W.L. Observation of ion motion in hydrogen Stark profiles. Phys. Rev. Lett. 1973, 31, 1431–1434. [Google Scholar] [CrossRef]
- Griem, H.R. Spectral Line Broadening by Plasmas; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Wiese, W.L.; Kelleher, D.E.; Helbig, V. Variation in Balmer-line Stark profiles with atom-ion reduced mass. Phys. Rev. A 1975, 11, 1854–1864. [Google Scholar] [CrossRef]
- Demura, A.V.; Lisitsa, V.S.; Sholin, G.V. On the ion motion effect in Stark profiles of hydrogen lines in a plasma. In Proceedings of the XIIth ICPIG, Eindhoven, The Netherlands, 1975; p. 37.
- Demura, A.V.; Lisitsa, V.S.; Sholin, G.V. Theory of Thermal Corrections to Stark Profiles of Hydrogen Spectral Lines; Preprint IAE-2672; Kurchatov Institute of Atomic Energy: Moscow, Russia, 1976; pp. 1–47. [Google Scholar]
- Demura, A.V.; Lisitsa, V.S.; Sholin, G.V. Effect of reduced mass in Stark broadening of hydrogen lines. Sov. Phys. J. Exp. Theor. Phys. 1977, 46, 209–215. [Google Scholar]
- Gruntzmacher, K.; Wende, B. Discrepancies between the Stark broadening theories for hydrogen and measurements of Ly-α Stark profiles in a dense equilibrium plasma. Phys. Rev. A 1977, 16, 243–246. [Google Scholar] [CrossRef]
- Seidel, J. Hydrogen Stark broadening by model electronic microfields. Z. Naturforschung. 1977, 32, 1195–1206. [Google Scholar]
- Seidel, J. Effects of ion motion on hydrogen Stark profiles. Z. Naturforschung. 1977, 32, 1207–1214. [Google Scholar]
- Voslamber, D. Effect of emitter-ion dynamics on the line core of Lyman-α. Phys. Lett. A 1977, 61, 27–29. [Google Scholar] [CrossRef]
- Gruntzmacher, K.; Wende, B. Stark broadening of the hydrogen resonance line Lβ in a dense equilibrium plasma. Phys. Rev. A 1978, 18, 2140–2149. [Google Scholar] [CrossRef]
- Stamm, R.; Voslamber, D. On the role of ion dynamics in the Stark broadening of hydrogen lines. J. Quant. Spectrosc. Radiat. Transf. 1979, 22, 599–609. [Google Scholar] [CrossRef]
- Voslamber, D.; Stamm, R. Influence of different ion dynamical effects on Lyman lines. In Spectral Line Shapes Volume 1; Wende, B., Ed.; Walter de Gruyter & Co.: Berlin, Germany, 1981; pp. 63–72. [Google Scholar]
- Seidel, J.; Stamm, R. Effects of radiator motion on plasma-broadened hydrogen Lyman-β. J. Quant. Spectrosc. Radiat. Transf. 1982, 27, 499–503. [Google Scholar] [CrossRef]
- Stamm, R.; Talin, B.; Pollock, E.L.; Iglesias, C.A. Ion-dynamics effects on the line shapes of hydrogenic emitters in plasmas. Phys. Rev. A 1986, 34, 4144–4152. [Google Scholar] [CrossRef]
- Calisti, A.; Stamm, R.; Talin, B. Effect of the ion microfield fluctuations on the Lyman-α fine-structure doublet of hydrogenic ions in dense plasmas. Europhys. Lett. 1987, 4, 1003–1008. [Google Scholar] [CrossRef]
- Boercker, D.B.; Dufty, J.W.; Iglesias, C.A. Radiative and transport properties of ions in strongly coupled plasmas. Phys. Rev. A 1987, 36, 2254. [Google Scholar] [CrossRef]
- Demura, A.V. Theory of Joint Distribution Functions of Ion. Microfield and Its Space and Time Derivatives in Plasma with Complex. Ionization Composition; Preprint IAE-4632/6; Kurchatov Institute of Atomic Energy: Moscow, Russia, 1988; pp. 1–17. [Google Scholar]
- Calisti, A.; Stamm, R.; Talin, B. Simulation calculation of the ion-dynamic effect on overlapping neutral helium lines. Phys. Rev. A 1988, 38, 4883–4886. [Google Scholar] [CrossRef]
- Demura, A.V. Microfield Fluctuations in Plasma with Low Frequency Oscillations. In XIXth ICPIG Contributed Papers; Labat, J.M., Ed.; Faculty of Physics, University of Belgrade: Belgrade, 1990; Volume 2, pp. 352–353. [Google Scholar]
- Calisti, A.; Khelfaoui, F.; Stamm, R.; Talin, B.; Lee, R.W. Model for the line shapes of complex ions in hot and dense plasmas. Phys. Rev. A 1990, 42, 5433–5440. [Google Scholar] [CrossRef]
- Rautian, S.G.; Shalagin, A.M. Kinetic Problems of Nonlinear Spectroscopy; North Holland: New York, NY, USA, 1991. [Google Scholar]
- Anufrienko, A.V.; Godunov, A.L.; Demura, A.V.; Zemtsov, Y.K.; Lisitsa, V.S.; Starostin, A.N.; Taran, M.D.; Shchipakov, V.A. Nonlinear interference effects in Stark broadening of ion lines in a dense plasma. Sov. Phys. J. Exp. Theor. Phys 1990, 71, 728–741. [Google Scholar]
- Anufrienko, A.V.; Bulyshev, A.E.; Godunov, A.L.; Demura, A.V.; Zemtsov, Y.K.; Lisitsa, V.S.; Starostin, A.N. Nonlinear interference effects and ion dynamics in the kinetic theory of Stark broadening of the spectral lines of multicharged ions in a dense plasma. JETP 1993, 76, 219–228. [Google Scholar]
- Sobelman, I.I.; Vainstein, L.A.; Yukov, E.A. Excitation of Atoms and Broadening of Spectral Lines; Springer: Heidelberg, Germany; New York, NY, USA, 1995. [Google Scholar]
- Talin, B.; Calisti, A.; Godbert, L.; Stamm, R.; Lee, R.W.; Klein, L. Frequency-fluctuation model for line-shape calculations in plasma spectroscopy. Phys. Rev. A 1995, 51, 1918–1928. [Google Scholar] [CrossRef]
- Gigosos, M.A.; Cardenoso, V. New plasma diagnosis tables of hydrogen Stark broadening including ion dynamics. J. Phys. B 1996, 29, 4795–4838. [Google Scholar] [CrossRef]
- Demura, A.V. Instantaneous joint distribution of ion microfield and its time derivatives and effects of dynamical friction in plasmas. J. Exp. Theor. Phys. 1996, 83, 60–72. [Google Scholar]
- Alexiou, S.; Calisti, A.; Gautier, P.; Klein, L.; Leboucher-Dalimier, E.; Lee, R.W.; Stamm, R.; Talin, B. Aspects of plasma spectroscopy: Recent advances. J. Quant. Spectrosc. Radiat. Transf. 1997, 58, 399–413. [Google Scholar] [CrossRef]
- Kosarev, I.N.; Stehle, C.; Feautrier, N.; Demura, A.V.; Lisitsa, V.S. Interference of radiating states and ion dynamics in spectral line broadening. J. Phys. B 1997, 30, 215–236. [Google Scholar] [CrossRef]
- Griem, H. Principles of Plasma Spectroscopy; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Stehle, C.; Hutcheon, R. Extensive tabulation of Stark broadened hydrogen line profiles. Astron. Astrophys. Suppl. Ser. 1999, 140, 93–97. [Google Scholar] [CrossRef]
- Barbes, A.; Gigosos, M.A.; Gonzalez, M.A. Analysis of the coupling between impact and quasistatic field mechanisms in Stark broadening. J. Quant. Spectrosc. Radiat. Transf. 2001, 68, 679–688. [Google Scholar] [CrossRef]
- Gigosos, M.A.; Gonzalez, M.A.; Cardenoso, V. Computer simulated Balmer-alpha, -beta and -gamma Stark line profiles for non-equilibrium plasma diagnostics. Spectrochim. Acta B 2003, 58, 1489–1504. [Google Scholar] [CrossRef]
- Demura, A.V.; Rosmej, F.B.; Stamm, R. Density Matrix Approach to Description of Doubly Excited States in Dense Plasmas. In Spectral Line Shapes; (18th International Conference on Spectral Line Shapes, Auburn, Alabama 4-9 June 2006); Oks, E., Pindzola, M., Eds.; AIP Conference Proceedings vol. 874; AIP: Melville, NY, USA, 2006; pp. 112–126. [Google Scholar]
- Calisti, A.; Ferri, S.; Mosse, C.; Talin, B. Modélisation des profils de raie dans les plasmas: PPP—Nouvelle version. J. Phys. IV Fr. 2006, 138, 95–103. [Google Scholar] [CrossRef]
- Stambulchik, E.; Maron, Y. A study of ion-dynamics and correlation effects for spectral line broadening in plasma: K-shell lines. J. Quant. Spectrosc. Radiat. Transf. 2006, 99, 730–749. [Google Scholar] [CrossRef]
- Oks, E.A. Stark Broadening of Hydrogen and Hydrogenlike. Spectral Lines in Plasmas. The Physical Insight; Alpha Science International Ltd.: Oxford, UK, 2006. [Google Scholar]
- Calisti, A.; Ferri, S.; Mosse, C.; Talin, B.; Lisitsa, V.; Bureyeva, L.; Gigosos, M.A.; Gonzalez, M.A.; del Rio Gaztelurrutia, T.; Dufty, J.W. Slow and fast micro-field components in warm and dense hydrogen plasmas. ArXiv e-prints 2007. [arXiv:physics.plasm-ph/0710.2091]. [Google Scholar]
- Calisti, A.; del Rio Gaztelurrutia, T.; Talin, B. Classical molecular dynamics model for coupled two component plasma. High Energy Density Phys. 2007, 3, 52–56. [Google Scholar] [CrossRef]
- Ferri, S.; Calisti, A.; Mosse, C.; Talin, B.; Gigosos, M.A.; Gonzalez, M.A. Line shape modeling in warm and dense hydrogen plasma. High Energy Density Phys. 2007, 3, 81–85. [Google Scholar] [CrossRef]
- Stambulchik, E.; Alexiou, S.; Griem, H.; Kepple, P.C. Stark broadening of high principal quantum number hydrogen Balmer lines in low-density laboratory plasmas. Phys. Rev. A 2007, 75, 016401. [Google Scholar]
- Calisti, A.; Ferri, S.; Talin, B. Classical molecular dynamics model for coupled two component plasma. High Energy Density Phys. 2009, 5, 307–311. [Google Scholar] [CrossRef]
- Godbert-Mouret, L.; Rosato, J.; Capes, H.; Marandet, Y.; Ferri, S.; Koubiti, M.; Stamm, R.; Gonzalez, M.A.; Gigosos, M.A. Zeeman-Stark line shape codes including ion dynamics. High Energy Density Phys. 2009, 5, 162–165. [Google Scholar] [CrossRef]
- Stambulchik, E.; Maron, Y. Plasma line broadening and computer simulations: A mini-review. High Energy Density Phys. 2010, 6, 9–14. [Google Scholar] [CrossRef]
- Calisti, A.; Mosse, C.; Ferri, S.; Talin, B.; Rosmej, F.; Bureyeva, L.A.; Lisitsa, V.S. Dynamic Stark broadening as the Dicke narrowing effect. Phys. Rev. E 2010, 81, 016406. [Google Scholar] [CrossRef]
- Demura, A.V. Physical Models of Plasma Microfield. Int. J. Spectrosc. 2010, 671073:1–671073:42. [Google Scholar]
- Calisti, A.; Talin, B. Classical Molecular Dynamics Model for Coupled Two-Component Plasmas—Ionization Balance and Time Considerations. Contrib. Plasma Phys. 2011, 51, 524–528. [Google Scholar] [CrossRef]
- Calisti, A.; Ferri, S.; Mosse, C.; Talin, B.; Gigosos, M.A.; Gonzalez, M.A. Microfields in hot dense hydrogen plasmas. High Energy Density Phys. 2011, 7, 197–202. [Google Scholar] [CrossRef]
- Ferri, S.; Calisti, A.; Mosse, C.; Mouret, L.; Talin, B.; Gigosos, M.A.; Gonzalez, M.A.; Lisitsa, V. Frequency-fluctuation model applied to Stark-Zeeman spectral line shapes in plasmas. Phys. Rev. E 2011, 84, 026407. [Google Scholar] [CrossRef]
- Mancini, R.C.; Iglesias, C.A.; Calisti, A.; Ferri, S.; Florido, R. The effect of improved satellite line shapes on the argon Heβ spectral feature. High Energy Density Phys. 2013, 9, 731–736. [Google Scholar] [CrossRef]
- Iglesias, C.A. Efficient algorithms for stochastic Stark-profile calculations. High Energy Density Phys. 2013, 9, 209–221. [Google Scholar] [CrossRef]
- Iglesias, C.A. Efficient algorithms for Stark-Zeeman spectral line shape calculations. High Energy Density Phys. 2013, 9, 737–744. [Google Scholar] [CrossRef]
- Stambulchik, E. Review of the 1st Spectral Line Shapes in Plasmas code comparison workshop. High Energy Density Phys. 2013, 9, 528–534. [Google Scholar] [CrossRef]
- Calisti, A.; Demura, A.; Gigosos, M.; Gonzalez-Herrero, D.; Iglesias, C.; Lisitsa, V.; Stambulchik, E. Influence of micro-field directionality on line shapes. Atoms 2014, 2, 259–276. [Google Scholar] [CrossRef]
- Ferri, S.; Calisti, A.; Mossé, C.; Rosato, J.; Talin, B.; Alexiou, S.; Gigosos, M.A.; González, M.A.; González-Herrero, D.; Lara, N.; Gomez, T.; Iglesias, C.; Lorenzen, S.; Mancini, R.C.; Stambulchik, E. Ion Dynamics Effect on Stark-Broadened Line Shapes: A Cross-Comparison of Various Models. Atoms 2014, 2, 299–318. [Google Scholar] [CrossRef]
- Alexiou, S.; Dimitrijevic, M.; Sahal-Brechot, S.; Stambulchik, E.; Duan, B.; Gonzalez-Herrero, D.; Gigosos, M.A. The second woorkshop on lineshape comparison: Isolated lines. Atoms 2014, 2, 157–177. [Google Scholar] [CrossRef]
- Briggs, J.S.; Rost, J.M. Time dependence in quantum mechanics. Eur. Phys. J. D 2000, 10, 311–318. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).